Prediction of the Fiber Orientation State and the Resulting Structural and Thermal Properties of Fiber Reinforced Additive Manufactured Composites Fabricated Using the Big Area Additive Manufacturing Process
Abstract
:1. Introduction
2. Fiber Orientation Modeling
2.1. Fiber Interactions: Isotropic Rotary Diffusion (IRD)
2.2. Fiber Interactions: Isotropic Rotary Diffusion—Reduced Strain Closure (IRD-RSC)
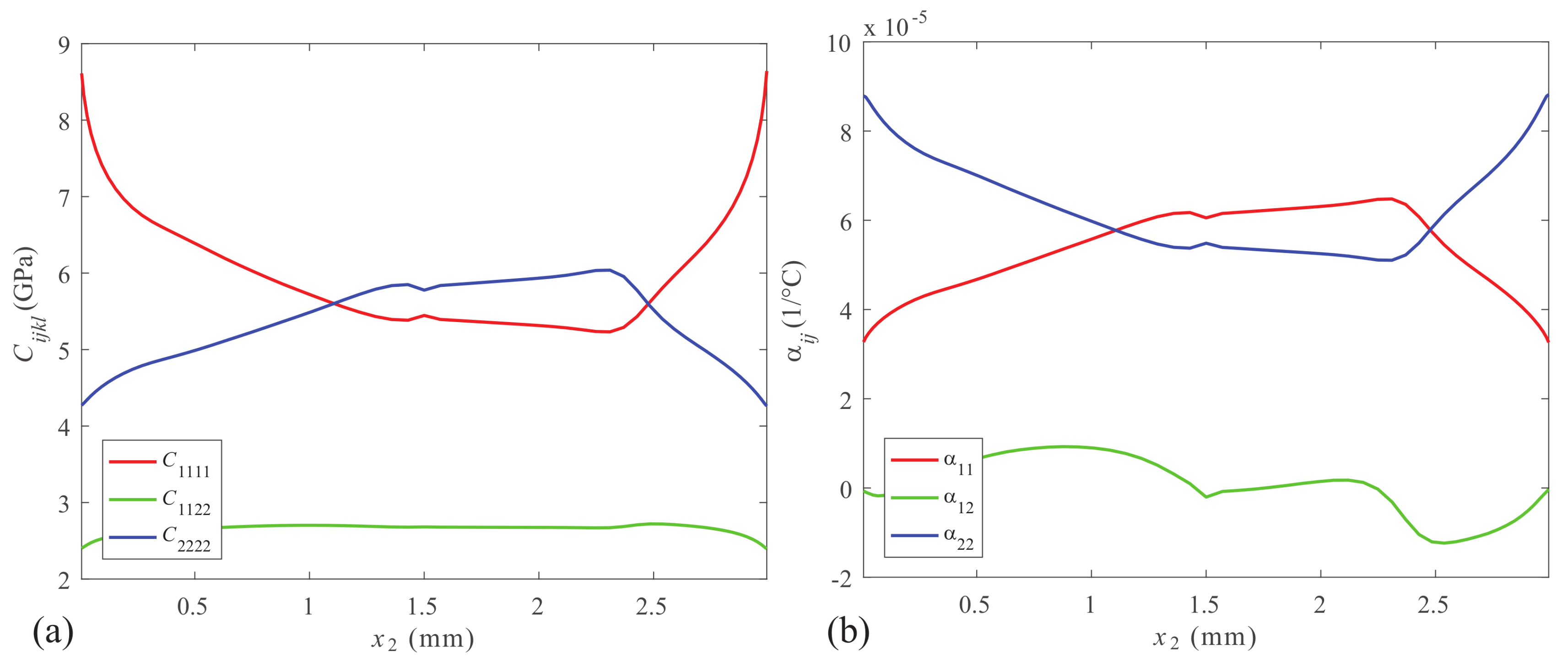
2.3. Mechanical Stiffness Tensor Predictions from Orientation
2.4. CTE Tensor Predictions from Orientation
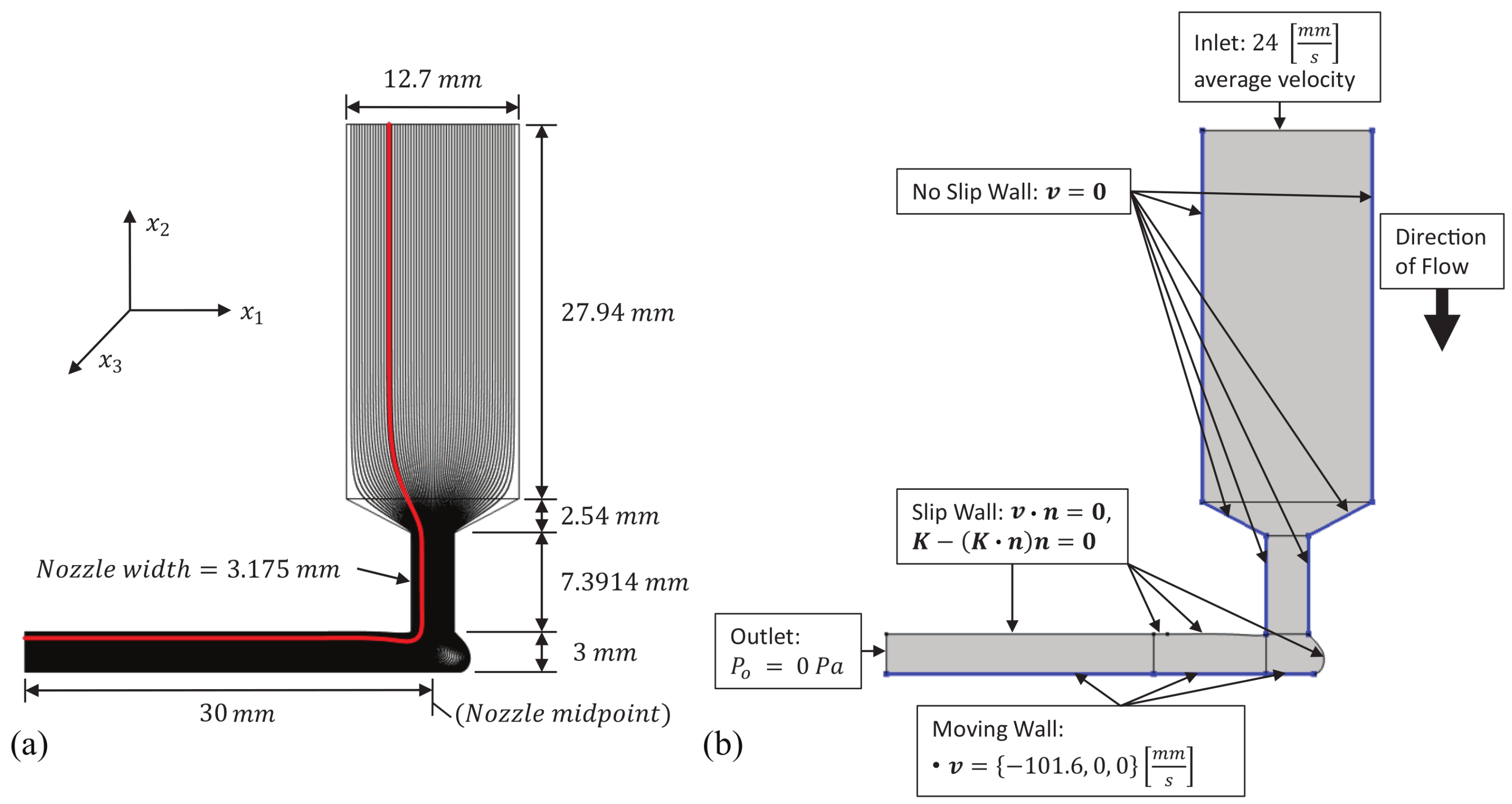
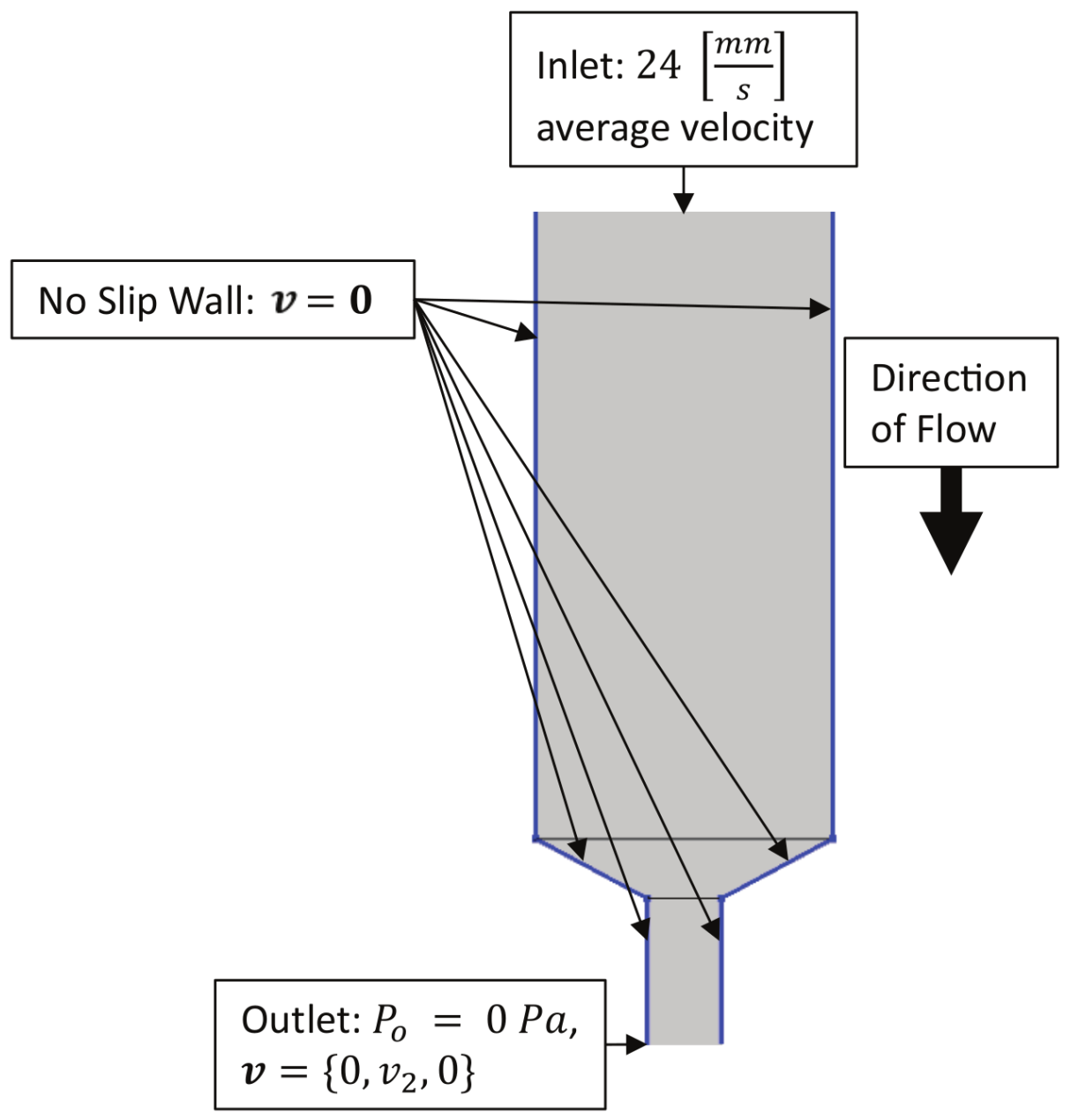
3. Flow Modeling
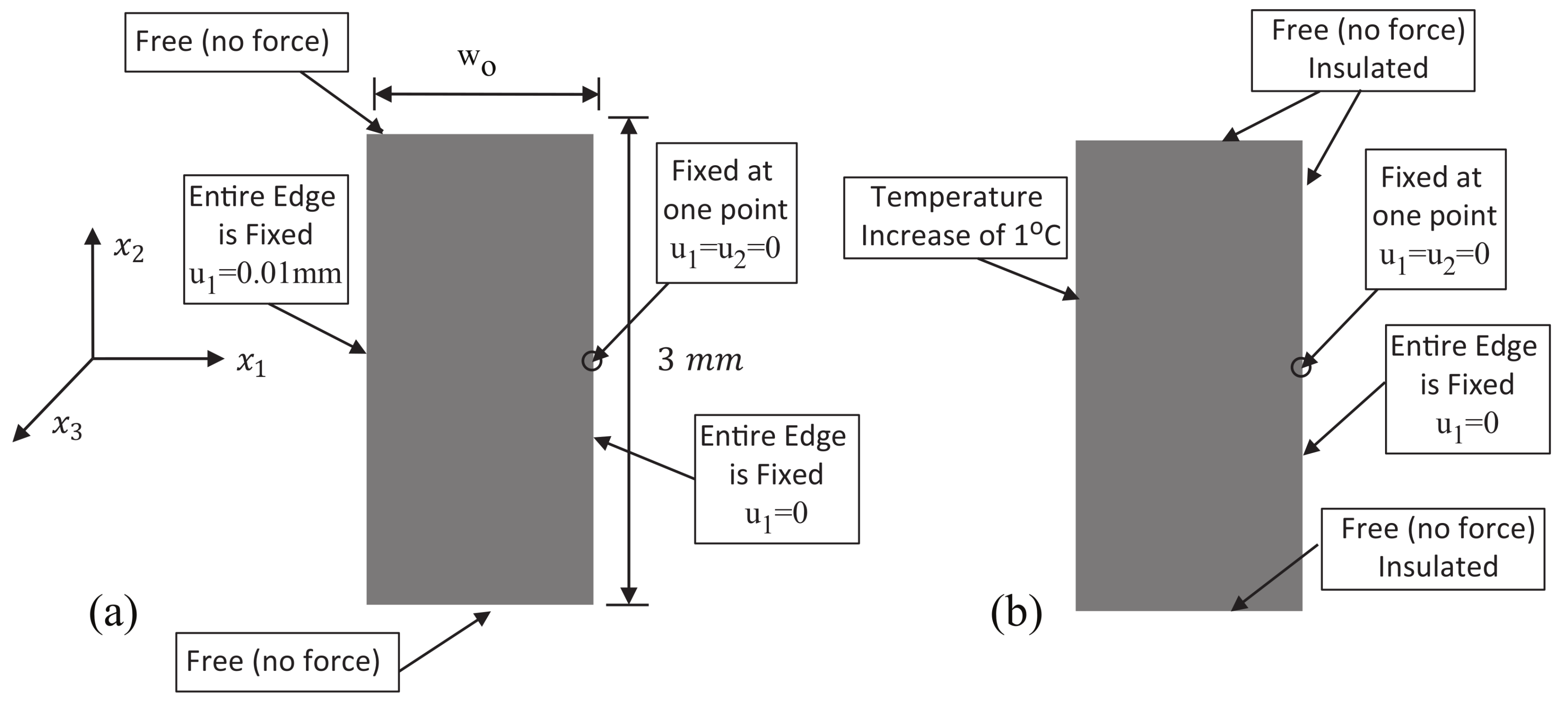
4. Results
4.1. Results for a Single Flow Type—IRD,
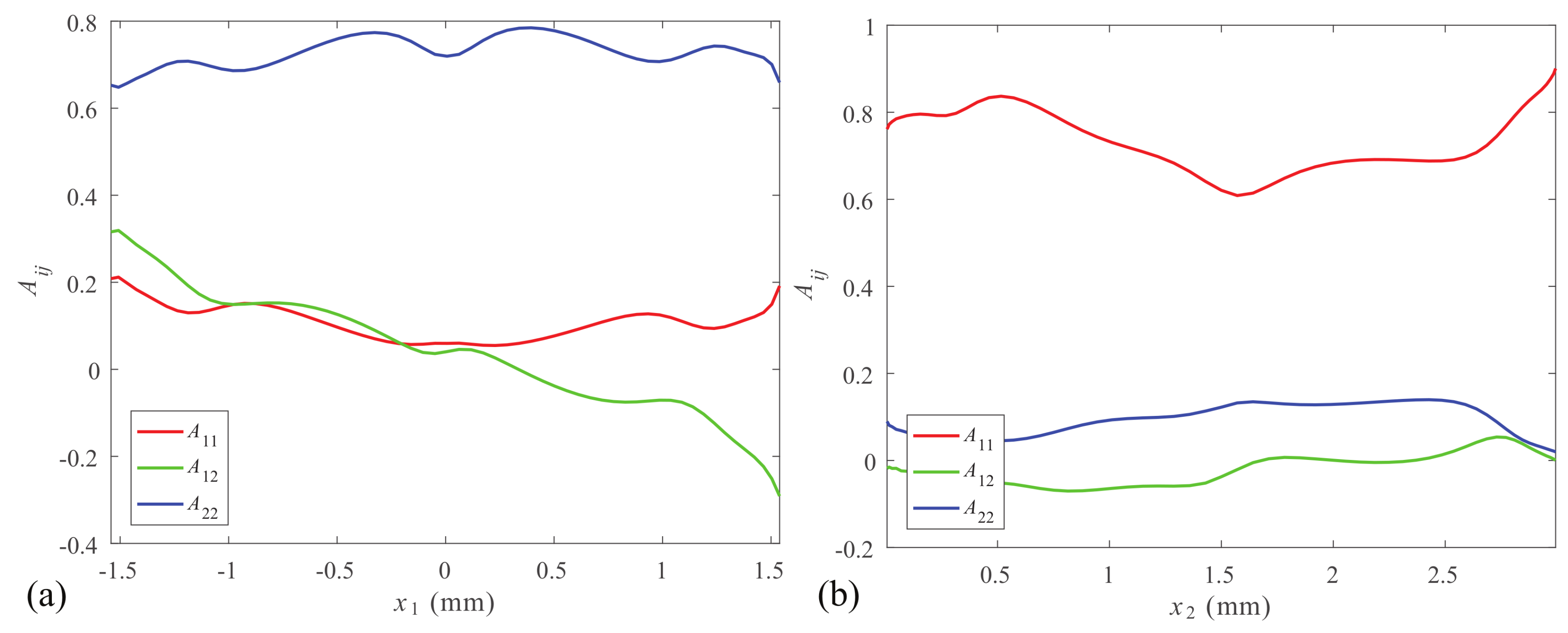
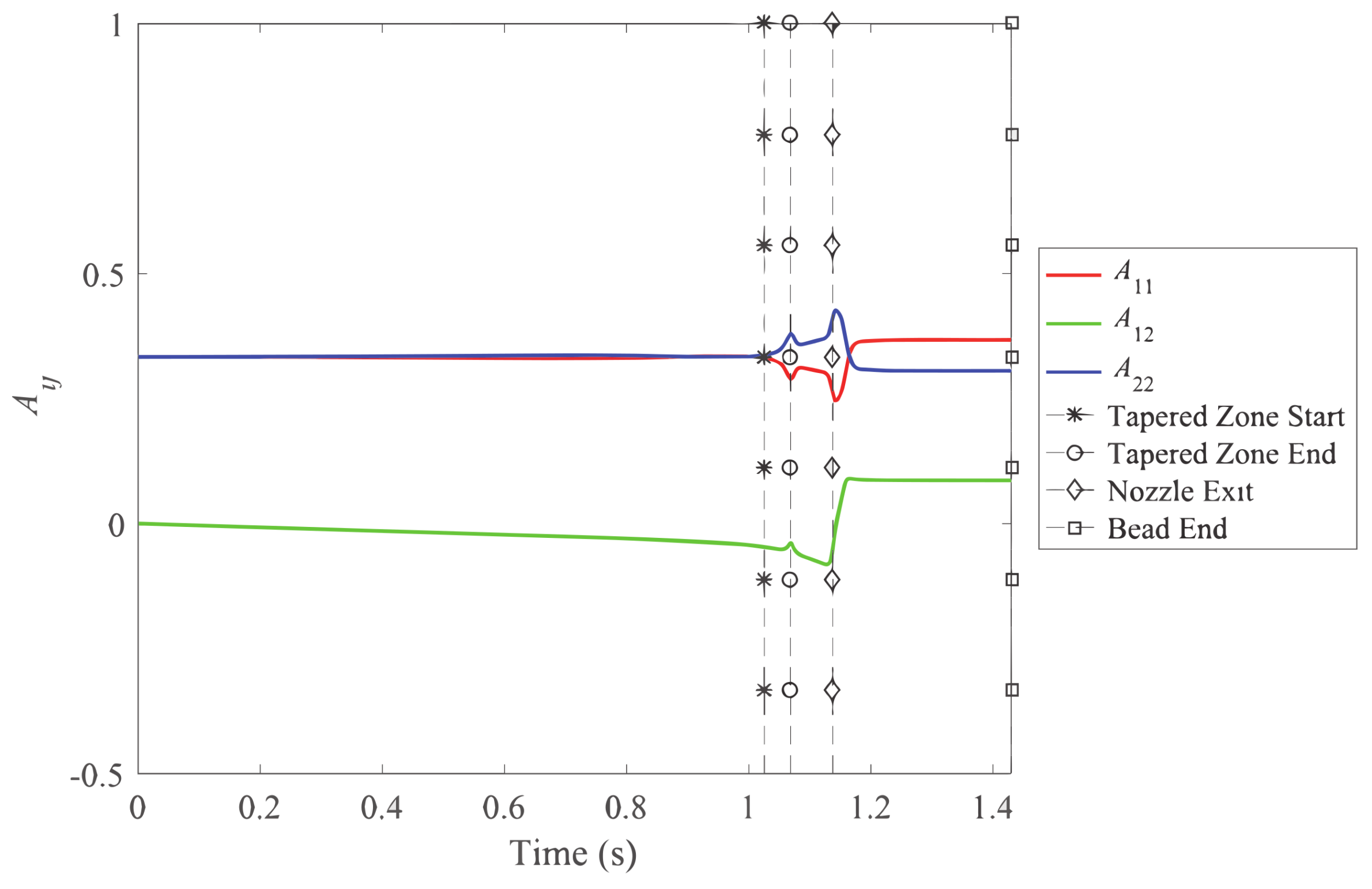
4.1.1. Orientation Tensors along a Streamline
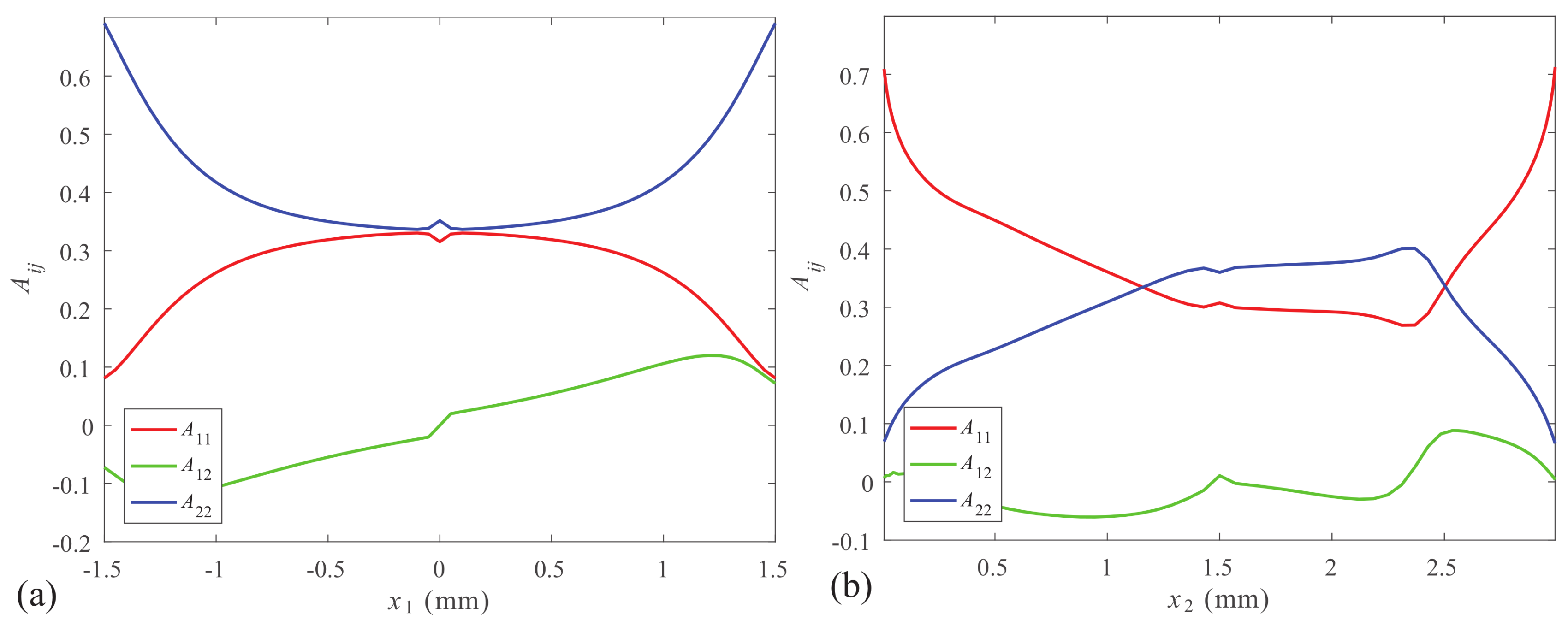
4.1.2. Orientation Tensors at the Exit and End
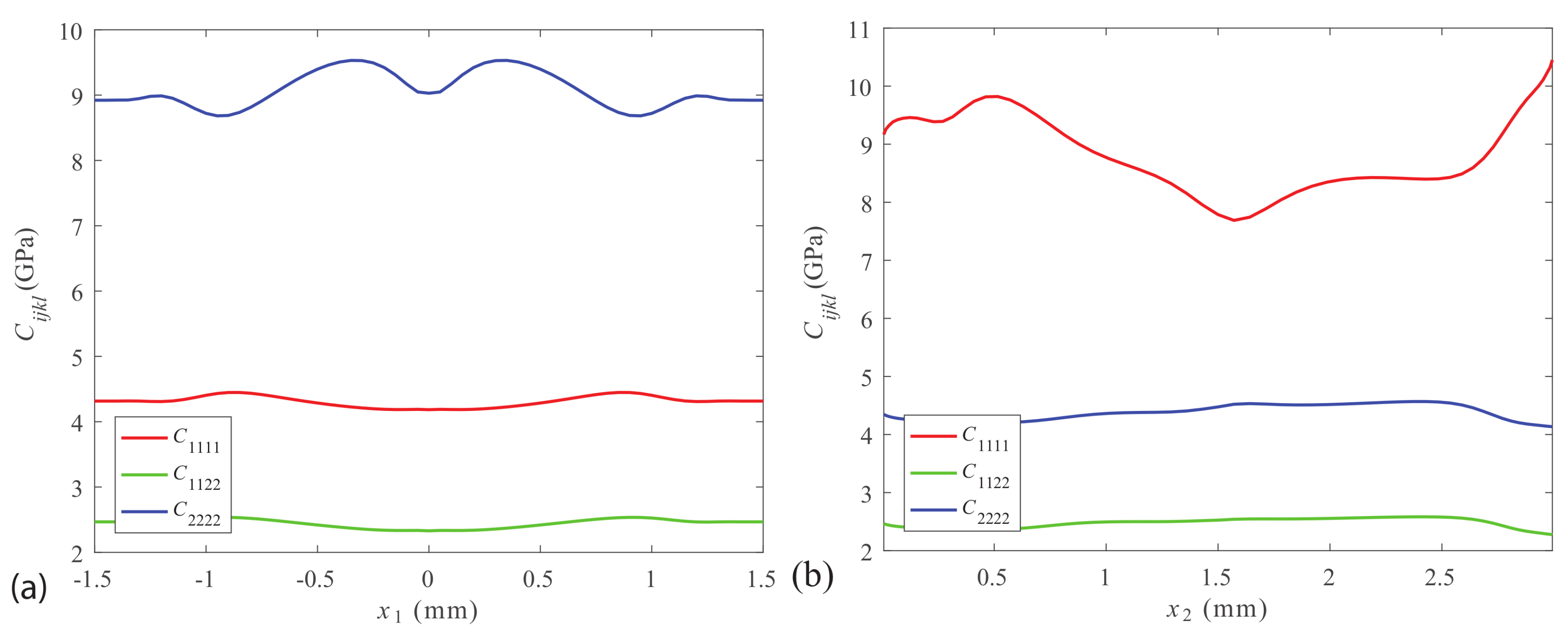
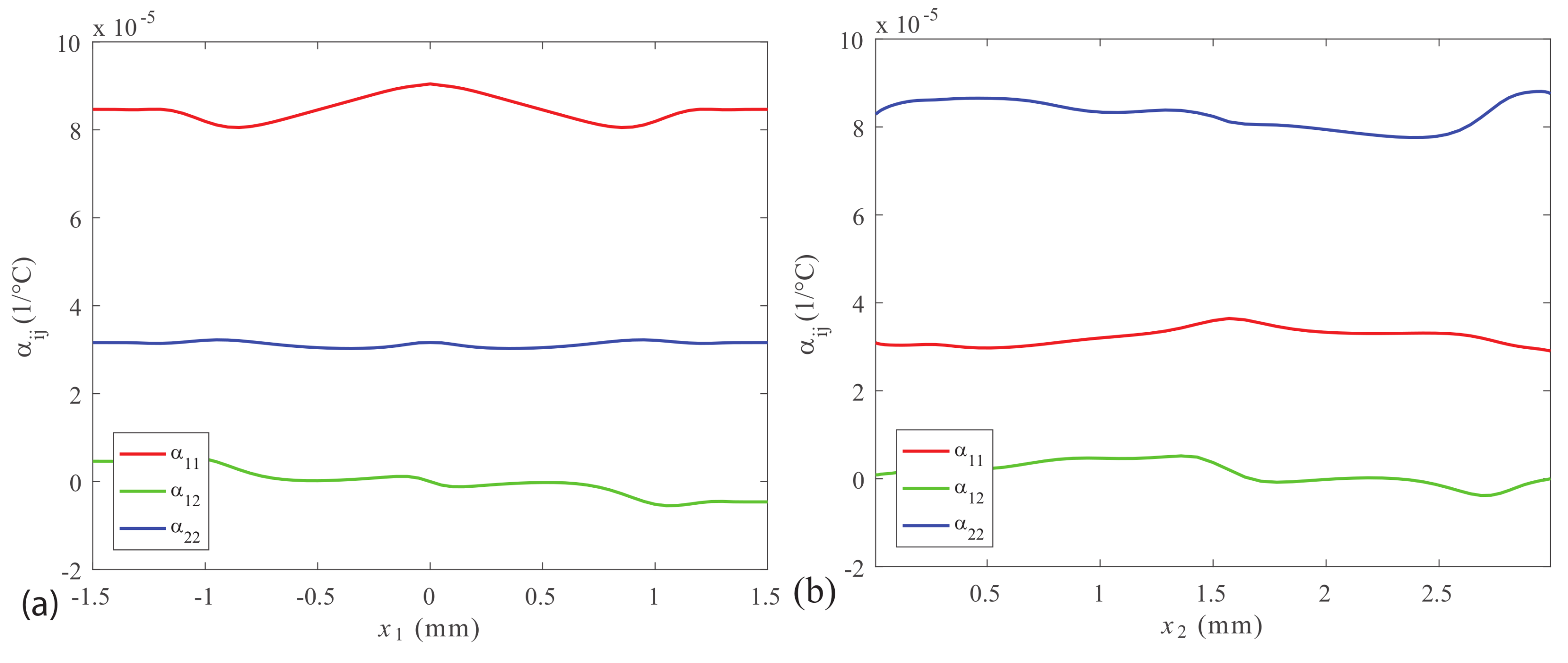
4.1.3. Stiffness and CTE at the Exit and End
4.1.4. Effective Longitudinal Properties
4.2. Contrasting Results between IRD and RSC
4.3. Effective Longitudinal Properties—All Flow Conditions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kannan, S.; Senthilkumaran, D.; Elangovan, K. Development of Composite Materials by Rapid Prototyping Technology using FDM Method. In Proceedings of the IEEE International Conference on Current Trends in Engineering and Technology (ICCTET), Coimbatore, India, 3 July 2013; pp. 281–283. [Google Scholar]
- Lind, R.; Post, B.; Blue, C.; Love, L. Enhanced Additive Manufacturing with a Reciprocating Leveling and Force Sensing Platen; Technical Report 201403257; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2014.
- Duty, C.; Kunc, V.; Compton, B.; Post, B.; Erdman, D.; Smith, R.; Lind, R.; Lloyd, P.; Love, L. Structure and Mechanical Behavior of Big Area Additive Manufacturing (BAAM) Materials. Rapid Prototyp. J. 2017, 23, 181–189. [Google Scholar] [CrossRef]
- Kishore, V.; Ajinjeru, C.; Nycz, A.; Post, B.; Lindahl, J.; Kunc, V.; Duty, C. Infrared preheating to improve interlayer strength of big area additive manufacturing (BAAM) components. Addit. Manuf. 2017, 14, 7–12. [Google Scholar] [CrossRef]
- Narahara, H.; Shirahama, Y.; Koresawa, H. Improvement and Evaluation of the Interlaminar Bonding Strength of FDM Parts by Atmospheric-Pressure Plasma. Proc. CIRP 2016, 42, 754–759. [Google Scholar] [CrossRef]
- Lau, K.; Hung, P.; Zhu, M.; Hui, D. Properties of natural fibre composites for structural engineering applications. Compos. Part B Eng. 2018, 136, 222–233. [Google Scholar] [CrossRef]
- Soutis, C. Fibre reinforced composites in aircraft construction. Prog. Aerosp. Sci. 2015, 41, 143–151. [Google Scholar] [CrossRef]
- Sfondrini, M.; Cacciafesta, V.; Scribante, A. Shear bond strength of fibre-reinforced composite nets using two different adhesive systems. Eur. J. Orthod. 2011, 33, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Cacciafesta, V.; Sfondrini, M.; Lena, A.; Scribante, A.; Vallittu, P.; Lassila, L. Flexural strengths of fiber-reinforced composites polymerized with conventional light-curing and additional postcuring. Am. J. Orthodont. Dent. Orthop. 2007, 132, 524–527. [Google Scholar] [CrossRef] [PubMed]
- Love, L.; Kunk, V.; Rios, O.; Duty, C.; Elliott, A.; Post, B.; Smith, R.; Blue, C. The Importance of Carbon Fiber to Polymer Additive Manufacturing. J. Mater. Res. 2014, 29, 1893–1898. [Google Scholar] [CrossRef]
- Tekinalp, H.; Kunc, V.; Velez-Garcia, G.; Duty, C.; Love, L.; Naskar, A.; Blue, C.; Ozcan, S. Highly Oriented Carbon Fiber-Polymer Composites via Additive Manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Cintra, J.S.; Tucker, C. Orthotropic Closure Approximations for Flow-Induced Fiber Orientation. J. Rheol. 1995, 39, 1095–1122. [Google Scholar] [CrossRef]
- Koch, D. A Model for Orientational Diffusion in Fiber Suspensions. Phys. Fluids 1995, 7, 2086–2088. [Google Scholar] [CrossRef]
- Huynh, H.M. Improved Fiber Orientation Predictions for Injection-Molded Composites. Master’s Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2001. [Google Scholar]
- Wang, J.; O’Gara, J.; Tucker, C. An Objective Model for Slow Orientation Kinetics in Concentrated Fiber Suspensions: Theory and Rheological Evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Phelps, J.; Tucker, C. An Anisotropic Rotary Diffusion Model for Fiber Orienation in Short- and Long Fiber Thermoplastics. J. Non-Newt. Fluid Mech. 2009, 156, 165–176. [Google Scholar] [CrossRef]
- Ortman, K.; Baird, D. Using Startup of Steady Shear Flow in a Sliding Plate Rheometer to Determine Material Parameters for the Purpose of Predicting Long Fiber Orientation. J. Rheol. 2012, 56, 955–981. [Google Scholar] [CrossRef]
- Camacho, C.; Tucker, C.; Yalvac, S.; McGee, R. Stiffness and Thermal Expansion Predictions for Hybird Short Fiber Composites. Polym. Compos. 1990, 11, 229–239. [Google Scholar] [CrossRef]
- Gusev, A.; Heggli, M.; Lusti, H.; Hine, P. Orientation Averaging for Stiffness and Thermal Expansion of Short Fiber Composites. Adv. Eng. Mater. 2002, 4, 931–933. [Google Scholar] [CrossRef]
- Jack, D.; Smith, D. Elastic Properties of Short-Fiber Polymer Composites, Derivation and Demonstration of Analytical Forms for Expectation and Variance from Orientation Tensors. J. Compos. Mater. 2008, 42, 277–308. [Google Scholar] [CrossRef]
- Jeffery, G. The Motion of Ellipsoidal Particles Immersed in a Viscous Fluid. Proc. R. Soc. Lond. A 1923, 102, 161–179. [Google Scholar] [CrossRef]
- Bay, R.; Tucker, C. Fiber orientation in simple injection moldings. Part I: Theory and numerical methods. Polym. Compos. 1992, 13, 317–331. [Google Scholar] [CrossRef]
- Montgomery-Smith, S.J.; Jack, D.; Smith, D. A Systematic Approach to Obtaining Numerical Solutions of Jeffery’s Type Equations using Spherical Harmonics. Compos. Part A 2010, 41, 827–835. [Google Scholar] [CrossRef]
- Dinh, S.; Armstrong, R. A Rheological Equation of State for Semiconcentrated Fiber Suspensions. J. Rheol. 1984, 28, 207–227. [Google Scholar] [CrossRef]
- Lipscomb, G.I.; Denn, M.; Hur, D.; Boger, D. Flow of Fiber Suspensions in Complex Geometries. J. Non-Newt. Fluid Mech. 1988, 26, 297–325. [Google Scholar] [CrossRef]
- Verweyst, B.; Tucker, C.L., III. Fiber Suspensions in Complex Geometries: Flow-Orientation Coupling. Can. J. Chem. Eng. 2002, 80, 1093–1106. [Google Scholar] [CrossRef]
- Chung, D.; Kwon, T. Numerical Studies of Fiber Suspensions in an Axisymmetric Radial Diverging Flow: The Effects of Modeling and Numerical Assumptions. J. Non-Newt. Fluid Mech. 2002, 107, 67–96. [Google Scholar] [CrossRef]
- Advani, S.; Tucker, C. Closure Approximations for Three-Dimensional Structure Tensors. J. Rheol. 1990, 34, 367–386. [Google Scholar] [CrossRef]
- Nguyen, N.; Bapanapalli, S.; Kunc, V.; Phelps, J.; Tucker, C. Prediction of the Elastic-Plastic Stress/Strain Response for Injection-Molded Long-Fiber Thermoplastics. J. Compos. Mater. 2009, 43, 217–246. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids. Vol. 2: Kinetic Theory, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Phan-Thien, N.; Fan, X.J.; Tanner, R.; Zheng, R. Folgar-Tucker Constant for a Fibre Suspension in a Newtonian Fluid. J. Non-Newt. Fluid Mech. 2002, 103, 251–260. [Google Scholar] [CrossRef]
- Sepehr, M.; Carreau, P.; Grmela, M.; Ausias, G.; Lafleur, P. Comparison of Rheological Properties of Fiber Suspensions with Model Predictions. J. Polym. Eng. 2004, 24, 579–610. [Google Scholar] [CrossRef]
- Strautins, U.; Latz, A. Flow-Driven Orientation Dynamics of Semiflexible Fiber Systems. Rheol. Acta 2007, 46, 1057–1064. [Google Scholar] [CrossRef]
- Nguyen, N.; Bapanapalli, S.; Holbery, J.; Smith, M.; Kunc, V.; Frame, B.; Phelps, J.; Tucker, C. Fiber Length and orientation in Long-Fiber Injection-Molded Thermoplastics—Part I: Modeling of Microstructure and Elastic Properties. J. Compos. Mater. 2008, 42, 1003–1029. [Google Scholar] [CrossRef]
- Agboola, B.; Jack, D.; Montgomery-Smith, S. Effectiveness of Recent Fiber-interaction Diffusion Models for Orientation and the Part Stiffness Predictions in Injection Molded Short-fiber Reinforced Composites. Compos. Part A 2012, 43, 1959–1970. [Google Scholar] [CrossRef]
- Stair, S.; Jack, D. Comparison of Experimental and Modeling Results for Cure Induced Curvature of a Carbon Fiber Laminate. Polym. Compos. 2017, 38, 2488–2500. [Google Scholar] [CrossRef]
- Zhang, D.; Smith, D.; Jack, D.; Montgomery-Smith, S. Numerical Evaluation of Single Fiber Motion for Short-Fiber-Reinforced Composite Materials Processing. J. Manuf. Sci. Eng. 2011, 133, 051002. [Google Scholar] [CrossRef]
- Doi, M. Molecular Dynamics and Rheological Properties of Concentrated Solutions of Rodlike Polymers in Isotropic and Liquid Crystalline Phases. J. Polym. Sci. Part B Polym. Phys. 1981, 19, 229–243. [Google Scholar] [CrossRef]
- Hand, G. A Theory of Anisotropic Fluids. J. Fluid Mech. 1962, 13, 33–46. [Google Scholar] [CrossRef]
- Chung, D.; Kwon, T. Improved Model of Orthotropic Closure Approximation for Flow Induced Fiber Orientation. Polym. Compos. 2001, 22, 636–649. [Google Scholar] [CrossRef]
- Chung, D.; Kwon, T. Invariant-Based Optimal Fitting Closure Approx. for the Numerical Prediction of Flow-Induced Fiber Orientation. J. Rheol. 2002, 46, 169–194. [Google Scholar] [CrossRef]
- Jack, D.; Schache, B.; Smith, D. Neural Network Based Closure for Modeling Short-Fiber Suspensions. Polym. Compos. 2010, 31, 1125–1141. [Google Scholar] [CrossRef]
- Montgomery-Smith, S.J.; Jack, D.; Smith, D. The Fast Exact Closure for Jeffery’s Equation with Diffusion. J. Non-Newt. Fluid Mech. 2011, 166, 343–353. [Google Scholar] [CrossRef]
- Montgomery-Smith, S.J.; He, W.; Jack, D.; Smith, D. Exact Tensor Closures for the Three Dimensional Jeffery’s Equation. J. Fluid Mech. 2011, 680, 321–335. [Google Scholar] [CrossRef]
- Jack, D.; Smith, D. An Invariant Based Fitted Closure of the Sixth-order Orientation Tensor for Modeling Short-Fiber Suspensions. J. Rheol. 2005, 49, 1091–1116. [Google Scholar] [CrossRef]
- Jack, D.; Smith, D. Sixth-order Fitted Closures for Short-fiber Reinforced Polymer Composites. J. Thermoplast. Compos. 2006, 19, 217–246. [Google Scholar] [CrossRef]
- Velez-Garcia, G.; Mazahir, S.; Hofmann, J.; Wapperom, P.; Barid, D.; Zink-Sharp, A.; Kunc, V. Improvement in Orientation Measurement for Short and Long Fiber Injection Molded Composites. In Proceedings of the 10th Annual SPE Automotive Composites Conference and Exposition, Detroit, MI, USA, 15–16 September 2010. [Google Scholar]
- Caselman, E. Elastic Property Prediction of Short Fiber Composites Using a Uniform Mesh Finite Element Method. Master’s Thesis, University of Missouri, Columbia, MO, USA, 2007. [Google Scholar]
- Halpin, J. Stiffness and Expansion Estimates for Oriented Short Fiber Composites. J. Compos. Mater. 1969, 3, 732–734. [Google Scholar] [CrossRef]
- Tucker, C.; Liang, E. Stiffness Predictions for Unidirectional Short-Fiber Composites: Review and Evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Tandon, G.; Weng, G. The Effect of Aspect Ratio of Inclusions on the Elastic Properties of Unidirectionally Aligned Composites. Polym. Compos. 1984, 5, 327–333. [Google Scholar] [CrossRef]
- Lielens, G.; Pirotte, P.; Couniot, A.; Dupret, F.; Keunings, R. Prediction of Thermo-Mech Properties for Compression Moulded Composites. Compos. Part A 1998, 29, 63–70. [Google Scholar] [CrossRef]
- Zhang, C. Modeling of Flexible Fiber Motion and Prediction of Material Properties. Master’s Thesis, Baylor University, Waco, TX, USA, 2011. [Google Scholar]
- Schapery, R. Thermal Expansion Coefficients of Composite Materials Based on Energy Principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Heller, B.; Smith, D.; Jack, D. Simulation of Planar Deposition Polymer Melt Flow and Fiber Orientation in Fused Filament Fabrication. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 7–9 August 2017; pp. 1096–1111. [Google Scholar]
- Tadmor, Z.; Gogos, C. Principles of Polymer Processing, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Athanasopulos, I.; Makrakis, G.; Rodrigues, J.F. Free Boundary Problems: Theory and Applications; Chapman and Hill/CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]

| Location | Model | (GPa) | /C | ||
|---|---|---|---|---|---|
| Deposited Bead | IRD | 0.01 | 1 | 6.82 | 32.2 |
| Deposited Bead | RSC | 0.01 | 1/10 | 4.82 | 45.5 |
| Deposited Bead | RSC | 0.01 | 1/30 | 4.18 | 53.3 |
| Deposited Bead | IRD | 0.003 | 1 | 7.69 | 30.3 |
| Deposited Bead | RSC | 0.003 | 1/10 | 4.88 | 45.1 |
| Deposited Bead | RSC | 0.003 | 1/30 | 4.19 | 53.2 |
| Nozzle Exit | IRD | 0.01 | 1 | 7.10 | 31.3 |
| Nozzle Exit | RSC | 0.01 | 1/10 | 5.07 | 42.4 |
| Nozzle Exit | RSC | 0.01 | 1/30 | 4.40 | 49.5 |
| Nozzle Exit | IRD | 0.003 | 1 | 7.89 | 29.9 |
| Nozzle Exit | RSC | 0.003 | 1/10 | 5.20 | 41.7 |
| Nozzle Exit | RSC | 0.003 | 1/30 | 4.45 | 49.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russell, T.; Heller, B.; Jack, D.A.; Smith, D.E. Prediction of the Fiber Orientation State and the Resulting Structural and Thermal Properties of Fiber Reinforced Additive Manufactured Composites Fabricated Using the Big Area Additive Manufacturing Process. J. Compos. Sci. 2018, 2, 26. https://doi.org/10.3390/jcs2020026
Russell T, Heller B, Jack DA, Smith DE. Prediction of the Fiber Orientation State and the Resulting Structural and Thermal Properties of Fiber Reinforced Additive Manufactured Composites Fabricated Using the Big Area Additive Manufacturing Process. Journal of Composites Science. 2018; 2(2):26. https://doi.org/10.3390/jcs2020026
Chicago/Turabian StyleRussell, Timothy, Blake Heller, David A. Jack, and Douglas E. Smith. 2018. "Prediction of the Fiber Orientation State and the Resulting Structural and Thermal Properties of Fiber Reinforced Additive Manufactured Composites Fabricated Using the Big Area Additive Manufacturing Process" Journal of Composites Science 2, no. 2: 26. https://doi.org/10.3390/jcs2020026





