A CFAR-Enhanced Spectral Whitening Method for Acoustic Sensing via UAVs
Abstract
:1. Introduction
2. Background Information
3. CFAR-Enhanced Whitening
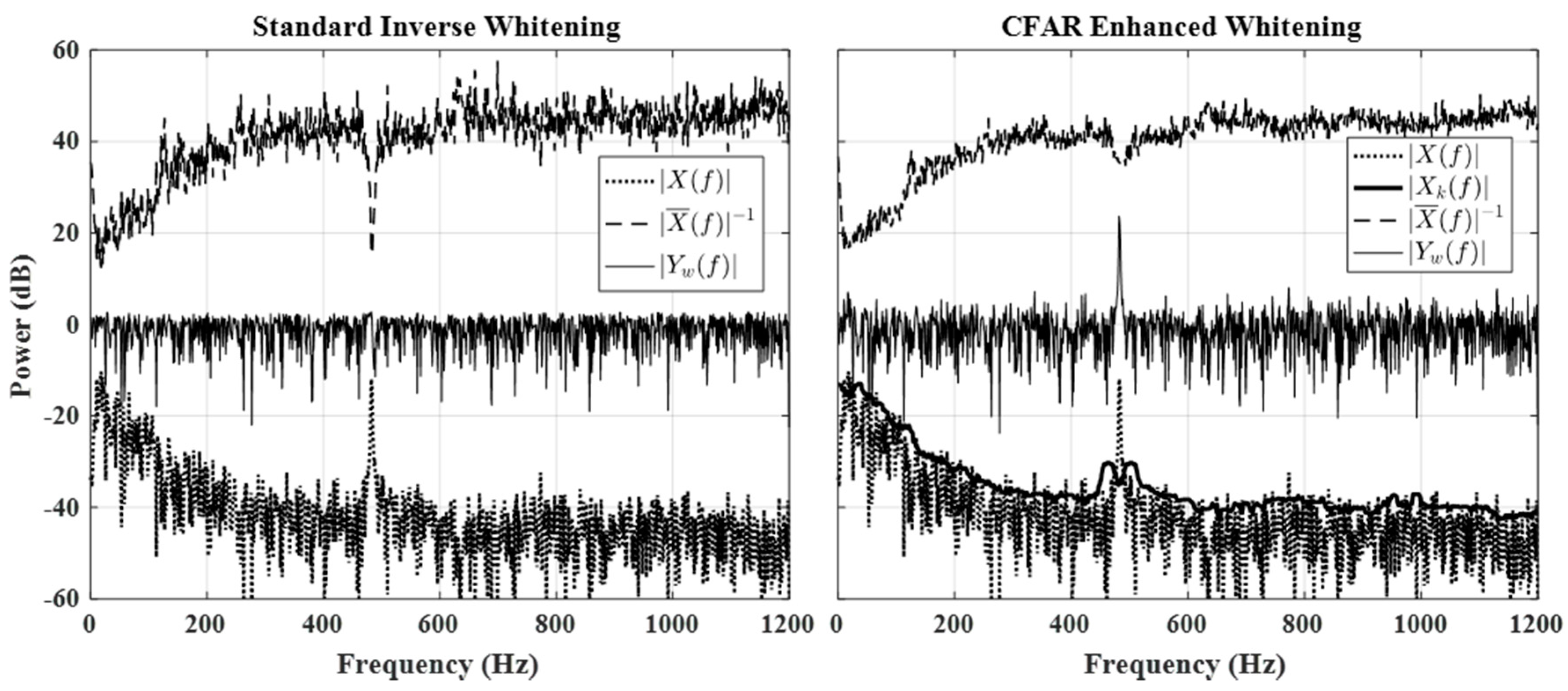
3.1. Description
3.2. Validation
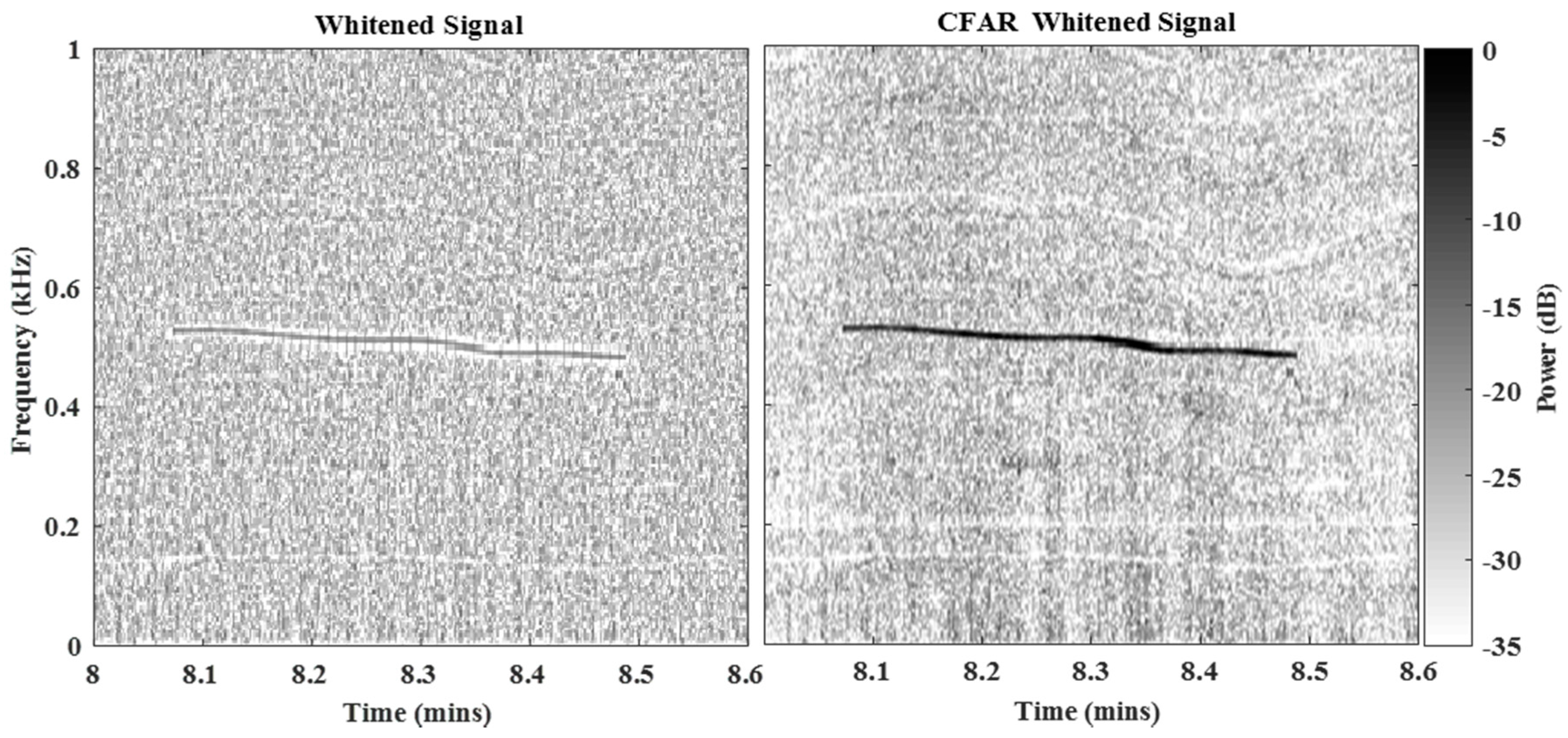
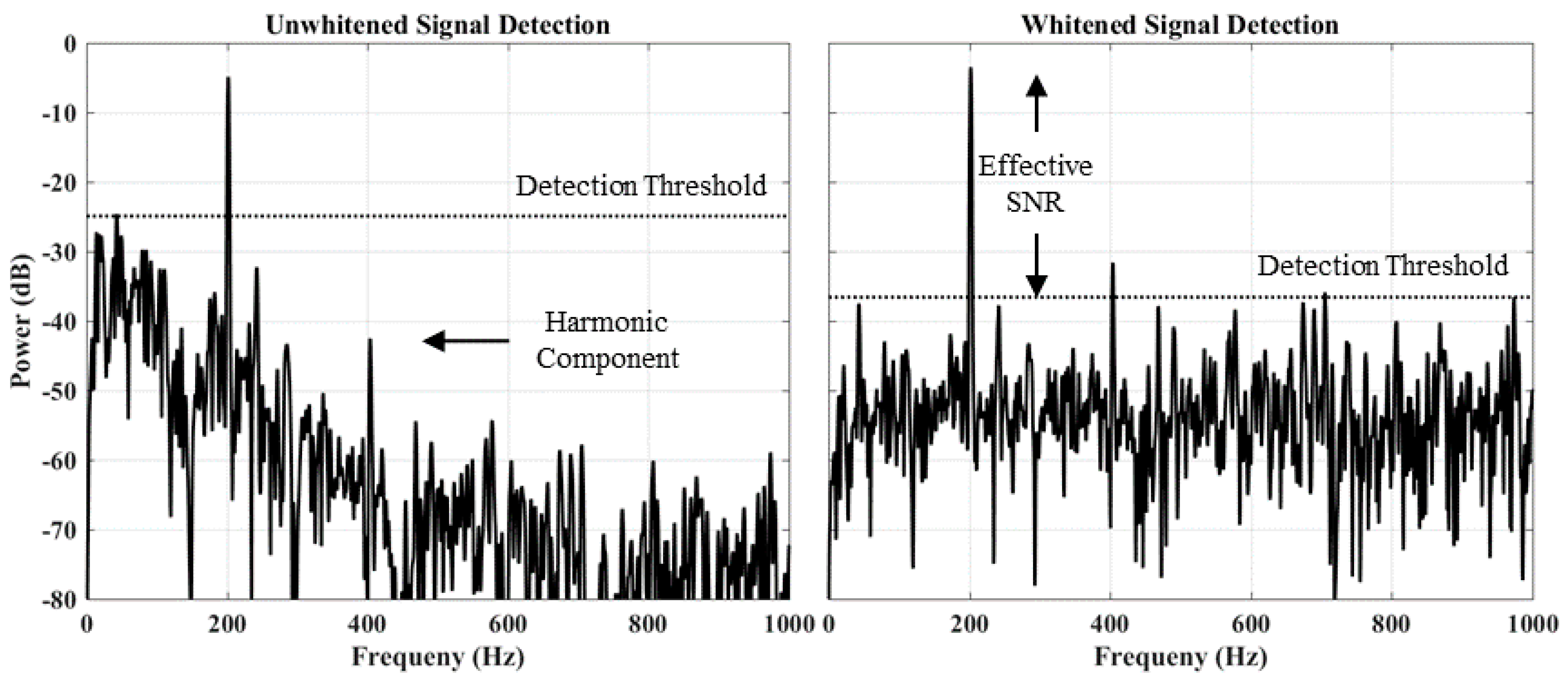
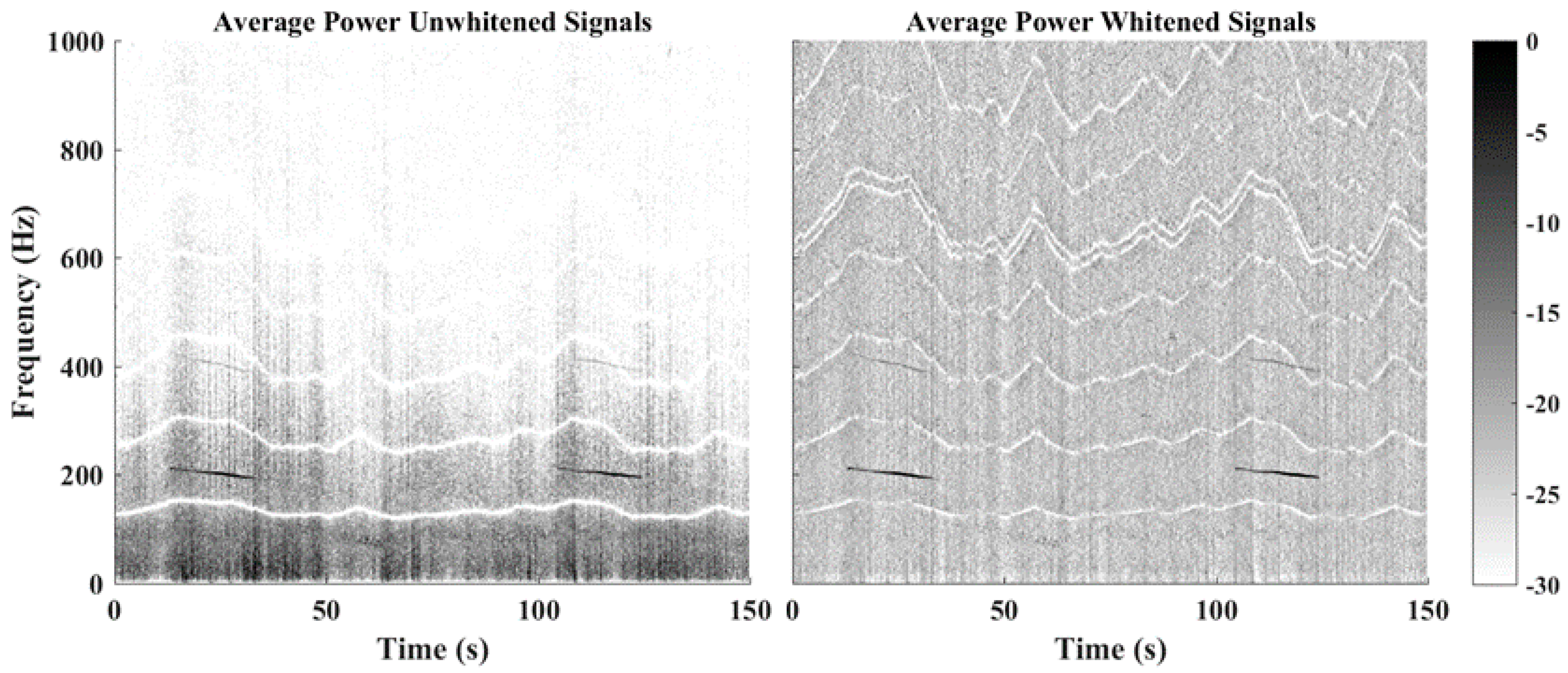
4. Experimental Results & Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Farnell, A. Designing Sound; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Thomas, R. (Ed.) Springer Handbook of Acoustics; Springer: New York, NY, USA, 2007; p. 113. [Google Scholar]
- Michel, U.; Dobrzynski, W.; Splettstoesser, W.; Delfs, J.; Isermann, U.; Obermeier, F. Aircraft noise. In Handbook of Engineering Acoustics, 1st ed.; Muller, M.M.G., Ed.; Springer Heidelberg: New York, NY, USA, 2013; p. 489. [Google Scholar]
- Richards, M.A. Fundamentals of Radar Signal Processing; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Sarma, A.; Tufts, D.W. Robust adaptive threshold for control of false alarms. IEEE Signal Process. Lett. 2001, 8, 261–263. [Google Scholar] [CrossRef]
- Ohata, T.; Nakamura, K.; Mizumoto, T.; Taiki, T.; Nakadai, K. Improvement in outdoor sound source detection using a quadrotor-embedded microphone array. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Okutani, K.; Yoshida, T.; Nakamura, K.; Nakadai, K. Outdoor auditory scene analysis using a moving microphone array embedded in a quadrocopter. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; p. 3288. [Google Scholar]
- Ferguson, B.; Wyber, R. Detection and localization of a ground based impulsive sound source using acoustic sensors onboard a tactical unmanned aerial vehicle. In Proceedings of the Battlefield Acoustic Sensing for ISR Applications, Neuilly-sur-Seine, France, 9–10 October 2006; pp. 16-1–16-8. [Google Scholar]
- Robertson, D.N.; Pham, T.; Edge, H.; Porter, B.; Shumaker, J.; Cline, D. Acoustic sensing from small-size UAVs. Proc. SPIE 2007, 6562. [Google Scholar] [CrossRef]
- Harvey, B.; O’Young, S. Detection of continuous ground-based acoustic sources via unmanned aerial vehicles. J. Unmanned Veh. Syst. 2015, 4, 83–95. [Google Scholar] [CrossRef]
- Harvey, B. Signal Processing Methods for the Detection & Localization of Acoustic Sources via Unmanned Aerial Vehicles. Ph.D., Memorial University of Newfoundland, St. John’s, NL, Canada, 2017. [Google Scholar]
- Harvey, B.; O’Young, S. Robust distribution-free CFAR detection of nonstationary narrowband signals. Dig. Signal Process. 2017. submitted. [Google Scholar]
- Lyons, R.G. Understanding Digital Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Lee, M.W. Spectral Whitening in the Frequency Domain; Open-File Report 86-108; United States Department of the Interior: Denver, CO, USA, 1986.
- Blake, S. OS-CFAR theory for multiple targets and nonuniform clutter. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 785–790. [Google Scholar] [CrossRef]
- Finn, H.M.; Johnson, P.S. Adaptive detection mode with threshold control as a function of spatially sampled clutter estimation. RCA Rev. 1968, 29, 414–464. [Google Scholar]
- Jalil, A.; Yousaf, H.; Baig, M.I. Analysis of CFAR techniques. In Proceedings of the 2016 13th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 12–16 January 2016. [Google Scholar]
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 608–621. [Google Scholar] [CrossRef]
- Ritcey, J.A. Performance analysis of the censored mean-level detector. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 443–454. [Google Scholar] [CrossRef]
- Gandhi, P.P.; Kassam, S.A. Analysis of CFAR processors in nonhomogeneous background. IEEE Trans. Aerosp. Electron. Syst. 1988, 24, 427–445. [Google Scholar] [CrossRef]
- Tan, L.; Jiang, J. Novel adaptive IIR filter for frequency estimation and tracking [DSP Tips&Tricks]. IEEE Signal Process. Mag. 2009, 26, 186–189. [Google Scholar]
- Tan, L.; Jiang, J. Real-time frequency tracking using novel adaptive harmonic IIR notch filter. Technol. Interface J. 2009, 9. [Google Scholar]
- Tan, L.; Jiang, J. Simplified gradient adaptive harmonic IIR notch filter for frequency estimation and tracking. Am. J. Signal Process. 2015, 5, 6–12. [Google Scholar]
- Tan, L.; Jiang, J.; Wang, L. Adaptive harmonic IIR notch filters for frequency estimation and tracking. In Adaptive Filtering; Garcia, L., Ed.; InTech: Rijeka, Croatia, 2011; p. 313. [Google Scholar]
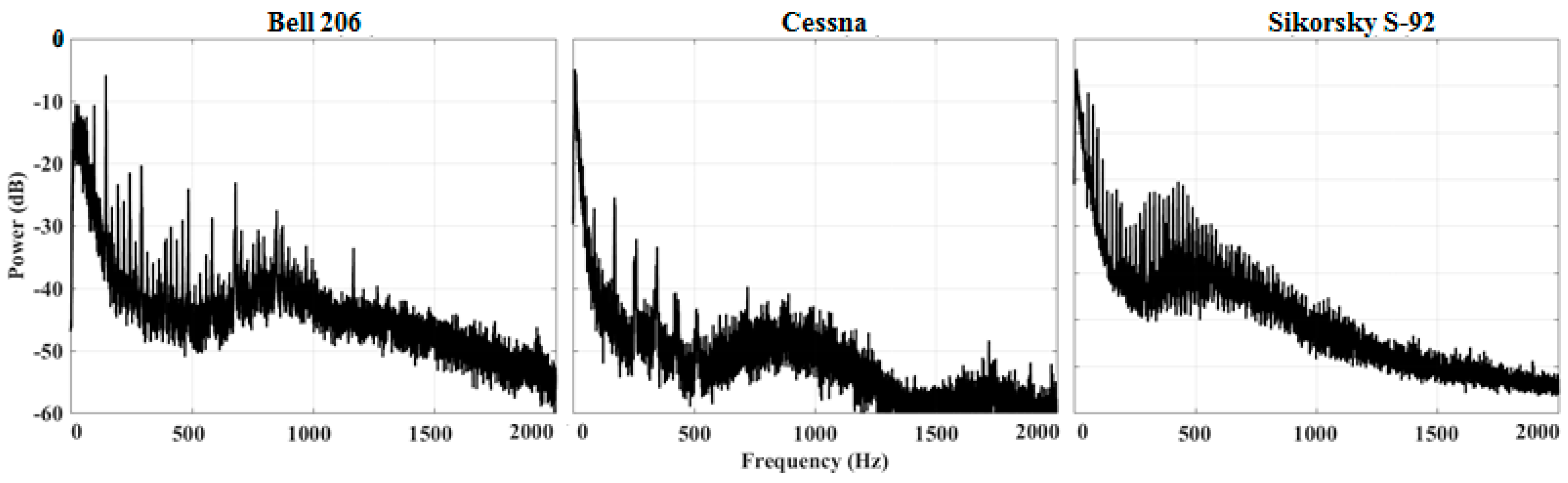
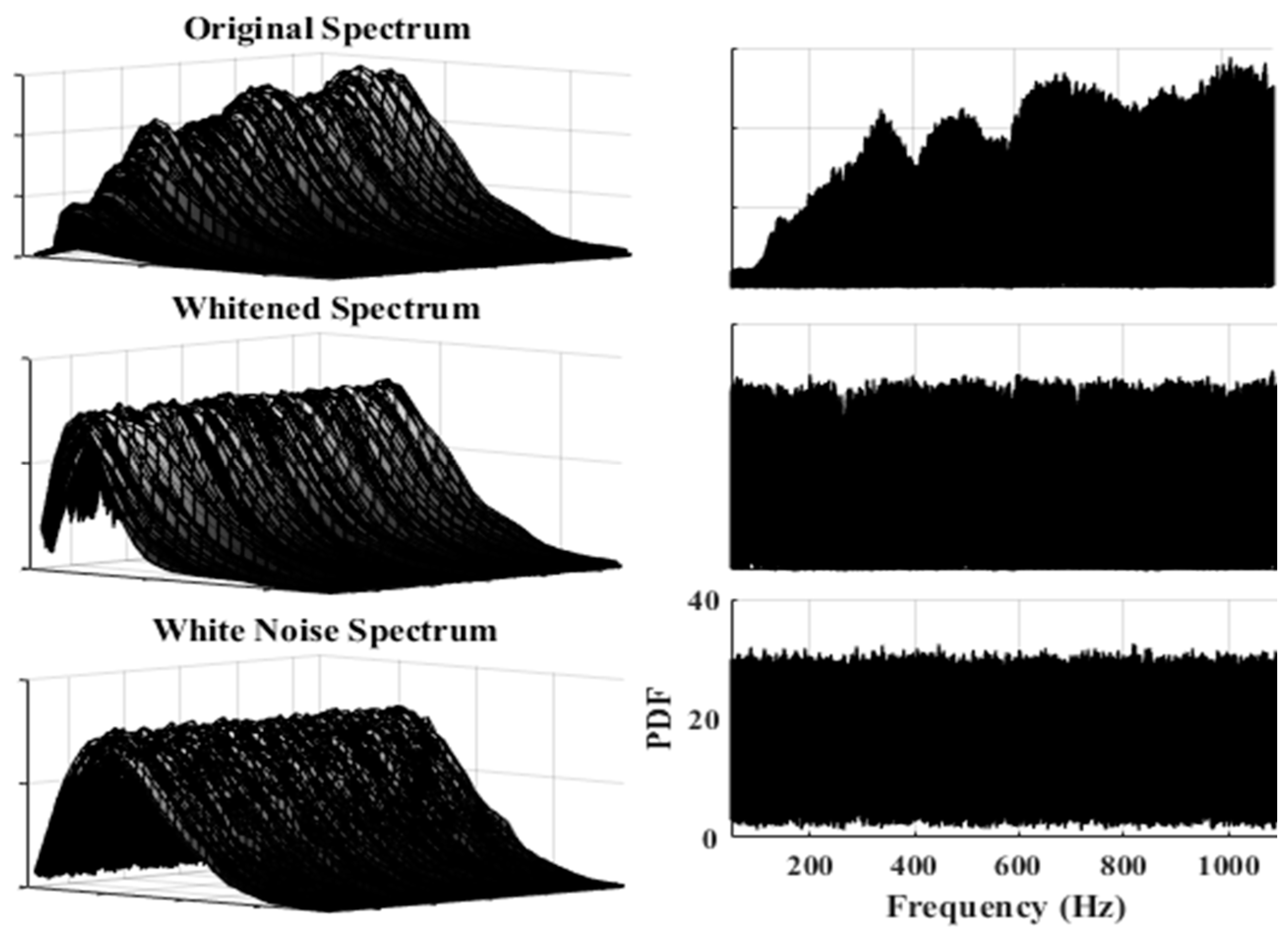
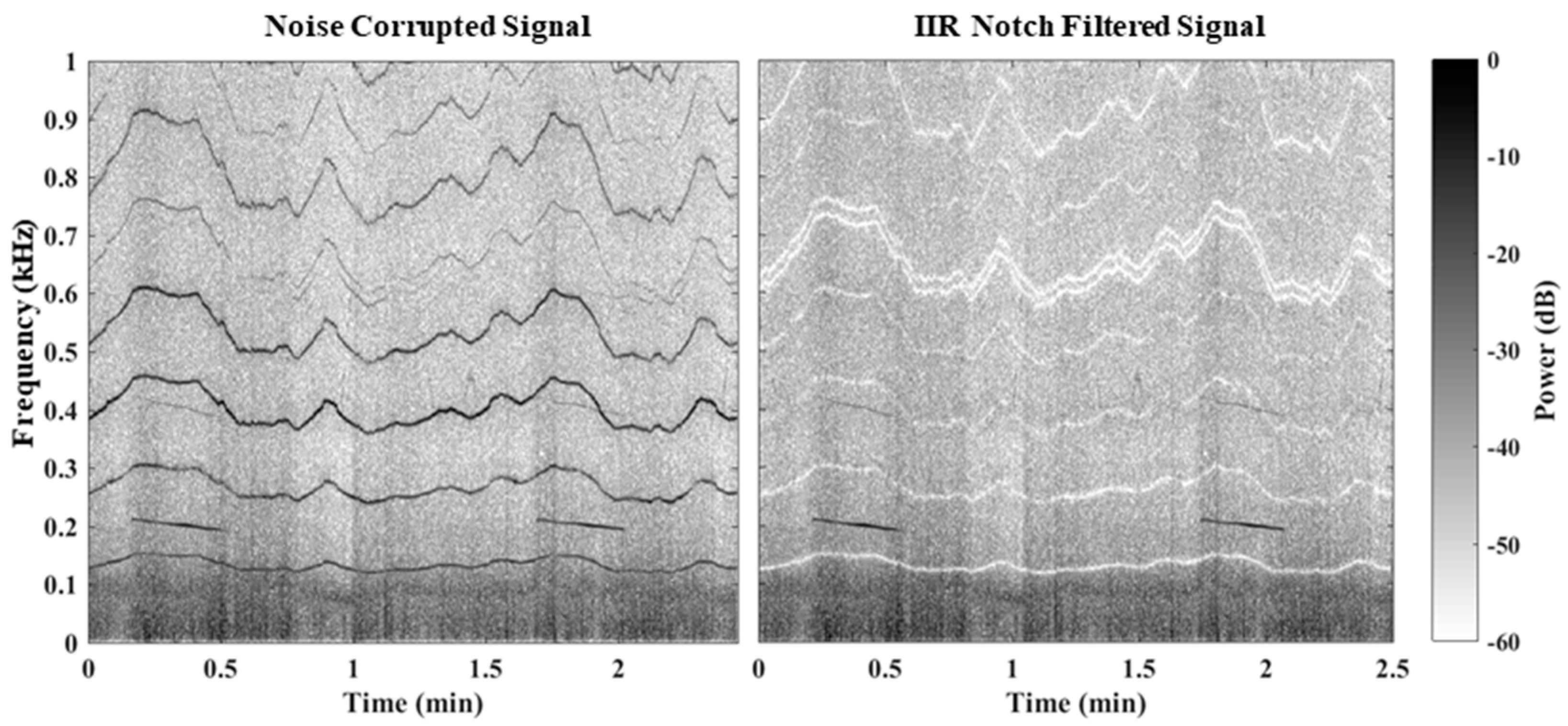
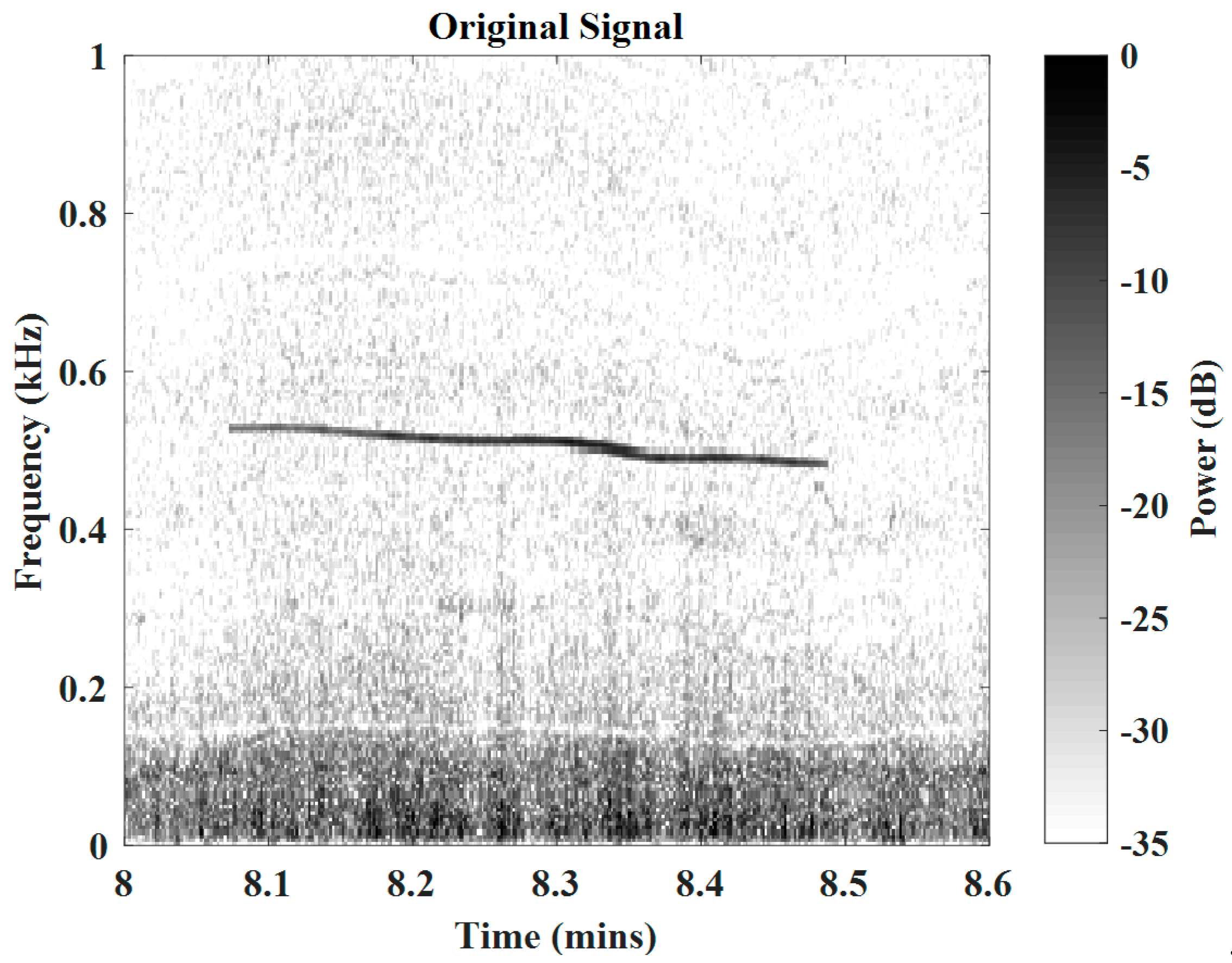
| Sampling Frequency () | 48 kHz | Number of Signals | 4 |
| Decimation Factor | 8 | FFT Window | 0.5 s |
| IIR Step Size () | 5 × 10−4 | Window Overlap | 50% |
| Notch Radius () | 0.995 | Padded Length () | 12,000 pts |
| Harmonics Removed () | 8 | Spectral Resolution () | 0.5 Hz/bin |
| Detector Type | OS-CFAR | Noise Samples ( | 101 |
| Forgetting Factor () | 0.2 | Order Statistic ( | |
| Flooring Factor () | 0.5 | Guard Cell Band () | 5.5 Hz |
| Noise Band () | 50 Hz | Guard Cells () | 12 |
| Noise Sample Band () | 1–1000 Hz | Consecutive Detections () | 2 |
| Test Band () | 150–550 Hz | Cell Deviation () | 1 |
| Guard Cell Band () | 10.5 Hz | Maxima Tested () | 2 |
| Noise Samples () | 1998 pts | 1.0 × 10−3 | |
| Test Cells () | 801 pts | 6.5 × 10−1 | |
| Guard Cells (G) | 22 pts | 8.2 × 10−4 | |
| Order Statistic () | 2 | 2.5 × 10−3 | |
| Consecutive Trials () | 2 |
| = 200 Hz | = 500 Hz | |||
|---|---|---|---|---|
| Unwhitened | Whitened | Unwhitened | Whitened | |
| Detection Rate (ST, BI, RBI) | 64%, 54%, 55% | 100%, 97%, 99% | 69%, 37%, 51% | 100%, 63%, 83% |
| Max SNR | 28 dB | 38.3 dB | 26.5 dB | 47.4 dB |
| Average SNR | 12.4 dB | 19.7 dB | 8.2 dB | 32.5 dB |
| Initial Detection | 13.25 s | 13 s | 11 s | 10.5 s |
| Second Detection | 20.25 s | 13.25 s | 12 s | 10.75 s |
| Observed Frequency Range | 212–190 Hz | 523–479 Hz | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harvey, B.; O’Young, S. A CFAR-Enhanced Spectral Whitening Method for Acoustic Sensing via UAVs. Drones 2018, 2, 1. https://doi.org/10.3390/drones2010001
Harvey B, O’Young S. A CFAR-Enhanced Spectral Whitening Method for Acoustic Sensing via UAVs. Drones. 2018; 2(1):1. https://doi.org/10.3390/drones2010001
Chicago/Turabian StyleHarvey, Brendan, and Siu O’Young. 2018. "A CFAR-Enhanced Spectral Whitening Method for Acoustic Sensing via UAVs" Drones 2, no. 1: 1. https://doi.org/10.3390/drones2010001





