Aggregation Operator and Its Application in Assessing First-Class Discipline Construction in Industry-Characteristic Universities
Abstract
1. Introduction
- We combine the advantages of CFS, CuFS, and FOFS in representing uncertain information to propose a new type of fuzzy set called CCFOFS. This new type of fuzzy set can represent uncertain information more comprehensively and is more suitable for dealing with fuzzy multi-attribute assessment problems. We apply it to the assessment of first-class discipline construction in industry-characteristic universities.
- We propose the CCFOFDWPPMM operator, which can consider the variability of parameter operations and is more compatible than traditional operation rules. This operator can effectively avoid the influence of singular values and solve decision-making problems involving interrelationships between attributes in different partitions, which is more in line with the reality of multi-attribute assessment.
- Taking into account the different degrees of importance of each attribute, we combine the IDOCRIW-weighting method with the proposed CCFOFDWPPMM operator to propose a new multi-attribute assessment method, and apply this method to the assessment of first-class discipline construction in industry-characteristic universities.
- We provide an indicator system suitable for first-class discipline construction in industry-characteristic universities, focusing on the four dimensions of “talent cultivation”, “scientific research”, “social services”, and “open education,” highlighting the core characteristics of first-class discipline construction in industry-characteristic universities. This indicator system breaks through the constraints of the comprehensive university assessment system framework and highlights the special mission of industry-characteristic universities in serving national strategies and specific industries.
2. Preliminaries
2.1. Fractional Orthotriple Fuzzy Set
2.2. Complex Cubic Fuzzy Set
2.3. The Dombi Operations
2.4. PA Operator
- (1)
- ;
- (2)
- ;
- (3)
- If , then .
2.5. MM Operator
- (1)
- When the parameter vector , the MM operator degrades to the geometric mean (GM) operator:
- (2)
- When , the MM operator degrades to the arithmetic mean (AM) operator:
- (3)
- When , the MM operator degrades to the BM operator:
- (4)
- When , the MM operator degrades to the Maclaurin symmetric mean (MSM) operator [33]:
2.6. PMM Operator
3. Complex Cubic Fractional Orthotriple Fuzzy Aggregation Operators
3.1. Complex Cubic Fractional Orthotriple Fuzzy Set
- (1)
- If , then ;
- (2)
- If , then ;
- (3)
- If , then
- (a)
- If , then ;
- (b)
- If , then ;
- (c)
- If , then .
3.2. Dombi Operations for Complex Cubic Fractional Orthotriple Fuzzy Set
3.3. Complex Cubic Fractional Orthotriple Fuzzy Dombi-Partitioned Muirhead Mean Operator
- (1)
- When the parameter vector , the CCFOFDPMM operator degrades to the CCFOFDPGM operator:
- (2)
- When , the CCFOFDPMM operator degrades to the CCFOFDPAM operator:
- (3)
- When , the CCFOFDPMM operator degrades to the CCFOFDPBM operator:
- (4)
- When , the CCFOFDMM operator degrades to the CCFOFDPMSM operator:
3.4. Complex Cubic Fractional Orthotriple Dombi-Weighted Power-Partitioned Muirhead Mean Operator
- (1)
- ;
- (2)
- ;
- (3)
- If , then .
- (1)
- When , the CCFOFDWPPMM operator degrades to the CCFOFDWPPGM operator:
- (2)
- When , the CCFOFDWPPMM operator degrades to the CCFOFDWPPAM operator:
- (3)
- When , the CCFOFDWPPMM operator degrades to the CCFOFDWPPBM operator:
- (4)
- When , the CCFOFDWPPMM operator degrades to the CCFOFDWPPMSM operator:
4. Constructing an Assessment Indicator System for the Construction of First-Class Disciplines
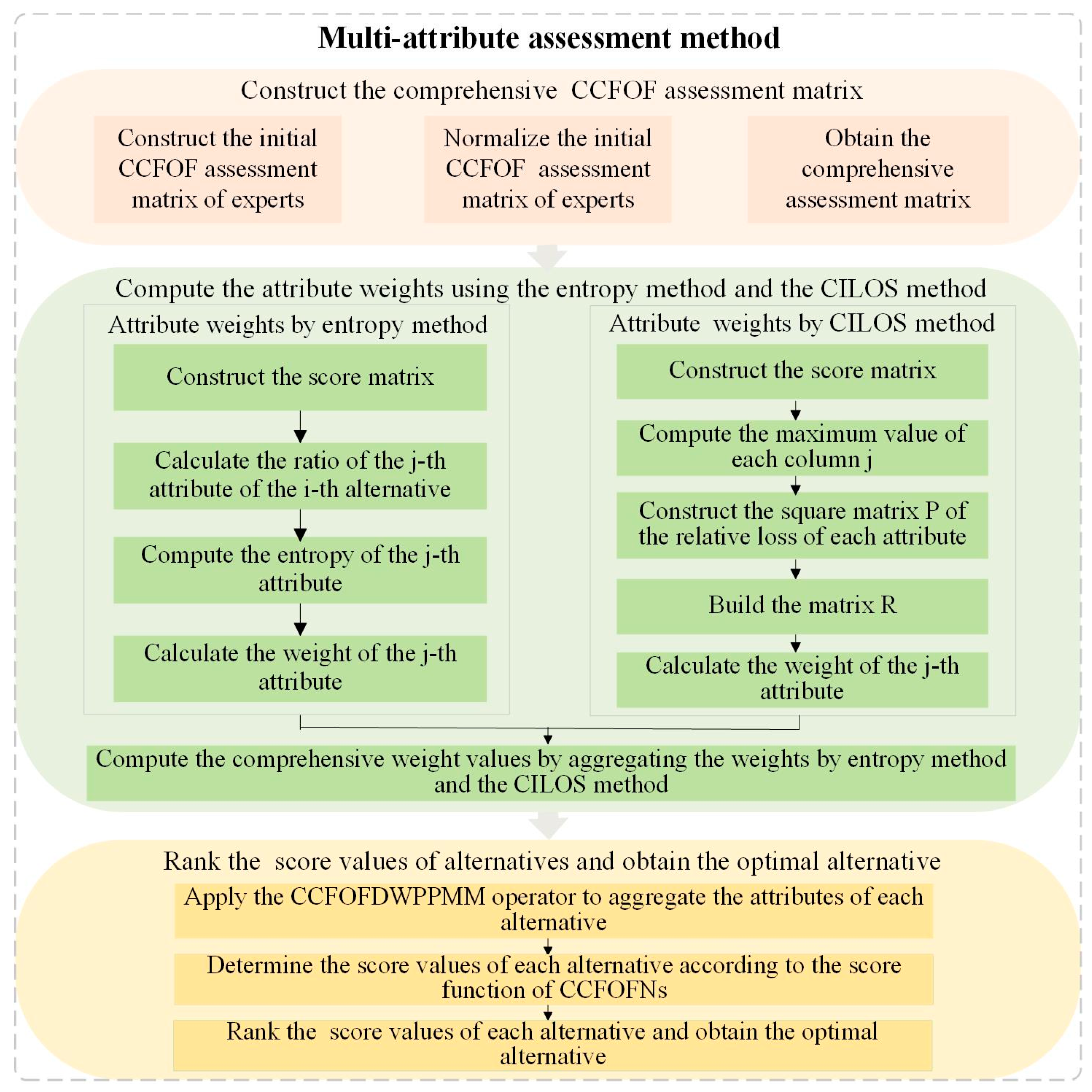
5. Multi-Attribute Assessment Method Based on the CCFOFDWPPMM Operator and the IDOCRIW Method
6. Example Analysis
6.1. Assessment Process
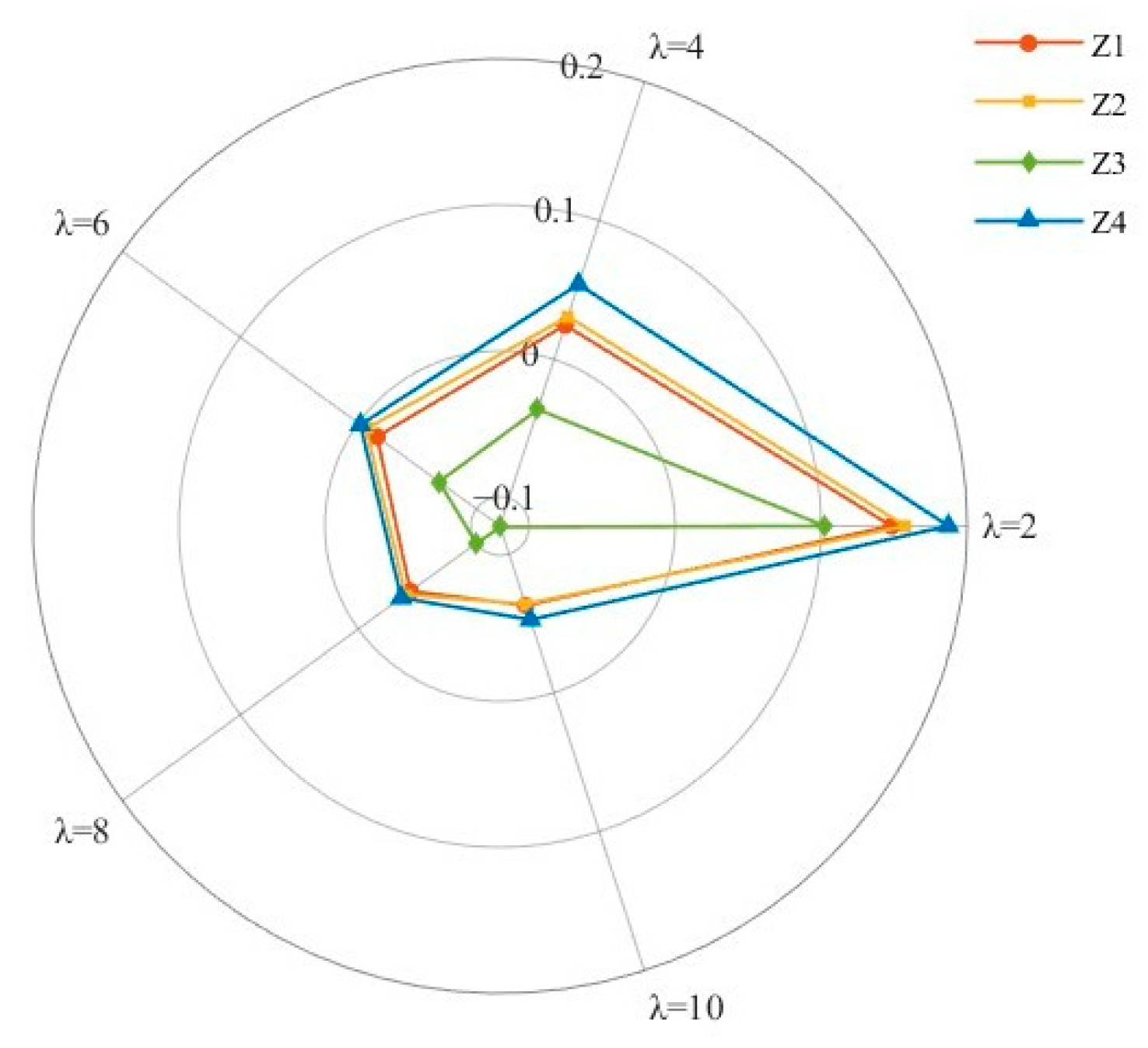
6.2. Sensitivity Analysis
6.3. Comparative Analysis
6.4. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCFOFS | Complex cubic fractional orthotriple fuzzy set |
| CCFOFDWPPMM | Complex cubic fractional orthotriple fuzzy Dombi-weighted power-partitioned Muirhead mean |
| PA | Power average |
| PMM | Partitioned Muirhead mean |
| IDOCRIW | Integrated Determination of Objective Criteria Weights |
| Grey-AHP | The grey analytic hierarchy process |
| IFS | Intuitionistic Fuzzy set |
| MD | Membership degree |
| NMD | Non-membership degree |
| PyFS | Pythagorean fuzzy set |
| q-ROFS | q-rung orthopair fuzzy set |
| FOFS | Fractional orthogonal fuzzy set |
| HD | Hesitation degree |
| CFS | Complex fuzzy set |
| CuFS | Cubic fuzzy set |
| CCFS | Complex cubic fuzzy set |
| BM | Bonferroni mean |
| HM | Heronian mean |
| MM | Muirhead mean |
| PPMM | Power-partitioned Muirhead mean |
| CCFOF | Complex cubic fractional orthotriple fuzzy |
| CILOS | Criterion impact loss |
| PDHL | Probabilistic double-hierarchy linguistic |
| WA | Weighted average |
| WG | Weighted geometric |
| OWA | Ordered weighted average |
| OWG | Ordered weighted geometric |
| GM | Geometric mean |
| AM | Arithmetic mean |
| MSM | Maclaurin symmetric mean |
| CCFOFN | Complex cubic orthotriple fractional fuzzy number |
| CCFOFDPMM | Complex cubic fractional orthotriple fuzzy Dombi-partitioned Muirhead mean |
Appendix A
Appendix B
| Partition | Attribute | Z1 | Z2 |
|---|---|---|---|
| O1 | F1 | (([0.12,0.60]ej[π/2,π], [0.41,0.81]ej[π/2,π/2], [0.39,0.8]ej[π/2,π/2]), (0.35,0.61,0.5)ej(π/2,π,π)) | (([0.12,0.61]ej[π/2,π/2], [0.39,0.79]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.37,0.59,0.4)ej(π/2,π/2,π/2)) |
| F2 | (([0.23,0.76]ej[π/2,π/2], [0.24,0.65]ej[π/2,π/2], [0.24,0.7]ej[π/2,π/2]), (0.50,0.45,0.6)ej(π/2,π,π/2)) | (([0.20,0.73]ej[π/2,π/2], [0.27,0.68]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.47,0.47,0.4)ej(π/2,π/2,π/2)) | |
| F3 | (([0.29,0.88]ej[π/3,π/2], [0.12,0.48]ej[π/2,π/2], [0.1,0.4]ej[π/2,π/2]), (0.58,0.30,0.4)ej(π/2,π/2,π/2)) | (([0.20,0.73]ej[π/2,π/2], [0.27,0.68]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.47,0.48.0,4)ej(π/2,π/2,π/2)) | |
| F4 | (([0.13,0.80]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2]), (0.46,0.40,0.38)ej(π/2,π/2,π/2)) | (([0.25,0.80]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2], [0.24,0.63]ej[π/2,π/2]), (0.53,0.40,0.4)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.05,0.71]ej[π/2,π/2], [0.29,0.71],ej[π/2,π/2], [0.2,0.7],ej[π/2,π/2]), (0.38,0.50,0.4)ej(π/2,π/2,π)) | ([0.06,0.70]ej[π/2,π/2], [0.29,0.71]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.38,0.50,0.5)ej(π/2,π/2,π/2)) |
| F6 | (([0.02,0.85],ej[π/3,π/2], [0.15,0.52]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.44,0.33,0.4)ej(π/2,π/2,π/2)) | (([0.05,0.89]ej[π/2,π/2], [0.11,0.45]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.47,0.28,0.3)ej(π/2,π/2,π/2)) | |
| F7 | (([0.04,0.62]ej[π/2,π/2], [0.39,0.79]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.33,0.58,0.6)ej(π/2,π/2,π/2)) | (([0.01,0.69]ej[π/2,π/2], [0.31,0.73]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.35,0.52,0.4)ej(π/2,π/2,π/2)) | |
| F8 | (([0.12,0.81]ej[π/2,π], [0.19,0.59]ej[π/2,π/2], [0.20.6]ej[π/2,π/2]), (0.46,0.39,0.4)ej(π/2,π/2,π/2)) | (([0.20,0.70]ej[π/2,π/2], [0.30,0.71]ej[π/2,π/2], [0.30,0.6]ej[π/2,π/2]), (0.45,0.50,0.4)ej(π/2,π/2,π/2)) | |
| O3 | F9 | (([0.05,0.79]ej[π/2,π/2], [0.21,0.61]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.42,0.41,0.3)ej(π/2,π/2,π/2)) | (([0.10,0.87]ej[π/2,π/2], [0.13,0.50]ej[π/2,π/2], [0.2,0.50]ej[π/2,π/2]), (0.48,0.31,0.42)ej(π/2,π/2,π/2)) |
| F10 | (([0.02,0.84]ej[π/2,π/2], [0.16,0.54]ej[π/3,π/2], [0.2,0.5]ej[π/3,π/2]), (0.43,0.35,0.4)ej(π/2,π/2,π/2)) | (([0.07,0.89]ej[π/2,π/2], [0.10,0.45]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.48,0.28,0.3)ej(π/2,π/2,π/2)) | |
| F11 | (([0.05,0.83]ej[π/2,π/2], [0.17,0.55]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.44,0.36,0.3)ej(π/2,π,π)) | (([0.10,0.87]ej[π/2,π/2], [0.13,0.49]ej[π/3,π/2], [0.2,0.5]ej[π/3,π/2]), (0.49,0.31,0.3)ej(π/2,π/2,π/2)) | |
| F12 | (([0.21,0.78]ej[π/2,π], [0.22,0.62]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.49,0.42,0.3)ej(π/2,π/2,π/2)) | (([0.25,0.80]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2], [0.3,0.50]ej[π/2,π/2]), (0.53,0.40,0.3)ej(π/2,π/2,π/2)) | |
| O4 | F13 | (([0.03,0.78]ej[π/2,π/2], [0.22,0.62]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.41,0.42,0.3)ej(π/2,π,π)) | (([0.04,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.43,0.39,0.3)ej(π/2,π/2,π/2)) |
| F14 | (([0.04,0.85]ej[π/2,π/2], [0.15,0.52]ej[π/2,π/2], [0.21,0.5]ej[π/2,π/2]), (0.45,0.33,0.34)ej(π/2,π/2,π/2)) | (([0.04,0.86]ej[π/2,π/2], [0.14,0.51]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.45,0.33,0.36)ej(π/2,π,π)) | |
| F15 | (([0.05,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.43,0.39,0.3)ej(π/2,π/2,π/2)) | (([0.12,0.87]ej[π/2,π/2], [0.13,0.49]ej[π/2,π/2], [0.2,0.49]ej[π/2,π/2]), (0.49,0.31,0.35)ej(π/2,π/2,π/2)) | |
| F16 | (([0.10,0.85]ej[π/2,π/2], [0.15,0.52]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.48,0.34,0.35)ej(π/2,π,π) | (([0.07,0.59]ej[π/2,π/2], [0.41,0.81]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.33,0.61,0.5)ej(π/2,π/2,π/2)) | |
| Partition | Attribute | Z3 | Z4 |
| O1 | F1 | (([0.05,0.52]ej[π/2,π/2], [0.48,0.85]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.29,0.67,0.5)ej(π/3,π/2,π/2)) | (([0.34,0.87]ej[π/3,π/2], [0.13,0.50]ej[π/2,π/2], [0.2,0.50]ej[π/2,π/2]), (0.60,0.31,0.4)ej(π/2,π/2,π/2)) |
| F2 | (([0.1,0.71]ej[π/3,π/2], [0.29,0.71]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.45,0.50,0.4)ej(π/3,π/2,π/2)) | (([0.3,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.28,0.61]ej[π/2,π/2], (0.50,0.39,0.4)ej(π/2,π/2,π/2)) | |
| F3 | (([0.04,0.74]ej[π/2,π], [0.26,0.68]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.39,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.32,0.71]ej[π/2,π/2], [0.29,0.71]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.46,0.50,0.5)ej(π/2,π/2,π/2)) | |
| F4 | (([0.1,0.74]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.50,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.3,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.50,0.39,0.4)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.05,0.66]ej[π/2,π], [0.34,0.75]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.35,0.54,0.4)ej(π/2,π/2,π/2)) | (([0.22,0.80]ej[π/2,π/2], [0.20,0.59]ej[π/2,π/2], [0.20,0.6]ej[π/2,π/2]), (0.55,0.40,0.3)ej(π/2,π/2,π/2)) |
| F6 | (([0.05,0.85]ej[π/2,π], [0.15,0.53]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.45,0.34,0.3)ej(π/2,π/2,π/2)) | (([0.21,0.78]ej[π/2,π/2], [0.22,0.63]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.49,0.43,0.4)ej(π/2,π/2,π/2)) | |
| F7 | (([0.01,0.66]ej[π/2,π/2], [0.34,0.75]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.34,0.54,0.4)ej(π/2,π/2,π/2)) | (([0.13,0.90]ej[π/2,π/2], [0.10,0.43]ej[π/2,π/2], [0.15,0.45]ej[π/2,π/2]), (0.52,0.27,0.34)ej(π/2,π/2,π/2)) | |
| F8 | (([0.04,0.63]ej[π/2,π], [0.37,0.77]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.39,0.57,0.4)ej(π/2,π/2,π/2)) | (([0.17,0.82]ej[π/3,π/2], [0.18,0.57]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.49,0.37,0.43)ej(π/2,π/2,π)) | |
| O3 | F9 | (([0.07,0.82]ej[π/2,π/2], [0.18,0.57]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.45,0.37,0.2)ej(π/2,π/2,π/2)) | (([0.06,0.78]ej[π/2,π/2], [0.22,0.62]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.42,0.42,0.3)ej(π/2,π/2,π/2)) |
| F10 | (([0.11,0.85]ej[π/2,π], [0.15,0.53]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.48,0.34,0.4)ej(π/2,π/2,π/2)) | (([0.19,0.87]ej[π/2,π/2], [0.13,0.49]ej[π/2,π/2], [0.2,0.51]ej[π/2,π/2]), (0.53,0.31,0.4)ej(π/2,π/2,π/2)) | |
| F11 | (([0.05,0.74]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.31,0.69]ej[π/2,π/2]), (0.39,0.46,0.3)ej(π/2,π/2,π/2)) | (([0.25,0.84]ej[π/2,π], [0.16,0.54]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.55,0.35,0.4)ej(π/2,π/2,π/2)) | |
| F12 | (([0.18,0.53]ej[π/2,π], [0.47,0.85]ej[π/2,π/2], [0.5,0.8]ej[π/2,π/2]), (0.35,0.66,0.5)ej(π/2,π/2,π/2)) | (([0.13,0.74]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.44,0.47,0.3)ej(π/2,π,π)) | |
| O4 | F13 | (([0.05,0.75]ej[π/3,π/2], [0.25,0.66]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.40,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.06,0.88]ej[π/2,π/2], [0.12,0.47]ej[π/2,π/2], [0.2,0.4]ej[π/2,π/2]), (0.55,0.29,0.4)ej(π/2,π/2,π/2)) |
| F14 | (([0.04,0.80]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2]), (0.42,0.40,0.34)ej(π/2,π/2,π/2)) | (([0.06,0.89]ej[π/2,π/2], [0.11,0.46]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.48,0.28,0.3)ej(π/2,π/2,π/2)) | |
| F15 | (([0.07,0.83]ej[π/2,π/2], [0.17,0.55]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.45,0.36,0.4)ej(π/2,π/2,π/2)) | (([0.09,0.75]ej[π/2,π/2], [0.25,0.66]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.42,0.46,0.35)ej(π/2,π/2,π/2)) | |
| F16 | (([0.09,0.47]ej[π/3,π/2], [0.53,0.88]ej[π/2,π/2], [0.52,0.7]ej[π/2,π/2]), (0.28,0.71,0.7)ej(π/2,π/2,π/2)) | (([0.07,0.45]ej[π/2,π/2], [0.55,0.89]ej[π/2,π/2], [0.44,0.69]ej[π/2,π/2]), (0.26,0.72,0.45)ej(π/2,π,π)) |
| Partition | Attribute | Z1 | Z2 |
|---|---|---|---|
| O1 | F1 | (([0.1,0.56]ej[π/2,π], [0.4,0.8]ej[π/2,π], [0.36,0.81]ej[π/2,π/2]), (0.37,0.6,0.5)ej(π/2,π/2,π)) | (([0.15,0.62]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2], [0.45,0.81]ej[π/2,π/2]), (0.39,0.6,0.35)ej(π/2,π,π)) |
| F2 | (([0.2,0.6]ej[π/2,π/2], [0.25,0.6]ej[π/2,π/2], [0.2,0.7]ej[π/2,π/2]), (0.55,0.5,0.61)ej(π/2,π,π/2)) | (([0.23,0.7]ej[π/2,π/2], [0.24,0.7]ej[π/2,π/2], [0.34,0.75]ej[π/2,π]), (0.47,0.47,0.4)ej(π/2,π/2,π)) | |
| F3 | (([0.31,0.82]ej[π/3,π/2], [0.15,0.5]ej[π/2,π/2], [0.15,0.39]ej[π/2,π/2]), (0.6,0.31,0.42)ej(π/2,π,π)) | (([0.22,0.7]ej[π/2,π/2], [0.3,0.65]ej[π/2,π/2], [0.35,0.71]ej[π/2,π/2]), (0.5,0.42.0,4)ej(π/2,π/2,π/2)) | |
| F4 | (([0.15,0.82]ej[π/2,π/2], [0.22,0.64]ej[π/2,π/2], [0.25,0.63]ej[π/2,π]), (0.45,0.45,0.35)ej(π/2,π/2,π/2)) | (([0.26,0.76]ej[π/2,π], [0.21,0.64]ej[π/2,π/2], [0.2,0.62]ej[π/2,π/2]), (0.47,0.39,0.38)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.06,0.74]ej[π/2,π/2], [0.29,0.7],ej[π/2,π/2], [0.21,0.67],ej[π/2,π]), (0.4,0.50,0.45)ej(π/2,π/2,π)) | (([0.06,0.70]ej[π/2,π/2], [0.29,0.71]ej[π/3,π/2], [0.32,0.75]ej[π/2,π]), (0.4,0.45,0.35)ej(π/2,π/2,π)) |
| F6 | (([0.05,0.8],ej[π/3,π/2], [0.2,0.5]ej[π/3,π/2], [0.3,0.45]ej[π/2,π/2]), (0.41,0.32,0.44)ej(π/2,π/2,π/2)) | (([0.05,0.83]ej[π/2,π/2], [0.15,0.43]ej[π/2,π/2], [0.23,0.58]ej[π/2,π/2]), (0.48,0.32,0.31)ej(π/2,π/2,π)) | |
| F7 | (([0.04,0.62]ej[π/2,π/2], [0.4,0.79]ej[π/2,π/2], [0.45,0.78]ej[π/3,π]), (0.35,0.56,0.5)ej(π/2,π/2,π/2)) | (([0.02,0.64]ej[π/2,π/2], [0.32,0.71]ej[π/2,π/2], [0.31,0.64]ej[π/2,π/2]), (0.4,0.51,0.34)ej(π/2,π/2,π/2)) | |
| F8 | (([0.15,0.83]ej[π/2,π], [0.24,0.56]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.5,0.42,0.41)ej(π/2,π/2,π/2)) | (([0.18,0.70]ej[π/2,π/2], [0.39,0.71]ej[π/2,π/2], [0.30,0.7]ej[π/2,π/2]), (0.54,0.45,0.5)ej(π/2,π/2,π/2)) | |
| O3 | F9 | (([0.03,0.73]ej[π/3,π/2], [0.2,0.59]ej[π/2,π/2], [0.21,0.56]ej[π/2,π/2]), (0.4,0.41,0.32)ej(π/2,π/2,π/2)) | (([0.08,0.87]ej[π/3,π/2], [0.13,0.50]ej[π/2,π/2], [0.2,0.50]ej[π/2,π/2]), (0.48,0.31,0.42)ej(π/2,π/2,π/2)) |
| F10 | (([0.02,0.72]ej[π/2,π/2], [0.16,0.53]ej[π/2,π/2], [0.13,0.35]ej[π/3,π/2]), (0.38,0.4,0.34)ej(π/2,π,π)) | (([0.05,0.78]ej[π/2,π/2], [0.12,0.43]ej[π/2,π/2], [0.22,0.38]ej[π/2,π/2]), (0.44,0.38,0.36)ej(π/2,π,π)) | |
| F11 | (([0.03,0.77]ej[π/2,π/2], [0.18,0.56]ej[π/2,π/2], [0.22,0.54]ej[π/2,π/2]), (0.45,0.39,0.39)ej(π/2,π,π)) | (([0.11,0.82]ej[π/3,π/2], [0.13,0.42]ej[π/3,π/2], [0.21,0.5]ej[π/3,π/2]), (0.43,0.25,0.23)ej(π/2,π/2,π/2)) | |
| F12 | (([0.05,0.71]ej[π/2,π], [0.25,0.6]ej[π/2,π/2], [0.25,0.62]ej[π/2,π/2]), (0.44,0.49,0.36)ej(π/2,π/2,π/2)) | (([0.13,0.75]ej[π/2,π/2], [0.24,0.65]ej[π/2,π/2], [0.23,0.55]ej[π/2,π/2]), (0.51,0.31,0.33)ej(π/2,π/2,π)) | |
| O4 | F13 | (([0.04,0.8]ej[π/2,π/2], [0.21,0.52]ej[π/2,π/2], [0.38,0.46]ej[π/2,π/2]), (0.42,0.43,0.36)ej(π/2,π,π)) | (([0.03,0.75]ej[π/2,π/2], [0.13,0.52]ej[π/2,π/2], [0.2,0.56]ej[π/2,π/2]), (0.41,0.4,0.3)ej(π/2,π/2,π/2)) |
| F14 | (([0.05,0.8]ej[π/2,π/2], [0.17,0.53]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.42,0.43,0.49)ej(π/2,π/2,π/2)) | (([0.04,0.56]ej[π/2,π/2], [0.12,0.5]ej[π/2,π/2], [0.2,0.51]ej[π/2,π/2]), (0.45,0.44,0.46)ej(π/2,π,π)) | |
| F15 | (([0.12,0.72]ej[π/2,π/2], [0.13,0.5]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.41,0.36,0.3)ej(π/2,π/2,π/2)) | (([0.15,0.68]ej[π/2,π/2], [0.14,0.41]ej[π/2,π/2], [0.2,0.49]ej[π/2,π/2]), (0.49,0.3,0.3)ej(π/2,π/2,π/2)) | |
| F16 | (([0.10,0.81]ej[π/2,π/2], [0.19,0.5]ej[π/2,π/2], [0.21,0.45]ej[π/2,π/2]), (0.5,0.4,0.5)ej(π/2,π,π)) | (([0.1,0.69]ej[π/2,π/2], [0.35,0.8]ej[π/2,π/2], [0.4,0.81]ej[π/2,π/2]), (0.36,0.71,0.51)ej(π/2,π/2,π/2)) | |
| Partition | Attribute | Z3 | Z4 |
| O1 | F1 | (([0.1,0.5]ej[π/2,π/2], [0.42,0.68]ej[π/2,π/2], [0.34,0.7]ej[π/2,π/2]), (0.3,0.62,0.45)ej(π/2,π/2,π/2)) | (([0.24,0.78]ej[π/3,π/2], [0.13,0.4]ej[π/2,π/2], [0.2,0.4]ej[π/2,π/2]), (0.55,0.25,0.35)ej(π/2,π/2,π/2)) |
| F2 | ([0.13,0.7]ej[π/3,π/2], [0.29,0.71]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.45,0.50,0.4)ej(π/3,π/2,π)) | (([0.2,0.7]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2], [0.2,0.55]ej[π/2,π/2]), (0.50,0.4,0.4)ej(π/2,π/2,π/2)) | |
| F3 | (([0.14,0.74]ej[π/2,π], [0.26,0.68]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.4,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.22,0.71]ej[π/3,π/2], [0.25,0.72]ej[π/2,π/2], [0.2,0.7]ej[π/2,π/2]), (0.46,0.50,0.5)ej(π/2,π/2,π/2)) | |
| F4 | (([0.1,0.8]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.50,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.20,0.78]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.5,0.39,0.4)ej(π/2,π/2,π)) | |
| O2 | F5 | (([0.06,0.66]ej[π/2,π/2], [0.4,0.79]ej[π/2,π/2], [0.35,0.7]ej[π/2,π/2]), (0.4,0.54,0.4)ej(π/2,π/2,π/2)) | (([0.36,0.78]ej[π/2,π/2], [0.23,0.59]ej[π/2,π/2], [0.24,0.6]ej[π/2,π/2]), (0.6,0.43,0.36)ej(π/3,π/2,π/2)) |
| F6 | (([0.05,0.85]ej[π/2,π], [0.25,0.58]ej[π/2,π/2], [0.22,0.45]ej[π/2,π]), (0.45,0.34,0.3)ej(π/2,π/2,π/2)) | (([0.2,0.8]ej[π/3,π/2], [0.32,0.73]ej[π/2,π/2], [0.31,0.66]ej[π/2,π/2]), (0.45,0.43,0.34)ej(π/2,π/2,π/2)) | |
| F7 | (([0.02,0.68]ej[π/2,π/2], [0.4,0.65]ej[π/2,π/2], [0.5,0.6]ej[π/2,π/2]), (0.4,0.5,0.45)ej(π/2,π/2,π)) | (([0.21,0.86]ej[π/2,π/2], [0.13,0.45]ej[π/2,π/2], [0.14,0.42]ej[π/2,π/2]), (0.53,0.34,0.3)ej(π/2,π/2,π/2)) | |
| F8 | (([0.06,0.6]ej[π/2,π], [0.3,0.7]ej[π/2,π/2], [0.33,0.67]ej[π/2,π/2]), (0.4,0.62,0.56)ej(π/2,π/2,π)) | (([0.17,0.78]ej[π/3,π/2], [0.23,0.5]ej[π/2,π/2], [0.22,0.63]ej[π/2,π/2]), (0.5,0.4,0.33)ej(π/2,π/2,π/2)) | |
| O3 | F9 | (([0.08,0.76]ej[π/3,π/2], [0.18,0.57]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.45,0.37,0.2)ej(π/2,π/2,π/2)) | (([0.13,0.81]ej[π/3,π/2], [0.27,0.64]ej[π/2,π/2], [0.23,0.64]ej[π/2,π/2]), (0.41,0.42,0.5)ej(π/2,π/2,π/2)) |
| F10 | (([0.1,0.8]ej[π/2,π], [0.12,0.51]ej[π/2,π/2], [0.12,0.5]ej[π/2,π/2]), (0.44,0.54,0.54)ej(π/2,π,π)) | (([0.2,0.83]ej[π/2,π/2], [0.23,0.7]ej[π/2,π/2], [0.27,0.74]ej[π/2,π/2]), (0.53,0.31,0.4)ej(π/2,π,π)) | |
| F11 | (([0.04,0.74]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.31,0.69]ej[π/2,π/2]), (0.39,0.5,0.3)ej(π/2,π/2,π/2)) | (([0.3,0.84]ej[π/2,π], [0.16,0.54]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.55,0.35,0.45)ej(π/2,π/2,π/2)) | |
| F12 | (([0.11,0.52]ej[π/2,π], [0.43,0.82]ej[π/2,π/2], [0.2,0.7]ej[π/2,π/2]), (0.35,0.69,0.53)ej(π/2,π/2,π/2)) | (([0.19,0.64]ej[π/2,π/2], [0.29,0.7]ej[π/2,π/2], [0.32,0.75]ej[π/2,π/2]), (0.44,0.48,0.32)ej(π/2,π,π)) | |
| O4 | F13 | ([0.05,0.7]ej[π/3,π/2], [0.22,0.69]ej[π/2,π/2], [0.34,0.6]ej[π/2,π/2], (0.41,0.47,0.45)ej(π/2,π/2,π/2)) | ([0.22,0.89]ej[π/2,π/2], [0.22,0.47]ej[π/2,π/2], [0.26,0.4]ej[π/2,π/2], (0.5,0.3,0.4)ej(π/2,π/2,π/2)) |
| F14 | (([0.06,0.67]ej[π/2,π/2], [0.21,0.63]ej[π/2,π/2], [0.20,0.65]ej[π/2,π/2]), (0.42,0.40,0.39)ej(π/2,π/2,π/2)) | (([0.2,0.7]ej[π/2,π/2], [0.19,0.49]ej[π/2,π/2], [0.26,0.6]ej[π/2,π/2]), (0.49,0.28,0.34)ej(π/2,π/2,π/2)) | |
| F15 | (([0.08,0.8]ej[π/2,π/2], [0.15,0.57]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.46,0.35,0.4)ej(π/2,π/2,π/2)) | (([0.19,0.76]ej[π/2,π/2], [0.22,0.65]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.45,0.41,0.32)ej(π/2,π/2,π/2)) | |
| F16 | (([0.09,0.42]ej[π/3,π/2], [0.51,0.8]ej[π/2,π/2], [0.42,0.71]ej[π/2,π/2]), (0.21,0.71,0.76)ej(π/2,π/2,π/2)) | (([0.18,0.5]ej[π/2,π/2], [0.45,0.8]ej[π/2,π/2], [0.4,0.6]ej[π/2,π/2]), (0.21,0.76,0.4)ej(π/2,π,π)) |
| Partition | Attribute | Z1 | Z2 |
|---|---|---|---|
| O1 | F1 | (([0.15,0.62]ej[π/2,π/2], [0.4,0.78]ej[π/2,π/2], [0.35,0.68]ej[π/2,π/2]), (0.3,0.56,0.5)ej(π/2,π/2,π)) | (([0.16,0.56]ej[π/2,π/2], [0.38,0.75]ej[π/2,π/2], [0.41,0.78]ej[π/2,π/2]), (0.36,0.51,0.44)ej(π/2,π/2,π/2)) |
| F2 | (([0.25,0.78]ej[π/2,π/2], [0.26,0.67]ej[π/2,π/2], [0.26,0.76]ej[π/2,π/2]), (0.35,0.36,0.56)ej(π/2,π/2,π/2)) | (([0.23,0.72]ej[π/2,π/2], [0.21,0.65]ej[π/2,π/2], [0.31,0.67]ej[π/2,π/2]), (0.45,0.44,0.47)ej(π/2,π/2,π/2)) | |
| F3 | (([0.2,0.5]ej[π/3,π/2], [0.12,0.4]ej[π/3,π/2], [0.1,0.4]ej[π/3,π/2]), (0.58,0.30,0.4)ej(π/2,π/2,π/2)) | (([0.21,0.72]ej[π/2,π/2], [0.23,0.7]ej[π/2,π/2], [0.33,0.7]ej[π/2,π/2]), (0.46,0.44.0,94)ej(π/2,π/2,π/2)) | |
| F4 | (([0.2,0.80]ej[π/2,π/2], [0.25,0.68]ej[π/2,π/2], [0.21,0.62]ej[π/2,π/2]), (0.5,0.43,0.4)ej(π/2,π/2,π/2)) | (([0.25,0.82]ej[π/2,π/2], [0.22,0.67]ej[π/2,π/2], [0.24,0.63]ej[π/2,π/2]), (0.58,0.49,0.44)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.04,0.68]ej[π/2,π/2], [0.25,0.72]ej[π/2,π/2], [0.21,0.67]ej[π/2,π/2]), (0.39,0.50,0.54)ej(π/2,π/2,π)) | (([0.06,0.70]ej[π/2,π/2], [0.26,0.61]ej[π/2,π/2], [0.34,0.72]ej[π/2,π/2]), (0.34,0.50,0.54)ej(π/2,π/2,π/2)) |
| F6 | (([0.03,0.81]ej[π/3,π/2], [0.14,0.51]ej[π/2,π/2], [0.21,0.45]ej[π/2,π/2]), (0.43,0.43,0.49)ej(π/2,π/2,π/2)) | (([0.05,0.82]ej[π/2,π/2], [0.1,0.44]ej[π/2,π/2], [0.21,0.5]ej[π/2,π/2]), (0.46,0.29,0.3)ej(π/2,π/2,π/2)) | |
| F7 | (([0.05,0.62]ej[π/2,π/2], [0.4,0.79]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.33,0.58,0.55)ej(π/2,π/2,π/2)) | (([0.01,0.69]ej[π/2,π/2], [0.31,0.72]ej[π/2,π/2], [0.27,0.63]ej[π/2,π/2]), (0.37,0.54,0.46)ej(π/2,π/2,π/2)) | |
| F8 | (([0.1,0.81]ej[π/2,π], [0.19,0.6]ej[π/2,π/2], [0.20.6]ej[π/2,π/2]), (0.46,0.39,0.45)ej(π/2,π/2,π/2)) | (([0.21,0.70]ej[π/2,π/2], [0.30,0.71]ej[π/2,π/2], [0.32,0.6]ej[π/2,π/2]), (0.45,0.54,0.4)ej(π/2,π/2,π/2)) | |
| O3 | F9 | (([0.04,0.72]ej[π/2,π/2], [0.23,0.66]ej[π/2,π/2], [0.21,0.62]ej[π/2,π/2]), (0.42,0.41,0.3)ej(π/2,π/2,π/2)) | (([0.09,0.84]ej[π/2,π/2], [0.15,0.54]ej[π/2,π/2], [0.21,0.55]ej[π/2,π/2]), (0.49,0.3,0.4)ej(π/2,π/2,π/2)) |
| F10 | (([0.03,0.78]ej[π/2,π/2], [0.2,0.5]ej[π/3,π/2], [0.24,0.54]ej[π/3,π/2]), (0.42,0.34,0.42)ej(π/2,π/2,π/2)) | (([0.05,0.81]ej[π/2,π/2], [0.13,0.41]ej[π/2,π/2], [0.21,0.56]ej[π/2,π/2]), (0.49,0.38,0.31)ej(π/2,π/2,π/2)) | |
| F11 | (([0.05,0.76]ej[π/2,π/2], [0.18,0.58]ej[π/2,π/2], [0.21,0.45]ej[π/2,π/2]), (0.45,0.39,0.35)ej(π/2,π,π)) | (([0.09,0.82]ej[π/2,π/2], [0.12,0.45]ej[π/3,π/2], [0.21,0.56]ej[π/3,π/2]), (0.41,0.32,0.3)ej(π/2,π/2,π/2)) | |
| F12 | (([0.23,0.72]ej[π/2,π], [0.21,0.69]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.5,0.47,0.38)ej(π/2,π/2,π/2)) | (([0.15,0.7]ej[π/2,π/2], [0.21,0.61]ej[π/2,π/2], [0.34,0.50]ej[π/2,π/2]), (0.53,0.43,0.3)ej(π/2,π/2,π/2)) | |
| O4 | F13 | (([0.03,0.7]ej[π/2,π/2], [0.21,0.6]ej[π/2,π/2], [0.33,0.61]ej[π/2,π/2]), (0.41,0.45,0.38)ej(π/2,π,π)) | (([0.05,0.73]ej[π/2,π/2], [0.29,0.5]ej[π/2,π/2], [0.21,0.56]ej[π/2,π/2)], (0.41,0.39,0.3)ej(π/2,π/2,π/2)) |
| F14 | (([0.04,0.86]ej[π/2,π/2], [0.13,0.51]ej[π/2,π/2], [0.22,0.56]ej[π/2,π/2]), (0.41,0.39,0.35)ej(π/2,π/2,π/2)) | (([0.07,0.8]ej[π/2,π/2], [0.12,0.45]ej[π/2,π/2], [0.21,0.51]ej[π/2,π/2]), (0.49,0.23,0.26)ej(π/2,π,π)) | |
| F15 | (([0.05,0.8]ej[π/2,π/2], [0.14,0.5]ej[π/2,π/2], [0.21,0.6]ej[π/2,π/2]), (0.4,0.39,0.31)ej(π/2,π/2,π/2)) | (([0.1,0.83]ej[π/2,π/2], [0.12,0.5]ej[π/2,π/2], [0.25,0.5]ej[π/2,π/2]), (0.41,0.41,0.4)ej(π/2,π/2,π/2)) | |
| F16 | (([0.10,0.59]ej[π/2,π/2], [0.19,0.51]ej[π/2,π/2], [0.21,0.58]ej[π/2,π/2]), (0.5,0.4,0.5)ej(π/2,π,π)) | (([0.07,0.51]ej[π/2,π/2], [0.42,0.71]ej[π/2,π/2], [0.43,0.6]ej[π/2,π/2]), (0.34,0.51,0.6)ej(π/2,π/2,π/2)) | |
| Partition | Attribute | Z3 | Z4 |
| O1 | F1 | (([0.11,0.58]ej[π/3,π/2], [0.34,0.39]ej[π/3,π/2], [0.34,0.4]ej[π/3,π/2]), (0.29,0.67,0.5)ej(π/3,π/2,π/2)) | (([0.21,0.83]ej[π/2,π/2], [0.2,0.59]ej[π/2,π/2], [0.23,0.6]ej[π/2,π/2]), (0.56,0.39,0.44)ej(π/2,π/2,π/2)) |
| F2 | (([0.09,0.54]ej[π/3,π/2], [0.21,0.61]ej[π/2,π/2], [0.23,0.67]ej[π/2,π/2]), (0.4,0.45,0.49)ej(π/3,π/2,π/2)) | (([0.23,0.6]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2),] (0.50,0.39,0.4)ej(π/2,π/2,π/2)) | |
| F3 | (([0.04,0.74]ej[π/2,π], [0.23,0.61]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.39,0.46,0.41)ej(π/2,π/2,π/2)) | (([0.26,0.71]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2], [0.23,0.77]ej[π/2,π/2]), (0.5,0.4,0.45)ej(π/2,π/2,π/2)) | |
| F4 | (([0.12,0.67]ej[π/2,π/2], [0.24,0.67]ej[π/2,π/2], [0.23,0.7]ej[π/2,π/2]), (0.45,0.46,0.4)ej(π/2,π/2,π/2)) | (([0.23,0.81]ej[π/2,π/2], [0.2,0.59]ej[π/2,π/2], [0.22,0.6]ej[π/2,π/2]), (0.51,0.39,0.4)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.04,0.66]ej[π/2,π], [0.38,0.75]ej[π/2,π/2], [0.34,0.67]ej[π/2,π/2]), (0.33,0.51,0.44)ej(π/2,π/2,π/2)) | (([0.26,0.78]ej[π/2,π/2], [0.21,0.6]ej[π/2,π/2], [0.22,0.65]ej[π/2,π/2]), (0.54,0.42,0.39)ej(π/2,π/2,π/2)) |
| F6 | (([0.05,0.8]ej[π/2,π], [0.15,0.53]ej[π/2,π/2], [0.22,0.5]ej[π/2,π/2]), (0.45,0.34,0.3)ej(π/2,π/2,π/2)) | (([0.21,0.78]ej[π/2,π/2], [0.22,0.63]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.49,0.43,0.4)ej(π/2,π/2,π/2)) | |
| F7 | (([0.03,0.65]ej[π/2,π/2], [0.1,0.57]ej[π/2,π/2], [0.19,0.6]ej[π/2,π/2]), (0.31,0.52,0.43)ej(π/2,π/2,π/2)) | (([0.39,0.87]ej[π/2,π/2], [0.33,0.47]ej[π/2,π/2], [0.19,0.49]ej[π/2,π/2]), (0.52,0.27,0.34)ej(π/2,π/2,π/2)) | |
| F8 | (([0.14,0.63]ej[π/2,π], [0.37,0.77]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.39,0.57,0.4)ej(π/2,π/2,π/2)) | (([0.2,0.8]ej[π/3,π/2], [0.15,0.56]ej[π/2,π/2], [0.21,0.56]ej[π/2,π/2]), (0.51,0.38,0.4)ej(π/2,π/2,π)) | |
| O3 | F9 | (([0.06,0.8]ej[π/2,π/2], [0.2,0.54]ej[π/2,π/2], [0.23,0.56]ej[π/2,π/2]), (0.4,0.39,0.27)ej(π/2,π/2,π/2)) | (([0.18,0.8]ej[π/2,π/2], [0.23,0.6]ej[π/2,π/2], [0.21,0.62]ej[π/2,π/2]), (0.4,0.41,0.43)ej(π/2,π/2,π/2)) |
| F10 | (([0.12,0.83]ej[π/2,π], [0.16,0.54]ej[π/2,π/2], [0.21,0.53]ej[π/2,π/2]), (0.43,0.36,0.43)ej(π/2,π/2,π/2)) | (([0.2,0.8]ej[π/2,π/2], [0.19,0.56]ej[π/2,π/2], [0.25,0.58]ej[π/2,π/2]), (0.51,0.41,0.44)ej(π/2,π/2,π/2)) | |
| F11 | (([0.04,0.71]ej[π/2,π/2], [0.22,0.65]ej[π/2,π/2], [0.32,0.61]ej[π/2,π/2]), (0.32,0.48,0.34)ej(π/2,π/2,π/2)) | (([0.28,0.87]ej[π/2,π], [0.2,0.54]ej[π/2,π/2], [0.27,0.6]ej[π/2,π/2]), (0.59,0.36,0.42)ej(π/2,π/2,π/2)) | |
| F12 | (([0.08,0.54]ej[π/2,π], [0.3,0.7]ej[π/2,π/2], [0.4,0.76]ej[π/2,π/2]), (0.33,0.45,0.5)ej(π/2,π/2,π/2)) | (([0.18,0.72]ej[π/2,π/2], [0.21,0.69]ej[π/2,π/2], [0.29,0.7]ej[π/2,π/2]), (0.41,0.5,0.37)ej(π/2,π,π)) | |
| O4 | F13 | (([0.06,0.71]ej[π/3,π/2], [0.28,0.61]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.42,0.5,0.4)ej(π/2,π/2,π/2)) | (([0.22,0.77]ej[π/2,π/2], [0.13,0.48]ej[π/2,π/2], [0.21,0.43]ej[π/2,π/2]), (0.5,0.3,0.4)ej(π/2,π/2,π/2)) |
| F14 | (([0.04,0.76]ej[π/2,π/2], [0.21,0.61]ej[π/2,π/2], [0.21,0.61]ej[π/2,π/2]), (0.32,0.40,0.34)ej(π/2,π/2,π/2)) | (([0.16,0.8]ej[π/2,π/2], [0.14,0.48]ej[π/2,π/2], [0.21,0.59]ej[π/2,π/2]), (0.47,0.3,0.3)ej(π/2,π/2,π/2)) | |
| F15 | (([0.07,0.82]ej[π/2,π/2], [0.16,0.59]ej[π/2,π/2], [0.26,0.63]ej[π/2,π/2]), (0.47,0.39,0.45)ej(π/2,π/2,π/2)) | (([0.19,0.7]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2], [0.31,0.65]ej[π/2,π/2]), (0.45,0.46,0.36)ej(π/2,π/2,π/2)) | |
| F16 | (([0.08,0.46]ej[π/3,π/2], [0.51,0.82]ej[π/2,π/2], [0.51,0.72]ej[π/2,π/2]), (0.3,0.72,0.7)ej(π/2,π/2,π/2)) | (([0.27,0.41]ej[π/2,π/2], [0.43,0.67]ej[π/2,π/2], [0.44,0.56]ej[π/2,π/2]), (0.2,0.51,0.45)ej(π/2,π,π)) |
| Partition | Attribute | Z1 | Z2 |
|---|---|---|---|
| O1 | F1 | (([0.1,0.56]ej[π/2,π], [0.13,0.5]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.36,0.56,0.51)ej(π/2,π,π)) | (([0.1,0.62]ej[π/2,π/2], [0.36,0.72]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.37,0.59,0.4)ej(π/2,π/2,π/2)) |
| F2 | (([0.19,0.77]ej[π/2,π/2], [0.27,0.69]ej[π/2,π/2], [0.23,0.7]ej[π/2,π/2]), (0.48,0.46,0.56)ej(π/2,π/2,π/2)) | (([0.3,0.72]ej[π/2,π/2], [0.25,0.66]ej[π/2,π/2], [0.32,0.71]ej[π/2,π/2]), (0.48,0.49,0.5)ej(π/2,π/2,π/2)) | |
| F3 | (([0.29,0.88]ej[π/3,π/2], [0.4,0.7]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.58,0.30,0.4)ej(π/2,π/2,π/2)) | (([0.15,0.6]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2], [0.1,0.67]ej[π/2,π/2]), (0.49,0.44.0,49)ej(π/2,π/2,π/2)) | |
| F4 | (([0.21,0.80]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2], [0.20,0.60]ej[π/2,π/2]), (0.46,0.40,0.38)ej(π/2,π/2,π/2)) | (([0.25,0.80]ej[π/2,π/2], [0.21,0.60]ej[π/2,π/2], [0.24,0.63]ej[π/2,π/2]), (0.54,0.41,0.47)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.07,0.75]ej[π/2,π/2], [0.28,0.73],ej[π/2,π/2], [0.21,0.72],ej[π/2,π/2]), (0.39,0.51,0.41)ej(π/2,π/2,π)) | (([0.06,0.70]ej[π/2,π/2], [0.25,0.71]ej[π/2,π/2], [0.23,0.67]ej[π/2,π/2]), (0.35,0.51,0.51)ej(π/2,π/2,π/2)) |
| F6 | (([0.04,0.82],ej[π/3,π/2], [0.15,0.52]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.44,0.3,0.4)ej(π/2,π/2,π/2)) | (([0.04,0.89]ej[π/2,π/2], [0.11,0.45]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.47,0.3,0.3)ej(π/2,π/2,π/2)) | |
| F7 | (([0.03,0.61]ej[π/2,π/2], [0.39,0.79]ej[π/2,π/2], [0.4,0.8]ej[π/2,π/2]), (0.33,0.58,0.6)ej(π/2,π/2,π/2)) | (([0.02,0.63]ej[π/2,π/2], [0.31,0.73]ej[π/2,π/2], [0.3,0.6]ej[π/2,π/2]), (0.35,0.52,0.4)ej(π/2,π/2,π/2)) | |
| F8 | (([0.02,0.81]ej[π/2,π], [0.19,0.59]ej[π/2,π/2], [0.21.64]ej[π/2,π/2]), (0.45,0.48,0.4)ej(π/2,π/2,π/2)) | (([0.02,0.73]ej[π/2,π/2], [0.23,0.71]ej[π/2,π/2], [0.31,0.58]ej[π/2,π/2]), (0.45,0.50,0.4)ej(π/2,π/2,π/2)) | |
| O3 | F9 | (([0.05,0.79]ej[π/2,π/2], [0.22,0.56]ej[π/2,π/2], [0.21,0.6]ej[π/2,π/2]), (0.43,0.41,0.34)ej(π/2,π/2,π/2)) | (([0.11,0.83]ej[π/2,π/2], [0.15,0.52]ej[π/2,π/2], [0.21,0.59]ej[π/2,π/2]), (0.44,0.32,0.41)ej(π/2,π/2,π/2)) |
| F10 | (([0.03,0.8]ej[π/2,π/2], [0.2,0.5]ej[π/3,π/2], [0.2,0.54]ej[π/3,π/2]), (0.4,0.35,0.45)ej(π/2,π/2,π/2)) | (([0.07,0.78]ej[π/2,π/2], [0.13,0.5]ej[π/2,π/2], [0.21,0.45]ej[π/2,π/2]), (0.42,0.38,0.33)ej(π/2,π/2,π/2)) | |
| F11 | (([0.05,0.81]ej[π/2,π/2], [0.16,0.55]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.48,0.4,0.43)ej(π/2,π,π)) | (([0.09,0.78]ej[π/2,π/2], [0.15,0.45]ej[π/3,π/2], [0.28,0.51]ej[π/3,π/2]), (0.5,0.41,0.3)ej(π/2,π/2,π/2)) | |
| F12 | (([0.11,0.78]ej[π/2,π], [0.29,0.62]ej[π/2,π/2], [0.2,0.61]ej[π/2,π/2], (0.5,0.4,0.25)ej(π/2,π/2,π/2)) | (([0.15,0.72]ej[π/2,π/2], [0.11,0.67]ej[π/2,π/2], [0.36,0.58]ej[π/2,π/2]), (0.54,0.40,0.3)ej(π/2,π/2,π/2)) | |
| O4 | F13 | (([0.03,0.7]ej[π/2,π/2], [0.21,0.72]ej[π/2,π/2], [0.31,0.61]ej[π/2,π/2]), (0.42,0.4,0.3)ej(π/2,π,π)) | (([0.04,0.67]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2], [0.21,0.67]ej[π/2,π/2]), (0.45,0.4,0.3)ej(π/2,π/2,π/2)) |
| F14 | (([0.05,0.83]ej[π/2,π/2], [0.16,0.62]ej[π/2,π/2], [0.22,0.51]ej[π/2,π/2]), (0.45,0.4,0.4)ej(π/2,π/2,π/2)) | (([0.05,0.67]ej[π/2,π/2], [0.15,0.52]ej[π/2,π/2], [0.21,0.55]ej[π/2,π/2]), (0.46,0.33,0.39)ej(π/2,π,π)) | |
| F15 | (([0.05,0.69]ej[π/2,π/2], [0.11,0.51]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.45,0.36,0.31)ej(π/2,π/2,π/2)) | (([0.11,0.83]ej[π/2,π/2], [0.17,0.42]ej[π/2,π/2], [0.21,0.56]ej[π/2,π/2]), (0.5,0.35,0.35)ej(π/2,π/2,π/2)) | |
| F16 | (([0.10,0.61]ej[π/2,π/2], [0.17,0.56]ej[π/2,π/2], [0.23,0.59]ej[π/2,π/2]), (0.5,0.34,0.5)ej(π/2,π,π)) | (([0.06,0.6]ej[π/2,π/2], [0.4,0.76]ej[π/2,π/2], [0.41,0.78]ej[π/2,π/2]), (0.34,0.65,0.5)ej(π/2,π/2,π/2)) | |
| Partition | Attribute | Z3 | Z4 |
| O1 | F1 | (([0.04,0.54]ej[π/2,π/2], [0.43,0.76]ej[π/2,π/2], [0.34,0.6]ej[π/2,π/2]), (0.24,0.29,0.3)ej(π/3,π/2,π/2)) | (([0.27,0.84]ej[π/3,π/2], [0.2,0.54]ej[π/2,π/2], [0.21,0.51]ej[π/2,π/2]), (0.61,0.32,0.34)ej(π/2,π/2,π/2)) |
| F2 | (([0.09,0.7]ej[π/3,π/2], [0.29,0.74]ej[π/2,π/2], [0.3,0.57]ej[π/2,π/2]), (0.5,0.50,0.4)ej(π/3,π/2,π/2)) | (([0.2,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.22,0.56]ej[π/2,π/2]), (0.54,0.4,0.39)ej(π/2,π/2,π/2)) | |
| F3 | (([0.03,0.73]ej[π/2,π], [0.26,0.66]ej[π/2,π/2], [0.3,0.7]ej[π/2,π/2]), (0.34,0.46,0.48)ej(π/2,π/2,π/2)) | (([0.26,0.78]ej[π/2,π/2], [0.23,0.71]ej[π/2,π/2], [0.31,0.67]ej[π/2,π/2]), (0.47,0.51,0.56)ej(π/2,π/2,π/2)) | |
| F4 | (([0.05,0.74]ej[π/2,π/2], [0.27,0.64]ej[π/2,π/2], [0.32,0.67]ej[π/2,π/2]), (0.46,0.46,0.5)ej(π/2,π/2,π/2)) | (([0.20,0.81]ej[π/2,π/2], [0.19,0.59]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.50,0.4,0.45)ej(π/2,π/2,π/2)) | |
| O2 | F5 | (([0.07,0.65]ej[π/2,π], [0.33,0.72]ej[π/2,π/2], [0.31,0.68]ej[π/2,π/2]), (0.36,0.52,0.41)ej(π/2,π/2,π/2)) | (([0.3,0.81]ej[π/2,π/2], [0.21,0.57]ej[π/2,π/2], [0.21,0.62]ej[π/2,π/2]), (0.56,0.42,0.38)ej(π/2,π/2,π/2)) |
| F6 | (([0.04,0.81]ej[π/2,π], [0.15,0.53]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2]), (0.45,0.34,0.3)ej(π/2,π/2,π/2)) | (([0.28,0.79]ej[π/2,π/2], [0.21,0.66]ej[π/2,π/2], [0.31,0.63]ej[π/2,π/2]), (0.47,0.42,0.48)ej(π/2,π/2,π/2)) | |
| F7 | (([0.02,0.63]ej[π/2,π/2], [0.31,0.72]ej[π/2,π/2], [0.26,0.69]ej[π/2,π/2]), (0.28,0.34,0.4)ej(π/2,π/2,π/2)) | (([0.23,0.82]ej[π/2,π/2], [0.14,0.47]ej[π/2,π/2], [0.15,0.45]ej[π/2,π/2]), (0.57,0.3,0.38)ej(π/2,π/2,π/2)) | |
| F8 | (([0.04,0.63]ej[π/2,π], [0.37,0.77]ej[π/2,π/2], [0.33,0.68]ej[π/2,π/2]), (0.49,0.54,0.4)ej(π/2,π/2,π/2)) | (([0.18,0.81]ej[π/3,π/2], [0.18,0.56]ej[π/2,π/2], [0.2,0.6]ej[π/2,π/2]), (0.49,0.37,0.43)ej(π/2,π/2,π)) | |
| O3 | F9 | (([0.07,0.67]ej[π/2,π/2], [0.2,0.57]ej[π/2,π/2], [0.21,0.69]ej[π/2,π/2]), (0.46,0.38,0.22)ej(π/2,π/2,π/2)) | (([0.1,0.73]ej[π/2,π/2], [0.23,0.63]ej[π/2,π/2], [0.26,0.63]ej[π/2,π/2]), (0.41,0.41,0.32)ej(π/2,π/2,π/2)) |
| F10 | (([0.10,0.81]ej[π/2,π], [0.16,0.59]ej[π/2,π/2], [0.21,0.55]ej[π/2,π/2]), (0.44,0.54,0.4)ej(π/2,π/2,π/2)) | (([0.2,0.80]ej[π/2,π/2], [0.16,0.42]ej[π/2,π/2], [0.22,0.58]ej[π/2,π/2]), (0.54,0.39,0.43)ej(π/2,π/2,π/2)) | |
| F11 | (([0.06,0.7]ej[π/2,π/2], [0.22,0.6]ej[π/2,π/2], [0.3,0.54]ej[π/2,π/2]), (0.4,0.47,0.39)ej(π/2,π/2,π/2)) | (([0.22,0.81]ej[π/2,π], [0.14,0.5]ej[π/2,π/2], [0.21,0.63]ej[π/2,π/2]), (0.54,0.4,0.41)ej(π/2,π/2,π/2)) | |
| F12 | (([0.12,0.5]ej[π/2,π], [0.41,0.81]ej[π/2,π/2], [0.41,0.56]ej[π/2,π/2]), (0.31,0.61,0.45)ej(π/2,π/2,π/2)) | (([0.11,0.71]ej[π/2,π/2], [0.45,0.63]ej[π/2,π/2], [0.41,0.61]ej[π/2,π/2]), (0.45,0.43,0.36)ej(π/2,π,π)) | |
| O4 | F13 | (([0.05,0.76]ej[π/3,π/2], [0.24,0.61]ej[π/2,π/2], [0.4,0.7]ej[π/2,π/2]), (0.40,0.36,0.3)ej(π/2,π/2,π/2)) | (([0.2,0.8]ej[π/2,π/2], [0.2,0.5]ej[π/2,π/2], [0.3,0.5]ej[π/2,π/2]), (0.52,0.3,0.49)ej(π/2,π/2,π/2)) |
| F14 | (([0.05,0.67]ej[π/2,π/2], [0.21,0.61]ej[π/2,π/2], [0.20,0.62]ej[π/2,π/2]), (0.43,0.40,0.43)ej(π/2,π/2,π/2)) | (([0.19,0.8]ej[π/2,π/2], [0.34,0.45]ej[π/2,π/2], [0.22,0.75]ej[π/2,π/2]), (0.4,0.3,0.37)ej(π/2,π/2,π/2)) | |
| F15 | (([0.07,0.81]ej[π/2,π/2], [0.17,0.52]ej[π/2,π/2], [0.21,0.68]ej[π/2,π/2]), (0.5,0.3,0.4)ej(π/2,π/2,π/2)) | (([0.36,0.71]ej[π/2,π/2], [0.25,0.61]ej[π/2,π/2], [0.31,0.7]ej[π/2,π/2]), (0.45,0.46,0.35)ej(π/2,π/2,π/2)) | |
| F16 | (([0.08,0.5]ej[π/3,π/2], [0.5,0.78]ej[π/2,π/2], [0.51,0.67]ej[π/2,π/2]), (0.3,0.71,0.7)ej(π/2,π/2,π/2)) | (([0.23,0.41]ej[π/2,π/2], [0.51,0.8]ej[π/2,π/2], [0.49,0.7]ej[π/2,π/2]), (0.28,0.71,0.4)ej(π/2,π,π)) |
| Partition | Attribute | Z1 | Z2 |
|---|---|---|---|
| O1 | F1 | (([0.24,0.84]ej2π[0.25,0.3], [0.18,0.49]ej2π[0.06,0.1], [0.17,0.46]ej2π[0.06,0.06]), (0.63,0.31,0.26)ej2π(0.25,0.11,0.13)) | (([0.26,0.85]ej2π[0.25,0.25], [0.19,0.48]ej2π[0.06,0.06], [0.2,0.51]ej2π[0.06,0.06]), (0.66,0.3,0.2)ej2π(0.25,0.1,0.1)) |
| F2 | (([0.43,0.9]ej2π[0.25,0.25], [0.12,0.37]ej2π[0.06,0.06], [0.11,0.43]ej2π[0.06,0.06]), (0.71,0.22,0.31)ej2π(0.25,0.1,0.06)) | (([0.46,0.91]ej2π[0.25,0.25], [0.11,0.38]ej2π[0.06,0.06], [0.15,0.42]ej2π[0.06,0.06]), (0.76,0.23,0.23)ej2π(0.25,0.06,0.09)) | |
| F3 | (([0.48,0.86]ej2π[0.18,0.25], [0.14,0.37]ej2π[0.06,0.06], [0.07,0.43]ej2π[0.06,0.06]), (0.85,0.14,0.2)ej2π(0.25,0.1,0.1)) | (([0.380.91]ej2π[0.25,0.25], [0.12,0.38]ej2π[0.06,0.06], [0.15,0.42]ej2π[0.06,0.06]), (0.77,0.22,0.68)ej2π(0.25,0.06,0.06)) | |
| F4 | (([0.34,0.95]ej2π[0.25,0.25], [0.1,0.35]ej2π[0.06,0.06], [0.1,0.33]ej2π[0.06,0.06]), (0.77,0.21,0.18)ej2π(0.25,0.06,0.06)) | (([0.5,0.94]ej2π[0.25,0.26], [0.1,0.35]ej2π[0.06,0.06], [0.1,0.34]ej2π[0.06,0.06]), (0.8,0.22,0.21)ej2π(0.25,0.06,0.06)) | |
| O2 | F5 | (([0.11,0.91]ej2π[0.25,0.25], [0.13,0.42]ej2π[0.06,0.06], [0.1,0.4]ej2π[0.06,0.1]), (0.68,0.26,0.24)ej2π(0.25,0.06,0.13)) | (([0.13,0.91]ej2π[0.25,0.25], [0.13,0.4]ej2π[0.06,0.06], [0.15,0.42]ej2π[0.06,0.1]), (0.65,0.25,0.25)ej2π(0.25,0.06,0.1)) |
| F6 | (([0.06,0.95]ej2π[0.18,0.25], [0.07,0.26]ej2π[0.06,0.06], [0.11,0.24]ej2π[0.06,0.06]), (0.72,0.18,0.22)ej2π(0.25,0.06,0.06)) | (([0.10.96]ej2π[0.25,0.25], [0.06,0.22]ej2π[0.06,0.06], [0.1,0.27]ej2π[0.06,0.06]), (0.76,0.14,0.14)ej2π(0.25,0.06,0.1)) | |
| F7 | (([0.08,0.87]ej2π[0.25,0.25], [0.19,0.51]ej2π[0.06,0.06], [0.2,0.51]ej2π[0.06,0.1]), (0.62,0.3,0.3)ej2π(0.25,0.06,0.06)) | (([0.03,0.89]ej2π[0.25,0.25], [0.15,0.43]ej2π[0.06,0.06], [0.14,0.34]ej2π[0.06,0.06]), (0.65,0.27,0.2)ej2π(0.25,0.06,0.06)) | |
| F8 | (([0.06,0.95]ej2π[0.25,0.4], [0.11,0.32]ej2π[0.06,0.06], [0.09,0.33]ej2π[0.06,0.1]), (0.76,0.21,0.21)ej2π(0.25,0.06,0.06)) | (([0.06,0.91]ej2π[0.25,0.25], [0.15,0.42]ej2π[0.06,0.06], [0.15,0.35]ej2π[0.06,0.1]), (0.76,0.26,0.21)ej2π(0.25,0.06,0.06)) | |
| O3 | F9 | (([0.08,0.93]ej2π[0.25,0.4], [0.1,0.33]ej2π[0.06,0.06], [0.1,0.32]ej2π[0.06,0.1]), (0.71,0.2,0.15)ej2π(0.25,0.06,0.06)) | (([0.2,0.96]ej2π[0.25,0.4], [0.07,0.27]ej2π[0.06,0.06], [0.1,0.28]ej2π[0.06,0.06]), (0.76,0.15,0.2)ej2π(0.25,0.06,0.06)) |
| F10 | (([0.05,0.94]ej2π[0.25,0.25], [0.09,0.26]ej2π[0.05,0.06], [0.1,0.26]ej2π[0.04,0.06]), (0.7,0.17,0.2)ej2π(0.25,0.1,0.1)) | (([0.12,0.95]ej2π[0.25,0.25], [0.06,0.22]ej2π[0.06,0.06], [0.1,0.25]ej2π[0.06,0.06]), (0.75,0.18,0.16)ej2π(0.25,0.1,0.1)) | |
| F11 | (([0.09,0.94]ej2π[0.25,0.25], [0.08,0.3]ej2π[0.06,0.06], [0.1,0.25]ej2π[0.06,0.06]) (0.75,0.19,0.19)ej2π(0.25,0.13,0.13)) | (([0.21,0.95]ej2π[0.22,0.25], [0.06,0.23]ej2π[0.04,0.06], [0.11,0.27]ej2π[0.04,0.06]) (0.74,0.16,0.14)ej2π(0.25,0.06,0.06)) | |
| F12 | (([0.15,0.92]ej2π[0.25,0.4], [0.12,0.36]ej2π[0.06,0.06], [0.1,0.33]ej2π[0.06,0.06]), (0.77,0.23,0.16)ej2π(0.25,0.06,0.06)) | (([0.32,0.92]ej2π[0.25,0.25], [0.1,0.35]ej2π[0.06,0.06], [0.15,0.28]ej2π[0.06,0.06]), (0.81,0.19,0.15)ej2π(0.25,0.06,0.1)) | |
| O4 | F13 | (([0.07,0.92]ej2π[0.25,0.25], [0.1,0.36]ej2π[0.06,0.06], [0.16,0.31]ej2π[0.06,0.06]) (0.71,0.21,0.17)ej2π(0.25,0.13,0.13)) | (([0.08,0.92]ej2π[0.25,0.25], [0.11,0.29]ej2π[0.06,0.06], [0.1,0.33]ej2π[0.06,0.06]) (0.72,0.2,0.14)ej2π(0.25,0.06,0.06)) |
| F14 | (([0.1,0.96]ej2π[0.25,0.25], [0.07,0.31]ej2π[0.06,0.06], [0.1,0.29]ej2π[0.06,0.06]), (0.72,0.19,0.2)ej2π(0.25,0.06,0.06)) | (([0.1,0.89]ej2π[0.25,0.25], [0.06,0.25]ej2π[0.06,0.06], [0.1,0.27]ej2π[0.06,0.06]), (0.75,0.17,0.19)ej2π(0.25,0.13,0.13)) | |
| F15 | (([0.12,0.93]ej2π[0.25,0.25], [0.07,0.27]ej2π[0.06,0.06], [0.09,0.32]ej2π[0.06,0.06]), (0.71,0.18,0.14)ej2π(0.25,0.06,0.06)) | (([0.24,0.94]ej2π[0.25,0.25], [0.07,0.23]ej2π[0.06,0.06], [0.1,0.26]ej2π[0.06,0.06]), (0.75,0.17,0.17)ej2π(0.25,0.06,0.06)) | |
| F16 | (([0.22,0.88]ej2π[0.25,0.25], [0.08,0.27]ej2π[0.06,0.06], [0.1,0.29]ej2π[0.06,0.06]), (0.78,0.18,0.24)ej2π(0.25,0.13,0.13)) | (([0.15,0.84]ej2π[0.25,0.25], [0.19,0.49]ej2π[0.06,0.06], [0.2,0.49]ej2π[0.06,0.06]), (0.63,0.36,0.28)ej2π(0.25,0.06,0.06)) | |
| Partition | Attribute | Z3 | Z4 |
| O1 | F1 | (([0.11,0.81]ej2π[0.21,0.25], [0.21,0.48]ej2π[0.06,0.06], [0.17,0.41]ej2π[0.06,0.06]), (0.53,0.34,0.23)ej2π(0.18,0.06,0.06)) | (([0.48,0.95]ej2π[0.19,0.25], [0.08,0.28]ej2π[0.06,0.06], [0.1,0.28]ej2π[0.06,0.06]), (0.84,0.16,0.19)ej2π(0.25,0.06,0.06)) |
| F2 | (([0.21,0.87]ej2π[0.18,0.25], [0.13,0.42]ej2π[0.06,0.06], [0.13,0.38]ej2π[0.06,0.06]), (0.73,0.25,0.22)ej2π(0.18,0.06,0.1)) | (([0.44,0.9]ej2π[0.25,0.25], [0.09,0.32]ej2π[0.06,0.06], [0.11,0.31]ej2π[0.06,0.06]), (0.79,0.19,0.19)ej2π(0.25,0.06,0.06)) | |
| F3 | (([0.08,0.92]ej2π[0.25,0.4], [0.12,0.37]ej2π[0.06,0.06], [0.14,0.41]ej2π[0.06,0.06]), (0.67,0.23,0.21)ej2π(0.25,0.06,0.06)) | (([0.5,0.92]ej2π[0.22,0.25], [0.13,0.41]ej2π[0.06,0.06], [0.13,0.43]ej2π[0.06,0.06]), (0.76,0.24,0.26)ej2π(0.25,0.06,0.06)) | |
| F4 | (([0.15,0.92]ej2π[0.25,0.25], [0.12,0.37]ej2π[0.06,0.06], [0.14,0.4]ej2π[0.06,0.06]), (0.76,0.23,0.21)ej2π(0.25,0.06,0.06)) | (([0.44,0.95]ej2π[0.25,0.25], [0.09,0.32]ej2π[0.06,0.06], [0.1,0.32]ej2π[0.06,0.06]), (0.79,0.19,0.21)ej2π(0.25,0.06,0.09)) | |
| O2 | F5 | (([0.11,0.89]ej2π[0.25,0.31], [0.18,0.46]ej2π[0.06,0.06], [0.16,0.4]ej2π[0.06,0.06]), (0.64,0.27,0.21)ej2π(0.25,0.06,0.06)) | (([0.52,0.94]ej2π[0.25,0.25], [0.1,0.31]ej2π[0.06,0.06], [0.1,0.34]ej2π[0.06,0.06]), (0.83,0.21,0.18)ej2π(0.22,0.06,0.06)) |
| F6 | (([0.1,0.95]ej2π[0.25,0.4], [0.09,0.28]ej2π[0.06,0.06], [0.1,0.25]ej2π[0.06,0.06]), (0.74,0.16,0.14)ej2π(0.25,0.06,0.06)) | (([0.44,0.94]ej2π[0.22,0.25], [0.12,0.38]ej2π[0.06,0.06], [0.14,0.34]ej2π[0.06,0.06]), (0.76,0.21,0.2)ej2π(0.25,0.06,0.06)) | |
| F7 | (([0.03,0.88]ej2π[0.25,0.25], [0.16,0.4]ej2π[0.06,0.06], [0.19,0.37]ej2π[0.06,0.06]), (0.59,0.25,0.21)ej2π(0.25,0.06,0.1)) | (([0.37,0.97]ej2π[0.25,0.25], [0.12,0.23]ej2π[0.06,0.06], [0.08,0.23]ej2π[0.06,0.06]), (0.81,0.14,0.16)ej2π(0.25,0.06,0.06)) | |
| F8 | (([0.1,0.87]ej2π[0.25,0.4], [0.17,0.45]ej2π[0.06,0.06], [0.15,0.4]ej2π[0.06,0.06]), (0.7,0.31,0.23)ej2π(0.25,0.06,0.1)) | (([0.37,0.95]ej2π[0.18,0.25], [0.09,0.29]ej2π[0.06,0.06], [0.1,0.32]ej2π[0.06,0.06]), (0.81,0.14,0.16)ej2π(0.25,0.06,0.12)) | |
| O3 | F9 | (([0.15,0.92]ej2π[0.25,0.25], [0.09,0.3]ej2π[0.06,0.06], [0.1,0.35]ej2π[0.06,0.06]), (0.7,30.18,0.11)ej2π(0.25,0.06,0.06)) | (([0.18,0.94]ej2π[0.25,0.25], [0.12,0.34]ej2π[0.06,0.06], [0.11,0.34]ej2π[0.06,0.06]), (0.7,0.2,0.21)ej2π(0.25,0.06,0.09)) |
| F10 | (([0.23,0.95]ej2π[0.25,0.4], [0.07,0.28]ej2π[0.06,0.06], [0.09,0.27]ej2π[0.06,0.06]), (0.74,0.24,0.23)ej2π(0.25,0.1,0.1)) | (([0.41,0.95]ej2π[0.25,0.25], [0.09,0.33]ej2π[0.06,0.06], [0.11,0.36]ej2π[0.06,0.06]), (0.7,0.2,0.21)ej2π(0.25,0.1,0.1)) | |
| F11 | (([0.1,0.92]ej2π[0.25,0.25], [0.11,0.36]ej2π[0.06,0.06], [0.15,0.36]ej2π[0.06,0.06]), (0.65,0.24,0.16)ej2π(0.25,0.06,0.06)) | (([0.1,0.96]ej2π[0.25,0.4], [0.17,0.27]ej2π[0.06,0.06], [0.15,0.33]ej2π[0.06,0.06]), (0.83,0.18,0.21)ej2π(0.25,0.06,0.06)) | |
| F12 | (([0.21,0.8]ej2π[0.25,0.4], [0.2,0.53]ej2π[0.06,0.06], [0.2,0.45]ej2π[0.06,0.06]), (0.61,0.35,0.25)ej2π(0.25,0.06,0.06)) | (([0.3,0.91]ej2π[0.25,0.25], [0.17,0.39]ej2π[0.06,0.06], [0.16,0.4]ej2π[0.06,0.06]), (0.73,0.24,0.17)ej2π(0.25,0.13,0.13)) | |
| O4 | F13 | (([0.11,0.92]ej2π[0.18,0.25], [0.12,0.36]ej2π[0.06,0.06], [0.17,0.36]ej2π[0.06,0.06]), (0.7,0.23,0.23)ej2π(0.25,0.06,0.06)) | (([0.19,0.95]ej2π[0.25,0.25], [0.08,0.24]ej2π[0.06,0.06], [0.12,0.22]ej2π[0.06,0.06]), (0.8,0.14,0.21)ej2π(0.25,0.06,0.06)) |
| F14 | (([0.11,0.91]ej2π[0.25,0.25], [0.1,0.33]ej2π[0.06,0.06], [0.1,0.34]ej2π[0.06,0.06]), (0.66,0.19,0.18)ej2π(0.25,0.06,0.06)) | (([0.19,0.94]ej2π[0.25,0.25], [0.12,0.24]ej2π[0.06,0.06], [0.11,0.37]ej2π[0.06,0.06]), (0.74,0.14,0.16)ej2π(0.25,0.06,0.06)) | |
| F15 | (([0.16,0.95]ej2π[0.25,0.25], [0.07,0.3]ej2π[0.06,0.06], [0.11,0.35]ej2π[0.06,0.06]), (0.76,0.17,0.21)ej2π(0.25,0.06,0.06)) | (([0.28,0.92]ej2π[0.25,0.25], [0.12,0.37]ej2π[0.06,0.06], [0.14,0.4]ej2π[0.06,0.06]), (0.74,0.22,0.17)ej2π(0.25,0.06,0.06)) | |
| F16 | (([0.18,0.75]ej2π[0.18,0.25], [0.26,0.56]ej2π[0.06,0.06], [0.25,0.41]ej2π[0.06,0.06]), (0.51,0.42,0.43)ej2π(0.25,0.06,0.06)) | (([0.22,0.73]ej2π[0.25,0.25], [0.25,0.56]ej2π[0.06,0.06], [0.2,20.37]ej2π[0.06,0.06]), (0.45,0.41,0.21)ej2π(0.25,0.13,0.13)) |
References
- Liu, X.; Wu, X.; Zhang, W. A New DEA Model and Its Application in Performance Evaluation of Scientific Research Activities in the Universities of China’s Double First-Class Initiative. Socioecon. Plan. Sci. 2024, 92, 101839. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, M.; Yin, P.; Liang, L. Performance Evaluation of Scientific Research System in Chinese Universities: A View of Goal Congruence. Socioecon. Plan. Sci. 2023, 87, 101548. [Google Scholar] [CrossRef]
- Dong, B.; Wang, Y.; Chen, B.; Zhang, R.; Zhang, S. Sustainable Development of Industry-Specific Universities in China under the “Double First-Class” Initiative: A Niche Perspective. Sustainability 2025, 17, 5736. [Google Scholar] [CrossRef]
- Cabras, I.; Goumagias, N.D.; Fernandes, K.; Cowling, P.; Li, F.; Kudenko, D.; Devlin, S.; Nucciarelli, A. Exploring Survival Rates of Companies in the UK Video-Games Industry: An Empirical Study. Technol. Forecast. Soc. Change 2017, 117, 305–314. [Google Scholar] [CrossRef]
- Suh, Y.; Woo, C.; Koh, J.; Jeon, J. Analysing the Satisfaction of University–Industry Cooperation Efforts Based on the Kano Model: A Korean Case. Technol. Forecast. Soc. Change 2019, 148, 119740. [Google Scholar] [CrossRef]
- Meissner, D.; Zhou, Y.; Fischer, B.; Vonortas, N. A Multilayered Perspective on Entrepreneurial Universities: Looking into the Dynamics of Joint University-Industry Labs. Technol. Forecast. Soc. Change 2022, 178, 121573. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R. Pythagorean Membership Grades in Multicriteria Decision Making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized Orthopair Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Abosuliman, S.S.; Abdullah, S.; Qiyas, M. Three-Way Decisions Making Using Covering Based Fractional Orthotriple Fuzzy Rough Set Model. Mathematics 2020, 8, 1121. [Google Scholar] [CrossRef]
- Qiyas, M.; Naeem, M.; Khan, N. Fractional Orthotriple Fuzzy Choquet-Frank Aggregation Operators and Their Application in Optimal Selection for EEG of Depression Patients. AIMS Math. 2023, 8, 6323–6355. [Google Scholar] [CrossRef]
- Zang, Y.; Sun, Y.; Wen, Y.; Miao, J. Fractional Orthotriple Fuzzy Dombi Power Partitioned Muirhead Mean Operators and Their Application for Evaluating the Government Information Disclosure on Public Health Emergencies. Systems 2023, 11, 451. [Google Scholar] [CrossRef]
- Qiyas, M.; Khan, N.; Karabasevic, D.; Alvi, M.L. Decision Support Model under the Fractional Orthotriple Fuzzy Information. Eng. Appl. Artif. Intell. 2025, 144, 110114. [Google Scholar] [CrossRef]
- Zhou, X.; Deng, Y.; Huang, Z.; Yan, F.; Li, W. Complex Cubic Fuzzy Aggregation Operators with Applications in Group Decision-Making. IEEE Access 2020, 8, 223869–223888. [Google Scholar] [CrossRef]
- Ramot, D.; Milo, R.; Friedman, M.; Kandel, A. Complex Fuzzy Sets. IEEE Trans. Fuzzy Syst. 2002, 10, 171–186. [Google Scholar] [CrossRef]
- Bustince, H.; Barrenechea, E.; Pagola, M.; Fernandez, J. Interval-Valued Fuzzy Sets Constructed from Matrices: Application to Edge Detection. Fuzzy Sets Syst. 2009, 160, 1819–1840. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, J.; Li, X. A Hybrid Method for Pythagorean Fuzzy Multiple-Criteria Decision Making. Int. J. Inf. Technol. Decis. Making 2016, 15, 403–422. [Google Scholar] [CrossRef]
- Jin, L.; Mesiar, R.; Senapati, T.; Jana, C.; Ma, C.; García-Zamora, D.; Yager, R.R. Ordered Weighted Geometric Averaging Operators for Basic Uncertain Information. Inf. Sci. 2024, 663, 120275. [Google Scholar] [CrossRef]
- Yager, R.R. On Ordered Weighted Averaging Aggregation Operators in Multicriteria Decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Güler, M.; Büyüközkan, G. Cybersecurity Maturity Assessment Using an Incomplete Hesitant Fuzzy AHP Method and Bonferroni Means Operator. Expert Syst. Appl. 2025, 282, 127268. [Google Scholar] [CrossRef]
- Thilagavathy, A.; Mohanaselvi, S. T-Spherical Fuzzy TOPSIS Method Based on Distance Measures and Hamacher Heronian Mean Averaging Aggregation Operators and Its Application to Waste Management. Appl. Soft Comput. 2024, 162, 111868. [Google Scholar] [CrossRef]
- Muirhead, R.F. Some Methods Applicable to Identities and Inequalities of Symmetric Algebraic Functions of n Letters. Proc. Edinburgh Math. Soc. 1902, 21, 144–162. [Google Scholar] [CrossRef]
- Yang, Z.; Li, X.; He, P. A Decision Algorithm for Selecting the Design Scheme for Blockchain-Based Agricultural Product Traceability System in q-Rung Orthopair Fuzzy Environment. J. Cleaner Prod. 2021, 290, 125191. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Scott, P.J.; Jiang, X. Multi-Criteria Group Decision Making Based on Archimedean Power Partitioned Muirhead Mean Operators of q-Rung Orthopair Fuzzy Numbers. PLoS ONE 2019, 14, e0221759. [Google Scholar] [CrossRef]
- Dombi, J. A General Class of Fuzzy Operators, the Demorgan Class of Fuzzy Operators and Fuzziness Measures Induced by Fuzzy Operators. Fuzzy Sets Syst. 1982, 8, 149–163. [Google Scholar] [CrossRef]
- Jana, C.; Senapati, T.; Pal, M.; Yager, R.R. Picture Fuzzy Dombi Aggregation Operators: Application to MADM Process. Appl. Soft Comput. 2019, 74, 99–109. [Google Scholar] [CrossRef]
- Deveci, M.; Pamucar, D.; Gokasar, I.; Pedrycz, W.; Wen, X. Autonomous Bus Operation Alternatives in Urban Areas Using Fuzzy Dombi-Bonferroni Operator Based Decision Making Model. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15714–15723. [Google Scholar] [CrossRef]
- Liu, P.; Shen, J.; Zhang, P. Multi-Attribute Group Decision-Making Method Using Single-Valued Neutrosophic Credibility Numbers with the Dombi Extended Power Aggregation Operator and Its Application in Intelligent Transportation System Data Collection Scheme Selection. Eng. Appl. Artif. Intell. 2024, 133, 108639. [Google Scholar] [CrossRef]
- Zang, Y.; Zhao, J.; Jiang, W.; Zhao, T. Advanced Linguistic Complex T-Spherical Fuzzy Dombi-Weighted Power-Partitioned Heronian Mean Operator and Its Application for Emergency Information Quality Assessment. Sustainability 2024, 16, 3069. [Google Scholar] [CrossRef]
- Więckowski, J.; Kizielewicz, B.; Shekhovtsov, A.; Sałabun, W. RANCOM: A Novel Approach to Identifying Criteria Relevance Based on Inaccuracy Expert Judgments. Eng. Appl. Artif. Intell. 2023, 122, 106114. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean Fuzzy MCDM Method Based on CoCoSo and CRITIC with Score Function for 5G Industry Evaluation. Artif. Intell. Rev. 2020, 53, 3813–3847. [Google Scholar] [CrossRef]
- Yang, S.; Pan, Y.; Zeng, S. Decision Making Framework Based Fermatean Fuzzy Integrated Weighted Distance and TOPSIS for Green Low-Carbon Port Evaluation. Eng. Appl. Artif. Intell. 2022, 114, 105048. [Google Scholar] [CrossRef]
- Gou, X.; Xu, Z.; Herrera, F. Consensus Reaching Process for Large-Scale Group Decision Making with Double Hierarchy Hesitant Fuzzy Linguistic Preference Relations. Knowl. Based Syst. 2018, 157, 20–33. [Google Scholar] [CrossRef]
- dos Santos, B.M.; Godoy, L.P.; Campos, L.M.S. Performance Evaluation of Green Suppliers Using Entropy-TOPSIS-F. J. Clean. Prod. 2019, 207, 498–509. [Google Scholar] [CrossRef]
- Tajik, M.; Makui, A.; Tosarkani, B.M. Sustainable Cathode Material Selection in Lithium-Ion Batteries Using a Novel Hybrid Multi-Criteria Decision-Making. J. Energy Storage 2023, 66, 107089. [Google Scholar] [CrossRef]
- Naz, S.; Tasawar, A.; Fatima, A.; Butt, S.A.; Gonzalez, Z.C. An Efficient 2-Tuple Linguistic Cubic q-Rung Orthopair Fuzzy CILOS-TOPSIS Method: Evaluating the Hydrological Geographical Regions for Watershed Management in Pakistan. J. Supercomput. 2025, 81, 103. [Google Scholar] [CrossRef]
- Das, A. Water Pollution and Water Quality Assessment and Application of Criterion Impact Loss (CILOS), Geographical Information System (GIS), Artificial Neural Network (ANN) and Decision-Learning Technique in River Water Quality Management: An Experiment on the Mahanadi Catchment, Odisha, India. Desalin. Water Treat. 2025, 321, 100969. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Podvezko, V. Integrated Determination of Objective Criteria Weights in MCDM. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 267–283. [Google Scholar] [CrossRef]
- Heidary Dahooie, J.; Raafat, R.; Qorbani, A.R.; Daim, T. An Intuitionistic Fuzzy Data-Driven Product Ranking Model Using Sentiment Analysis and Multi-Criteria Decision-Making. Technol. Forecast. Soc. Chang. 2021, 173, 121158. [Google Scholar] [CrossRef]
- Ali, T.; Aghaloo, K.; Chiu, Y.-R.; Ahmad, M. Lessons Learned from the COVID-19 Pandemic in Planning the Future Energy Systems of Developing Countries Using an Integrated MCDM Approach in the off-Grid Areas of Bangladesh. Renew. Energy 2022, 189, 25–38. [Google Scholar] [CrossRef]
- Liu, P.; Shen, M.; Wu, X.; Yu, L. Probabilistic Double Hierarchy Linguistic Risk Analysis Based on Failure Mode and Effects Analysis and S-ARAS Method. Inf. Sci. 2023, 648, 119608. [Google Scholar] [CrossRef]
- Yager, R.R. The Power Average Operator. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 2001, 31, 724–731. [Google Scholar] [CrossRef]
- Dill, D.D.; Soo, M. Academic Quality, League Tables, and Public Policy: A Cross-National Analysis of University Ranking Systems. High. Educ. 2005, 49, 495–533. [Google Scholar] [CrossRef]
- Mayerle, S.F.; Rodrigues, H.F.; Neiva De Figueiredo, J.; De Genaro Chiroli, D.M. Optimal Student/School/Class/Teacher/Classroom Matching to Support Efficient Public School System Resource Allocation. Socioecon. Plan. Sci. 2022, 83, 101341. [Google Scholar] [CrossRef]
- Mussard, M.; James, A.P. Engineering the Global University Rankings: Gold Standards, Limitations and Implications. IEEE Access 2018, 6, 6765–6776. [Google Scholar] [CrossRef]
- Hendel, D.D.; Stolz, I. A Comparative Analysis of Higher Education Ranking Systems in Europe. Tert. Educ. Manag. 2008, 14, 173–189. [Google Scholar] [CrossRef]
- Li, J.; Xue, E. A Social Networking Analysis of Education Policies of Creating World-Class Universities for Higher Education Sustainability in China. Sustainability 2022, 14, 10243. [Google Scholar] [CrossRef]
- Zhao, Y.; He, F.; Feng, Y. Research on the Current Situation of Employment Mobility and Retention Rate Predictions of “Double First-Class” University Graduates Based on the Random Forest and BP Neural Network Models. Sustainability 2022, 14, 8883. [Google Scholar] [CrossRef]
- Abulibdeh, A.; Zaidan, E.; Abulibdeh, R. Navigating the Confluence of Artificial Intelligence and Education for Sustainable Development in the Era of Industry 4.0: Challenges, Opportunities, and Ethical Dimensions. J. Clean. Prod. 2024, 437, 140527. [Google Scholar] [CrossRef]
- Durrans, B.; Whale, J.; Calais, M. Benchmarking a Sustainable Energy Engineering Undergraduate Degree against Curriculum Frameworks and Pedagogy Standards from Industry and Academia. Energies 2020, 13, 822. [Google Scholar] [CrossRef]
- Bai, M.; Liu, Y.; Qi, M.; Roy, N.; Shu, C.; Khan, F.; Zhao, D. Current Status, Challenges, and Future Directions of University Laboratory Safety in China. J. Loss Prev. Process Ind. 2022, 74, 104671. [Google Scholar] [CrossRef]
- Nepeina, K.; Istomina, N.; Bykova, O. The Role of Field Training in STEM Education: Theoretical and Practical Limitations of Scalability. Eur. J. Investig. Health Psychol. Educ. 2020, 10, 511–529. [Google Scholar] [CrossRef]
- Jain, N.; Thomas, A.; Gupta, V.; Ossorio, M.; Porcheddu, D. Stimulating CSR Learning Collaboration by the Mentor Universities with Digital Tools and Technologies—An Empirical Study during the COVID-19 Pandemic. Manag. Decis. 2022, 60, 2824–2848. [Google Scholar] [CrossRef]
- Wang, C.; Wang, D. Managing the Integration of Teaching Resources for College Physical Education Using Intelligent Edge-Cloud Computing. J. Cloud Comput. Adv. Syst. Appl. 2023, 12, 82. [Google Scholar] [CrossRef]
- Al-Amri, A.S.; Mathew, P.; Zubairi, Y.Z.; Jani, R. Optimal Standards to Measure the Quality of Higher Education Institutions in Oman: Stakeholders’ Perception. SAGE Open 2020, 10, 2158244020947440. [Google Scholar] [CrossRef]
- Guan, J.; Zhao, Q. The Impact of University-Industry Collaboration Networks on Innovation in Nanobiopharmaceuticals. Technol. Forecast. Soc. Chang. 2013, 80, 1271–1286. [Google Scholar] [CrossRef]
- Wang, S.; Tang, L.; Chen, Z. The Impact of Policy Adoption of University-Affiliated Think Tanks on Economic Growth: A Fixed Effects Model Test Based on China’s Provincial Panel Data. High. Educ. Policy 2024, 37, 116–137. [Google Scholar] [CrossRef]
- Xue, E.; Tian, S.; Li, J. Doctoral Cultivation System and Mechanism of University Think Tank in China. Educ. Philos. Theory 2023, 55, 1464–1473. [Google Scholar] [CrossRef]
- Chang, S. Examining Key Technologies among Academic Patents through an Analysis of Standard-Essential Patents. SAGE Open 2022, 12, 21582440221114331. [Google Scholar] [CrossRef]
- Yan, M.; Wu, C. Soft Magnetic Composites with Enhanced Performance and Their Key Production Technologies. J. Zhejiang Univ. Sci. A 2017, 18, 163–166. [Google Scholar] [CrossRef]
- Cheng, Z.; Xiao, T.; Chen, C.; Xiong, X. Evaluation of Scientific Research in Universities Based on the Idea of Education for Sustainable Development. Sustainability 2022, 14, 2474. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Zhao, M.; Lai, X.; Chang, L.; Wang, Z. Efficiency of Higher Education Financial Resource Allocation from the Perspective of ‘Double First-Class’ Construction: A Three-Stage Global Super Slacks-Based Measure Analysis. Educ. Inf. Technol. 2024, 29, 12047–12075. [Google Scholar] [CrossRef]
- Yan, Z. Construction and Application of Vocational Training Platform for Enterprise Employees. Mob. Inf. Syst. 2022, 2022, 4091808. [Google Scholar] [CrossRef]
- López-Pérez, M.; Melero, I.; Sesé, F. Does Specific CSR Training for Managers Impact Shareholder Value? Implications for Education in Sustainable Development. Corp. Soc. Responsib. Environ. Manag. 2017, 24, 435–448. [Google Scholar] [CrossRef]
- Aoki, T.; Ito, K. What Is the Role of Universities in Disaster Response, Recovery, and Rehabilitation? Focusing on Our Disaster Victim Identification Project. IEEE Commun. Mag. 2014, 52, 30–37. [Google Scholar] [CrossRef]
- Mao, K.; Wang, J.; Li, L.; Zhang, Y.; Tian, W.; Su, G.; Qiu, S.; Corradini, M. Development of Cladding Oxidation Analysis Code [COAC] and Application for Early Stage Severe Accident Simulation of AP1000. Prog. Nucl. Energy 2015, 85, 352–365. [Google Scholar] [CrossRef]
- Yang, X.; You, Y. How the World-Class University Project Affects Scientific Productivity? Evidence from a Survey of Faculty Members in China. High. Educ. Policy 2018, 31, 583–605. [Google Scholar] [CrossRef]
- Anderson, T.R.; Daim, T.U.; Lavoie, F.F. Measuring the Efficiency of University Technology Transfer. Technovation 2007, 27, 306–318. [Google Scholar] [CrossRef]
- Gómez-Aguayo, A.; Azagra-Caro, J.; Benito-Amat, C. The Steady Effect of Knowledge Co-Creation with Universities on Business Scientific Impact throughout the Economic Cycle. Scientometrics 2024, 129, 2771–2799. [Google Scholar] [CrossRef]
- Greenhalgh, T.; Jackson, C.; Shaw, S.; Janamian, T. Achieving Research Impact through Co-Creation in Community-Based Health Services: Literature Review and Case Study. Milbank Q. 2016, 94, 392–429. [Google Scholar] [CrossRef]
- Fan, X.; Yang, X.; Chen, L. Diversified Resources and Academic Influence: Patterns of University-Industry Collaboration in Chinese Research-Oriented Universities. Scientometrics 2015, 104, 489–509. [Google Scholar] [CrossRef]
- Davey, T.; Martínez-Martínez, S.; Ventura, R.; Galán-Muros, V. The Creation of Academic Spin-Offs: University-Business Collaboration Matters. J. Technol. Transf. 2024, 50, 1567–1601. [Google Scholar] [CrossRef]
- Cai, Y. Towards a New Model of EU-China Innovation Cooperation: Bridging Missing Links between International University Collaboration and International Industry Collaboration. Technovation 2023, 119, 102553. [Google Scholar] [CrossRef]
- Heitor, M. How University Global Partnerships May Facilitate a New Era of International Affairs and Foster Political and Economic Relations. Technol. Forecast. Soc. Change 2015, 95, 276–293. [Google Scholar] [CrossRef]
- Ryan, J. Teaching and Learning for International Students: Towards a Transcultural Approach. Teach. Teach. 2011, 17, 631–648. [Google Scholar] [CrossRef]
- Shi-jin, W.; Gui-rong, J. Impact Mechanism of International Students’ Cultural Values on the Intention—Based on the Plan Behavior Theory in China. J. Knowl. Econ. 2024, 15, 383–407. [Google Scholar] [CrossRef]
- Zhou, J.; Mei, L.; Chen, J. Leveraging University Competitiveness: Evidence from Alliance Portfolio Practices at Zhejiang University. Emerg. Mark. Financ. Trade 2019, 55, 827–842. [Google Scholar] [CrossRef]
- Shin, J.; Li, X.; Byun, B.; Nam, I. Building a Coordination System of HRD, Research and Industry for Knowledge and Technology-Driven Economic Development in South Asia. Int. J. Educ. Dev. 2020, 74, 102161. [Google Scholar] [CrossRef]

| A non-empty finite set | A collection of alternatives | ||
| A set of non-negative real numbers | A group of attributes | ||
| The distance of and | A group of experts | ||
| Support of for | The weights of attributes | ||
| A vector of parameters | Weights of experts | ||
| b subregions | The initial assessment matrix | ||
| The number of arguments in the partition | The comprehensive assessment matrix | ||
| Complex cubic fractional orthotriple fuzzy number | The score matrix | ||
| The score function of | The attribute weights according to the entropy method | ||
| The accuracy function of | The attribute weights according to the CILOS method | ||
| The entropy of the j-th attribute | The ratio of the j-th attribute of the i-th alternative |
| Exclusion Indicator | Violated Standards | Specific Reasons |
|---|---|---|
| Industry fiscal resource investment [44] | Strong correlation with the assessment of first-class discipline construction in industry-characteristic universities | This indicator reflects the scale of resources rather than the effectiveness of their use, but first-class discipline construction in industry-characteristic universities emphasizes “output orientation” rather than input scale, and the correlation between the two is weak. |
| Industry teacher title structure [45] | Expert-assessed feasibility | The proportion of senior professional titles cannot directly reflect the quality of teaching staff, and experts find it difficult to quantify “structural rationality,” which can easily lead to the misconception of “focusing solely on titles.” |
| Industry recognition Academic reputation [46] | Expert-assessed feasibility | Relies on subjective impression surveys; experts may be subject to assessment bias due to differences in regional or disciplinary backgrounds, making it impossible to establish universal assessment standards. |
| Industry Student Satisfaction [47] | Frequency of occurrence ≥ 3 times | Only two documents mention this, and there is a lack of universal assessment value. |
| Construction Assessment for First-Class Disciplines | Talent Cultivation (O1) | Competitiveness of Graduates in Core Industry Positions (F1) | [48,49] |
| Industry Target Alignment (F2) | [50,51] | ||
| Industry Practice Platform Support (F3) | [52,53] | ||
| Industry–Academia Integration (F4) | [54,55] | ||
| Scientific Research (O2) | Industry Standards and Patent Value (F5) | [56,57] | |
| Industry Think-Tank Influence Strength (F6) | [58,59] | ||
| Contributions to Breakthroughs in Key Technologies in the Industry (F7) | [60,61] | ||
| Industry Innovation Platform Level (F8) | [62,63] | ||
| Social Service (O3) | High-End Training Brand in the Industry (F9) | [64,65] | |
| Adequacy of Emergency Service Response (F10) | [66,67] | ||
| Effectiveness of Technology Transfer (F11) | [68,69] | ||
| Industry Ecosystem Co-Construction Participation Rate (F12) | [70,71] | ||
| Open Education (O4) | International Rule-Making Authority (F13) | [72,73] | |
| Depth of International Cooperation (F14) | [74,75] | ||
| International Student Industry Suitability (F15) | [76,77] | ||
| Industry Resource Coordination Density (F16) | [78,79] |
| Parameter | Score Function Result | Ranking Result |
|---|---|---|
| Aggregation Operator | Ranking of Score Values | Ranking Result |
|---|---|---|
| CCFOFDWA | ||
| CCFOFDWG | ||
| CCFOFDWPAM | ||
| CCFOFDWPGM | ||
| CCFOFDWPBM | ||
| CCFOFDWPMSM | ||
| CCFOFDWPPMM |
| Aggregation Operator | Whether to Enhance the Flexibility | Whether to Consider Interrelationship of Both Attributes | Whether to Consider Interrelationship of Multiple Attributes | Whether to Reduce the Negative Effect | Whether to Consider Partitioning of Attributes |
|---|---|---|---|---|---|
| CCFOFDWA | Yes | No | No | No | No |
| CCFOFDWG | Yes | No | No | No | No |
| CCFOFDWPAM | Yes | No | No | No | Yes |
| CCFOFDWPGM | Yes | No | No | No | Yes |
| CCFOFDWPBM | Yes | Yes | No | No | Yes |
| CCFOFDWPMSM | Yes | Yes | Yes | No | Yes |
| CCFOFDWPPMM | Yes | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, Y.; Cui, K.; Li, S.; Li, X. Aggregation Operator and Its Application in Assessing First-Class Discipline Construction in Industry-Characteristic Universities. Fractal Fract. 2025, 9, 576. https://doi.org/10.3390/fractalfract9090576
Zang Y, Cui K, Li S, Li X. Aggregation Operator and Its Application in Assessing First-Class Discipline Construction in Industry-Characteristic Universities. Fractal and Fractional. 2025; 9(9):576. https://doi.org/10.3390/fractalfract9090576
Chicago/Turabian StyleZang, Yuqi, Kaijie Cui, Siyu Li, and Xingguo Li. 2025. "Aggregation Operator and Its Application in Assessing First-Class Discipline Construction in Industry-Characteristic Universities" Fractal and Fractional 9, no. 9: 576. https://doi.org/10.3390/fractalfract9090576
APA StyleZang, Y., Cui, K., Li, S., & Li, X. (2025). Aggregation Operator and Its Application in Assessing First-Class Discipline Construction in Industry-Characteristic Universities. Fractal and Fractional, 9(9), 576. https://doi.org/10.3390/fractalfract9090576






