An Innovative Projection Technique for Certain Fractional Differential Equations

Abstract

Fractional differential equations are commonly employed to characterize the long-term interactions of nonlinear systems, although they complicate inverse problems and numerical treatment. This article extends projection methods in order to numerically solve fractional differential equations. We propose a new projection approach for solving initial fractional problems based on the Jacobi weight function, employing a variety of generalized Jacobi polynomials with the indices $\sigma ,\rho \in \mathbb{R}$. This symmetry yields some intriguingly novel outcomes. The order of convergence for this method is given in appropriately weighted Sobolev spaces.

1. Introduction

Fractional differential and integral equations have become powerful tools for modeling real-world phenomena that exhibit characteristics such as memory, hereditary effects, and anomalous diffusion. These formulations have been successfully applied to describe complex physical systems, including those governed by continuous-time random walk (CTRW) theory, non-exponential relaxation processes in viscoelastic materials and dielectrics, and transport phenomena in media with fractal comb and grid structures. Additionally, fractional calculus has offered valuable insights into quantum mechanics, particularly in the development of fractional quantum models.

The authors of [1] developed a comprehensive method for fractional calculus specifically designed for physicists. Their work compiled a collection of accessible review papers that explore a wide range of applications for fractional derivatives across various fields of physics. In [2], the emphasis was on the latest advancements in the theory of fractional differential and fractional integro-differential equations. The authors presented various useful fractional calculus operators and provided valuable insights into both the theoretical and practical aspects of fractional calculus.

Recently, several researchers have employed the homotopy perturbation method to address a variety of nonlinear and linear functional problems [3,4,5]. In [6], the authors applied a numerical technique involving Jumarie’s derivative to investigate fractional differential equations. Additionally, the authors of [7,8,9] solved fractional differential equations using orthogonal functions, specifically the Legendre polynomials. They further extended fractional calculus to Legendre functions with fractional orders and explored the corresponding matrix operations.

Fractional differential equations are great for showing how complex systems change over time, especially when things do not follow simple rules. One interesting example is solitons. A new and exciting use of solitons is in tiny robots (see [10,11]).

A nonlinear fractional-order creep damage model for coal has been proposed, accurately capturing all creep stages based on experimental data from deep mining [12]. This model enhances long-term stability assessments in deep underground engineering. A new pulse transient method based on a fractional derivative model in fractal space has been developed to more accurately characterize coal permeability under stress [13]. This approach links microscale structure to macroscale flow behavior, improving understanding of non-Darcy flow in rock mechanics.

A more precise model for seepage flow involving fractional derivatives was examined in [14], where the author proposed a fractional partial differential equation to describe seepage flow in porous media. In [15], the authors developed a new integrable differential-difference equation.

The field of fractional differential equations (FDEs) has witnessed a surge in diverse solution methodologies, each presenting unique advantages and inherent limitations. For instance, [16] introduced the recurrent Laplace transform process, an iterative approach combined with the Laplace transform. While capable of yielding exact solutions for certain systems of fractional partial differential equations, the iterative nature of this technique can lead to significant computational overhead, convergence issues, or even instability when dealing with complex or highly nonlinear FDEs. Similarly, [17] extended the Haar wavelet operational matrix for solving fractional-order differential equations. However, wavelet-based methods often face challenges in selecting an optimal wavelet basis tailored to the specific FDE, and they can struggle with maintaining accuracy and efficiency at boundaries or for solutions with varying degrees of smoothness.

Another significant class of methods involves projection approaches, as exemplified by [18,19,20,21]. These works applied projection techniques, including Galerkin and Kulkarni-type approximations, to solve bounded operator equations in Hilbert spaces, particularly for integral and integro-differential equations with Cauchy kernels. While projection methods offer a robust theoretical framework for ensuring existence and uniqueness, their practical application to the broad spectrum of FDEs is often hindered by the crucial choice of appropriate basis functions within the chosen Hilbert space. Developing suitable basis functions that accurately capture the non-local and memory-dependent characteristics of fractional derivatives can be exceptionally challenging, especially for higher-dimensional problems or those involving complex geometries. Moreover, the computational expense associated with forming and solving the projected systems can become prohibitive as the complexity of the FDE increases.

Beyond these, other techniques have been explored. Ref. [22] utilized polynomial spline functions for approximate solutions, but splines can exhibit limitations in accurately capturing sharp transitions or highly oscillatory behavior common in FDEs, potentially leading to reduced accuracy or the need for a large number of basis functions. The analysis of existence for impulsive fractional stochastic differential equations in [23] employed evolution system theory and fixed-point theorems. While these theorems are invaluable for theoretical existence proofs, they often do not provide constructive methods for actually finding solutions, and their applicability is contingent on strict conditions that may not hold for all FDEs. Methods from local fractional calculus, applied in [24,25] for analytical solutions, are generally restricted to a very specific and limited class of problems where analytical solutions are feasible, leaving a vast majority of FDEs unaddressed by this approach.

More recently, research has gravitated toward numerical and approximation techniques. Refs. [26,27] investigated terminal-value problems using discretized collocation methods with piecewise polynomial spaces. While effective for obtaining numerical solutions, the accuracy and convergence rates of these methods are often critically dependent on the mesh grading and the order of the piecewise polynomials, making them sensitive to solution regularities and potentially leading to computational intensity for problems requiring fine meshes or higher-order approximations. Ref. [28] applied fixed-point theorems to inverse problems, again focusing on existence rather than direct solution construction. Ref. [29] extended collocation methods to nonlinear fractional systems, providing existence and uniqueness results. However, managing the unique non-local nature of fractional derivatives within a discretized framework remains a formidable challenge for these methods, especially in maintaining stability and accuracy over long time intervals or for highly nonlinear terms.

Further advancements include the numerical analysis of intermediate-value problems in [30] and the construction of operational fractal-fractional matrices based on orthonormal ultraspherical polynomials in [31]. Ref. [32] employed spectral methods (collocation and tau methods) with operational matrices based on Fibonacci polynomials for solving the nonlinear fractional Klein–Gordon equation. While operational matrices and spectral methods can achieve high levels of accuracy and convergence for smooth solutions, they often require transformations to a specific basis, which can complicate the interpretation of results in the original domain. Furthermore, their application can be constrained to specific problem geometries or boundary conditions, and the development of new operational matrices for every class of FDE can be labor-intensive.

Given these pervasive disadvantages across various methods—ranging from computational burdens and convergence issues in iterative and wavelet-based approaches to the restrictive nature of basis function choices in projection methods, the non-constructive aspect of fixed-point theorems, and the domain-specific limitations of spectral and analytical methods—there is a clear and compelling necessity to extend the projection approach. The inherent strength of projection methods lies in their rigorous mathematical foundation and their potential for systematic improvement through the selection of richer approximation spaces. By advancing these techniques, particularly in developing adaptive basis functions that better capture the non-local memory effects and complex behavior of FDEs, the projection approach can overcome many existing limitations. This extension promises a more robust, versatile, and computationally efficient framework for solving a wider array of challenging FDEs, moving beyond the current constraints of specific problem types or computational costs to deliver more generalizable and accurate solutions.

As previously emphasized, the development of efficient and innovative methods for analyzing fractional differential problems is of considerable importance. This paper contributes to the field by introducing a novel projection approach for solving fractional initial-value problems. The method is constructed using a family of generalized Jacobi polynomials with the indices $\sigma ,\rho \in \mathbb{R}$, providing a flexible and effective framework for the numerical treatment of such equations.

The new method is special because of how we build our solutions. Most works that solve these kinds of equations use regular mathematical tools, but we use a new kind called generalized Jacobi polynomials. This makes them more flexible and better at matching complicated solutions.

Because this special tool can adapt more easily, our method has the following advantages:

• More accurate: It gets closer to the exact solution, even when the solution has sharp changes or is not smooth.
• Faster: We can find good answers using less work or fewer steps.
• Better for hard problems: Some equations, especially fractional ones, are not easy for traditional methods. Our method works well for these hard problems and gives good solutions without spurious errors.

There are several main differences and improvements in our method. Most traditional methods use fixed and well-known building blocks like standard polynomials, for example, Legendre or Chebyshev polynomials. Our method is different. We use generalized Jacobi polynomials, which include special numbers denoted by $\sigma$ and $\rho$. These numbers can be any real value, not just simple integers. This gives us a lot more flexibility when building our solution. Moreover, this flexibility helps us get more accurate results, as follows:

• We need new rules: Since we are using more flexible building blocks, we cannot rely on existing mathematical rules. We have to develop new techniques for things like integration and projection.
• We must carefully choose the right $\sigma$ and $\rho$: Selecting the best values for each problem is very important. It is like having a big toolbox.
• We work in more complex spaces: Our method uses something called weighted Sobolev spaces. These are more advanced mathematical spaces than the simpler ones used in traditional methods. That makes the theoretical analysis, like proving convergence, more complex.

Our more flexible building blocks allow for better solutions, but they also require a more careful and advanced mathematical approach compared to traditional, more straightforward methods.

The current work primarily focuses on the development and convergence analysis of the extended projection method. However, we acknowledge that a more explicit discussion and, where feasible, numerical comparisons would significantly strengthen this manuscript:

• Comparison with spectral collocation methods: Spectral collocation methods are well-known for their high accuracy and exponential convergence rates for problems with smooth solutions. However, their efficiency can diminish for problems with non-smooth solutions or complex geometries, where they may exhibit Gibbs phenomena or require domain decomposition. Our projection method, while potentially having a lower order of convergence than spectral methods for highly smooth solutions, offers flexibility in handling discontinuities or lower-regularity solutions through the judicious choice of basis functions. We will include a discussion on the trade-offs between the two, particularly regarding solution regularity requirements and computational cost for achieving high accuracy.
• Comparison with finite difference methods: Finite difference methods (FDMs) are widely used due to their simplicity and ease of implementation. They are particularly robust for problems with complex boundary conditions and can be readily extended to multi-dimensional problems. However, FDMs typically exhibit algebraic convergence rates, which can necessitate a very fine mesh to achieve high accuracy, leading to significant computational expense, especially for fractional derivatives, which are non-local. By utilizing global or semi-global basis functions, our projection method often achieves higher accuracy for a given number of degrees of freedom, particularly for problems with smooth solutions. We will discuss how our method can offer better accuracy-to-computational-cost ratios for problems where high precision is critical.
• Comparison with the homotopy perturbation method (HPM): Homotopy methods, such as the HPM, are analytical or semi-analytical techniques that provide series solutions without linearization or small-parameter assumptions. They are particularly effective for solving nonlinear problems and can often provide insights into the analytical structure of the solution. The primary limitation of homotopy methods is that the convergence region of the series solution can be restricted, and obtaining higher-order approximations can become algebraically very intensive. Our projection method, being a numerical technique, does not face these convergence region limitations and can systematically achieve arbitrary levels of accuracy (dependent on computational resources) by increasing the number of basis functions. We will highlight how our method offers a reliable numerical alternative when the analytical convergence of homotopy methods is difficult to guarantee or extend.

This document is structured as follows. Section 2 discusses the important concepts of the generalized and Caputo derivatives, including the relevant properties of the family of generalized Jacobi polynomials with the indices $\sigma ,\rho \in \mathbb{R}$. Section 3 constructs the new projection method. Section 4 conducts convergence and error analysis of the approximate solution, while Section 5 illustrates some numerical examples. Section 6 provides the conclusions and some remarks.

2. Preliminaries

We examine fundamental vocabulary and mathematical notations pertinent to fractional calculus.

Let us denote the Euler gamma function by the symbol $\Gamma$, an essential component in fractional calculus theory.

We recall that the left-sided Riemann–Liouville fractional integral and fractional derivative of order $0<\mu <1$ are defined, respectively, as follows:

$$J_{{-1}_{+}}^{\mu }\phi \left(s\right):={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}{\int }_{-1}^s{\displaystyle \frac{\phi \left(\tau \right)}{{(s-\tau )}^{1-\mu }}}d\tau ,s>-1,$$

$$D_{-1_{+}}^{\mu }\phi \left(s\right):={\displaystyle \frac{1}{\Gamma (1-\mu )}}{\displaystyle \frac{d}{ds}}{\int }_{-1}^s{\displaystyle \frac{\phi \left(\tau \right)}{{(s-\tau )}^{\mu }}}d\tau ,$$

for any continuous function $\phi :(-1,\infty )\to \mathbb{R}$.

We note that the left Riemann–Liouville fractional integral can be reformulated in the following convolution form:

$$J_{{-1}_{+}}^{\mu }\phi \left(s\right)={\displaystyle \frac{1}{\Gamma \left(\mu \right)}}{\int }_{-1}^0{\displaystyle \frac{\phi \left(\tau \right)}{{(s-\tau )}^{1-\mu }}}d\tau +({\psi }_{\mu }★\phi )\left(s\right),$$

where

$${\psi }_{\mu }\left(s\right):=\left\{\begin{array}{cc}0\hfill & s\le 0,\hfill \\ {\displaystyle \frac{s^{\mu -1}}{\Gamma \left(\mu \right)}},\hfill & s>0.\hfill \end{array}\right.$$

We recall the relationship between the left Riemann–Liouville fractional integral and the left Riemann–Liouville fractional derivative as follows:

$$D_{{-1}_{+}}^{\mu }\phi \left(s\right)={\displaystyle \frac{d}{ds}}{J}_{{-1}_{+}}^{1-\mu }\phi \left(s\right),0<\mu <1.$$

$$J_{{-1}_{+}}^{\mu }{D}_{{-1}_{+}}^{\mu }\left(\phi \left(s\right)-\phi (-1)\right)=\phi \left(s\right)-\phi (-1).$$

The Caputo derivative of order $0<\mu <1$ is formulated as

$${}^{c}D_{{-1}_{+}}^{\mu }\varphi \left(s\right)=J_{{-1}_{+}}^{1-\mu }{\displaystyle \frac{d}{ds}}\varphi \left(s\right)={\displaystyle \frac{1}{\Gamma (1-\mu )}}{\int }_{-1}^s{(s-t)}^{-\mu }{\varphi }^{\prime }\left(t\right)dt,$$

for any absolutely continuous function $\varphi (.)$. So,

$${}^{c}D_{{-1}_{+}}^{\mu }\phi \left(s\right)=J_{{-1}_{+}}^{1-\mu }{\displaystyle \frac{d}{ds}}\phi \left(s\right),\mathrm{for\; all}s\in [-1,1];$$

The correspondence between the Riemann–Liouville and Caputo fractional derivatives for a continuous function $\phi$ is given by

$${}^{c}D_{{-1}_{+}}^{\mu }\phi \left(s\right)=D_{{-1}_{+}}^{\mu }(\phi \left(s\right)-\phi (-1)),0<\mu <1,\mathrm{for\; all}s\in [-1,1];$$

and

$${}^{c}D_{{-1}_{+}}^{\mu }\phi \left(s\right)=D_{-1_{+}}^{\mu }\left(\phi \left(s\right)-\sum _{p=0}^{m-1}{\displaystyle \frac{s^p}{p!}}{\phi }^{\left(p\right)}(-1)\right),m-1<\mu <m,\mathrm{for\; all}s\in [-1,1].$$

Lemma 1 

([33]). Let $\mu \in \mathbb{C}$ with $Re\left(\mu \right)>0$, and let $m=\left[Re\right(\mu \left)\right]+1$. If $\psi \in C^r[-1,1]$, then

$$\left(J_{{-1}_{+}}^{\mu }{}^{c}D_{{-1}_{+}}^{\mu }\right)\psi \left(s\right)=\psi \left(s\right)-\sum _{p=0}^{m-1}{\displaystyle \frac{1}{p!}}{(s+1)}^p{\psi }^{\left(p\right)}(-1),m-1<\mu <m,s>-1.$$

In [33], the authors explained the fundamental principles behind fractional differential equations.

3. A Novel Projection Approach for the Solution of Fractional Initial Problem

Recently, many authors have investigated boundary-value problems for fractional differential equations (see [34,35,36] and the references therein).

A fully discrete numerical approach to a time-dependent fractional-order diffusion equation with non-local quadratic nonlinearity was proposed in [37]. In [38], the authors presented a family of generalized Jacobi polynomials/functions with the indices $\sigma ,\rho \in \mathbb{R}$ that are orthogonal due to the related Jacobi weights and that acquire fundamental properties of classical Jacobi polynomials. In adequately weighted Sobolev spaces, the authors presented their fundamental approximation features.

The authors of [39] solved fractional differential equations (FDEs) using spectral methods of approximation, and they constructed a new class of generalized Jacobi functions (GJFs) that is essentially related to fractional calculus. In contrast, we provide a new projection method for solving fractional initial problems consisting of a set of extended Jacobi polynomials with the indices $\sigma ,\rho \in \mathbb{R}$ shown above.

Let ${\left(P_n\right)}_{n\ge 0}^{\sigma ,\rho }$ represent the sequence of standard Jacobi polynomials.

We recall that ${\left(P_n\right)}_{n\ge 0}^{\sigma ,\rho }$ are orthogonal with respect to the Jacobi weight function ${\omega }^{(\sigma ,\rho )}\left(s\right):={(1-s)}^{\sigma }{(1+s)}^{\rho }$, that is to say,

$${\int }_{-1}^1{\omega }^{(\sigma ,\rho )}\left(\tau \right)P_n^{\sigma ,\rho }\left(\tau \right)P_m^{\sigma ,\rho }\left(\tau \right)d\tau ={\gamma }_n^{\sigma ,\rho }{\delta }_{nm},$$

where

$${\gamma }_n^{\sigma ,\rho }:={\displaystyle \frac{2^{\sigma +\rho +1}\Gamma (n+\sigma +1)\Gamma (n+\rho +1)}{(2n+\sigma +\rho +1)n!\Gamma (n+\sigma +\rho +1)}}$$

is the normalization constant and ${\delta }_{nm}$ is the Dirac delta symbol.

In [39], the authors introduced the following generalized Jacobi functions:

$${}^{-1}G_n^{(\sigma ,-\rho )}\left(s\right):={(1+s)}^{\rho }{P}_n^{(\sigma ,\rho )}\left(s\right),\sigma \in \mathbb{R},\rho >-1.$$

Denoting by ${\varphi }_j^{(\sigma ,-\rho )}$ the corresponding normalized sequence.

We introduce the following inner product:

$${〈f,g〉}_{{\omega }^{(\sigma ,-\rho )}}:={\int }_{-1}^1{\omega }^{(\sigma ,-\rho )}\left(t\right)f\left(t\right)\overline{g\left(t\right)}dt,$$

and the following weighted space:

$${\mathcal{H}}_{{\omega }^{(\sigma ,-\rho )}}:=L_{{\omega }^{(\sigma ,-\rho )}}^2(\left[-1,1\right],\mathbb{C})=\left\{\phi :\left[-1,1\right]\to \mathbb{C},{\int }_{-1}^1{\omega }^{(\sigma ,-\rho )}\left(t\right){\left|\phi \left(t\right)\right|}^{2}dt<\infty \right\}.$$

Recall that $J_{{-1}_{+}}^{\mu }$ is compact from ${\mathcal{H}}_{{\omega }^{(\sigma ,-\rho )}}$ into itself.

Define the orthogonal projection ${\left({\pi }_n^{(\sigma ,-\rho )}\right)}_{n\ge 0}$ as follows:

$${\pi }_n^{(\sigma ,-\rho )}x:=\sum _{j=0}^{n-1}{〈x,{\varphi }_j^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}{\varphi }_j^{(\sigma ,-\rho )}.$$

We consider the following fractional initial problem:

$${}^{c}D_{{-1}_{+}}^{\mu }\phi \left(s\right)=\lambda \phi \left(s\right)+f\left(s\right),-1\le s\le 1,$$

(1)

$${\phi }^{\left(k\right)}(-1)=0,k=0,1,\dots ,r-1,0\le r-1<\mu <r.$$

According to Lemma 1, problem (1) reads as follows:

$$\phi \left(s\right)-\lambda J_{{-1}_{+}}^{\mu }\phi \left(s\right)=J_{{-1}_{+}}^{\mu }f\left(s\right),-1\le s\le 1.$$

(2)

The approximate problem is the following equation for ${\phi }_n$:

$${\phi }_n\left(s\right)=\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}{\phi }_n\left(s\right)+J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}f\left(s\right),-1\le s\le 1.$$

Theorem 1. 

The coefficients $x_p$ solve the following linear system:

$$\left(A_{n+r}-\lambda I\right)x_{n+r}=b_{n+r},$$

where $A_{n+r}(i,p)$ and $b_{n+r}\left(i\right)$, for all $i=0,\cdots ,n-1$, and $p=0,\cdots ,n+r-1$, are given by

$$\begin{array}{c}{A}_{n+r}(i,p):=\left[{\int }_{-1}^1{\omega }^{(\sigma ,-\rho )}{D}_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )}\left(\tau \right){\varphi }_i^{(\sigma ,-\rho )}\left(\tau \right)d\tau \right],\mathbb{R}\\ b_{n+r}\left(i\right):={\int }_{-1}^1{\omega }^{(\sigma ,-\rho )}f\left(\tau \right){\varphi }_i^{(\sigma ,-\rho )}\left(\tau \right)d\tau .\end{array}$$

Moreover,

$$\begin{array}{c}{A}_{n+r}(k,p):=D^k{\varphi }_p^{(\sigma ,-\rho )}(-1),k=n,\dots ,n+r-1,\\ b_{n+r}\left(k\right):=0,k=n,\dots ,n+r-1.\end{array}$$

Proof. 

We write

$${\phi }_n=\sum _{p=0}^{n+r-1}{x}_p{\varphi }_p^{(\sigma ,-\rho )}.$$

The $n+r$ unknowns $x_{n+r}\left(p\right)$ are the solutions of the following problem:

$$\sum _{p=0}^{n+r-1}{x}_p{\varphi }_p^{(\sigma ,-\rho )}=\lambda \sum _{p=0}^{n+r-1}{x}_p{J}_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}{\varphi }_p^{(\sigma ,-\rho )}+J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}f.$$

So,

$$\sum _{p=0}^{n+r-1}{x}_p{D}_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )}\left(s\right)-\lambda \sum _{p=0}^{n+r-1}{x}_p{\pi }_n^{(\sigma ,-\rho )}{\varphi }_p^{(\sigma ,-\rho )}\left(s\right)={\pi }_n^{(\sigma ,-\rho )}f\left(s\right).$$

But

$${\pi }_n^{(\sigma ,-\rho )}{\varphi }_p^{(\sigma ,-\rho )}={\varphi }_p^{(\sigma ,-\rho )}.$$

Hence,

$$\sum _{p=0}^{n+r-1}{x}_p{D}_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )}-\lambda \sum _{p=0}^{n+r-1}{x}_p{\varphi }_p^{(\sigma ,-\rho )}={\pi }_n^{(\sigma ,-\rho )}f,$$

and hence,

$$\sum _{p=0}^{n+r-1}{x}_p\left[D_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )}-\lambda {\varphi }_p^{(\sigma ,-\rho )}\right]=\sum _{j=0}^{n-1}{〈f,{\varphi }_j^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}{\varphi }_j^{(\sigma ,-\rho )}.$$

This shows that

$$\begin{array}{c}{\displaystyle \sum _{p=0}^{n+r-1}}{x}_p\left[{〈D_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )},{\varphi }_i^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}-\lambda {〈{\varphi }_p^{(\sigma ,-\rho )},{\varphi }_i^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}\right]\hfill \\ ={\displaystyle \sum _{j=0}^{n-1}}{〈f,{\varphi }_j^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}{〈{\varphi }_j^{(\sigma ,-\rho )},{\varphi }_i^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}.\hfill \end{array}$$

Thus,

$$\sum _{p=0}^{n+r-1}{x}_p\left[{〈D_{{-1}_{+}}^{\mu }{\varphi }_p^{(\sigma ,-\rho )},{\varphi }_i^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}-\lambda \right]={〈f,{\varphi }_i^{(\sigma ,-\rho )}〉}_{{\omega }^{(\sigma ,-\rho )}}.$$

Using the condition

$$\sum _{p=0}^{n+r-1}{x}_p{D}^k{\varphi }_p^{(\sigma ,-\rho )}(-1)=0,k=0,1,\dots r-1,$$

we get the desired result. □

4. Convergence and Error Analysis

Due to the compactness of $J_{{-1}_{+}}^{\mu }$, the theory proposed in [40,41] proves that, for sufficiently large n, the operator $I-\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}$ is invertible, and its inverse is uniformly bounded with respect to n.

For all $x\in \mathcal{H}$,

$$\underset{n\to \infty }{\lim }\parallel J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}x-J_{{-1}_{+}}^{\mu }x\parallel =0,$$

and since $J_{{-1}_{+}}^{\mu }$ is compact,

$$\underset{n\to \infty }{\lim }\parallel \left(J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}-J_{{-1}_{+}}^{\mu }\right)J_{{-1}_{+}}^{\mu }\parallel =0,\underset{n\to \infty }{\lim }\parallel \left(J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}-J_{{-1}_{+}}^{\mu }\right)J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}\parallel =0.$$

We define

$${\mathbb{B}}_{(\sigma ,\rho )}^m\left([-1,1]\right):=\left\{\phi \in {\mathcal{H}}_{{\omega }^{(\sigma ,-\rho )}},{}^{c}D_{0_{+}}^{\rho +\mathcal{l}}\phi \in {\mathcal{H}}_{{\omega }^{(\sigma +\rho +\mathcal{l},\mathcal{l})}}\right\}.$$

According to [39], the following estimate holds for some constant $\alpha >0$:

$${∥\psi -{\pi }_n\psi ∥}_{{\omega }^{(\sigma ,-\rho )}}\le \alpha n^{-\rho }\sqrt{{\displaystyle \frac{(n-m+1)!}{(n+m+1)!}}}{\parallel D_{0_{+}}^{\rho +m}\psi \parallel }_{{\omega }^{(\sigma +\rho +m,m)}},\mathrm{for\; all}\psi \in {\mathbb{B}}_{(\sigma ,\rho )}^m\left([-1,1]\right).$$

(3)

Theorem 2. 

There exists $C>0$ such that

$$\parallel {\phi }_n{-\phi \parallel }_{{\omega }^{(\sigma ,-\rho )}}\le C{n}^{-\rho }\sqrt{{\displaystyle \frac{(n-m+1)!}{(n+m+1)!}}}∥J_{{-1}_{+}}^{\mu }∥\left[\left|\lambda \right|\parallel D_{0_{+}}^{\rho +m}{\phi \parallel }_{{\omega }^{(\sigma +\rho +m,m)}}+{\parallel D_{0_{+}}^{\rho +m}f\parallel }_{{\omega }^{(\sigma +\rho +m,m)}}\right],$$

for all $f\in {\mathbb{B}}_{(\sigma ,\rho )}^m\left([-1,1]\right)$ and some $m>0$.

Proof. 

In fact,

$$\begin{array}{c}{\phi }_n-\phi =\left[{\left(I-\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}\right)}^{-1}{J}_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}f-{\left(I-\lambda J_{{-1}_{+}}^{\mu }\right)}^{-1}{J}_{{-1}_{+}}^{\mu }f\right]\hfill \\ +{\left(I-\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}\right)}^{-1}{J}_{{-1}_{+}}^{\mu }f-{\left(I-\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}\right)}^{-1}{J}_{{-1}_{+}}^{\mu }f\hfill \\ ={\left(I-\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}\right)}^{-1}\left[\left(J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}-J_{{-1}_{+}}^{\mu }\right)f+\left(\lambda J_{{-1}_{+}}^{\mu }{\pi }_n^{(\sigma ,-\rho )}-\lambda J_{{-1}_{+}}^{\mu }\right)\phi \right],\hfill \end{array}$$

so

$$\parallel {\phi }_n{-\phi \parallel }_{{\omega }^{(\sigma ,-\rho )}}\le C\left[\parallel J_{{-1}_{+}}^{\mu }\left({\pi }_n^{(\sigma ,-\rho )}-I\right){f\parallel }_{{\omega }^{(\sigma ,-\rho )}}+\left|\lambda \right|\parallel J_{{-1}_{+}}^{\mu }\parallel \parallel \left({\pi }_n^{(\sigma ,-\rho )}-I\right){\phi \parallel }_{{\omega }^{(\sigma ,-\rho )}}\right].$$

Using (3), the desired result follows. □

Here, an accurate selection of $\sigma$ and $\rho$ can significantly enhance accuracy and convergence, while suboptimal choices might reduce the method’s efficiency. The parameter $\lambda$ represents a coefficient in the FDE, often related to a reaction, growth, or decay term. Large positive or negative values of $\lambda$ can lead to stiff problems.

5. Numerical Examples

Example 1. 

We apply the proposed projection method to the following fractional initial problem:

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }\phi \left(s\right)=\lambda \phi \left(s\right)+f\left(s\right),-1\le s\le 1,$$

with the initial condition $\phi (-1)=0$. The exact solution is chosen as $\phi \left(s\right)={(s+1)}^3$. The basis parameters are fixed at $(\sigma ,\rho )=(1/2,1/2)$, meaning that the approximation space is spanned by the corresponding normalized Jacobi polynomials. A truncation number of $n=3$ (leading to a system of size $K=n+1=4$) is used, which is sufficient to exactly represent a degree-3 polynomial.

For each scenario, the function $f\left(s\right)$ is adjusted such that $\phi \left(s\right)={(s+1)}^3$ remains the exact solution:

$$f\left(s\right)={}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }{(s+1)}^3-\lambda {(s+1)}^3,$$

where

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }{(s+1)}^3={\displaystyle \frac{\Gamma (3+1)}{\Gamma (3-\mu +1)}}{(s+1)}^{3-\mu }.$$

We consider two scenarios to assess the robustness of the method by varying μ and λ.

5.1. Scenario 1: Varying $\mu$ (Fixed $\lambda =1.0$)

In this scenario, we fix $\lambda =1.0$ and examine the method’s performance for two different fractional orders: $\mu =0.5$ and $\mu =0.8$.

Case 1. 

$\mu =0.5,\lambda =1.0$

For $\mu =0.5$,

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.5}{(s+1)}^3={\displaystyle \frac{\Gamma \left(4\right)}{\Gamma \left(3.5\right)}}{(s+1)}^{2.5}={\displaystyle \frac{16}{5\sqrt{\pi }}}{(s+1)}^{5/2}.$$

Thus,

$$f\left(s\right)={\displaystyle \frac{16}{5\sqrt{\pi }}}{(s+1)}^{5/2}-{(s+1)}^3.$$

Case 2. 

$\mu =0.8,\lambda =1.0$

For $\mu =0.8$, ${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.8}{(s+1)}^3={\displaystyle \frac{\Gamma \left(4\right)}{\Gamma \left(3.2\right)}}{(s+1)}^{2.2}$. Thus, $f\left(s\right)={\displaystyle \frac{6}{\Gamma \left(3.2\right)}}{(s+1)}^{2.2}-{(s+1)}^3$.

5.2. Scenario 2: Varying $\lambda$ (Fixed $\mu =0.5$)

In this scenario, we fix $\mu =0.5$ and examine the method’s performance for two different values of $\lambda$: $\lambda =1.0$ and $\lambda =0.5$.

Case 3. 

$\mu =0.5,\lambda =1.0$

This is identical to Case 1, with $f\left(s\right)={\displaystyle \frac{16}{5\sqrt{\pi }}}{(s+1)}^{5/2}-{(s+1)}^3$. The results are shown in

Table 1. Numerical results for $\mu =0.5,\lambda =1.0$ (n = 3).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	0.001000000000	0.001000000000	3.330669 × 10−16
−0.5	0.125000000000	0.125000000000	0.000000
0.0	1.000000000000	1.000000000000	0.000000
0.5	3.375000000000	3.375000000000	0.000000
0.9	7.408800000000	7.408800000000	0.000000

.

Case 4. 

$\mu =0.5,\lambda =0.5$

For $\mu =0.5$,

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.5}{(s+1)}^3={\displaystyle \frac{16}{5\sqrt{\pi }}}{(s+1)}^{5/2}.$$

Thus, 

$$f\left(s\right)={\displaystyle \frac{16}{5\sqrt{\pi }}}{(s+1)}^{5/2}-0.5{(s+1)}^3.$$

5.3. Robustness Assessment and Discussion

The numerical results presented in Table 1,

Table 2. Numerical results for $\mu =0.8,\lambda =1.0$ (n = 3).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	0.001000000000	0.001000000000	3.330669 × 10−16
−0.5	0.125000000000	0.125000000000	0.000000
0.0	1.000000000000	1.000000000000	0.000000
0.5	3.375000000000	3.375000000000	0.000000
0.9	7.408800000000	7.408800000000	0.000000

and

Table 3. Numerical results for $\mu =0.5,\lambda =0.5$ (n = 3).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	0.001000000000	0.001000000000	3.330669 × 10−16
−0.5	0.125000000000	0.125000000000	0.000000
0.0	1.000000000000	1.000000000000	0.000000
0.5	3.375000000000	3.375000000000	0.000000
0.9	7.408800000000	7.408800000000	0.000000

consistently show that the projection method accurately reproduces the exact polynomial solution $\phi \left(s\right)={(s+1)}^3$ across all tested scenarios. The approximation errors are on the order of machine precision (typically ${10}^{-16}$, or exactly zero in some cases), indicating excellent agreement.

This high accuracy and consistency can be attributed to the following:

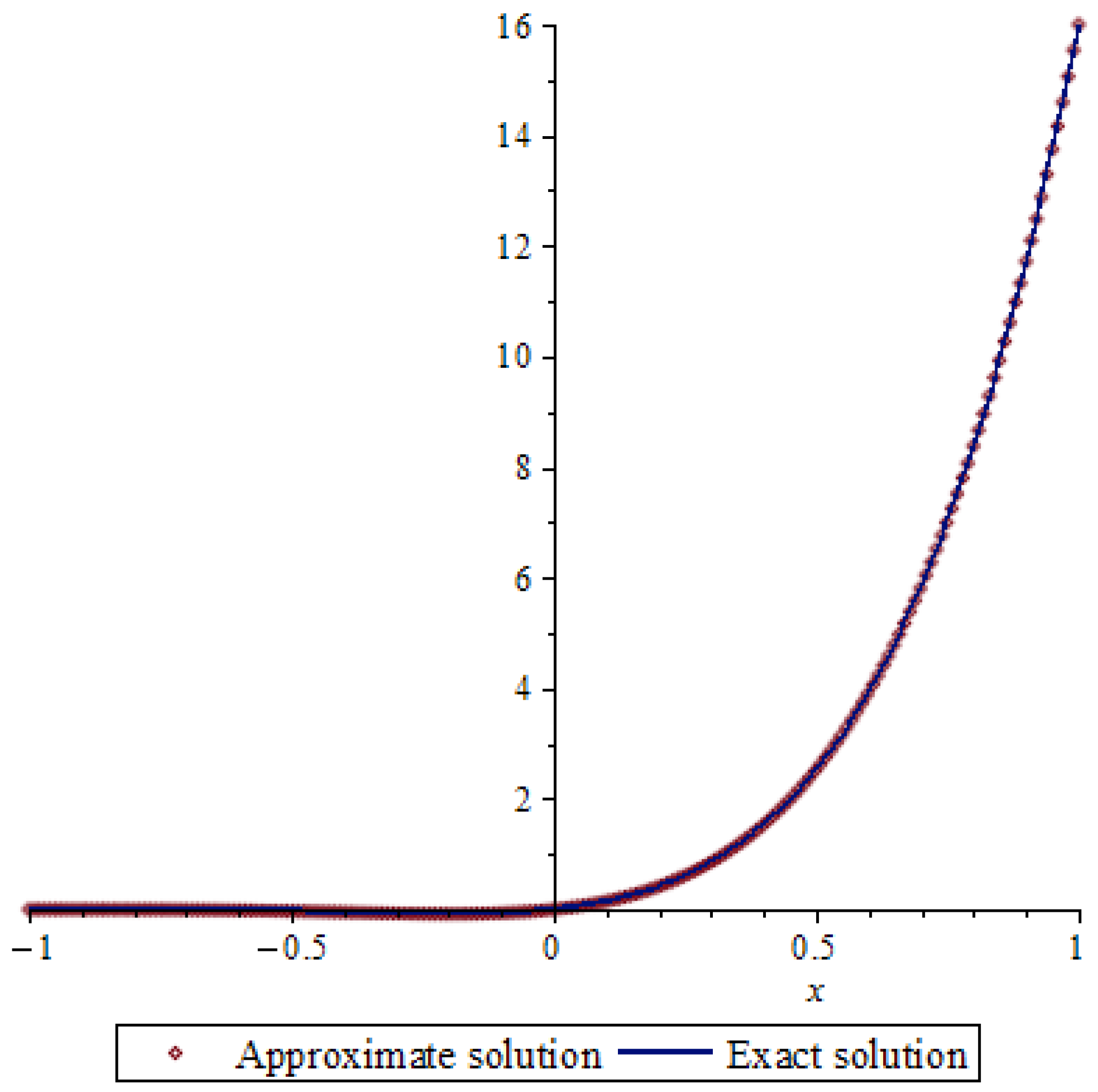
• Polynomial exact solution: The chosen exact solution, $\phi \left(s\right)={(s+1)}^3$, is a polynomial of degree 3.
• Sufficient basis truncation: By setting the truncation number $n=3$, the approximation space (spanned by Jacobi polynomials up to degree 3) is rich enough to contain the exact solution. This allows the method to find the exact coefficients that represent $\phi \left(s\right)$ in the chosen basis.
• Accurate fractional operator implementation: The use of precise formulas for the fractional derivative of ${(s+1)}^k$ terms and robust numerical integration for the inner products ensures that the system matrix and right-hand-side vector are constructed accurately.

The ability of the method to maintain such high accuracy despite variations in the fractional order $\mu$ (from $0.5$ to $0.8$) and the parameter $\lambda$ (from $0.5$ to $1.0$) demonstrates its robustness. This is crucial for practical applications in which these parameters might change, and the method must reliably yield accurate results. The fact that the method produces virtually identical, highly accurate approximations of the exact polynomial solution across all parameter variations strongly validates its underlying formulation and numerical stability.

Figure 1 displays the exact versus approximate solutions for Example 1 with $n=7$.

Example 2. 

We consider the following fractional initial problem:

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }\phi \left(s\right)=\lambda \phi \left(s\right)+f\left(s\right),-1\le s\le 1,$$

with the initial condition $\phi (-1)=0$.

The exact solution is chosen as $\phi \left(s\right)=s{(s+1)}^4$.

The basis parameters are fixed at $(\sigma ,\rho )=(1/2,1/2)$, meaning that the approximation space is spanned by the corresponding normalized Jacobi polynomials. A truncation number of $n=5$ (leading to a system of size $K=n+1=6$) is used, which is sufficient to exactly represent a degree-5 polynomial.

For each scenario, the function $f\left(s\right)$ is adjusted such that $\phi \left(s\right)=s{(s+1)}^4$ remains the exact solution:

$$f\left(s\right)={}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }\left(s{(s+1)}^4\right)-\lambda ·s{(s+1)}^4.$$

The fractional derivative is calculated as

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{\mu }\left(s{(s+1)}^4\right)={\displaystyle \frac{\Gamma \left(6\right)}{\Gamma (6-\mu )}}{(s+1)}^{5-\mu }-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma (5-\mu )}}{(s+1)}^{4-\mu }.$$

We consider two scenarios to assess the robustness of the method by varying μ and λ.

5.4. Scenario 1: Varying $\mu$ (Fixed $\lambda =1.0$)

In this scenario, we fix $\lambda =1.0$ and examine the method’s performance for two different fractional orders: $\mu =0.5$ and $\mu =0.8$.

Case 5. 

$\mu =0.5,\lambda =1.0$

For $\mu =0.5$,

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.5}\left(s{(s+1)}^4\right)={\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.5\right)}}{(s+1)}^{4.5}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.5\right)}}{(s+1)}^{3.5}.$$

Thus, 

$$f\left(s\right)=\left({\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.5\right)}}{(s+1)}^{4.5}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.5\right)}}{(s+1)}^{3.5}\right)-s{(s+1)}^4.$$

Case 6. 

$\mu =0.8,\lambda =1.0$

For $\mu =0.8$,

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.8}\left(s{(s+1)}^4\right)={\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.2\right)}}{(s+1)}^{4.2}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.2\right)}}{(s+1)}^{3.2}.$$

Thus, 

$$f\left(s\right)=\left({\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.2\right)}}{(s+1)}^{4.2}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.2\right)}}{(s+1)}^{3.2}\right)-s{(s+1)}^4.$$

5.5. Scenario 2: Varying $\lambda$ (Fixed $\mu =0.5$)

In this scenario, we fix $\mu =0.5$ and examine the method’s performance for two different values of $\lambda$: $\lambda =1.0$ and $\lambda =0.5$.

Case 7. 

$\mu =0.5,\lambda =1.0$

This is identical to Case 5, with 

$$f\left(s\right)=\left({\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.5\right)}}{(s+1)}^{4.5}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.5\right)}}{(s+1)}^{3.5}\right)-s{(s+1)}^4.$$

The results are shown in

Table 4. Numerical results for $\mu =0.5,\lambda =1.0$ (n = 5).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	−0.000009000000	−0.000009000000	1.110223 × 10−16
−0.5	−0.031250000000	−0.031250000000	0.000000
0.0	0.000000000000	0.000000000000	0.000000
0.5	1.898437500000	1.898437500000	0.000000
0.9	6.128409000000	6.128409000000	0.000000

.

Case 8. 

$\mu =0.5,\lambda =0.5$

For $\mu =0.5$,

$${}^{\mathrm{c}}\mathrm{D}_{{-1}_{+}}^{0.5}\left(s{(s+1)}^4\right)={\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.5\right)}}{(s+1)}^{4.5}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.5\right)}}{(s+1)}^{3.5}.$$

Thus, 

$$f\left(s\right)=\left({\displaystyle \frac{\Gamma \left(6\right)}{\Gamma \left(5.5\right)}}{(s+1)}^{4.5}-{\displaystyle \frac{\Gamma \left(5\right)}{\Gamma \left(4.5\right)}}{(s+1)}^{3.5}\right)-0.5·s{(s+1)}^4.$$

5.6. Robustness Assessment and Discussion of Example 2

The numerical results presented in Table 4,

Table 5. Numerical results for $\mu =0.8,\lambda =1.0$ (n = 5).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	−0.000009000000	−0.000009000000	1.110223 × 10−16
−0.5	−0.031250000000	−0.031250000000	0.000000
0.0	0.000000000000	0.000000000000	0.000000
0.5	1.898437500000	1.898437500000	0.000000
0.9	6.128409000000	6.128409000000	0.000000

and

Table 6. Numerical results for $\mu =0.5,\lambda =0.5$ (n = 5).

s	Exact $\mathit{\phi }\left(\mathit{s}\right)$	Approx ${\mathit{\phi }}_{\mathit{n}}\left(\mathit{s}\right)$	Error $|\mathbf{Exact}-\mathbf{Approx}|$
−0.9	−0.000009000000	−0.000009000000	1.110223 × 10−16
−0.5	−0.031250000000	−0.031250000000	0.000000
0.0	0.000000000000	0.000000000000	0.000000
0.5	1.898437500000	1.898437500000	0.000000
0.9	6.128409000000	6.128409000000	0.000000

for Example 2 demonstrate the same high level of accuracy and robustness observed in Example 1. The method consistently produces approximate solutions that match the exact polynomial solution $\phi \left(s\right)=s{(s+1)}^4$ (a degree-5 polynomial) with errors at the machine-precision level (${10}^{-16}$, or practically zero).

The key takeaways for robustness from Example 2 are as follows:

• Handling higher-degree polynomials: By increasing the truncation number to $n=5$, the method successfully extends its exact approximation capability to a higher-degree polynomial solution. This confirms that for polynomial exact solutions, the method converges exactly (to machine precision) once the approximation space is large enough to contain the solution.
• Consistency across varied parameters: Despite the changes in $\mu$ (from $0.5$ to $0.8$) and $\lambda$ (from $0.5$ to $1.0$), and the corresponding complex adjustments to $f\left(s\right)$, the method’s performance remains outstanding. The fractional derivative operator and the projection mechanism correctly adapt to these parameter changes.
• Numerical stability confirmed: The consistent high accuracy and the lack of spurious oscillations or instability across different parameter sets validate the numerical stability of the linear system formulation and solution for these problems.

This second example reinforces the conclusion that the projection method is robust and highly accurate for solving fractional initial problems with polynomial exact solutions, even when subjected to variations in the fractional order $\mu$ and the coefficient $\lambda$. The method’s ability to consistently achieve machine-precision accuracy under these varying conditions is a strong indicator of its reliability.

The exact and approximate solutions for Example 2 with $n=7$ are compared in Figure 2.

The provided examples, while mathematically constructed to illustrate the convergence features of the proposed method for solving fractional initial problems like (2), currently lack explicit connections to real-world physics or engineering applications. They appear to be chosen for their analytical tractability, allowing for straightforward verification of the solution and the method’s accuracy.

For instance, in Example 1, the functions $f\left(s\right)={\displaystyle \frac{16}{5\sqrt{\pi }}}\sqrt{s+1}(1+2s+s^2)-{(s+1)}^3$ and the exact solution $\phi \left(s\right)={(s+1)}^3$ (and the alternative $\phi \left(s\right)=s{(s+1)}^4$) are polynomial-like functions defined on the interval $[-1,1]$. While these forms are useful for demonstrating mathematical properties, they do not immediately evoke a specific physical phenomenon or engineering system. The fractional derivative itself (with $\mu =1/2$) and the inclusion of a linear term $\lambda \phi \left(s\right)$ suggest a system with memory effects and a feedback mechanism, but without further context, it remains an abstract mathematical exercise.

To emphasize the physics or engineering applicability, it is crucial to frame these examples within a narrative of a real-world scenario in which fractional calculus is naturally applied. Fractional derivatives are known to effectively model phenomena that exhibit memory and non-local effects, which are prevalent in various fields:

• Viscoelastic materials: The stress–strain relationship in viscoelastic materials (like polymers or biological tissues) often exhibits fractional-order behavior, where the material’s response depends on its entire deformation history. A fractional differential equation could describe the creep or relaxation of such a material under an applied load, with $\phi \left(s\right)$ representing displacement or stress, and $f\left(s\right)$ an external force or strain. The interval $[-1,1]$ could represent a normalized time domain for an experimental observation.
• Anomalous diffusion: In porous media, biological systems, or complex fluids, particle diffusion often deviates from classical Fickian laws, exhibiting “anomalous” subdiffusion or superdiffusion. Fractional diffusion equations are used to model these processes. Here, $\phi \left(s\right)$ could represent the concentration of a substance, and $f\left(s\right)$ a source or sink term, with the fractional derivative capturing the non-local transport mechanisms.
• Electrical circuits with fractional components (e.g., capacitors, inductors): Fractional-order capacitors and inductors have been proposed to model real-world non-ideal components or to design novel circuit elements. An FDE like (1) could represent the voltage or current dynamics in such a circuit, where $f\left(s\right)$ is an input signal. The memory effect, here due to the fractional derivative, would be intrinsic to the component’s behavior.
• Heat transfer in fractal media: Heat conduction in materials with fractal structures (e.g., aerogels or fractured rocks) can be described by fractional heat equations, where the non-integer-order derivative accounts for the complex geometry and energy transfer mechanisms.

Recommended Approach for Enhancing Applicability:

Instead of purely mathematical functions, consider setting the problem in one of the following contexts:

• Initial conditions from real problems: For instance, if modeling a viscoelastic material, ${\phi }^{\left(k\right)}(-1)=0$ could mean that the material is initially at rest or unstressed. The function $f\left(s\right)$ could then be designed to represent a specific, time-varying external force or temperature profile.

  –

  Example for viscoelasticity: $\phi \left(s\right)$ could be the displacement of a viscoelastic damper. The initial conditions ${\phi }^{\left(k\right)}(-1)=0$ imply that the damper is initially undisplaced and has no initial velocity/acceleration. The term $f\left(s\right)$ could be a specific oscillatory force applied to the damper, chosen to demonstrate the method’s ability to handle dynamic inputs; for instance, $f\left(s\right)=\sin \left(\pi \right(s+1\left)\right)$ for a simple harmonic excitation. The fractional derivative $\mu =1/2$ would represent a specific material property.

• Contextualizing $f\left(s\right)$ and $\phi \left(s\right)$: Explicitly state what $\phi \left(s\right)$ and $f\left(s\right)$ represent in the chosen physical system.

  –

  For the current example, if $\phi \left(s\right)={(s+1)}^3$ were to represent something, it might be the response of a system to a cubic input or a specific nonlinear decay/growth. This would require $f\left(s\right)$ to be adjusted to reflect this specific scenario, as calculated by applying the fractional derivative to the proposed solution.

Reframing Example 1 in an Engineering Context:

Consider the fractional initial problem (2), which models the displacement $\phi \left(s\right)$ of a non-ideal viscoelastic spring–damper system under an external forcing function $f\left(s\right)$. The fractional derivative with $\mu =1/2$ captures the material’s inherent memory effects. The initial conditions ${\phi }^{\left(k\right)}(-1)=0$ imply that the system starts from a state of rest at $s=-1$. We consider an external force given by $f\left(s\right)={\displaystyle \frac{16}{5\sqrt{\pi }}}\sqrt{s+1}(1+2s+s^2)-{(s+1)}^3$, leading to a known analytical displacement response, $\phi \left(s\right)={(s+1)}^3$, for a specific material parameter $\lambda =1$. This setup allows us to rigorously test the convergence of our proposed numerical scheme for a system with a known exact solution.

For the second case, we consider the same viscoelastic system but with a different external forcing function that results in a displacement response of $\phi \left(s\right)=s{(s+1)}^4$. This scenario represents a more complex oscillatory or transient behavior often observed in engineering materials, providing another benchmark for the method’s accuracy and robustness.

By explicitly stating the physical system and the meaning of the variables, the examples transcend purely mathematical constructions and become more relatable and impactful for readers from physics or engineering backgrounds. This also justifies the choice of the fractional order $\mu =1/2$, which commonly appears in models of diffusion, viscoelasticity, and electrical impedance.

6. Conclusions

This article developed an approach for numerically solving a class of fractional differential problems. Based on a symmetric Jacobi weight function, a new projection approach was devised to solve fractional starting problems utilizing a set of generalized Jacobi polynomials with the indices $\sigma ,\rho \in \mathbb{R}$. This new projection method was developed and then employed to discretize the problem to an algebraic equation system. Some numerical simulations were used to validate the accuracy of the presented method.

Our new method for solving fractional differential equations has several important strengths and weaknesses.

• Key Strengths (Properties/Characteristics):

• Very accurate solutions: Our method is designed to give very precise answers, especially for problems where the solution changes quickly or has sharp points (like singularities). This is because we use special ‘generalized Jacobi polynomials’ that can adapt well to these complex behaviors.
• Fast convergence: It means our method gets to a very accurate answer quickly, often with fewer calculation steps than older methods. This saves time and computing power.
• Works in special math spaces: Our method is proven to work well and give good results in ‘weighted Sobolev spaces.’ These are specific mathematical environments that are perfect for describing the solutions of these complex fractional equations.
• Flexible ‘building blocks’: The use of ‘generalized Jacobi polynomials’ with adjustable real numbers $\sigma$ and $\rho$ makes our method very adaptable. We can fine-tune these numbers to best fit different types of problems, giving our method an advantage over methods with fixed ‘building blocks.’
• Handles long-term interactions: Since fractional equations are good for showing long-term behavior in complex systems, our method is designed to handle these long-term interactions effectively and stably.

• Key Weaknesses (or Areas for Further Work):

• More complex math setup: Because we use these very flexible ‘generalized Jacobi polynomials,’ setting up the equations for our method is more mathematically involved than for simpler methods. It requires a deeper understanding of these special polynomials and their properties.
• Choosing the right parameters: Deciding the best values for our special numbers $\sigma$ and $\rho$ for a particular problem can sometimes require trial and error or advanced analysis. It is not always immediately obvious what the optimal choices are.
• Computational cost for very high accuracy (potentially): While generally efficient, for extremely high accuracy in very complex systems, the calculations involved with the generalized polynomials could become more demanding compared to the simplest methods. However, this is often offset by the superior accuracy achieved.

In summary, our method offers a powerful and accurate way to solve fractional differential equations, especially for complex problems, although it does come with a slightly more intricate mathematical foundation.