Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete
Abstract
1. Introduction
2. Fractional Creep Model
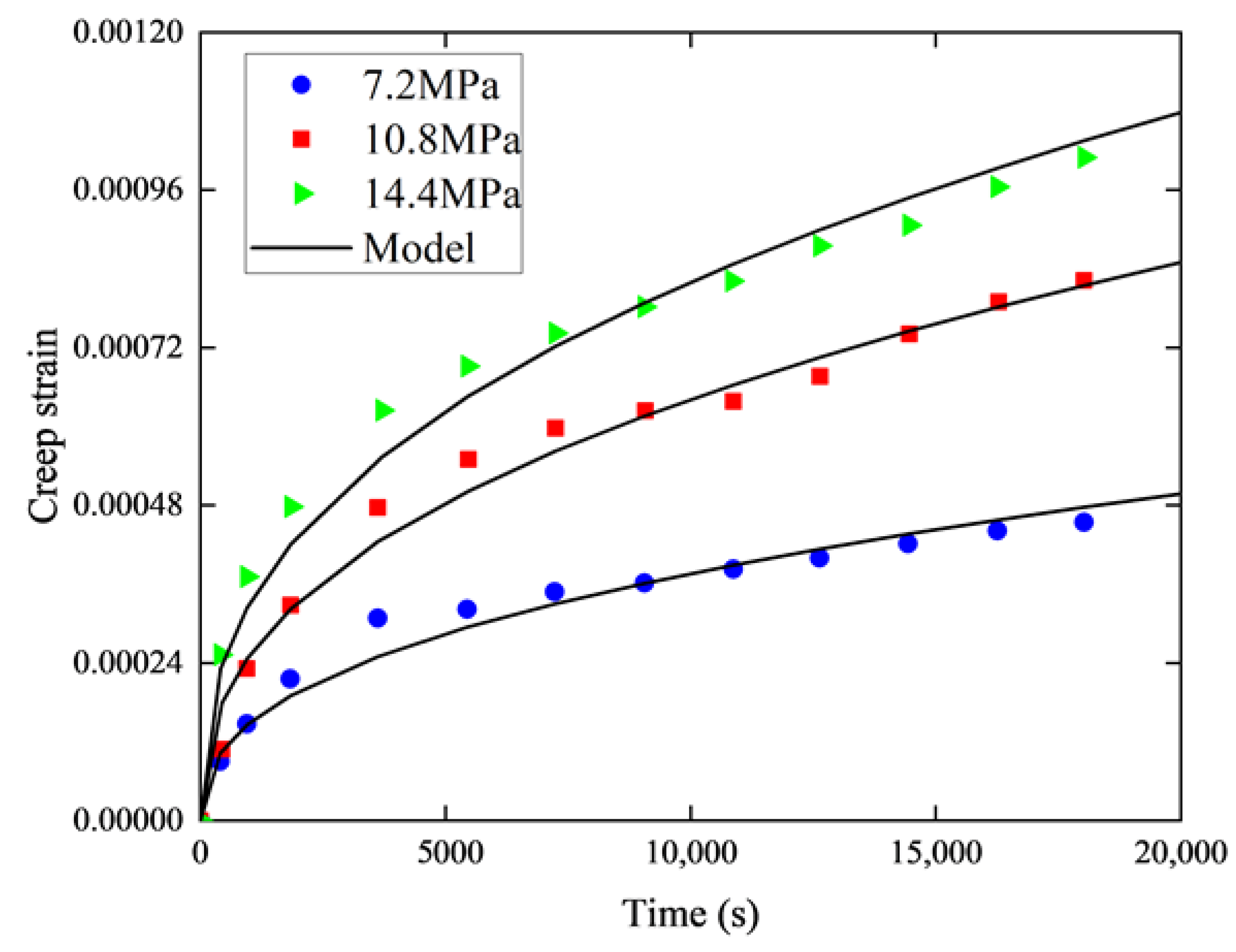
3. Results and Discussion
4. Prediction of Concrete Creep
5. Conclusions
- (i)
- The fractional creep model can accurately describe the experimental data and has good adaptability as well as robustness under different temperatures and applied stresses.
- (ii)
- The value of the fractional order tends to increase with the increase in temperature. This intuitively reflects that high temperatures accelerate the creep process of concrete, making its mechanical properties gradually softer.
- (iii)
- The prediction formula containing the average fractional-order value at each temperature was established, and the creep deformation of concrete was predicted only by changing the applied stress, which provides an innovative and practical method for predicting the temperature-dependent creep behavior of concrete.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Xu, Q.; Chen, S. Approaches of concrete creep using micromechanics: Numerical simulation and predictive model. Model. Simul. Mater. Sci. Eng. 2019, 27, 055012. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, S.; Sun, B.; Chen, L. Creep characteristics and time-dependent creep model of tunnel lining structure concrete. Mech. Time-Depend. Mater. 2021, 25, 365–382. [Google Scholar] [CrossRef]
- Mussabayev, T.T.; Nuguzhinov, Z.S.; Nemova, D.; Kayupov, T.; Tolkynbaev, T.A.; Akmakanova, A.Z.; Khafizova, G.S. Creep of Concrete in Shell Structures: Nonlinear Theory. Materials 2023, 16, 5587. [Google Scholar] [CrossRef] [PubMed]
- Houhou, N.; Benzarti, K.; Quiertant, M.; Chataigner, S.; Fléty, A.; Marty, C. Analysis of the nonlinear creep behavior of concrete/FRP-bonded assemblies. J. Adhes. Sci. Technol. 2014, 28, 1345–1366. [Google Scholar] [CrossRef]
- Baktheer, A.; Chudoba, R. Experimental and theoretical evidence for the load sequence effect in the compressive fatigue behavior of concrete. Mater. Struct. 2021, 54, 1–23. [Google Scholar] [CrossRef]
- Li, R.; Liu, L.; An, H.; Wang, Y. Study on Dynamic Constitutive Model of Polypropylene Concrete under Real-Time High-Temperature Conditions. Appl. Sci. 2022, 12, 1482. [Google Scholar] [CrossRef]
- Gernay, T.; Franssen, J.-M. A formulation of the Eurocode 2 concrete model at elevated temperature that includes an explicit term for transient creep. Fire Saf. J. 2012, 51, 1–9. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Wu, J.; Jiang, W. A thermomechanical coupling constitutive model of concrete including elastoplastic damage. Appl. Sci. 2021, 11, 604. [Google Scholar] [CrossRef]
- Liang, M.; Chang, Z.; Wan, Z.; Gan, Y.; Schlangen, E.; Šavija, B. Interpretable Ensemble-Machine-Learning models for predicting creep behavior of concrete. Cem. Concr. Compos. 2022, 125, 104295. [Google Scholar] [CrossRef]
- Stanisauskis, E.; Mashayekhi, S.; Pahari, B.; Mehnert, M.; Steinmann, P.; Oates, W. Fractional and fractal order effects in soft elastomers: Strain rate and temperature dependent nonlinear mechanics. Mech. Mater. 2022, 172, 104390. [Google Scholar] [CrossRef]
- Qin, X.; Yin, W. A novel fractal model for effective thermal conductivity in granular porous media. Geothermics 2023, 108, 102625. [Google Scholar] [CrossRef]
- Qu, M.L.; Tian, S.Q.; Fan, L.W.; Yu, Z.T.; Ge, J. An experimental investigation and fractal modeling on the effective thermal conductivity of novel autoclaved aerated concrete (AAC)-based composites with silica aerogels (SA). Appl. Therm. Eng. 2020, 179, 115770. [Google Scholar] [CrossRef]
- Jiang, J.; Zheng, L.; Jones, M.R.; Lu, Z.; Li, J. Estimating thermal conductivity of lightweight nanoporous cement pastes using a hybrid fractal model. Constr. Build. Mater. 2022, 327, 126941. [Google Scholar] [CrossRef]
- Li, T.; Hou, R.; Liu, G.; Han, Q.; Li, D. Investigations on Creep Behavior and Fractal Derivative Constitutive Model of Sandstone under Different Drying-Wetting Cycles. KSCE J. Civ. Eng. 2022, 26, 69–78. [Google Scholar] [CrossRef]
- Bouras, Y.; Vrcelj, Z. Fractional and fractal derivative-based creep models for concrete under constant and time-varying loading. Constr. Build. Mater. 2023, 367, 130324. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New fractional variable-order creep model with short memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Shitikova, M.V. Fractional operator viscoelastic models in dynamic problems of mechanics of solids: A Review. Mech. Solids 2022, 57, 1–33. [Google Scholar] [CrossRef]
- Mainardi, F.; Spada, G. Creep, relaxation and viscosity properties for basic fractional models in rheology. Eur. Phys. J. Spéc. Top. 2011, 193, 133–160. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef]
- Katicha, S.W.; Apeagyei, A.K.; Flintsch, G.W.; Loulizi, A. Universal linear viscoelastic approximation property of fractional viscoelastic models with application to asphalt concrete. Mech. Time-Depend. Mater. 2014, 18, 555–571. [Google Scholar] [CrossRef]
- Zatar, W.; Xiao, F.; Chen, G.S.; Hulsey, J.L. Identification of viscoelastic property of pile-soil interactions with fractional derivative model. J. Low Freq. Noise, Vib. Act. Control. 2021, 40, 1392–1400. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, L.; Bao, T.; Liu, Y. Fractional order creep model for dam concrete considering degree of hydration. Mech. Time-Depend. Mater. 2019, 23, 361–372. [Google Scholar] [CrossRef]
- Xu, H.; Jiang, X. Creep constitutive models for viscoelastic materials based on fractional derivatives. Comput. Math. Appl. 2017, 73, 1377–1384. [Google Scholar] [CrossRef]
- Sapora, A.; Cornetti, P.; Carpinteri, A.; Baglieri, O.; Santagata, E. The use of fractional calculus to model the experimental creep-recovery behavior of modified bituminous binders. Mater. Struct. 2016, 49, 45–55. [Google Scholar] [CrossRef]
- Tang, H.; Wang, D.; Huang, R.; Pei, X.; Chen, W. A new rock creep model based on variable-order fractional derivatives and continuum damage mechanics. Bull. Eng. Geol. Environ. 2018, 77, 375–383. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, L.; Liu, H. A fractional elasto-viscoplastic model for describing creep behavior of soft soil. Acta Geotech. 2021, 16, 67–76. [Google Scholar] [CrossRef]
- Bouras, Y.; Zorica, D.; Atanacković, T.M.; Vrcelj, Z. A non-linear thermo-viscoelastic rheological model based on fractional derivatives for high temperature creep in concrete. Appl. Math. Model. 2018, 55, 551–568. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Z.; Zhu, S.; He, Z.; Zhu, D.; Liu, J.; Meng, S. Nonlinear creep damage constitutive model of concrete based on fractional calculus theory. Materials 2019, 12, 1505. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, J.G.T.; de Castro, J.T.P.; Meggiolaro, M.A. Modeling concrete and polymer creep using fractional calculus. J. Mater. Res. Technol. 2021, 12, 1184–1193. [Google Scholar] [CrossRef]
- Smit, W.; de Vries, H. Rheological models containing fractional derivatives. Rheol. Acta 1970, 9, 525–534. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.; Freed, A.; Luchko, Y. Algorithms for the fractional calculus: A selection of numerical methods. Comput. Methods Appl. Mech. Eng. 2005, 194, 743–773. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Yang, C.; Huang, R.; Liu, D.; Qiu, W.; Zhang, R.; Tang, Y. Analysis and warning prediction of tunnel deformation based on multifractal theory. Fractal Fract. 2024, 8, 108. [Google Scholar] [CrossRef]
- Kati, N.; Ucar, F. An Intelligent Model for Supercapacitors with a Graphene-Based Fractal Electrode to Investigate the Cyclic Voltammetry. Fractal Fract. 2023, 7, 218. [Google Scholar] [CrossRef]











| T (°C) | 22 | 204 | 316 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (MPa) | 7.2 | 10.8 | 14.4 | 7.2 | 10.8 | 14.4 | 7.2 | 10.8 | 14.4 |
| E (MPa) | 20,841 | 20,345 | 18,570 | 11,720 | 11,458 | 11,298 | 4811 | 4390 | 4652 |
| (s) | 3.34 × 106 | 1.70 × 106 | 1.73 × 106 | 1.09 × 105 | 1.04 × 105 | 8.64 × 104 | 4.14 × 105 | 3.68 × 105 | 3.91 × 105 |
| 0.3078 | 0.2993 | 0.2977 | 0.3683 | 0.3630 | 0.3629 | 0.4028 | 0.4059 | 0.3948 |
| T (°C) | 22 | 204 | 316 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | 7.2 | 10.8 | 14.4 | 7.2 | 10.8 | 14.4 | 7.2 | 10.8 | 14.4 | |
| Bouras’s model | RMSE | 3.20 × 10−5 | 1.81 × 10−5 | 2.54 × 10−5 | 3.29 × 10−5 | 2.68 × 10−5 | 3.57 × 10−5 | 3.96 × 10−5 | 5.01 × 10−5 | 2.10 × 10−5 |
| R2 | −0.8034 | 0.8222 | 0.9395 | 0.9132 | 0.9787 | 0.9831 | 0.9235 | 0.9636 | 0.9951 | |
| Proposed Model | RMSE | 5.80 × 10−6 | 5.19 × 10−6 | 1.44 × 10−5 | 2.03 × 10−5 | 2.14 × 10−5 | 2.31 × 10−5 | 2.56 × 10−5 | 3.63 × 10−5 | 4.25 × 10−5 |
| R2 | 0.9477 | 0.9889 | 0.9593 | 0.9724 | 0.9890 | 0.9927 | 0.9734 | 0.9841 | 0.9835 | |
| T (°C) | 22 | 204 | 316 |
|---|---|---|---|
| E (MPa) | 20,712 | 11,492 | 4618 |
| (s) | 1.76 × 106 | 9.98 × 104 | 3.91 × 105 |
| 0.3034 | 0.3647 | 0.4012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Gong, L.; Meng, R. Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete. Fractal Fract. 2024, 8, 482. https://doi.org/10.3390/fractalfract8080482
Chen J, Gong L, Meng R. Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete. Fractal and Fractional. 2024; 8(8):482. https://doi.org/10.3390/fractalfract8080482
Chicago/Turabian StyleChen, Jiecheng, Lingwei Gong, and Ruifan Meng. 2024. "Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete" Fractal and Fractional 8, no. 8: 482. https://doi.org/10.3390/fractalfract8080482
APA StyleChen, J., Gong, L., & Meng, R. (2024). Application of Fractional Calculus in Predicting the Temperature-Dependent Creep Behavior of Concrete. Fractal and Fractional, 8(8), 482. https://doi.org/10.3390/fractalfract8080482









