1. Introduction
Nanocrystals have a typical grain size of several tens of nanometers. There is experimental evidence that conventional grain interior dislocation-mediated activities prevail in nanocrystals coarser than 100 nm, whereas in nanocrystals smaller than 50 nm, the deformation is accommodated mostly at the grain boundaries (GB). Grain rotation, though not usually treated as an important plastic deformation mechanism in bulk-sized materials, is very relevant in nanomechanics [
1]. For instance, oriented attachment of nanocrystals [
2] and radiation-induced texture [
3] involve the grain rotation of nanocrystals. However, the grain rotation mechanism remains puzzling because some processes, such as lattice diffusion, dislocations, disclinations, and curvature-driven grain boundary migration, may play roles, which complicates investigations into the grain rotation mechanisms [
3,
4]. In this article, we review the previous theories, computer simulations, and experimental investigations into grain rotation. It is expected that the established knowledge and experimental techniques will advance future explorations significantly.
2. Theories of Grain Rotation
Many experimental studies have proved that grain rotation plays an essential role in the plastic deformation of nanocrystalline materials [
1,
3,
5,
6,
7,
8,
9,
10,
11,
12]. Inspired by the experimental observations of grain rotation, a lot of theoretical models were developed in the last decade to describe the plastic deformation associated with the grain boundary activity accompanied by grain rotation. To explain the grain orientation changes induced by the rigid body rotation in thin films of gold, a phenomenological theoretical model was addressed to explore the kinetics of grain rotation behaviors [
4]. In this model, the aggregate energy gradient due to the misorientation for all grain boundaries surrounding a grain and the diffusion fluxes of vacancies along the grain boundary are taken into account. The predicted grain rotation rate agrees well with the experimental observation, which is grain-size dependent. Kobayashi et al. developed a phase field model to simulate the two-dimensional grain boundaries dynamics [
13], in which the solidification and the anisotropic phase boundary energies are involved, as well as the crystalline order induced into an adjoining amorphous phase. This model can simulate the grain boundary motion and grain rotation during the grain boundaries’ evolution.
Following the Raj–Ashby theory for diffusion-accommodated grain-boundary sliding [
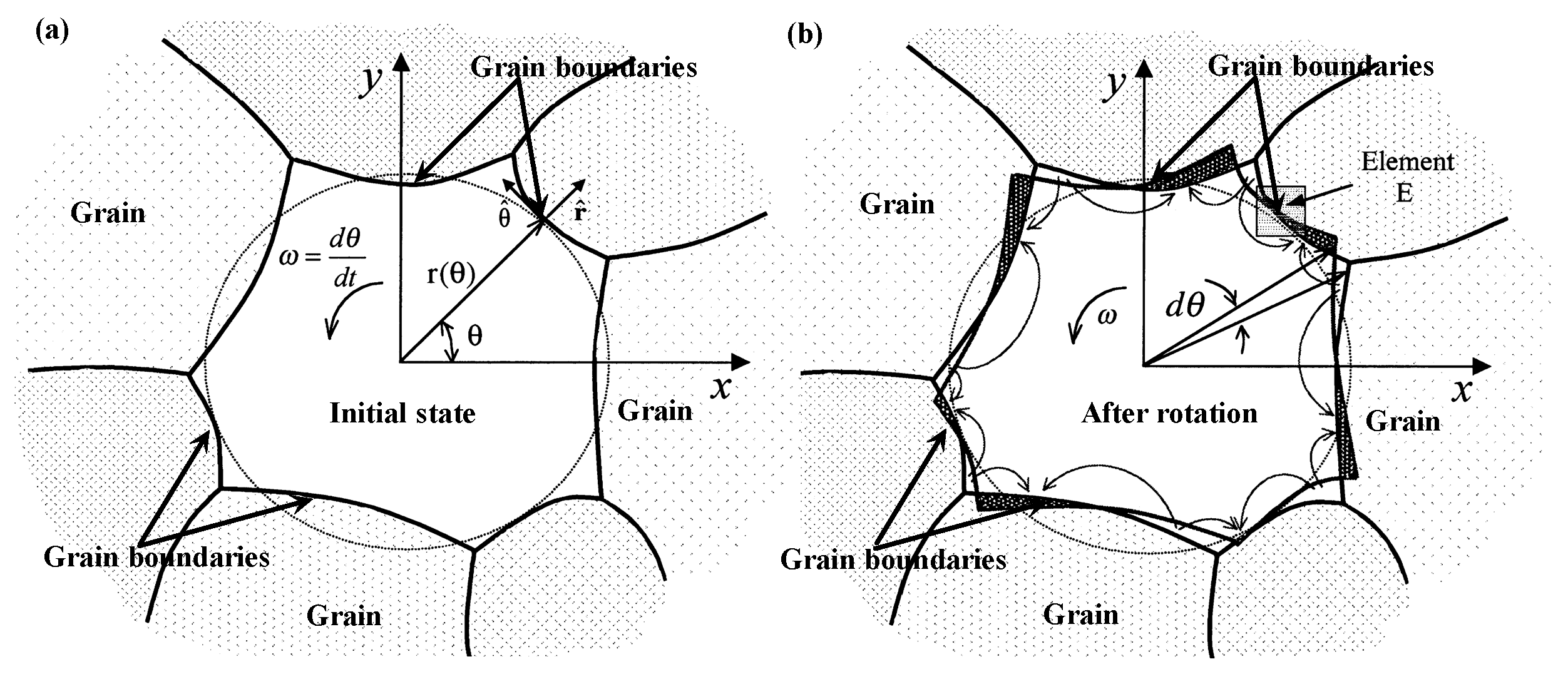
14], Moldovan et al. developed the elasticity and diffusive flow models to explore the grain rotation issue in polycrystalline materials through considering grain boundaries’ (GB) diffusion along the grain periphery and lattice diffusion in the grain interior, both of which could induce grain rotation [
15], as shown in
Figure 1. The proposed general expression for the rotation rate could be applied to simulate the grain-rotation-induced grain coalescence for grain growth. Moldovan used this general theory of grain rotation in the framework of a mean field theory to explain the grain growth induced by the grain rotation, and the dominant grain-rotation coalescence mechanism leads to the power-law of grain growth [
16].
Since the GB sliding originating from the shear and normal forces acts on the grain boundaries [
17], Cahn and Taylor presented a unified method to monitor the grain boundary motion under the postulate of a coupled tangential motion in two crystals produced during the motion of the interface [
18]. In their theoretical framework, the normal and tangential motions of grain boundaries, the grain sliding rigidly along the boundary, and grain rotation can all be compiled into a unified theoretical formulation. The rotation of circular cylindrical grains can then be predicted through considering the reduction of total surface/interface free energy. To identify the orientation dependence of grain rotation as observed in experiments [
6], Winther et al. adopted the Sachs and Taylor models to analyze the relationship between the grain rotation path and grain orientation, as well as the self-consistent model [
19]. The previous orientation-based models could not characterize the grain rotation behavior in all regions, and the Sachs model [
20] is the lower bound model and the Taylor model [
21] is the upper bound model. That is the reason why the prediction based on the Taylor and Sachs models are inconsistent with the experimental grain rotations in Al [
5].
To avoid the assumption of the specific orientation of grain boundaries in the theoretical models of grain boundary dynamics, Caillard et al. proposed a shear-migration coupling model in which the random orientations of grain boundaries are involved [
20]. Such a geometrical model could help in describing the grain rotations and GB-based plasticity in nanocrystals very well. The grain boundary energy and stress-driven grain rotations are quantified in a kinetic model proposed by Yang et al. [
21]. In their model, the contribution of triple junction and grain shape in grain rotations are analyzed in detail. They found that the power law of grain size for the grain rotation rates is sensitive to the driving forces and the GB migration. These grain rotation models [
4,
15,
18] are also applied to predict the grain-rotation-induced grain growth in nanoceramics. It was revealed that during grain-rotation-induced coalescence, the formation of low-energy, low-angle grain boundaries depend on the rotation step and temperature, as well as grain size [
22].
For the crack-free and pre-cracked nanocrystalline materials, the theoretical models were developed to characterize the nanoscale grain rotation originated from the grain boundary sliding and grain boundary dislocation climb [
23,
24]. It was concluded that the rotation deformation rate is dominated by diffusion, facilitating the climb of grain boundary dislocations. Ovid’ko and Sheinerman further presented a model to analyze the fast nanoscale rotation in the nanocrystalline materials occurring through local ideal shear processes. An extreme condition, such as very high applied stress and plastic strain rate, could lead to such shear-induced fast grain rotation [
25,
26]. Bobylev and Ovid’ko also revealed the mechanism of stress-driven GB rotation in their model and the predictions are agree well with the experimental observations [
27]. In addition, the GB viscosity could also affect the grain boundary sliding and grain rotation [
28,
29,
30]. For example, Kim et al. considered the contribution of the boundary viscosity on the GB sliding rate, rotation rate, and stress distribution, and they found that with increasing boundary viscosity, the sliding rate and rotation rate decrease, as well as the normal stress on the GBs [
28,
29,
30].
Note that grain rotation plays an important role in the plastic deformation in polycrystalline materials, especially in the nanograined materials. The theoretical models mentioned above provide a comprehensive description for the grain boundary activities that are associated with grain rotations. It could be helpful to develop an elastoplastic framework for the plastic deformation in polycrystalline metals by considering grain rotation behaviors. There are still several challenges in theoretical models for grain rotations. For example: (1) How to distinguish the grain rotation behaviors in face-centered cubic (FCC), body-centered cubic (BCC), and hexagonal close packing (HCP) metals? (2) How to characterize the grain rotation under a high strain rate in the models? (3) Can the present models be applied to describe the grain rotation behaviors of polycrystalline materials at extreme conditions such as high temperature or high pressure?
3. Molecular Dynamics Simulations of Grain Rotation
Molecular dynamics (MD) simulation is a powerful method to investigate the grain boundary dynamics at the atomic scale. Upmanyu et al. conducted the MD simulations to monitor the grain rotation and grain boundary migration [
31]. It was found that the local minima in the grain boundary energy results in the grain rotation, and the rotation rate decreases with increasing grain size. They also used the interface parameters obtained from MD simulations in phase field modeling to reproduce the grain boundary dynamics, and a good agreement in grain rotation rate is achieved for the above two simulation approaches.
Since the coupled behavior between the normal grain boundary motion and the tangential translation of grains was confirmed using MD simulations [
31], Cahn et al. examined the factor of the GB motion coupled to grain translation using the MD simulations, and found that the coupling factor is multivalued [
32]. They also addressed a geometric model to predict the misorientation dependence of this factor, which agrees with the MD results. Farkas et al. studied the grain growth kinetics in 4-nm nanocrystalline Ni by using the three-dimensional MD simulations and revealed that the grain rotation and the decrease in grain boundary energy dominate the grain growth in the ultrafine nanograins of Ni [
33].
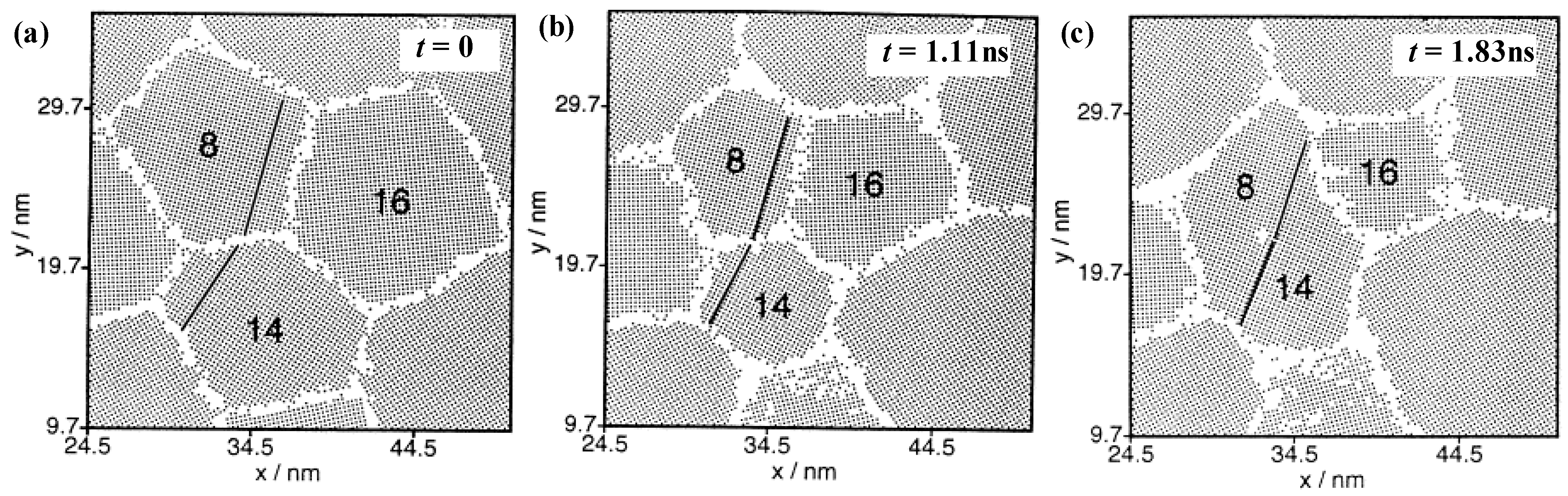
To verify the contribution of grain rotation on the plastic deformation and grain growth, Haslam et al. addressed the MD simulations to give the first evidence of grain rotation and grain growth, as shown in
Figure 2, and indicated that the rotation–coalescence mechanism coupled with the grain boundary migration [
34]. For the coupling behavior of the normal and tangential grain boundary motions predicted in Cahn and Taylor [
18], Trautt and Mishin [
35] carried out MD simulations to give an insight into the dynamics of grain boundary motion. They found that the normal and tangential motions are not perfectly coupled to one another, and grain boundary motion involves a proportion of sliding.
Hasnaoui et al. performed large-scale MD simulations to support the GB sliding as the primary plastic deformation as mentioned in the model of Hahn et al. [
36,
37], while they found that the grain rotation can also act as one important deformation mechanism in nanocrystalline materials [
38]. Haslam et al. further performed MD simulations to study the grain growth in nanocrystalline materials under stress and they found that the grain growth comes from the grain boundary migration and grain rotation, both of which can be accelerated by deformation [
39]. Sansoz and Dupont also used atomistic simulations to study the stress-driven grain growth during nanocrystalline aluminum indentation [
40]. The grain rotation is also identified as one important mechanism for grain growth. During the deformation of nanocrystalline Ni, three-dimensional MD simulations also demonstrated that the grain rotation and GB activity act as the analogous part of the intergranular plasticity mechanism found in nanocrystalline metals [
41]. Even though the MD simulations could provide the mechanisms of grain rotation at the atomic scale, it is still a challenge for the MD simulations to monitor the grain rotation behaviors in the cases of deformation under lower strain rate and a polycrystalline structure with multi-modal grain size distribution.
4. TEM Characterizations of Grain Rotation
For determining the change of grain orientation, scanning electron microscopy (SEM) imaging combined with electron back scattering diffraction is a well-developed method. This method has been extensively used for coarse-grained materials (grain size over 1 μm) or fine grains (grain size between 100 nm and 1 μm), while is not suitable for measuring sub-10 nm grains. TEM is a powerful technique to record the grain orientations, together with position, size, morphology, and topological connectivity among grains of polycrystalline materials. This information can be recorded using electron back scattered diffraction (EBSD) or X-ray based techniques, too. The spatial resolution for EBSD is around 20 nm, and over 200 nm for three-dimensional (3D) X-ray techniques, in contrast to a spatial resolution down to 1 nm for TEM [
42]. To record grain orientation or boundary misorientation using TEM, several methods can be used, e.g., selection area diffraction or Kikuchi patterns. Among those methods, Kikuchi patterns have an outstanding advantage in that both the orientation and microstructure image can be recorded at the same time. In 1995, Liu et al. developed a rapid method to determine the orientations and misorientations of crystalline foils with TEM [
43]. With this method, the orientation of crystallite can be measured by the relative position of Kikuchi patterns through tilting the specimen to allow the low-index zone axes to be close to the beam direction. Afterward, for a region of interest with many crystallites, the orientations of different crystallites can be determined by moving the specimen to obtain the Kikuchi patterns of these crystallites. The misorientations between two crystallites can be calculated. The accuracy for the orientation is about 1°. For misorientation angles and axes between two crystallites, the accuracies are 0.3° and 3°, respectively [
43]. Another TEM-based orientation mapping method, namely automated crystal orientation mapping, was proposed by R.A. Schwarzer in 1998 [
44]. This method was developed to extend crystallographic orientation mapping to specimens that cannot be measured using EBSD-SEM techniques [
44,
45,
46,
47]. Particularly, it is very effective for severely deformed metals. This method has been frequently used to map grain orientations in ultrafine grained samples that are prepared using severe plastic deformation. In this method, the Bragg spot pattern, rather than Kikuchi lines, is employed, which is more sensitive to lattice parameters than an SEM-based method [
44]. It can be used for both orientation mapping and phase mapping.
To provide direct evidence for grain rotation, in situ TEM observations is essential. An in situ straining stage combined with lattice imaging can provide the changes in grain misorientation. Nevertheless, the study addressing the grain rotation for nanograined samples with TEM is rare. An early study was carried out in 1995. The deformation behavior of nanoscaled gold thin films, with grain sizes of 10 nm and film thicknesses of l0–20 nm, has been investigated using in situ high resolution transmission electron microscopy [
48]. The grain rotation was characterized by measuring the variation in the angular relationship between the lattice fringes of two neighboring grains. Because of the small scattering angle of electron diffraction, fringe images are generally observed only for the crystal planes whose normals are approximately perpendicular to the incident beam direction. The variation of the misorientation by grain rotation is then measured by the variation of the angle between the lattice fringes. This technique works well when the rotation axis is parallel to the electron beam and the normal of film. They pointed out that the lattice fringe contrast might change in some of the grains, but not in others. The loss of lattice fringe contrast in a certain grain may be transient. Grains rotated with respect to each other are extensively observed, which implies the plastic strain takes place via grain boundary sliding. The local strain tensor and the level of plastic strain associated with the deformation were also measured with TEM [
48]. The two-dimensional (2D) strain tensor was obtained by measuring the shape change of a triangle in the deforming zone. The normal strain in three different directions can be determined via a measurement of the change in the length of the sides of the triangle. However, it is difficult to evaluate the accuracy for the strain measurement. There are inevitable errors when identifying the same material point step by step, which is necessary when placing the triangle. Even with the uncertainties in strain determination, the gold films with a grain size of 10 nm can be deformed to an 30% plastic strain with no apparent dislocation activity. The grain rotation, combined with the lack of dislocation activity, both imply that deformation at the nanoscale is accommodated by grain boundary sliding. In contrast, it is further found that traditional dislocation-based plasticity takes place when silver films with coarser grain sizes around 110 nm were strained in a similar manner [
48].
Wang et al. investigated the deformation behavior of nanocrystalline Ni under an in situ tensile deformation using transmission electron microscopy [
49]. They used a technique that combined the use of nanobeam electron diffraction and dark field images techniques. Both the individual grain rotation and neighboring grain rotation/growth were recorded [
49]. Recently, a grain rotation by grain boundary dislocations in nanocrystalline platinum was reported by Wang et al. [
1]. A transition of a plastic deformation mode from cross-grain dislocation glide in larger grains (>6 nm) to a coordinated rotation of multiple grains for grains with diameter <6 nm was observed. It was found that the grain rotation is realized by a dislocation climb at the grain boundary, rather than grain boundary sliding or diffusional creep. The atomic-scale images indicate that the evolution of the misorientation angle between neighboring grains is related to the change of the Frank–Bilby dislocation content near the grain boundary [
1].
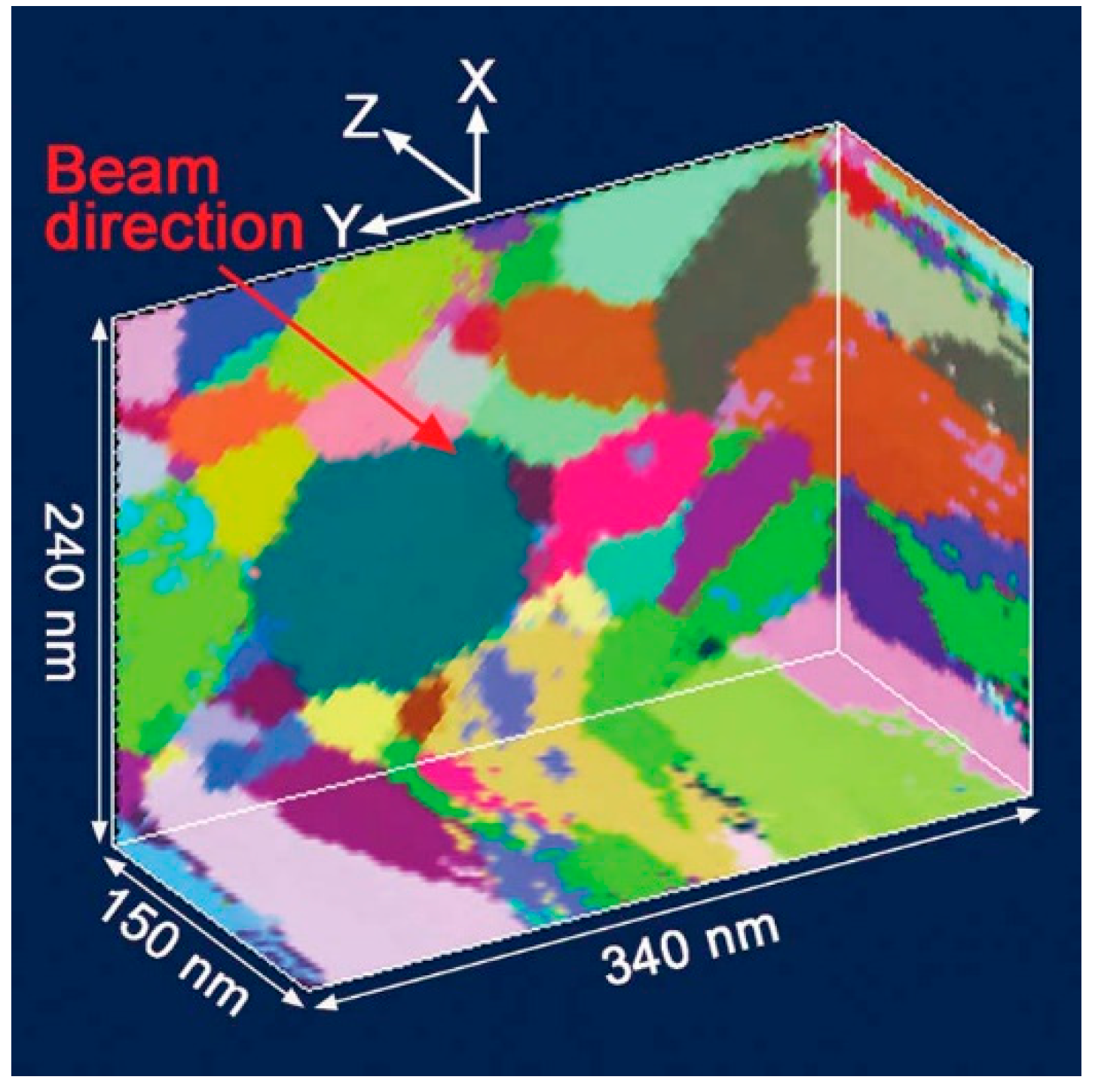
Usually, the foils for TEM characterizations often have a thickness of about 50–100 nm, which puts the grain size limitation for TEM measurements as several nanometers. The first solution is to prepare thin foils with a thickness similar to or lower than the grain size. Recently, a three-dimensional (3D) method for orientation mapping with TEM was developed by Liu et al. [
42]. This method allows for recording the orientation and morphology of nanograins when the thickness of thin foils is much larger than the grain size.
Figure 3 is an example of a 3D grain-orientation map for a 150-nm-thick aluminum film. The data collection is based on conical-scanning dark-field imaging. To enable the reconstruction of a 3D orientation map for all grains in a sample volume, images are recorded at many tilt angles. A new approach for the orientation determination and 3D reconstruction was also developed, based on the grain sweeper and grain spotter algorithms [
42]. Although several mechanisms for grain rotation of nanograins have been revealed by the usage of in situ TEM observation, the as-used foils generally contain only single-layer grains. This type of constraint condition is quite different from those of foils with multi-layered nanograins. In future, a combination of 3D orientation mapping technique and in situ TEM staging techniques can provide a powerful capability to study the grain rotation of nanograins.
5. X-ray Characterizations of Grain Rotation
The computation models usually cannot deal with texture evolution well and often overestimate the rate of texture development. The lack of local-scale experimental input is the main reason, and the models are built on global assumptions without considering the local surroundings of individual grains. In order to obtain the local-scale dynamic data, Margulies et al. used three-dimensional (3D) X-ray diffraction microscopy [
5] to examine a high-purity aluminum sample (3 mm thick and 300 µm across in diameter) at various strain levels. The grain rotation and grain subdivision were measured during the deformation of polycrystals. This technique allows for simultaneous measurements on multiple grains and provides statistical analysis for ensembles of the sample grains. A 3D grain map can be extracted to record the information on neighboring relations. From the grain boundary maps in the deformation, the changes in the grain shape and texture evolution can be generated. This technique bridges the grain and subgrain length scales. The measurements can provide the necessary information for establishing and testing the local models, e.g., finite-element analysis algorithms. Experimental information on grain rotations are not consistent with the traditional Taylor and Sachs models, indicating that the local dynamic information is important for the solid modeling of grain rotation.
For the grain rotation at the nanoscale, several mechanisms have been proposed, such as grain boundary sliding with atomic shuffling, stress-induced disclination dipoles, and disorder-enhanced mobility of atoms at grain boundaries. At the Berlin Electron Storage Ring Society for Synchrotron Radiation (BESSY), Zizak and co-workers investigated the radiation-induced deformation properties of nanocrystalline titanium by examining the bombardment-induced texture changes. They found that a substantially large amount of strain is induced by the collective rotations of multiple nanocrystals [
3], which, in contrast, is immeasurably small or absent in microcrystals. Grain rotation can be correlated with the radiation-induced movement of amorphous matter at grain boundaries. The nanograins float around by the disclination dipoles at grain boundaries. In nanocrystalline ceramics, the plastic strain is thought to originate from the grain boundaries and the grain interiors do not deform plastically (we have found that this assumption is not true in real cases). Although there is no complete freedom for grains to rotate, the mutual hindrance is small. The rotation rate and shear rate are coupled. In nanocrystalline metals, the authors assume that the plastic strain occurs exclusively in the grain interior, presumably in the form of dislocation loops. The transient stress fields arising from subsequent ion bombardment may induce an array of dislocations and thus pileups at the grain boundaries. When the pileup stress exceeds a critical value, climbing dislocations occur due to splitting. Disclination dipoles move along the grain boundaries, inducing shear and grain rotation. Shear and grain rotation need not stop simultaneously. Grain rotation will cease when the dislocation arrays pass a triple line with no disclination dipoles formed.
Another synchrotron-based technique, X-ray absorption near-edge structure spectroscopy and photoelectron emission spectromicroscopy (XANES-PEEM), has been found to be useful for characterizing the grain rotation of materials that have a strong X-ray linear dichroism effect. The polarization-dependent imaging contrast (PIC) mapping with XANES-PEEM detected the gradual ordering processes in mollusk shell nacre [
50]; the mineral blocks that have alternating orientations in sea urchin teeth [
51]; and the mechanism of secondary-nucleation-mediated co-orientation, also in sea urchin teeth [
52]. Gilbert et al. explored this technique further and determined the orientations of individual calcite nanocrystals with a spatial resolution of 10 nm [
11]. The XANES spectra of the carbon K edge were collected from a single crystal of calcite at different angles of the linear polarization vector. The polar angle represents the angle between the linear polarization vector and the calcite c axis, which completely describes the calcite crystal and its c-axis direction. The intensities of the π* (pi antibonding) and σ* (sigma antibonding) peak are anticorrelated: at large polar angles (90°) the π* peak has a minimum and σ* peak has a maximum intensity. The intensity of the π* peak is the strongest at low polar angles (0°). XANES-PEEM can achieve spatial resolution on the order of several nanometers. This experimental technique will be especially useful for elucidating the well-controlled nanoscale organization of biominerals.
For the plastic deformation of nanomaterials, an inverse Hall–Petch size dependence has been reported for the strength of nanometals below a critical length scale because in the plastic deformation at the lower nanoscale, dislocation activity fades away and GB sliding, diffusion, and grain rotation take over the role [
53]. GB-mediated mechanisms are reported yielding a d
−4 dependence on grain rotation rate, where d represents the grain size [
54], i.e., grain rotation activity is greatly enhanced in ultra-fine nanocrystals. Crystallographic alignment due to grain rotation has been observed in 2-to-3-nm ferrihydrite nanocrystals [
55,
56,
57], which seems to be the supportive evidence for the grain rotation enhancement with decreasing grain size. In contrast, computer simulations reveal that GB mobility weakens with decreasing grain size [
33,
58]. Although the in situ examinations of grain rotation of micrometer and coarser crystals during plastic deformation are feasible [
5,
59], in situ measurement of grain rotation at the nanoscale is difficult and remains to be explored. In radial diamond-anvil-cell X-ray diffraction (rDAC XRD) experiments, Chen et al. investigated the texturing of bulk-sized platinum embedded in nickel particle with sizes from 500 nm down to 3 nm [
60]. They found that the texture intensity of the platinum of the same grain size drops rapidly with decreasing grain size of the surrounding nickel medium, which indicates that grain rotation occurs in a more active mode in the smaller nickel nanocrystals. It has been established that dislocations glide in preferred directions giving rise to a deformation texture whereas grain rotation through GB sliding alone will randomize the grain orientation distribution and thereby destroys texture formation. Basically, under uniaxial compression, the texture of a polycrystalline material is mainly determined by the slip activities, i.e., the maximum texture strength for fcc platinum at (110) is expected [
60], similar to the texture pattern for fcc nickel (
Figure 4). However, the observed big change in the texture profile of platinum indicates that some other external factors introduced in the experiments destroyed the typical correlation between the texture profile and slip activities. The authors conclude that the grain rotation of the nickel nanocrystals in the mixtures of the platinum sample was responsible for the texture loss of platinum [
60].
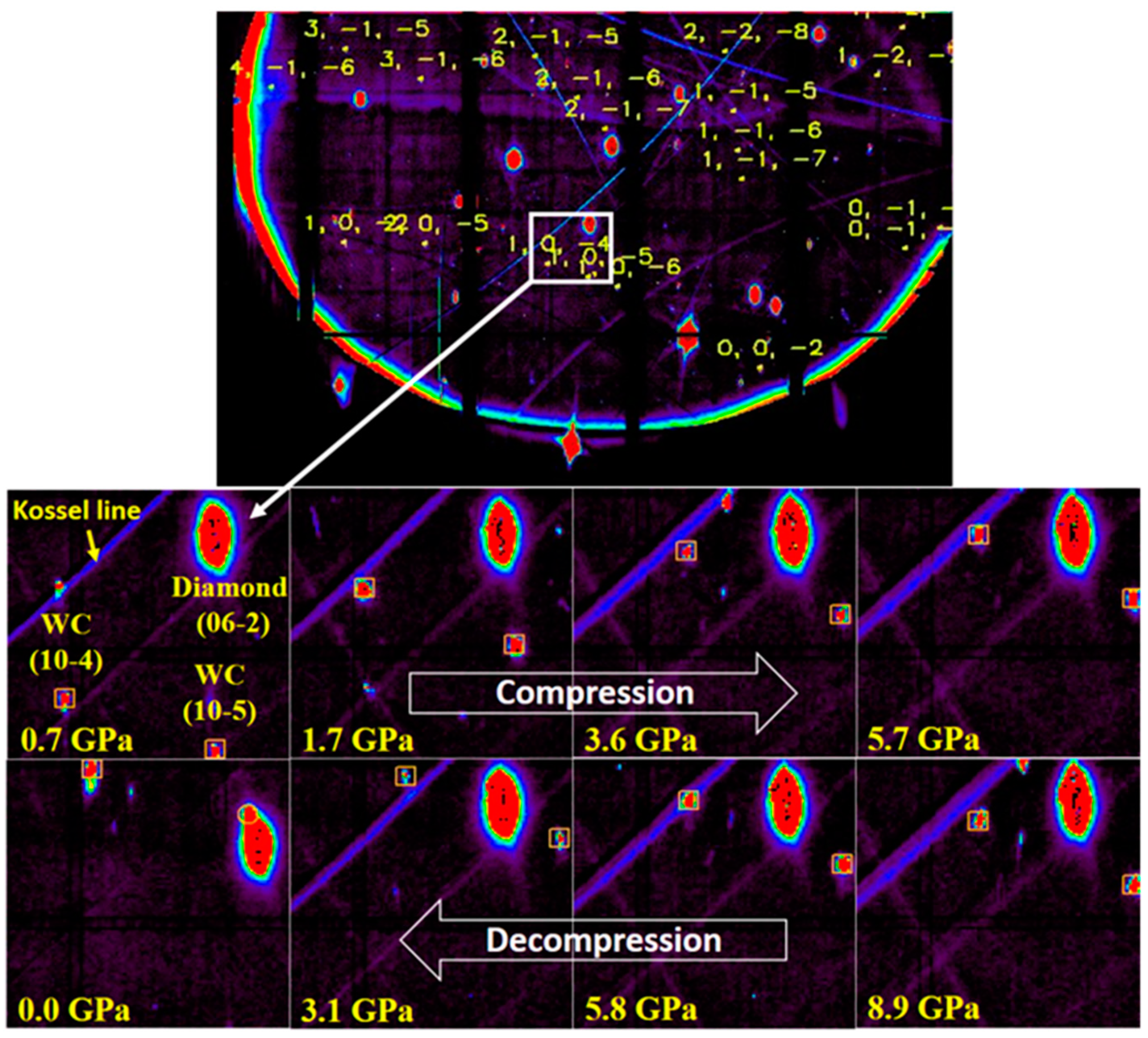
Texture measurements do not give direct information regarding grain rotation. As a continuing exploration of the above observation in rDAC XRD experiments, Zhou and co-workers used Laue X-ray micro-diffraction to track the orientation marker in nanosized media of different sizes and investigated the size dependence of grain rotation [
12]. For good detection signals, 6~8 µm tungsten carbide (WC) particles were mixed with nickel particles to measure the rotation magnitude of nickel nanograins. The very small amount of WC was well-diluted in the nickel nanocrystals. In order to extract the size effect on the grain rotation, they compared in the same differential stress conditions. They observed that the WC marker crystals in the nickel medium of the 70 nm grain size rotated more than in any other sized nickel media. It is inferred that the trend turnover in the size dependence of the grain rotation originates from the crossover between two different mechanisms: the grain boundary dislocation-mediated and grain interior dislocation-mediated rotation mechanisms. The activities of the grain interior dislocations are evidenced by a separate study on the deformation texturing of the nickel nanocrystals. This new finding will help to better unveil the deformation mysteries of nanomaterials and to optimize material properties. As shown in
Figure 4, the same sample volume can be mostly kept in the beam in the deformation. Laue XRD measurements can generate the direct information of grain rotation. Due to the beam size used in the study of Zhou et al. [
12], the smallest grains that can be identified directly from the individual diffraction spots are of 1 μm in diameter. The emerging Laue XRD techniques with a nanosized beam can identify grains with a size down to 10 nm and has great potential for exploration on this topic.
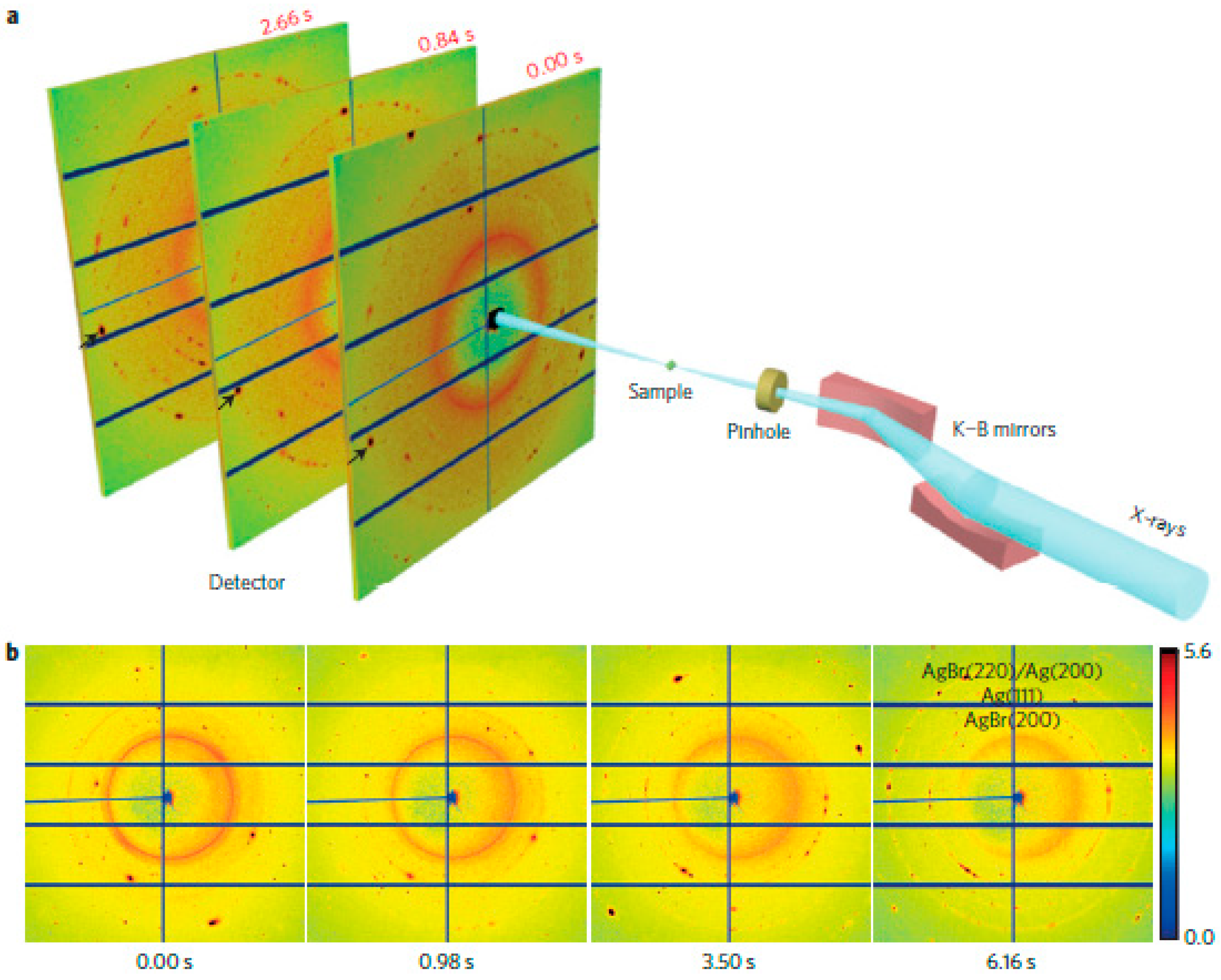
Mechanical properties of materials are also affected by dynamic processes [
61]. TEM can image grain lattice and grain boundaries with atomic resolution, but its temporal resolutions are very limited; meanwhile, XRD can give better temporal resolution and works more flexibly with different sample environments, but provides only the average structure of grains. Huang and co-workers developed an in situ X-ray nanodiffraction method by combining a brilliant synchrotron beam, Kirkpatrick–Baez (KB) mirrors, and a high-resolution X-ray detector (PILATUS 6M or 1M, DECTRIS AG, Baden, Switzerland) [
62], as shown in
Figure 5. They obtained the diffraction patterns from individual grains with a temporal resolution of several milliseconds. In this study, by tracking in situ the photolysis of AgBr grains and the formation of Ag nanograins, they observed lattice deformation and grain rotation during chemical reactions for the first time. If combined with various sample environments, such as high pressure, high temperature, and external fields, this in situ X-ray nanodiffraction technique will be even more powerful for grain rotation studies and can find wide applications in multiple disciplines.
6. Summary
In this article, the theoretical models, computer simulations, and experimental studies on grain rotation are reviewed. Grain rotation is actually related to multiscale physics and a spectrum of techniques are needed for various investigations. The information at the atomic level, such as chemical bonding, crystal defects, local strain/stress environments, etc., are necessary for examining the grain rotation behaviors and mechanisms. The information at the nanoscale and microscale may correlate grain rotation with the macroscopic properties of materials such as texturing, materials strengthening, crystal growth, phase transition, etc. A few techniques are reviewed in this article only as representative cases. The advances in techniques enable grain rotation probing with high spatial and temporal resolutions, which provides more and better information for improving the theoretical models of grain rotation, and broader applications are expected in materials science, physics, chemistry, and nanoscience.