Effect of Water Drawdown and Dynamic Loads on Piled Raft: Two-Dimensional Finite Element Approach
Abstract
:1. Introduction
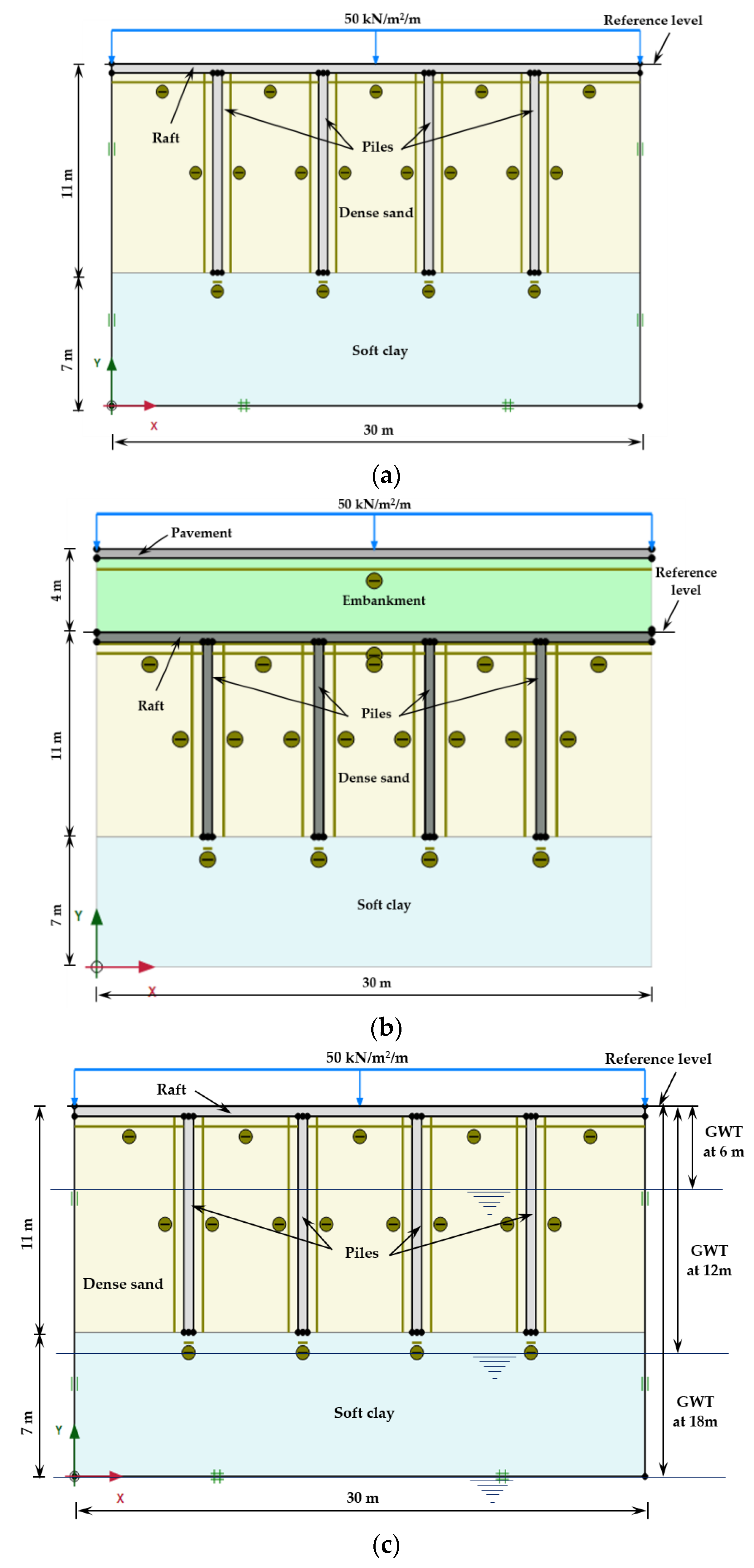
2. Finite Element Modeling and Model Setup
3. Results and Discussion
3.1. Case (i): Piled Raft Constructed in Sand Underlain by Clay
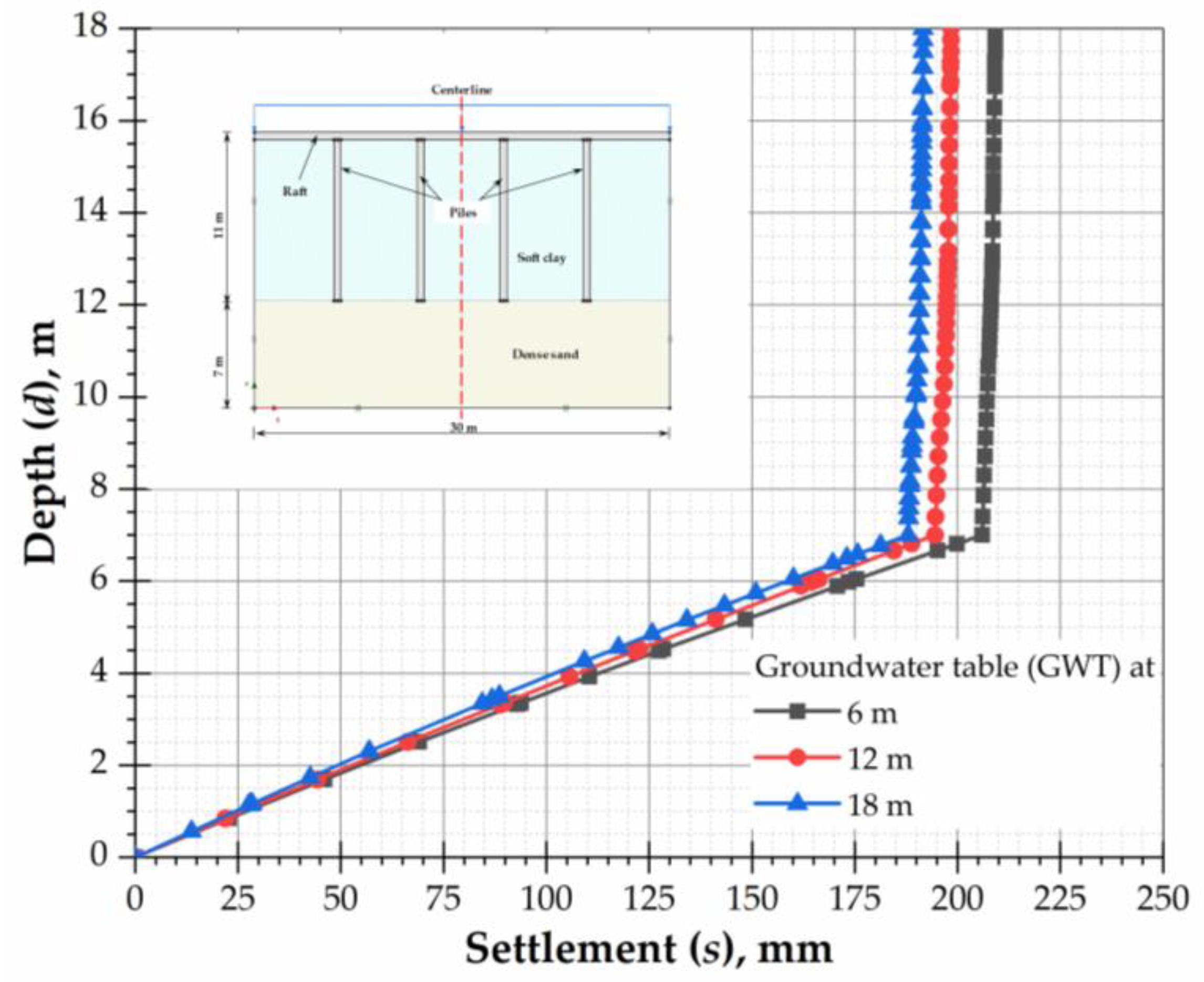
3.2. Case (ii): Piled Raft Constructed in Clay Underlain by Sand
3.3. Case (iii): Piled Embankment in Sand Underlain by Clay
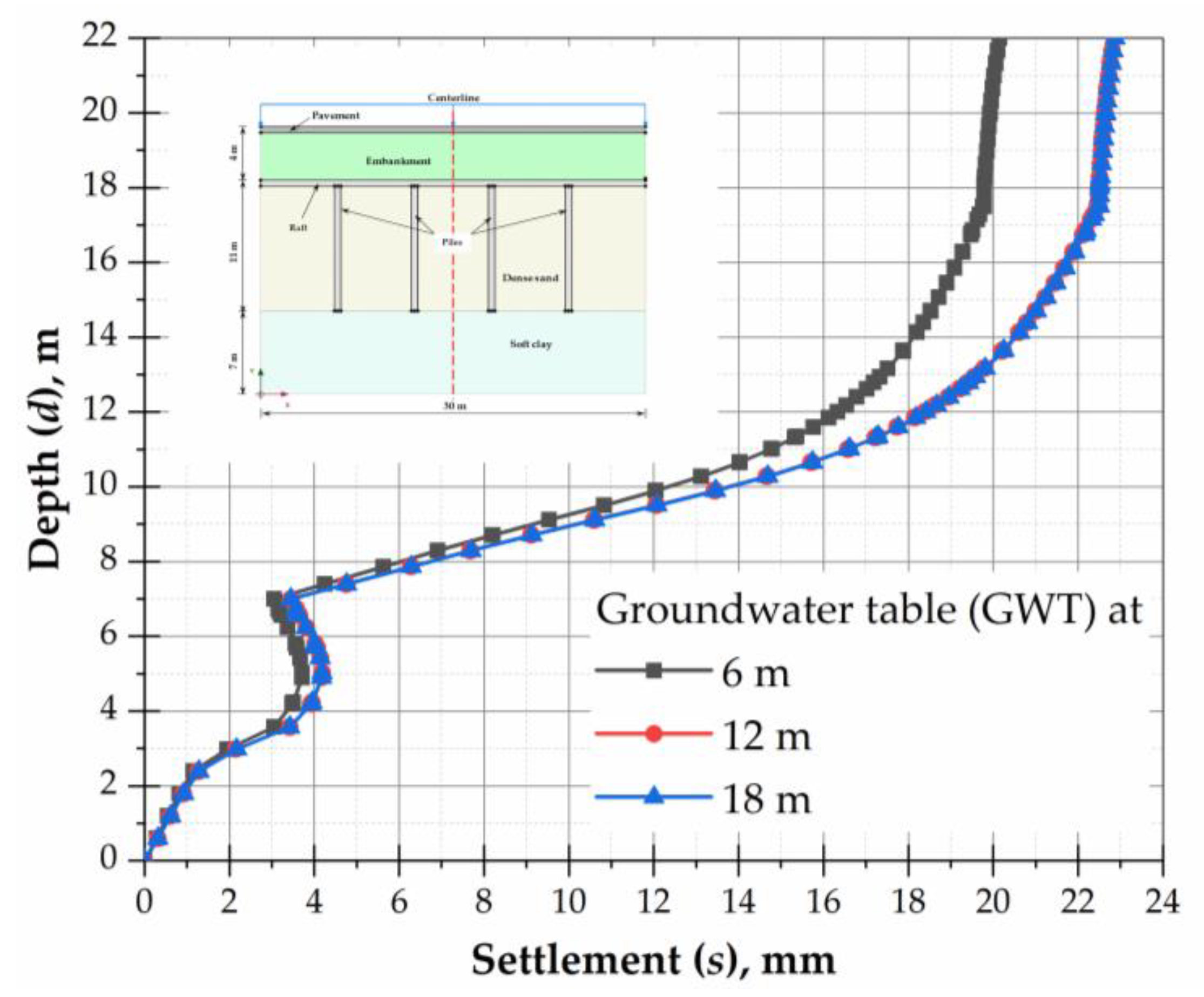
3.4. Case (iv): Piled Raft Embankment in Clay Underlain by Sand
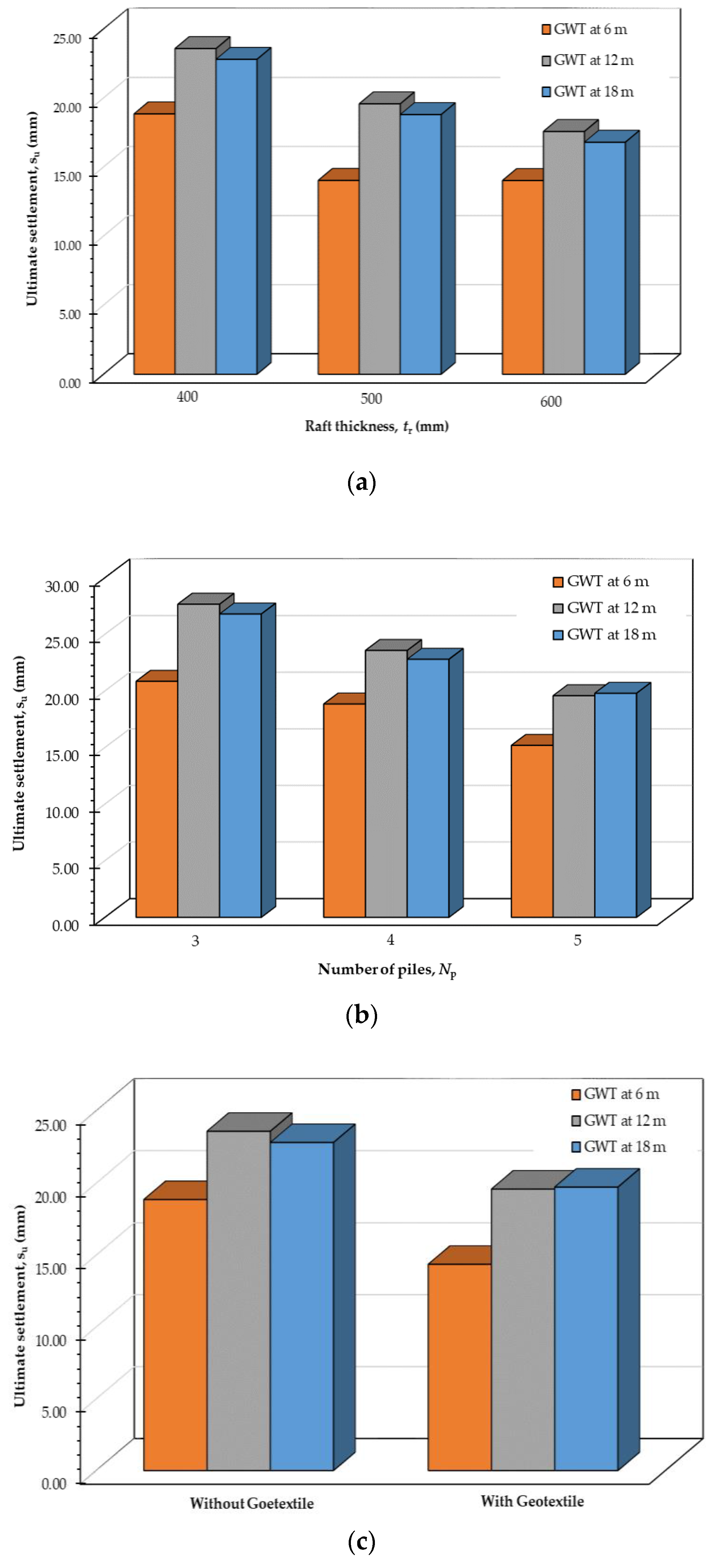
4. Improved Performance of Piled Raft
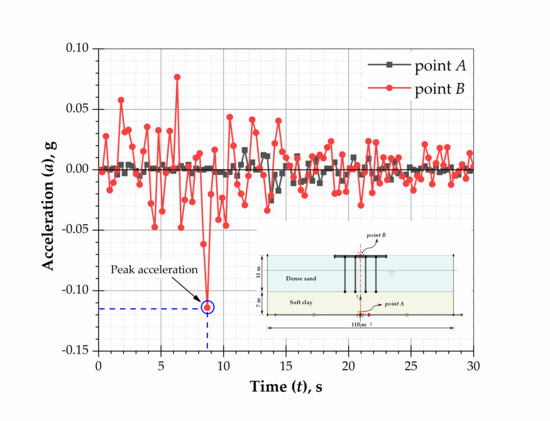
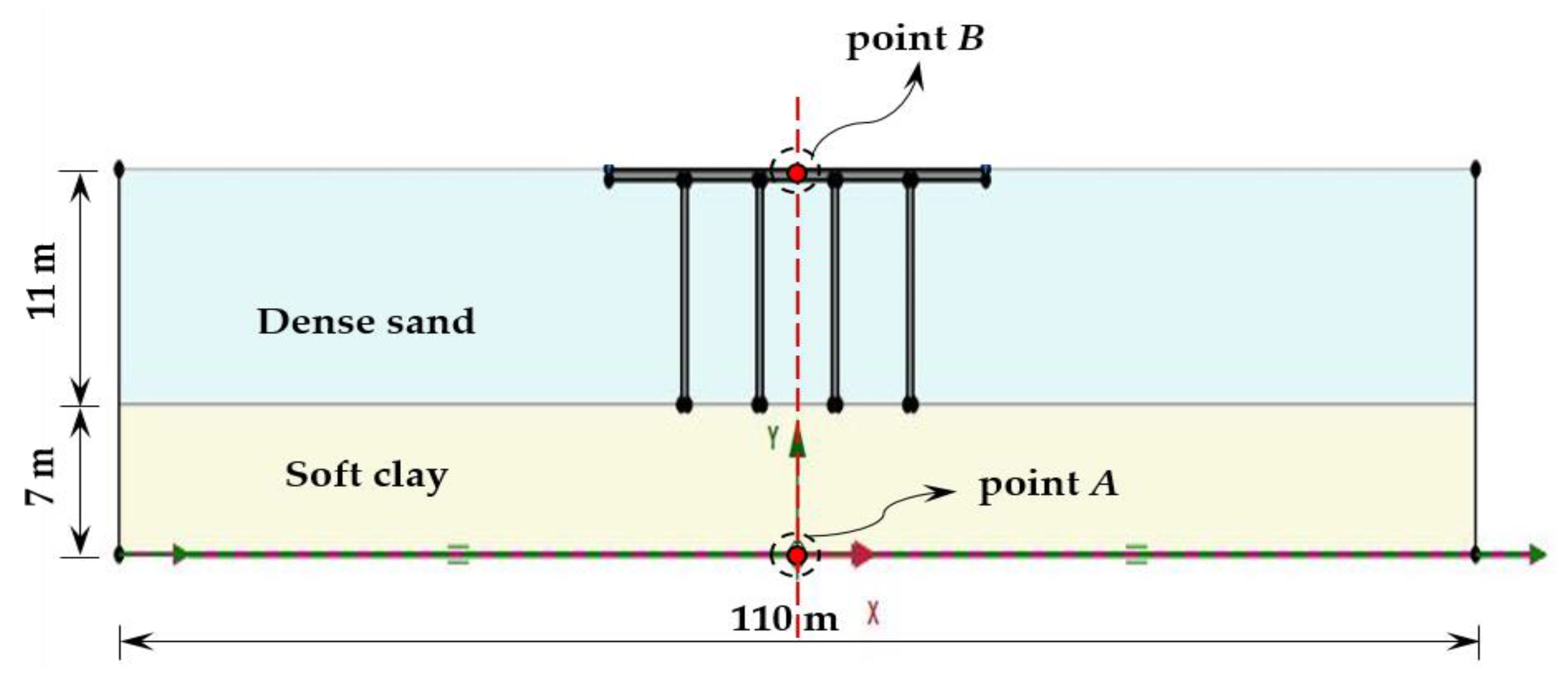
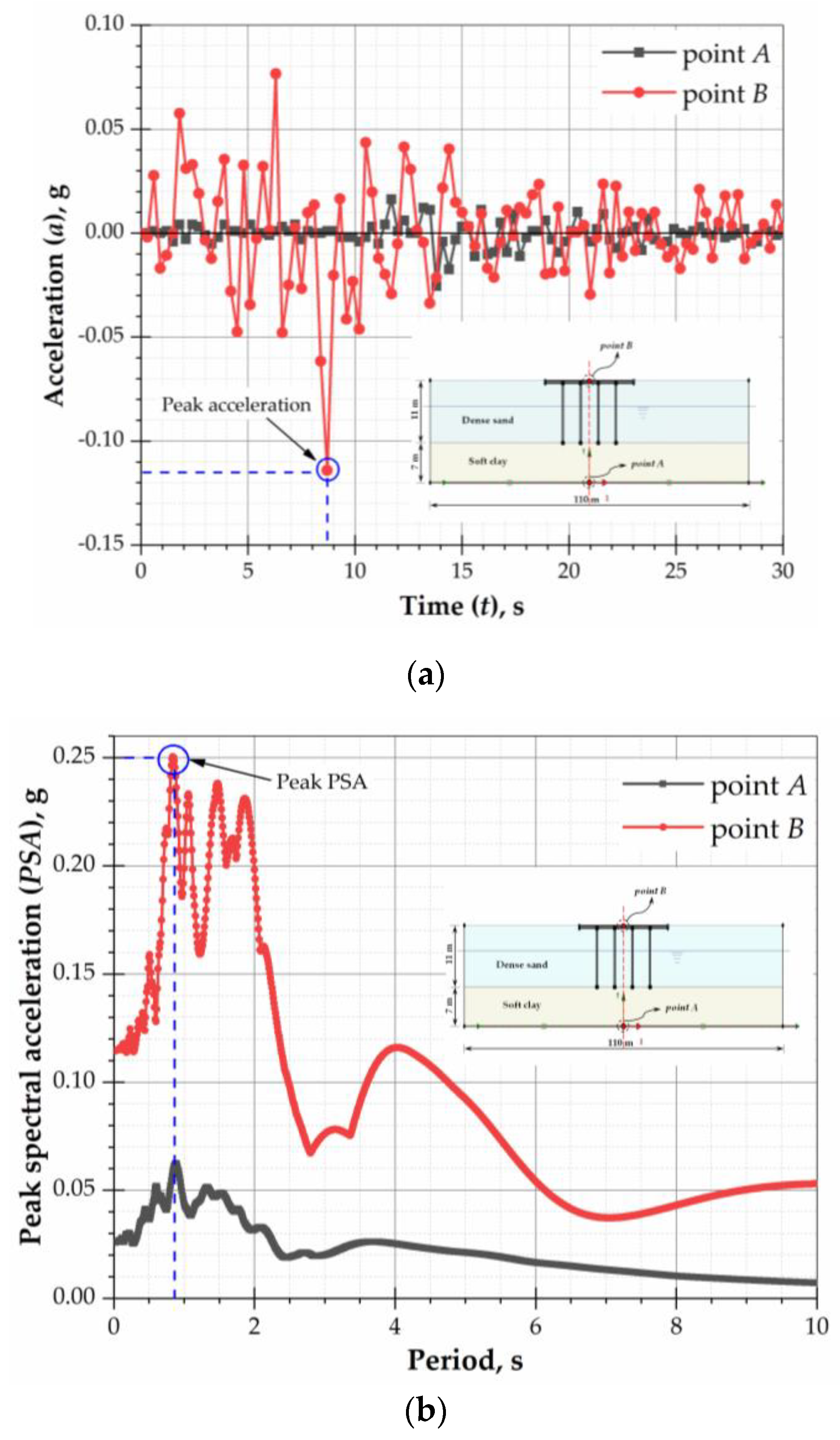
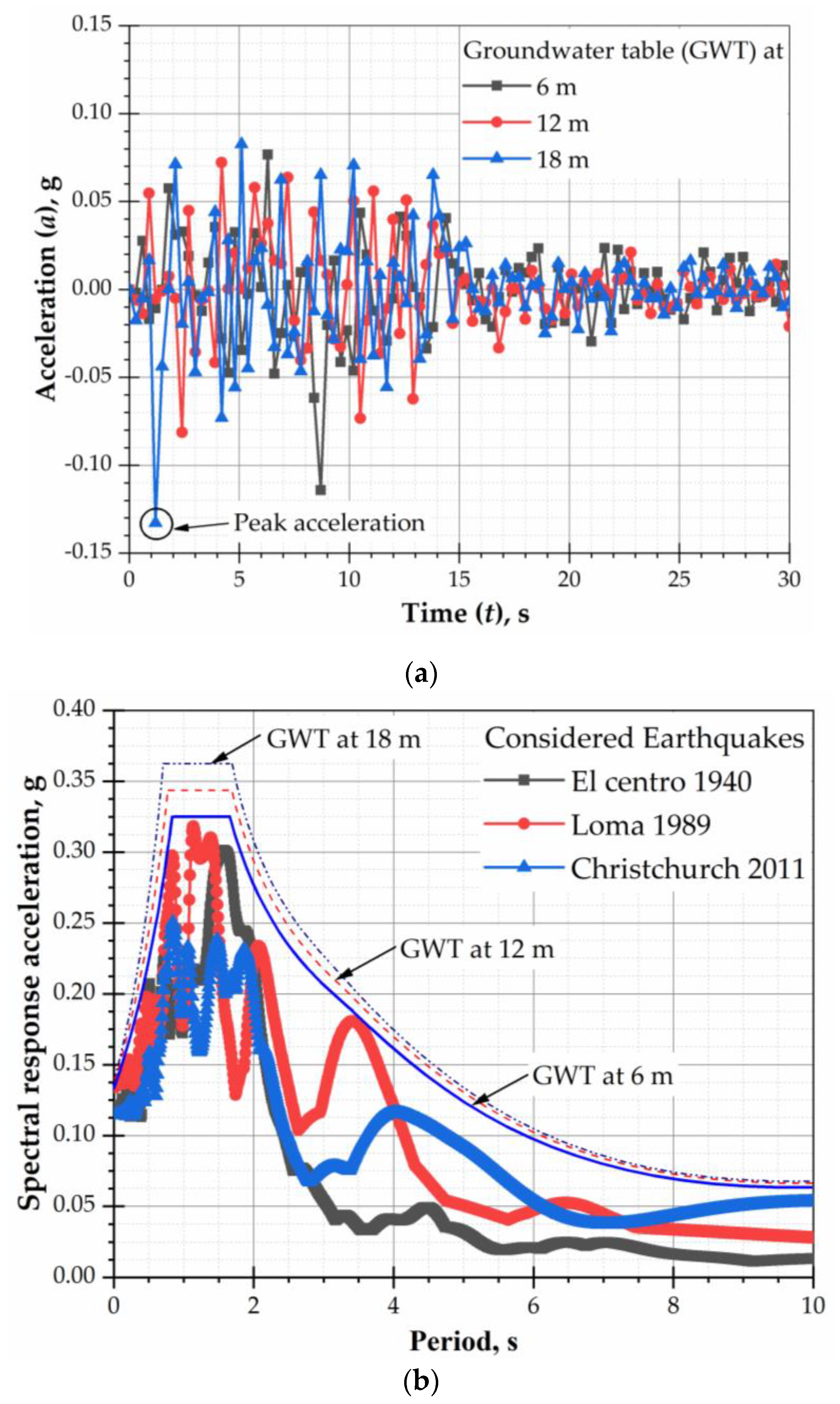
5. Seismic Response Analysis
6. Conclusions
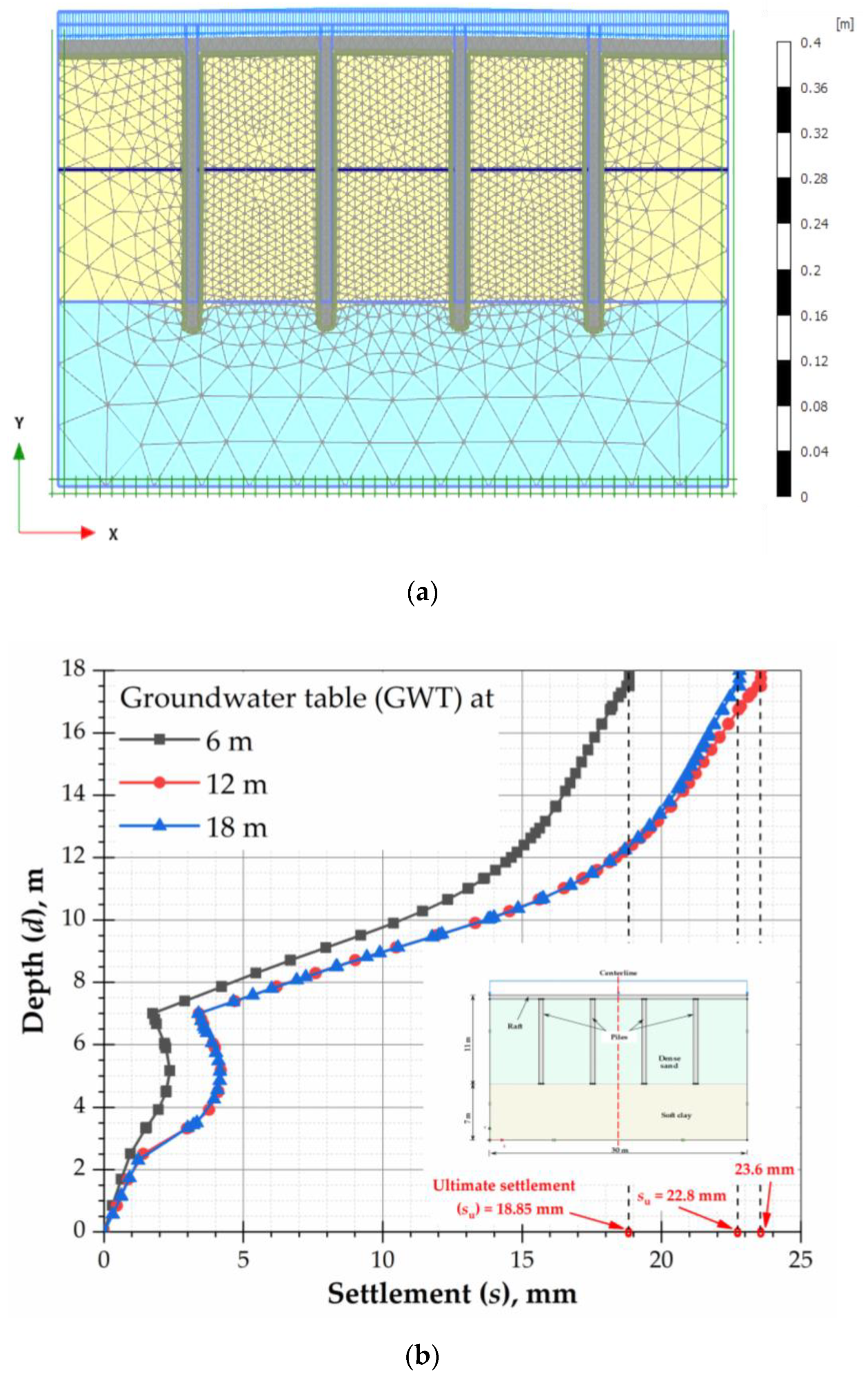
- The level of groundwater has a substantial effect on the settlement of piled raft foundation. The ground response is significantly influenced by the GWT fluctuation. The lower GWT gives low site frequency resulting in increases of peak ground acceleration. The peak acceleration increases by 20% when GWT is located at 18 m compared to 6 m and 12 m. Thus, the seismic response of the foundation system also affects the level of groundwater. This aspect should be considered in the design of piled raft.
- Three strengthening techniques are considered to improve the performance of piled raft. The settlement is reduced by up to 20% by introducing more number of piles compared to other considered strengthening techniques. It is worth noting that the liquefaction risk can be reduced by increasing the number of piles.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burland, J. Piles as settlement reducers. In Proceedings of the 19th National Italian Geotechnical Conference, Padova, Italy, 19–21 September 1995; Volume 2, pp. 21–34. [Google Scholar]
- Sawada, K.; Takemura, J. Centrifuge model tests on piled raft foundation in sand subjected to lateral and moment loads. Soils Found. 2014, 54, 126–140. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, D.D.C.; Kim, D.-S.; Jo, S.-B. Parametric study for optimal design of large piled raft foundations on sand. Comput. Geotech. 2014, 55, 14–26. [Google Scholar] [CrossRef]
- Basile, F. Non-linear analysis of vertically loaded piled rafts. Comput. Geotech. 2015, 63, 73–82. [Google Scholar] [CrossRef]
- Mali, S.; Singh, B. Behavior of large piled-raft foundation on clay soil. Ocean Eng. 2018, 149, 205–216. [Google Scholar] [CrossRef]
- Maharaj, D.K.; Gandhi, S.R. Non-linear finite element analysis of piled-raft foundations. Inst. Civ. Eng. Geotech. Eng. 2004, 157, 107–113. [Google Scholar] [CrossRef]
- Butterfield, R.; Banerjee, P.K. The problem of pile group–pile cap interaction. Geotechnique 1971, 21, 135–142. [Google Scholar] [CrossRef]
- Kuwabara, F. An elastic analysis for piled raft foundations in a homogeneous soil. Soils Found. 1989, 29, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Poulos, H.G. Tall building foundations: Design methods and applications. Innov. Infrastruct. Solut. 2016, 1, 10. [Google Scholar] [CrossRef] [Green Version]
- Poulos, H.G. Piled raft foundations: Design and applications. Geotechnique 2001, 51, 95–113. [Google Scholar] [CrossRef]
- Moormann, C. Geotechnical long-term monitoring: Impact of groundwater-lowering on adjacent high-rise buildings. In Field Measurements in Geomechanics; CRC Press: Borarton, FL, USA, 2003; pp. 250–257. [Google Scholar]
- Rahardjo, H.; Nio, A.S.; Leong, E.C.; Song, N.Y. Effects of groundwater table position and soil properties on stability of slope during rainfall. J. Geotech. Geoenviron. Eng. 2010, 136, 1555–1564. [Google Scholar] [CrossRef]
- Calin, N.; Radu, C.; Bica, I. Dewatering system of a deep of excavation in urban area–Bucharest case study. Procedia Eng. 2017, 209, 210–215. [Google Scholar] [CrossRef]
- You, Y.; Yan, C.; Xu, B.; Liu, S.; Che, C. Optimization of dewatering schemes for a deep foundation pit near the Yangtze River, China. J. Rock Mech. Geotech. Eng. 2018, 10, 555–566. [Google Scholar] [CrossRef]
- Viggiani, C.; Mandolini, A.; Russo, G. Piles and Pile Foundations; CRC Press: London, UK, 2014. [Google Scholar]
- Kumar, A.; Choudhury, D.; Katzenbach, R. Effect of earthquake on combined pile–raft foundation. Int. J. Geomech. 2016, 16, 04016013. [Google Scholar] [CrossRef]
- Das, B.; Saha, R.; Haldar, S. Effect of in-situ variability of soil on seismic design of piled raft supported structure incorporating dynamic soil-structure-interaction. Soil Dyn. Earthq. Eng. 2016, 84, 251–268. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H. Seismic response of clay-pile-raft-superstructure systems subjected to far-field ground motions. Soil Dyn. Earthq. Eng. 2017, 101, 209–224. [Google Scholar] [CrossRef]
- Yamashita, K.; Hamada, J.; Onimaru, S.; Higashino, M. Seismic behavior of piled raft with ground improvement supporting a base-isolated building on soft ground in Tokyo. Soils Found. 2012, 52, 1000–1015. [Google Scholar] [CrossRef] [Green Version]
- Buckman, S. Earthquakes down under: A rare but real hazard. Conversation 2015, 1–4. Available online: http://ro.uow.edu.au/cgi/viewcontent.cgi?article=3576&context=smhpapers (accessed on 5 March 2019).
- Standards Australia. Structural Design Actions Part 4: Earthquake Actions in Australia; Standards Australia International: Sydney, Australia, 2007. [Google Scholar]
- Geoscience Australia. Historic Earthquakes of Australia. Available online: https://geoscience-au.maps.arcgis.com/apps/MapSeries/index.html?appid=72ad590cc9364e41b06907406bb7712e (accessed on 5 March 2019).
- Cho, J.; Lee, J.H.; Jeong, S.; Lee, J. The settlement behavior of piled raft in clay soils. Ocean Eng. 2012, 53, 153–163. [Google Scholar] [CrossRef]
- Alnuaim, A.M.; El Naggar, H.; El Naggar, M.H. Evaluation of Piled Raft Performance Using a Verified 3D Nonlinear Numerical Model. Geotech. Geol. Eng. 2017, 35, 1831–1845. [Google Scholar] [CrossRef]
- Manafpour, A.R.; Moradi, V. Investigating conventional FE modelling for dynamic soil-structure interaction under horizontal and vertical ground motions. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Amorosi, A.; Boldini, D.; Elia, G. Parametric study on seismic ground response by finite element modelling. Comput. Geotech. 2010, 37, 515–528. [Google Scholar] [CrossRef]
- Basack, S.; Nimbalkar, S. Numerical solution of single pile subjected to torsional cyclic load. Int. J. Geomech. 2017, 17, 04017016. [Google Scholar] [CrossRef]
- Basack, S.; Nimbalkar, S. Measured and predicted response of pile groups in soft clay subjected to cyclic lateral loading. Int. J. Geomech. 2018, 18, 04018073. [Google Scholar] [CrossRef]
- Engin, H.K.; Brinkgreve, R.B.J. Investigation of pile behavior using embedded piles. In Proceedings of the 17th International Conference on Soil Mechanics and Geotechnical Engineering, Alexandria, Egypt, 5–9 October 2009; pp. 1189–1192. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Swolfs, W.M.; Engin, E.; Waterman, D.; Chesaru, A.; Bonnier, P.G.; Galavi, V. PLAXIS 2D 2010. Available online: http://plaxis.us/updater/Plaxis%202D/2013.02.16773.4521/files/classic/manuals/english/2D2012-0-Gen-Info.pdf (accessed on 5 March 2019).
- Wulandari, P.S.; Tjandra, D. Analysis of piled raft foundation on soft soil using PLAXIS 2D. Procedia Eng. 2015, 125, 363–367. [Google Scholar] [CrossRef] [Green Version]
- Rowe, R.K.; Liu, K.W. Three-dimensional finite element modelling of a full-scale geosynthetic-reinforced, pile-supported embankment. Can. Geotech. J. 2015, 52, 2041–2054. [Google Scholar] [CrossRef]
- Wang, K.; Zhuang, Y.; Liu, H.; Xiao, H. Multilayered low-strength geogrid-reinforced piled embankment. Geotech. Res. 2018, 5, 231–246. [Google Scholar] [CrossRef] [Green Version]
- GeoNet New Zealand. The New Zealand GeoNet Strong Motion Data Products. Available online: https://www.geonet.org.nz/data/types/strong_motion (accessed on 28 June 2019).
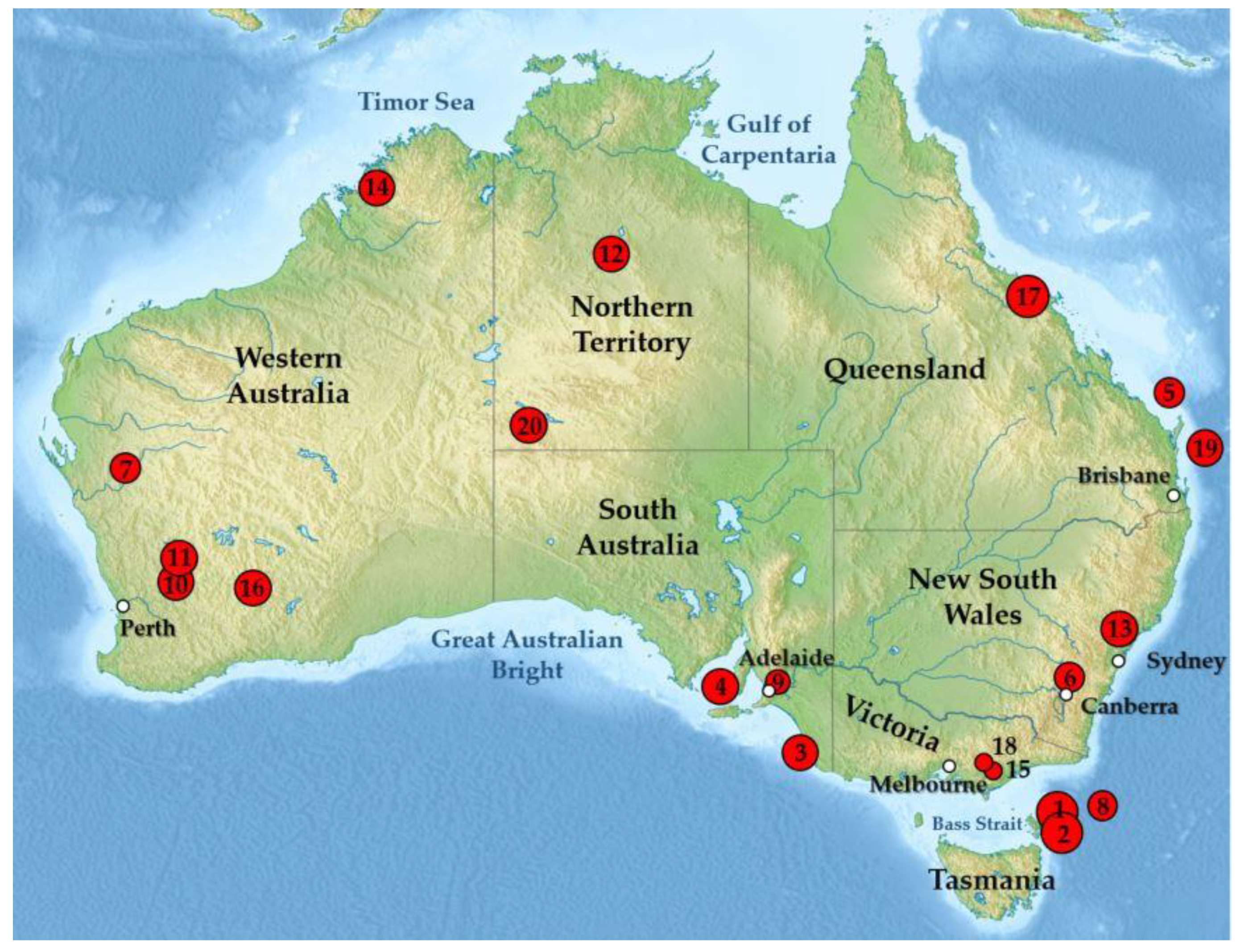


| Location No. | Year | Location | State | Magnitude (M) |
|---|---|---|---|---|
| 1. | 2016 | Petermann Ranges | Northern Territory | 6.1 |
| 2. | 2015 | Offshore East of Fraser Island | Queensland | 5.4 |
| 3. | 2012 | Moe | Victoria | 5.4 |
| 4. | 2011 | Near Bowen | Queensland | 7.1 |
| 5. | 2010 | Kalgoorlie | Western Australia | 5.0 |
| 6. | 2000 | Boolarra South | Victoria | 5.0 |
| 7. | 1997 | Collier Bay | Western Australia | 6.2 |
| 8. | 1989 | Newcastle | New South Wales | 5.4 |
| 9. | 1988 | Tennant Creek | Northern Territory | 6.6 |
| 10. | 1979 | Cadoux | Western Australia | 6.1 |
| 11. | 1968 | Meckering | Western Australia | 6.5 |
| 12. | 1954 | Adelaide | South Australia | 5.4 |
| 13. | 1946 | Offshore East of Flinders Island | Tasmania | 5.8 |
| 14. | 1941 | Meeberrie | Western Australia | 6.3 |
| 15. | 1934 | Gunning | New South Wales | 5.6 |
| 16. | 1918 | Offshore Gladstone | Queensland | 6.0 |
| 17. | 1902 | Warooka | South Australia | 6.0 |
| 18. | 1897 | Offshore Beachport | South Australia | 6.5 |
| 19. | 1892 | Tasman Sea NE | Tasmania | 6.9 |
| 20. | 1885 | Tasman Sea | Tasmania | 6.8 |
| Parameter | Clay | Sand | Embankment | Piled-Raft | Pavement Base |
|---|---|---|---|---|---|
| Material Model | HS Small | HS Small | Hardening Soil | Linear elastic | Linear elastic |
| Drainage Type | Drained | Drained | Drained | Non-porous | Non-porous |
| Soil unit weight above phreatic level, γunsat (kN/m3) | 16 | 20 | 16 | 24 | 15 |
| Soil unit weight below phreatic level, γsat (kN/m3) | 18 | 20 | 19 | - | - |
| Young modulus at reference level, E’ (kN/m2) | - | - | - | 3 × 107 | 3 × 107 |
| Secant stiffness in standard drained triaxial test, E50ref (kN/m2) | 2.0 × 104 | 3.0 × 104 | 2.5 × 104 | - | - |
| Tangent stiffness for primary oedometer loading, Eoedref (kN/m2) | 2.6 × 104 | 3.6 × 104 | 2.5 × 104 | - | - |
| Unloading/reloading stiffness, Eurref (kN/m2) | 9.5 × 104 | 1.1 × 105 | 7.5 × 104 | - | - |
| Power for stress-level dependency of stiffness, m | 0.5 | 0.5 | 0.5 | - | - |
| Poisson’s ratio, ν‘ | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 |
| Friction angle, φ’ (deg) | 18 | 30 | 30 | - | - |
| Cohesion, c’ref (kN/m2) | 10 | 5 | 1 | - | |
| Shear strain at which Gs = 0.7Go, γ0.7 | 1.2 × 10−4 | 1.5 × 10−4 | - | - | - |
| Shear modulus at very small strains, Goref (kN/m2) | 2.7 × 105 | 1.0 × 105 | - | - | - |
| Case | GWT at | Peak Stress, σmax (kPa) | Maximum Strain, εmax (%) | Ultimate Settlement, su (mm) |
|---|---|---|---|---|
| Case (i) | 6 m | 263.45 | 2.15 | 18.85 |
| 12 m | 289.55 | 3.75 | 23.58 | |
| 18 m | 305.21 | 4.52 | 22.80 | |
| Case (ii) | 6 m | 254.43 | 0.31 | 20.92 |
| 12 m | 375.95 | 0.37 | 19.85 | |
| 18 m | 394.24 | 0.42 | 19.17 | |
| Case (iii) | 6 m | 511.19 | 0.44 | 20.15 |
| 12 m | 520.21 | 0.45 | 22.85 | |
| 18 m | 570.85 | 0.44 | 22.87 | |
| Case (iv) | 6 m | 489.57 | 0.24 | 20.15 |
| 12 m | 519.12 | 0.27 | 22.85 | |
| 18 m | 549.43 | 0.30 | 22.87 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meena, N.K.; Nimbalkar, S. Effect of Water Drawdown and Dynamic Loads on Piled Raft: Two-Dimensional Finite Element Approach. Infrastructures 2019, 4, 75. https://doi.org/10.3390/infrastructures4040075
Meena NK, Nimbalkar S. Effect of Water Drawdown and Dynamic Loads on Piled Raft: Two-Dimensional Finite Element Approach. Infrastructures. 2019; 4(4):75. https://doi.org/10.3390/infrastructures4040075
Chicago/Turabian StyleMeena, Naveen Kumar, and Sanjay Nimbalkar. 2019. "Effect of Water Drawdown and Dynamic Loads on Piled Raft: Two-Dimensional Finite Element Approach" Infrastructures 4, no. 4: 75. https://doi.org/10.3390/infrastructures4040075