1. Introduction
Inertial migration effects have long been observed in macroscopic systems in studies regarding the flow of cells through capillaries and rheology experiments with suspensions of spherical particles [
1,
2,
3,
4]. Saffman later provided the theoretical basis that attributed this apparent migration of particles and cells to the inner region of capillary tubes and blood vessels to non-linearities of the Navier-Stokes (N-S) equations [
5]. With the advent of microfluidic technologies, inertial migration has acquired significant attention, thanks to its associated passive focusing capabilities in devices in which some form of suspended particulate flows in a driving fluid [
6,
7]. Microfluidic devices composed of serpentines or spiral channels are particularly suitable for experiments in which efficient conditions for inertial focusing are sought, because transverse flows that spontaneously emerge in curved geometries assist particles and cells in reaching stable positions faster [
8,
9,
10,
11,
12,
13]. Experimental and theoretical developments in the physics of inertial migration have improved our understanding of this phenomena [
14,
15,
16] and have led to the study of the underpinning mechanics for real-life conditions with finite Reynolds number (
Re) and finite particle size approximations [
17,
18,
19,
20]. The Reynolds number (which is used in fluid dynamics to quantify, in relative terms, the importance of viscous over inertial forces) is defined as
, where
is the fluid density,
its velocity,
is a characteristic length of the system, and
is the viscosity of the fluid.
In parallel to the development of the theory of inertial migration of particles, numerical methods have emerged as a powerful tool to predict inertial forces and particle focusing positions. Aiming at reducing the computational complexity of the simulated dynamics of particles in confined flows, many authors have proposed the use of an iterative procedure according to which the variables of the problem are referred to a moving frame of reference fixed to the moving sphere [
21,
22,
23,
24,
25]. Since the sphere is stationary with respect to this frame of reference, the velocity of the backwards-moving walls and the angular velocity of the particle are then iteratively updated until the particle moves force and torque free. This method helps find the inertial force distribution over the particle in a section of the channel. The use of such a physically constrained system, however, requires prior knowledge of the velocity and spin direction of the analyzed particle, which makes it unsuitable for complex channel geometries. Liu et al. proposed the use of an explicit formula for the lift force to predict the trajectories of particles in complex geometries using a Lagrangian tracking method [
26]. The coefficients of this formula, however, need to be determined through computational fluid dynamics (CFD) simulations of N-S equations solved for flows in straight channels.
Given the complexity of simulating particle migration conditions, some authors have proposed the use of lattice Boltzmann methods (LBM) [
27,
28,
29,
30], due to their lower memory consumption with respect to the more generally used finite element method (FEM) [
31]. Nonetheless, LBM is prone to cause instability issues in particle-fluid interaction simulations owing to its inherent inefficient representation of the solid boundary interface [
32]. Additionally, this method relies on analytical solutions [
28] that, in some cases, are only valid for very small Reynolds numbers. In order to improve the treatment of particle-fluid interactions at the boundary level, a coupling between LBM and the immersed boundary method (IBM) [
33] was proposed (IB-LBM) [
32]. Employing the IB-LBM method, Jiang et at. studied the focusing conditions of spherical particles in a symmetric serpentine [
34]. The drawback of the IB-LBM method is that the velocity field of the fluid and the particle are found by including a body force term into the lattice Boltzmann equation. This body force is in turn deduced from the deformation suffered by the boundary of the solid-fluid interface. Consequently, one must provide the simulation code with an appropriate stiffness factor—not too small so that it prevents flow perturbations caused by the deformation of the particle, but not too big so that no measurable distortion is obtained preventing the simulation to converge [
32]. The requirement for a measurable deformation in the IB-LBM method may also be the cause for particles moving close to the center of symmetry of a given channel geometry, remaining in those positions, even when inertial focusing conditions are reached [
34], a situation that is not reflected in the real experiment.
Fluid-structure interaction methods (FSI) are normally employed in systems in which deformations of a solid structure are expected, given their interaction with some fluid [
35,
36,
37,
38]. Because of computational restrictions, this method is rarely employed in simulations in which one of its components translates a long distance, e.g., a particle moving through a microfluidic channel. However, although scarce, previous work demonstrates the convenience of applying FSI methods for moving particles [
39,
40,
41]. The strength of this method is that it provides a solution that fully describes the physics of the process since the particle and the flow are defined with unconstrained components during the simulation—it can model how a moving object and the surrounding fluid affect each other.
In this paper, we propose a new two-way coupling FSI 3D model scheme for an asymmetric serpentine to simulate the influence of drag and inertial forces of the fluid over a particle with unrestricted degrees of freedom. In order to test the accuracy of this model, we obtained images of focused fluorescent particles in a microfluidic device and then compared the luminous streak with the obtained trajectory in the simulation process. The flow rate and geometry of the simulated domain were adjusted to match the experimental values in the microfluidic device. The simulation results from the free-rotating particle also allowed to find the angular velocity components of the particle, providing a set of variables that are hardly attainable under postulated assumptions alone. Using a provided definition for the transverse flow (Dean flow), we present a phenomenological relationship about the behavior of the rotating particle and its interaction with the Dean and gradients of the flow. We believe that the description about the evolution of the angular velocity of the particle can be incorporated in a variety of systems, e.g., spirals [
10,
42,
43], symmetric serpentines [
44], and expansion/contraction chambers [
45], to name a few, in order to define pre-set angular velocity components in less computation-intensive simulations like the ones we find in the literature for the more-simple straight channel case [
21,
22,
23,
24,
25]. This would allow a substantial time improvement for simulations involving complex microfluidic systems in which some form of transverse flow is present.
2. Model and Methods
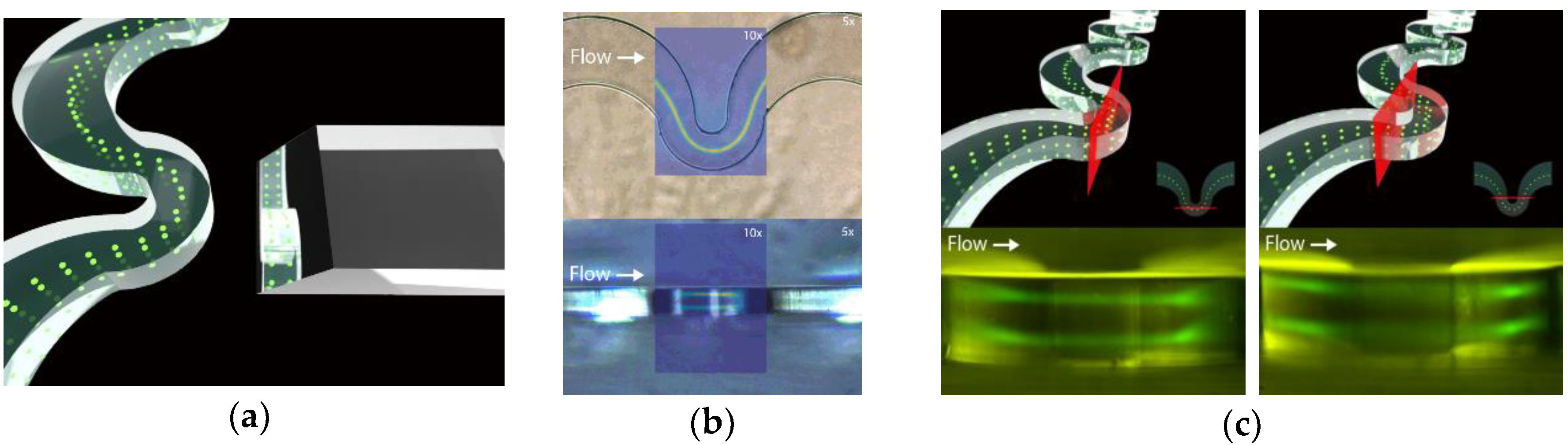
In order to test the suitability of our simulation model, a microfluidic device with the same serpentine geometry was created employing conventional photolithography techniques. SU8 (SU8-2150, MicroChem Corp., Newton, MA, USA) was spun on a 3-inche silicon wafer at 3500 RPM to obtain the desired channel height. The design of the serpentine was transferred from a chromium mask onto the SU8 layer using a UV mask aligner (MG 1410, SÜSS MicroTec AG, Garching, Germany). The microfluidic chip was elaborated in polydimethylsiloxane (PDMS) (Sylgard 184 from Dow Corning Corp., Midland, MI, USA). In addition to the conventional channels, the PDMS device also incorporated cavities to insert micromachined glass mirrors in the vicinity of the serpentine. The PDMS cavities devoted to the mirror had to be casted from micromachined structures directly stuck onto the Si wafer and placed very close to the fluidic channel. The mirrors were oriented at 45° and its field of view covered the entire height of the fluidic channel. This allowed to visualize the two stable trajectories of inertially focused fluorescent polystyrene particles (
Figure 1).
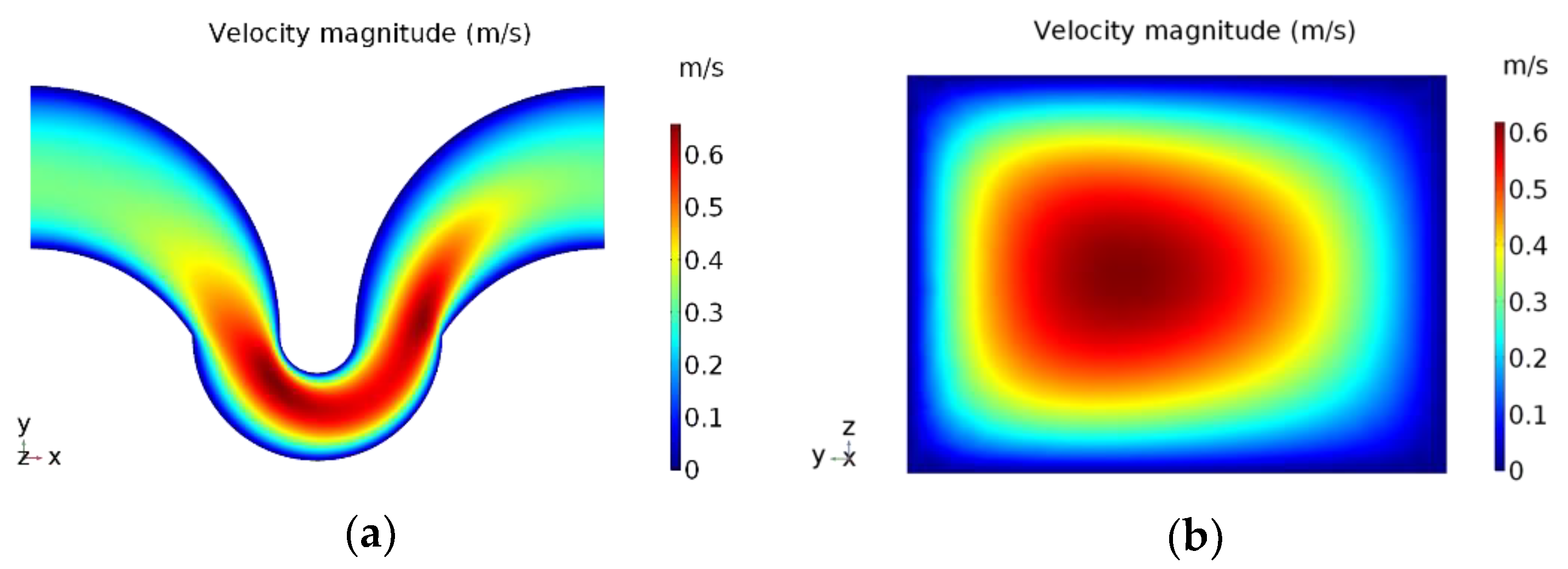
For simulation involving only the fluid, which was used to find the solution for the transverse flow, a 3D periodic unit of the serpentine (
Figure 2) was used as the computational domain. Periodic flow conditions were required to set a pressure difference between a source boundary, where the fluid enters the domain, and a destination group through which the fluid exits the domain. The pressure difference was set at 857 Pa so that the desired flow rate of 130 μL/min was obtained during the simulation; the same used in the experiment with the fluidic device. We chose this geometry and flow rate for the simulation because the experimental results showed very good focusing conditions for particles that were optimal after 24 big-small curve doublets. The mesh also incorporated a finer mesh region inside the small turn in order to improve the simulation results in the region around which Dean vortex centers are expected to develop. The governing equations for momentum and mass conservation solved during the computation step were:
where
is the velocity field of the flow,
the pressure,
the unit identity matrix, and
and
the density and viscosity of the fluid, respectively.
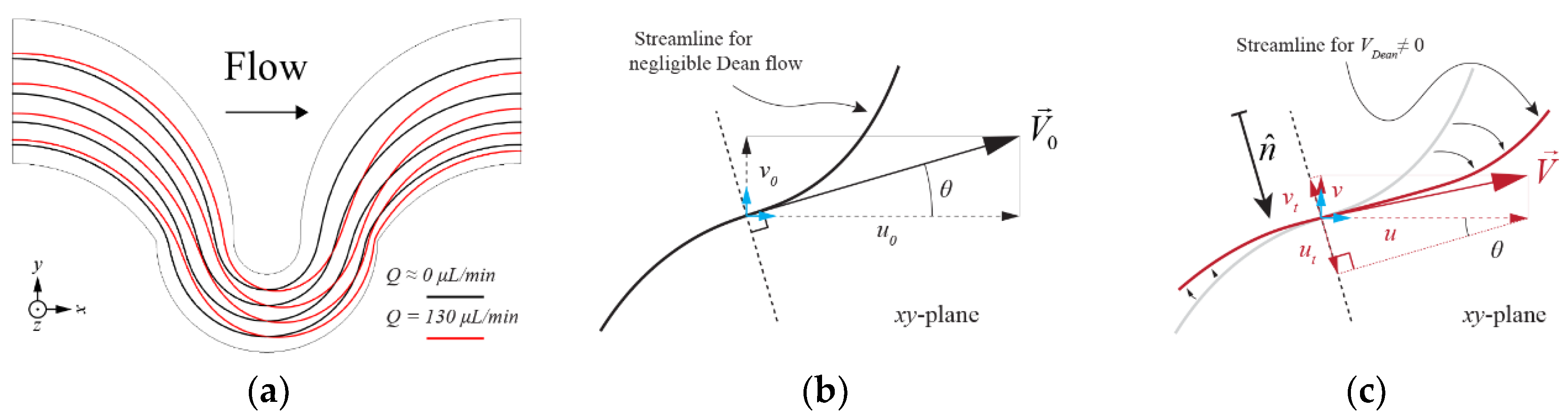
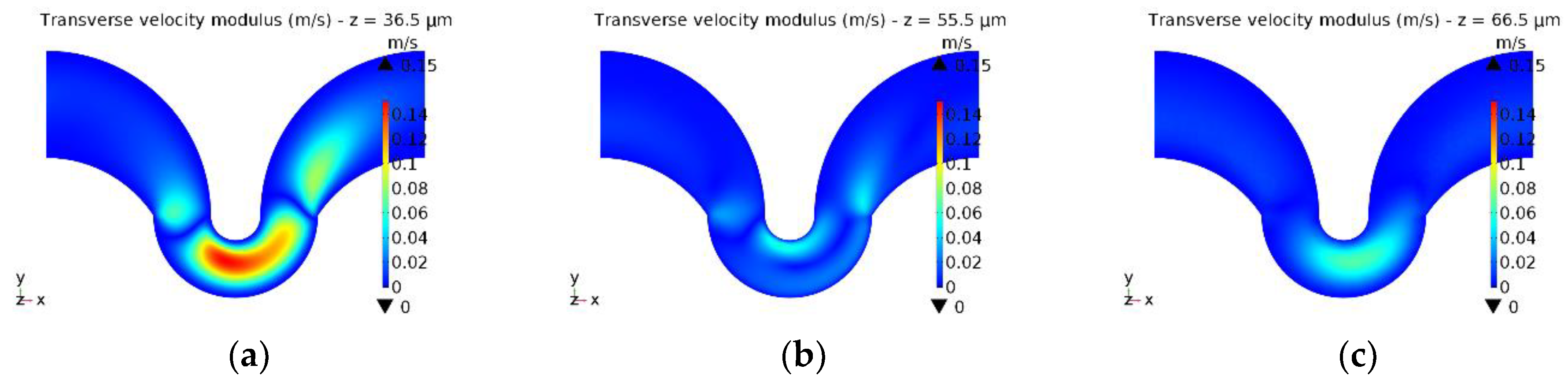
Bounded flows with some degree of curvature may facilitate the emergence of a flow field distribution that is perpendicular to the streamwise flow called Dean flow. These flows originate from the difference in velocity at the inner region of the fluidic channel with respect to the near-wall regions, which in comparison, due to the parabolic velocity profile, tend to be negligible. When the flow rate is sufficiently low, the viscosity between the flow elements in a moving mass of fluid suffices to force the streamlines of fluid to follow the curvature of the channel. The dimensionless parameter used to characterize the strength of transverse flows is the Dean number, ; where is the hydraulic diameter, where and are the width and height of the channel, respectively, and is the radius of the curved channel.
We propose a new approach by which the direction and magnitude of Dean flows can be numerically calculated at the pointwise level inside a simulation domain employing a FEM. The flow field is simulated at low and high flow rates and the differences between them are measured point-by-point in order to infer the magnitude and direction of the resulting transverse (Dean) flow. In our calculations, we chose the transverse components of the flow field at a given point to be the velocity field in the
z direction (
w), and the velocity field components in the
x-y plane (
u and
v for
x and
y components, respectively). The latter coordinates are projected along a direction perpendicular to the streamlines obtained for the simulation at low flow rates (
Figure 3). This method can be applied to any channel geometry, provided that the solutions for two different regimes, creeping flow, and regular laminar flow, can be obtained.
The analytical expression of the transverse flow field is then defined point-by-point and expressed in terms of the variables obtained in a simulation involving a low flow rate (
Q(
v0 = 1 μm/s) ≈ 1.8 × 10
−4 μL/min),
u0 and
v0, and the variables obtained in the studied flow rate (
Q(
v0 = 0.67 m/s) = 130 μL/min)
u,
v and
w:
Dean patterns are commonly represented as flow field projections in a section of a microfluidic channel [
26,
34,
45,
46]. Such representation is indirectly based on the assumption that the streamlines of a hypothetical creeping flow are perpendicular to the said plane because its tangent components are taken as the Dean flow components. Reference cross-sectional planes (based on the geometry of the channel) to represent such flows can yield inaccurate results since, in general, it cannot be guaranteed that the streamlines of a flow, for which inertial effects can be neglected, are indeed perpendicular to the reference plane at any point. This is particularly true for the case of channels with complex geometries, such as serpentines or mixers, where new techniques have to be applied in order to visualize the complicated flow patterns that emerge [
47,
48].
The FSI simulation (in addition to N-S equations) also incorporated a term for the load on the solid boundary and a moving wall condition (displacement of the solid) for the fluid domain:
were
is the normal vector to the boundary of the sphere,
is the velocity of the fluid-solid interface, which acts as a moving wall for the fluid, and
is the structural displacement of the solid.
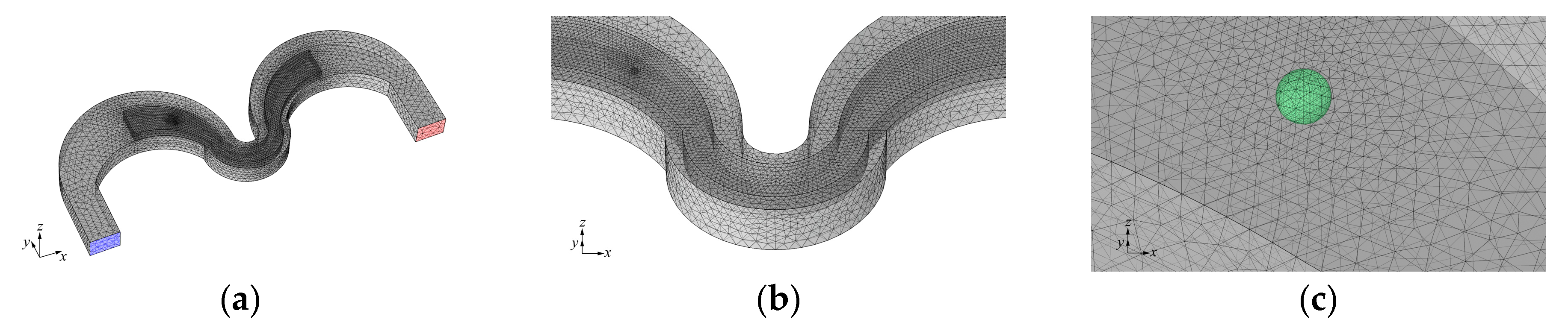
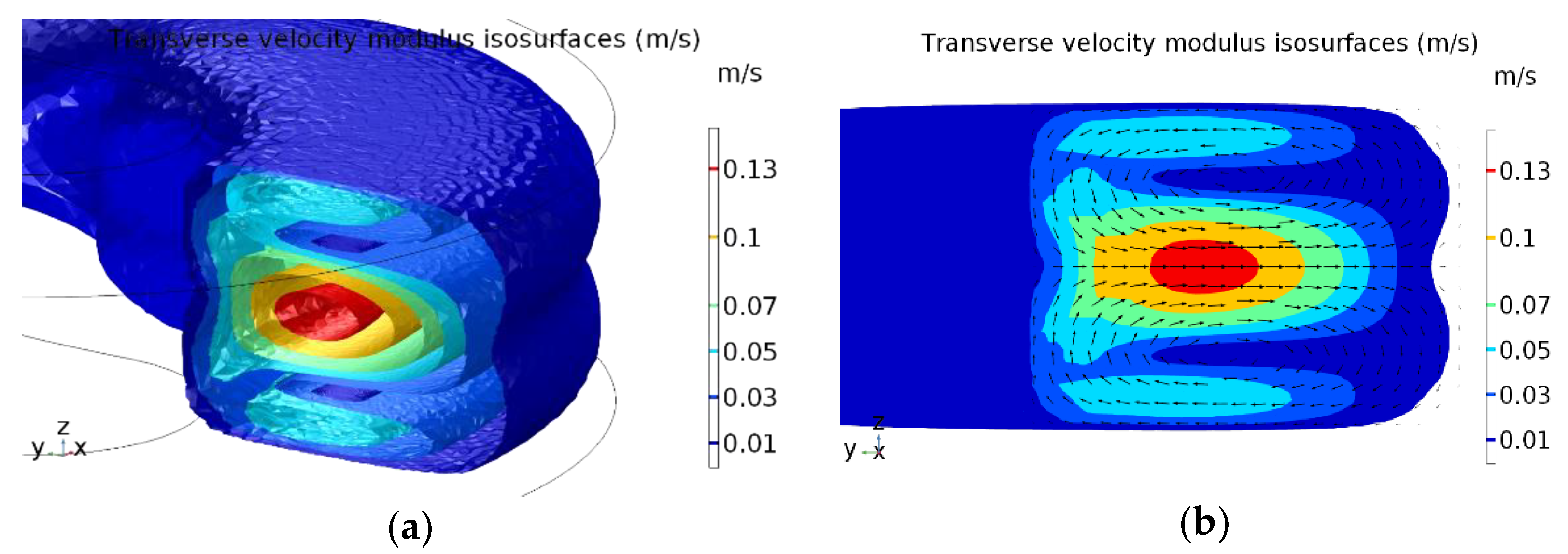
Figure 4 depicts the 3D fluid domain employed during the FSI simulation process. Unlike the stationary case, we opted not to use a periodic domain in the simulation involving the interaction between the particle and the flow. The reason is that periodic flow conditions only allow the use of pressure differences between the source and destination boundaries of the domain. The problem of using a pressure difference as a driving source for the flow in a transient simulation is that the pressure difference between the source and the destination boundaries—the pressure needed to obtain the desired flow rate—fixes the time it takes the flow to achieve stationary conditions, a regime that is expected as the particle travels through the region of interest (the small curve). Unfortunately, in our geometry, the time it takes the flow to achieve such conditions is so long that the particle penetrates the region of interest, while the flow hasn’t yet achieved stationary conditions (stationary flow rate and velocity profiles). Instead, by fixing an inflow velocity field distribution as a boundary condition for the inlet modulated by a smooth time dependent function, we can artificially set the time it takes the fluid domain to achieve a fully developed flow, a time that will be short enough so that the particle enters the small turn long after this condition is achieved. With this new boundary condition, we designed a new domain that comprised of a straight channel section, where the flow first develops, followed by a succession of big-small-big turns whose geometric parameters coincide with the microfluidic chip used to focus Ø = 10 μm particles in the experimental section. Like in the CFD simulation, the flow rate was set at 130 μL/min. The inlet velocity flow profile is approximated to that of a rectangular section channel by the expression:
where step (
t[1/
s]) is a dimensionless smoothed step function included to improve the convergence at the beginning of the time dependent simulation.
is a normalizing factor at the inlet boundary condition so that
at the center of the inlet. Similarly, the expression in the numerator ensures that
decays from the center of the channel out down to 0 at the walls in accordance with the no slip wall boundary condition for the flow introduced in the simulation. Notice that in the selected reference frame
has only a
y-component at the inlet (
Figure 4a). A 0 Pa pressure condition is set at the outlet.
is chosen so that, after stationary conditions are achieved, the desired flow rate is obtained in the channel (with our channel section,
Q(
v0 = 0.74 m/s) ≈ 130 μL/min). The flow rate is monitored by integrating the obtained flow fields across an arbitrary section of the channel. The length of the straight section ensures that the approximated velocity profile will have enough time to be fully developed at its end, before entering the first of the two big turns. Likewise, the big turn was completely included in the computational domain to ensure that the developed flow at the entry of the small turn was as similar as possible to the periodic case.
The mesh of the fluid domain was composed of two differentiated regions with two different mesh sizes (
Figure 4b). The finer mesh region was restricted to the upper half of the channel. It was devoted to act as an “envelope” domain for a particle in the upper stable trajectory; it was placed in such a way that, during the simulations, the particle would remain inside this domain at all times. The finer mesh allows the solver to calculate the variables of the problem more precisely, since it can resolve the gradients of pressure and velocity in the vicinity of the sphere more reliably. The domain also included a spherical mesh 10 μm in diameter (
Figure 4c), representing a particle, whose material properties were adjusted to match those of polystyrene. The series of FSI simulations consisted of numerically solving pathline trajectories of these spherical particles with different initial positions. The initial and final positions in the resulting simulation were located well away from the entry and exit of the small turn of the serpentine so that the particle’s behavior in this region was entirely captured. The mesh of the sphere itself was customized with lower element sizes than the predefined ones in order to obtain a reliable measurement of the calculated reaction forces.
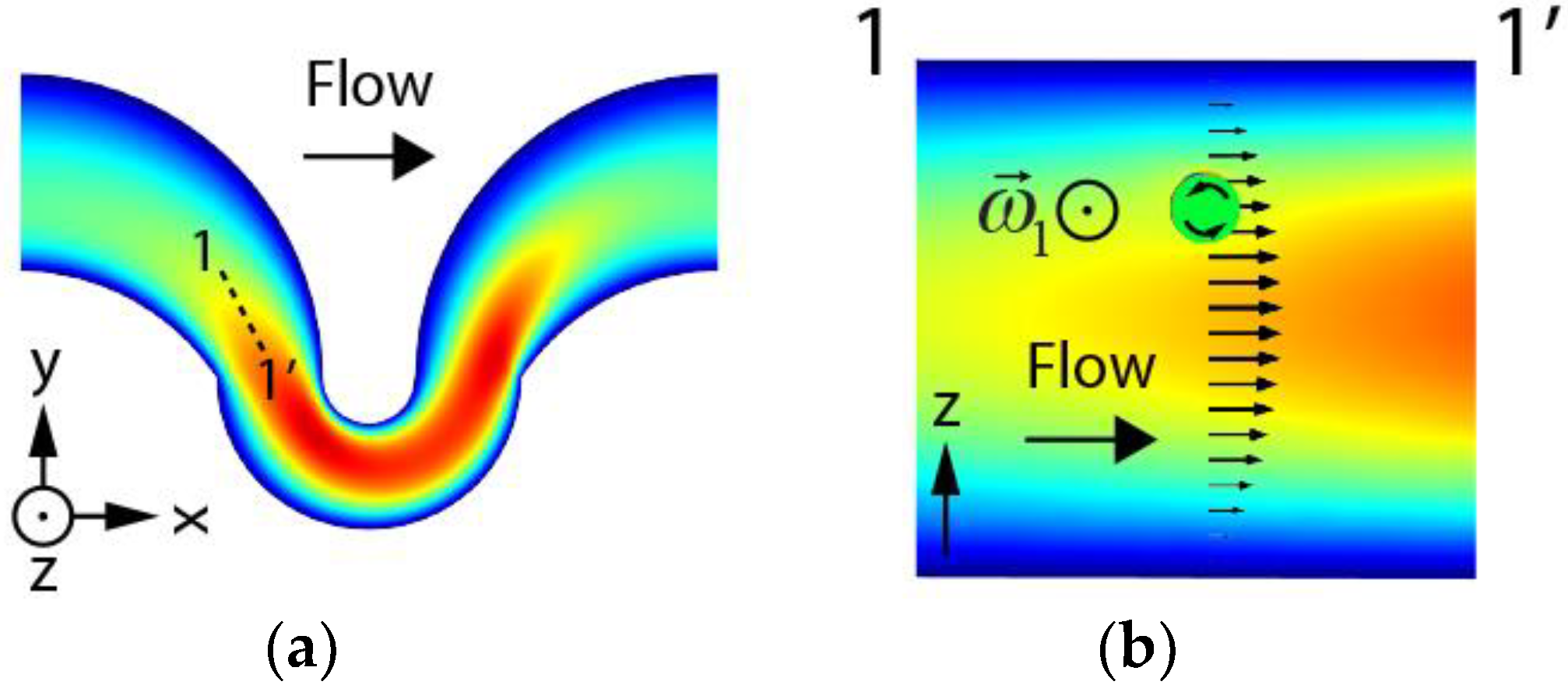
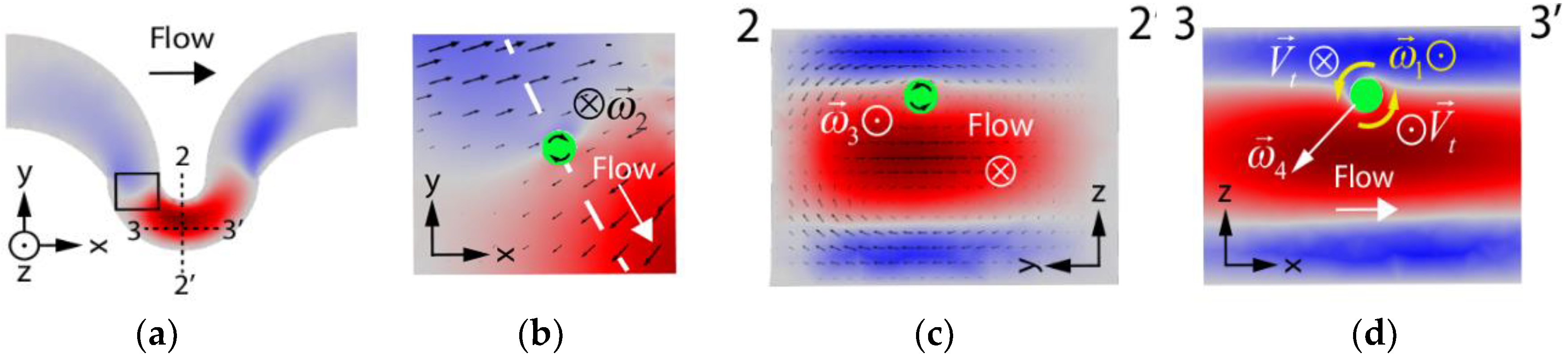
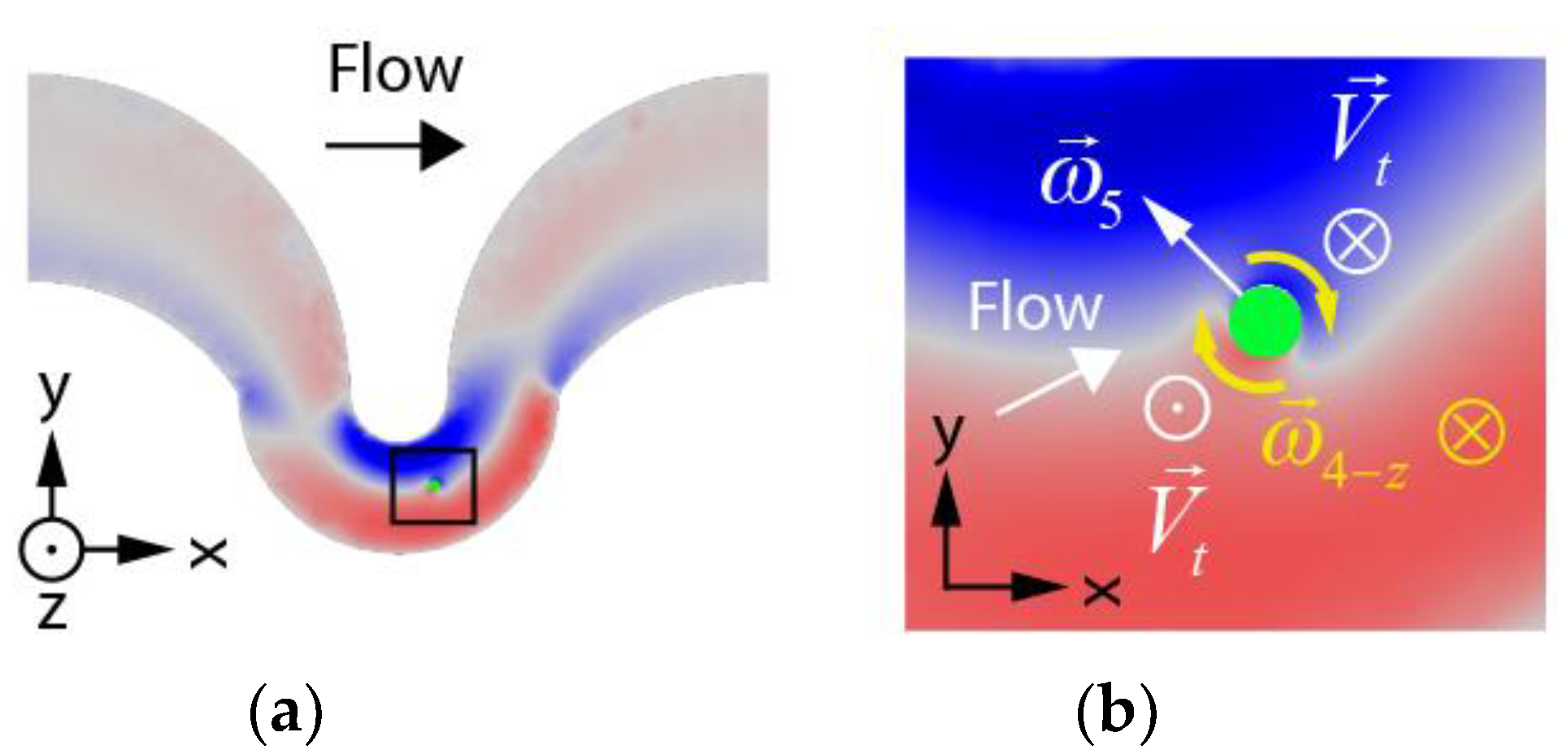
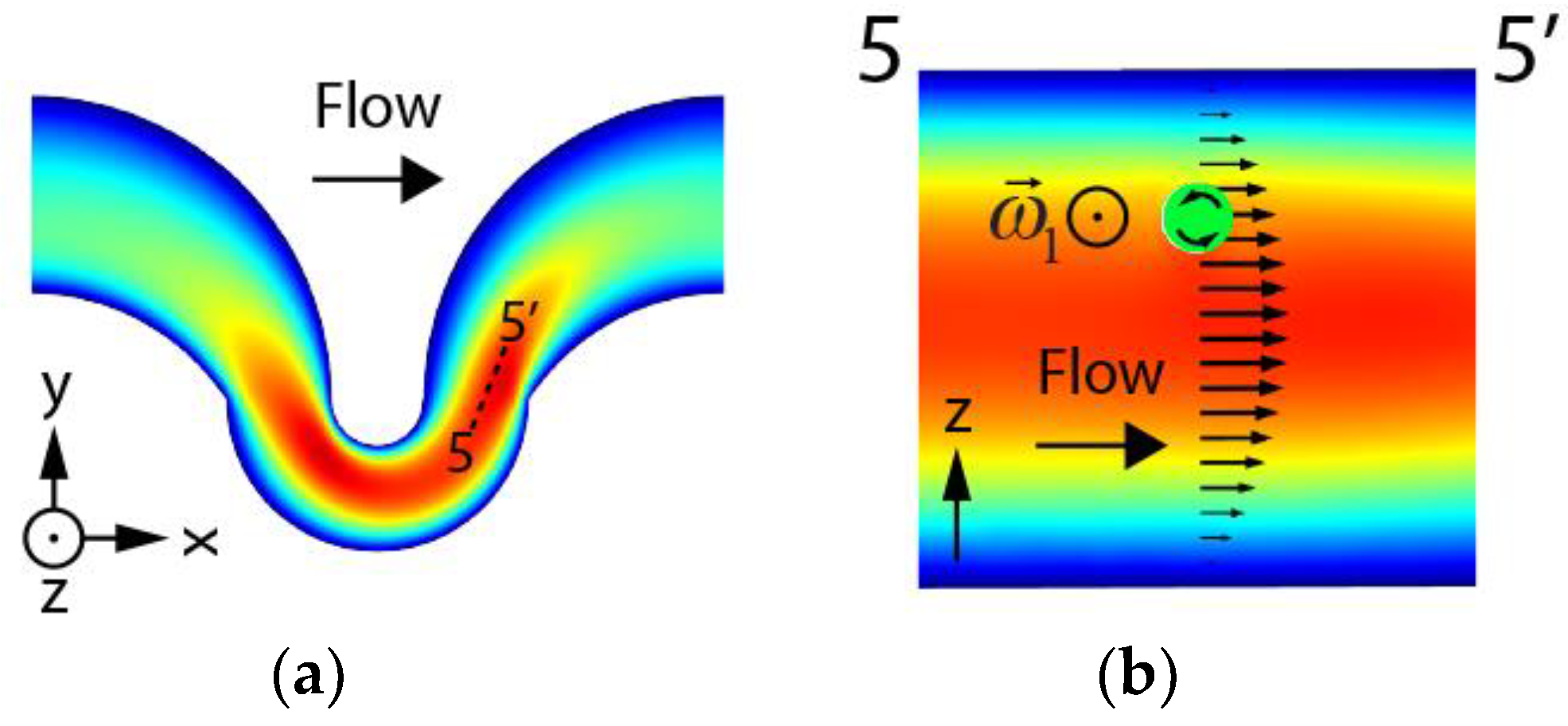
Since the flow and pressure profiles solutions are symmetric in z, the study of one of the two trajectories is enough to characterize the effects of the Dean flow when no interaction between particles is considered. In order to reduce the computational complexity and the number of degrees of freedom of the simulation, a coarser mesh was used in the rest of the fluid domain, a domain which only contained fluid throughout the simulation. It has to be stressed that due to the geometry of the problem and the complexity of the flow patterns arising in the channel, the 3D simulation could not make use of symmetries that would speed up the convergence of the solutions. Likewise, inertial terms in the N-S equations (which lead to non-linearities) could not be neglected in order for inertial migration effects to arise in the solutions.
In our problem, the FSI formulation couples the flow field and pressure solutions from N-S equations for an incompressible flow to solid mechanics equations, namely, the reaction forces over the solid boundary of the particle. The use of the FSI formulation for the time-dependent study in COMSOL (version 5.0, COMSOL Inc., Stockholm, Sweden) incorporates an arbitrary Lagrangian-Eulerian (ALE) method that takes into account the deformation of the mesh in the fluid domain caused by the movement of the particle being displaced under the influence of the surrounding flow. No constraint is applied on the particle, so it becomes a freely moving mesh. This circumstance imposes the use of an automatic remeshing feature at the mesh surrounding the particle, otherwise the fluid domain would be deformed indefinitely over time as the particle (the spherical mesh) moves along the channel (
Figure 5).
4. Conclusions
We presented CFD and FSI simulation results for the flow in an asymmetric serpentine and an unrestricted free spherical particle. A custom-made microfluidic device was fabricated in order to compare the numerical results with the experiment conducted at the same conditions. The micro-mirrors inserted in the microfluidic device were useful to verify the existence of two stable trajectories, mirrored in z, for the focused particles and to make an estimation of the height of the streak to use it as the initial conditions in the FSI time-dependent simulation.
We also introduced a new methodology, based entirely on the results of numerical simulations, to obtain the transverse flow magnitude in a curved geometry. The fact that this method is based on the measurable differences between a creeping flow and the flow containing transverse lateral flows helps find the direction and magnitude of the transverse flow at any point in the fluidic domain without any geometric bias such as the ones that may be introduced by section planes when Dean patterns are represented.
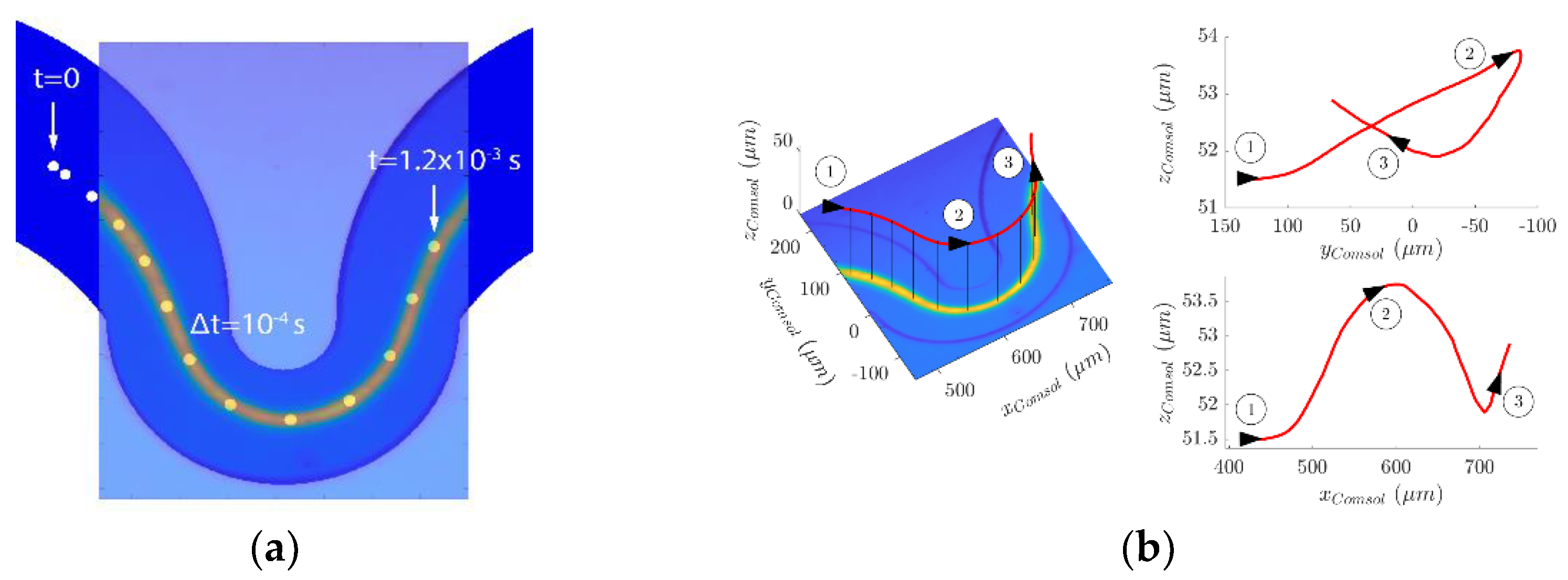
FSI results suggest that particles focused under inertial focusing conditions tend to be entrained in the centerlines of the Dean vortices, something already observed by Jiang et al. [
34] with the IB-LBM method. This fact seems to be relativizing the importance of Dean drag contribution to inertial focusing conditions in curved channels; particles appear to have a preference to be focused at regions with small local lateral flow intensities. The comparison between the trajectory found in the simulation and the experimental one shows good agreement between them validating the join application of FSI + ALE + remeshing features in COMSOL.
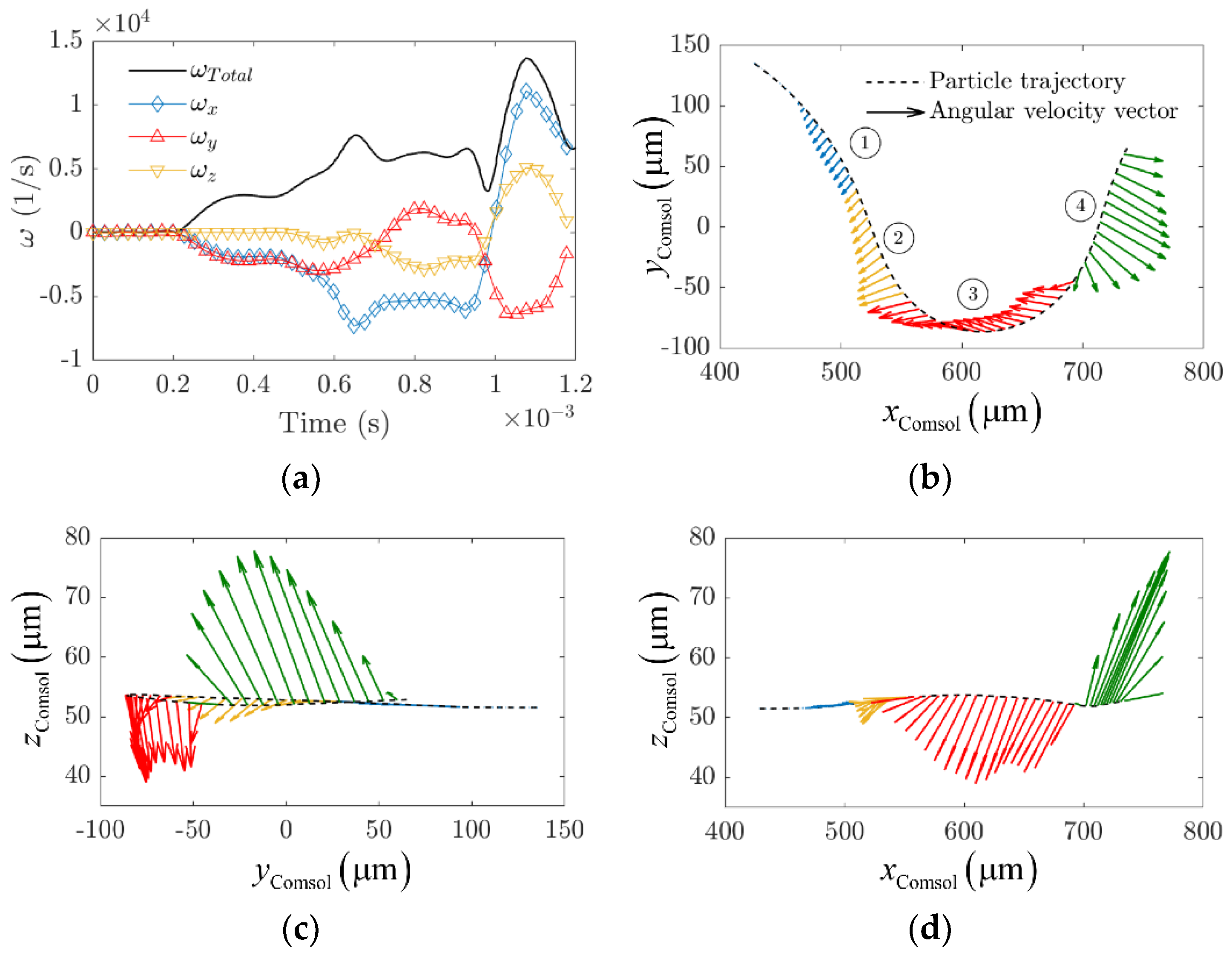
The obtention of the rotational components of the translating sphere revealed the complexity of the particle’s dynamics as it moves along its trajectory. This behavior clearly differs from the one observed in straight channels due to the presence of Dean flows in the small curve. Provided that particles seem to be translating along Dean vortices centerlines under focusing conditions, this fact can already be used as a simplification of the simulation by means of constrained variables because centerlines can be obtained with conventional CFD simulations alone. The elucidation of the theory behind the apparent movement and focusing of particles through vortices’ centerlines will require further studies (its response to flow rate changes and particle’s confinement ratio, among others). We believe that our analysis on angular velocity components can be incorporated to simpler simulation models to infer, at least as a first approximation, the evolution of the angular velocity of the particle on its path through a curved geometry, suppressing the need to perform computationally intensive simulations with coupled solvers. The use of a complex structure (the asymmetric serpentine) has probably improved our understanding of the particle’s behavior in a way that it probably couldn’t be achieved if we had simulated focusing conditions in a simpler geometry (a spiral or a curved channel for instance), for which Dean inversions and abrupt gradient changes hardly occur.