Steady Flux Regime During Convective Mixing in Three-Dimensional Heterogeneous Porous Media

Abstract

Density-driven convective mixing in porous media can be influenced by the spatial heterogeneity of the medium. Previous studies using two-dimensional models have shown that while the initial flow regimes are sensitive to local permeability variation, the later steady flux regime (where the dissolution flux is relatively constant) can be approximated with an equivalent anisotropic porous media, suggesting that it is the average properties of the porous media that affect this regime. This work extends the previous results for two-dimensional porous media to consider convection in three-dimensional porous media. Through the use of massively parallel numerical simulations, we verify that the steady dissolution rate in the models of heterogeneity considered also scales as $\sqrt{k_v{k}_h}$ in three dimensions, where $k_v$ and $k_h$ are the vertical and horizontal permeabilities, respectively, providing further evidence that convective mixing in heterogeneous models can be approximated with equivalent anisotropic models.

1. Introduction

Density-driven convective mixing of CO${}_2$ in a saline aquifer is a fascinating phenomena that can accelerate the dissolution of CO${}_2$ into the resident formation brine, reducing the risk of any leakage to the shallower subsurface. Understanding the fundamental characteristics of density-driven convective mixing is important in order to establish its role in long-term geological storage of CO${}_2$.

Many theoretical, numerical and experimental studies examining the important features of density-driven convective mixing and its importance to CO${}_2$ storage in saline aquifers have appeared in the scientific literature (e.g., References [1,2,3,4,5,6,7,8,9,10,11,12,13]), see Reference [14] for a detailed review of the published scientific literature regarding convective dissolution of CO${}_2$ in saline aquifers. For a typical storage scenario, CO${}_2$ injected into a saline aquifer will rise under buoyancy and spread beneath an impermeable caprock, forming a thin, laterally extensive plume. Diffusion-driven dissolution of CO${}_2$ into the resident brine slightly increases its density, resulting in a gravitational instability. After a finite incubation time, the instability leads to convective mixing, characterised by the complex downward motion of fingers of dense CO${}_2$-rich brine.

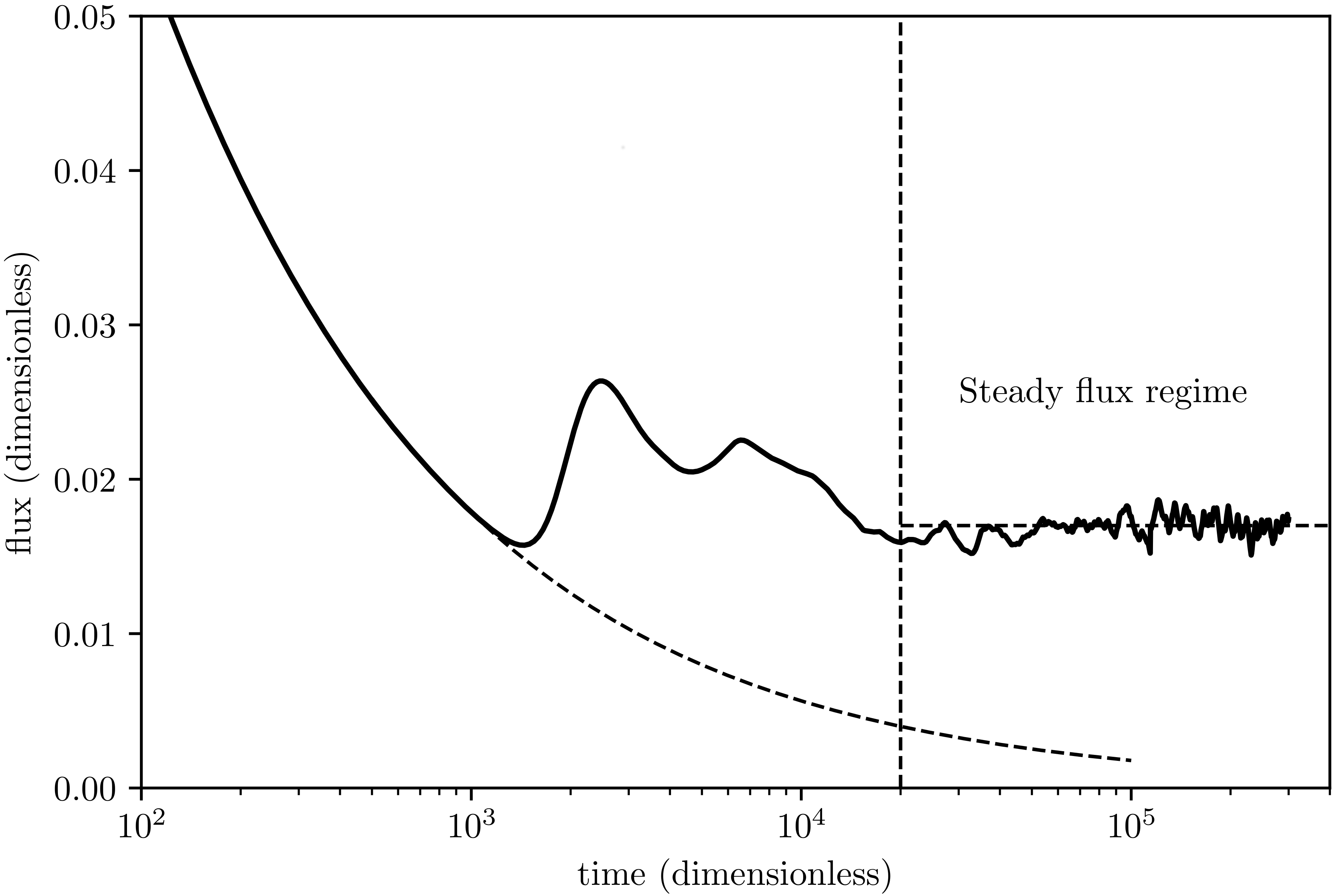
A large proportion of the theoretical studies concerning density-driven convective mixing in porous media that have appeared in the scientific literature have focussed on understanding the critical time for the onset of convection and the associated critical wavelength of fingers at the onset of convection in idealised homogeneous models (e.g., References [1,2,3,4,5,7,10,13,14]). One significant feature of density-driven convective mixing that has also received attention is the establishment of a steady long-term mass flux during the period after the fingers stabilise and before they reach the base of the aquifer, see Figure 1. Despite the complicated nature of the flow, only modest fluctuations in the rate of dissolution are observed in numerical simulations in this regime [9,10,15].

Solutal convection in realistic geological formations is typically a fine-scale process that occurs at a length scale several orders of magnitude below the typical computational resolution possible in field-scale simulations. For example, high-resolution simulations of convective mixing may use computational domains that are only a few metres in size, with spatial resolution at the cm or mm scale necessary in order to accurately model the complicated convective mixing process. The size and resolution of these models is in stark contrast to field-scale simulations of CO${}_2$ storage, where the computational expense commonly constrains the size of computational grid blocks to metres to tens of metres. The consequence of this disparity is to inhibit, and therefore delay, the onset of convective mixing in simulation studies with large grid blocks, which results in an underestimate of the total dissolved CO${}_2$ fraction [3].

Comparatively few studies have attempted to include the effect of enhanced dissolution due to density-driven convective mixing at the fine scale in large-scale simulation studies using coarse grid blocks. Initial attempts to include convective mixing in a coarse-scale model have included using a rudimentary sink term in the uppermost portion of the model to remove an amount of mobile CO${}_2$ equal to the theoretical estimate of the long-term average mass flux in order [16], or including the effect of convection through an upscaled representation of the mass transfer rate in a vertical equilibrium model [17,18]. Common to both of these studies are the assumptions that the onset time of the convective mixing process is small in comparison to the total simulation time, and that the dissolution rate can be approximated with the estimate of the steady flux. Using these models, it was found that including the enhanced dissolution due to sub-grid convective mixing reduced the up-dip migration of the gas-phase CO${}_2$, and therefore the total time that the plume is mobile.

It is clear that the presence of a steady flux regime is likely to be significant in the development of an appropriate upscaling scheme for enhanced dissolution due to convective mixing, enabling this fine-scale process to be included in much larger grid blocks through some suitable mechanism. The availability of accurate theoretical estimates of the mass flux in the steady flux regime therefore underpins the establishment of upscaled models. For isotropic homogenous models, detailed numerical simulation studies have verified the functional form of the average dissolution rate in the steady flux regime, for both two-dimensional and three-dimensional models [9]. In practice, coarse simulation models are often constructed by upscaling fine-scale heterogeneous geological models to representative anisotropic homogeneous models with effective permeabilities. In this anisotropic case, a theoretical estimate of the average dissolution rate in the steady flux regime was shown to scale as $\sqrt{k_v{k}_h}$ for two-dimensional porous media only, where $k_v$ and $k_h$ are the effective vertical and horizontal permeabilities, respectively [15].

In this study, we consider the effect of anisotropy on the average long-term mass flux of CO${}_2$ in a three-dimensional saline aquifer, extending the work of Green and Ennis-King [15] for two dimensions. Numerical simulations of anisotropic porous media are used to verify that the scaling result for two-dimensional anisotropic porous media is also valid for three-dimensional porous media, despite the increased degrees of freedom present in three dimensions in comparison to two dimensions. Using high-resolution numerical simulations of heterogeneous three-dimensional porous media, we demonstrate that the average long-term mass flux is adequately represented by an equivalent anisotropic homogenous model, even though the vertical connectivity of these models is highly complex. Finally, we discuss how these results may be used as part of an upscaling method to incorporate the effects of subgrid-scale enhanced dissolution due to convective mixing in coarse-scale simulations of CO${}_2$ storage in saline aquifers.

2. Background Theory

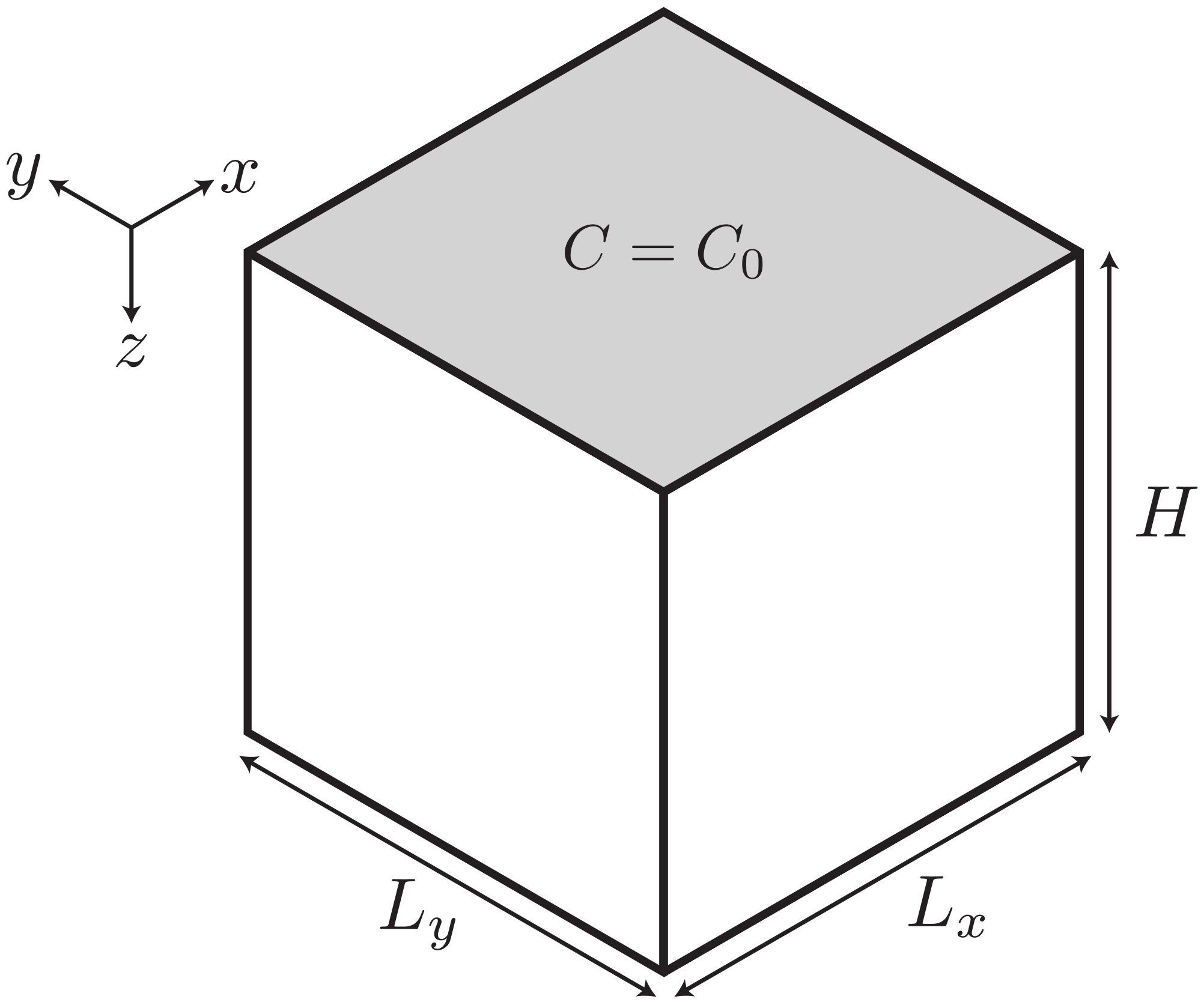
In this section, we present a brief overview of the theoretical background to the problem of density-driven convective mixing in porous media in three dimensions. For simplicity, we consider a cuboid model of height H and lengths $L_x$ and $L_y$ in the x and y directions, respectively, see Figure 2. The solute concentration, C, at the top surface ($z=0$) is fixed at equilibrium saturation $C_0$. All parameters used in this analysis and their units are described in the table of nomenclature,

Table 1. Nomenclature.

Symbol	Definition	SI Units
C	Solute concentration (kg solute/kg solvent)	-
D	Effective diffusion coefficient	m${}^2$ s${}^{-1}$
F	Dissolution flux	kg m${}^{-2}$ s${}^{-1}$
g	Gravity	m s${}^{-2}$
H	Height of model	m
$k_h$	Horizontal permeability	m${}^2$
$k_v$	Vertical permeability	m${}^2$
$L_x$	Length of model in x direction	m
$L_y$	Length of model in y direction	m
P	Pressure	Pa
t	Time	s
$\mathbf{u}=(u,v,w)$	Fluid velocity	m s${}^{-1}$
$\gamma =k_v/h_h$	Permeability anisotropy	-
$\mu$	Viscosity	kg m${}^{-1}$ s${}^{-1}$
$\rho$	Fluid density	kg m${}^{-3}$
$\varphi$	Porosity	-

.

Density-driven convective mixing of dissolved CO${}_2$ in porous media is a complex phenomenon governed by coupled partial differential equations, namely Darcy’s law and the convection-diffusion equation for transport of the dissolved solute. They are commonly expressed as

$$\mathbf{u}=-\frac{k}{\mu }\left(\nabla P-{\rho }_f\mathbf{g}\right),$$

(1)

and

$$\varphi \frac{\partial C}{\partial t}+\mathbf{u}·\nabla C=\varphi D{\nabla }^{2}C,$$

(2)

where $\mathbf{u}$ is the Darcy velocity, k is permeability, $\mu$ is the dynamic viscosity, P is the pressure, ${\rho }_f$ is the fluid density, $\mathbf{g}$ is the acceleration due to gravity, $\varphi$ is the porosity of the porous medium, C is the solute concentration, t is time, and D is the effective diffusion coefficient (the product of diffusivity and tortuosity [2]). We also assume that the fluid is incompressible, whereby

$$\nabla ·\mathbf{u}=0.$$

(3)

Equations (1) and (2) are coupled by the change in fluid density as a result of the dissolved solute, which is typically provided using a relation of the form

$${\rho }_f={\rho }_0\left(1+\frac{\Delta \rho }{{\rho }_0{C}_0}C\right),$$

(4)

where ${\rho }_0$ is the density of the unsaturated fluid, $C_0$ is the maximum solute concentration (i.e., the concentration at solute equilibrium), and $\Delta \rho =\rho -{\rho }_0$ is the maximum density increase with concentration. We restrict our study to the case where $\Delta \rho >0$, i.e., the density of the fluid increases monotonically with increasing solute concentration, as is the case for CO${}_2$ dissolved in brine.

In order to simplify the problem, we invoke the Boussinesq approximation [19], in which case the dependence of ${\rho }_f$ on C is only retained in the buoyancy term in Equation (1). This simplifying assumption effectively linearises the dependence of density on concentration, which is appropriate for CO${}_2$ dissolved in brine due to the weak dependence of partial molar volume on concentration [2].

The governing equations are closed with appropriate boundary and initial conditions. Assuming that the porous media is an infinitely long, horizontal reservoir of fixed height H, the boundary conditions at the top ($z=0$) and bottom ($z=H$) surfaces are given by

$$\begin{array}{cc}\hfill w(x,0,t)=0,& w(x,H,t)=0,\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill C(x,0,t)=C_0,& \frac{\partial C(x,z,t)}{\partial z}{|}_{z=H}=0,\hfill \end{array}$$

(6)

respectively, where w is the vertical component of velocity. These boundary conditions correspond to a Dirichlet boundary at the upper surface (where the concentration is fixed at its equilibrium value), and a no-flux boundary at the lower surface. The presence of a fixed concentration boundary at the upper surface is supported by previous studies, where it was observed that the interface between the supercritical CO${}_2$ and brine remains sharp despite the presence of fingers of CO${}_2$ saturated brine sinking into the less dense unsaturated brine [3,20]. In reality, this assumption is a simplification of the true interface at the boundary layer, where two phases coexist. The initial conditions are

$$\mathbf{u}(x,z,0)=0,C(x,z,0)=0,$$

(7)

which correspond to no initial velocity and zero initial solute concentration in the reservoir (apart from the top boundary).

Significant insight into the problem can be obtained by non-dimensionalising the governing equations using suitable scales. As we are primarily interested in the steady flux regime during convective mixing in porous media, we only consider cases where the height of the model is much larger than the vertical distance over which convective instability forms [2]. Consequently, we scale lengths with the length over which convection and diffusion balance, so that horizontal lengths are scaled by $\varphi \mu D/(k_v{\gamma }^{1/2}\Delta \rho g)$ and vertical lengths are scaled by $\varphi \mu D/(k_v\Delta \rho g)$ [2], where $k_h$ and $k_v$ are the horizontal and vertical permeabilities, respectively (We only consider the case where permeability is the same in both horizontal directions for simplicity), and $\gamma =k_v/k_h$ is the permeability anisotropy. Similarly, horizontal velocities are scaled by $k_v\Delta \rho g/\left(\mu {\gamma }^{1/2}\right)$ while vertical velocity is scaled by $k_v\Delta \rho g/\mu$. Concentration C is scaled by $C_0$, time is scaled by ${\left(\varphi \mu \right)}^{2}D/{(k_v\Delta \rho g)}^2$, and pressure is scaled by $\varphi \mu D/k_v$. The governing equations, boundary conditions and initial conditions become

$$\begin{array}{cc}\hfill {\mathbf{u}}^{*}& =-\nabla P^{*}+C^{*}\widehat{z},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \frac{\partial C^{*}}{\partial t^{*}}& +{\mathbf{u}}^{*}·\nabla C^{*}=\gamma {\nabla }_h^2{C}^{*}+\frac{{\partial }^2{C}^{*}}{\partial z^{*2}},\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill w^{*}(x^{*},0,t^{*})=0,& w^{*}(x^{*},Ra,t^{*})=0,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill C^{*}(x^{*},0,t^{*})=1,& \frac{\partial C^{*}(x^{*},z^{*},t^{*})}{\partial z^{*}}{|}_{z^{*}=Ra}=0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\mathbf{u}}^{*}(x^{*},z^{*},0)=0,& C^{*}(x^{*},z^{*},0)=0,\hfill \end{array}$$

(12)

where the superscript asterisk denotes a dimensionless variable, ${\nabla }_h=\partial /\partial x+\partial /\partial y$, and $Ra$ is the Rayleigh number, given by

$$Ra=\frac{k_z\Delta \rho g{C}_{0}H}{\varphi \mu D}.$$

(13)

This dimensionless number is a measure of the relative importance of density-driven convection to purely diffusive motion. When $Ra$ is sufficiently large, convection may occur. Using stability analysis, it has been shown that no convection is possible for $Ra<32.5$ [10]. For $32.5<Ra<75$, convection is possible, with a minimum onset time depending on $Ra$ [10]. When $Ra>75$, the earliest possible time for the onset of a convective instability is independent of $Ra$ [10].

We note that the Rayleigh number does not appear in the dimensionless governing equations, Equations (8) and (9). Rather, it appears only in the boundary condition at the base of the model, Equation (10), where the lower boundary is at a dimensionless depth $Ra$. This is due to the length scale used in the parameterisation being the length at which diffusion and advection balance, rather than any geometrical length present in the model [21]. We choose this scaling as we are primarily interested in the steady flux regime, where the presence of a lower boundary does not influence the flux (a semi-infinite model) [21]. This is convenient for numerical models, as $Ra$ can be varied by simply changing the height of the model, with no scaling of the spatial resolution required as $Ra$ is varied.

Significant research effort has been undertaken to determine critical properties of density-driven convective mixing, such as the time for the onset of convection, and the wavelength of the initial perturbations for tractable cases of homogeneous porous media, both isotropic [3,4,5,10,20] and anisotropic [2,3,4,13]. A detailed review of these studies and the estimated values for critical parameters has been provided by Emamai-Meybodi et al. [14], to which the reader is referred for more information.

One of the most interesting features of solutal convection is the establishment of a steady flux regime, where the mass flux over the top boundary is relatively constant, with only small fluctuations about an average value observed despite the complex interaction between the fingers of saturated fluid and the unsaturated background fluid. High resolution numerical simulations have shown that the mass flux oscillates about a constant value in the long term, with temporal variations of the order of 15% (e.g., References [9,12,21]). This phenomena has also been observed experimentally in Hele-Shaw cells (e.g., References [8,22,23]).

The functional form of this long-term mass flux of CO${}_2$ per unit width in a two-dimensional model, $F_m$, is given by [9]

$$F_m\approx 0.017\frac{k{C}_0\Delta \rho g}{\mu },$$

(14)

where the constant $0.017$ is calculated from numerical results. Analogous results for three dimensions have demonstrated that the mass flux exhibits similar long-term behaviour as the two-dimensional case, albeit with a slightly increased prefactor [9,24].

Following Neufeld et al. [8], Green and Ennis-King [15] developed a simple theoretical scaling for the average dissolution flux in the steady flux regime in anisotropic two-dimensional porous media, which we provide here for completeness. The conceptual model is as follows: Downward moving plumes of CO${}_2$-rich water are interspersed with upwelling plumes of fresh water. Once the upwelling plumes reach the top of the reservoir, they are forced laterally into a mixing region [8]. The lateral flow in the mixing region acts to stabilise the diffusive boundary layer, which has thickness $\delta ={(Dl/u)}^{1/2}$, where l is the width of the upwelling plume, and u is the lateral fluid velocity in the mixing region.

When the porous media is isotropic, the lateral fluid velocity is equal to the vertical velocity of fluid in the upwelling plume [8]. If the porous media is anisotropic, however, the principle of conservation of mass dictates that the ratio of the thickness of the horizontal mixing region to the width of the upwelling plume is equal to $\gamma$. It then follows that ratio of the vertical fluid velocity in the upwelling plume to the lateral fluid velocity in the mixing region must scale as ${\gamma }^{-1}$. The width of the upwelling plume is inversely proportional to $k_v$ to first order [2], while vertical velocity in the upwelling plumes scales as $k_v$. The total flux into the porous media across the upper boundary, which is equal to the flux across the boundary layer $F_{bl}\sim \varphi D\Delta \rho /\delta$ [8], therefore scales as ${\left(k_v{k}_h\right)}^{1/2}$ in an anisotropic porous media.

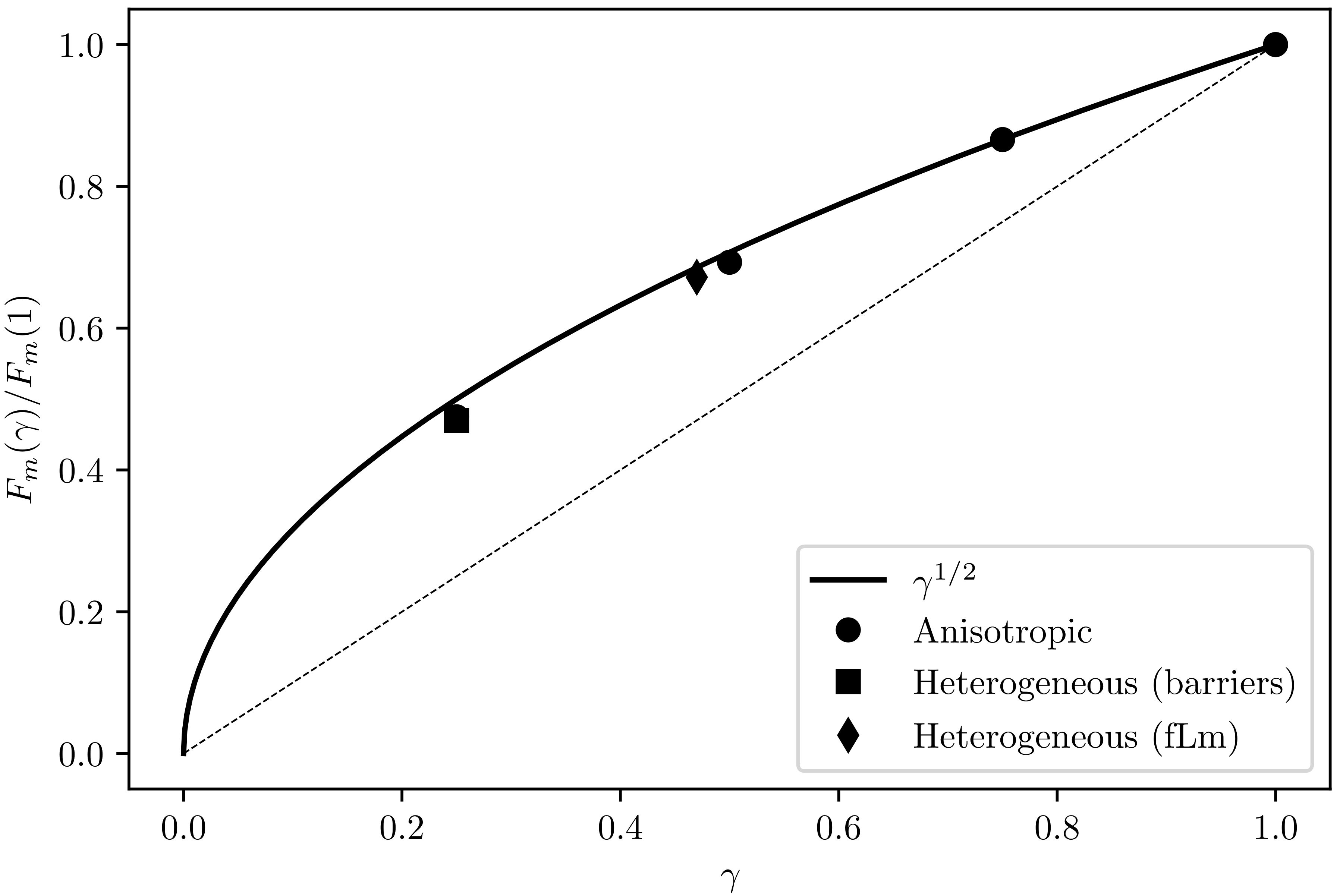
This result suggests that it is the geometric mean of the vertical and horizontal permeabilities that should be used in the estimate of the mass flux in the steady flux regime [15], in which case the average long-term mass flux for a two-dimensional anisotropic porous media is

$$F_m\left(\gamma \right)\approx 0.017{\gamma }^{1/2}\frac{k_h{C}_0\Delta \rho g}{\mu },$$

(15)

i.e., Equation (14) scaled by ${\gamma }^{1/2}$ and replacing k with $k_h$. This functional relationship has been verified through two-dimensional numerical simulations of anisotropic homogeneous porous media [15,25].

Green and Ennis-King [26] demonstrated through numerical simulations that the average mass flux in the steady flux regime during solutal convection in a two-dimensional heterogeneous porous medium was well represented by an anisotropic homogeneous porous medium with equivalent permeabilities in the vertical and horizontal directions. Several subsequent studies have also observed that the steady flux rate is dependent on the average properties of the porous medium, suggesting that heterogeneous porous media may be suitably modelled using anisotropic homogeneous porous media [15,27,28,29,30].

3. Numerical Method

To date, the scaling relationship for the average mass flux in the steady flow regime, Equation (15), has not been demonstrated for anisotropic and heterogeneous three-dimensional models. It is important to verify (or otherwise disprove) the theoretical scaling presented by Green and Ennis-King [15] for two-dimensional convective mixing in the three-dimensional case. To that end, we have undertaken a series of high-resolution simulations of density-driven convective mixing in both anisotropic and heterogeneous porous media.

High-resolution numerical simulations were performed using Numbat [31] (https://github.com/cpgr/numbat), an open-source application developed by the authors using the Multiphysics Object-Oriented Simulation Environment (MOOSE) software framework [32] (http://www.mooseframework.org). Numbat solves either the dimensional (Equations (1)–(4)) or dimensionless (Equations (8) and (9)) form of the governing equations using the finite element method, and leverages powerful features of the open-source MOOSE framework, such as adaptive mesh refinement, automatic parallelism, and both continuous and discontinuous Galerkin methods to enable massively parallel simulations of density-driven convective mixing in porous media. In this study, numerical simulations using both the dimensional and dimensionless forms are used to determine the average mass flux in the steady flux regime in three-dimensional models. Fully unstructured computational meshes were used in this study, with a fine discretisation near the top boundary to adequately resolve the initial fingers, and a coarser discretisation towards the base of the model where fingers are large. At least several million elements are used in each of the three-dimensional meshes. Due to the large number of elements, each simulation was run using between 100 and 1000 cores on a large computational cluster.

The dimensionless form of the governing equations, Equation (8) and (9), are solved using a stream function formulation [21,33]. For details, see Appendix A.

Numbat has been benchmarked against previously published results in two and three dimensions, detailed by Pruess and Zhang [34] and Pau et al. [9]. Qualitatively, the results obtained using Numbat are consistent with those studies. The steady flux values in these cases are similar to those reported by Pruess and Zhang [34] and Pau et al. [9]. Small differences in the onset time are observed, but these are likely the result of the difference in the random noise used to seed the instability. Full details are provided in the Numbat user manual [31].

It is well known that the onset time of convection is sensitive to the initial disturbance used to seed the gravitational instability that is the driver of convective mixing [14], whereas the steady mass flux is insensitive to the choice of initial disturbance [14]. In this study, the gravitational instability is seeded by perturbing the model in a controlled manner. For dimensional simulations, a random noise of amplitude $1\%$ is added to the initial porosity field [26], while for the dimensionless simulations, a reproducible random noise is added to the initial diffusive concentration field [21].

No-flow boundaries are imposed on the upper and lower faces of the model, while lateral periodicity is imposed through periodic boundary conditions. The upper boundary is fixed at a given concentration, either $C=1$ for the dimensionless model, or $C=C_0$ for the dimensional case, for some equilibrium concentration $C_0$.

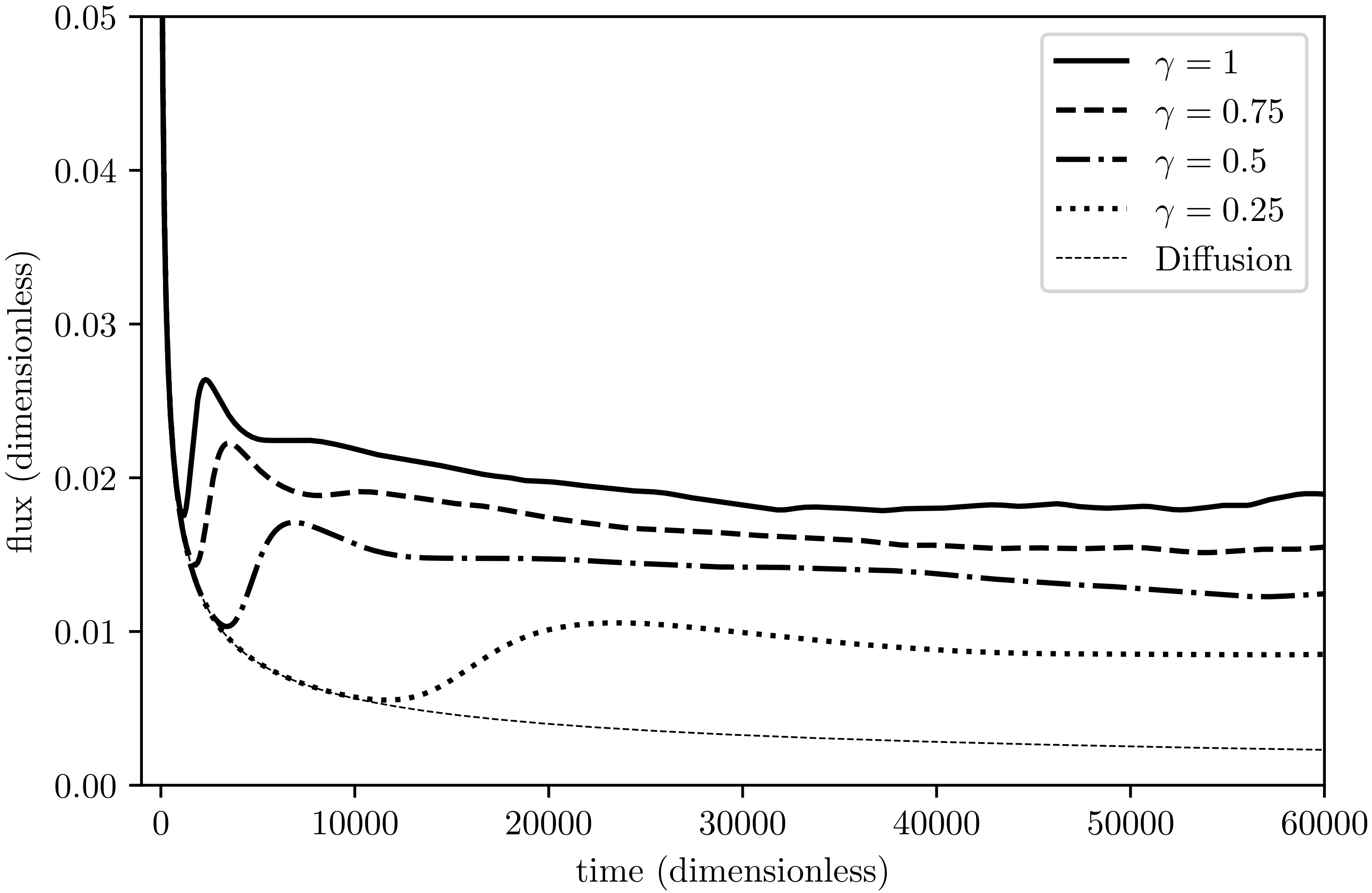
Anisotropy is imposed through varying the anisotropy ratio $\gamma$ in the dimensionless model. The computational models used in these anisotropic simulations have a dimensionless length of 3000 in each of the horizontal directions, and a dimensionless length of 5000 in the vertical direction. The height of the model corresponds to a Rayleigh number of $Ra=5000$ [10]. The horizontal lengths are chosen so that a sufficiently large number of fingers are present in the model. The wavelength of the fingers at the onset of convection has the functional form ${\lambda }_c=c\left(\gamma \right)\varphi \mu D/(k\Delta \rho g)$, where the parameter $c\left(\gamma \right)$ has been estimated by various authors as $95{\gamma }^{-0.758}$ [2], $96.23{\gamma }^{-0.849}$ [4], or $115.3{\gamma }^{-0.83}$ [13]. These estimates suggest that there will be at least one hundred fingers in the model at the onset of convection for the smallest value of anisotropy ratio, and up to several hundred for the isotropic case.

Two models of reservoir heterogeneity are considered in this study. Following the use of horizontal flow barriers as a simplified proxy for realistic heterogeneity (such as shale filled reservoirs) in two-dimensional studies of convective mixing [15,26,27,28,30], we extend this idea to three dimensions using flat elliptical disks of various aspect ratios to represent flow barriers. The major and minor axes of the elliptical disks are drawn from Gaussian distributions $N(250,75)$ and $N(100,25)$, respectively, where $N(\mu ,\sigma )$ refers to a Gaussian distribution with mean $\mu$ and standard deviation $\sigma$. 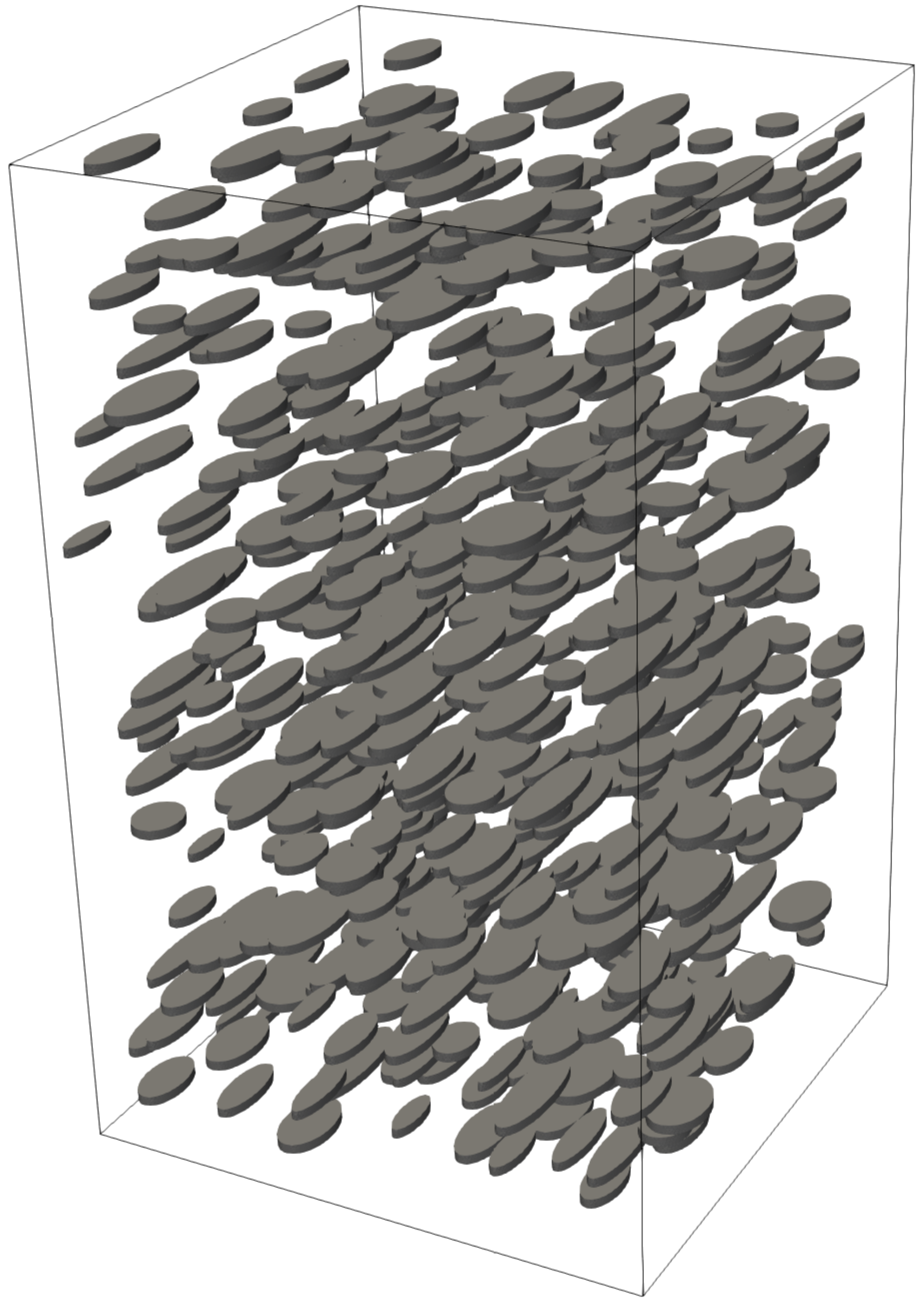Barrier dimensions were chosen so as to be larger than the typical finger length in the upper region of the computational mesh to provide a significant impediment to downwards flow. The distribution of barriers used in this study is depicted in Figure 3. The mesh was suitably refined in the vicinity of the barriers to accurately capture their geometry. The distribution of barriers shown in Figure 3 results in a permeability anisotropy of $\gamma =0.25$. As for the anisotropic models, the dimensionless forms of the governing equations are solved in this case. The horizontal dimensions again have a dimensionless length of 3000, while the model has a dimensionless height of 5000.

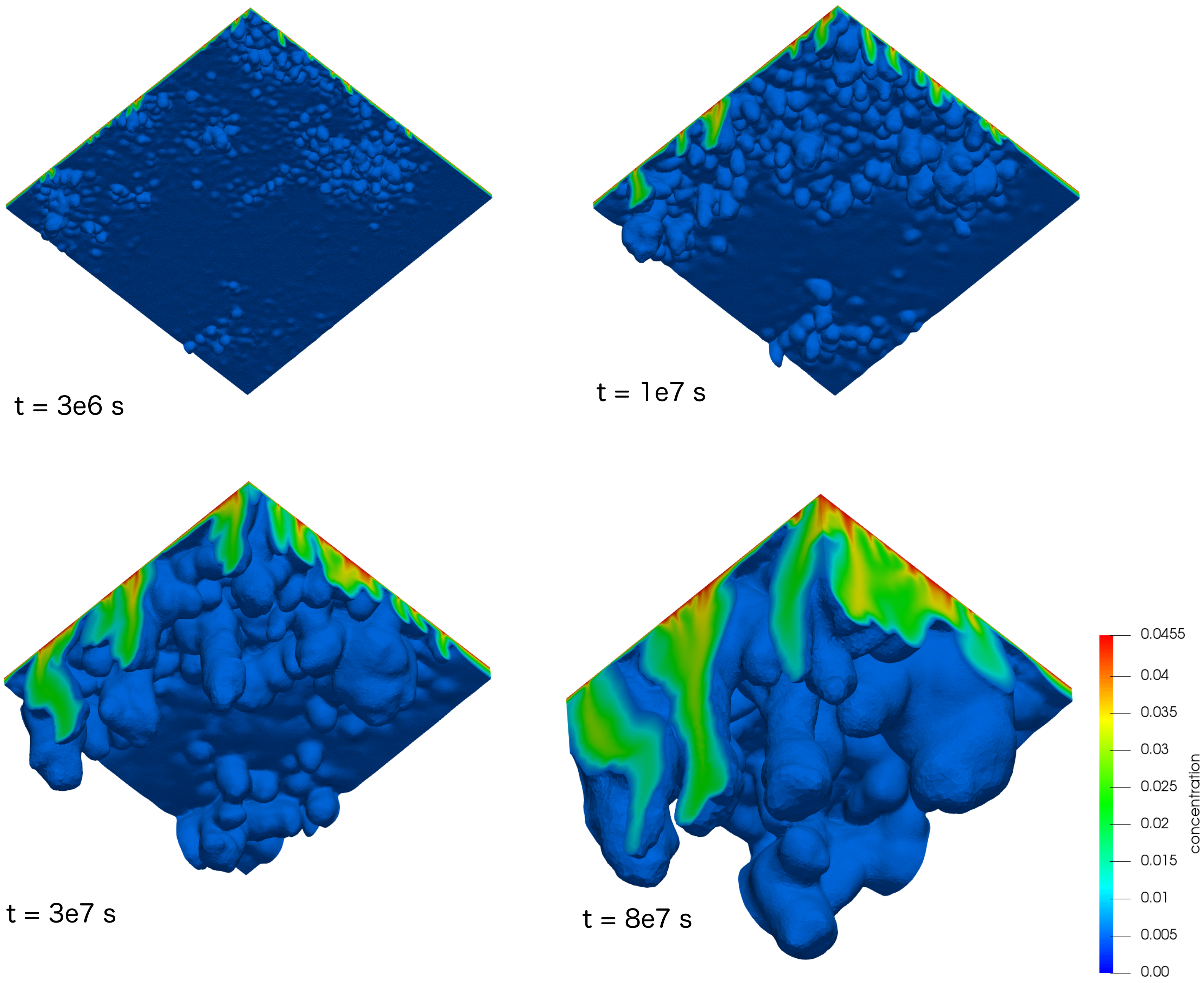
The second model of heterogeneity uses fractional Lévy motion (fLm) to generate a spatially-varying permeability field, as non-Gaussian structure has been observed in sedimentary formations [35,36,37]. A model with fLm structure was generated using a midpoint displacement algorithm with successive random additions [38] drawn from a Lévy distribution with width parameter $\alpha =1.25$ and Hurst parameter $H=0.1$ [39]. A heterogeneous permeability field was then constructed as $k=k_{0}exp\left[L(\alpha ,H)\right]$, where $k_0=4\times {10}^{-13}$ m${}^2$ is a mean permeability (approximately 400 mD), and $L(\alpha ,H)$ is a random number sampled from the Lévy distribution with width parameter $\alpha$ and Hurst parameter H. This results in a heterogeneous model with permeability varying over three orders of magnitude, see Figure 4. Within each cell, the vertical permeability was scaled so that the overall permeability anisotropy was $\gamma =0.5$. All other reservoir properties are representative of a low salinity aquifer at a depth of approximately 1 km, and are given in

Table 2. Parameters used in the dimensional simulations (representative of a low salinity aquifer at a depth of approximately 1 km).

Pressure, P	11.4 MPa
Temperature, T	59 ${}^{\circ }$C
Salt mass fraction, $C_s$	$0.01$
Porosity, $\varphi$	0.25
Viscosity, $\mu$	$0.485\times {10}^{-3}$ kg m${}^{-1}$ s${}^{-1}$
Unsaturated brine density, ${\rho }_0$	$994.8$ kg m${}^{-3}$
Saturated brine density, $\rho$	$1004.7$ kg m${}^{-3}$
Saturated CO${}_2$ mass fraction, $C_0$	$0.0455$
Effective diffusion coefficient, D	$2\times {10}^{-9}$ m${}^2$ s${}^{-1}$

. The dimensions of the model are 10 m in all directions.

In contrast to the two-dimensional case, where multiple statistical realisations of heterogeneity are used to investigate their effect on solutal convection [15,26], the computational expense of three-dimensional simulations precludes a probabilistic study. As a result, only two statistical realisations of each permeability heterogeneity are considered.

4. Results

4.1. Anisotropic Porous Media

Numerical simulations of three-dimensional convective mixing in homogeneous but anisotropic porous media were performed for permeability anisotropies $\gamma =1$, $0.75$, $0.5$ and $0.25$ using the dimensionless form of the governing equations. Figure 5 presents a comparison of an isotropic model ($\gamma =1$) with an anisotropic model ($\gamma =0.5$). As this comparison shows, we observe that anisotropy delays the onset of convection in comparison with the isotropic case, as evidenced by the slower formation of downwelling fingers in the anisotropic case, see Figure 5. This is in line with previous findings for convective mixing in two-dimensional porous media [2,15].

Figure 5 also demonstrates that the lateral dimension of the fingers at the onset of convection is larger for $\gamma =0.5$ in comparison for $\gamma =1$ (remembering that lateral dimensions scale as ${\gamma }^{-1/2}$). This can be observed by comparing the initial finger pattern at $t=3000$ for the isotropic case with the finger pattern for the anisotropic case at a similar finger depth (at a later time t = 10,000 due to the delayed onset of convection in the anisotropic case in comparison to the isotropic case), where fewer fingers can be seen.

The effect of permeability anisotropy can be quantified by comparing the temporal evolution of the flux across the top boundary for the isotropic and anisotropic cases, which is calculated as

$$F\left(t\right)=\frac{\varphi \rho D}{L_x{L}_y}{\int }_0^{L_x}{\int }_0^{L_y}\frac{\partial C}{\partial z}{|}_{z=0}dxdy,$$

(16)

where $L_x$ and $L_y$ are the lengths of the computational model in the x and y directions, respectively, see Figure 2.

As Figure 6 demonstrates, decreasing $\gamma$ delays the onset of convection, which results in a smaller average flux in the steady flux regime.

For the isotropic case ($\gamma =1$), the average flux in the steady flux regime was calculated as $0.018$, slightly larger than the accepted value for two-dimensional models ($0.017$). This finding is commensurate with the previous observations of steady flux in isotropic homogeneous porous media in three dimensions [9]. Likewise, we observe smaller oscillations about this average flux in three dimensions, which is likely the result of the increased number of fingers in the three-dimensional model.

4.2. Heterogeneous Porous Media

One of the important results presented in earlier studies of density-driven convective mixing in two-dimensional heterogeneous porous media is that the steady flux in a heterogeneous model is well-approximated by the flux in an equivalent anisotropic homogeneous model [15,26], which implies that a heterogeneous model of the porous media can be replaced with a simpler anisotropic homogeneous model. We now present numerical results to verify this in three dimensions using the two examples of permeability heterogeneity discussed earlier.

The temporal evolution of the concentration in the heterogeneous model with elliptical flow barriers is presented in Figure 7. Initially, small fingers form around the barriers, with an increased concentration observed on the upper surface of the barriers. As time increases, the downwelling fingers merge to form larger fingers which totally encapsulate the barriers. These then flow downwards until they reach the next barrier, and the process is repeated.

It is clearly evident from Figure 7 that the barriers have a significant effect on the dynamics of the fingers, impeding their downward motion and resulting in extremely complex finger patterns. Nevertheless, the average flux in the steady flux regime for this complex model is well approximated by the average flux in an equivalent anisotropic homogeneous model, see Figure 8. In contrast, we observe that the onset time for convection is much earlier for the heterogeneous barrier model in comparison to the equivalent anisotropic model, providing more evidence that the onset time is sensitive to the local permeability whereas the steady flux is governed by the global average permeability [15,26]. In fact, comparing the onset time for the heterogeneous model in Figure 8 with the onset time for the isotropic porous medium in Figure 6, we find that they are nearly identical. As both models use an equivalent formulation, with the permeability in the background of the heterogeneous model equivalent to the isotropic case, this result provides further evidence for the hypothesis that it is the local permeability that influences the onset of convective mixing in heterogeneous porous media [15,26].

In the second case of heterogeneity, the dimensional form of the governing equations are solved for the case of permeability heterogeneity constructed using a fractional Lévy motion model. In this case, convective fingers are observed to form in the higher permeability regions initially, with no fingers observed in the regions of lower permeability, see Figure 9. At this early time, we conclude that it is the local permeability that controls the onset and growth of fingers. As time increases, these initially small fingers merge to form larger fingers, as usual. Eventually, the fingers become large enough, after which it is the average permeability that governs their motion, and we observe that fingers are now present throughout the porous media, even in those regions where the permeability is low.

This is clearly illustrated in the temporal progression depicted in Figure 10, where the contours of concentration are provided along a horizontal slice a distance of 0.5 m from the upper surface of the model. After ${10}^7$ s, fingers can be observed in the regions of higher permeability, with no fingers present in the regions of lower permeability. As time increases, we can observe that the fingers join into laterally extensive plumes that begin to include the lower permeability region.

The flux across the top boundary for the fractional Lévy motion model of permeability heterogeneity is presented in Figure 11, alongside the flux in an anisotropic homogeneous model with equivalent effective permeabilities in the vertical and horizontal directions. Again, the steady flux in the heterogeneous model is well approximated by the flux in the equivalent anisotropic model, providing further evidence that the complex motion in the steady flux regime of density-driven convective mixing in heterogeneous porous media can be adequately modelled using simpler anisotropic homogeneous models with effective permeabilities.

The calculated steady fluxes for all three-dimensional cases considered are summarised in Figure 12, where the average flux is calculated from the numerical results in the steady-flux regime. These results clearly demonstrate that the theoretical scaling for the steady flux in anisotropic porous media presented by Green and Ennis-King [15] for two-dimensional porous media is also applicable to density-driven convective mixing in three-dimensional porous media, but with the prefactor increased to $0.018$:

$$F_m\left(\gamma \right)\approx 0.018{\gamma }^{1/2}\frac{k_h{C}_0\Delta \rho g}{\mu }.$$

(17)

This is despite the increased complexity observed in three-dimensional porous media in contrast to two-dimensional porous media due to the added degrees of freedom. Importantly, these results demonstrate that this scaling may also be appropriate in heterogeneous three-dimensional porous media, suggesting that the long-term dissolution in a heterogeneous model may be well approximated with a simple anisotropic model.

5. Discussion

High-resolution numerical simulations of density-driven convective mixing in three-dimensional porous media have been undertaken to examine the applicability of the theoretical scaling for the steady flux in two-dimensional models developed by Green and Ennis-King [15] to three-dimensional models. In so doing, it was demonstrated that the average mass flux in the steady flux regime also scales as $\sqrt{k_h{k}_v}$ in three dimensional anisotropic porous media.

Two models of permeability heterogeneity were considered, and in each case, it was demonstrated that the magnitude of the average flux in the steady flux regime for these models of permeability heterogeneity were well represented by anisotropic homogeneous porous models with effective permeabilities that provide an equivalent Darcy flux. This finding extends the earlier findings for two-dimensional heterogeneous porous media [15,26] to the more realistic case of three-dimensional models. Qualitatively similar behaviour between heterogeneous and homogeneous three-dimensional models were obtained by Soltanian et al. [29] for different models of heterogeneity when comparing the dynamics of convection using a different measure of convection to the steady flux considered here.

In both cases of heterogeneity studied here, we observed that the onset time of convection was shorter in the heterogeneous model in comparison to the equivalent anisotropic model. This lends further support to the hypothesis that local regions of comparatively high permeability can influence the critical onset time and wavelength of the fingers in heterogeneous media [15]. These regions of high local permeability are not present in the anisotropic model, having been averaged out through upscaling to effective permeabilities. As a result, the onset time is delayed in anisotropic models in comparison to heterogeneous models. This is in contrast to the steady flux, which appears to be insensitive to local permeability and is instead governed by the large-scale effective permeability [15,26].

The observation that convection occurs much sooner in heterogeneous models in comparison to an equivalent anisotropic homogeneous model while still exhibiting similar average flux in the steady flux regime over the long term suggests that it may be possible to incorporate the enhanced dissolution due to convection at the fine-scale in coarse-scale simulations, by assuming that convection begins immediately and that the rate of mass flux into the liquid phase is constant while a gas phase remains present. This lends support to initial attempts to include enhanced dissolution due to convection at the sub-grid scale using these simplifying assumptions [16,17,18].

Due to the fundamental importance of convective mixing on the rate of dissolution and hence the total amount of CO${}_2$ that is immobilised in the denser liquid phase, upscaled models that implement this accelerated dissolution are necessary for reliable numerical predictions of the long-term fate of CO${}_2$ storage in saline aquifers. These upscaled models must be informed by theoretical estimates of the dissolution events, such as average dissolution in the steady flux regime [9,15,21]. As previously discussed, results such as those presented here, as well as earlier studies [15,26,27,29], suggest that it may be possible to approximate the steady flux regime in heterogenous porous media using an upscaled model with effective parameters. Additionally, if the onset time for convection is small in comparison to the total simulation time, then the dissolution flux may, to first order, be approximated by the steady flux for all time (as implemented in previous attempts to incorporate enhanced dissolution due to convection in large-scale models as discussed above [16,17,18]). This implies that it may be possible to adequately represent a heterogeneous model with an anisotropic model with equivalent effective permeabilities, even though the onset time in the heterogeneous model is likely to be earlier than in the anisotropic model. This follows from the observation that if the rate of dissolution in both heterogeneous and anisotropic models is similar, then the relative difference between the total dissolved solute due to the difference in onset time in both cases becomes smaller as time increases. If the total simulation time greatly exceeds the onset time, then the difference due to the delayed onset time in the anisotropic model is likely to be small in comparison to the total dissolved amount.

The results presented in this study have been obtained using an idealised representation of the physics involved. Only a single fluid phase has been considered, with an unlimited supply of saturated fluid provided using a constant concentration boundary condition at the top surface. This is a commonly used simplification of the more realistic two-phase boundary that would exist at the interface of the saturated and unsaturated fluids. The presence of a capillary transition zone has also been ignored, as has the possibility of geochemical reactions. Different realisations of permeability heterogeneity may result in cases where the steady flux regime is not adequately represented using an equivalent anisotropic model. A detailed review of the impact that these complicating factors may have on the convective mixing process can be found in Emami-Meybodi et al. [14], to which the reader is referred for further details.