A TITO Control Strategy to Increase Productivity in Uncertain Exothermic Continuous Chemical Reactors
Abstract
:1. Introduction
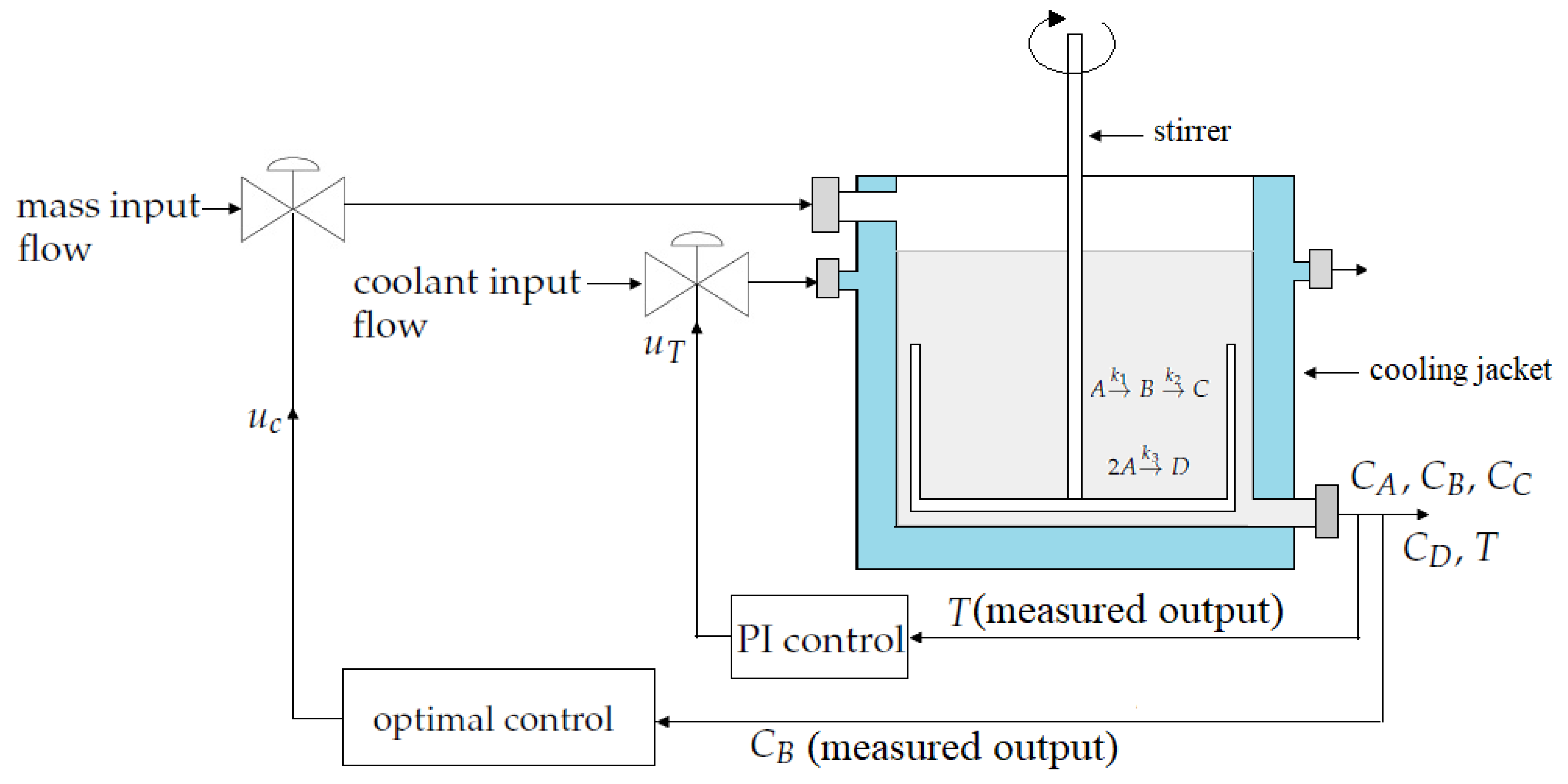
2. Mathematical Model of a Continuous Stirred Tank Reactor(CSTR)
- Mass balance equations:
- Energy balance equation:
3. Control Strategy Design
3.1. PI Temperature Control
3.2. Optimal Control Design
- The state equation:
- The terminal constraints:
- The initial conditions:
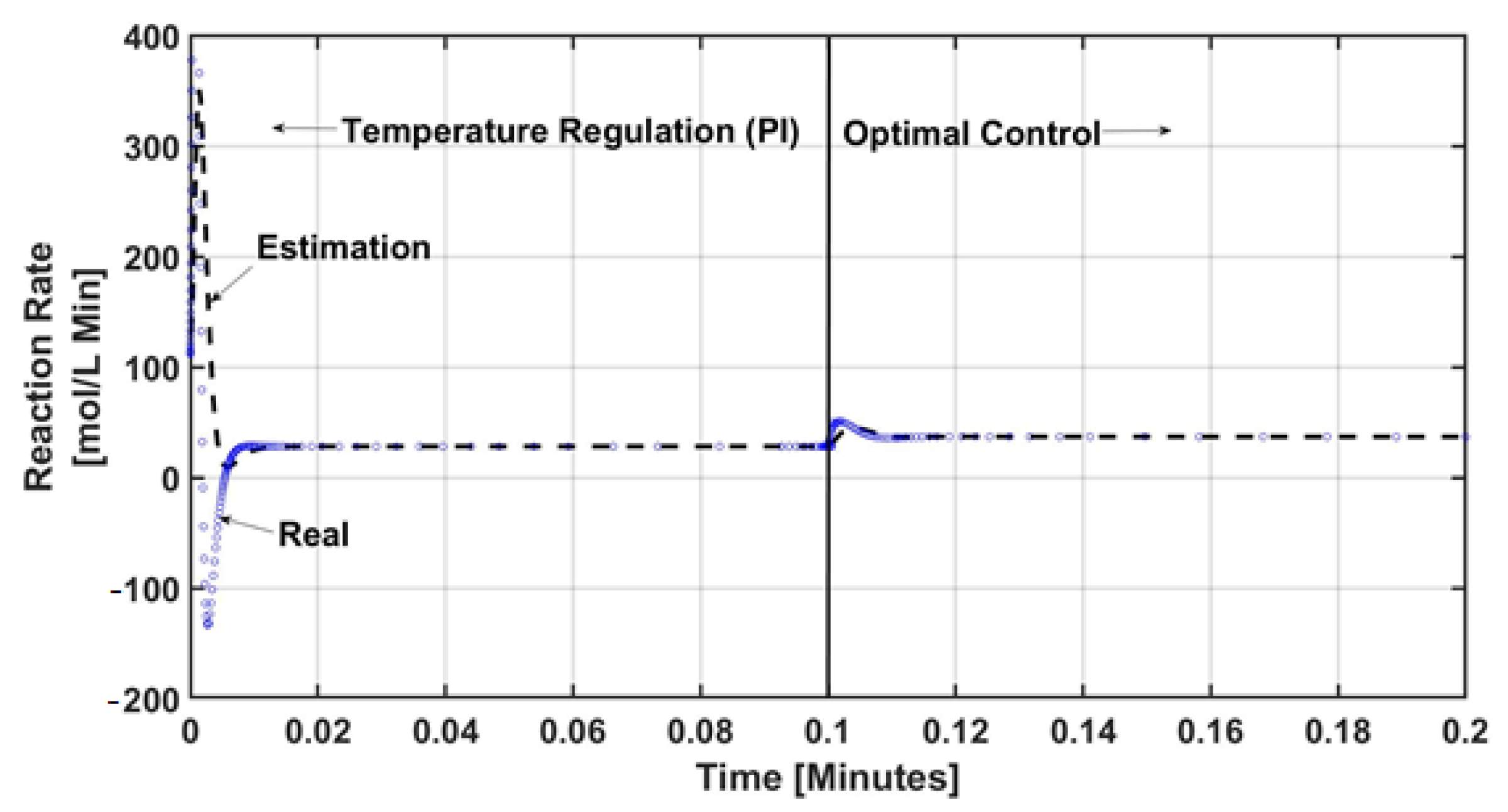
3.3. Uncertainty Estimator Design
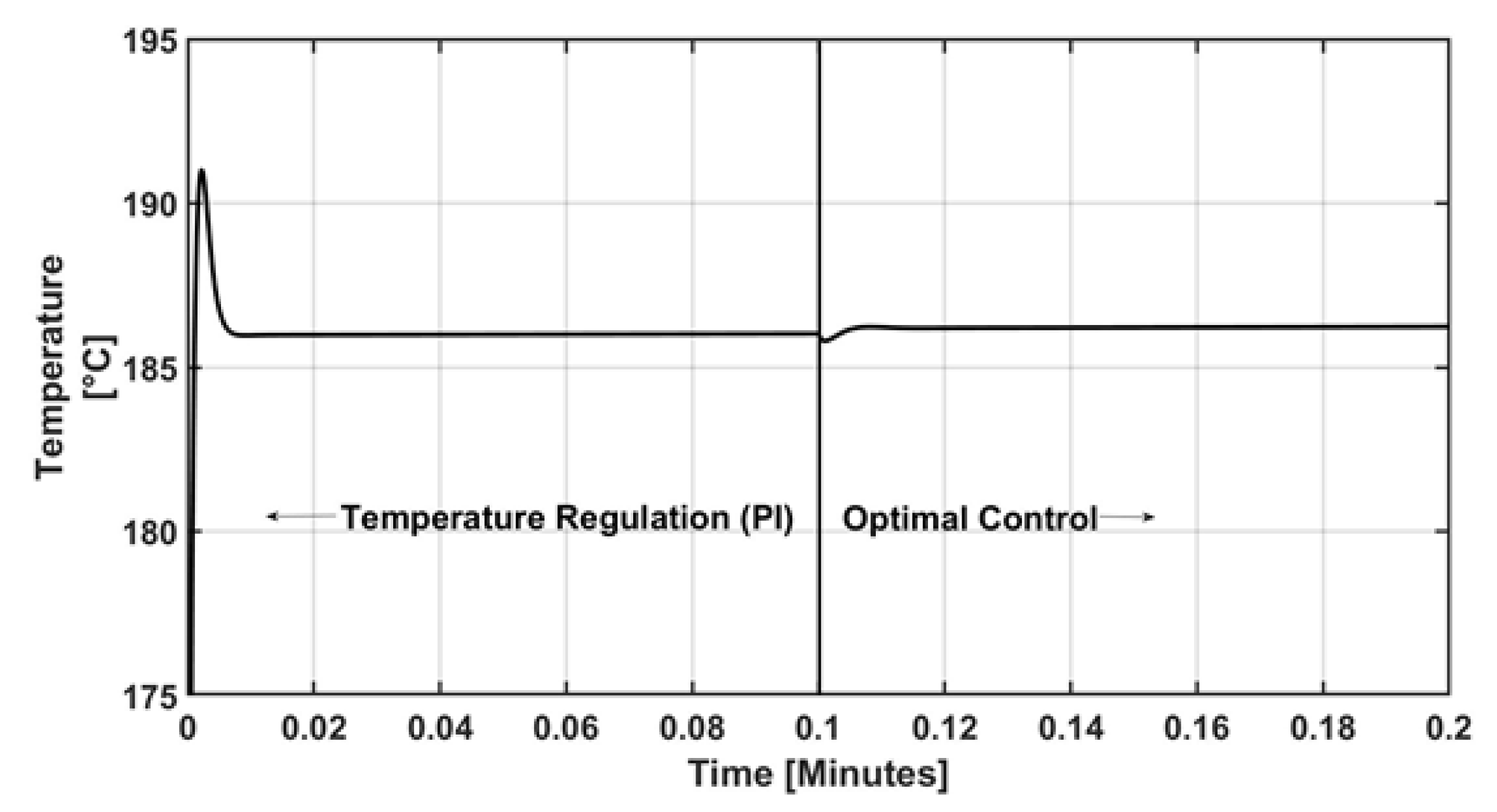
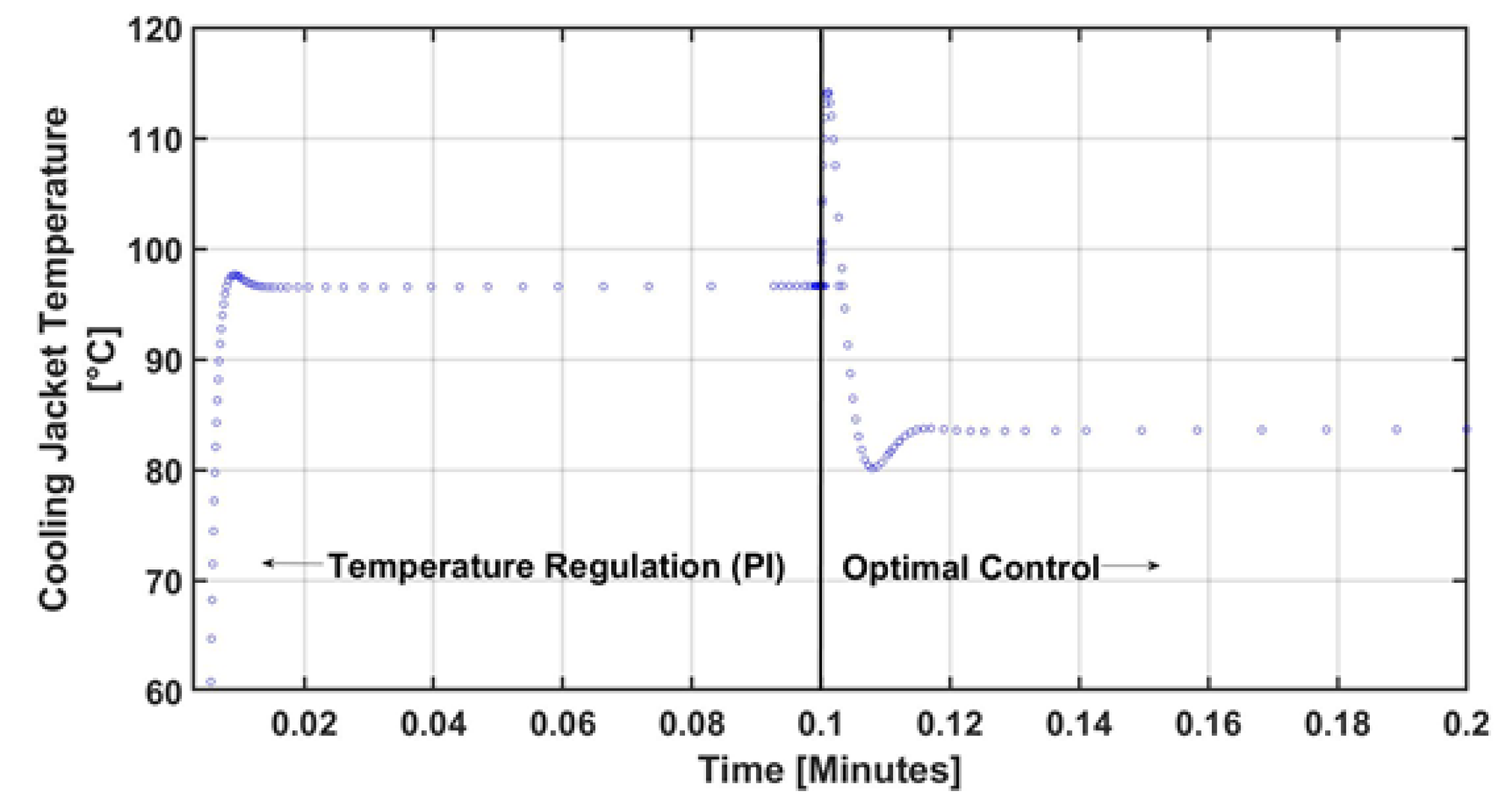
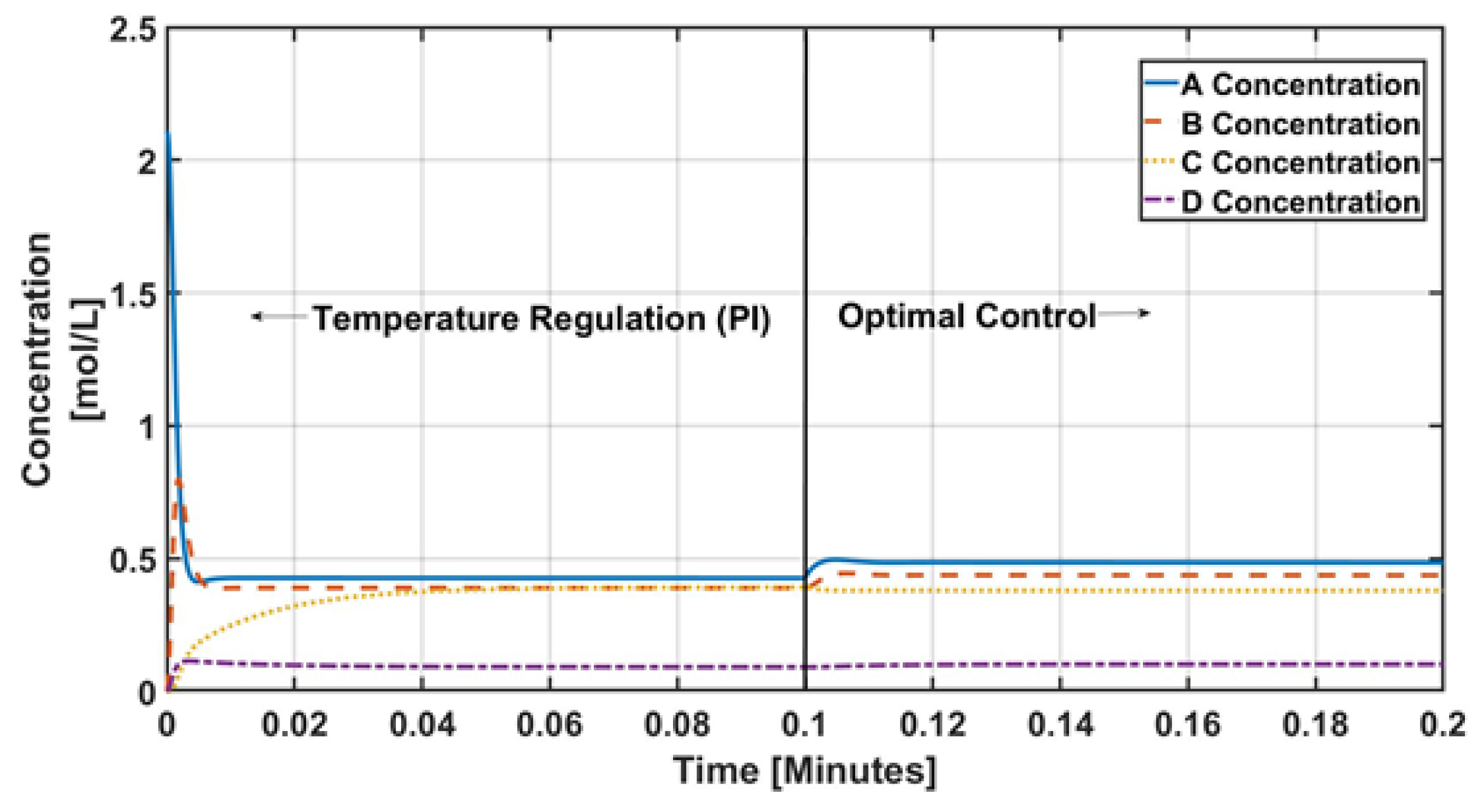
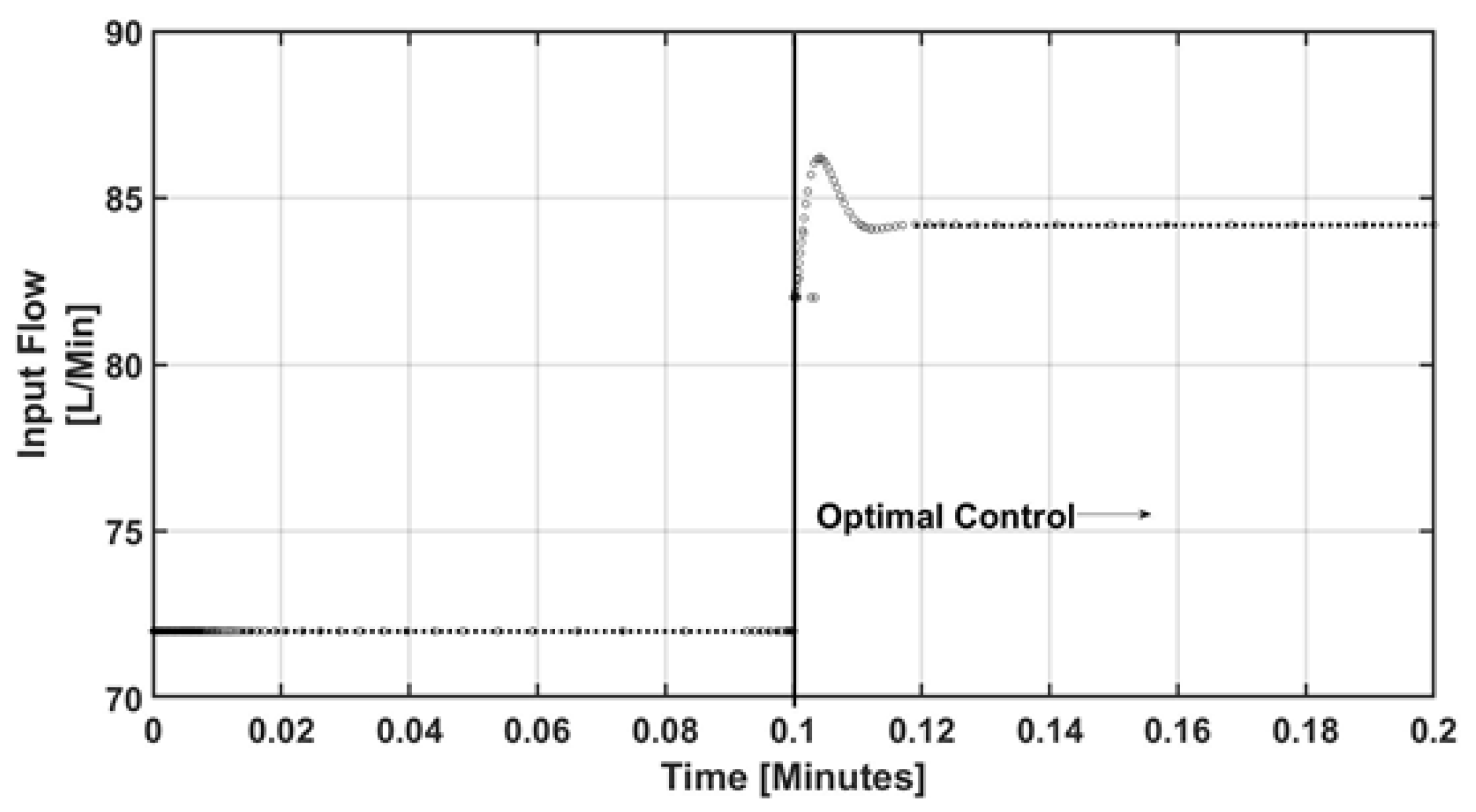
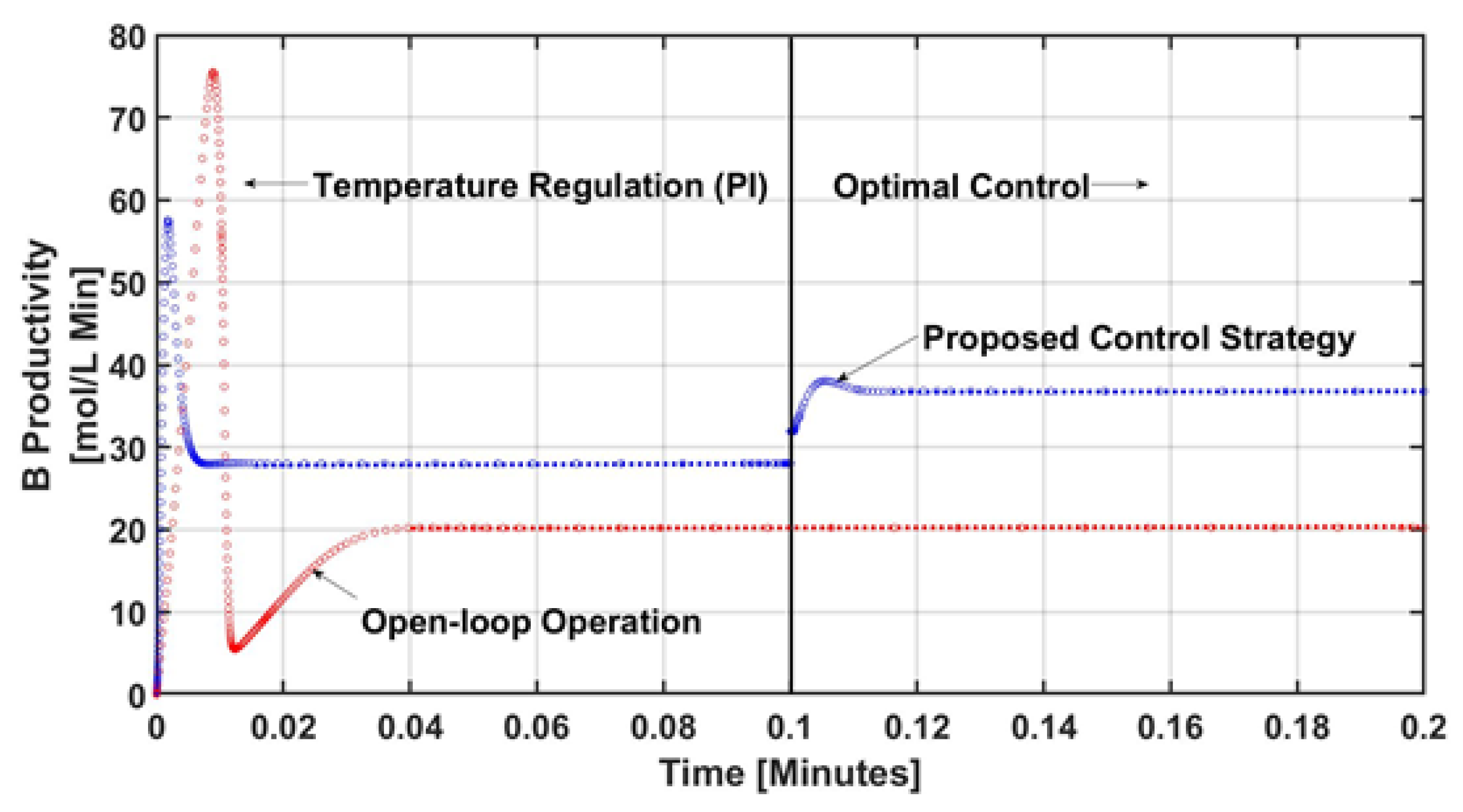
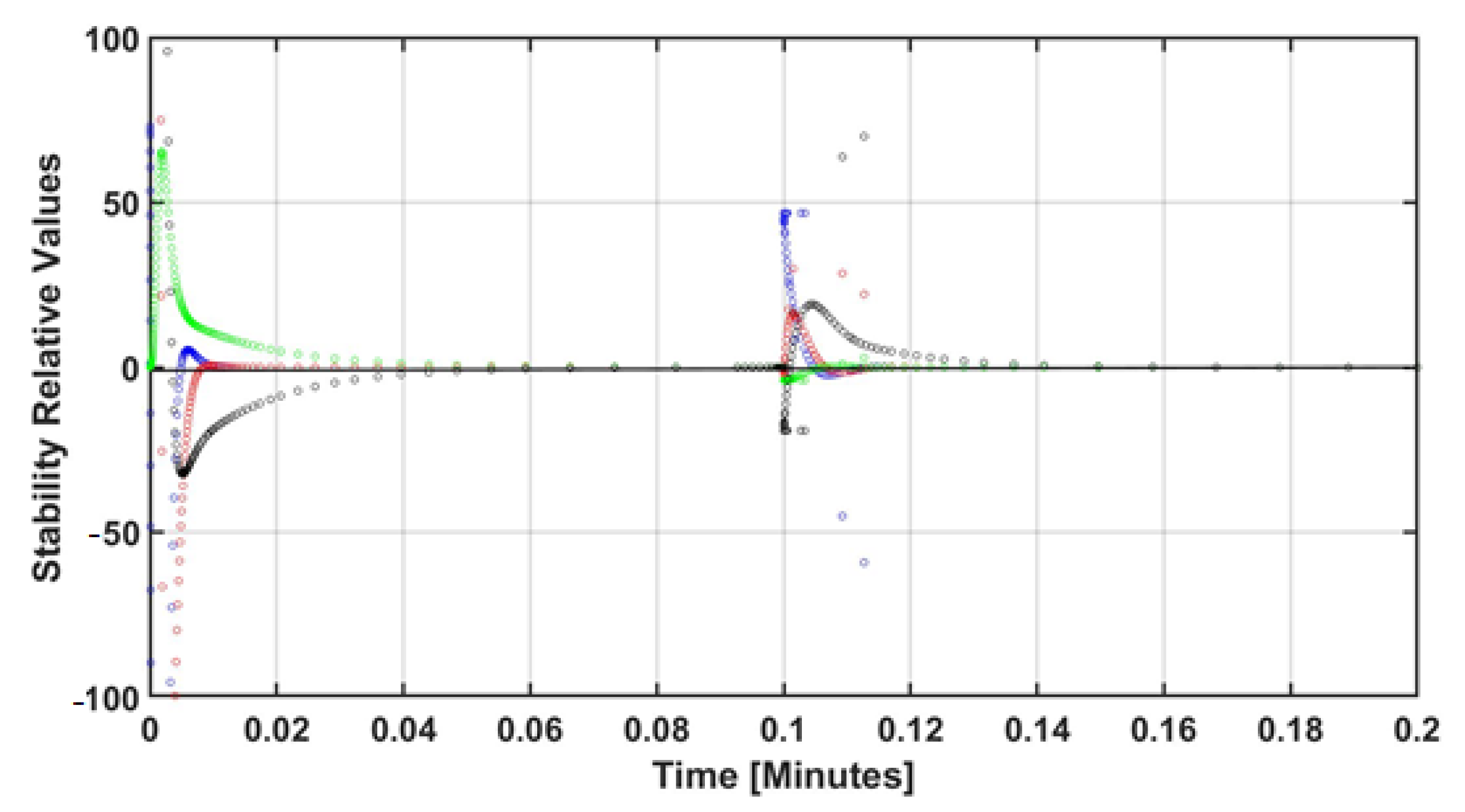
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roberge, D.; Noti, C.; Irle, E.; Eyholzer, M.; Rittiner, B.; Penn, G.; Schenkel, B. Control of Hazardous Processes in Flow: Synthesis of 2-Nitroethanol. J. Flow Chem. 2014, 4, 26–34. [Google Scholar] [CrossRef] [Green Version]
- Chehade, G.; Dincer, I. Advanced Kinetic Modelling and Simulation of a New Small Modular Ammonia Converter. Chem. Eng. Sci. 2021, 236, 116512. [Google Scholar] [CrossRef]
- Contreras, L.A.; Franco, H.A.; Alvarez, J. Saturated output-feedback nonlinear control of a 3-continuous exothermic reactor train. IFAC-Pap. Online 2018, 51, 425–430. [Google Scholar] [CrossRef]
- Gavalas, G.R. Uniform Systems with Chemical Change. In Nonlinear Differential Equations of Chemically Reacting Systems; Springer Tracts in Natural Philosophy; Springer: Berlin/Heidelberg, Germany, 1968; Volume 17. [Google Scholar]
- Ackermann, J.; Kaesbauer, D. Design of robust PID controllers. In Proceedings of the European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 522–527. [Google Scholar]
- Aguilar, R.; Poznyak, A.; Martínez-Guerra, R.; Maya-Yescas, R. Temperature control in catalytic cracking reactors via a robust PID controller. J. Process Control 2002, 12, 695–705. [Google Scholar] [CrossRef]
- Oriolo, G.; De Luca, A.; Vendittelli, M. WMR control via dynamic feedback linearization: Design, implementation, and experimental validation. IEEE Trans. Control Syst. Technol. 2002, 10, 835–852. [Google Scholar] [CrossRef]
- Barkhordari, M.; Jahed-Motlagh, M.R. Stabilization of a CSTR with two arbitrarily switching modes using modal state feedback linearization. Chem. Eng. J. 2009, 155, 838–843. [Google Scholar] [CrossRef]
- Rubio, J.J. Robust feedback linearization for nonlinear processes control. ISA Trans. 2018, 74, 155–164. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Z.; Durand, H.; Albalawi, F.; Christofides, P.D. On integration of feedback control and safety systems: Analyzing two chemical process applications. Chem. Eng. Res. Des. 2018, 132, 616–626. [Google Scholar] [CrossRef] [Green Version]
- Kravaris, C.; Kantor, J.C. Geometric methods for nonlinear process control. 2. Controller synthesis. Ind. Eng. Chem. Res. 1990, 29, 2310–2323. [Google Scholar] [CrossRef]
- Alvarez-Gallegos, J. Nonlinear regulation of a Lorenz system by feedback linearization techniques. Dyn. Control 1994, 4, 277–298. [Google Scholar] [CrossRef]
- Jana, A.K. Nonlinear State Estimation and Generic Model Control of a Continuous Stirred Tank Reactor. Int. J. Chem. React. Eng. 2007, 5, A42. [Google Scholar] [CrossRef]
- Cott, B.J.; Macchietto, S. Temperature control of exothermic batch reactors using generic model control. Ind. Eng. Chem. Res. 1989, 28, 1177–1184. [Google Scholar] [CrossRef]
- Chu, Y.; You, F. Model-based integration of control and operations: Overview, challenges, advances, and opportunities. Comput. Chem. Eng. 2015, 83, 2–20. [Google Scholar] [CrossRef]
- Baruah, S.; Dewan, L. A comparative study of PID based temperature control of CSTR using Genetic Algorithm and Particle Swarm Optimization. In Proceedings of the International Conference on Emerging Trends in Computing and Communication Technologies (ICETCCT), Dehradun, India, 17–18 November 2017; pp. 1–6. [Google Scholar]
- Khanduja, N.; Bhushan, B. CSTR Control Using IMC-PID, PSO-PID, and Hybrid BBO-FF-PID Controller. In Applications of Artificial Intelligence Techniques in Engineering; Malik, H., Srivastava, S., Sood, Y., Ahmad, A., Eds.; Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; Volume 697. [Google Scholar]
- Romero-Bustamante, J.A.; Moguel-Castañeda, J.G.; Puebla, H.; Hernandez-Martinez, E. Robust Cascade Control for Chemical Reactors: An Approach based on Modelling Error Compensation. Int. J. Chem. React. Eng. 2017, 15. [Google Scholar] [CrossRef]
- Murugesan, R.; Solaimalai, J.; Chandran, K. Computer-Aided Controller Design for a Nonlinear Process Using a Lagrangian-Based State Transition Algorithm. Circuits Syst. Signal Process 2020, 39, 977–996. [Google Scholar] [CrossRef]
- Zerari, N.; Chemachema, M. Robust adaptive neural network prescribed performance control for uncertain CSTR system with input nonlinearities and external disturbance. Neural Comput. Applic. 2020, 32, 10541–10554. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, S.; Cao, Z.; Lu, J.; Gao, F. A Systematic Min–Max Optimization Design of Constrained Model Predictive Tracking Control for Industrial Processes against Uncertainty. IEEE Trans. Control Syst. Technol. 2018, 26, 2157–2164. [Google Scholar] [CrossRef]
- Maurer, J.; Freund, H. Efficient calculation of constraint back-offs for optimization under uncertainty: A case study on maleic anhydride synthesis. Chem. Eng. Sci. 2018, 192, 306–317. [Google Scholar]
- Rodríguez-Pérez, B.E.; Flores-Tlacuahuac, A.; Ricardez-Sandoval, L.; Lozano, F.J. Optimal Water Quality Control of Sequencing Batch Reactors Under Uncertainty. Ind. Eng. Chem. Res. 2018, 57, 9571–9590. [Google Scholar] [CrossRef]
- Jia, R.; You, F. Multi-stage economic model predictive control for a gold cyanidation leaching process under uncertainty. AIChE J. 2021, 67, e17043. [Google Scholar] [CrossRef]
- Aguilar, R.; Martínez-Guerra, R.; Poznyak, A. Reaction heat estimation in continuous chemical reactors using high gain observers. Chem. Eng. J. 2002, 87, 351–356. [Google Scholar] [CrossRef]
- Aguilar-López, R. State estimation for nonlinear systems under model unobservable uncertainties: Application to continuous reactor. Chem. Eng. J. 2005, 108, 139–144. [Google Scholar] [CrossRef]
- Harinath, E.; Foguth, L.C.; Paulson, J.A.; Braatz, R.D. Nonlinear model predictive control using polynomial optimization methods. In Proceedings of the IEEE American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1–6. [Google Scholar]
- Hashem, I.; Telen, D.; Nimmegeers, P.; Logist, F.; Van Impe, J. A novel algorithm for fast representation of a Pareto front with adaptive resolution: Application to multi-objective optimization of a chemical reactor. Comput. Chem. Eng. 2017, 106, 544–558. [Google Scholar] [CrossRef]
- Puschke, J.; Djelassi, H.; Kleinekorte, J.; Hannemann-Tamás, R.; Mitsos, A. Robust dynamic optimization of batch processes under parametric uncertainty: Utilizing approaches from semi-infinite programs. Comput. Chem. Eng. 2018, 116, 253–267. [Google Scholar] [CrossRef]
- Maurer, J.; Freund, H. Optimization under uncertainty in chemical engineering: Comparative evaluation of unscented transformation methods and cubature rules. Chem. Eng. Sci. 2018, 183, 329–345. [Google Scholar]
- Bernardo, F.P.; Pistikopoulos, E.N.; Saraiva, P.M. Integration and computational issues in stochastic design and planning optimization problems. Ind. Eng. Chem. Res. 1999, 38, 3056–3068. [Google Scholar] [CrossRef]
- Bernardo, F.P.; Pistikopoulos, E.N.; Saraiva, P.M. Quality costs and robustness criteria in chemical process design optimization. Comput. Chem. Eng. 2001, 25, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Seow, V.Y.; Chen, X.; Too, H.P. Multidimensional heuristic process for high-yield production of astaxanthin and fragrance molecules in Escherichia coli. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Yuan, J.; Liu, C.; Zhang, X.; Xie, J.; Feng, E.; Yin, H.; Xiu, Z. Optimal control of a batch fermentation process with nonlinear time-delay and free terminal time and cost sensitivity constraint. J. Process Control 2016, 44, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Gurubel, K.J.; Osuna-Enciso, V.; Coronado-Mendoza, A.; Cuevas, E. Optimal control strategy based on neural model of nonlinear systems and evolutionary algorithms for renewable energy production as applied to biofuel generation. J. Renew. Sustain. Energy 2017, 9, 033101. [Google Scholar] [CrossRef]
- Goud, H.; Swarnkar, P. Investigations on Metaheuristic Algorithm for Designing Adaptive PID Controller for Continuous Stirred Tank Reactor. MAPAN 2019, 34, 113–119. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liao, L. Near-optimal control of nonlinear dynamical systems: A brief survey. Annu. Rev. Control 2019, 47, 71–80. [Google Scholar] [CrossRef]
- Bailo, R.; Bongini, M.; Carrillo, J.A.; Kalise, D. Optimal consensus control of the Cucker-Smale model. IFAC-Pap. OnLine 2018, 51, 1–6. [Google Scholar] [CrossRef]
- Lara-Cisneros, G.; Aguilar-López, R.; Femat, R. On the dynamic optimization of methane production in anaerobic digestion via extremum-seeking control approach. Comput. Chem. Eng. 2015, 75, 49–59. [Google Scholar] [CrossRef]
- Verleysen, K.; Coppitters, D.; Parente, A.; De Paepe, W.; Contino, F. How can power-to-ammonia be robust? Optimization of an ammonia synthesis plant powered by a wind turbine considering operational uncertainties. Fuel 2020, 266, 117049. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J.; Puebla, H. On classical PI control of chemical reactors. Chem. Eng. Sci. 2001, 56, 2111–2121. [Google Scholar] [CrossRef]
- Amte, V.; Nistala, S.; Malik, R.; Mahajani, S. Attainable regions of reactive distillation—Part III. Complex reaction scheme: Van de Vusse reaction. Chem. Eng. Sci. 2011, 66, 2285–2297. [Google Scholar] [CrossRef]
- Van de Vusse, J.G. Plug-flow type reactor versus tank reactor. Chem. Eng. Sci. 1964, 19, 994–997. [Google Scholar] [CrossRef]
- Trierweiler, J.O. A Systematic Approach to Control Structure Design. Ph.D. Thesis, Universität Dortmund, Dortmund, Germany, 1997. [Google Scholar]
- Rubi, V.A.; Deo, A.; Kumar, N. Temperature control of CSTR using PID Controller. Int. J. Eng. Comput. Sci. 2015, 4, 11902–11905. [Google Scholar]
- Kumar, M.; Prasad, D.; Giri, B.S.; Singh, R.S. Temperature control of fermentation bioreactor for ethanol production using IMC-PID controller. Biotechnol. Rep. 2019, 22, e00319. [Google Scholar] [CrossRef]
- Aguilar-López, R. Chaos Suppression via Euler-Lagrange Control Design for a Class of Chemical Reacting System. Math. Probl. Eng. 2018, 3802801. [Google Scholar] [CrossRef]
- Flores-Flores, J.P.; Martínez-Guerra, R. PI observer design for a class of nondifferentially flat systems. Int. J. Appl. Math. Comput. Sci. 2019, 29, 655–665. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Guerra, R.; Cruz-Victoria, J.C.; Gonzalez-Galan, R.; Aguilar-Lopez, R. A new reduced-order observer design for the synchronization of Lorenz systems. Chaos Solitons Fractals 2006, 28, 511–517. [Google Scholar] [CrossRef]
- Aguilar-Lopez, R.; Maya-Yescas, R. Inverse dynamics: A problem on transient controllability for industrial plants. Inverse Probl. Sci. Eng. 2008, 16, 811–827. [Google Scholar] [CrossRef]
- Babatunde, A.O.; Ray, W.H. Process Dynamics Modeling Control; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
| Description | Parameter | Value | Units |
|---|---|---|---|
| Heat transfer area | A | 0.215 | m |
| Temperature initial condition | 387.05 | K | |
| Heat transfer coefficient | U | 67.2 | kJ·minmK |
| Heat capacity | kJ·kg K | ||
| Nominal cooling jacket temperature | 125 | C | |
| Reacting mixture density | 934.2 | kg·m | |
| Reactor volume | V | 0.01 | m |
| Concentration initial conditions | |||
| Pre-exponential kinetic factors | |||
| Activation energies | |||
| Reaction heat |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar-López, R.; Mata-Machuca, J.L.; Godinez-Cantillo, V. A TITO Control Strategy to Increase Productivity in Uncertain Exothermic Continuous Chemical Reactors. Processes 2021, 9, 873. https://doi.org/10.3390/pr9050873
Aguilar-López R, Mata-Machuca JL, Godinez-Cantillo V. A TITO Control Strategy to Increase Productivity in Uncertain Exothermic Continuous Chemical Reactors. Processes. 2021; 9(5):873. https://doi.org/10.3390/pr9050873
Chicago/Turabian StyleAguilar-López, Ricardo, Juan Luis Mata-Machuca, and Valeria Godinez-Cantillo. 2021. "A TITO Control Strategy to Increase Productivity in Uncertain Exothermic Continuous Chemical Reactors" Processes 9, no. 5: 873. https://doi.org/10.3390/pr9050873






