Improving the Classification Efficiency of an ANN Utilizing a New Training Methodology
Abstract
:1. Introduction
2. Weight Constrained Neural Network Training Algorithm
| Algorithm 1: Weight Constrained Neural Network Training Algorithm |
|
3. Experimental Analysis
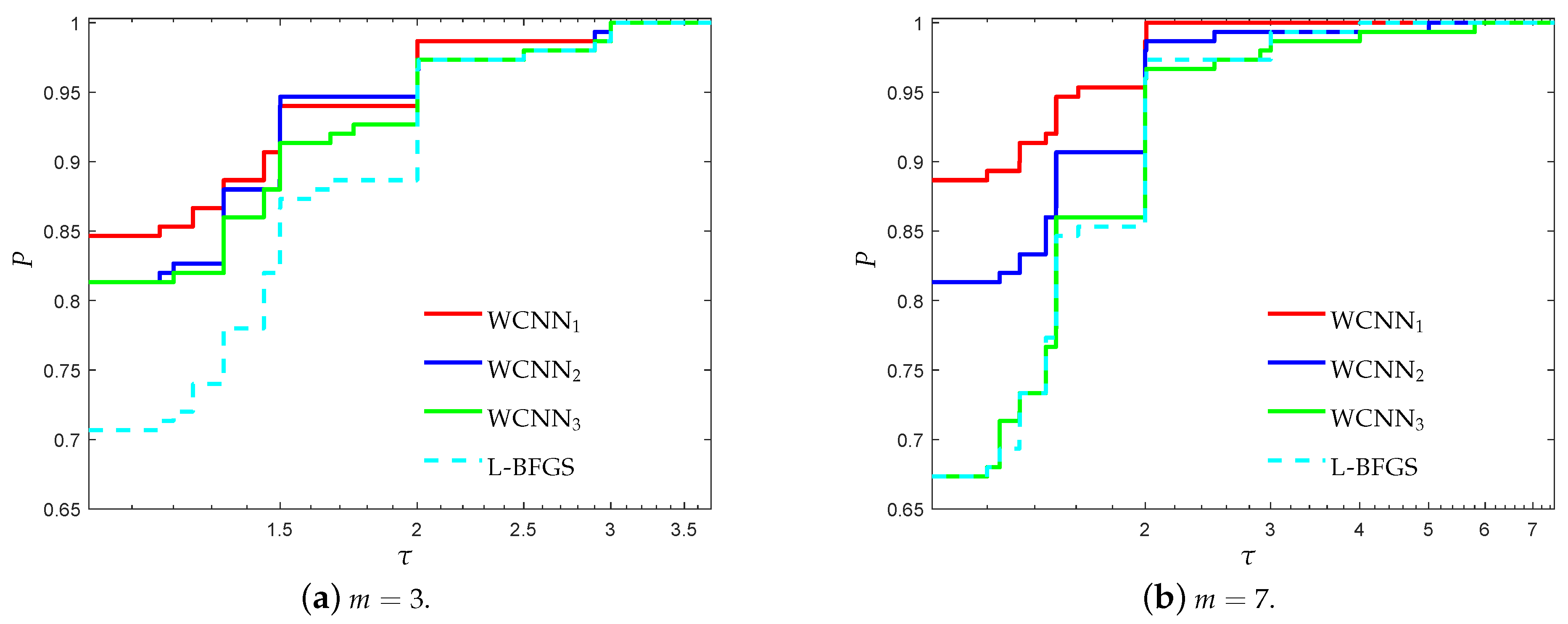
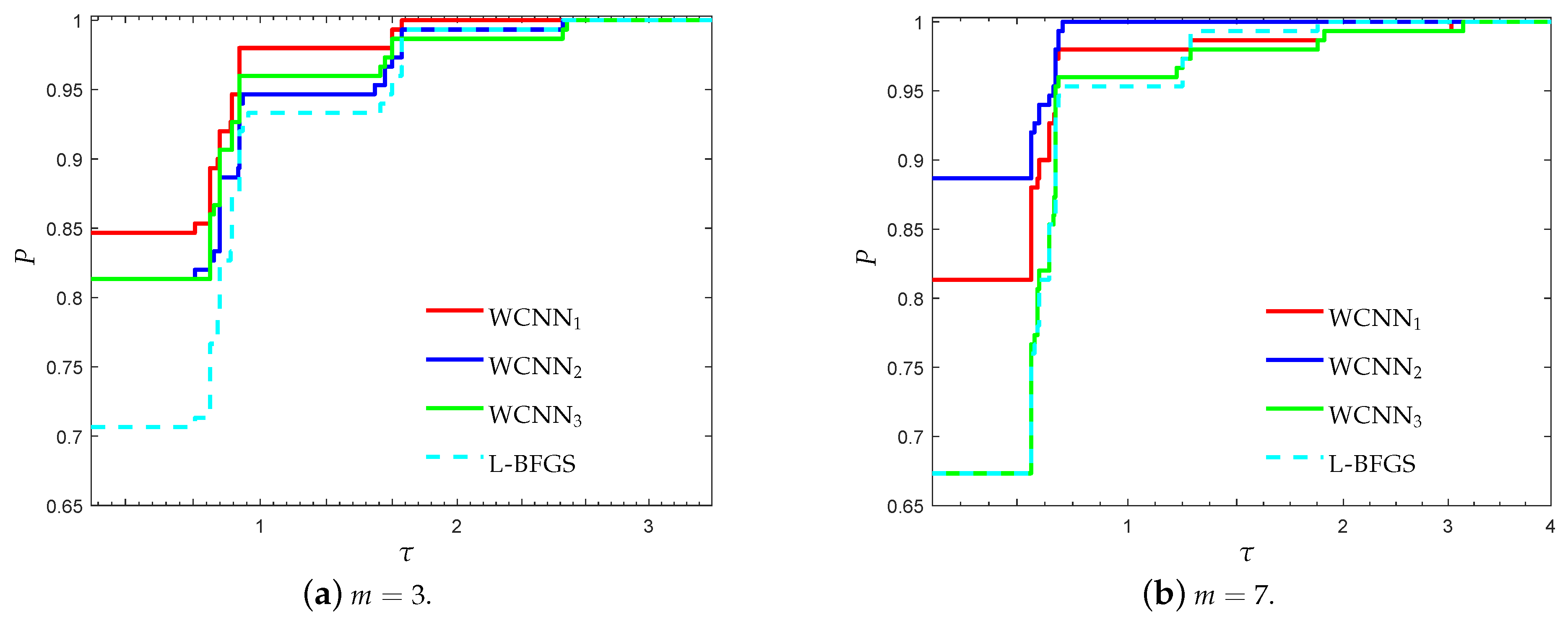
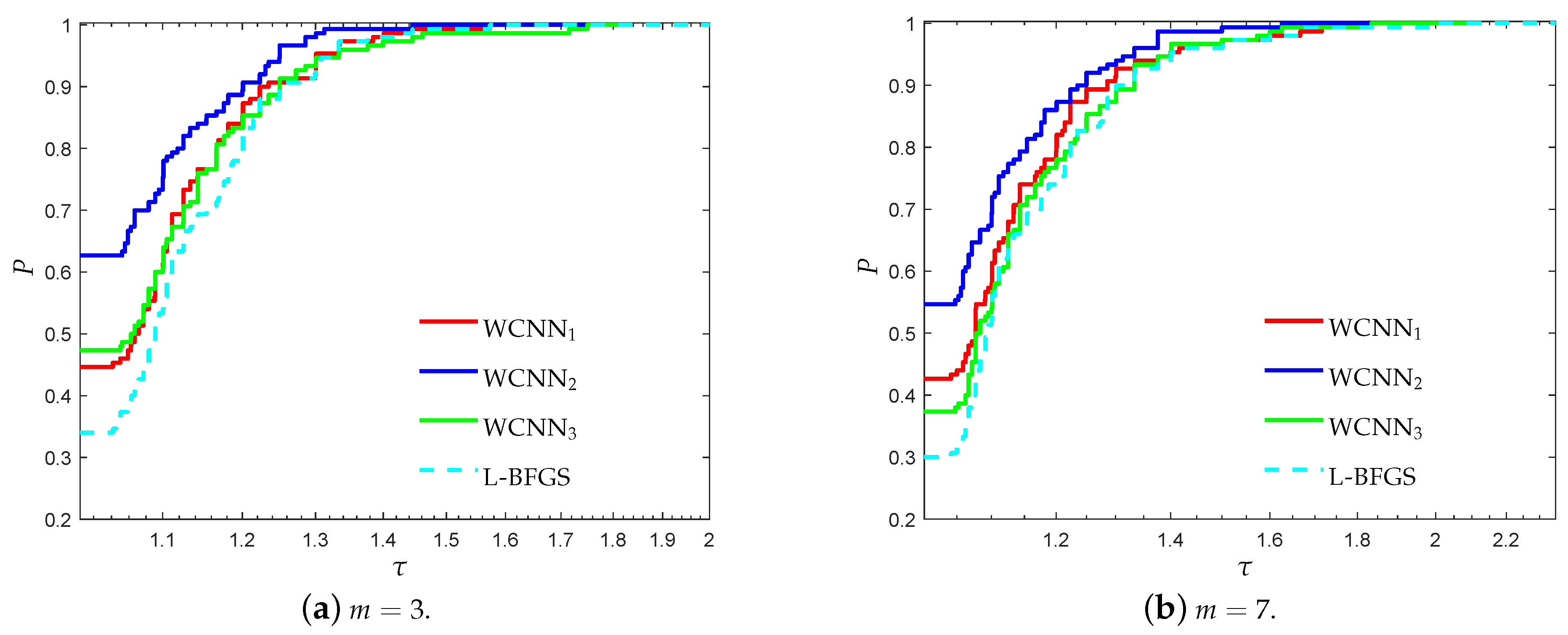
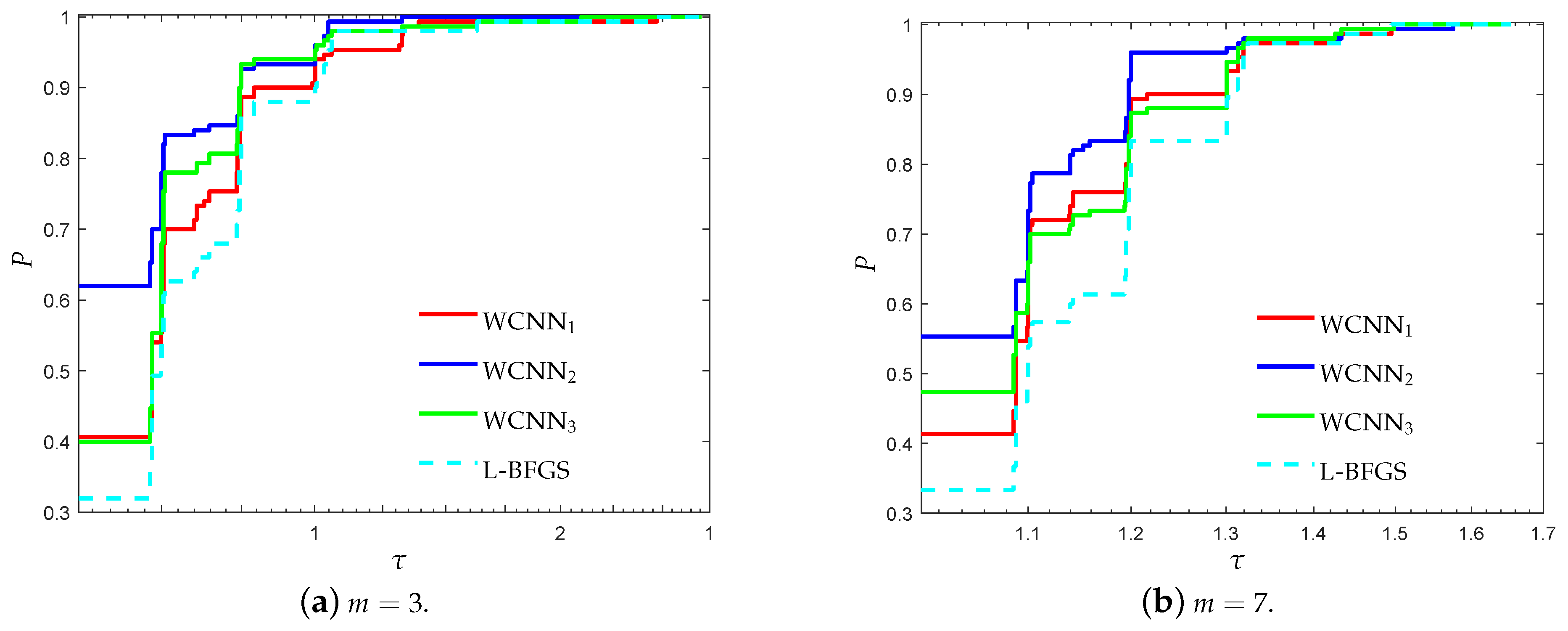
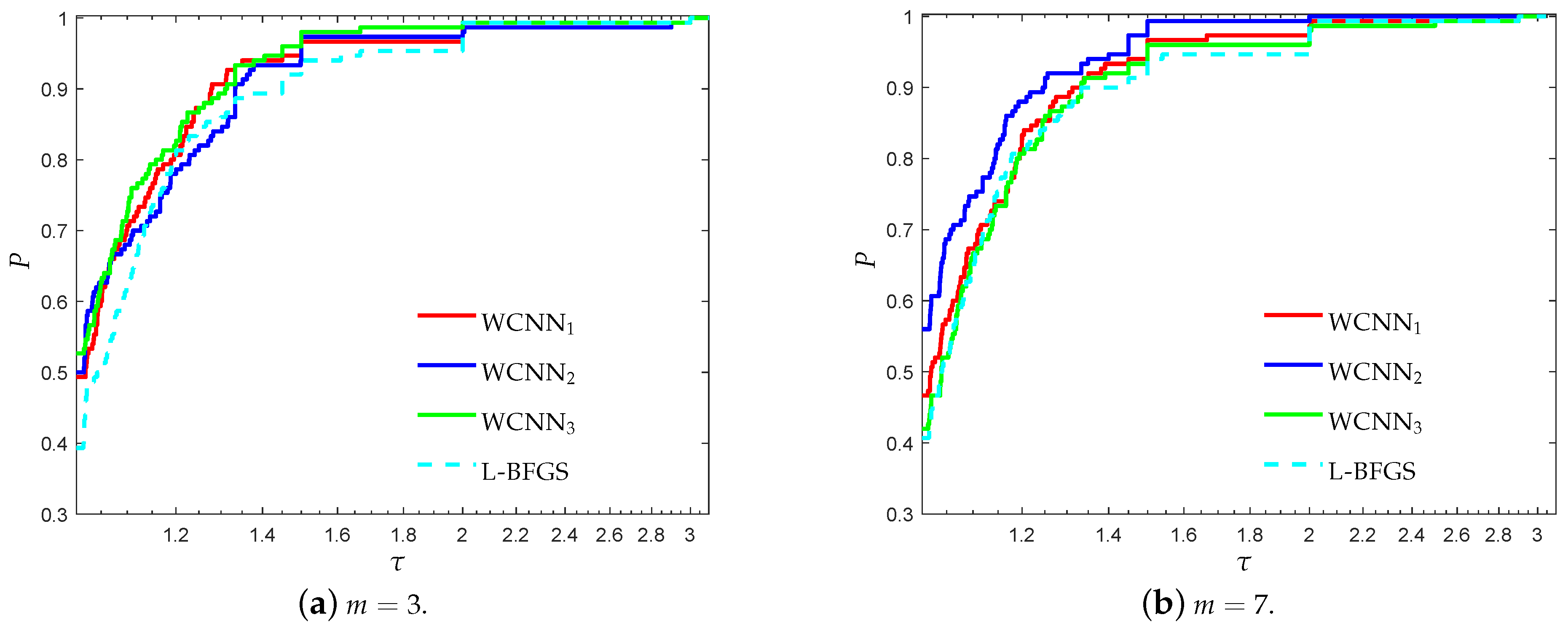
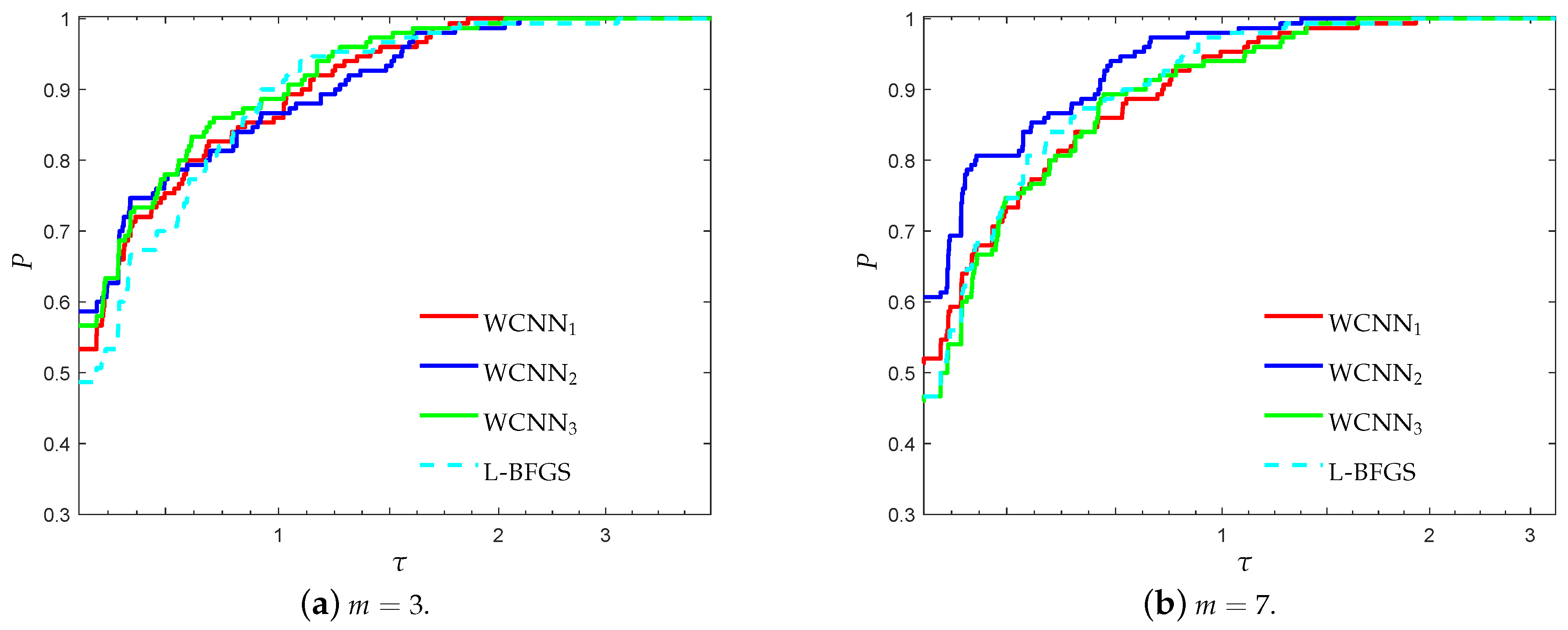
3.1. Performance Evaluation Against L-BFGS Algorithm
- “WCNN1” stands for Algorithm 1 with bounds on the weights .
- “WCNN2” stands for Algorithm 1 with bounds on the weights .
- “WCNN3” stands for Algorithm 1 with bounds on the weights .
- “L-BFGS” stands for the limited-memory BFGS.
3.1.1. Breast Cancer Classification Problem
3.1.2. Australian Credit Card Classification Problem
3.1.3. Diabetes Classification Problem
3.1.4. Escherichia coli Classification Problem
3.1.5. Coimbra Classification Problem
3.1.6. SPECT Heart Classification Problem
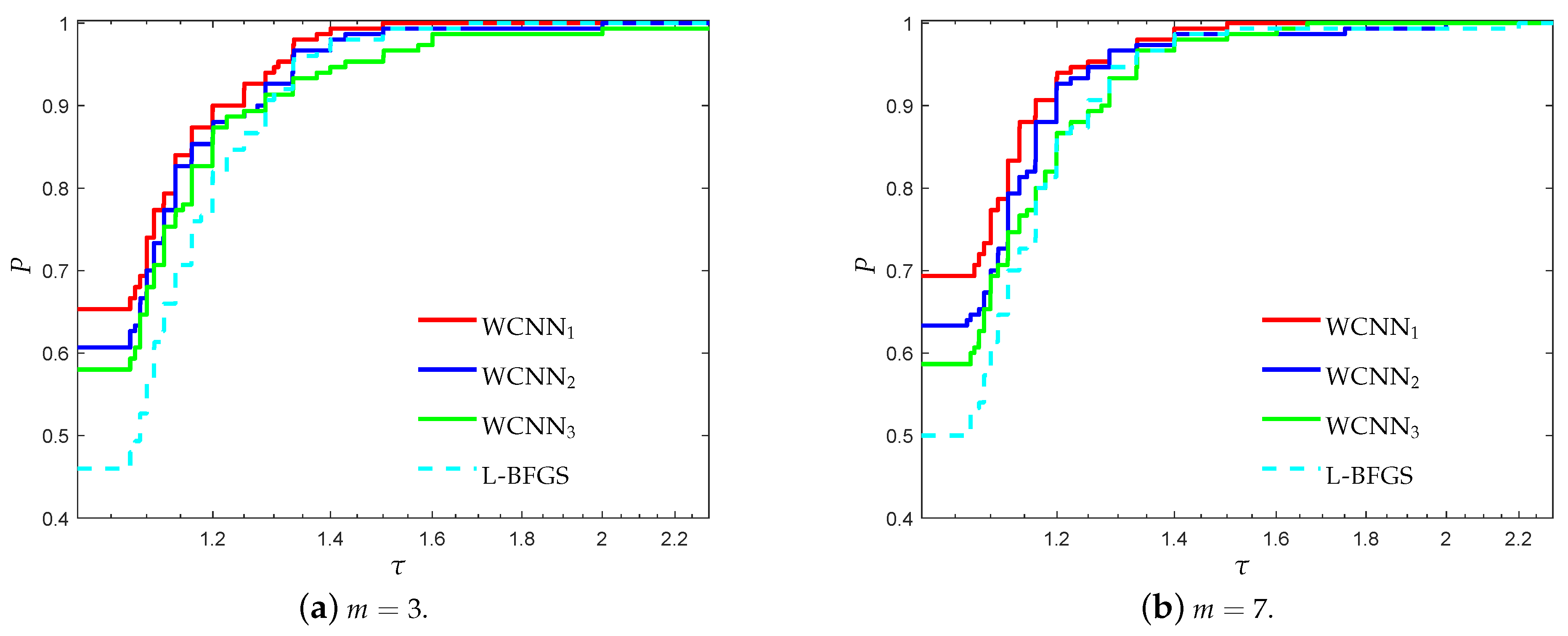
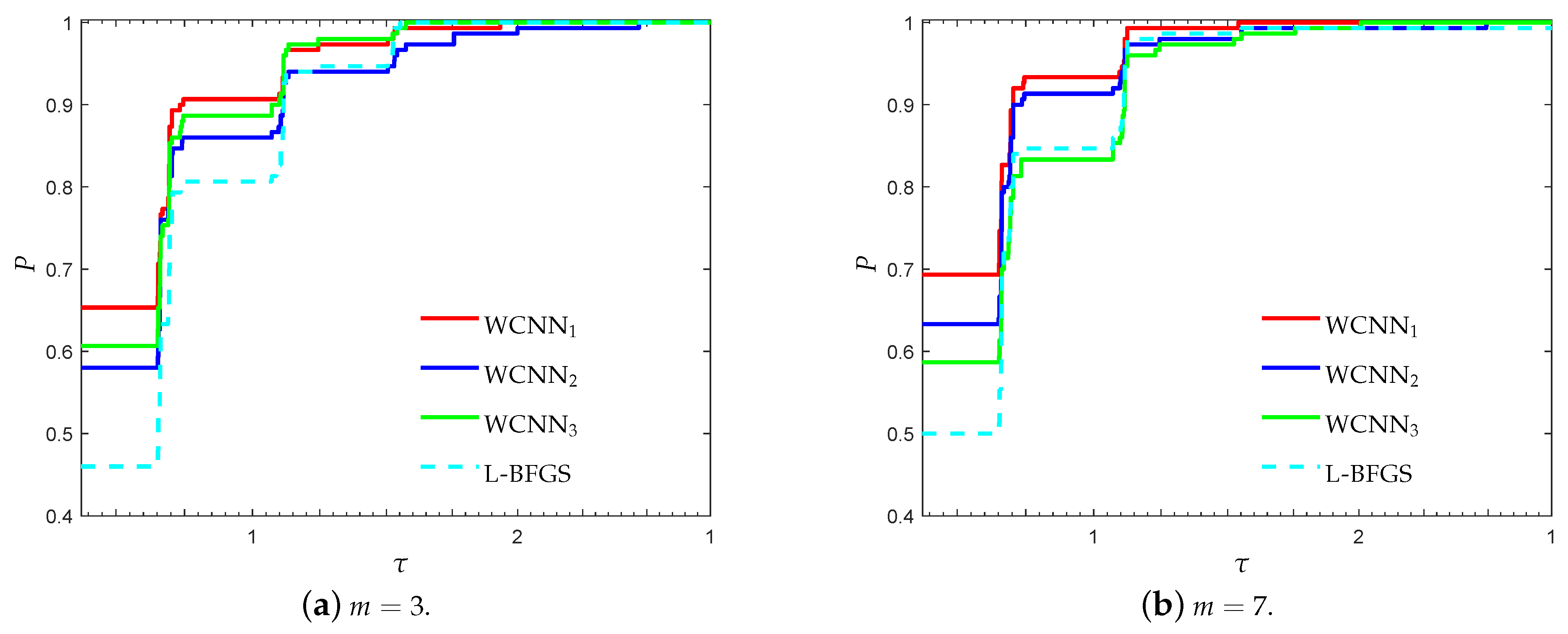
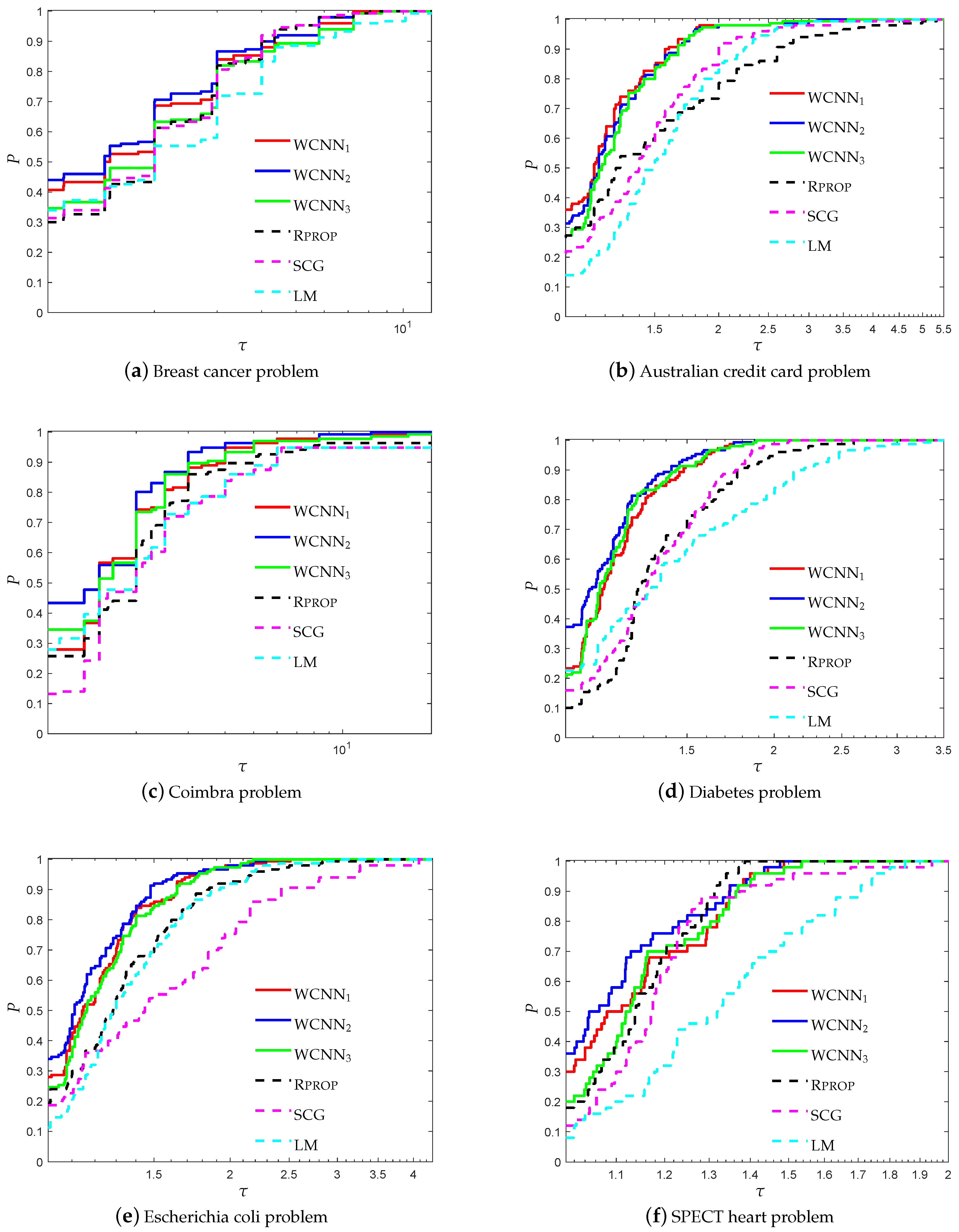
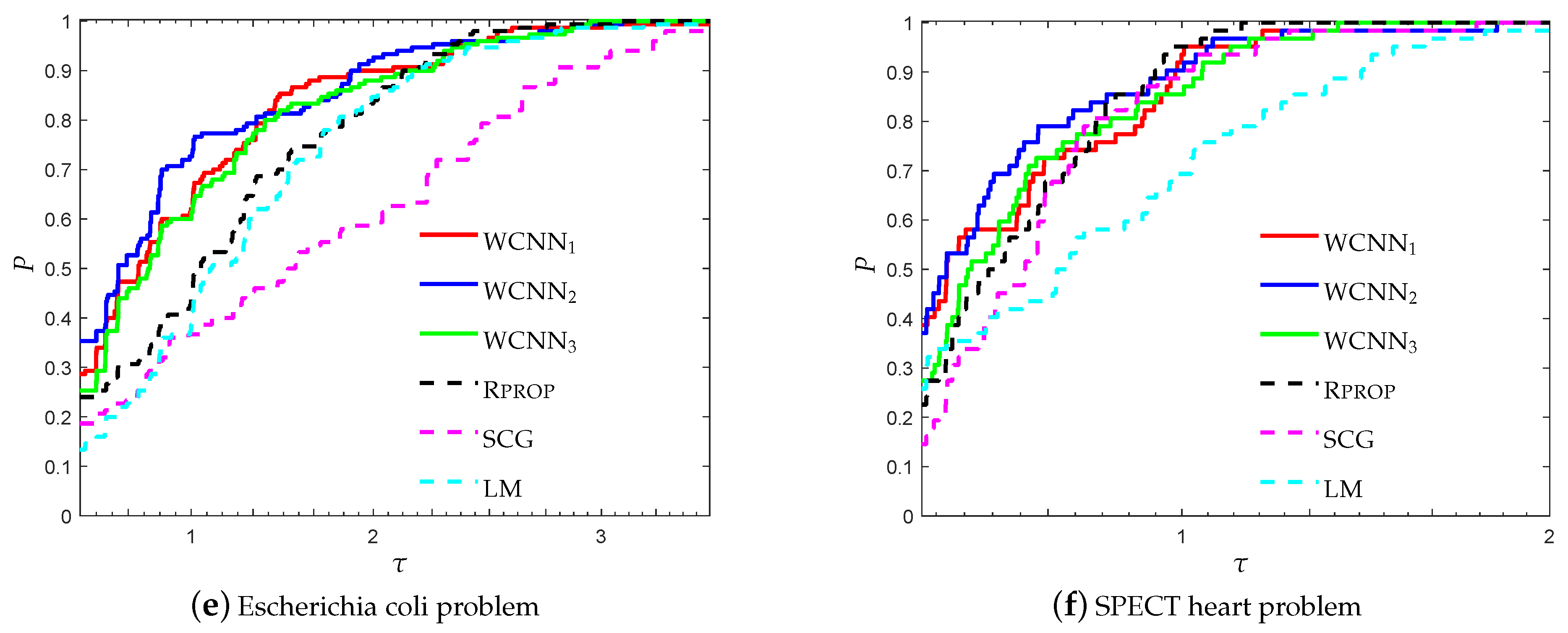
3.2. Performance Evaluation against State-of-the-Art Training Algorithms
- “WCNN1” stands for Algorithm 1 with and bounds on the weights .
- “WCNN2” stands for Algorithm 1 with and bounds on the weights .
- “WCNN3” stands for Algorithm 1 with and bounds on the weights .
- “Rprop” stands for Resilient backpropagation.
- “SCG” stands for scaled conjugate gradient.
- “LM” stands for Levenberg-Marquardt training algorithm.
4. Discussion, Conclusions and Future Research
Funding
Conflicts of Interest
References
- Azar, A.T.; Vaidyanathan, S. Computational Intelligence Applications in Modeling and Control; Springer: New York, NY, USA, 2015. [Google Scholar]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design; Martin Hagan: Boston, MA, USA, 2014. [Google Scholar]
- Dinh, T.A.; Kwon, Y.K. An empirical study on importance of modeling parameters and trading volume-based features in daily stock trading using neural networks. Inform. Multidiscip. Dig. Publ. Inst. 2018, 5, 36. [Google Scholar] [CrossRef]
- Frey, S. Sampling and Estimation of Pairwise Similarity in Spatio-Temporal Data Based on Neural Networks. Inform. Multidiscip. Dig. Publ. Inst. 2017, 4, 27. [Google Scholar] [CrossRef]
- Maren, A.J.; Harston, C.T.; Pap, R.M. Handbook of Neural Computing Applications; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Moya Rueda, F.; Grzeszick, R.; Fink, G.A.; Feldhorst, S.; Ten Hompel, M. Convolutional Neural Networks for Human Activity Recognition Using Body-Worn Sensors. Inform. Multidiscip. Dig. Publ. Inst. 2018, 5, 26. [Google Scholar] [CrossRef]
- Hamada, M.; Hassan, M. Artificial neural networks and particle swarm optimisation algorithms for preference prediction in multi-criteria recommender systems. Inform. Multidiscip. Dig. Publ. Inst. 2018, 5, 25. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Rumelhart, D., McClelland, J., Eds.; The MIT Press: London, UK, 1986; pp. 318–362. [Google Scholar]
- Golovashkin, D.; Sharanhovich, U.; Sashikanth, V. Accelerated TR-L-BFGS Algorithm for Neural Network. US Patent Application 14/823,167, 16 February 2017. [Google Scholar]
- Liu, Q.; Liu, J.; Sang, R.; Li, J.; Zhang, T.; Zhang, Q. Fast Neural Network Training on FPGA Using Quasi-Newton Optimisation Method. IEEE Trans. Very Larg. Scale Integr. Syst. 2018, 26, 1575–1579. [Google Scholar] [CrossRef]
- Badem, H.; Basturk, A.; Caliskan, A.; Yuksel, M.E. A new efficient training strategy for deep neural networks by hybridisation of artificial bee colony and limited–memory BFGS optimisation algorithms. Neurocomputing 2017, 266, 506–526. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. An improved spectral conjugate gradient neural network training algorithm. Int. J. Artif. Intell. Tools 2012, 21, 1250009. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. A new conjugate gradient algorithm for training neural networks based on a modified secant equation. Appl. Math. Comput. 2013, 221, 491–502. [Google Scholar] [CrossRef]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Peng, C.C.; Magoulas, G.D. Adaptive nonmonotone conjugate gradient training algorithm for recurrent neural networks. In Proceedings of the 19th IEEE International Conference on Tools with Artificial Intelligence, Paris, France, 29–31 October 2007; pp. 374–381. [Google Scholar]
- Peng, C.C.; Magoulas, G.D. Advanced adaptive nonmonotone conjugate gradient training algorithm for recurrent neural networks. Int. J. Artif. Intell. Tools 2008, 17, 963–984. [Google Scholar] [CrossRef]
- Peng, C.C.; Magoulas, G.D. Nonmonotone Levenberg–Marquardt training of recurrent neural architectures for processing symbolic sequences. Neural Comput. Appl. 2011, 20, 897–908. [Google Scholar] [CrossRef]
- Peng, C.C.; Magoulas, G.D. Nonmonotone BFGS-trained recurrent neural networks for temporal sequence processing. Appl. Math. Comput. 2011, 217, 5421–5441. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. A new class of nonmonotone conjugate gradient training algorithms. Appl. Math. Comput. 2015, 266, 404–413. [Google Scholar] [CrossRef]
- Karras, D.A.; Perantonis, S.J. An efficient constrained training algorithm for feedforward networks. IEEE Trans. Neural Netw. 1995, 6, 1420–1434. [Google Scholar] [CrossRef] [PubMed]
- Perantonis, S.J.; Karras, D.A. An efficient constrained learning algorithm with momentum acceleration. Neural Netw. 1995, 8, 237–249. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Nocedal, J. On the limited memory BFGS method for large scale optimisation methods. Math. Programm. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Dolan, E.; Moré, J. Benchmarking optimisation software with performance profiles. Math. Programm. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- Morales, J.L.; Nocedal, J. Remark on “Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound constrained optimisation”. ACM Trans. Math. Softw (TOMS) 2011, 38, 7. [Google Scholar] [CrossRef]
- Dua, D.; Karra Taniskidou, E. UCI Machine Learning Repository. In Proceedings of the ISIT Blogging, Part 3, Istanbul, Turkey, 31 July 2013. [Google Scholar]
- Nguyen, D.; Widrow, B. Improving the learning speed of 2-layer neural network by choosing initial values of adaptive weights. Biol. Cybern. 1990, 59, 71–113. [Google Scholar]
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feed-forward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Yu, J.; Wang, S.; Xi, L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing 2008, 71, 1054–1060. [Google Scholar] [CrossRef]
- Liang, P.; Labedan, B.; Riley, M. Physiological genomics of Escherichia coli protein families. Physiol. Genom. 2002, 9, 15–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anastasiadis, A.; Magoulas, G.; Vrahatis, M. New globally convergent training scheme based on the resilient propagation algorithm. Neurocomputing 2005, 64, 253–270. [Google Scholar] [CrossRef]
- Patrício, M.; Pereira, J.; Crisóstomo, J.; Matafome, P.; Gomes, M.; Seiça, R.; Caramelo, F. Using Resistin, glucose, age and BMI to predict the presence of breast cancer. BMC Cancer 2018, 18, 29. [Google Scholar] [CrossRef] [PubMed]
- Jeni, L.A.; Cohn, J.F.; De La Torre, F. Facing imbalanced data—Recommendations for the use of performance metrics. In Proceedings of the Humaine Association Conference on Affective Computing and Intelligent Interaction, Geneva, Switzerland, 2–5 September 2013; pp. 245–251. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Hager, W.W.; Zhang, H. A new active set algorithm for box constrained optimisation. SIAM J. Optim. 2006, 17, 526–557. [Google Scholar] [CrossRef]
- Birgin, E.G.; Martínez, J.M. Large-scale active-set box-constrained optimisation method with spectral projected gradients. Comput. Optim. Appl. 2002, 23, 101–125. [Google Scholar] [CrossRef]
- Magoulas, G.D.; Plagianakos, V.P.; Vrahatis, M.N. Hybrid methods using evolutionary algorithms for on-line training. In Proceedings of the International Joint Conference on Neural Networks, Washington, DC, USA, 15–19 July 2001; pp. 2218–2223. [Google Scholar]
- Parsopoulos, K.E.; Plagianakos, V.P.; Magoulas, G.D.; Vrahatis, M.N. Improving the particle swarm optimizer by function “stretching”. In Advances in Convex Analysis and Global Optimisation; Springer: New York, NY, USA, 2001; pp. 445–457. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimisation method for constrained optimisation problems. Theory Appl. New Trends Intell. Technol. 2002, 76, 214–220. [Google Scholar]





| Classification Problem | #Features | #Instances | Neural Network Architecture | Total Number of Weights |
|---|---|---|---|---|
| Breast cancer | 9 | 683 | 9-4-2-2 | 56 |
| Australian credit card | 15 | 690 | 15-16-8-2 | 410 |
| Diabetes | 8 | 768 | 8-4-4-2 | 66 |
| Escherichia coli | 7 | 336 | 7-16-8 | 264 |
| Coimbra | 9 | 100 | 9-5-2-2 | 68 |
| SPECT heart | 13 | 270 | 13-16-8-2 | 230 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livieris, I.E. Improving the Classification Efficiency of an ANN Utilizing a New Training Methodology. Informatics 2019, 6, 1. https://doi.org/10.3390/informatics6010001
Livieris IE. Improving the Classification Efficiency of an ANN Utilizing a New Training Methodology. Informatics. 2019; 6(1):1. https://doi.org/10.3390/informatics6010001
Chicago/Turabian StyleLivieris, Ioannis E. 2019. "Improving the Classification Efficiency of an ANN Utilizing a New Training Methodology" Informatics 6, no. 1: 1. https://doi.org/10.3390/informatics6010001





