On the Oscillatory Properties of Solutions of Second-Order Damped Delay Differential Equations
Abstract
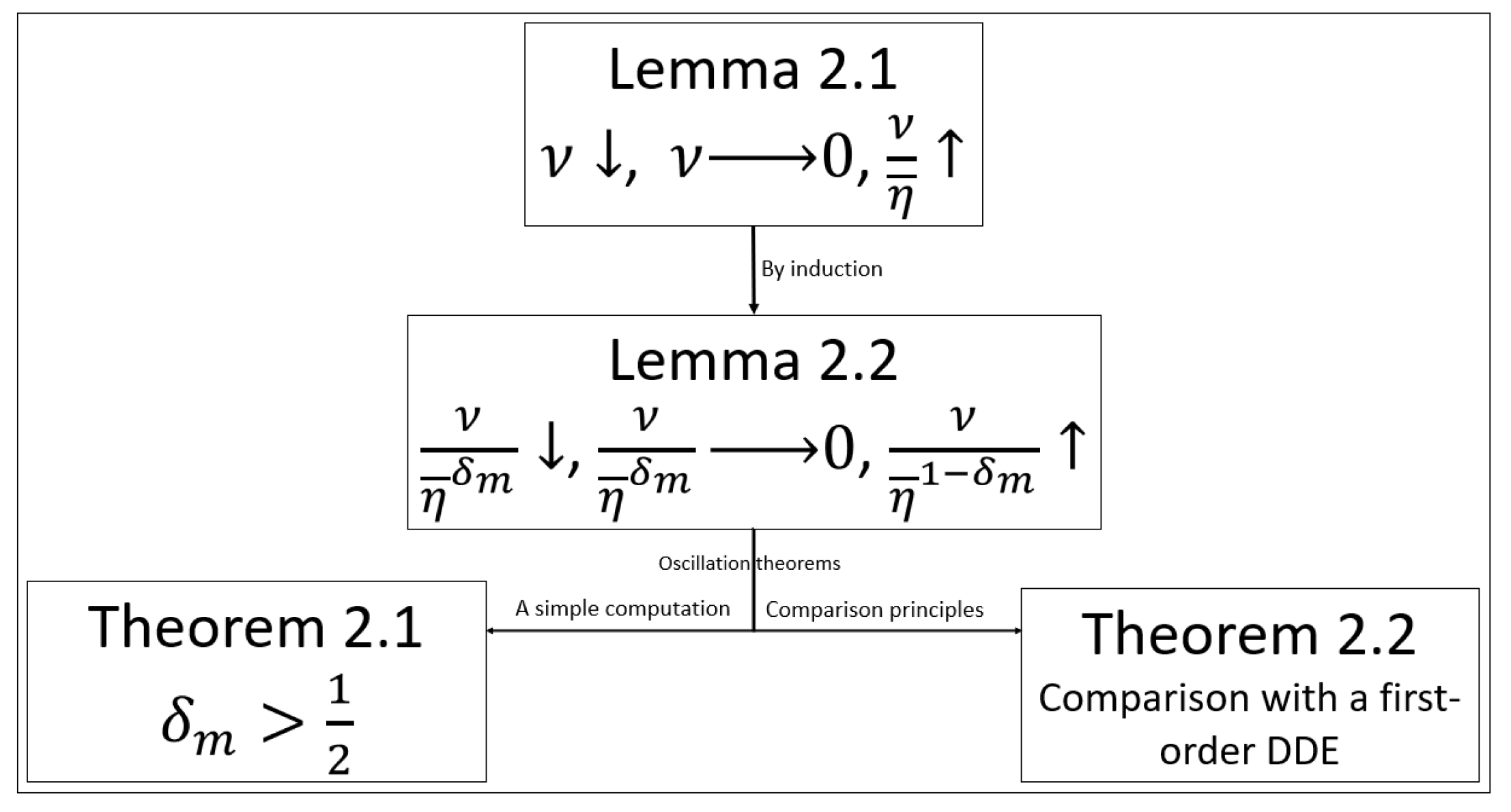
:1. Introduction
2. Main Results
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hale, J.K. Partial neutral functional differential equations. Rev. Roum. Math. Pures Appl. 1994, 39, 339–344. [Google Scholar]
- Bocharov, G.A.; Rihan, F.A. Numerical modelling in biosciences using delay differential equations. J. Comput. Appl. Math. 2000, 125, 183–199. [Google Scholar] [CrossRef] [Green Version]
- Rakkiyappan, R.; Velmurugan, G.; Rihan, F.; Lakshmanan, S. Stability analysis of memristor-based complex-valued recurrent neural networks with time delays. Complexity 2015, 21, 14–39. [Google Scholar] [CrossRef]
- Bahadorinejad, A.; Imani, M.; Braga-Neto, U.M. Adaptive particle filtering for fault detection in partially-observed Boolean dynamical systems. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 17, 1105–1114. [Google Scholar] [CrossRef] [PubMed]
- Imani, M.; Ghoreishi, S.F. Partially-Observed Discrete Dynamical Systems. In Proceedings of the American Control Conference (ACC), New Orleans, LA, USA, 26–28 May 2021. [Google Scholar]
- Wenger, J.; Hennig, P. Probabilistic Linear Solvers for Machine Learning. arXiv 2020, arXiv:2010.09691. [Google Scholar]
- Agarwal, R.P.; Grace, S.R.; O’Regan, D. Oscillation Theory for Second Order Linear, Half-Linear, Superlinear and Sublinear Dynamic Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Agarwal, R.P.; Bohner, M.; Li, W. Non-Oscillation and Oscillation Theory for Functional Differential Equations; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
- Gyori, I.; Ladas, G. Oscillation Theory of Delay Differential Equations with Applications; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Grace, S.R. Oscillation theorems for second order nonlinear differential equations with damping. Math. Nachr. 1989, 141, 117–127. [Google Scholar] [CrossRef]
- Grace, S.R. Oscillation of nonlinear differential equations of second order. Publ. Math. Debrecen. 1992, 40, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Grace, S.R.; Lalli, B.S. Oscillation theorems for certain second order perturbed nonlinear differential equation. J. Math. Anal. Appl. 1980, 77, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Grace, S.R.; Lalli, B.S. Asymptotic and oscillatory behavior of solutions of a class of second order differential equations with deviating arguments. J. Math. Anal. Appl. 1992, 145, 112–136. [Google Scholar] [CrossRef] [Green Version]
- Grace, S.R.; Lalli, B.S.; Yeh, C.C. Oscillation theorems for nonlinear second order differential equations with a nonlinear damping term. Siam. J. Math. Anal. 1984, 15, 1082–1093. [Google Scholar] [CrossRef]
- Kirane, M.; Rogovechenko, Y.V. Oscillation results for a second order damping differential equations with nonmontonous nonlinearity. J. Math. Anal. Appl. 2000, 250, 118–138. [Google Scholar] [CrossRef] [Green Version]
- Li, W.T.; Agarwal, R.P. Interval oscillation criteria for second order nonlinear differential equations with damping. Comput. Math. Appl. 2000, 40, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Li, W.T.; Zhang, M.Y. Oscillation criteria for second order nonlinear differential equations with damping term. Indian J. Pure Appl. Math. 1999, 30, 1017–1029. [Google Scholar]
- Rogovchenko, Y.V. Oscillation theorems for second-order equations with damping. Nonlinear Anal. Theor. 2000, 41, 1005–1028. [Google Scholar] [CrossRef]
- Wong, J.S. On Kamenev-type oscillation theorems for second-order differential equations with damping. J. Math. Anal. Appl. 2001, 258, 244–257. [Google Scholar] [CrossRef]
- Yan, J. Oscillation theorems for second order linear differential equations with damping. Proc. Am. Math. Soc. 1986, 98, 276–282. [Google Scholar] [CrossRef]
- Grace, S.R. On the oscillatory and asymptotic behavior of damping functional differential equations. Math. Jpn. 1991, 36, 220–237. [Google Scholar]
- Saker, S.H.; Pang, P.Y.; Agarwal, R.P. Oscillation theorem for second-order nonlinear functional differential equation with damping. Dyn. Syst. Appl. 2003, 12, 307–322. [Google Scholar]
- Tunc, E.; Kaymaz, A. On oscillation of second-order linear neutral differential equations with damping term. Dyn. Syst. Appl. 2019, 28, 289–301. [Google Scholar] [CrossRef] [Green Version]
- Philos, C.G. On the existence of nonoscillatory solutions tending to zero at ∞ for differential equations with positive delays. Arch. Math. 1981, 36, 168–178. [Google Scholar] [CrossRef]
- Kitamura, Y.; Kusano, T. Oscillation of first-order nonlinear differential equations with deviating arguments. Proc. Am. Math. Soc. 1980, 78, 64–68. [Google Scholar] [CrossRef]
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 18 | |||||
| 52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hendi, A.A.; Moaaz, O.; Cesarano, C.; Alharbi, W.R.; Abdou, M.A. On the Oscillatory Properties of Solutions of Second-Order Damped Delay Differential Equations. Mathematics 2021, 9, 1060. https://doi.org/10.3390/math9091060
Hendi AA, Moaaz O, Cesarano C, Alharbi WR, Abdou MA. On the Oscillatory Properties of Solutions of Second-Order Damped Delay Differential Equations. Mathematics. 2021; 9(9):1060. https://doi.org/10.3390/math9091060
Chicago/Turabian StyleHendi, Awatif A., Osama Moaaz, Clemente Cesarano, Wedad R. Alharbi, and Mohamed A. Abdou. 2021. "On the Oscillatory Properties of Solutions of Second-Order Damped Delay Differential Equations" Mathematics 9, no. 9: 1060. https://doi.org/10.3390/math9091060








