Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method
Abstract
:1. Introduction
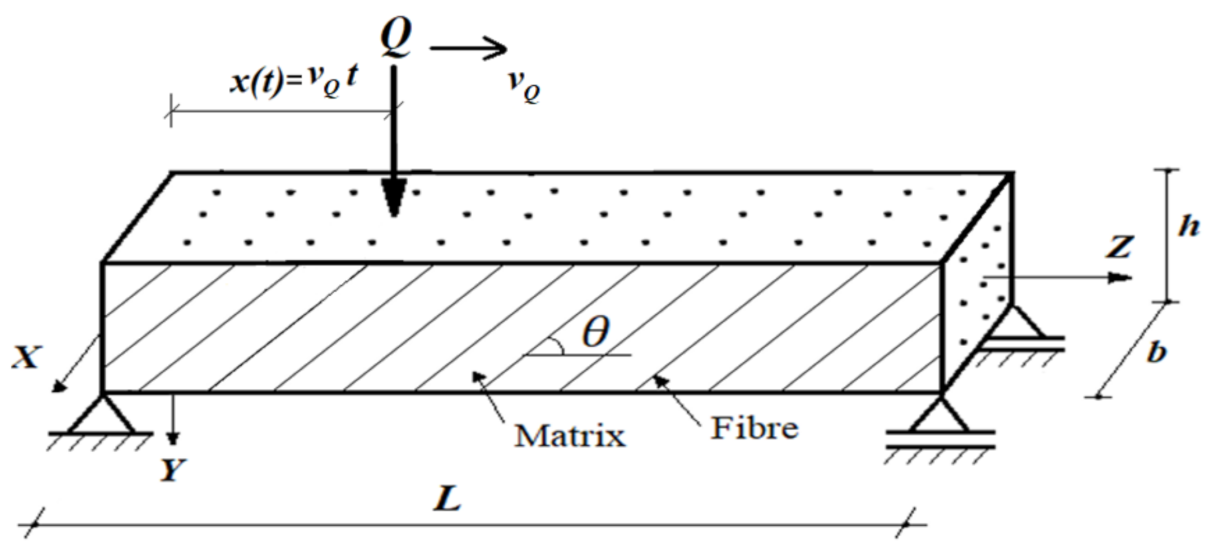
2. Materials and Methods
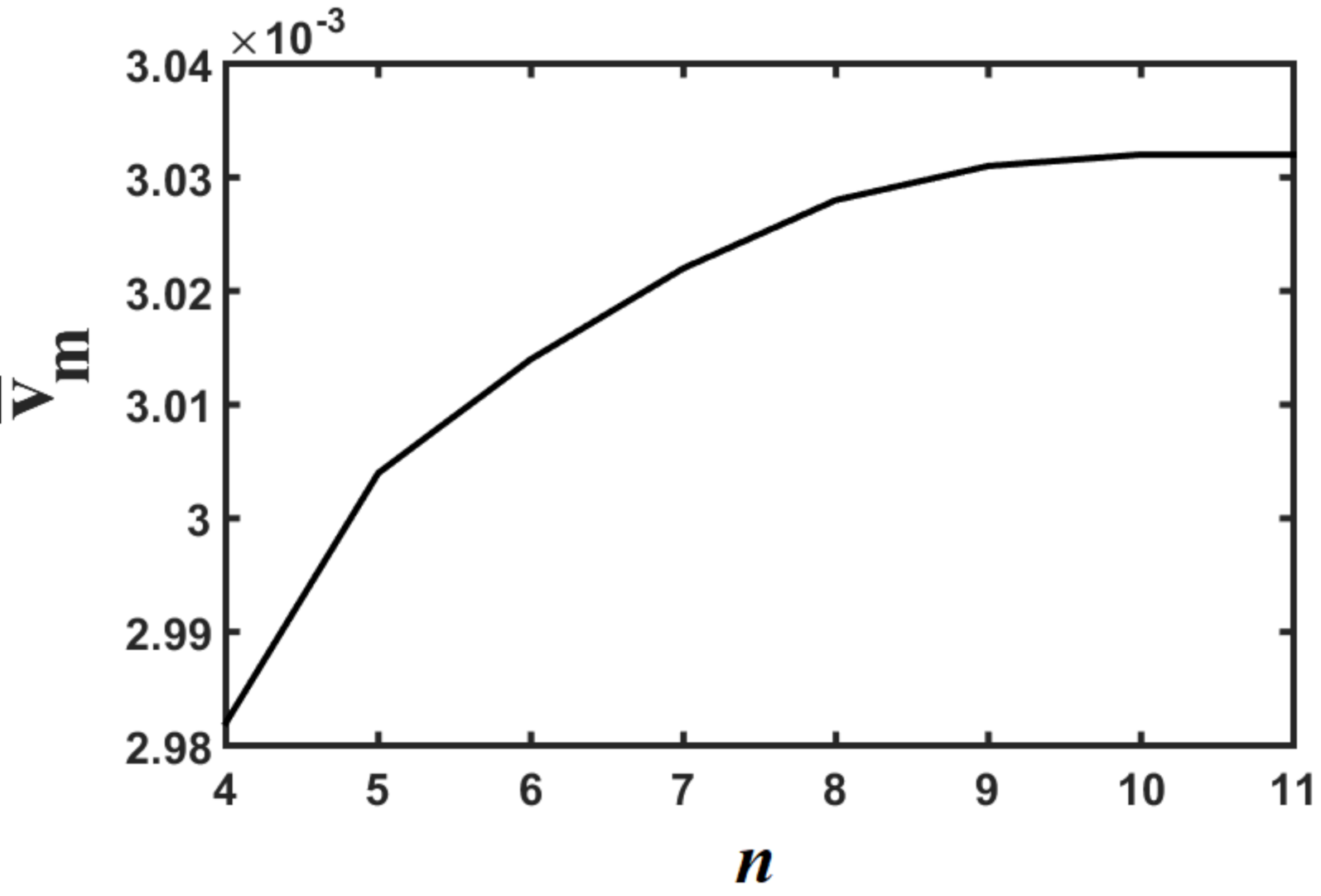
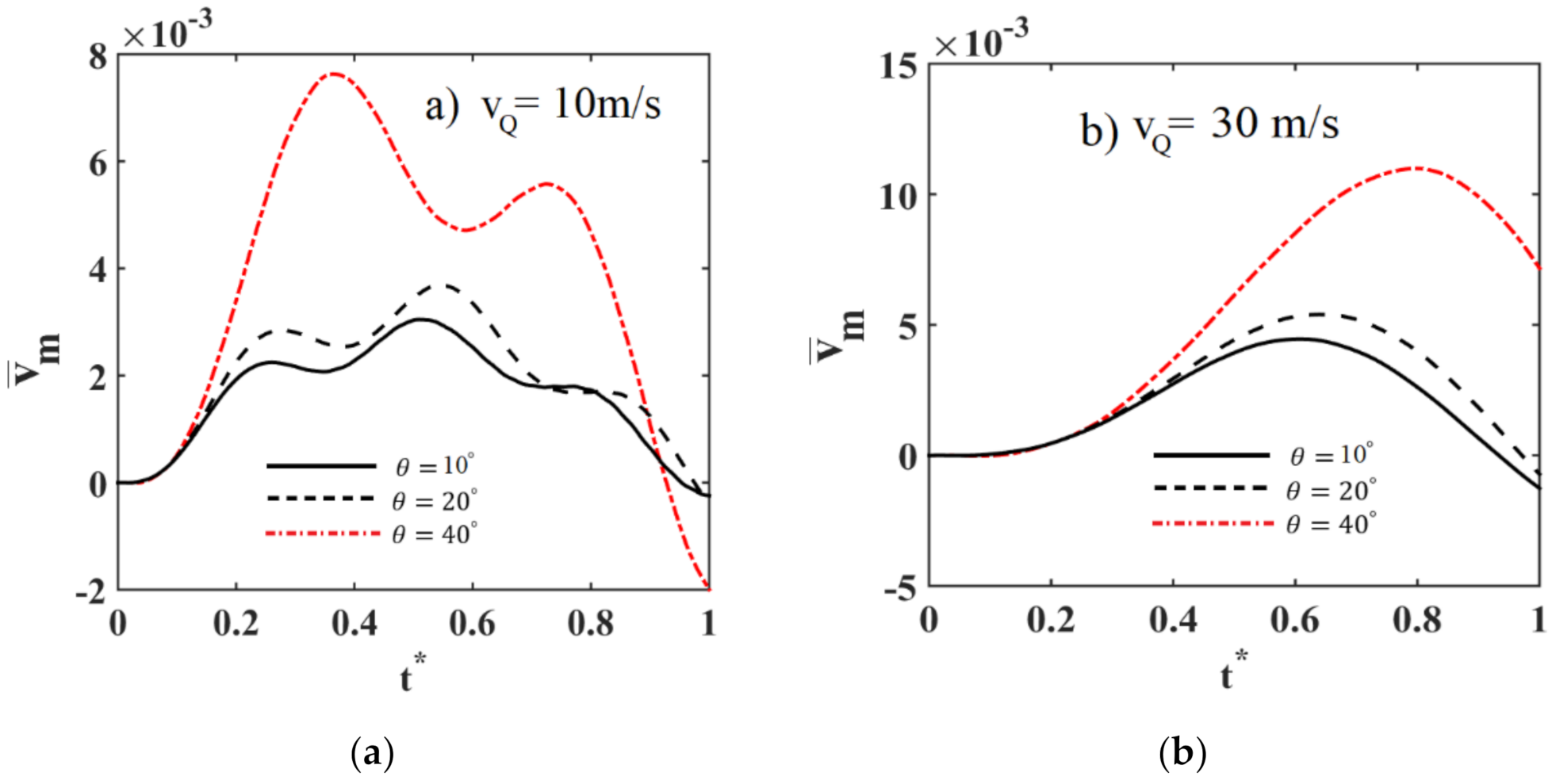
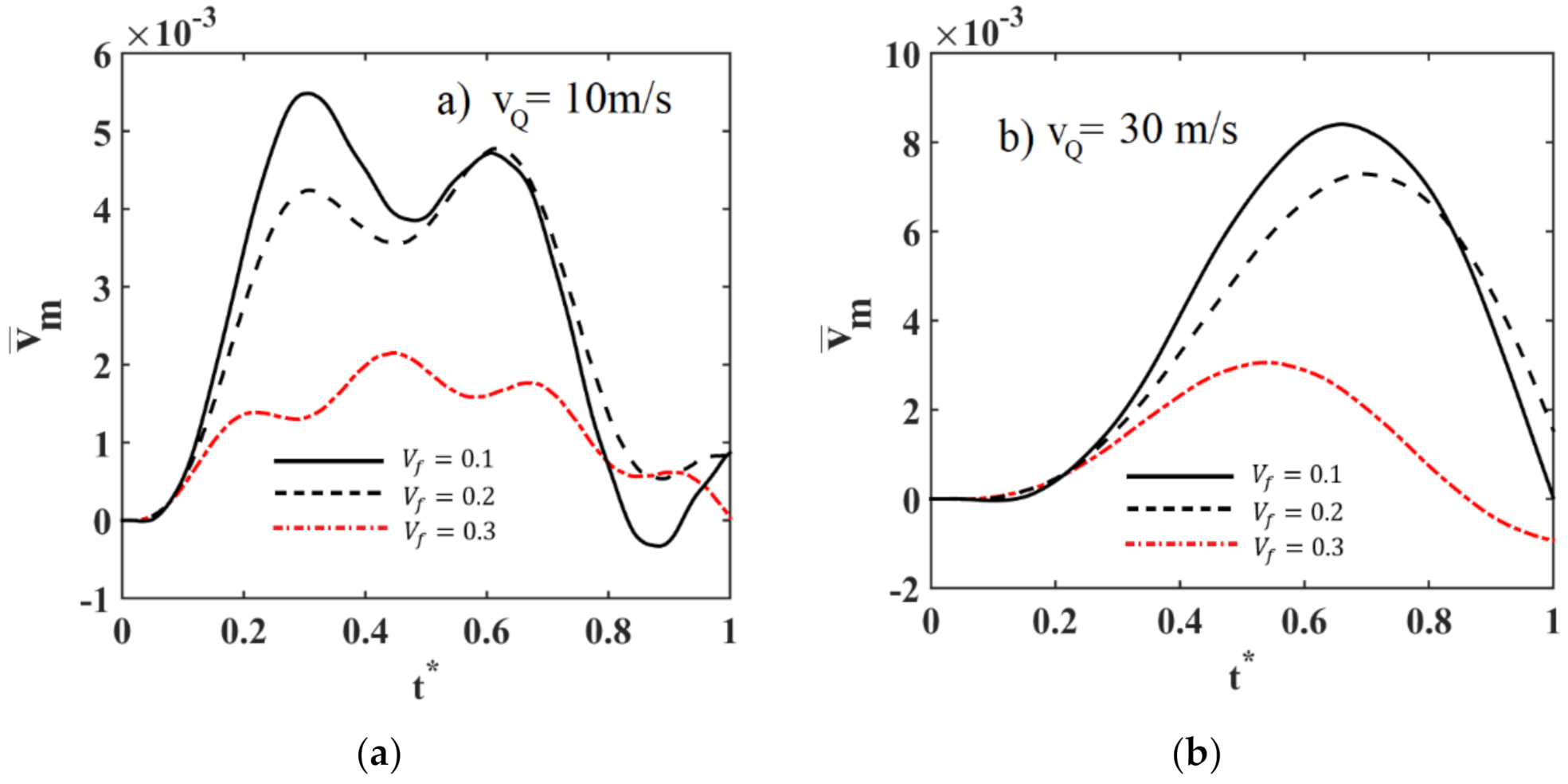
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shariat, M.; Shariati, M.; Madadi, A.; Wakil, K. Computational Lagrangian multiplier method by using for optimization and sensitivity analysis of rectangular reinforced concrete beams. Steel Compos. Struct. 2018, 29, 243–256. [Google Scholar] [CrossRef]
- Luo, Z.Y.; Sinaei, H.; Ibrahim, Z.; Shariati, M.; Jumaat, Z.; Wakil, K.; Pham, B.T.; Mohamad, E.T.; Khorami, M. Computational and experimental analysis of beam to column joints reinforced with CFRP plates. Steel Compos. Struct. 2019, 30, 271–280. [Google Scholar] [CrossRef]
- Huang, W.; Yan, W.; He, W.; Wang, K.; Long, L.; He, M.; Qin, S.; Yu, J. Synergistic flame-retardant effect of DOPO-based derivative and organo-montmorillonite on glass-fiber-reinforced polyamide 6 T. Polym. Adv. Technol. 2020, 31, 2083–2093. [Google Scholar] [CrossRef]
- Souza, P.R.; Nunes, C.S.; Freitas, A.R.; Belinato, J.R.; Pilau, E.J.; Fajardo, A.R.; Da Silva Filho, E.A.; Schreiner, W.H.; Muniz, E.C. Sub- and supercritical D-limonene technology as a green process to recover glass fibres from glass fibre-reinforced polyester composites. J. Clean. Prod. 2020, 254, 119984. [Google Scholar] [CrossRef]
- Amiri, A.; Krosbakken, T.; Schoen, W.; Theisen, D.; A Ulven, C. Design and manufacturing of a hybrid flax/carbon fiber composite bicycle frame. Proc. Inst. Mech. Eng. Part P 2018, 232, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Lawcock, G.; Ye, L.; Mai, Y.W. Novel fiber-reinforced metal laminates for aerospace applications—A review. 1. Background and general mechanical-properties. Sampe J. 1995, 31, 23–31. [Google Scholar]
- Lawcock, G.; Ye, L.; Mai, C.Y. Novel fiber-reinforced metal laminates for aerospace applications. 2. Notched strength and fatigue behavior. Sampe J. 1995, 31, 67–75. [Google Scholar]
- Henderson, J. Fibre-reinforced-polymer composites make the leap from aerospace to infrastructure. Proc. Inst. Civ. Eng. Civ. Eng. 2014, 167, 148. [Google Scholar] [CrossRef]
- Aamir, M.; Tolouei-Rad, M.; Giasin, K.; Nosrati, A. Recent advances in drilling of carbon fiber–reinforced polymers for aerospace applications: A review. Int. J. Adv. Manuf. Technol. 2019, 105, 2289–2308. [Google Scholar] [CrossRef]
- Samanta, A.K. Fibre reinforced composites: Multiplicity of application. Latest Trends Text. Fash. Des. 2018, 1, 1–3. [Google Scholar] [CrossRef]
- Prashanth, S.; Subbaya, K.M.; Nithin, K.; Sachhidananda, S. Fiber reinforced composites—A review. J. Mater. Sci. Eng. 2017, 6, 341. [Google Scholar] [CrossRef] [Green Version]
- Kiani, K.; Nikkhoo, A.; Mehri, B. Prediction capabilities of classical and shear deformable beam models excited by a moving mass. J. Sound Vib. 2009, 320, 632–648. [Google Scholar] [CrossRef]
- Kiani, K.; Mehri, B. Assessment of nanotube structures under a moving nanoparticle using nonlocal beam theories. J. Sound Vib. 2010, 329, 2241–2264. [Google Scholar] [CrossRef]
- Kiani, K. Application of nonlocal beam models to double-walled carbon nanotubes under a moving nanoparticle. Part I: Theoretical formulations. Acta Mech. 2010, 216, 165–195. [Google Scholar] [CrossRef]
- Kiani, K. Application of nonlocal beam models to double-walled carbon nanotubes under a moving nanoparticle. Part II: Parametric study. Acta Mech. 2011, 216, 197–206. [Google Scholar] [CrossRef]
- Yas, H.M.; Heshmati, M. Dynamic analysis of functionally graded nanocomposite beams reinforced by randomly oriented carbon nanotube under the action of moving load. Appl. Math. Model. 2012, 36, 1371–1394. [Google Scholar] [CrossRef] [Green Version]
- Khalili, S.; Jafari, A.; Eftekhari, S. A mixed Ritz-DQ method for forced vibration of functionally graded beams carrying moving loads. Compos. Struct. 2010, 92, 2497–2511. [Google Scholar] [CrossRef]
- Yan, T.; Kitipornchai, S.; Yang, J.; He, X.Q. Dynamic behaviour of edge-cracked shear deformable functionally graded beams on an elastic foundation under a moving load. Compos. Struct. 2011, 93, 2992–3001. [Google Scholar] [CrossRef]
- Teoh, L.; Huang, C.-C. The vibration of beams of fibre reinforced material. J. Sound Vib. 1977, 51, 467–473. [Google Scholar] [CrossRef]
- Eksi, S.; Kapti, A.O.; Genel, K. Buckling behavior of fiber reinforced plastic-metal hybrid-composite beam. Mater. Des. 2013, 49, 130–138. [Google Scholar] [CrossRef]
- Allien, J.V.; Kumar, H.; Desai, V. Semi-active vibration control of SiC-reinforced Al6082 metal matrix composite sandwich beam with magnetorheological fluid core. Proc. Inst. Mech. Eng. Part L 2019, 234, 408–424. [Google Scholar] [CrossRef]
- Jin, Q.; Ren, Y.; Peng, F.; Jiang, H. Imperfection sensitivity of free vibration of symmetrically/anti-symmetrically laminated FRC beams in thermally pre-and post-buckling equilibrium states. Acta Astronaut. 2020, 173, 240–251. [Google Scholar] [CrossRef]
- Akbaş, Ş.D. Post-buckling analysis of a fiber reinforced composite beam with crack. Eng. Fract. Mech. 2019, 212, 70–80. [Google Scholar] [CrossRef]
- Akbas, S.D. Large deflection analysis of a fiber reinforced composite beam. Steel Compos. Struct. 2018, 27, 567–576. [Google Scholar] [CrossRef]
- Akbas, S.D. Nonlinear behavior of fiber reinforced cracked composite beams. Steel Compos. Struct. 2019, 30, 327–336. [Google Scholar] [CrossRef]
- Nayak, S.; Pattnaik, S.; Panigrahi, I.; Nayak, R.; Panda, S. Small delamination detection in carbon fibre reinforced polymer composite beam by NDT and vibration analysis. Indian J. Eng. Mater. Sci. 2020, 27, 789–794. [Google Scholar]
- Liu, B.; Sun, Y. Free vibration analysis of carbon-fiber-reinforced Miuraori core sandwich beam: Theoretical prediction and numerical simulation. Mech. Adv. Mater. Struct. 2020, 1–10. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Dabbagh, A. Vibration analysis of graphene oxide powder-/carbon fiber-reinforced multi-scale porous nanocomposite beams: A finite-element study. Eur. Phys. J. Plus 2019, 134, 225. [Google Scholar] [CrossRef]
- Barretta, R.; Luciano, R.; Willis, J.R. On torsion of random composite beams. Compos. Struct. 2015, 132, 915–922. [Google Scholar] [CrossRef]
- Reddy, J.N.; Pang, S.D. Nonlocal continuum theories of beams for the analysis of carbon nanotubes. J. Appl. Phys. 2008, 103, 023511. [Google Scholar] [CrossRef]
- Liew, K.; Lei, Z.; Zhang, L. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Bending analysis of embedded carbon nanotubes resting on an elastic foundation using strain gradient theory. Acta Astronaut. 2016, 119, 1–12. [Google Scholar] [CrossRef]
- Civalek, Ö.; Uzun, B.; Yayli, M.Ö.; Akgöz, B. Size-dependent transverse and longitudinal vibrations of embedded carbon and silica carbide nanotubes by nonlocal finite element method. Eur. Phys. J. Plus 2020, 135, 1–28. [Google Scholar] [CrossRef]
- Vodenitcharova, T.; Zhang, L. Bending and local buckling of a nanocomposite beam reinforced by a single-walled carbon nanotube. Int. J. Solids Struct. 2006, 43, 3006–3024. [Google Scholar] [CrossRef] [Green Version]
- Ke, L.-L.; Yang, J.; Kitipornchai, S. Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams. Compos. Struct. 2010, 92, 676–683. [Google Scholar] [CrossRef]
- Yas, M.; Samadi, N. Free vibrations and buckling analysis of carbon nanotube-reinforced composite Timoshenko beams on elastic foundation. Int. J. Press. Vessel. Pip. 2012, 98, 119–128. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Ungbhakorn, V. Analytical solutions for bending, buckling and vibration responses of carbon nanotube-reinforced composite beams resting on elastic foundation. Comput. Mater. Sci. 2013, 71, 201–208. [Google Scholar] [CrossRef]
- Vo-Duy, T.; Ho-Huu, V.; Nguyen-Thoi, T. Free vibration analysis of laminated FG-CNT reinforced composite beams using finite element method. Front. Struct. Civ. Eng. 2019, 13, 324–336. [Google Scholar] [CrossRef]
- Shafiei, H.; Setoodeh, A.R. An analytical study on the nonlinear forced vibration of functionally graded carbon nano-tube-reinforced composite beams on nonlinear viscoelastic foundation. Arch. Mech. 2020, 72, 81–107. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Monajemi, A.A.; Afshari, H. Free and forced vibration analysis of viscoelastic damped FG-CNT reinforced micro composite beams. Microsyst. Technol. 2017, 26, 1–15. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y. Vibration of carbon nanotube reinforced composite beams based on the first and third order beam theories. Appl. Math. Model. 2014, 38, 3741–3754. [Google Scholar] [CrossRef]
- Khosravi, S.; Arvin, H.; Kiani, Y. Vibration analysis of rotating composite beams reinforced with carbon nanotubes in thermal environment. Int. J. Mech. Sci. 2019, 164, 105187. [Google Scholar] [CrossRef]
- Civalek, Ö.; Akbaş, Ş.; Akgöz, B.; Dastjerdi, S. Forced vibration analysis of composite beams reinforced by carbon nanotubes. Nanomaterials 2021, 11, 571. [Google Scholar] [CrossRef]
- Ansari, R.; Shojaei, M.F.; Mohammadi, V.; Gholami, R.; Sadeghi, F. Nonlinear forced vibration analysis of functionally graded carbon nanotube-reinforced composite Timoshenko beams. Compos. Struct. 2014, 113, 316–327. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Shahsavari, D.; Dimitri, R.; Tornabene, F. Nonlocal buckling analysis of composite curved beams reinforced with functionally graded carbon nanotubes. Molecules 2019, 24, 2750. [Google Scholar] [CrossRef] [Green Version]
- Fallah, A.; Dehkordi, M.B.; Nourbakhsh, H.; Beni, Y.T. Semi-exact solution for nonlinear dynamic analysis of graded carbon nanotube-reinforced beam with graded shape memory wires. Mech. Adv. Mater. Struct. 2021, 28, 568–582. [Google Scholar] [CrossRef]
- Kiani, Y.; Mirzaei, M. Nonlinear stability of sandwich beams with carbon nanotube reinforced faces on elastic foundation under thermal loading. Proc. Inst. Mech. Eng. Part C 2018, 233, 1701–1712. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Thermomechanical analysis of large deflection in shear deformable FG-CNT reinforced composite beams using perturbation technique. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Civalek, Ö.; Dastjerdi, S.; Akbaş, Ş.D.; Akgöz, B. Vibration analysis of carbon nanotube-reinforced composite microbeams. Math. Methods Appl. Sci. 2021, 11, 571. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, K.; Fu, T. Vibration analysis of functionally graded graphene oxide-reinforced composite beams using a new Ritz-solution shape function. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–14. [Google Scholar] [CrossRef]
- Song, M.; Gong, Y.; Yang, J.; Zhu, W.; Kitipornchai, S. Free vibration and buckling analyses of edge-cracked functionally graded multilayer graphene nanoplatelet-reinforced composite beams resting on an elastic foundation. J. Sound Vib. 2019, 458, 89–108. [Google Scholar] [CrossRef]
- Mojiri, H.R.; Salami, S.J. Free vibration and dynamic transient response of functionally graded composite beams reinforced with graphene nanoplatelets (GPLs) resting on elastic foundation in thermal environment. Mech. Based Des. Struct. Mach. 2020, 1–21. [Google Scholar] [CrossRef]
- Nematollahi, M.S.; Mohammadi, H.; Dimitri, R.; Tornabene, F. Nonlinear vibration of functionally graded graphene nanoplatelets polymer nanocomposite sandwich beams. Appl. Sci. 2020, 10, 5669. [Google Scholar] [CrossRef]
- Vinson, J.R.; Sierakowski, R.L. Behaviour of Structures Composed of Composite Materials, 2nd ed.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2002; ISBN 978-140-2009-04-4. [Google Scholar]
- Krawczuk, M.; Ostachowicz, W.; Żak, A. Modal analysis of cracked, unidirectional composite beam. Compos. Part B Eng. 1997, 28, 641–650. [Google Scholar] [CrossRef]
- Tao, C.; Fu, Y.-M.; Dai, H.-L. Nonlinear dynamic analysis of fiber metal laminated beams subjected to moving loads in thermal environment. Compos. Struct. 2016, 140, 410–416. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbaş, Ş.D.; Ersoy, H.; Akgöz, B.; Civalek, Ö. Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method. Mathematics 2021, 9, 1048. https://doi.org/10.3390/math9091048
Akbaş ŞD, Ersoy H, Akgöz B, Civalek Ö. Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method. Mathematics. 2021; 9(9):1048. https://doi.org/10.3390/math9091048
Chicago/Turabian StyleAkbaş, Şeref D., Hakan Ersoy, Bekir Akgöz, and Ömer Civalek. 2021. "Dynamic Analysis of a Fiber-Reinforced Composite Beam under a Moving Load by the Ritz Method" Mathematics 9, no. 9: 1048. https://doi.org/10.3390/math9091048





