On Extended Adjacency Index with Respect to Acyclic, Unicyclic and Bicyclic Graphs
Abstract
:1. Introduction
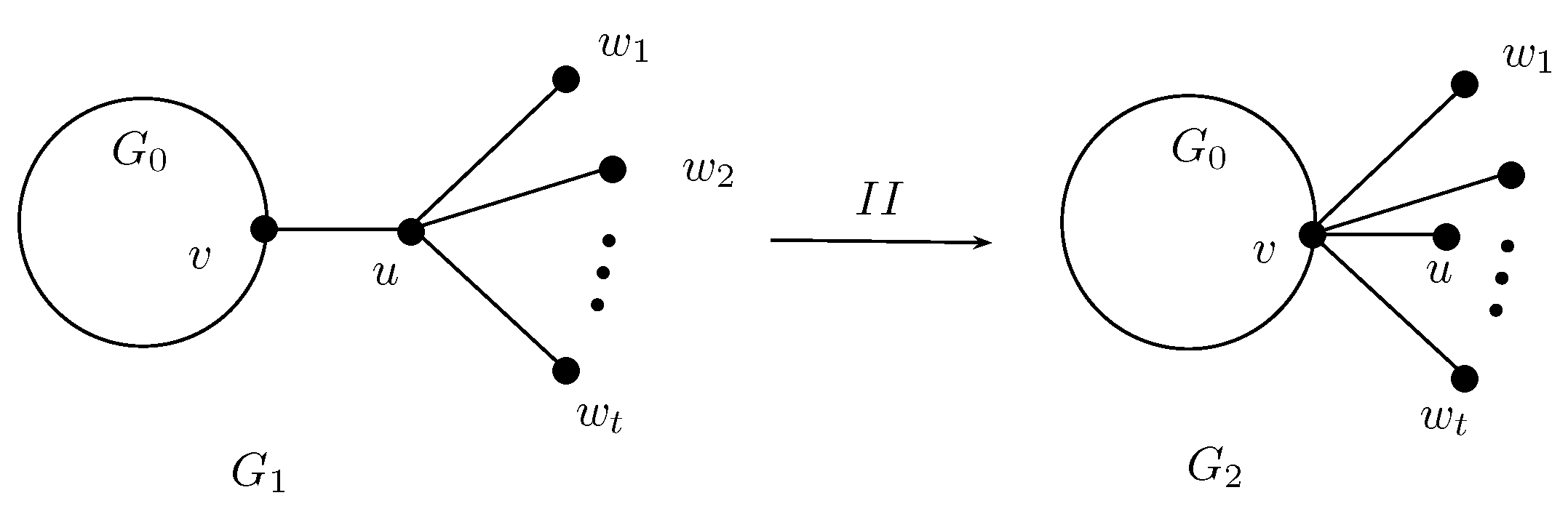
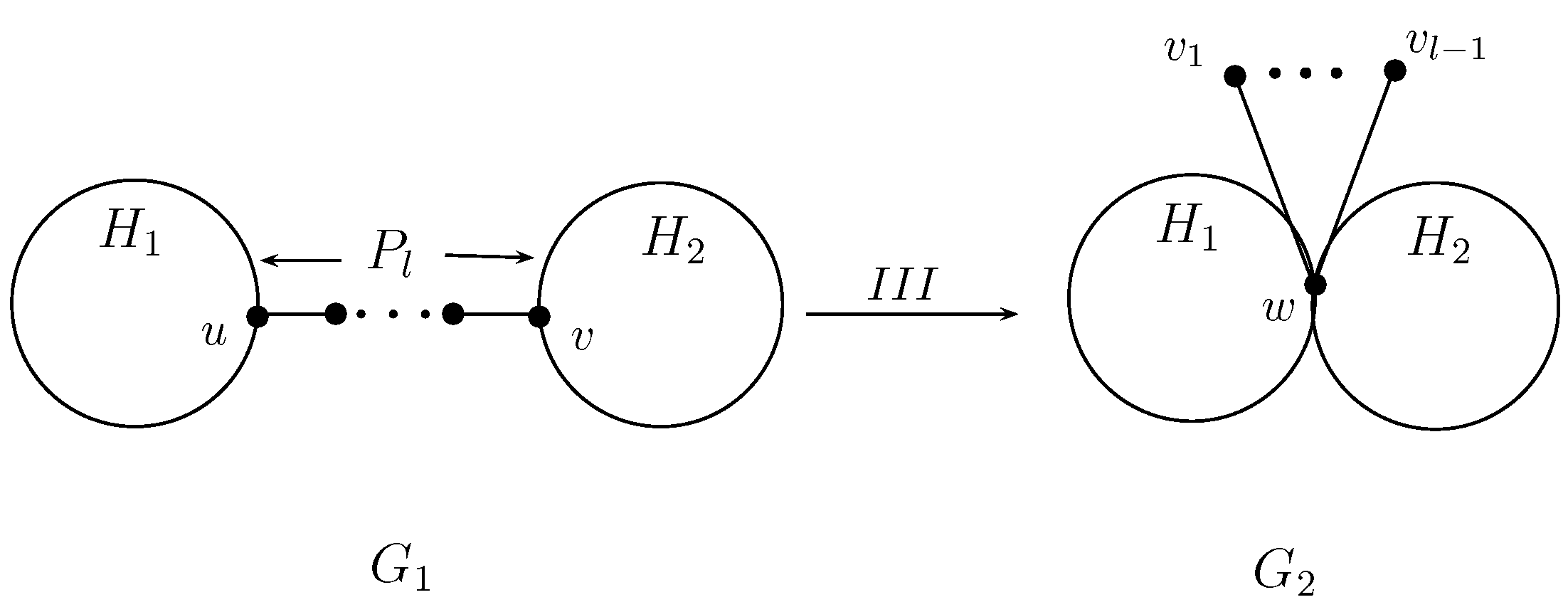
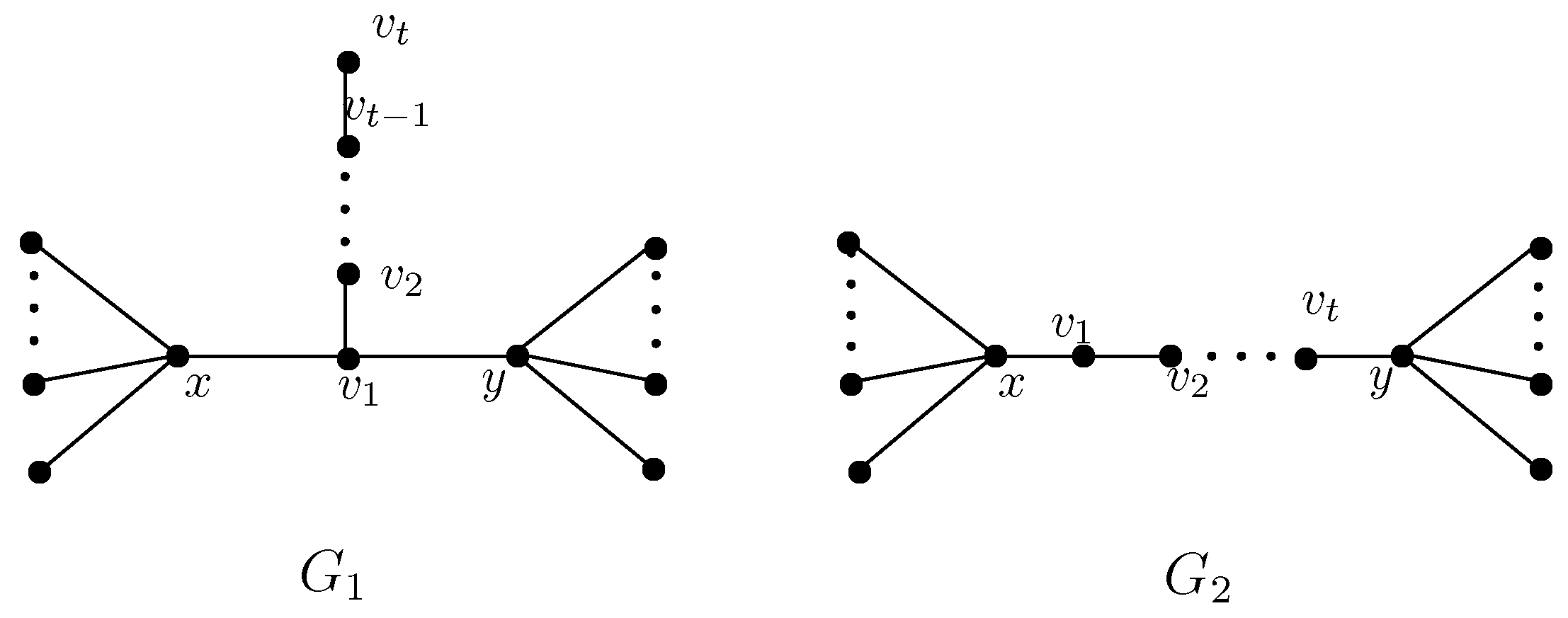
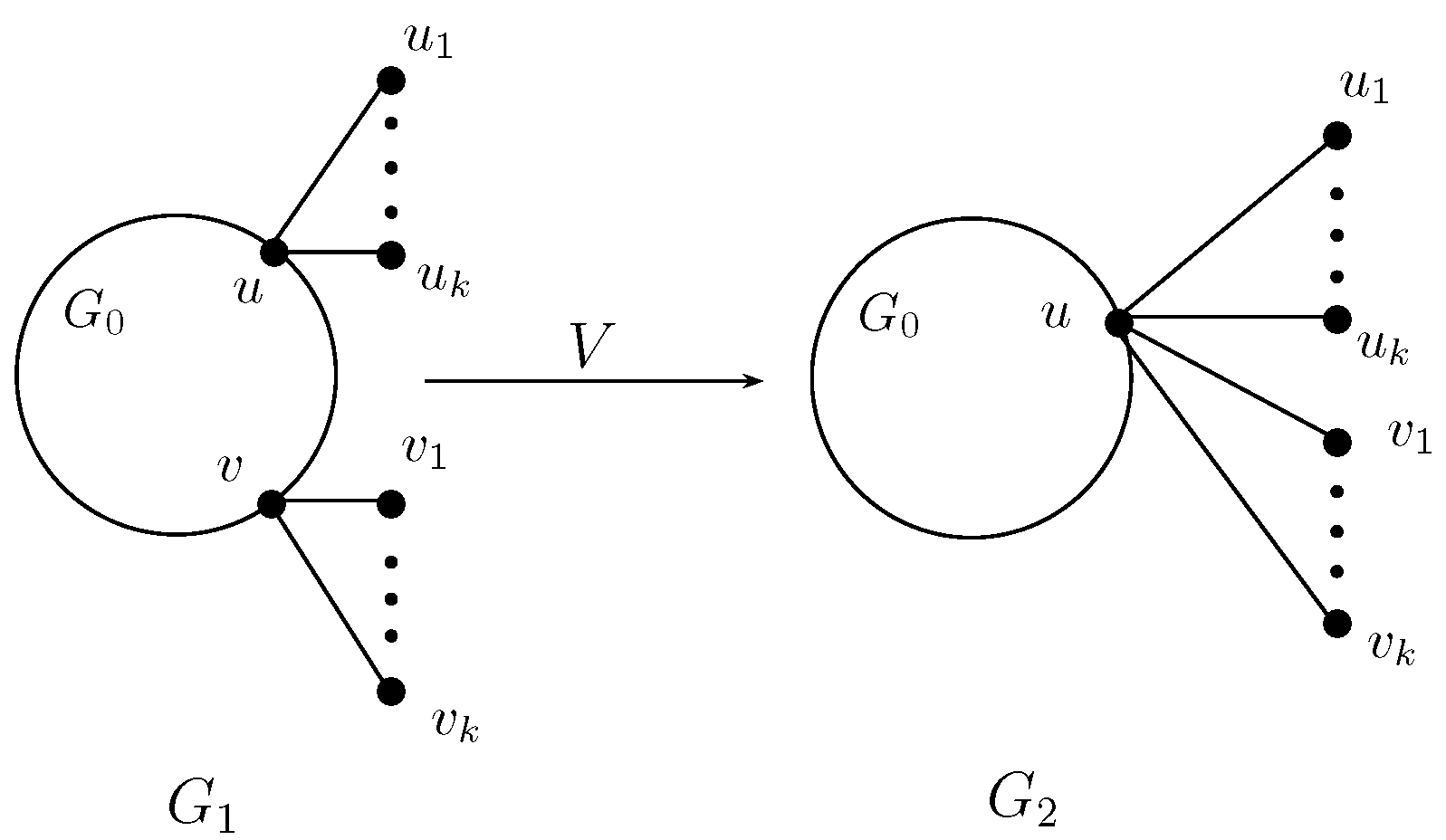
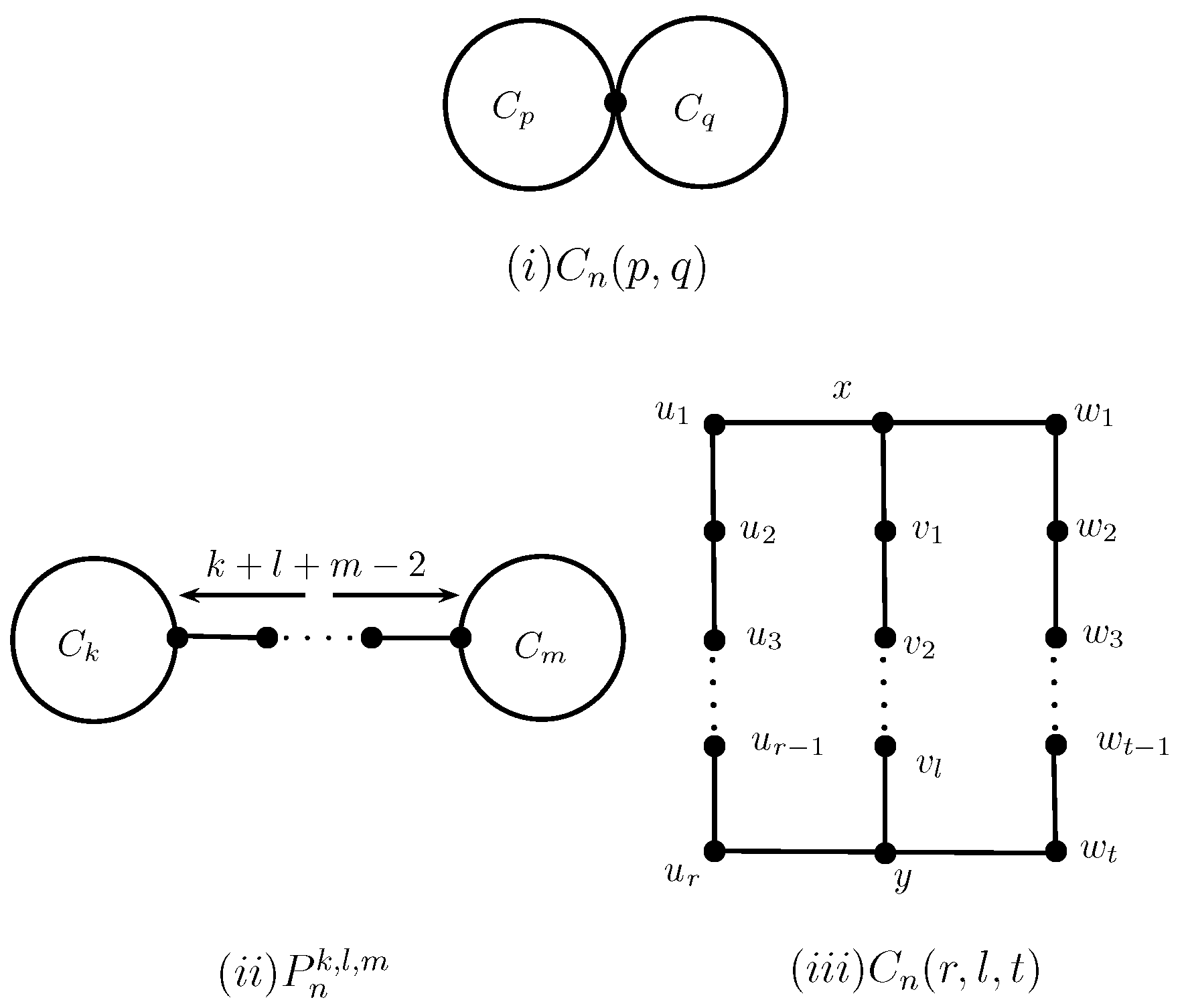
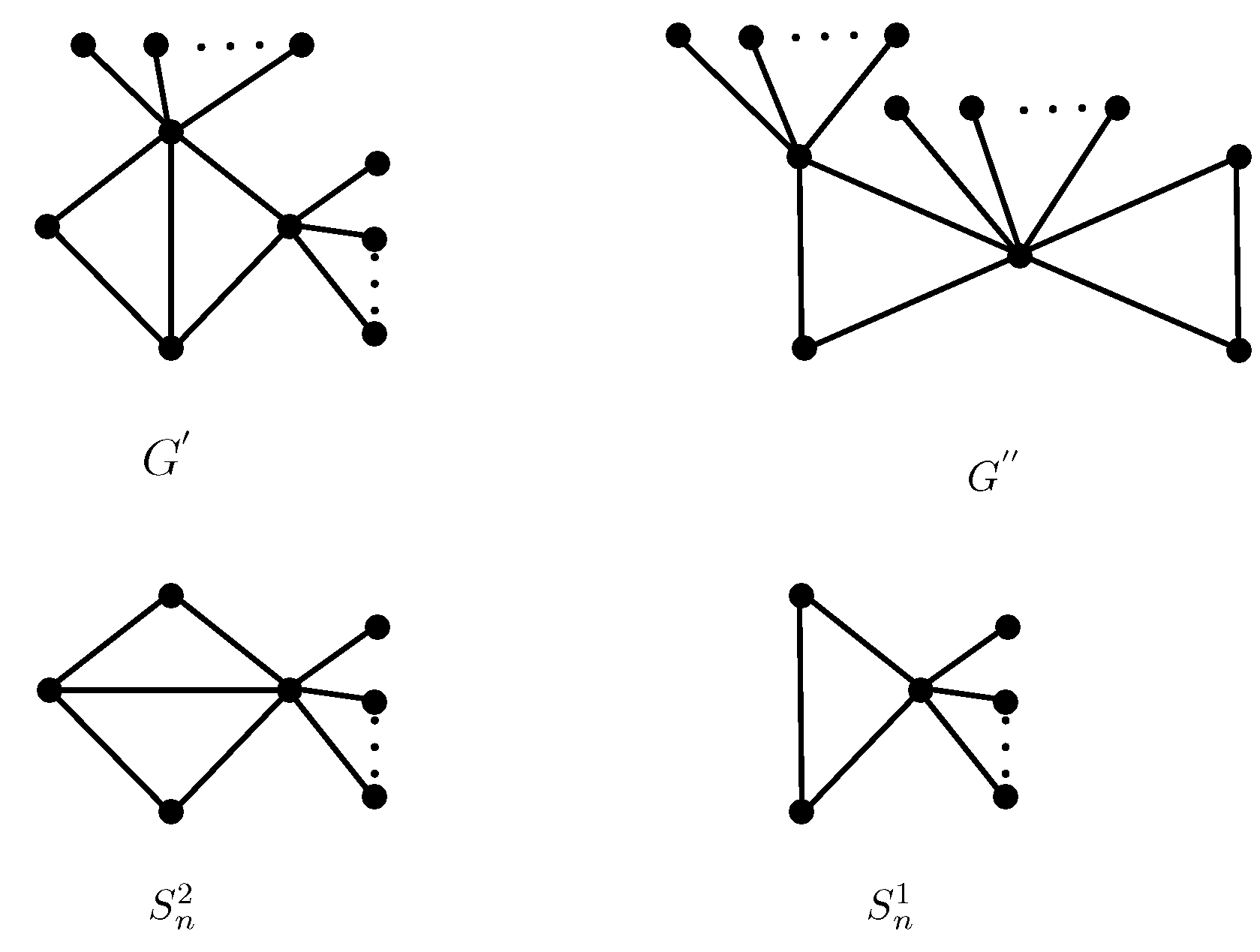
2. Some Graph Transformations
3. Main Results
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Katanić, V. Randic index and information. AKCE Int. J. Graphs Comb. 2018, 15, 307–312. [Google Scholar] [CrossRef]
- Suil, O.; Shi, Y. Sharp bounds for the Randic index of graphs with given minimum and maximum degree. Discrete Appl. Math. 2018, 247, 111–115. [Google Scholar]
- Bedratyuk, L.; Savenko, O. The star sequence and the general first Zagreb index. MATCH Commun. Math. Comput. Chem. 2018, 79, 407–414. [Google Scholar]
- Gutman, I.; Milovanović, E.; Milovanović, I. Beyond the Zagreb indices. AKCE Int. J. Graphs Comb. 2018, in press. [Google Scholar] [CrossRef]
- Liu, J.B.; Javed, S.; Javaid, M.; Shabbir, K. Computing first general Zagreb index of operations on graphs. IEEE Acess 2019, 7, 47494–47502. [Google Scholar] [CrossRef]
- Liu, J.B.; QAli, B.; Malik, A.M.; Hafiz, S.A.M.; Imran, M. Reformulated Zagreb indices of some derived graphs. Mathematics 2019, 7, 366. [Google Scholar] [CrossRef]
- Liu, J.B.; Wang, C.; Wang, S. Zagreb indices and multiplicative Zagreb indices of Eulerian graphs. Bull. Malays. Math. Sci. Soc. 2019, 42, 67–78. [Google Scholar] [CrossRef]
- Ramane, H.S.; Manjalapur, V.V.; Gutman, I. General sum-connectivity index, general product-connectivity index, general Zagreb index and coindices of line graph of subdivision graphs. AKCE Int. J. Graphs Comb. 2017, 14, 92–100. [Google Scholar] [CrossRef]
- Akhter, S.; Imran, M. Computing the forgotten topological index of four operations on graphs. AKCE Int. J. Graphs Comb. 2017, 14, 70–79. [Google Scholar] [CrossRef]
- Che, Z.; Chen, Z. Lower and upper bounds of the forgotten topological index. MATCH Commun. Math. Comput. Chem. 2017, 76, 635–648. [Google Scholar]
- Elumalai, S.; Mansour, T. A short note on tetracyclic graphs with extremal values of Randić index. Asian-Eur. J. Math. 2019, in press. [Google Scholar] [CrossRef]
- Elumalai, S.; Mansour, T.; Rostami, A.M. On the bounds of the forgotten topological index. Turk. J. Math. 2017, 41, 1687–1702. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Xu, L.; Hu, C.Y. Extended adjacency matrix indices and their applications. J. Chem. Inf. Comput. Sci. 1994, 34, 1140–1145. [Google Scholar] [CrossRef]
- Bianchi, M.; Cornaro, A.; Palacios, J.L.; Torriero, A. Upper and lower bounds for the mixed degree-Kirchhoff index. Filomat 2016, 30, 2351–2358. [Google Scholar] [CrossRef]
- Adiga, C.; Rakshit, B.R. Upper bounds for extended energy of graphs and some extended equienergetic graphs. Opusc. Math. 2018, 38, 5–13. [Google Scholar] [CrossRef]
- Gutman, I. Relation between energy and extended energy of a graph. Int. J. Appl. Graph Theory 2017, 1, 42–48. [Google Scholar]
- Gutman, I.; Furtula, B.; Das, K.C. Extended energy and its dependence on molecular structure. Can. J. Chem. 2017, 95, 526–529. [Google Scholar] [CrossRef]
- Ramane, H.S.; Manjalapur, V.V.; Gudodagi, G.A. On extended adjacency index and its spectral properties. 2019; Communicated. [Google Scholar]
- Ali, A.; Dimitrov, D. On the extremal graphs with respect to bond incident degree indices. Discrete Appl. Math. 2018, 238, 32–40. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.Y. A unified approach to the extremal Zagreb indices for trees, unicyclic graphs and bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2007, 57, 597–616. [Google Scholar]
- Ji, S.; Li, X.; Huo, B. On reformulated Zagreb indices with respect to acyclic, unicyclic and bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2014, 72, 723–732. [Google Scholar]
- Liu, J.B.; Pan, X.F. A unified approach to the asymptotic topological indices of various lattices. Appl. Math. Comput. 2015, 270, 62–73. [Google Scholar] [CrossRef]
- Pei, L.; Pan, X. Extremal values on Zagreb indices of trees with given distance k-domination number. J. Inequal. Appl. 2018, 2018, 16. [Google Scholar] [CrossRef] [PubMed]
- Xu, K.; Hua, H. A unified approach to extremal multiplicative Zagreb indices for trees, unicyclic and bicyclic graphs. MATCH Commun. Math. Comput. Chem. 2012, 68, 241–256. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory and Its Applications; MacMillan: London, UK, 1976. [Google Scholar]
- Harary, F. Graph Theory; Addison Wesley Reading: Reading, MA, USA, 1969. [Google Scholar]
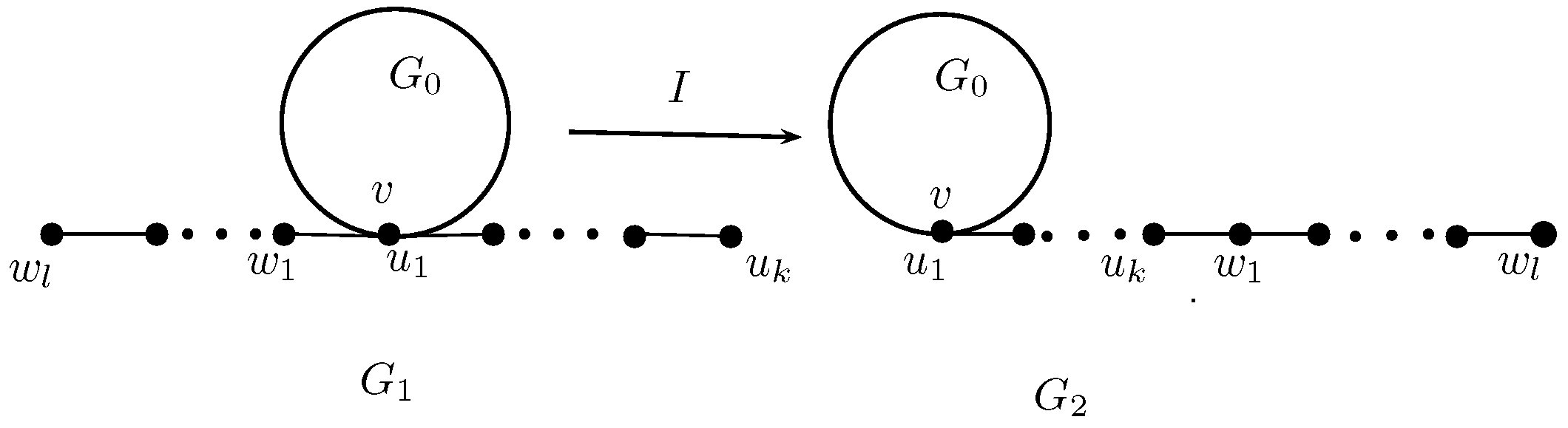
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Manjalapur, V.V.; Sajjan, S.P.; Mathai, M.M.; Liu, J.-B. On Extended Adjacency Index with Respect to Acyclic, Unicyclic and Bicyclic Graphs. Mathematics 2019, 7, 652. https://doi.org/10.3390/math7070652
Yang B, Manjalapur VV, Sajjan SP, Mathai MM, Liu J-B. On Extended Adjacency Index with Respect to Acyclic, Unicyclic and Bicyclic Graphs. Mathematics. 2019; 7(7):652. https://doi.org/10.3390/math7070652
Chicago/Turabian StyleYang, Bin, Vinayak V. Manjalapur, Sharanu P. Sajjan, Madhura M. Mathai, and Jia-Bao Liu. 2019. "On Extended Adjacency Index with Respect to Acyclic, Unicyclic and Bicyclic Graphs" Mathematics 7, no. 7: 652. https://doi.org/10.3390/math7070652




