Pricing Decision within an Inventory Model for Complementary and Substitutable Products

Abstract

A combination of substitutable and complementary products is very important for any business industry to make all-round profit from different aspects. How deterioration affects complementary products or substitutable products is discussed in this study. This study investigates the pricing and inventory decisions for complementary and substitutable items which are deteriorating in nature. Four models are analyzed where the demand of one product is dependent upon the selling price and the price of another product. This paper tries to compute the optimum prices and order quantities to optimize the total profit, which is the main aim. Theoretically, this model is solved by a classical optimization method. Numerical examples demonstrate the applicability of this model. Results conclude that the total profit is dependent on the degree of substitutability and complementarity. A sensitivity analysis of optimal solutions is given to test the stability of the proposed model.

1. Introduction

Everyday life starts with the use of a toothbrush and toothpaste, which are complementary products. Then, the energy for the whole day is derived from the breakfast where at least one seasonal fruit is mandatory for good health. The seasonal fruit can be replaced by another fruit based on the availability and price and is substitutable product. Whenever the increasing price of one product indicates the increasing sales rate of another product, then those products substitute each other [1]. Increasing the price of one item can help to increase the sale of another substitutable item. For example, Coca-Cola and Pepsi are two substitutable products as both can satisfy the purpose. One customer can buy Pepsi instead of Coca-Cola in any circumstances. Complementary products are used in combination with another product [2]. Single use of any part of complementary products has limited usage. The overall utility is increased whenever both products are used together. The market demand of complementary products depends upon both products [3]. Car and fuel, camera and memory card, toothpaste and brush—these are a few examples of complementary products. A car cannot move without proper fuel, which implies that the car is useless without fuel, and fuel is no longer important if the car is not there. To earn in all aspects, the manufacturer introduces substitutable as well as complementary products in the business. From the perspective of the inventory, complementary products need more storage and inventory, as both products are important. In reality, substitutable products give the manufacturer tough competition, as it is important to choose alternative products very wisely such that it can satisfy the demand as well as the quality of the original product. The pricing factor is the next important thing for substitutable products. The price of the alternative should be less than or equal to the original product. The situation may differ in case of the reverse situation when the alternative’s price is greater than the original price. The situation gets more complicated when the product deteriorates in nature.

There are several researches who focus on substitutable and complementary products, while none of them have investigated both inventory and pricing decisions of the products simultaneously. Moreover, this investigation is done for deteriorating products. In this paper, four models are discussed for pricing and inventory decisions of two types of items, which may be complementary or substitutable, and deteriorating or non-deteriorating. The rest of the present paper is organized as follows: Section 2 presents a literature review, whereas problem definition, notation, and assumptions are defined in Section 3, and the mathematical modeling is presented in Section 4. Numerical examples, a sensitivity analysis, and managerial insights are provided in Section 5. Section 6 concludes the achievements of this proposed model. The last section provides the References of the study.

2. Literature Review

Pricing policy is an important part in the field of supply chain management [4,5,6,7]. Several research articles have been studied on inventory and pricing decisions for single or multi-products inventory models [8,9,10]. However, few of them studied pricing decisions for complementary or substitutable products. In such cases, the price, quality, and durability of the products play a crucial role to attract customers [5,9]. On the other hand, retailers face the cross-selling phenomenon for complementary products. McGillivray and Silver [11] investigated the full substitutability and its effect on total cost within an inventory model. Zhang et al. [12] illustrated an inventory system when the demand of a minor and a major item is correlated with cross-selling. Zhang [13] discussed an inventory problem for multiple products with the inventory replenishment. They proposed a search method which gives a global optimum solution. Yue et al. [14] investigated a duopoly market dealing with complementary products.

An inventory model was discussed by Liu and Yuan [15] for two types of products where the consumption rates of those products are correlated, and the replenishment rates are coordinated. Wei et al. [9] analyzed a non-coordination supply chain management consisting of two manufactures with one retailer for two complementary type products with the help of five different game theories: manufacturer-leader Bertrand, manufacturer-leader Stackelberg, retailer-leader Bertrand, retailer-leader Stackelberg, and Nash game (NG) models. Guchhait et al. [16] studied an advertisement-dependent demand scenario within supply chain management. They used a Stackelberg game policy to solve the model. Shavandi et al. [17] extended the pricing and lot sizing model of Abad [18] for multiple products. They proposed several pricing strategies of multi-products for deteriorating items which may be complementary, substitutable, or independent. The aim of the research was to maximize the profit optimization, along with optimum prices and production quantities.

An inventory model was studied by Balkhi and Benkherouf [19] for deteriorating products. The market demand was stock dependent and time dependent. A procedure was proposed by them to achieve the optimum replenishment schedule. Anjos et al. [20] considered perishable products and presented a continuous pricing strategy where the optimal pricing strategy can be explicitly characterized and easily implemented. Dye [21] extended an inventory model for perishable items with a time-dependent backlog by assuming a price-sensitive demand and variable deterioration with time. In that article, an improved algorithm was proposed by them to find out the optimal selling price of a product and replenishment schedule. Panda et al. [22] considered a single-item economic order quantity (EOQ) model with discounted sale as products were perishable in nature, and the demand was stock dependent. Pang [23] studied optimal dynamic pricing policies and inventory control policies for deteriorating products within a periodic type inventory model. Sarkar and Saren [24] investigated the effect of the trade-credit policy for exponentially deteriorating products. Sarkar et al. [25] developed a two-echelon supply chain model for deteriorating items, where single-setup-multi-delivery (SSMD) transportation policy was adopted.

Sett et al. [26] and Sarkar et al. [27] studied fixed lifetime products and their replenishment policy. The deterioration rate was variable, and the backlog was time dependent. Sarkar et al. [28] applied preservation technology for seasonal deteriorating products while Ullah et al. [29] used the preservation for waste generation. Recycling of the deteriorated products was investigated by Iqbal and Sarkar [30]. The market demand can be affected by the deterioration and a backlog scenario may appear in that case. The service level can help to get rid of this situation [31]. Gürler and Yilmaz [32] studied a supply chain management with two substitutable products in a newsboy problem. Demands for both products were independent, and the aim of the research was to maximize the retailer’s and manufacturer’s profits jointly. Kim and Bell [33] proposed that the production system of a firm sold their products to multiple market segments for a specific period. A price-driven scenario was examined by them, and the effect on the pricing strategy and production capacity of the firm were discussed.

Stavrulaki [34] investigated an inventory model for substitutable products. They explained the combined effect of the demand stimulation for stochastic demand. Karakul and Chan [35] studied the analytical implications of product substitutability and procurement decisions in a newsboy problem with two products. Thereafter, they established the unimodality of the expected profit of their previous work [36] with respect to the procurement and price of quantities. Birge et al. [37] developed an inventory model for substitutable products where market demand follows a uniform distribution. Netessine et al. [38] determined the optimum procurement for multi-substitutable items under exogenous prices of an integrated inventory-pricing problem. Parlar and Goyal [39] developed two integrated production–inventory models of two substitutable products under different prices and assumptions [40]. Tang and Yin [41] discussed an improved procedure to find the optimum selling price within an inventory framework where demand is price sensitive for substitutable products. Xia [42] suggested a two-echelon supply chain model including competitive multiple suppliers and multiple buyers, where each supplier offers one type of substitutable product to the buyers. Netessine et al. [43] discussed about centralized inventory policy where market demand is substitutable.

Table 1. Author’s contributions table.

Author(s)	Inventory	Pricing	Deterioration	Complementary Products	Substitutable Products
Sarkar and Lee [2]		√		√
Sana [4]	√	√
Smith et al. [7]	√	√
Wei at al. [9]		√		√
Mcgillivray and Silver [11]	√				√
Yue et al. [14]		√		√
Balkhi and Benkherouf [19]	√		√
Dye [21]	√	√	√
Karakul and Chan [35]	√	√			√
Tang and Yin [41]	√	√			√
This study	√	√	√	√	√

gives the contribution from different authors associated with the area of research.

3. Problem Description, Notation, and Assumptions

3.1. Problem Definition

Consider a market where the retailer intends to determine the order quantities of different products. The products may be complementary or substitutable, for which two different scenarios exist.

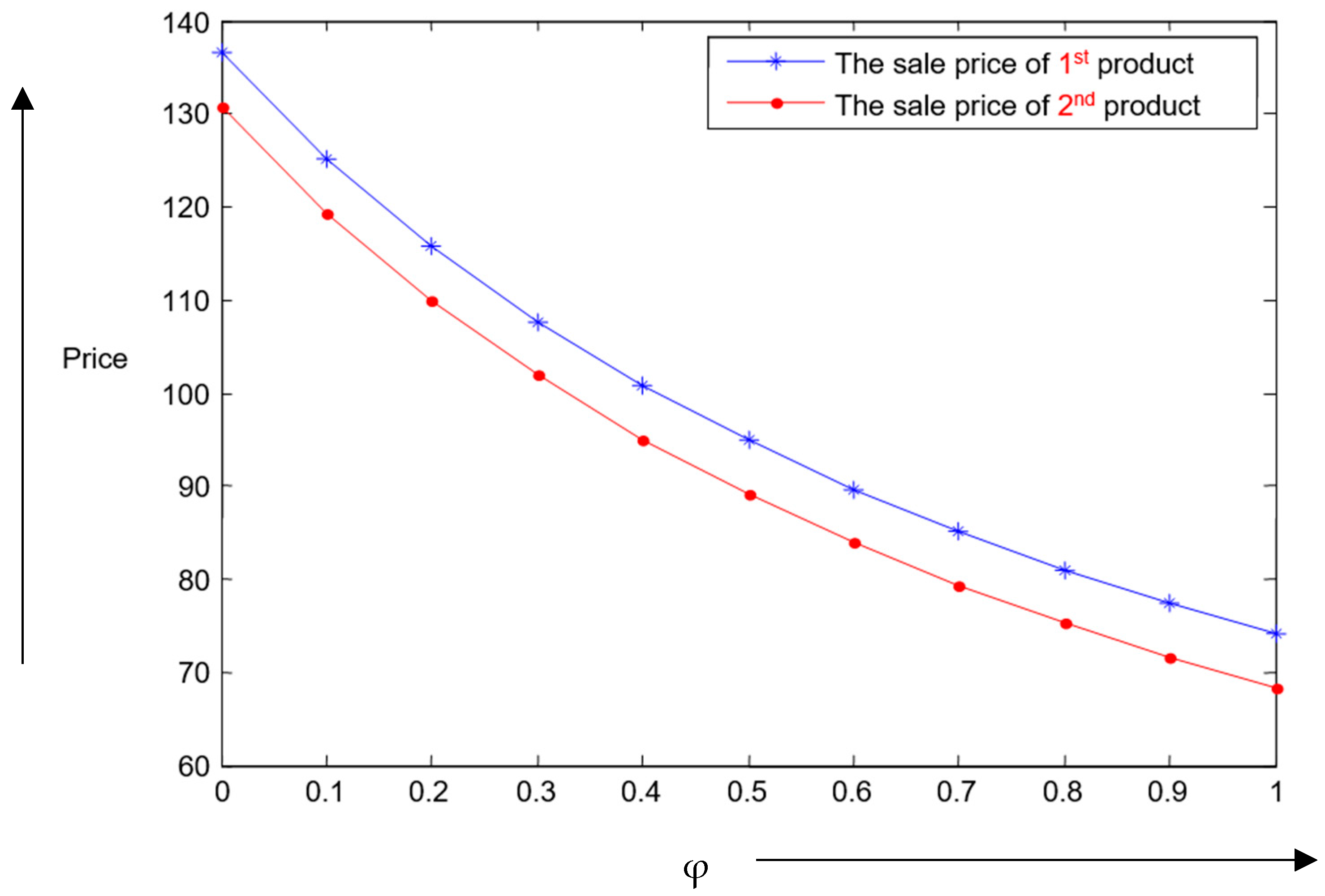
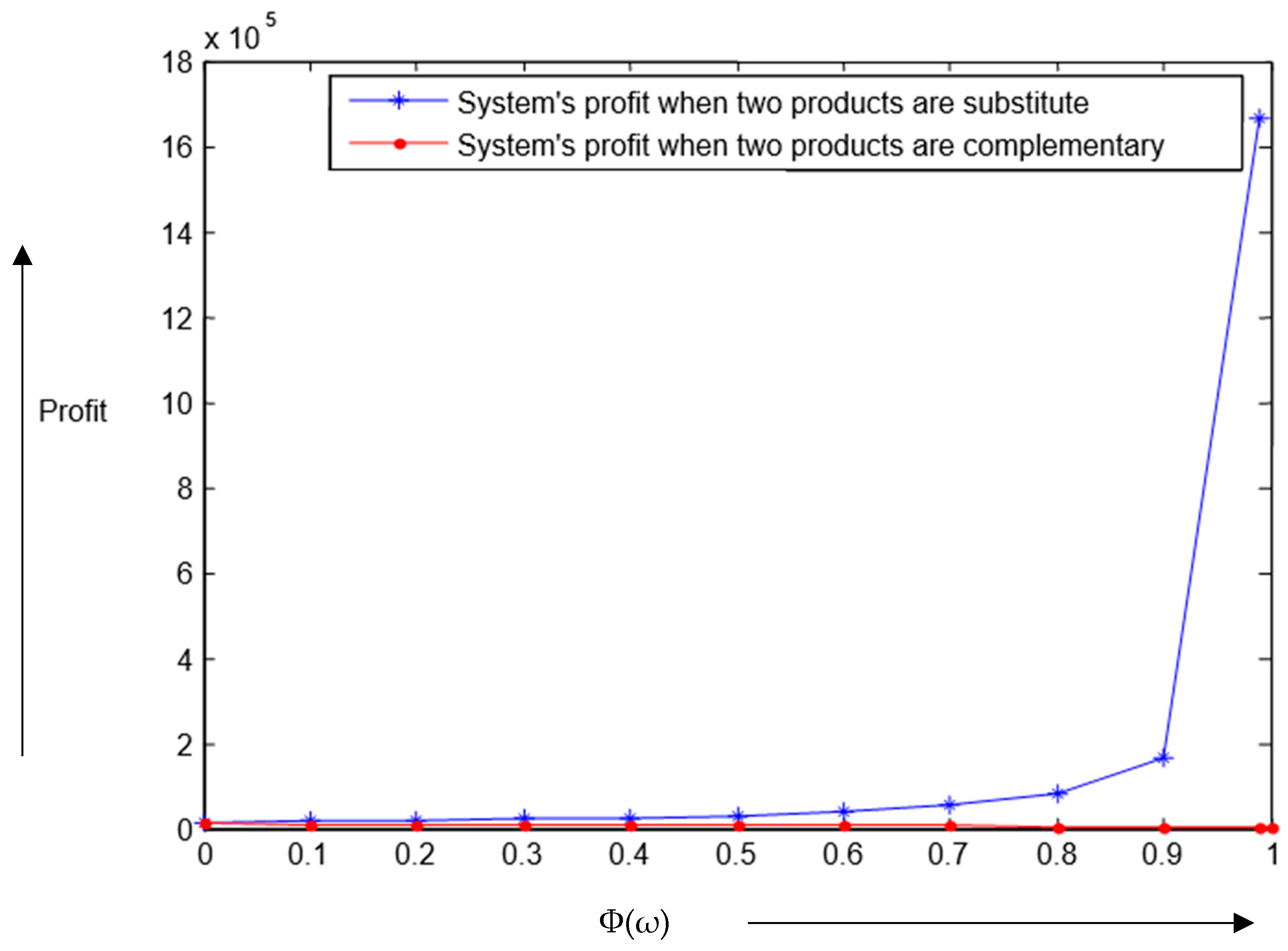
In case of complementary products, the retailer expects a higher consumption rate of a product when the consumption rate of its complementary product increases and vice versa. Moreover, the demand of every complementary product depends upon the price of the other such that the high price of one of them decreases the demand of the complementary product and vice versa. Obviously, the degree of complementarity between two products, which is between 0 and 1, has the main effect on the changes between their respective demands and prices. In this situation, the retailer determines the optimal order quantity and selling price of each product in such a way that the retailer can maximize the total profit.

In the second scenario, each product can be used instead of another one in the case of substitutable products. In this situation, the retailer faces the situation that the decreasing demand of a substitutable product increases the other product’s demand. The demand of each substitutable product depends upon its own price and the price of another one such that the higher price of one of them increases the demand of its substitutable product and vice versa because the customer intends to use the substitutable product, which has a lower price compared to the other. Generally, the degree of substitutability between two products, which is between 0 and 1, has the main effects on the changes between their demands and prices. Therefore, the retailer should determine the optimum order quantity such that the total profit should maximize.

3.2. Notation

The notation related to this study is given in the Nomenclature section at the end of the study.

3.3. Assumptions

Assumptions are used to formulate the model are as follows:

• A retailer maximizes the profit based on an economic order quantity (EOQ) model. The demand is dependent upon selling prices and lot sizes of two types of products. The demand of two complementary products is dependent upon each product’s selling price and the degree of complementarity.
• After a certain time, products start to deteriorate with a constant deterioration rate. As deterioration is considered in this model, deterioration cost per time unit for the product m is ${\eta }_m^{\prime }$ ($ per unit). The deterioration rate of product 1 and product 2 is $D_r$.
• The degree of complementarity between two products is given by $\theta$, where $0\le \phi \le 1,$ and the degree of substitutability between two products is given by d, where $0\le \omega \le 1$.
• The lead time is zero, and there are no shortages for both types of products.
• The time horizon is infinite.

4. Mathematical Model

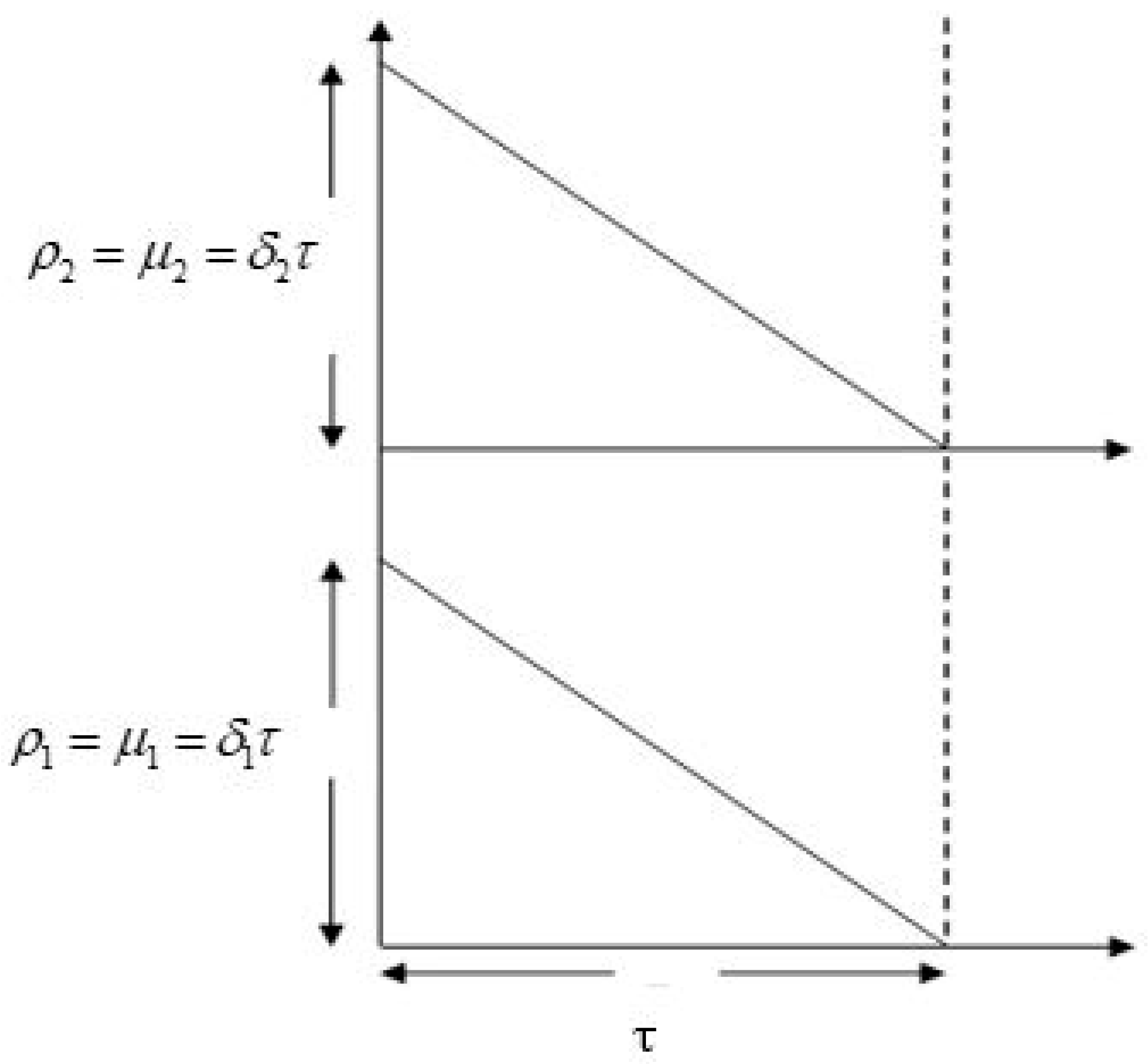
The scenarios for both non-deteriorating (Figure 1) and deteriorating (Figure 2) products are discussed.

In all cases, the aim is to find the optimal values of the order quantity, the cycle length, and selling prices for profit maximization.

4.1. Non-Deteriorating Complementary Products

This section discusses the complementary products when products are of a non-deteriorating type. The demand [35,44] of two complementary products, product 1 and product 2, are

$${\delta }_1({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_1-\beta \phi {\gamma }_2$$

(1)

$${\delta }_2({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_2-\beta \phi {\gamma }_1$$

(2)

respectively. Here, all parameters ($\alpha ,\beta ,\phi$) are non-negative. The retailer is trying to obtain the optimal values of decision variables. Therefore, the average profit is

$$\begin{array}{l}Maximize\\ {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)=({\gamma }_1-{\eta }_1){\delta }_1({\gamma }_1,{\gamma }_2)+({\gamma }_2-{\eta }_2){\delta }_2({\gamma }_1,{\gamma }_2)-\left(\frac{G_1+G_2}{\tau }+\frac{\left[{\lambda }_1{\delta }_1({\gamma }_1,{\gamma }_2)+{\lambda }_2{\delta }_2({\gamma }_1,{\gamma }_2)\right]}{2}\tau \right)\end{array}$$

(3)

Expression (1) gives the revenue from product 1. Expression (2) explains the revenue from product 2, and Expression (3) defines the summation of ordering costs and holding costs. The purpose is to maximize the profit, using the following theorem:

Theorem 1.

${\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)$is strictly concave if

$$G_1+G_2>\frac{\tau \beta }{2}\left[\tau ({\lambda }_1({\gamma }_1+{\gamma }_2\phi )+{\lambda }_2({\gamma }_2+{\gamma }_1\phi ))-4\phi {\gamma }_1{\gamma }_2-2({\gamma }_1^2+{\gamma }_2^2)\right].$$

Proof. 

See Appendix A.

Substituting the values of ${\delta }_1({\gamma }_1,{\gamma }_2)$ and ${\delta }_2({\gamma }_1,{\gamma }_2)$ within the first order derivative of the Equation (3) with respect to the decision variable τ, one can obtain

$$\frac{\partial {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)}{\partial \tau }=\frac{G_1+G_2}{{\tau }^2}+\frac{{\lambda }_1\left(\beta {\gamma }_1-\alpha +\beta \phi {\gamma }_2\right)+{\lambda }_2\left(\beta {\gamma }_2-\alpha +\beta \phi {\gamma }_1\right)}{2}$$

(4)

The first order derivatives of Equation (3) with respect to the variables ${\gamma }_1$ and ${\gamma }_2$ are given by

$$\frac{\partial {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_1}=\frac{\tau \beta ({\lambda }_1+\phi {\lambda }_2)}{2}+\alpha +\beta {\eta }_1-2\beta {\gamma }_1+\beta \phi {\eta }_2-2\beta \phi {\gamma }_2$$

(5)

$$\frac{\partial {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_2}=\frac{\tau \beta ({\lambda }_2+\phi {\lambda }_1)}{2}+\alpha +\beta {\eta }_2-2\beta {\gamma }_2+\beta \phi {\eta }_1-2\beta \phi {\gamma }_1$$

(6)

The required optimum values of ${\gamma }_1$ and ${\gamma }_2$ are as given by the following expressions as:

$${\gamma }_1^{*}=\frac{2\alpha +\beta (1+\phi )({\lambda }_1\tau +2{\eta }_1)}{4\beta (1+\phi )}$$

(7)

$${\gamma }_2^{*}=\frac{2\alpha +\beta (1+\phi )({\lambda }_2\tau +2{\eta }_2)}{4\beta (1+\phi )}$$

(8)

Using Equations (7) and (8) on the right-hand side of Equation (4) and equating them to zero, one can obtain

$${\alpha }_1{\tau }^3+{\alpha }_2{\tau }^2+{\alpha }_4=0$$

(9)

where

$${\alpha }_1=\beta ({\lambda }_1{}^2+{\lambda }_2{}^2+2\phi {\lambda }_1{\lambda }_2)$$

(10)

$${\alpha }_2=2\left[\beta ({\lambda }_1{\eta }_1+{\lambda }_2{\eta }_2)+\beta \phi ({\lambda }_1{\eta }_2+{\lambda }_2{\eta }_1)-\alpha ({\lambda }_1+{\lambda }_2)\right]$$

(11)

$${\alpha }_4=8(G_1+G_2)$$

(12)

Equation (9) is a cubic polynomial and the discriminant is

$$\Delta =-4{\alpha }_2{}^3{\alpha }_4-27{\alpha }_1{}^2{\alpha }_4{}^2$$

(13)

According to Δ, the discriminant has three types of values. Δ > 0 gives three real roots of distinct quality, Δ = 0 gives multiple real roots, and Δ < 0 gives one real root and two complex roots. The following improved solution procedure has been developed to solve the problem numerically.

Solution algorithm

Step 1.

Using Equations (10)–(12), calculate the coefficients of polynomial shown in Equation (9).

Step 2.

All positive real roots of Equation (9) are found by using MATLAB software. Go to the Step (3).

Step 3.

Determine the values $({\gamma }_1,{\gamma }_2)$ from Step (2).

Step 4.

For all combinations of $(\tau ,{\gamma }_1,{\gamma }_2)$, obtain the profit and check the concavity clause (Theorem 1). Select the maximum value as an optimal value of the profit. Then the related optimum decision variables are ${\tau }^{*}$, ${{\gamma }_1}^{*}$ and ${{\gamma }_2}^{*}$.

Step 5.

Determine the optimal values of the order quantities using ${\mu }_1^{*}={\delta }_1({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$ and ${\mu }_2^{*}={\delta }_2({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$.

4.2. Non-Deteriorating Substitutable Products

This section discusses about non-deteriorating substitutable products. The demand of two substitutable products, product 1 and product 2, is defined as follows:

$${\delta }_1({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_1+\beta \omega {\gamma }_2$$

(14)

$${\delta }_2({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_2+\beta \omega {\gamma }_1$$

(15)

where all parameters are non-negative. The average profit is

$${\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)=({\gamma }_1-{\eta }_1){\delta }_1({\gamma }_1,{\gamma }_2)+({\gamma }_2-{\eta }_2){\delta }_2({\gamma }_1,{\gamma }_2)-\left(\frac{G_1+G_2}{\tau }+\frac{\left[{\lambda }_1{\delta }_1({\gamma }_1,{\gamma }_2)+{\lambda }_2{\delta }_2({\gamma }_1,{\gamma }_2)\right]}{2}\tau \right)$$

(16)

The following theorem is used to maximize the above profit.

Theorem 2.

${\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)$is strictly concave

$$G_1+G_2>\frac{\tau \beta }{2}\left[\tau {\lambda }_1({\gamma }_1-{\gamma }_2\omega )+\tau {\lambda }_2({\gamma }_2-{\gamma }_1\omega )+4\omega {\gamma }_1{\gamma }_2-2({\gamma }_1^2+{\gamma }_2^2)\right].$$

Proof. 

See Appendix B.

Now, Equation (16) gives the following expression with respect to the variables τ, ${\gamma }_1$, and ${\gamma }_2$.

$$\frac{\partial {\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)}{\partial \tau }=\frac{G_1+G_2}{{\tau }^2}+\frac{{\lambda }_1(\beta {\gamma }_1-\alpha -\beta \omega {\gamma }_2)+{\lambda }_2(\beta {\gamma }_2-\alpha -\beta \omega {\gamma }_1)}{2}$$

(17)

$$\frac{\partial {\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_1}=\frac{\tau \beta ({\lambda }_1-\omega {\lambda }_2)}{2}+\alpha -2\beta {\gamma }_1+\beta {\eta }_1+2\beta \omega {\gamma }_2-\beta \omega {\eta }_2$$

(18)

$$\frac{\partial {\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_2}=\frac{\tau \beta ({\lambda }_2-\omega {\lambda }_1)}{2}+\alpha -2\beta {\gamma }_2+\beta {\eta }_2+2\beta \omega {\gamma }_1-\beta \omega {\eta }_1$$

(19)

Equations (18) and (19) give the optimum values of ${\gamma }_1$ and ${\gamma }_2$ as

$${\gamma }_1^{*}=\frac{2\alpha +\beta (1+\omega )({\lambda }_1\tau +2{\eta }_1)}{4\beta (1+\omega )},where0\le \omega <1$$

(20)

$${\gamma }_2^{*}=\frac{2\alpha +\beta (1+\omega )({\lambda }_2\tau +2{\eta }_2)}{4\beta (1+\omega )},where0\le \omega <1$$

(21)

Using Equations (20) and (21) on the right-hand side of Equation (17) and equating them to zero, one can obtain

$${\alpha }_1{\tau }^3+{\alpha }_2{\tau }^2+{\alpha }_4=0$$

(22)

where

$${\alpha }_1=\beta ({\lambda }_1{}^2-2\omega {\lambda }_1{\lambda }_2+{\lambda }_2{}^2)$$

(23)

$${\alpha }_2=2\left[-\alpha ({\lambda }_1+{\lambda }_2)+\beta ({\lambda }_1{\eta }_1+{\lambda }_2{\eta }_2)-\beta \omega ({\lambda }_1{\eta }_2+{\lambda }_2{\eta }_1)\right]$$

(24)

$${\alpha }_4=8(G_1+G_2)$$

(25)

According to the discussion about the discriminant of cubic polynomial above, the following solution procedure is suggested for the substitutable products case.

Solution algorithm

Step 1.

Using Equations (23)–(25), calculate the coefficients of the polynomial in Equation (22).

Step 2.

After finding all possible roots of Equation (22) with the help of MATLAB software, go to the Step (3).

Step 3.

From Step 2, determine the values of $({\gamma }_1,{\gamma }_2)$.

Step 4.

For all values of $(\tau ,{\gamma }_1,{\gamma }_2)$, determine the total profit and check the concavity clause (Theorem 2). Then select the maximum value as the optimum one. The related decision variables associated with the maximum profit are ${\tau }^{*},{{\gamma }_1}^{*}$, and ${{\gamma }_2}^{*}$.

Step 5.

Determine optimal values of order quantities using ${\mu }_1^{*}={\delta }_1({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$ and ${\mu }_2^{*}={\delta }_2({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$.

4.3. Deteriorating Complementary Products

In this case, it is assumed that the retailer is doing the business with two deteriorating complementary products. For both products, the deterioration rates are constant. The differential equation $\frac{d\rho (t)}{dt}=-D_r\rho (t)-\delta (\gamma )$ shows that the inventory level changes over time, where $\rho (\tau )=0$. Solving this differential equation yields $\rho (t)=\frac{\delta (\gamma )}{D_r}(e^{D_r(\tau -t)}-1)$, and according to Figure 2, the order quantity of each product is equal to $\mu =\rho \left(0\right)=\frac{\delta (\gamma )}{D_r}\left(e^{D_r\tau }-1\right)$. The holding cost is given by

$$\lambda {\displaystyle \underset{0}{\overset{\tau }{\int }}\rho (t)=\lambda {\displaystyle \underset{0}{\overset{\tau }{\int }}\frac{\delta (\gamma )}{D_r}(e^{D_r(\tau -t)}-1)dt}}=\frac{\lambda \delta (\gamma )}{D_r{}^2}(e^{D_r\tau }-D_r\tau -1)$$

(26)

Moreover, the deterioration cost is

$${\eta }^{\prime }\left(\underset{DeteriorationQuantity}{\underbrace{\rho (0)-\delta (\gamma )\tau }}\right)={\eta }^{\prime }\left(\frac{\delta (\gamma )}{D_r}(e^{D_r\tau }-1)-\delta (\gamma )\tau \right)$$

(27)

The total cost after utilizing the approximation of the Taylor series expansion, $e^{D_r\tau }=1+D_r\tau +\frac{{(D_r\tau )}^2}{2}$, is

$$TC=\frac{1}{\tau }\left[G+\stackrel{HoldingCost}{\overbrace{\frac{\lambda \delta (\gamma )}{D_r{}^2}(e^{D_r\tau }-D_r\tau -1)}}+\underset{DeteriorationCost}{\underbrace{\frac{{\eta }^{\prime }\delta (\gamma )}{D_r}(e^{D_r\tau }-1)-{\eta }^{\prime }\delta (\gamma )\tau }}\right]$$

$$\begin{array}{l}\stackrel{e^{D_r\tau }=1+D_r\tau +\frac{{(D_r\tau )}^2}{2}}{\to }\\ TC=\frac{1}{\tau }\left[G+\frac{\lambda \delta (\gamma )}{2}{\tau }^2+\frac{{\eta }^{\prime }\delta (\gamma )D_r{\tau }^2}{2}\right]=\frac{G}{\tau }+\frac{(\lambda +{\eta }^{\prime }{D}_r)\delta (\gamma )}{2}{\tau }^2\end{array}$$

(28)

The demand of two deteriorating complementary products, product 1 and product 2, is as follows (as defined in Section 4.1):

$${\delta }_1({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_1+\beta \phi {\gamma }_2$$

(29)

$${\delta }_2({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_2+\beta \phi {\gamma }_1$$

(30)

Finally, the average profit is

$$\begin{array}{ll}{\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)=& ({\gamma }_1-{\eta }_1){\delta }_1({\gamma }_1,{\gamma }_2)+({\gamma }_2-{\eta }_2){\delta }_2({\gamma }_1,{\gamma }_2)\\ & -[\frac{G_1+G_2}{\tau }+\frac{\tau ({\lambda }_1+{\eta }_1^{\prime }{D}_r){\delta }_1({\gamma }_1,{\gamma }_2)}{2}+\frac{\tau ({\lambda }_2+{\eta }_2^{\prime }{D}_r){\delta }_2({\gamma }_1,{\gamma }_2)}{2}]\end{array}$$

(31)

To optimize the profit, the following theorem is used.

Theorem 3.

${\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)$is strictly concave if

$$G_1+G_2>\frac{\tau \beta }{2}[-4\phi {\gamma }_1{\gamma }_2-2({\gamma }_1^2+{\gamma }_2^2)+\tau {\gamma }_1({\lambda }_1+\phi {\lambda }_2)+\tau {\gamma }_2({\lambda }_2+\phi {\lambda }_1)+\tau {\eta }_1^{\prime }{D}_r({\gamma }_1+\phi {\gamma }_2)+\tau {\eta }_2^{\prime }{D}_r({\gamma }_2+\phi {\gamma }_1)]$$

Proof. 

See Appendix C.

Here, the first order derivative of Equation (31) with respect to T yields

$$\frac{\partial {\pi }_c(\tau ,{\gamma }_1,{\gamma }_2)}{\partial \tau }=\frac{G_1+G_2}{{\tau }^2}+\frac{\left({\lambda }_1+{\eta }_1^{\prime }{D}_r\right)(\beta {\gamma }_1-\alpha +\beta \phi {\gamma }_2)+\left({\lambda }_2+{\eta }_2^{\prime }{D}_r\right)(\beta {\gamma }_2-\alpha +\beta \phi {\gamma }_1)}{2}$$

(32)

The first order derivatives of the Equation (31) for variables $p_1$ and $p_2$ are given by

$$\frac{\partial {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_1}=\frac{\tau \beta (({\lambda }_1+{\eta }_1^{\prime }{D}_r)+\phi ({\lambda }_2+{\eta }_2^{\prime }{D}_r))}{2}+\alpha -2\beta ({\gamma }_1+\phi {\gamma }_2)+\beta ({\eta }_1+\phi {\eta }_2)$$

(33)

$$\frac{\partial {\pi }_C(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_2}=\frac{\tau \beta (({\lambda }_2+{\eta }_2^{\prime }{D}_r)+\phi ({\lambda }_1+{\eta }_1^{\prime }{D}_r))}{2}+\alpha -2\beta ({\gamma }_2+\phi {\gamma }_1)+\beta ({\eta }_2+\phi {\eta }_1)$$

(34)

Optimum values of the decision variables $p_1$ and $p_2$ are

$${\gamma }_1^{*}=\frac{2\alpha +\beta (1+\phi )(2{\eta }_1+\tau {\lambda }_1+\tau {\eta }_1^{\prime }{D}_r)}{4\beta (1+\phi )}$$

(35)

$${\gamma }_2^{*}=\frac{2\alpha +\beta (1+\phi )(2{\eta }_2+\tau {\lambda }_2+\tau {\eta }_2^{\prime }{D}_r)}{4\beta (1+\phi )}$$

(36)

Using Equations (35) and (36) in Equation (32) and equating them to zero for optimality, one can obtain

$${\alpha }_1{\tau }^3+{\alpha }_2{\tau }^2+{\alpha }_4=0$$

(37)

where

$${\alpha }_1=\beta [({\gamma }_1^2+{\gamma }_2^2)+D_r^2({\eta }_1^{\prime 2}+{\eta }_2^{\prime 2})+2{\eta }_1^{\prime }{D}_r({\gamma }_1+\phi {\lambda }_2)+2{\eta }_2^{\prime }{D}_r({\lambda }_2+\phi {\lambda }_1)+2\phi ({\lambda }_1{\lambda }_2+{\eta }_1^{\prime }{\eta }_2^{\prime }{D}_r{}^2)]$$

(38)

$${\alpha }_2=-2[({\gamma }_1+{\eta }_1^{\prime }{D}_r)(\alpha -\beta ({\eta }_1+\phi {\eta }_2))+({\gamma }_2+{\eta }_2^{\prime }{D}_r)(\alpha -\beta ({\eta }_2+\phi {\eta }_1))]$$

(39)

$${\alpha }_4=8(G_1+G_2)$$

(40)

According to the discussion about the discriminant of cubic polynomial provided above (Section 4.1.), the following improved solution procedure is suggested for finding optimum solutions.

Solution algorithm

Step 1.

Using Equations (38)–(40), calculate coefficients of polynomial shown in the Equation (37).

Step 2.

Equation (37) gives all roots by using MATLAB software and then go to the Step (3).

Step 3.

Determine all values of $({\gamma }_1,{\gamma }_2)$ for period from the Step (2).

Step 4.

For all possible combinations of $(\tau ,{\gamma }_1,{\gamma }_2)$, determine the total profit and check the concavity clause (Theorem 3). Select the maximum value as the optimal value of the profit. Then optimal values of the decision variables are ${\tau }^{*},{{\gamma }_1}^{*}$, and ${{\gamma }_2}^{*}$.

4.4. Deteriorating Substitutable Products

This case discusses deteriorating substitutable products. The demand of two deteriorating substitutable products, product 1 and product 2, is

$${\delta }_1({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_1+\beta \omega {\gamma }_2$$

(41)

$${\delta }_2({\gamma }_1,{\gamma }_2)=\alpha -\beta {\gamma }_2+\beta \omega {\gamma }_1$$

(42)

where all parameters are non-negative. The average profit function is calculated as

$$\begin{array}{ll}{\pi }_S(\tau ,{\gamma }_1,{\gamma }_2)=& ({\gamma }_1-{\eta }_1){\delta }_1({\gamma }_1,{\gamma }_2)+({\gamma }_2-{\eta }_2){\delta }_2({\gamma }_1,{\gamma }_2)\\ & -[\frac{G_1+G_2}{\tau }+\frac{\tau ({\lambda }_1+{\eta }_1^{\prime }{D}_r){\delta }_1({\gamma }_1,{\gamma }_2)}{2}+\frac{\tau ({\lambda }_2+{\eta }_2^{\prime }{D}_r){\delta }_2({\gamma }_1,{\gamma }_2)}{2}]\end{array}$$

(43)

With the help of the following theorem, this profit can be optimized.

Theorem 4.

${\pi }_S(T,p_1,p_2)$is strictly concave if

$$G_1+G_2>\frac{\tau \beta }{2}[4\omega {\gamma }_1{\gamma }_2-2({\gamma }_1^2+{\gamma }_2^2)+\tau {\gamma }_1({\lambda }_1-\omega {\lambda }_2)+\tau {\gamma }_2({\lambda }_2-\omega {\lambda }_1)+\tau {\eta }_1^{\prime }{D}_r({\gamma }_1-\omega {\gamma }_2)+\tau {\eta }_2^{\prime }{D}_r({\gamma }_2-\omega {\gamma }_1)]$$

holds.

Proof. 

See Appendix D.

From the necessary condition, Equation (43) gives the following expressions

$$\frac{\partial {\pi }_s(\tau ,{\gamma }_1,{\gamma }_2)}{\partial \tau }=\frac{G_1+G_2}{{\tau }^2}+\frac{\left({\lambda }_1+{\eta }_1^{\prime }{D}_r\right)(\beta {\gamma }_1-\alpha -\beta \omega {\gamma }_2)+\left({\lambda }_2+{\eta }_2^{\prime }{D}_r\right)(\beta {\gamma }_2-\alpha -\beta \omega {\gamma }_1)}{2}$$

(44)

$$\frac{\partial {\pi }_s(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_1}=\frac{\tau \beta (({\lambda }_1+{\eta }_1^{\prime }{D}_r)-\omega ({\lambda }_2+{\eta }_2^{\prime }{D}_r))}{2}+\alpha -2\beta ({\gamma }_1-\omega {\gamma }_2)+\beta ({\eta }_1-\omega {\eta }_2)$$

(45)

$$\frac{\partial {\pi }_s(\tau ,{\gamma }_1,{\gamma }_2)}{\partial {\gamma }_2}=\frac{\tau \beta (({\lambda }_2+{\eta }_2^{\prime }{D}_r)-\omega ({\lambda }_1+{\eta }_1^{\prime }{D}_r))}{2}+\alpha -2\beta ({\gamma }_2-\omega {\gamma }_1)+\beta ({\eta }_2-\omega {\eta }_1)$$

(46)

Setting Equations (45) and (46) equal to zero, $p_1$ and $p_2$ are given as follows:

$${\gamma }_1^{*}=\frac{2\alpha +\beta (1-\omega )(2{\eta }_1+\tau {\lambda }_1+\tau {\eta }_1^{\prime }{D}_r)}{4\beta (1-\omega )},where0\le d<1$$

(47)

$${\gamma }_2^{*}=\frac{2\alpha +\beta (1-\omega )(2{\eta }_2+\tau {\lambda }_2+\tau {\eta }_2^{\prime }{D}_r)}{4\beta (1-\omega )},where0\le d<1$$

(48)

Using Equations (47) and (48) on the right-hand side of the Equation (44) and equating them to zero, one can obtain

$${\alpha }_1{\tau }^3+{\alpha }_2{\tau }^2+{\alpha }_4=0$$

(49)

where

$${\alpha }_1=\beta [({\gamma }_1^2+{\gamma }_2^2)+D_r^2({\eta }_1^{\prime 2}+{\eta }_2^{\prime 2})+2{\eta }_1^{\prime }{D}_r({\gamma }_1-\omega {\lambda }_2)+2{\eta }_2^{\prime }{D}_r({\lambda }_2-\omega {\lambda }_1)-2\omega ({\lambda }_1{\lambda }_2+{\eta }_1^{\prime }{\eta }_2^{\prime }{D}_r{}^2)]$$

(50)

$${\alpha }_2=-2[({\gamma }_1+{\eta }_1^{\prime }{D}_r)(\alpha -\beta ({\eta }_1-\omega {\eta }_2))+({\gamma }_2+{\eta }_2^{\prime }{D}_r)(\alpha -\beta ({\eta }_2-\omega {\eta }_1))]$$

(51)

$${\alpha }_4=8(G_1+G_2)$$

(52)

According to the discussion about discriminant of cubic polynomial provided above (Section 4.1), the following solution procedure can help to find the numerical solution for substitutable products.

Solution algorithm

Step 1.

Calculate the coefficients of polynomial from the Equation (49) by using Equations (50) to (52).

Step 2.

Equation (49) gives the roots of the equation using MATLAB software. Move to the Step 3.

Step 3.

Find $({\gamma }_1,{\gamma }_2)$ using Step 2.

Step 4.

For $(\tau ,{\gamma }_1,{\gamma }_2)$, obtain the profit and check the concavity clause (Theorem4). Choose the maximum value as the optimal value of the profit. Then related decision variables for the maximum profit are given by ${\tau }^{*},{{\gamma }_1}^{*}$, and ${{\gamma }_2}^{*}$.

Step 5.

Determine optimal values of order quantities using ${\mu }_1^{*}={\delta }_1({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$ and ${\mu }_2^{*}={\delta }_2({{\gamma }_1}^{*},{{\gamma }_2}^{*}){\tau }^{*}$.

5. Numerical Examples and Sensitivity Analysis

Four numerical examples are given to justify the mathematical model. All examples explain effects of changes of the degree of complementarity or substitutability.

5.1. Example 1: Non-Deteriorating Complementary Products

The values of all parameters are $G_1=120$, $G_2=100$, ${\lambda }_1=6,$, ${\lambda }_2=3$, $\alpha =100$, $\beta =0.4$, ${\eta }_1=20$, and ${\eta }_2=10$. By using Steps (1) to (5) of the proposed solution algorithm in Section 4.1, optimal values of $\tau$, ${\gamma }_1$, ${\gamma }_2$, ${\mu }_1$, and ${\mu }_2$ are obtained. These values with some variation of $\phi$ are depicted in the

Table 2. Optimum results for some variations of φ.

φ	Concavity	τ	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\prod }_{\mathit{C}}$
0	True	93.3221	274.9832	199.9916	−932.5924	1866.8	1247.6
	True	1.0290 *	136.5438 *	130.7719 *	46.7087 *	49.0849 *	10621 *
	False	−1.0180	-	-	-	-	-
0.1	True	85.9137	252.5069	183.0716	−715.2833	1432.3	944.4092
	True	1.0327 *	125.1854 *	119.4109 *	46.6255 *	48.7723 *	8548.6 *
	False	−1.0229	-	-	-	-	-
0.2	True	79.5269	233.4570	168.8118	−547.7619	1097.4	715.6247
	True	1.0362 *	115.7210 *	109.9438 *	46.4588 *	48.1415 *	7752.7 *
	False	−1.0229	-	-	-	-	-
0.3	True	73.9641	217.1000	156.6269	-416.8036	835.5901	539.8298
	True	1.0398 *	107.7135 *	101.9337 *	46.4588 *	48.1415 *	7752.7 *
	False	−1.0253	-	-	-	-	-
0.4	True	69.0754	202.8988	146.0923	−313.2069	628.5371	402.6596
	True	1.0433 *	100.8607 *	95.0682 *	46.3753 *	47.5031 *	6481.3 *
	False	−1.0278	-	-	-	-	-
0.5	True	64.7452	190.4512	136.8923	−230.4240	463.1133	294.2216
	True	1.0470 *	94.9038 *	89.1186 *	46.2917 *	47.5031 *	6481.3 *
	False	−1.0303	-	-	-	-	-
0.6	True	60.8831	179.4496	128.7873	−163.7025	329.8139	207.5357
	True	1.0606 *	89.7010 *	83.9130 *	46.2079 *	47.1809 *	5965.9 *
	False	−1.0328	-	-	-	-	-
0.7	True	57.4169	169.6547	121.5921	−109.5329	221.6201	137.5717
	True	1.0644 *	85.1110 *	79.3202 *	46.0401 *	46.5305 *	5108.5 *
	False	−1.0353	-	-	-	-	-
0.8	True	54.2887	160.8775	115.1610	−65.2832	133.2681	80.6367
	True	1.0581 *	81.0316 *	75.2380 *	46.0401 *	46.5305 *	5108.5 *
	False	−1.0379	-	-	-	-	-
0.9	True	51.4514	152.9666	109.3780	−28.9524	60.7553	33.9747
	True	1.0619 *	77.3824 *	71.5859 *	45.9560 *	46.2022 *	4748.4 *
	False	−1.0404	-	-	-	-	-
1.0	True	48.8661	145.7992	104.1496	1.0005	1.0005	−4.5010
	True	1.0658 *	74.0987 *	68.2993 *	45.8717 *	45.8717 *	4424.9 *
	False	−1.0430	-	-	-	-	-

“-“ means infeasible result; “*” means optimum solution.

. ‘*’ demonstrates optimum results. Table 2 reveals the increasing value of $\phi$ gives decreasing values of ${\gamma }_1^{*}$, ${\gamma }_2^{*}$, ${\mu }_1^{*}$, ${\mu }_2^{*}$, and ${\pi }_C({\tau }^{*},{\gamma }_1^{*},{\gamma }_2^{*})$, but gives an increasing value of ${\tau }^{*}$. More precisely, these changes on ${\gamma }_1^{*}$ and ${\gamma }_2^{*}$ are shown in Figure 3. Bold font indicates the optimum results.

5.2. Example 2: Non-Deteriorating Substitutable Products

Values of parameters are $G_1=150$, $G_2=155$, ${\lambda }_1=4.5$, ${\lambda }_2=4$, $\alpha =100$, $\beta =0.3$, ${\eta }_1=15$, and ${\eta }_2=13$. Steps (1) to (5) of the solution algorithm proposed in the Section 4.2 help to obtain optimum values of $\tau$, ${\gamma }_1$, ${\gamma }_2$, ${\mu }_1$, and ${\mu }_2$ for different values of d.

Table 3. Optimum results for some variations of ω.

$\mathit{\omega }$	Concavity	τ	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\prod }_{\mathit{C}}$
0	True	149.7187	342.6002	322.8854	−416.2286	469.2757	56.4733
	True	1.2292 *	175.5495	174.3959 *	58.1837 *	58.6091 *	14,799 *
	False	−1.2170	-	-	-	-	-
0.1	True		380.5094	358.6400	−566.5791	638.3149	77.4294
	True		194.0644 *	192.9112 *	58.3172 *	58.7838 *	16,647 *
	False	−1.2170	-	-	-	-	-
0.2	True	188.4626	427.8537	403.2959	−783.6958	882.4670	107.5095
	True	1.2228 *	217.2090 *	216.0561 *	58.4503 *	58.9578 *	18,957 *
	False	−1.2149	-	-	-	-	-
0.3	True	216.0547	488.6568	460.6500	−1110.2	1249.7	152.5353
	True		246.9673 *	245.8149 *	58.5830 *	59.1312 *	21,929 *
	False	−1.2107	-	-	-	-	-
0.4	True	252.7386	569.6088	537.0164	−1627.8	1831.9	223.6789
	True	1.2165 *	286.6464 *	285.4943 *	58.7153 *	59.3039 *	25,894 *
	False	−1.2107	-	-	-	-	-
0.5	True	303.8947	682.7149	643.7281	−2508.7	2822.8	344.5513
	True	1.2134 *	342.1984 *	341.0467 *	58.8472 *	59.4761 *	31,445 *
	False	−1.2086	-	-	-	-	-
0.6	True	380.1918	851.8825	803.3585	−4167.0	4688.3	572.1289
	True	1.2103 *	425.5283 *	424.3770 *	58.9787 *	59.6475 *	39,774 *
	False	−1.2065	-	-	-	-	-
0.7	True	506.2033	1132.5	1068.3	−7808.6	8784.9	1073.6
	True	1.2073 *	564.4137 *	563.2628 *	59.1098 *	59.8184 *	53,659 *
	False	−1.2044	-	-	-	-	-
0.8	True	753.9936	1689.1	1593.8	−18,250	20,531	2525.4
	True	1.2043 *	842.1881 *	841.0376 *	59.2405 *	59.9887 *	81,433 *
	False	−1.2013	-	-	-	-	-
0.9	True	1465.2	3322.5	3138.4	−72,373	81,420	10,300
	True	1.2013 *	1675.5 *	1674.4 *	59.3708 *	60.1583 *	164,760 *
	False	-	-	-	-	-	-
1.0	Undefined	22659	∞	∞	∞	∞	Undefined
	Undefined	1.1983	−∞	∞	∞	−∞	Undefined
	Undefined	−1.1982	−∞	∞	−∞	∞	Undefined

“-“ means infeasible result; “*” means optimum solution.

reveals that when $\omega$ increases, ${\tau }^{*}$, ${\gamma }_1^{*}$, and ${\gamma }_2^{*}$ decrease, but ${\mu }_1^{*}$, ${\mu }_2^{*}$, and ${\pi }_S({\tau }^{*},{\gamma }_1^{*},{\gamma }_2^{*})$ increase. The changes on ${\gamma }_1^{*}$ and ${\gamma }_2^{*}$ are shown in Figure 4. Figure 5 reveals that the profit decreases whenever the degree of complementarity increases and vice-versa. Therefore, the retailer who intends to work on complementary products should select two products with a smaller degree of complementary to make more profit. But if he/she intends to work on substitutable products, he/she should select two products with a larger degree of substitutability.

5.3. Example 3: Deteriorating Complementary Products

The values of parameters for this example are $G_1=120$, $G_2=100$, ${\lambda }_1=6$, ${\lambda }_2=3$, $\alpha =100$, $\beta =0.4$, ${\eta }_1=20,{\eta }_2=10,{\eta }_1^{\prime }=10,{\eta }_2^{\prime }=5$ and $D_r=0.01$. Using Steps (1) to (5) of the proposed solution algorithm in Section 4.3, the optimal values of $\tau ,{\gamma }_{1,}{\gamma }_{2,}{\mu }_1$, and ${\mu }_2$ are obtained.

Table 4. Optimum results for some variations of φ (deterioration case).

φ	Concavity	τ	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\prod }_{\mathit{C}}$
0	True	91.7921	274.9829	199.9914	−1503.0	3008.7	1247.6
	True	1.0208 *	136.5567 *	130.7784 *	46.5584 *	48.9299 *	10,618 *
	False	−1.0096	-	-	-	-	-
0.1	True	84.5050	252.5065	183.0715	−1105.7	2214.1	944.3665
	True	1.0242 *	125.1983 *	119.4174 *	46.4762 *	48.6187 *	9486.7 *
	False	−1.0120	-	-	-	-	-
0.2	True	78.2230	233.4567	168.8117	−817.1057	1637.0	715.5786
	True	1.0277 *	115.7340 *	109.9503 *	46.3938 *	48.3057 *	8545.1 *
	False	−1.0144	-	-	-	-	-
0.3	True	72.7513	217.0996	156.6267	−602.9090	1208.7	539.7803
	True	1.0313 *	107.7265 *	101.9402 *	46.3114 *	47.9908 *	7749.2 *
	False	−1.0168	-	-	-	-	-
0.4	True	67.9427	202.8984	146.0921	−441.0527	885.1454	402.6065
	True	1.0348 *	100.8638 *	95.0748 *	46.2288 *	47.6741 *	7067.7 *
	False	−1.0193	-	-	-	-	-
0.5	True	63.6836	190.4508	136.8921	−316.9006	636.9689	294.1649
	True	1.0384 *	94.9169 *	89.1251 *	46.1462 *	47.3553 *	6477.9 *
	False	−1.0218	-	-	-	-	-
0.6	True	59.8847	179.4492	128.7871	−220.4678	444.2343	207.4755
	True	1.0421 *	89.7142 *	83.9196 *	46.0634 *	47.0346 *	5962.4 *
	False	−1.0243	-	-	-	-	-
0.7	True	56.4753	169.6543	121.5918	−144.7758	292.9846	137.5079
	True	1.0458 *	85.1242 *	79.3268 *	45.9805 *	46.7119 *	5508.2 *
	False	−1.0268	-	-	-	-	-
0.8	True	53.3984	160.8770	115.1607	−84.8435	173.2576	80.5692
	True	1.0495 *	81.0449 *	75.2447 *	45.8975 *	46.3871 *	5105.1 *
	False	−1.0293	-	-	-	-	-
0.9	True	50.6076	152.9660	109.3778	−37.0492	77.8092	33.9034
	True	1.0533 *	77.3957 *	71.5926 *	45.8144 *	46.0602 *	4745.0 *
	False	−1.0318	-	-	-	-	-
1.0	True	48.0647	145.7986	104.1493	1.2845	1.2845	−4.5761
	True	1.0571 *	74.1121 *	68.3060 *	45.7312 *	45.7312 *	4421.4 *
	False	−1.0344	-	-	-	-	-

“-“ means infeasible result; “*” means optimum solution.

shows that ${\gamma }_1^{*},{\gamma }_2^{*}$, ${\mu }_1^{*}$, ${\mu }_2^{*}$, and ${\pi }_C({\tau }^{*},{\gamma }_1^{*},{\gamma }_2^{*})$ decrease when $\phi$ increases, but at that time, ${\tau }^{*}$ increases (similar to Section 5.1). The changes on ${\gamma }_1^{*}$ and ${\gamma }_2^{*}$ are shown in Figure 6 precisely.

5.4. Example 4: Deteriorating Substitutable Products

Fixed parametric values are $G_1=150,G_2=155,{\lambda }_1=4.5,{\lambda }_2=4,$ $\alpha =100,$ $\beta =0.3,$ ${\eta }_1=15,{\eta }_2=13,{\eta }_1^{\prime }=7,{\eta }_2^{\prime }=6$, and $D_r=0.01$. For different values of ω, one can use Steps (1) to (5) of proposed solution algorithm in Section 4.4. From the

Table 5. Optimum results for some variations of ω (deterioration case).

ω	Concavity	τ	${\mathit{\gamma }}_1$	${\mathit{\gamma }}_2$	${\mathit{\mu }}_1$	${\mathit{\mu }}_2$	${\prod }_{\mathit{S}}$
0	True	147.4584	342.6379	322.8369	−940.472	1060.9	56.9563
	True	1.2199 *	175.5604 *	174.4049 *	58.0953 *	58.5208 *	14,795 *
	False	−1.2099	-	-	-	-	-
0.1	True	164.4331	380.5500	358.5848	−1423.5	1604.6	78.1010
	True	1.2167 *	194.0753 *	192.9202 *	58.2279 *	58.6945 *	16,643 *
	False	−1.2078	-	-	-	-	-
0.2	True	185.6144	427.8978	403.2320	−2254.3	2539.8	108.4521
	True	1.2136 *	217.2198 *	216.0651 *	58.3600 *	58.8676 *	18,954 *
	False	−1.2057	-	-	-	-	-
0.3	True	212.7872	488.7046	460.5742	−3816.6	4298.5	153.8840
	True	1.2104 *	246.9782 *	245.8238 *	56.4918 *	59.0400 *	21,926 *
	False	−1.2036	-	-	-	-	-
0.4	True	248.9126	569.6604	536.9240	−7146.8	8047.2	225.6693
	True	1.2073 *	286.6572 *	285.5032 *	58.6231 *	59.2118 *	25,890 *
	False	−1.2015	-	-	-	-	-
0.5	True	299.2879	682.7698	643.6106	−15,703	17,678	347.6315
	True	1.2043 *	342.2092 *	341.0556 *	58.7540 *	59.3829 *	31441 *
	False	−1.1994	-	-	-	-	-
0.6	True	374.4167	851.9377	803.1996	−45,423	51134	577.2581
	True	1.2012 *	425.5390 *	424.3859 *	58.8845 *	59.5534 *	39,770 *
	False	−1.1974	-	-	-	-	-
0.7	True	498.4871	1132.6	1068.0	−224,880	253,130	1083.2

“-“ means infeasible result; “*” means optimum solution.

, it can be concluded that ${\tau }^{*}$, ${\gamma }_1^{*}$, and ${\gamma }_2^{*}$ decrease with increased values of ω, but ${\mu }_1^{*}$, ${\mu }_2^{*}$, and ${\pi }_S({\tau }^{*},{\gamma }_1^{*},{\gamma }_2^{*})$ increase (similar Section 5.2). The changes on ${\gamma }_1^{*}$ and ${\gamma }_2^{*}$ are presented in the Figure 7. Figure 8 describes that the profit decreases when the complementarity degree increases, but profit increases while the degree of substitutability increases. As a result, the retailer who intends to work on complementary products should select two products with a smaller degree of complementary in order to make more profit. If he/she intends to work on substitutable products, he/she should select two products with a larger degree of substitutability.

Managerial insights

Numerical studies justify the theoretical implications of this research in each case separately. The degree of complementarity of a product has an inverse impact on the selling price, i.e., the increasing complementarity gives less profit. This implies that if one product is more dependent or complement to the other product, the selling of the one product is dependent upon the other product. In the case that one of the complementary products is not available at the right time, the chances to sale of the other product are smaller. To handle this situation, industry managers need to take more care of the inventory and safety stock of the complementary products.

For the case of substitutable products, the increasing rate of the degree of substitutability has a direct impact on the profit. This implies that if customers can get any similar substitutable product, the customer is satisfied with the service. The absence of the original product does not have any impact on the profit. This study suggests to industry managers that they should introduce similar types of alternative products to the shops or their centers such that they can survive facing losses from original products. It helps to keep the brand image of the industry as well as the retailer. The scenario is the same for the case of deteriorated substitutable and complementary products. Therefore, the industry needs to create their strategies carefully for complementary products rather than substitutable products.

6. Conclusions

Four pricing models for two types of products which may be complementary or substitutable and non-deteriorating or deteriorating were studied analytically as well as numerically. For all cases, it was observed that selling prices and lot sizes of both products as well as the average profit were decreased, and the period length was increased while the degree of complementarity was increased and vice versa. The selling prices and order quantities of both products as well as average profit were increased, and the cycle length was decreased with increased values of the degree of substitutability. This study concluded that sell of complementary products should be with some smaller degree of complementarity and substitutable products with bigger degree of substitutability in order to make more profit. The present model can help a manager to fix optimal selling prices, ordered quantities, and cycle length for different scenarios so that the joint profit is maximized. In the existing literature, some research articles are focused on substitutable and complementary products but none of them have investigated both inventory and pricing decisions of products simultaneously. Therefore, the present article is quite new compared to existing literature. Lead time is considered as zero in this study, but in reality it is not possible. This study can be extended with random lead time and backorder. The business can be spread through multiple number of retailers. Extra service facilities can be included within the study [45,46,47,48] for deteriorating products and non-zero random lead time. The quality improvement [49,50] and preservation technology [28,29] for deteriorating products can improve the study in a realistic way.