An Enhanced Tuna Swarm Algorithm for Link Scheduling Strategies in Wireless Sensor Networks
Abstract
1. Introduction
2. Related Work
2.1. Link Scheduling Approaches
2.2. Emerging Trends and Nascent Works
2.3. Tuna Swarm Optimization Approaches
3. Preparation Work
3.1. Network Topology Model
3.2. Node Energy of WSNs
3.3. Link Scheduling Model
4. Materials and Methods
4.1. Tuna Swarm Optimization Algorithm
- Step 1: Algorithm Initialization.Assume that in a D-dimensional search space, there are N tunas. The position of the i-th tuna at iteration t is denoted as:The population positions are randomly initialized within the search space:where and are the lower bound and upper bound vectors of the search space, respectively, and is a random number within the range [0, 1].
- Step 2: Iteration Process.represents the maximum number of iterations. From iteration to , the following steps are repeated:
- -
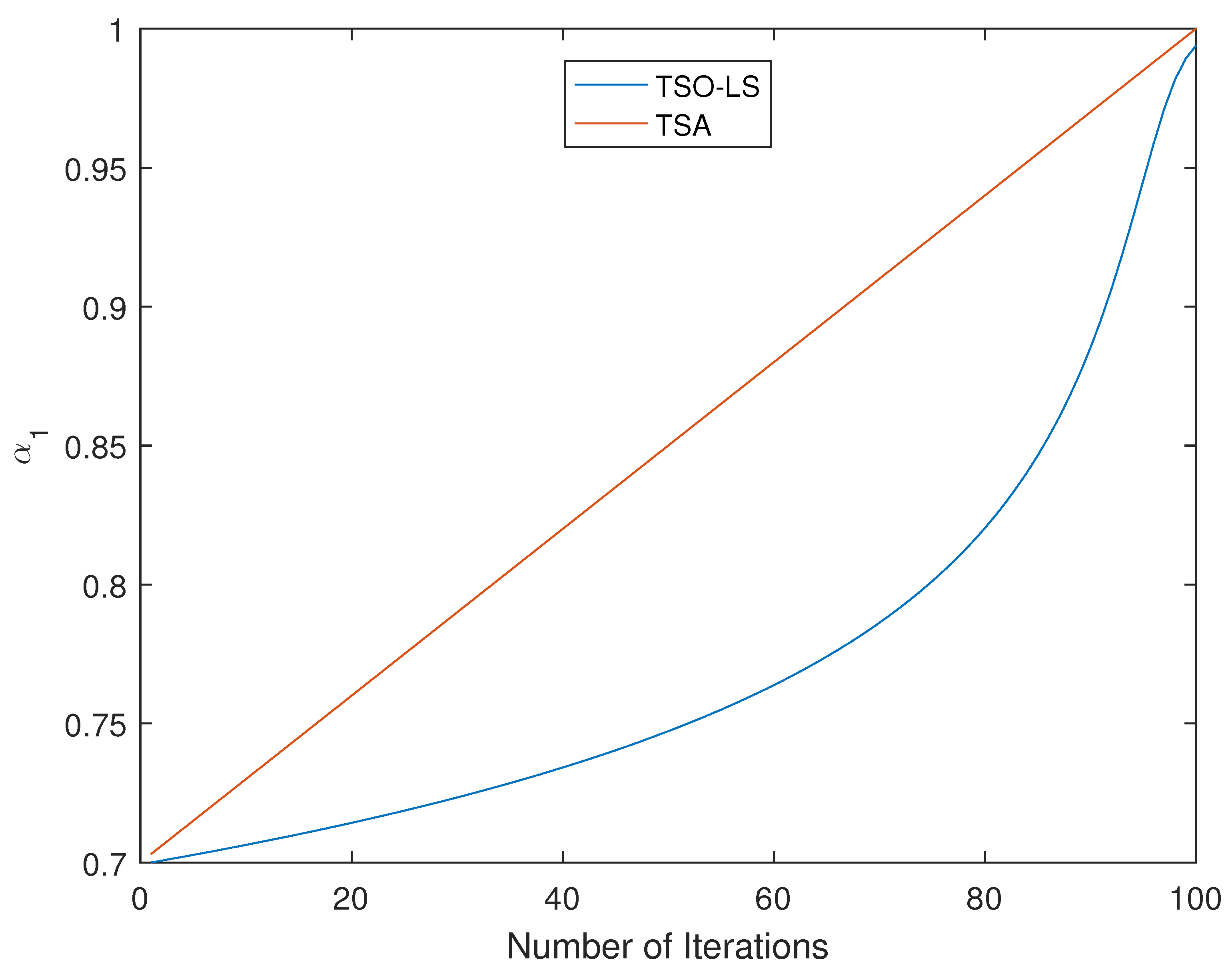
- Step 2.1: Update Control Parameters.First, calculate the current parameter , which increases linearly from the constant value to 1 as iterations progress, thereby balancing exploration and exploitation. Here, a is a constant used to control subsequent spiral movements.Simultaneously, compute the parameter p used in parabolic foraging:
- -
- Step 2.2: Position Update.For each tuna individual i in the population, generate a random number in the range [0, 1], and select a foraging strategy based on its value.Case A: Spiral Foraging (When )In this mode, the tuna moves towards the best individual and a selected leader individual . First, calculate according to the following formula, where l and b are random numbers:Then, determine the leading individual:Finally, the position update formula for the tuna population is given as follows:where is the best individual from the i-th iteration, and is the leading individual. Formula (15) means that its position update depends entirely on the global best individual and its own current position. It can be regarded as a leading individual exploring near the best position and its own current location.Case B: Parabolic Foraging (When )During this phase, the tuna forms a parabolic encirclement with the best individual as the focus. First, generate a random direction factor :Then, based on another random number , select the position update method:if :where is a random number within the range [0, 1].if :
- -
- Step 2.3: Boundary Handling.Check whether the new position remains within the search boundaries . If it exceeds the boundaries, clamp it to the boundary values.
- -
- Step 2.4: Evaluation and Selection.Calculate the fitness values of the new positions for all tuna individuals. If the new position of any tuna yields a better fitness value, replace its old position with the new one. Subsequently, update the global best individual for the entire population.
- Step 3: Algorithm Termination.When the iteration counter t reaches , the algorithm stops. The output at this point represents the global optimal solution found by the algorithm.
4.2. TSO-LS Algorithm
- 1.
- Optimization of the individual update mechanism for accelerated scheduling solution; To rapidly obtain high-quality link scheduling schemes, the individual update mechanism of the algorithm has been optimized. Specifically, an adaptive weighting factor is introduced, whose value is dynamically adjusted based on the current iteration count. This effectively accelerates the algorithm’s convergence in the search through the link scheduling solution space. The calculation formula for the weighting factor is:where is the value of in Formula (11) at the t-th iteration, and is a constant. In this way, the algorithm can maintain strong exploration capability in the early stages while gradually enhancing its exploitation capability as the number of iterations increases, thereby achieving the goal of rapid convergence.
- 2.
- Optimization of the individual update mechanism for accelerated scheduling solution;To prevent the generated link scheduling schemes from converging to a local optimum, the selection strategy for the leading individual has been refined. During each iteration, in addition to considering individual fitness (i.e., the quality of the scheduling scheme), a weighting based on the distance between individuals is introduced. This ensures more effective exploration of the entire solution space, thereby facilitating the discovery of globally superior scheduling schemes with better performance and fewer conflicts. The specific formula for selecting the leader is:Here, L denotes the selected leading individual. represents the fitness value of the i-th individual, calculated using Formula (19). A smaller fitness value indicates that the link scheduling scheme corresponding to that individual is more optimal. The term denotes the distance between the i-th individual and the current global optimal solution, which quantifies the proximity of the individual’s position in the solution space to the optimal solution.
- 3.
- Maintenance of population diversity to avoid suboptimal scheduling schemes solution;To prevent the algorithm from prematurely converging to a suboptimal link activation pattern, a population diversity maintenance mechanism is introduced. After each iteration, a randomly selected proportion of individuals are reinitialized, causing their positions to be randomly redistributed within the solution space. This helps preserve the diversity of scheduling strategies, thereby enhancing the algorithm’s ability to escape local optima in scheduling solutions.
4.3. TSO-LS Algorithm Implementation
- 1.
- Initialization Phase. Generate initial individuals in the tuna swarm. Each individual represents a potential link scheduling scheme, including the connection status between nodes and data transmission paths. To ensure diversity, the initial population is generated using random methods, and each individual is encoded to facilitate subsequent calculations and optimization.
- 2.
- Fitness Evaluation. For each individual, substitute parameters such as energy consumption and delay into Formula (19) to calculate its fitness value. A higher fitness value indicates a more optimal scheduling scheme.
- 3.
- Selection Operation. Based on the fitness values of individuals, select the top-performing individuals to proceed to the next generation.
- 4.
- Main Iteration Loop. For each tuna in the population, generate a random number in the range [0, 1]. If this random number is less than , execute spiral foraging; otherwise, execute parabolic foraging to obtain a new position. Check whether the new position is within the search boundaries. If it exceeds the boundaries, reset it to the boundary values.
- 5.
- Update the Optimal Solution. Calculate the fitness values of the new positions for all tuna. If there exists an individual with better fitness than the current optimal solution, update the optimal solution.
- 6.
- Loop Termination and Output. When the number of iterations reaches , the loop terminates. The algorithm outputs the global optimal solution.
5. Experiments and Results
5.1. Evaluation Metrics
5.2. Experimental Design
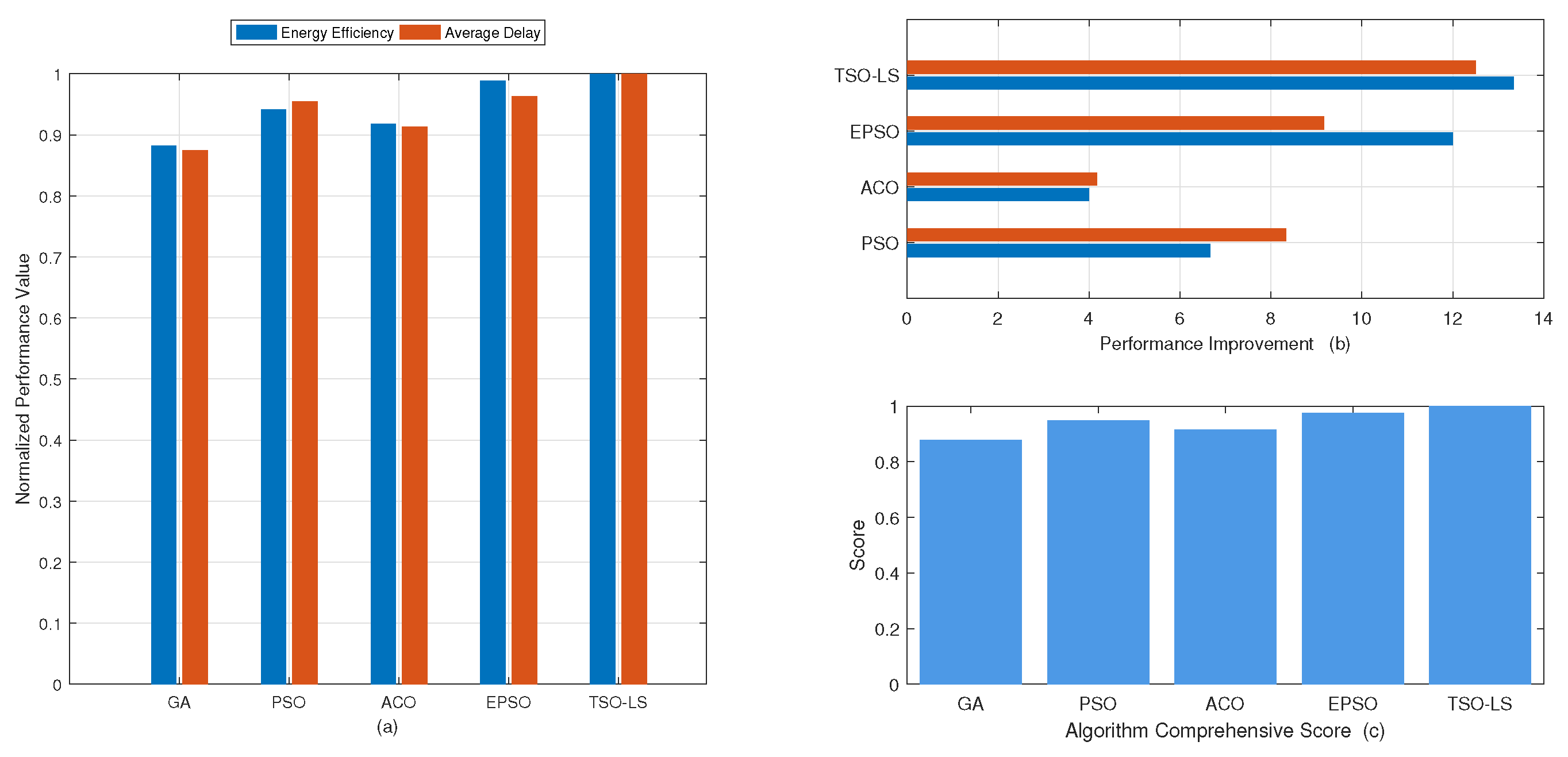
5.3. Comparison of Algorithms
6. Conclusions
Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masood, A. Survey on Energy-Efficient Techniques for Wireless Sensor Networks. arXiv 2021, arXiv:2105.10413. [Google Scholar] [CrossRef]
- Houssein, E.H.; Saad, M.R.; Djenouri, Y.; Hu, G.; Ali, A.A.; Shaban, H. Metaheuristic algorithms and their applications in wireless sensor networks: Review, open issues, and challenges. Clust. Comput. 2024, 27, 13643–13673. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhuo, X.; Liu, M.; Wei, Y.; Qu, F. A centralized cross-layer protocol for joint power control, link scheduling, and routing in UWSNs. IEEE Internet Things J. 2023, 11, 12823–12833. [Google Scholar] [CrossRef]
- Okdem, S.; Karaboga, D. Routing in wireless sensor networks using an ACO router chip. Sensors 2009, 9, 909–921. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Amgoth, T.; Annavarapu, C.S.R. ACO-based mobile sink path determination for wireless sensor networks under non-uniform data constraints. Appl. Soft Comput. 2018, 69, 528–540. [Google Scholar]
- Sharmin, A.; Anwar, F.; Motakabber, S.M.A.; Hashim, A.H.A. Secure ACO-Based Wireless Sensor Network Routing Algorithm for IoT. In Proceedings of the 2021 8th International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 22–23 June 2021; pp. 190–195. [Google Scholar]
- Kulkarni, R.V.; Venayagamoorthy, G.K. Particle swarm optimization in wireless-sensor networks: A brief survey. IEEE Trans. Syst. Man, Cybern. Part C (Appl. Rev.) 2010, 41, 262–267. [Google Scholar] [CrossRef]
- Tripathy, P.; Khilar, P.M. PSO based Amorphous algorithm to reduce localization error in Wireless Sensor Network. Pervasive Mob. Comput. 2024, 100, 101890. [Google Scholar] [CrossRef]
- Azharuddin, M.; Jana, P.K. Particle swarm optimization for maximizing lifetime of wireless sensor networks. Comput. Electr. Eng. 2016, 51, 26–42. [Google Scholar] [CrossRef]
- Tossa, F.; Abdou, W.; Ezin, E.C.; Gouton, P. Improving coverage area in sensor deployment using genetic algorithm. In Computational Science—ICCS 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 398–408. [Google Scholar]
- Shahi, B.; Dahal, S.; Mishra, A.; Kumar, S.V.; Kumar, C.P. A review over genetic algorithm and application of wireless network systems. Procedia Comput. Sci. 2016, 78, 431–438. [Google Scholar] [CrossRef]
- Hao, Z.; Hou, J.; Dang, J.; Dang, X.; Qu, N. Game algorithm based on link quality: Wireless sensor network routing game algorithm based on link quality. Int. J. Distrib. Sens. Netw. 2021, 17, 1550147721996248. [Google Scholar] [CrossRef]
- Mohammadi, N.; Bigham, B.S.; Kadivar, M. PDSLS: An approximation SINR-based Shortest Link Scheduling algorithm with power control. Comput. Commun. 2025, 236, 108137. [Google Scholar] [CrossRef]
- Zeng, B.; Liang, Z.; Zhao, C. Sinr-based slot reuse algorithm for multi-channel wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2025, 2025, 48. [Google Scholar] [CrossRef]
- Tian, H. Enhancing the effectiveness of wireless sensor networks through consensus estimation and universal coverage. Sci. Rep. 2025, 15, 24930. [Google Scholar] [CrossRef]
- Butt, F.A.; Jalil, M.; Liaquat, S.; Alawsh, S.A.; Naqvi, I.H.; Mahyuddin, N.M.; Muqaibel, A.H. Self-calibration of wireless sensor networks using adaptive filtering techniques. Results Eng. 2025, 25, 103775. [Google Scholar] [CrossRef]
- Kamel, S.; Al Qahtani, A.; Al-Shahrani, A.S.M. Particle Swarm Optimization for Wireless Sensor Network Lifespan Maximization. Eng. Technol. Appl. Sci. Res. 2024, 14, 13665–13670. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, Y. A survey of energy-efficient scheduling mechanisms in sensor networks. Mob. Netw. Appl. 2006, 11, 723–740. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.R.; Han, B.; Tang, A. Tuna swarm optimization: A novel swarm-based metaheuristic algorithm for global optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Tan, M.; Li, Y.; Ding, D.; Zhou, R.; Huang, C. An improved jade hybridizing with tuna swarm optimization for numerical optimization problems. Math. Probl. Eng. 2022, 2022, 7726548. [Google Scholar] [CrossRef]
- Xiao, X.; Tan, G.; Gao, C.; Tang, X.; Song, W.; Tian, Y. A Multi-Strategy Improved Tuna Swarm Optimization Algorithm for Cloud Task Scheduling. In Proceedings of the 2024 5th International Symposium on Computer Engineering and Intelligent Communications (ISCEIC), Wuhan, China, 8–10 November 2024; pp. 174–179. [Google Scholar]
- Wang, W.; Tian, J. An improved nonlinear tuna swarm optimization algorithm based on circle chaos map and levy flight operator. Electronics 2022, 11, 3678. [Google Scholar] [CrossRef]
- Srinivasan, B.; Kalimuthu, V.K.; Muthu, T.; Velumani, R. Modeling of tuna swarm algorithm based unequal clustering approach on internet of things assisted networks. Braz. Arch. Biol. Technol. 2024, 67, e24231115. [Google Scholar] [CrossRef]
- Daneshvar, S.M.M.H.; Mazinani, S.M. On the best fitness function for the WSN lifetime maximization: A solution based on a modified salp swarm algorithm for centralized clustering and routing. IEEE Trans. Netw. Serv. Manag. 2023, 20, 4244–4254. [Google Scholar] [CrossRef]
- Kapoor, R.; Sharma, S. Hybrid metaheuristic optimization for energy-efficient routing, clustering, and sleep scheduling in WSNs. In Wireless Ad-Hoc and Sensor Networks; CRC Press: Boca Raton, FL, USA, 2024; pp. 156–176. [Google Scholar]
- Yuan, J.; Peng, J.; Yan, Q.; He, G.; Xiang, H.; Liu, Z. Deep reinforcement learning-based energy consumption optimization for Peer-to-Peer (P2P) communication in wireless sensor networks. Sensors 2024, 24, 1632. [Google Scholar] [CrossRef]
- Jerbi, W.; Cheikhrouhou, O.; Guermazi, A.; Trabelsi, H. An enhanced MSU-TSCH scheduling algorithms for industrial wireless sensor networks. Concurr. Comput. Pract. Exp. 2024, 36, e7938. [Google Scholar] [CrossRef]
- Khiar, A.; Mazouzi, S.; Benaboud, R.; Haouassi, H. Binary Tuna Swarm Optimization Algorithm-Based Feature Selection for Intrusion Detection Systems. J. Commun. Softw. Syst. 2025, 21, 383–393. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Xue, G.; Bai, F.; Huang, S. Fast Non-Dominated Sorting Tuna Swarm Optimization Algorithm (FNS-TSO): Time-Energy-Impact Multi-Objective Optimization of Underwater Manipulator Trajectories. J. Mar. Sci. Eng. 2025, 13, 916. [Google Scholar] [CrossRef]
- Periasamy, J.K.; Mallick, S.; Chitti, S.; Sivasakthi, S.; Kv, B.; Puliyanjalil, E. Tuna Swarm Algorithm Based Robust Node Localization Scheme in Wireless Communication Networks. Int. Res. J. Multidiscip. Scope 2025, 6, 1426–1437. [Google Scholar] [CrossRef]
- Kannan, S.K.; Diwekar, U. An enhanced particle swarm optimization (PSO) algorithm employing quasi-random numbers. Algorithms 2024, 17, 195. [Google Scholar] [CrossRef]


| Algorithm Category | Algorithm Name | Network Lifetime |
|---|---|---|
| ACO-based | ACO Basic Routing [4] | 10% improvement compared to EEABR |
| ACO Mobile Sink [5] | 40–150% longer than WRP(uniform) | |
| PSO-based | PSO Lifetime Max [9] | 1800 rounds, 50% higher than PSOK |
| GA-based | GABLQ (Link Quality) [12] | 1428 rounds, 16.8% higher than LEACH-IMPT |
| Traditional | LEACH | 100 rounds |
| LEACH-IMPT | 600 rounds | |
| NWPSO | 837 rounds | |
| PSOK | 1200 rounds |
| Algorithm | Parameter | Value | Description |
|---|---|---|---|
| GA | Population Size | 100 | Number of individuals in each generation |
| Maximum Generations | 100 | Stopping criterion | |
| Crossover Rate | 0.85 | Probability of applying crossover | |
| Mutation Rate | 0.02 | Probability of bit mutation per individual | |
| PSO | Swarm Size | 50 | Number of particles |
| Maximum Iterations | 100 | Stopping criterion | |
| Cognitive Coefficient () | 1.5 | Individual learning factor | |
| Social Coefficient () | 1.5 | Social learning factor | |
| Inertia Weight () | 0.7–0.4 | Linearly decreasing from 0.7 to 0.4 | |
| ACO | Number of Ants | 50 | Population size |
| Maximum Iterations | 100 | Stopping criterion | |
| Pheromone Influence () | 1 | Weight of pheromone trail | |
| Heuristic Influence () | 2 | Weight of heuristic information | |
| Evaporation Rate () | 0.1 | Pheromone evaporation coefficient | |
| Initial Pheromone () | 0.5 | Starting pheromone level | |
| Q Constant | 100 | Pheromone deposit quantity | |
| EPSO | Swarm Size | 50 | Number of particles |
| Random Number Generation | Quasi-random | Halton Sequence | |
| Cognitive Coefficient () | 2 | Individual learning factor | |
| Social Coefficient () | 2 | Social learning factor | |
| Inertia Weight () | 0.75 | Constant | |
| TSO-LS | Population Size | 50 | Number of tuna in the swarm |
| Maximum Iterations | 100 | Stopping criterion | |
| Spiral Constant () | 0.7 | Controls spiral foraging intensity | |
| Strategy Parameter (z) | 0.05 | Probability threshold for spiral strategies | |
| , | 0.6, 1 | Formula (19) | |
| 6.1 | Formula (21) |
| GA | PSO | ACO | EPSO | TSO-LS | |
|---|---|---|---|---|---|
| Energy Efficiency | 0.75 | 0.80 | 0.78 | 0.84 | 0.85 |
| Average Delay | 12 ms | 11 ms | 11.5 ms | 10.9 ms | 10.5 ms |
| Throughput (Mbps) | Average Energy Consumption (mJ) | |
|---|---|---|
| ACO | 5.2 | 0.36 |
| EPSO | 5.4 | 0.32 |
| TSO-LS | 5.5 | 0.32 |
| PSO | 5.3 | 0.34 |
| GA | 5.1 | 0.41 |
| Iterations to Convergence | Final Fitness Value | |
|---|---|---|
| TSA | 154 | 0.918 |
| TSA + OUM | 110 | 0.939 |
| TSA + ESS | 128 | 0.942 |
| TSA + PDM | 156 | 0.945 |
| TSO-LS | 98 | 0.951 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.; Yang, Z.; Shen, Y.; Wang, Y. An Enhanced Tuna Swarm Algorithm for Link Scheduling Strategies in Wireless Sensor Networks. Mathematics 2025, 13, 3905. https://doi.org/10.3390/math13243905
Hong S, Yang Z, Shen Y, Wang Y. An Enhanced Tuna Swarm Algorithm for Link Scheduling Strategies in Wireless Sensor Networks. Mathematics. 2025; 13(24):3905. https://doi.org/10.3390/math13243905
Chicago/Turabian StyleHong, Sunyan, Zhe Yang, Yang Shen, and Yujian Wang. 2025. "An Enhanced Tuna Swarm Algorithm for Link Scheduling Strategies in Wireless Sensor Networks" Mathematics 13, no. 24: 3905. https://doi.org/10.3390/math13243905
APA StyleHong, S., Yang, Z., Shen, Y., & Wang, Y. (2025). An Enhanced Tuna Swarm Algorithm for Link Scheduling Strategies in Wireless Sensor Networks. Mathematics, 13(24), 3905. https://doi.org/10.3390/math13243905





