Ship Spare Parts Optimization Model Based on Ideal Point Method and Improved Ant Colony Algorithm
Abstract
1. Introduction
2. Problem Description and Basic Assumptions
2.1. Problem Description
2.2. Model Assumptions
2.3. Mathematical Problem Description
2.3.1. Decision Variables
2.3.2. System Reliability Function
2.3.3. System Total Cost Function
2.3.4. Constraint Conditions
3. Ship Spare Parts Optimization Model
3.1. Traditional R/C Model
3.2. IPM Model
3.2.1. Clarifying Dual Objectives
3.2.2. Determining Ideal Point and Anti-Ideal Point
3.2.3. Normalization Processing
3.2.4. Weighted Euclidean Distance Calculation
3.2.5. Constructing Single-Objective Function
4. Ship Spare Parts Optimization Algorithm Design
4.1. Multi-Dimensional Pheromone Matrix Design
4.2. Adaptive Pheromone Update Mechanism
- The R/C Model (Maximize Cost-Effectiveness Ratio) pheromone increment is proportional to the cost-effectiveness ratio:
- 2.
- The IPM Model (Minimize Objective Deviation) pheromone increment is inversely proportional to fitness:
4.3. Constraint Handling Strategy Innovation Design
- (1)
- Basic Constraint Filtering: This step filters out obviously infeasible solutions, significantly enhancing computational efficiency by ensuring complete constraint satisfaction and preventing boundary-violating solutions.
- (2)
- Global Constraint Handling: This stage repairs solutions based on cost-effectiveness selections, ensuring that the repaired solutions continue to satisfy all other constraints.
- (3)
- Performance Constraint Optimization: The marginal contribution of each spare part to system reliability is quantified, prioritizing the addition of spare parts that offer the greatest unit cost reliability improvement. Protection mechanisms are incorporated by setting increment limits to avoid ineffective repairs.
5. Simulation and Analysis
5.1. Simulation Parameters
5.2. Simulation Process
5.3. Simulation Results
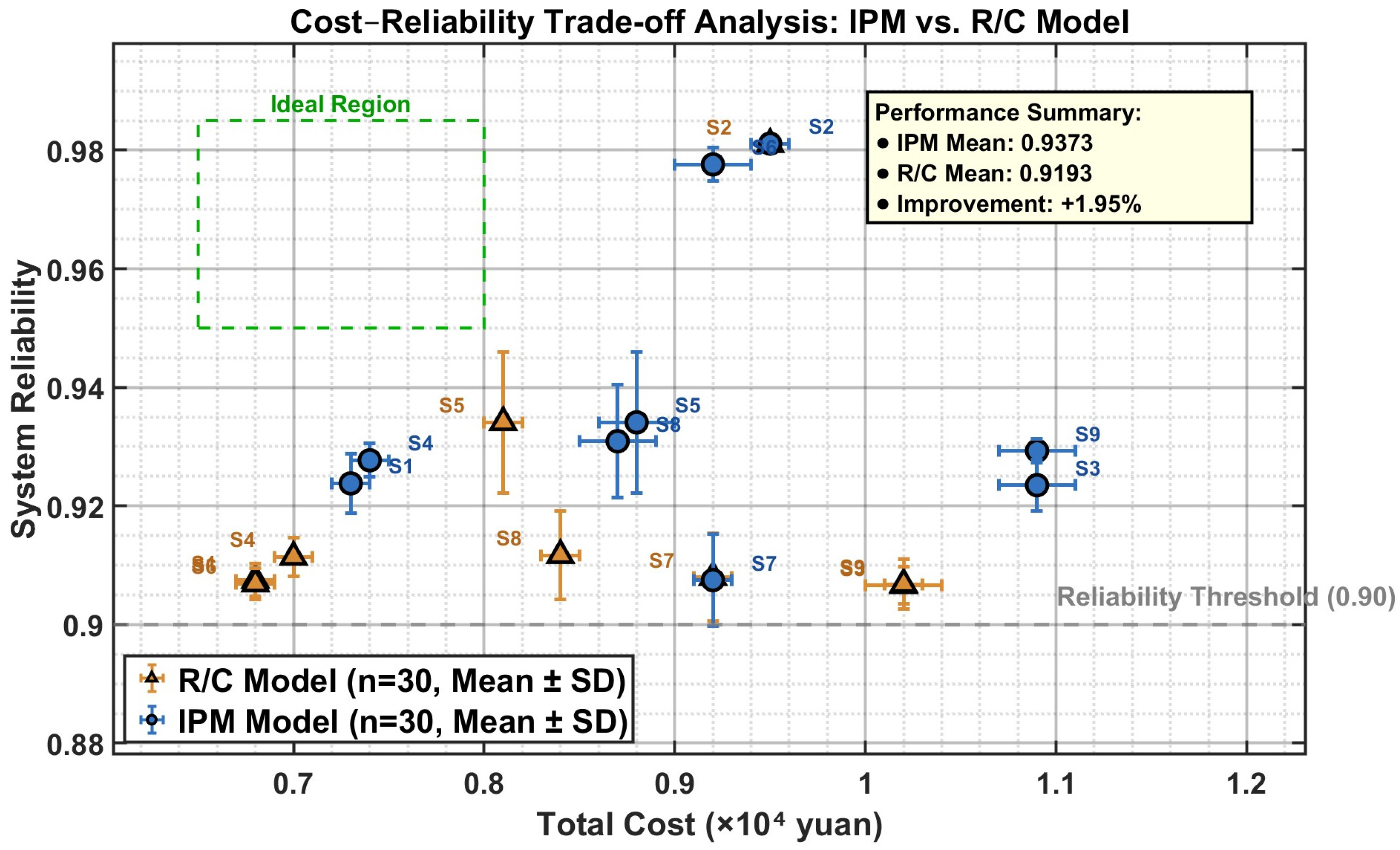
5.4. Results Analysis
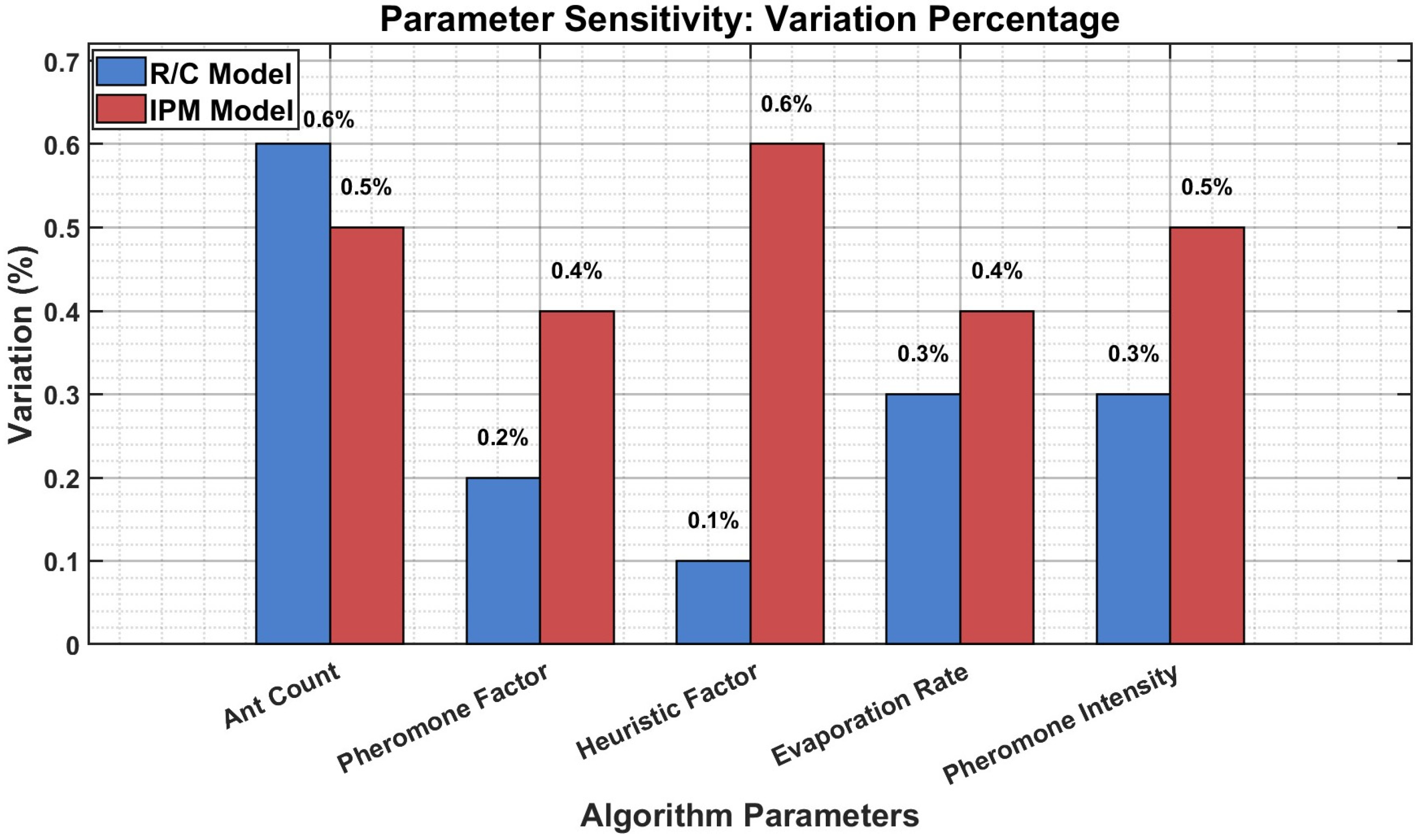
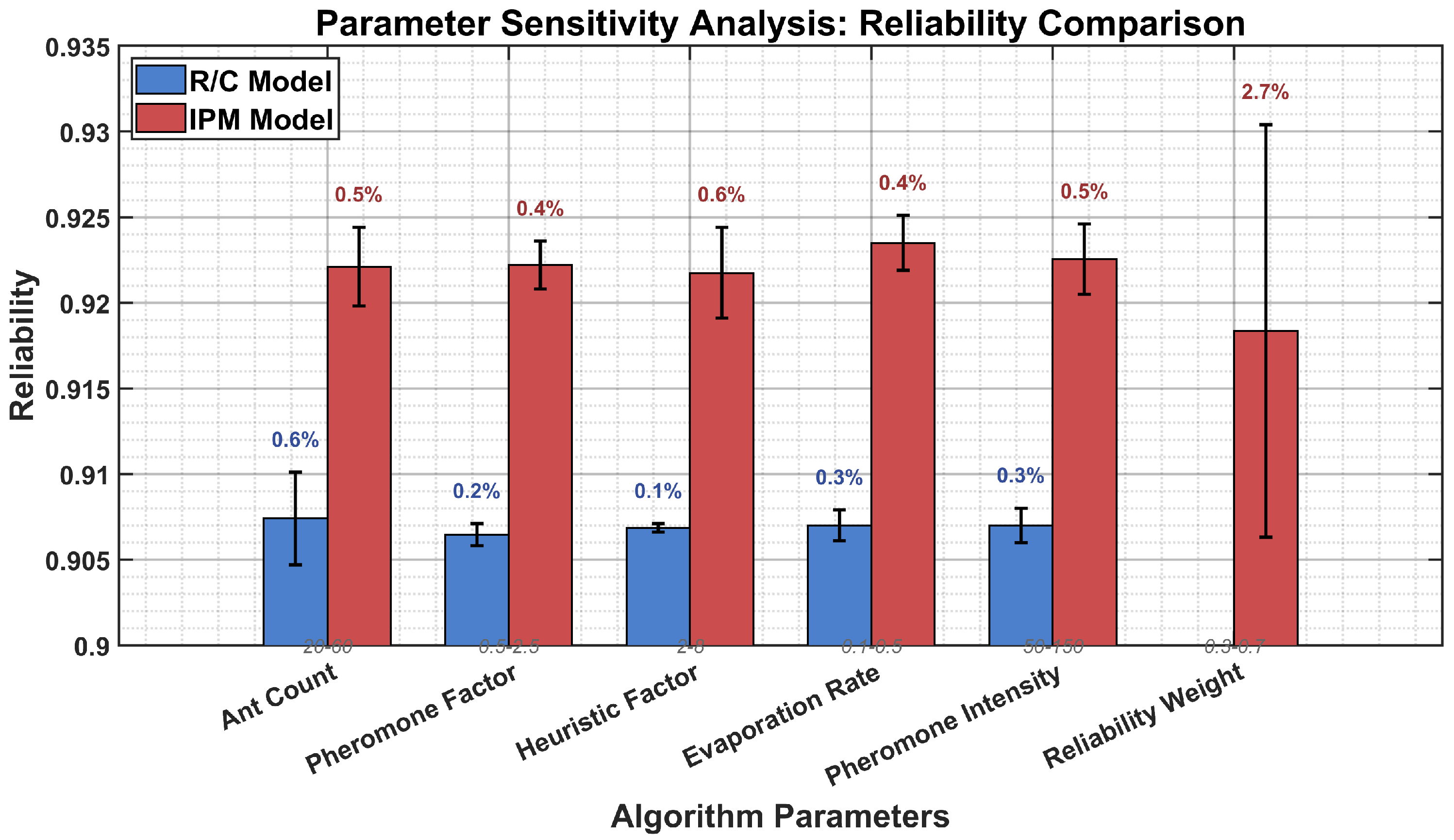
5.5. Parameter Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| Algorithm A1. Three-level Constraint Handling Mechanism |
| function [best_solution, best_reliability, best_cost] = RC_Model_ACO() Initialize pheromone matrix; Set best_ratio to zero; while not converged do for each ant do Generate feasible solution satisfying: - Minimum quantity constraints - Total quantity constraint - Minimum reliability requirement end Calculate system reliability R using Poisson distribution; Calculate total cost C from unit costs; Compute R/C ratio as fitness value; if R/C ratio > best_ratio then Update best solution; Update best_ratio; Record reliability and cost; end end Calculate pheromone increment for each solution; Update pheromone matrix based on solution quality; Apply pheromone evaporation; end return best_solution, best_reliability, best_cost; end |
Appendix A.2
| Algorithm A2. Improved Ant Colony Algorithm for Spare Parts Optimization |
| function [best_solution, best_reliability, best_cost] = Ideal_Point_Method_ACO() Determine ideal point (maximum reliability, minimum cost); Calculate normalization bounds for objectives; Initialize pheromone matrix; Set best_distance to infinity; while not converged do for each ant do Generate feasible solution satisfying: - Minimum quantity constraints - Total quantity constraint - Minimum reliability requirement end Calculate system reliability R using Poisson distribution; Calculate total cost C from unit costs; Normalize reliability to [0, 1] range; Normalize cost to [0, 1] range; Calculate weighted Euclidean distance to ideal point: distance = sqrt(w1 × (R_normalized - R_ideal)2 + w2 × (C_normalized - C_ideal)2); end if distance < best_distance then Update best solution; Update best_distance; Record reliability and cost; end end Calculate pheromone increment inversely proportional to distance; Update pheromone matrix based on solution quality; Apply pheromone evaporation; end return best_solution, best_reliability, best_cost; end |
References
- Xiao, B.; Liu, C.; Jiang, T.J. Multi objective optimization of ship spare parts maintenance based on Improved Genetic Algorithm. E3S Web Conf. 2021, 253, 02016. [Google Scholar] [CrossRef]
- Wang, H.; Liu, H.; Shao, S.; Zhang, Z. Methodology of shipboard spare parts requirements based on whole part repair strategy. Mathematics 2024, 12, 3053. [Google Scholar] [CrossRef]
- Zhang, J.R. Research on spare parts optimization method for complex electronic equipment based on monte carlo simulation. Consum. Electron. 2024, 9, 6–12. [Google Scholar]
- Dong, Z.Q.; Tang, S.K.; Li, C.Y.; Nie, L.; Zhou, X.D.; Ding, S.T.; Fan, Y.Y. Configuration method of naval gun equipment spare parts based on multi-agent simulation. Chin. J. Ship Res. 2022, 17, 228–234. [Google Scholar]
- Li, W.; Li, H.J.; Li, H. Optimization of spare parts configuration scheme for ship equipment based on multi-agent simulation. Proc. SPIE 2024, 13445, 134452L. [Google Scholar]
- Fu, L.Y.; Liu, C.Y.; Dong, Q.; Tang, L.; Weng, X.H.; Xian, K. Research on multi-objective configuration optimization of ship spare with exponential distribution demand. In Proceedings of the 2018 2nd International Conference on Management Engineering, Software Engineering and Service Sciences (ICMSS 2018), Wuhan, China, 13–15 January 2018. [Google Scholar]
- Li, Y.H.; Zhang, Y.; Yong, Q.; Chen, Z.M. Research on optimization method of ship spare parts allocation based on improved discrete crow search algorithm. Commun. Comput. Inf. Sci. 2024, 2139, 211–221. [Google Scholar]
- Liu, G.; Zhong, X.J.; Dong, P. Research on optimization model of ship electronic equipment spare parts based on genetic algorithm and neural network. Ship Sci. Technol. 2008, 30, 138–142. [Google Scholar]
- Jiang, W.; Sheng, W.; Yang, L.; Fan, Y.L. Optimization configuration of phased array radar spare parts under condition-based maintenance. Syst. Eng. Electron. 2017, 39, 2052–2057. [Google Scholar]
- Mei, D.; Wang, G.B.; Ye, Z.H.; Shen, J.; Feng, H. Optimization configuration of spare parts for motor control and power distribution systems. Electr. Mach. Control Appl. 2018, 45, 41–45, 63. [Google Scholar]
- Gong, L.X.; Fan, Y.M.; Liang, J.L.; Xiao, M.L.; Lei, B.W. Cost and availability-oriented ship redundant system and spare parts inventory optimization model. J. Nav. Univ. Eng. 2025, 37, 1–8. [Google Scholar]
- Tang, Z.; Lin, M.C.; Wang, C.Y. Critical Evaluation and Optimal Allocation Model of Ship Spare Parts. In Proceedings of the 4th International Conference on Modelling, Simulation and Applied Mathematics (MSAM 2020), Wuhan, China, 12–13 January 2020. [Google Scholar]
- Zhou, L.; Meng, J.; Li, Y.; Li, W. Optimization method for radiation interference cancellation equipment of ship spare parts configuration with criticality under multiple constraints. Syst. Eng. Electron. 2020, 42, 365–373. [Google Scholar]
- Dong, Z.Q.; Tang, S.K.; Zhou, X.D.; Nie, L.; Fan, Y.Y. Optimization configuration method of ship accompanying spare parts based on tabu search. Ship Eng. 2023, 45, 138–143. [Google Scholar]
- Zhang, R.; Liu, C.L.; Shao, H.W.; Zhou, H.F.; Zhang, J. Multi-constraint ship spare parts configuration optimization based on improved particle swarm algorithm. Ship Electron. Eng. 2023, 43, 102–108. [Google Scholar]
- Li, Z.Q.; Xu, T.X.; Dong, Q.; Zeng, X.; Liu, Y.D. Optimization configuration method for ship-borne spare parts based on PDF-CDF. Fire Control Command. Control. 2018, 43, 17–21. [Google Scholar]
- Zhai, Y.L.; Qi, R.; Shao, S.S. Ship spare parts utilization rate calculation and application under periodic supply conditions. Comput. Simul. 2025, 42, 16–21. [Google Scholar]
- Ruan, M.Z.; Qian, C.; Wang, R.; Wang, J.L. Ship formation spare parts configuration optimization under regular support mode. Syst. Eng. Theory Pract. 2018, 38, 2441–2448. [Google Scholar]
- Chai, Z.J.; Wang, Z.B. Application of improved particle swarm algorithm in ship spare parts configuration optimization problem. Comput. Digit. Eng. 2021, 49, 493–495+588. [Google Scholar]
- Li, Q.J. Ship electronic equipment spare parts optimization model based on ant colony algorithm and extreme learning machine. Ship Sci. Technol. 2022, 44, 158–161. [Google Scholar]
- Sha, J.; Leng, J.; Mao, H.; Pei, J.; Diao, K. Research Progress in Predictive Maintenance of Offshore Platform Structures Based on Digital Twin Technology. J. Mar. Sci. Appl. 2025, 24, 877–899. [Google Scholar] [CrossRef]
- Lv, Z.; Lv, H.; Fridenfalk, M. Digital Twins in the Marine Industry. Electronics 2023, 12, 2025. [Google Scholar] [CrossRef]
- Kalafatelis, A.S.; Nomikos, N.; Giannopoulos, A.; Alexandridis, G.; Karditsa, A.; Trakadas, P. Towards Predictive Maintenance in the Maritime Industry: A Component-Based Overview. J. Mar. Sci. Eng. 2025, 13, 425. [Google Scholar] [CrossRef]
- Budimir, D.; Medić, D.; Ružić, V.; Kulej, M. Integrated Approach to Marine Engine Maintenance Optimization: Weibull Analysis, Markov Chains, and DEA Model. J. Mar. Sci. Eng. 2025, 13, 798. [Google Scholar] [CrossRef]
- Karkaria, V.; Tsai, Y.; Chen, Y.; Chen, W. An optimization-centric review on integrating artificial intelligence and digital twin technologies in manufacturing. Eng. Optim. 2025, 57, 161–207. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, K.; Gao, S. Research on ship spare parts optimization model based on cost-effectiveness analysis. Electron. Des. Eng. 2016, 24, 1–4. [Google Scholar]


| (a) Sets and Indices. | ||
| Symbol | Description | |
| Index for spare part types, | ||
| Index for number of failures | ||
| (b) Model Parameters and Their Descriptions. | ||
| Symbol | Description | Unit |
| Unit price of spare part type | 104 yuan/piece | |
| Minimum cost at ideal point (IPM model) | 104 yuan | |
| Maximum cost at anti-ideal point (IPM model) | 104 yuan | |
| Upper limit of total cost | 104 yuan | |
| Total number of spare part types | − | |
| Lower limit of system reliability | − | |
| Maximum reliability at ideal point (IPM model) | − | |
| Minimum reliability at anti-ideal point (IPM model) | − | |
| Lower limit of total spare parts quantity | pieces | |
| Lower limit of spare parts quantity for type | pieces | |
| Upper limit of spare parts quantity for type | pieces | |
| Weight coefficient for cost objective (IPM model) | − | |
| Weight coefficient for reliability objective (IPM model, + = 1) | − | |
| (c) Decision Variables and Derived Quantities. | ||
| Symbol | Description | Unit |
| Total system cost function | 104 yuan | |
| Weighted Euclidean distance to ideal point (IPM model) | − | |
| System reliability function | − | |
| Spare parts quantity vector, | pieces | |
| Decision variable: quantity of spare parts type | pieces | |
| Normalized reliability deviation (IPM model) | − | |
| Normalized cost deviation (IPM model) | − | |
| Spare Part Type | Unit Price (104 Yuan) | Failure Rate (Times/Day) |
|---|---|---|
| Satcom Module | 0.05 | 0.01 |
| HF Radar Processor | 0.02 | 0.02 |
| Relay Controller | 0.17 | 0.015 |
| ECM Module | 0.03 | 0.025 |
| Scenario Number | Scenario Name | Failure Rate Change | Mission Duration Change | Cost Change | Various Spare Parts Minimum Configuration Changes | Reliability Requirement |
|---|---|---|---|---|---|---|
| 1 | Normal Conditions | - | - | - | - | 0.98 |
| 2 | High Reliability Requirement | - | - | - | - | - |
| 3 | Low Budget Conditions | - | - | 1.5 times | - | - |
| 4 | Satcom Module Scarcity | - | - | - | [3, 2, 1, 1] | - |
| 5 | Relay Controller Scarcity | - | - | - | [1, 2, 3, 1] | - |
| 6 | All-Type Spare Parts Constraint Enhancement | - | - | - | [2, 3, 2, 2] | - |
| 7 | Navigation Mission Extension | - | 1.5 times | - | - | - |
| 8 | Increased Failure Rate | 1.2 times | - | - | - | - |
| 9 | Core Component Price Fluctuation | - | - | Relay Controller cost: 0.34 million | [2, 3, 2, 2] | 0.98 |
| Symbol | Meaning | Value |
|---|---|---|
| Ant quantity | 40 | |
| Maximum iteration count | 100 | |
| Pheromone importance factor | 1.5 | |
| Heuristic factor importance | 5 | |
| Pheromone evaporation factor | 0.2 | |
| Pheromone increase intensity coefficient | 100 | |
| Spare part types | 4 | |
| Unit prices of spare parts (104 yuan) | [0.05, 0.02, 0.17, 0.03] | |
| Spare parts failure rates | [0.01, 0.02, 0.015, 0.025] | |
| Mission execution time (days) | 60 |
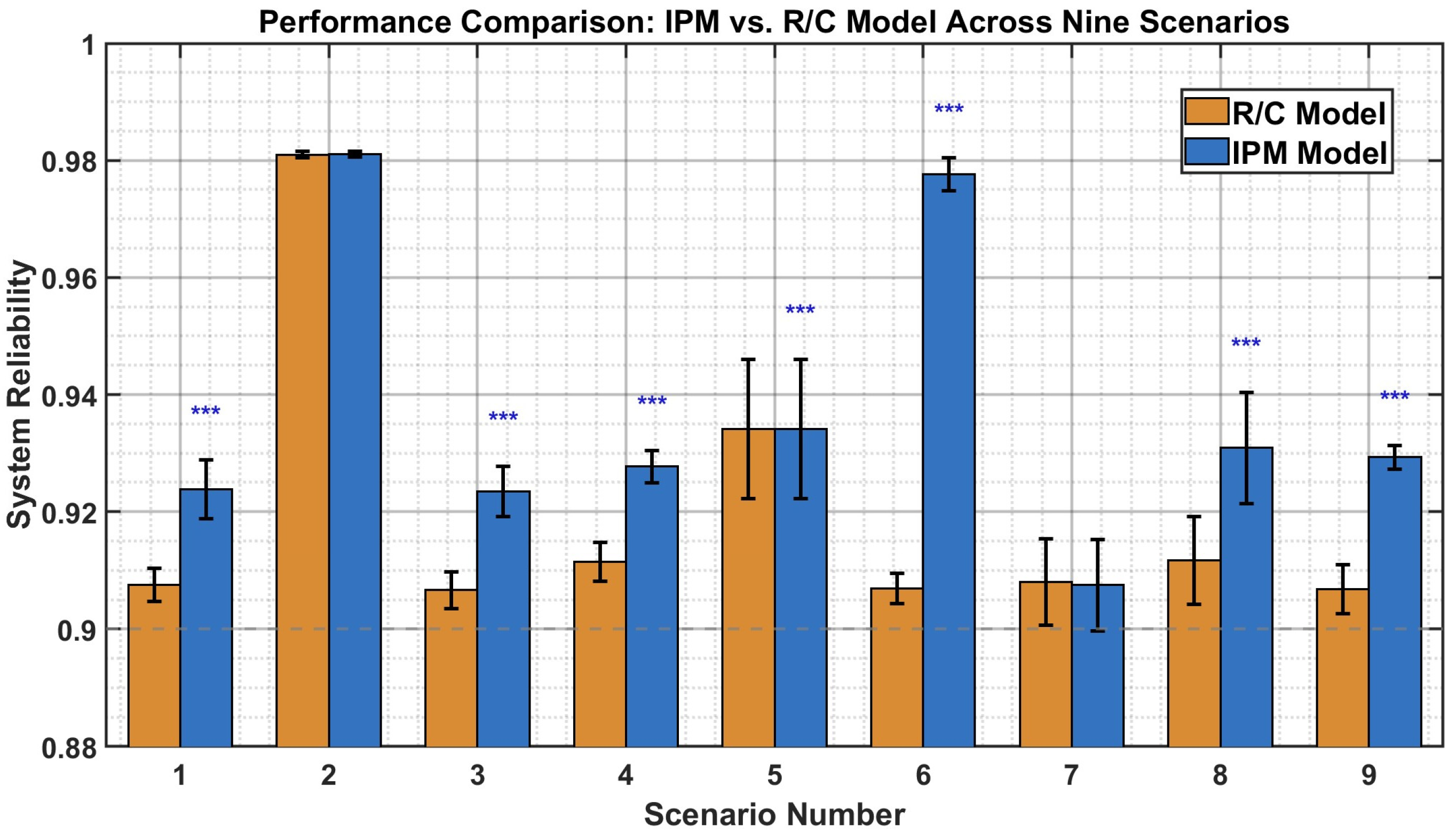
| Scenario | Method | Allocation [x1, x2, x3, x4] | Reliability | Cost (104 Yuan) | Objective |
|---|---|---|---|---|---|
| Scenario 1 | R/C | [3, 2, 1, 2] | 0.9075 ± 0.0028 | 0.68 ± 0.01 | 1.3315 ± 0.017 |
| IPM | [3, 3, 1, 2] | 0.9238 ± 0.0050 *** | 0.73 ± 0.01 | 0.1449 ± 0.001 | |
| Scenario 2 | R/C | [4, 4, 2, 3] | 0.9810 ± 0.0005 | 0.95 ± 0.01 | 1.0378 ± 0.010 |
| IPM | [4, 4, 2, 3] | 0.9811 ± 0.0005 | 0.95 ± 0.01 | 0.1735 ± 0.003 | |
| Scenario 3 | R/C | [3, 2, 1, 2] | 0.9066 ± 0.0031 | 1.02 ± 0.02 | 0.8916 ± 0.012 |
| IPM | [3, 3, 1, 2] | 0.9235 ± 0.0043 *** | 1.09 ± 0.02 | 0.1451 ± 0.002 | |
| Scenario 4 | R/C | [3, 2, 1, 2] | 0.9114 ± 0.0033 | 0.70 ± 0.01 | 1.3091 ± 0.017 |
| IPM | [3, 3, 1, 3] | 0.9277 ± 0.0028 *** | 0.74 ± 0.01 | 0.1317 ± 0.001 | |
| Scenario 5 | R/C | [3, 2, 3, 1] | 0.9341 ± 0.0119 | 0.81 ± 0.01 | 1.1552 ± 0.008 |
| IPM | [3, 3, 3, 2] | 0.9341 ± 0.0119 *** | 0.88 ± 0.02 | 0.0897 ± 0.001 | |
| Scenario 6 | R/C | [2, 3, 2, 2] | 0.9069 ± 0.0026 | 0.68 ± 0.01 | 1.3302 ± 0.020 |
| IPM | [3, 4, 3, 3] | 0.9776 ± 0.0028 *** | 0.92 ± 0.02 | 0.1226 ± 0.002 | |
| Scenario 7 | R/C | [4, 3, 2, 3] | 0.9080 ± 0.0074 | 0.92 ± 0.01 | 0.9881 ± 0.009 |
| IPM | [4, 3, 2, 3] | 0.9075 ± 0.0078 | 0.92 ± 0.01 | 0.1835 ± 0.001 | |
| Scenario 8 | R/C | [3, 3, 2, 2] | 0.9117 ± 0.0075 | 0.84 ± 0.01 | 1.0872 ± 0.005 |
| IPM | [3, 3, 2, 3] | 0.9309 ± 0.0095 *** | 0.87 ± 0.02 | 0.1668 ± 0.000 | |
| Scenario 9 | R/C | [3, 3, 1, 2] | 0.9068 ± 0.0042 | 1.02 ± 0.01 | 0.8906 ± 0.008 |
| IPM | [3, 3, 2, 2] | 0.9293 ± 0.0020 *** | 1.09 ± 0.02 | 0.1307 ± 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Sun, H.; Qi, R.; Li, X. Ship Spare Parts Optimization Model Based on Ideal Point Method and Improved Ant Colony Algorithm. Mathematics 2025, 13, 3862. https://doi.org/10.3390/math13233862
Ma T, Sun H, Qi R, Li X. Ship Spare Parts Optimization Model Based on Ideal Point Method and Improved Ant Colony Algorithm. Mathematics. 2025; 13(23):3862. https://doi.org/10.3390/math13233862
Chicago/Turabian StyleMa, Tianyu, Huiling Sun, Rui Qi, and Xiangjun Li. 2025. "Ship Spare Parts Optimization Model Based on Ideal Point Method and Improved Ant Colony Algorithm" Mathematics 13, no. 23: 3862. https://doi.org/10.3390/math13233862
APA StyleMa, T., Sun, H., Qi, R., & Li, X. (2025). Ship Spare Parts Optimization Model Based on Ideal Point Method and Improved Ant Colony Algorithm. Mathematics, 13(23), 3862. https://doi.org/10.3390/math13233862





