An Advanced Hybrid Optimization Algorithm for Vehicle Suspension Design Using a QUBO-SQP Framework
Abstract
1. Introduction
2. System Modeling and Problem Formulation
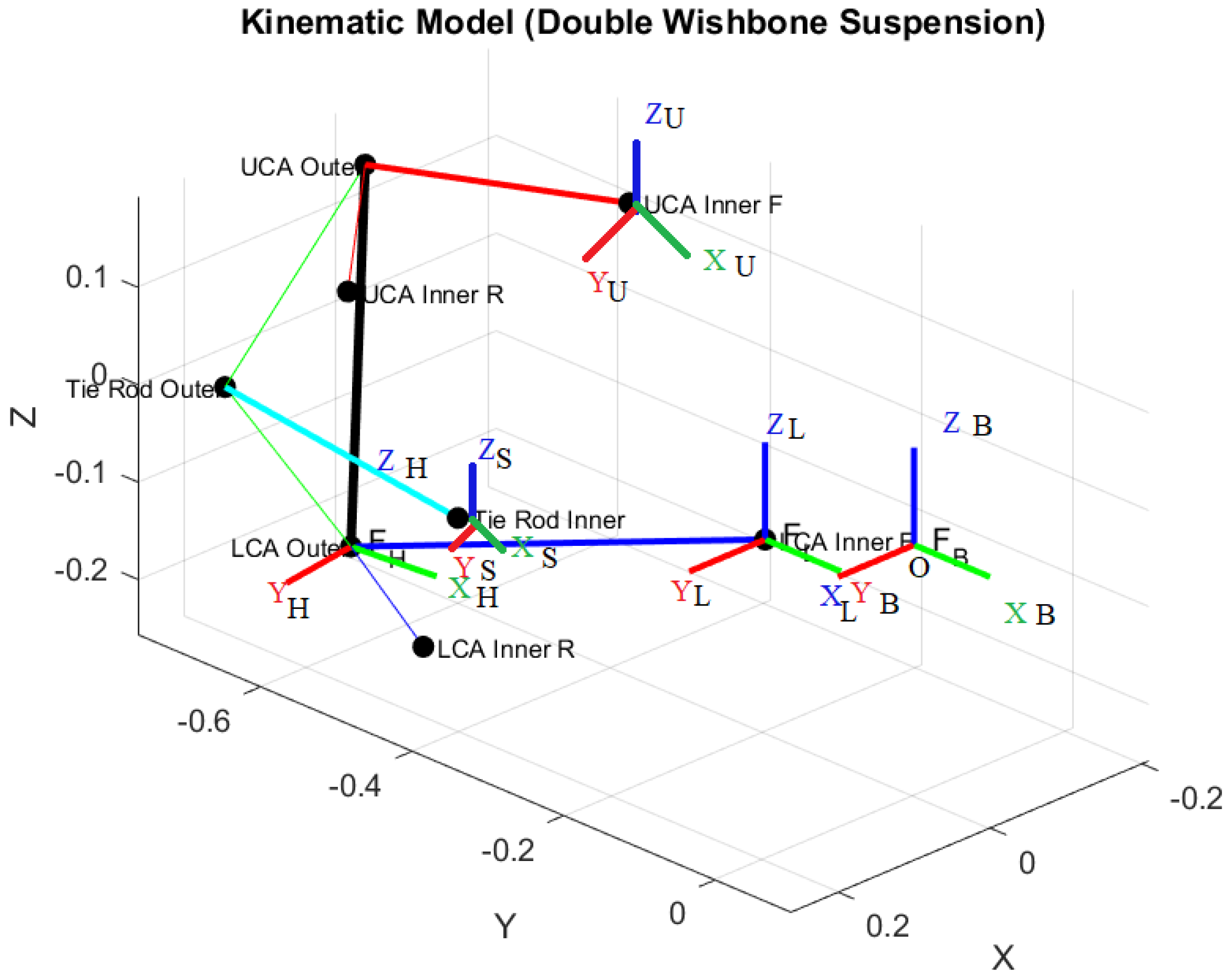
2.1. Kinematic Model of the Double-Wishbone Suspension
2.1.1. Geometric Hardpoints and Vectors
- , , : Global coordinates of the front-inner chassis pivots for the UCA, LCA, and TR, respectively.
- , : Vectors from the front-inner to the rear-inner chassis pivots for the UCA and LCA.
- : Vector from the LCA inner pivot () to the lower ball joint, defined in the LCA’s local frame.
- : Vector from the lower ball joint to the upper ball joint, defined in the Upright’s local frame.
- : Vector from the lower ball joint to the Tie Rod end, defined in the Upright’s local frame.
- : Vector from the UCA inner pivot () to the upper ball joint, defined in the UCA’s local frame.
- : Vector from the TR inner pivot () to the Tie Rod end, defined in the TR’s local frame.
2.1.2. Coordinate Systems
2.1.3. Mathematical Tools: Homogeneous Transformation Matrices
2.2. Loop-Closure Constraints
2.2.1. Upper Control Arm (UCA) Loop
2.2.2. Tie Rod (TR) Loop
2.3. Performance Objectives
2.4. Camber Angle (γ)
2.5. Caster Angle (τ)
2.6. The Formal Optimization Problem
3. The Hybrid QUBO-SQP Optimization Framework
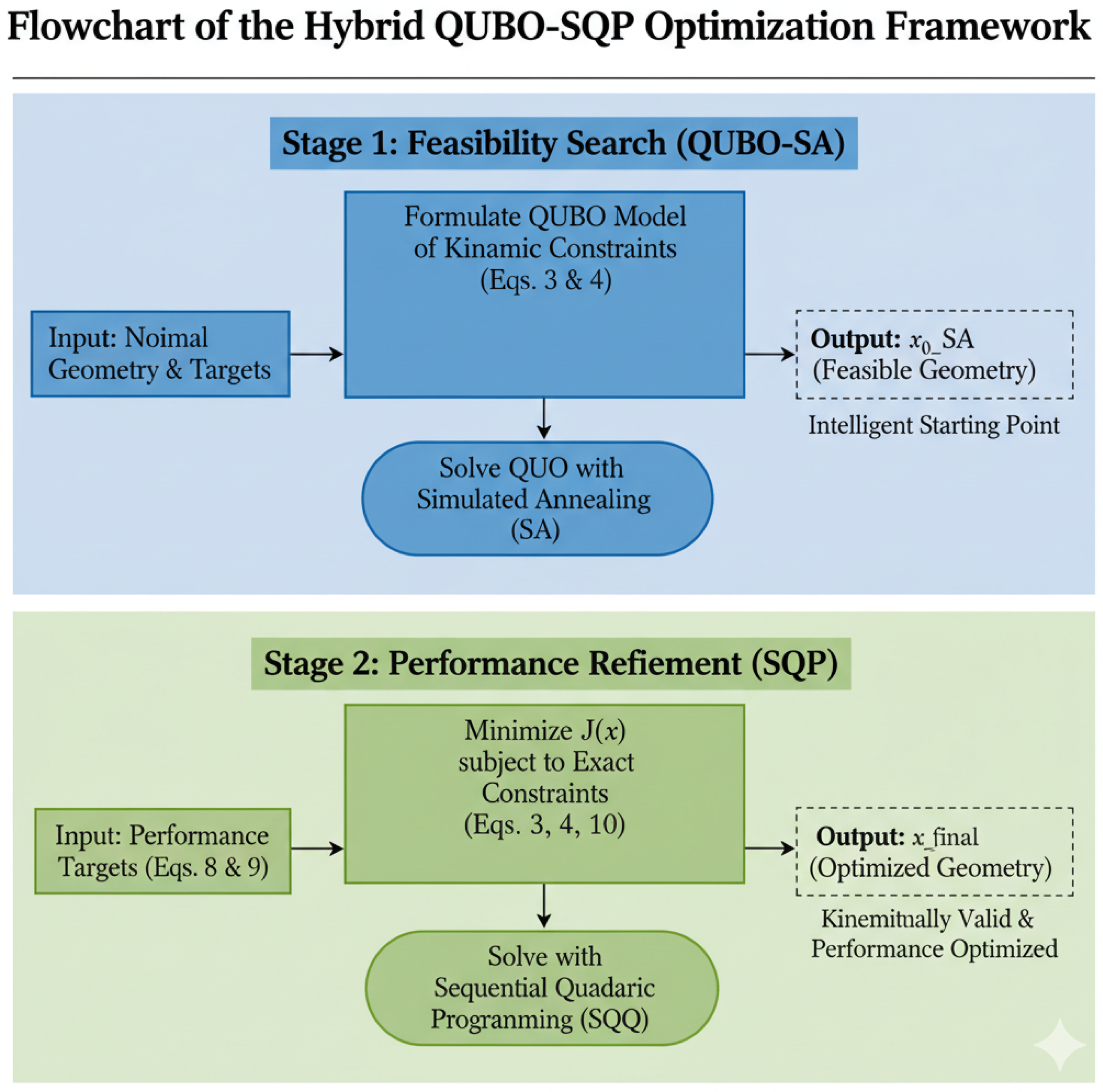
3.1. Framework Overview
- Input: The process begins with the nominal (initial) suspension geometry and the desired performance targets.
- Stage 1: Feasibility Search (QUBO-SA): The continuous design space is discretized into a binary representation. The nonlinear kinematic constraints (Equations (3) and (4)) are approximated as a quadratic polynomial of binary variables, forming a QUBO model. The QUBO is solved using a Simulated Annealer (SA) to find a binary solution that minimizes the constraint violation. This binary solution is decoded back into a continuous vector, . This vector represents a physically feasible, but not yet performance-optimized, suspension geometry.
- Stage 2: Performance Refinement (SQP): The feasible vector is used as the initial guess for the Sequential Quadratic Programming (SQP) optimizer. The SQP algorithm minimizes the high-precision performance objective (Equation (10)) subject to the exact, non-approximated trigonometric constraints (Equations (3) and (4)).
- Output: The final output, , is a suspension geometry that is both kinematically valid and performance-optimized.
3.2. Stage 1: QUBO Formulation for Feasibility Search
3.2.1. Discretization of Continuous Variables
3.2.2. Polynomial Approximation of Constraints
3.2.3. Hamiltonian Construction
3.2.4. Solver: Simulated Annealing (SA)
3.3. Stage 2: SQP for Performance Refinement
3.3.1. Algorithm: Sequential Quadratic Programming (SQP)
3.3.2. Problem Formulation for SQP
- Initial Guess:
- Objective Function: The exact performance objective from Equation (10), using the precise sin and cos functions.
| Algorithm 1 The Hybrid QUBO-SQP Framework |
| Require: Nominal geometry , Performance targets T Ensure: Optimized geometry 1: // Stage 1: Feasibility Search 2: Discretize continuous variables v into binary variables b using Equation (13). 3: Approximate kinematic constraints h to polynomials using Equations (14) and (15). 4: Construct QUBO Hamiltonian from using Equation (16). 5: 6: Decode back to continuous vector using Equation (13). 7: 8: // Stage 2: Performance Refinement 9: Set initial guess . 10: Define objective using Equation (10) (full precision). 11: Define constraints using Equations (3) and (4) (full precision). 12: 13: return |
4. Results and Discussion
4.1. Implementation Details
4.2. Optimization Performance and Convergence
4.2.1. Stage 1 (QUBO-SA Feasibility Search)
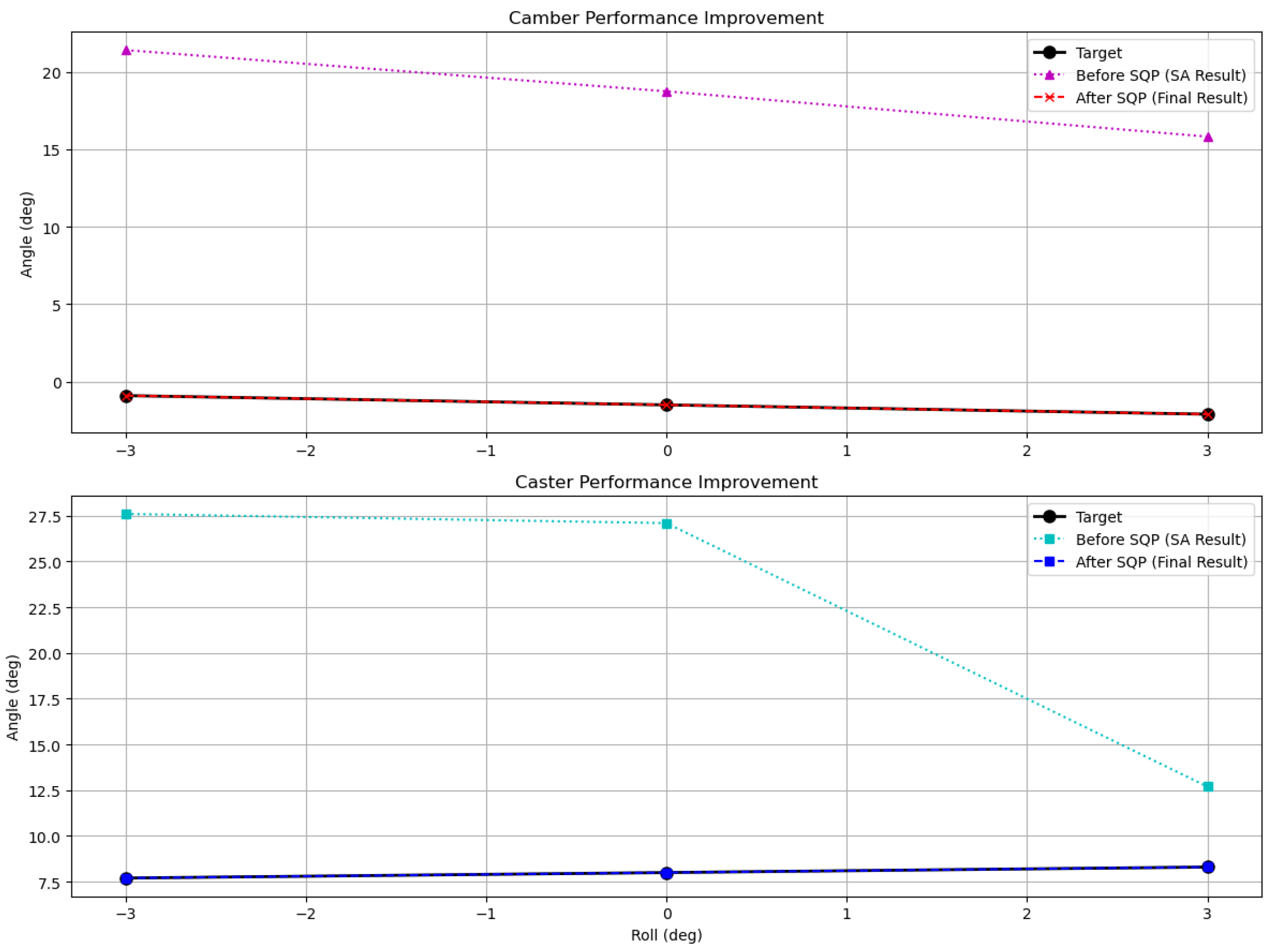
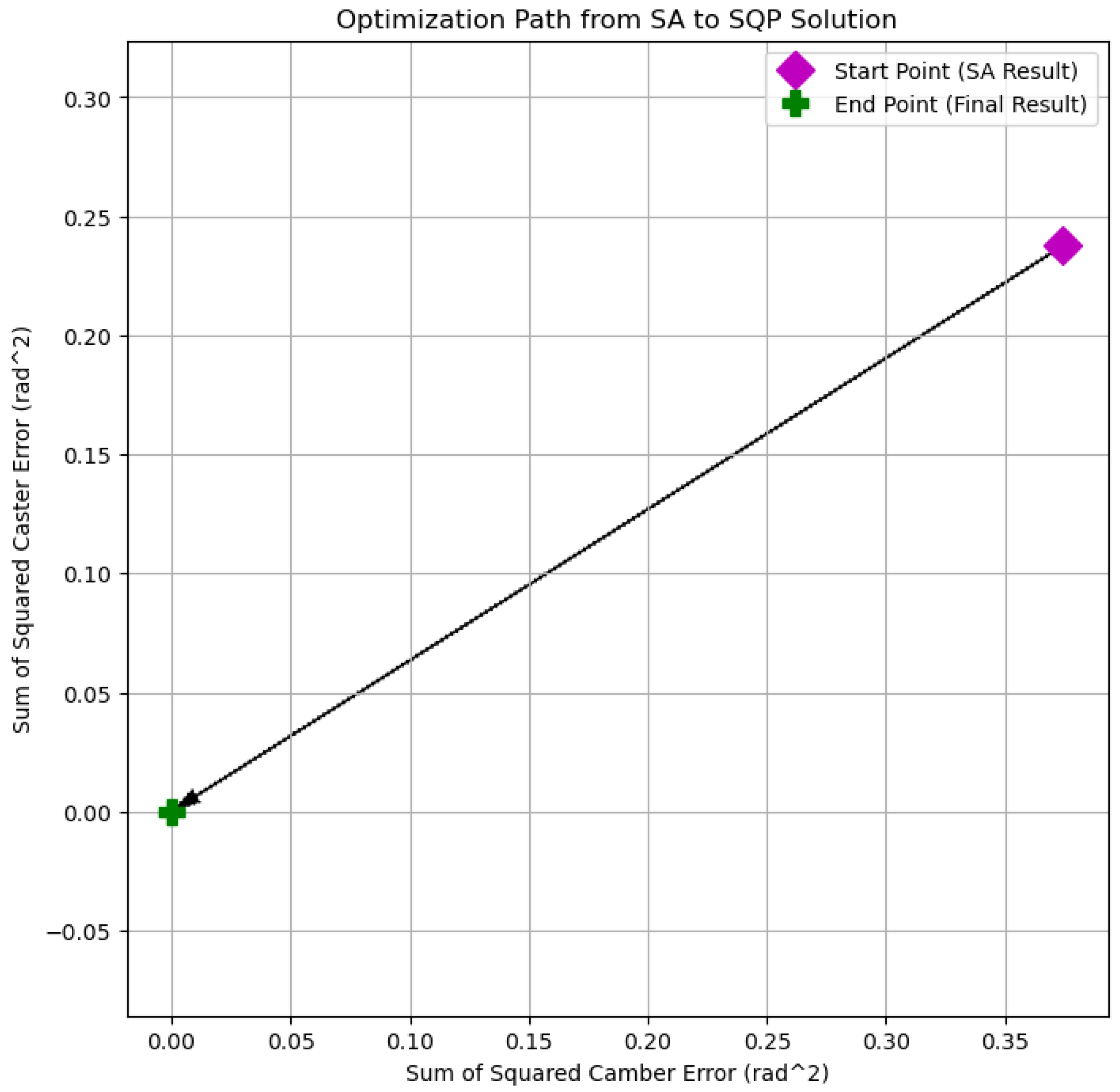
4.2.2. Stage 2 (SQP Performance Refinement)
4.3. Analysis of Geometric Changes
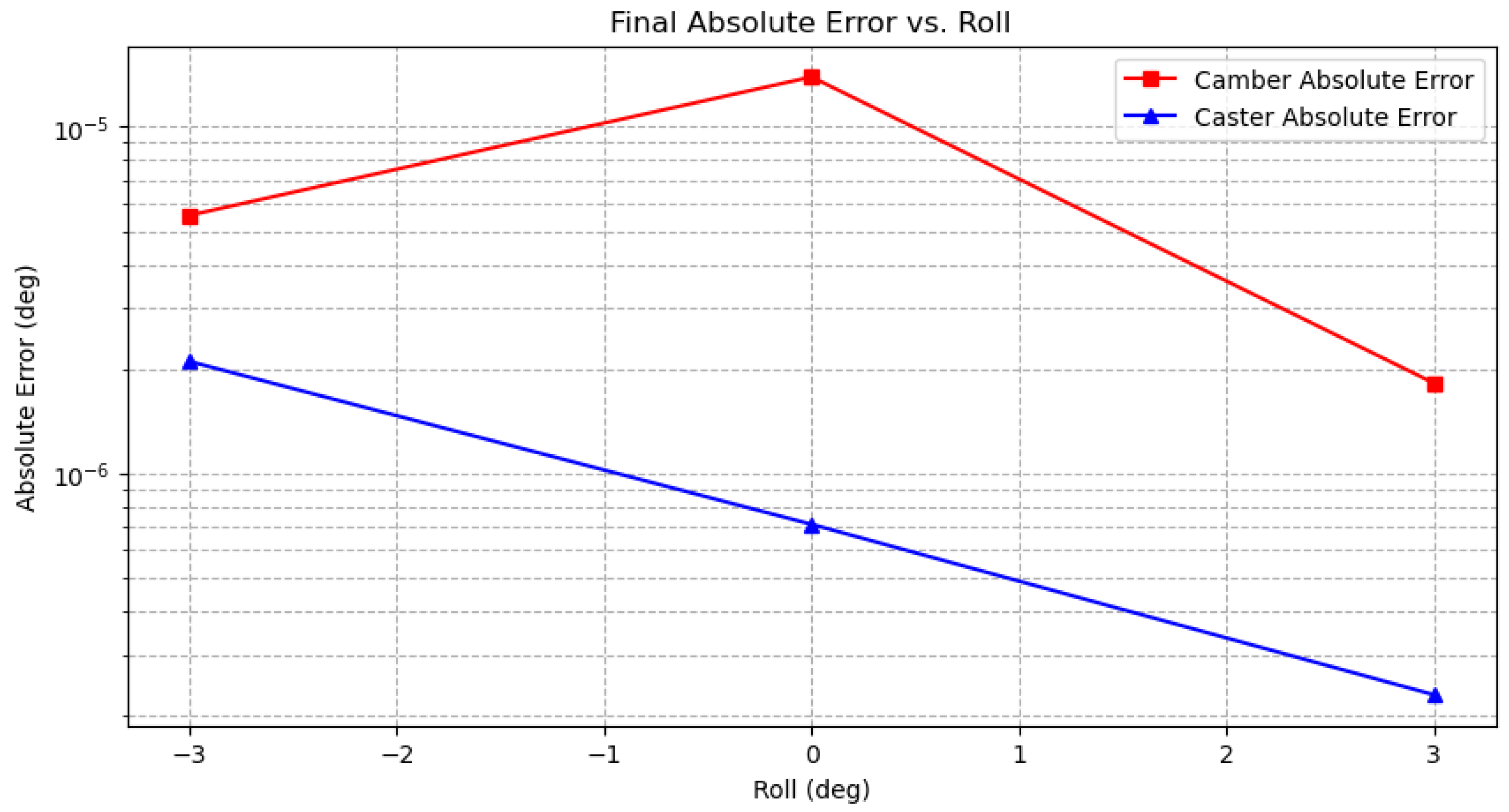
4.4. Analysis of Kinematic Performance
4.5. Comparison with State-of-the-Art Methods
4.6. Discussion of the Hybrid Approach
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QUBO | Quadratic Unconstrained Binary Optimization |
| SQP | Sequential Quadratic Programming |
| SA | Simulated Annealing |
| UCA | Upper Control Arm |
| LCA | Lower Control Arm |
| TR | Tie Rod |
| KPI | Key Performance Indicator |
| HT | Homogeneous Transformation |
| MSE | Mean Squared Error |
| NP-hard | Non-deterministic Polynomial-time hard |
Appendix A. Derivation of Abstract Geometric Vectors
Appendix A.1. Nominal Hard Point Data
Appendix A.2. Derivation of Optimization Vectors
- (UCA Front-Inner Pivot): Set directly from the global coordinates of the front UCA chassis pivot.
- (LCA Front-Inner Pivot): Set directly from the global coordinates of the front LCA chassis pivot.
- (TR Inner Pivot): Set directly from the global coordinates of the Tie Rod inner pivot.
- (UCA Rear Pivot Vector): The vector from the front to the rear UCA chassis pivot.
- (LCA Rear Pivot Vector): The vector from the front to the rear LCA chassis pivot.
- (UCA Outboard Vector, Local Frame): The vector from the UCA’s front-inner pivot to its outer ball joint. In the nominal state (zero rotation), this is defined in the global frame.
- (LCA Outboard Vector, Local Frame): The vector from the LCA’s front-inner pivot to its outer ball joint.
- (TR Outboard Vector, Local Frame): The vector from the TR’s inner pivot to its outer end.
- (Upright UCA Vector, Local Frame): The vector defining the location of the UCA ball joint relative to the LCA ball joint, representing the upper part of the upright.
- (Upright TR Vector, Local Frame): The vector defining the location of the TR ball joint relative to the LCA ball joint, representing the steering arm of the upright.
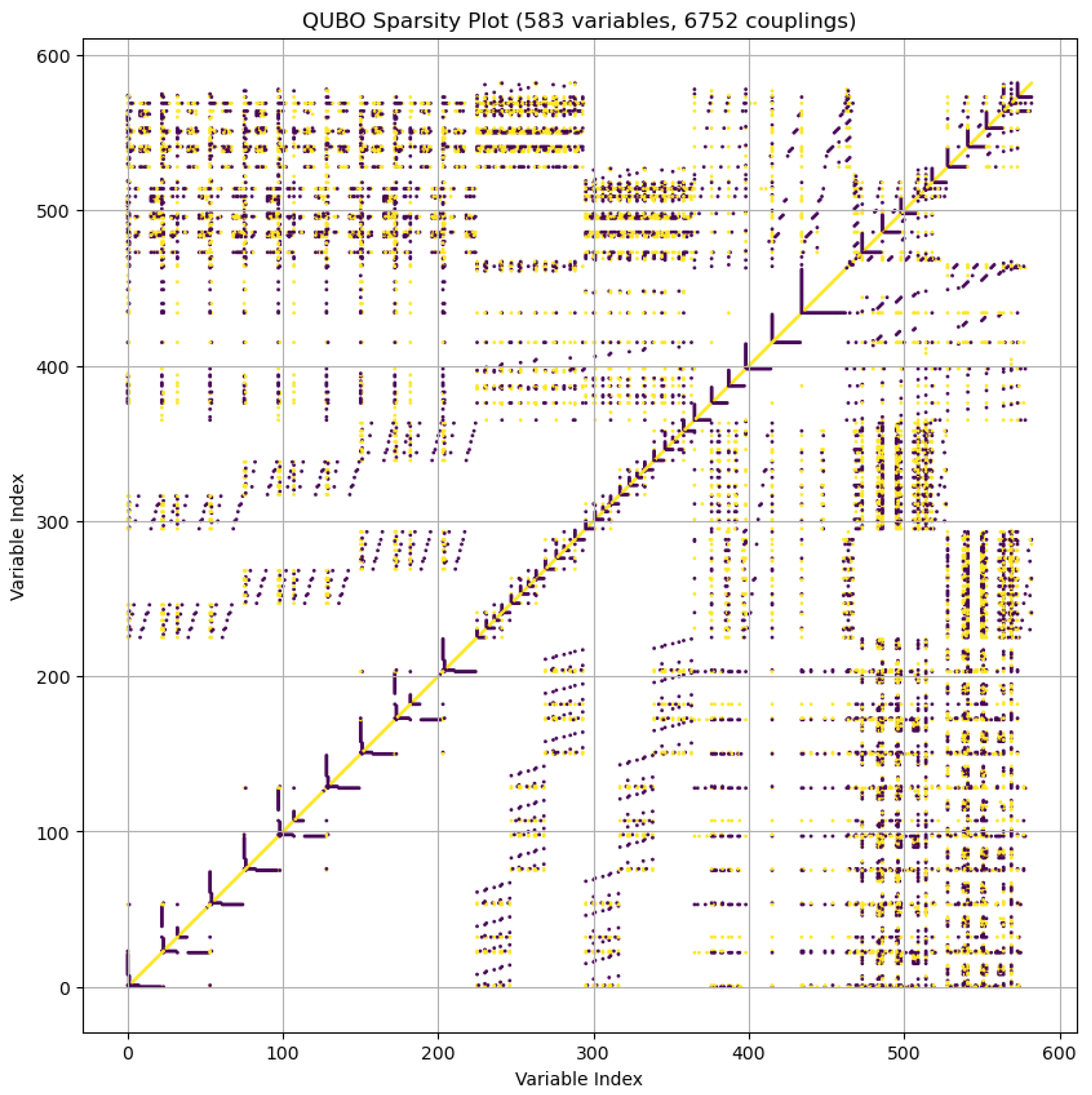
Appendix B. QUBO Model Size and Sparsity
Appendix B.1. Total Binary Variables
- Geometric Variables: binary variables.
- Angle Variables: binary variables.
Appendix B.2. QUBO Matrix Couplings
References
- Arshad, M.W.; Lodi, S. Optimization of Double Wishbone Suspension: Evaluating the Performance of Classes of Algorithms. In Proceedings of the 2024 International Conference on Applied Mathematics & Computer Science (ICAMCS), Venice, Italy, 28–30 September 2024; IEEE: New York, NY, USA, 2024; pp. 156–161. [Google Scholar] [CrossRef]
- Singh, A.; Pawar, S.; Soundalkar, M.; Ali, M.A. Design Optimization of the Control Arms of a Double Wishbone Suspension System Using Topological Approach. Int. J. Sci. Res. Eng. Manag. 2024, 8, IJSREM31250. [Google Scholar] [CrossRef]
- Wagh, S.Y.; Nandi, E. Design and Analytical Calculations of Double Wishbone for Formula Student Race Car. Int. J. Eng. Res. Technol. 2020, 9, 1029–1033. [Google Scholar] [CrossRef]
- Niu, Z.; Liu, S.; Li, B.; Pan, Z.; Wang, R. Explicit Solution to the Nonlinear Geometry of Double Wishbone Suspension by Decoupling Steering and Wheel Jumping DOF. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 1495–1504. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.; Pan, F.; Wang, S.; Ge, X. Multi-objective optimization study of vehicle suspension based on minimum time handling and stability. Proc. IMechE Part D 2020, 234, 2355–2363. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Z. Mathematical Modeling and Nonlinear Analysis of Stiffness of Double Wishbone Independent Suspension. J. Mech. Sci. Technol. 2021, 35, 5351–5357. [Google Scholar] [CrossRef]
- Ashtekar, V.; Bandyopadhyay, S. Forward Dynamics of the Double-Wishbone Suspension Mechanism Using the Embedded Lagrangian Formulation. In Mechanism and Machine Science: Select Proceedings of Asian MMS 2018; Springer: Singapore, 2020; pp. 843–859. [Google Scholar] [CrossRef]
- Upadhyay, P.; Deep, M.; Dwivedi, A.; Agarwal, A.; Bansal, P.; Sharma, P. Design and analysis of double wishbone suspension system. In Proceedings of the International Conference on Mechanical and Energy Technologies (ICMET 2019), Greater Noida, India, 7–8 November 2019; IOP Publishing: Bristol, UK, 2020; Volume 748, p. 012020. [Google Scholar] [CrossRef]
- Garg, S.; Dudeja, S.; Gupta, S.; Rastogi, V. Optimization of a Double Wishbone Suspension Geometry for Off-road Vehicles using Genetic Algorithm and Machine Learning. In Proceedings of the 2022 13th International Conference on Mechanical and Aerospace Engineering (ICMAE), Bratislava, Slovakia, 20–22 July 2022; IEEE: New York, NY, USA, 2022; pp. 472–477. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, Y.; Gao, D.; Pan, T.; Yang, J. Serial Combinational Optimization Method for Double Wishbone Suspension’s Pseudo Damage Improvement. Struct. Multidiscip. Optim. 2023, 66, 122. [Google Scholar] [CrossRef]
- Kulkarni, V.; Jadhav, A.; Basker, P. Finite Element Analysis and Topology Optimization of Lower Arm of Double Wishbone Suspension Using RADIOSS and Optistruct. Int. J. Sci. Res. 2014, 3, 639–643. [Google Scholar]
- Raikar, D.; Metar, M.; Attal, H. Design and Static Stress Analysis of Double Wishbone Suspension. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 249–257. [Google Scholar] [CrossRef]
- Metar, M. Structural Analysis of Double-Wishbone Suspension System. Int. J. Res. Appl. Sci. Eng. Technol. 2021, 9, 1681–1685. [Google Scholar] [CrossRef]
- Kumar, G.A.; Manepalli, P.; Narendran, R. Design optimization of double wishbone suspension system for motorcycle. In Proceedings of the International Conference on Advances in Thermal Engineering and Applications (ICATEA 2021), Online, 19–20 March 2021; IOP Publishing: Bristol, UK, 2021; Volume 2054, p. 012024. [Google Scholar] [CrossRef]
- Bhandarkar, S.; Nagose, A.; Sharma, D.; Bhasme, V. Design and Modification of Double Wishbone Suspension System in an ATV. Int. Res. J. Eng. Technol. 2020, 7, 6082–6087. [Google Scholar]
- Varthanan, P.A.; Jayasuriya, N.; Gowtham, V. Modification and Simulation of Double Wishbone Front Suspension in Safari SUV. J. Crit. Rev. 2020, 7, 150–157. [Google Scholar] [CrossRef]
- Prabaharan, T.; Herbert Bejaxhin, A.B.; Periyaswamy, P.; Ramanan, N.; Ramkumar, K. Lower Wishbone Modeling and Analysis for Commercial Vehicle Independent Suspension System. J. Mines Met. Fuels 2022, 70, 1143–1148. [Google Scholar] [CrossRef]
- Arshad, M.W.; Lodi, S.; Liu, D.Q. A Hybrid Quantum-Classical Approach Using D-Wave and SLSQP for Double Wishbone Suspension System Optimization. In Proceedings of the 2025 IEEE Conference on Artificial Intelligence (CAI), Santa Clara, CA, USA; 2025; pp. 16–19. [Google Scholar] [CrossRef]
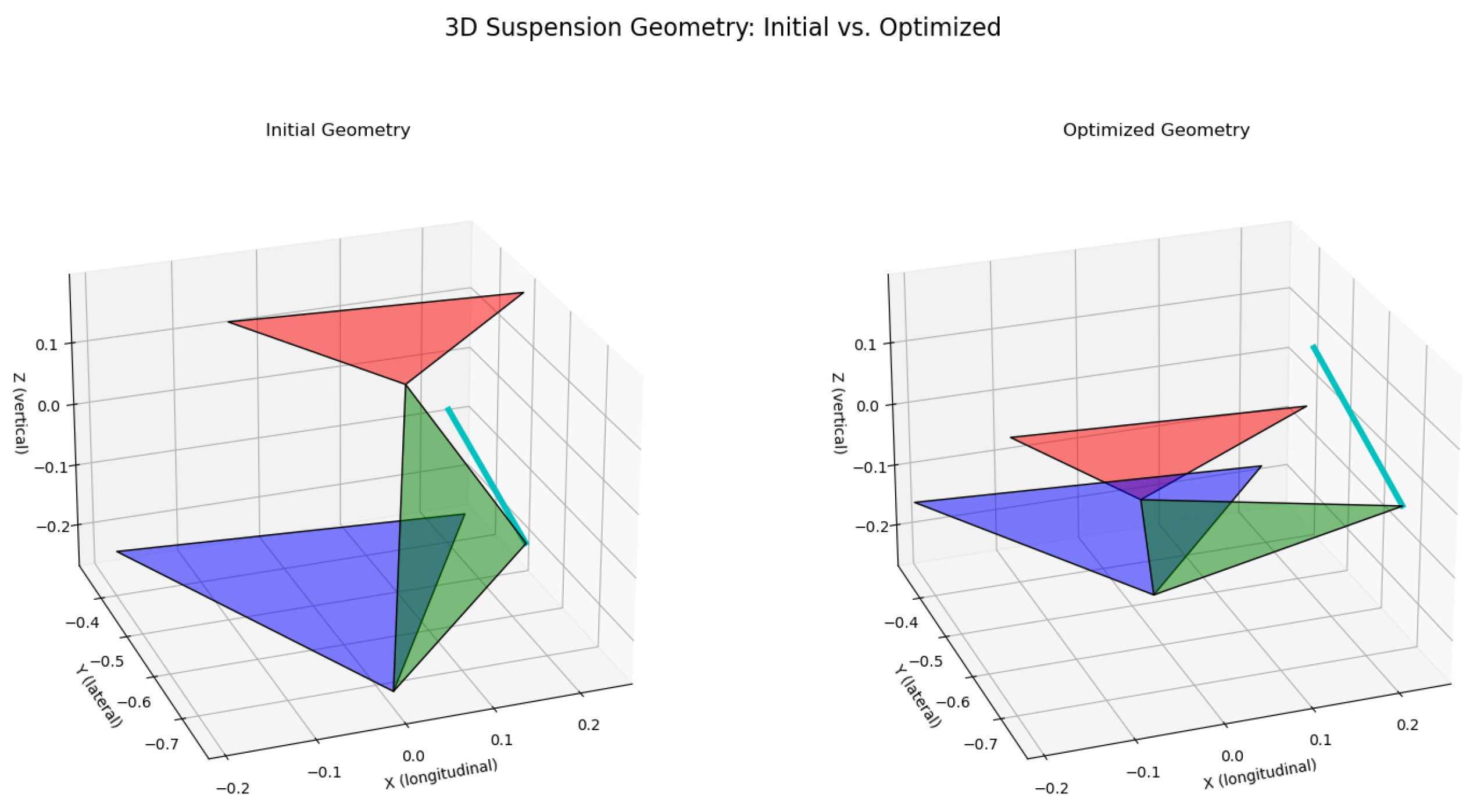
| Variable | Axis | Initial (m) | Optimized (m) |
|---|---|---|---|
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z | |||
| x | |||
| y | |||
| z |
| Variable | Displacement (mm) |
|---|---|
| Roll (deg) | Target Camber | SA Camber | Final Camber | Target Caster | SA Caster | Final Caster |
|---|---|---|---|---|---|---|
| Method | Feasibility Norm | Camber RMSE (°) | Caster RMSE (°) | CPU Time (s) |
|---|---|---|---|---|
| QUBO–SQP (Proposed) | ||||
| QUBO–GA | ||||
| QUBO–PSO | ||||
| QUBO–GD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, M.W.; Lodi, S.; Liu, D.Q. An Advanced Hybrid Optimization Algorithm for Vehicle Suspension Design Using a QUBO-SQP Framework. Mathematics 2025, 13, 3843. https://doi.org/10.3390/math13233843
Arshad MW, Lodi S, Liu DQ. An Advanced Hybrid Optimization Algorithm for Vehicle Suspension Design Using a QUBO-SQP Framework. Mathematics. 2025; 13(23):3843. https://doi.org/10.3390/math13233843
Chicago/Turabian StyleArshad, Muhammad Waqas, Stefano Lodi, and David Q. Liu. 2025. "An Advanced Hybrid Optimization Algorithm for Vehicle Suspension Design Using a QUBO-SQP Framework" Mathematics 13, no. 23: 3843. https://doi.org/10.3390/math13233843
APA StyleArshad, M. W., Lodi, S., & Liu, D. Q. (2025). An Advanced Hybrid Optimization Algorithm for Vehicle Suspension Design Using a QUBO-SQP Framework. Mathematics, 13(23), 3843. https://doi.org/10.3390/math13233843








