Event-Driven Average Estimation with Dispersion-Tolerant Poisson–Inverse Gaussian Approach

Abstract

Overdispersion is a major problem in the context of count data analysis, and the classical Poisson regression estimators are, in general, unreliable since they imply that the mean equals its variance. In this article, an event-driven class of average estimators, which is based on the Poisson–inverse Gaussian (P-IG) regression model, is formulated to overcome this shortcoming. P-IG regression is a mixture of Poisson and inverse Gaussian regression that is modeled to deal with the overdispersion that is often found in real data. It approximates such count data by a compound distribution with a heavy-tailed inverse Gaussian component. Suggested estimators are more effective in estimating the population means in situations of overdispersion using auxiliary data in the form of covariates. The design-based framework specifies the statistical properties of proposed estimators with respect to their bias and mean squared error (MSE). To confirm the effectiveness and the strength of the suggested methodology, a reasonable amount of simulations and real-data applications are carried out, contrasting it with customary Poisson-based estimators. The results indicate that the P-IG-based estimators are superior over their counterparts. The study provides a statistically valid and practically useful breakthrough in survey sampling and count data regression that can provide researchers and practitioners with a strong alternative to classical Poisson-regression-based mean estimator procedures.

1. Introduction

At every stage of a typical research process, conducting a sample survey is the initial step because it is a fundamental method for gathering data. Interviews may be conducted virtually or in person; arranged by individuals or groups; and conducted via mail, telephone, or in person methods. A questionnaire is one of the research instruments used across various disciplines, including education, medicine, economics, labor studies, industry studies, business studies, animal studies, and environmental studies. Personal, telephone, postal, and web-based surveys are the most common methods for conducting a survey. Surveys may be ineffective if flawed data collection methods are used. For this reason, the methods of data collection should be accurate to yield valid conclusions. As a result, developing an action plan based on strategic data collection approaches can significantly increase the quality of research and enhance the accuracy of results. Utilizing auxiliary technical variables closely related to the primary research variable can enhance the model and yield more valid and stable results [1,2,3].

Sampling theory is distinct from other statistical theories in that it is based on supplementary information to maximize estimation accuracy. Auxiliary information is typically featured during different stages of a sampling study, including stratification and determination of selection probabilities, to maximize the effectiveness of population parameter estimation. Generally, the objective of surveys is to estimate the population total or mean. There are several techniques that have been suggested by researchers in using auxiliary information and improving the accuracy of population average estimation; see [4,5,6,7]. In the case of a direct relationship between supplementary and primary variables, regression and ratio estimators are particularly notable for estimating the population mean.

Nevertheless, classical techniques tend to become less accurate when extreme values or outliers in the data set come into play. To solve these shortcomings, effective ratio and regression-based techniques have been suggested in the estimation of means. Moreover, many sophisticated methods that specifically account for extreme values in augmented datasets have been designed. For example, Oral and Oral [8] treat the deficiencies of the classical ratio estimator and propose a new one constructed on the modified maximum likelihood (MML) and order statistics. Their estimator is very robust and efficient in non-normal cases. Abid et al. [9] explored estimating the population mean by employing unconventional location parameters. Zaman [10,11] and Bulut and Zaman [12] introduced a category of robust ratio estimators by synthesizing the existing ratio estimators. Ref. [13] and Ibrahim et al. [14] consider the problem of outliers in ratio estimators and employ robust regressions such as LTS, LMS, and Huber estimations. Under data contamination, their results indicate that estimation accuracy has been boosted by a substantial margin compared to the conventional approaches. In addition, the new double-sampling estimator, implied by robust regression methods, was proposed by Zaman and Bulut [15]. Ref. [16] suggested ratio-based estimators employing quantile regression as a replacement for conventional regression estimators. Ali et al. [17] obtained estimators through a robust regression technique, which is specifically appropriate in sensitive surveys that can be conducted in simple random samples. More recently, Koc [18] came up with the new idea of using the Poisson regression coefficient to estimate means in a specific situation, namely, in the context of count data. Their study is unique because they are concerned with count data and the utilization of Poisson regression in the estimation of ratio-based average estimators.

The basic principle of a useful statistical analysis has been count data modeling and estimation of mean. It can be directly applied in such domains as epidemiology, ecology, economics, and industrial engineering. The Poisson regression model of count outcomes has historically been the statistical workhorse because it is simple in both mathematics and analysis, and because it has a straightforward expression linking the mean of the response variable with its variance (Cameron and Trivedi [19]). That is one of the reasons that Koc [18] came up with the new idea of using the Poisson regression coefficient in mean estimation. After that, many studies extended their work by defining average estimators using the regression coefficient of Poisson. For example, Koc et al. [20] extend this work to double sampling. Ref. [21] developed a Poisson regression-based estimator of the mean that aims to suit the simple random sampling scenario to count data. Their approach is an indication of the significance of matching estimation methods with the distribution of underlying data. Wani et al. [22] proposed an enhanced version of the Koc [18] estimator by incorporating power components from Shahzad et al. [21]. Raghav et al. [23] and Alomair and Shahzad [24] also extended this idea to Poisson and Tweedie–Poisson regression-based average estimators under probability sampling designed to improve the accuracy of count data.

However, the assumptions of the Poisson distribution do not always hold in the real world due to overdispersion in a data set. This violation may cause an underestimation of the standard errors and lead to inaccurate inference. To overcome these weaknesses, it is necessary to apply a more appropriate regression model that can accommodate dispersion. The P-IG regression model is another useful alternative, and it is a mixture of Poisson and inverse Gaussian. The model retains the simplicity of interpretation of the classical Poisson model and introduces a dispersion parameter to account for extra-Poisson variability; hence, it is particularly effective in fitting overdispersed counts (Sellers and Shmueli [25]; Farghali et al. [26]). The principal goal of the current research is to formulate mean estimators on the basis of the P-IG regression coefficient, which is more convenient than the classical Poisson estimators under conditions of overdispersion.

As far as we are aware, no prior research has investigated the problem of mean estimation in sampling theory using the P-IG regression coefficient. This gap is addressed in the present paper, where mean estimators based on the P-IG regression have been derived and tested, and their performance is compared with Poisson regression-based mean estimators. These estimators are based on auxiliary information, i.e., extra covariates or known quantities that enhance the efficiency and accuracy of statistical estimators (Sarndal et al. [27]; Rao [28]). The strategic application of auxiliary variables is a well-established procedure in survey sampling and small-area estimation; however, the incorporation of auxiliary variables into more sophisticated regression models involving count data has received relatively little attention. This aspect is also explored in the current research article.

The subsequent parts of the paper are arranged into four parts to discuss how the development and application of robust mean estimators concerning the P-IG regression coefficient are carried out. In Section 2, the background of count regression is reviewed, and the existing estimators developed by Koc [18] based on Poisson regression coefficients are explained. Section 3 contains the theory of the P-IG regression, its superiority over the classical equivalents, and the construction of the new family of average estimators, which are more efficient by utilizing auxiliary variable information. 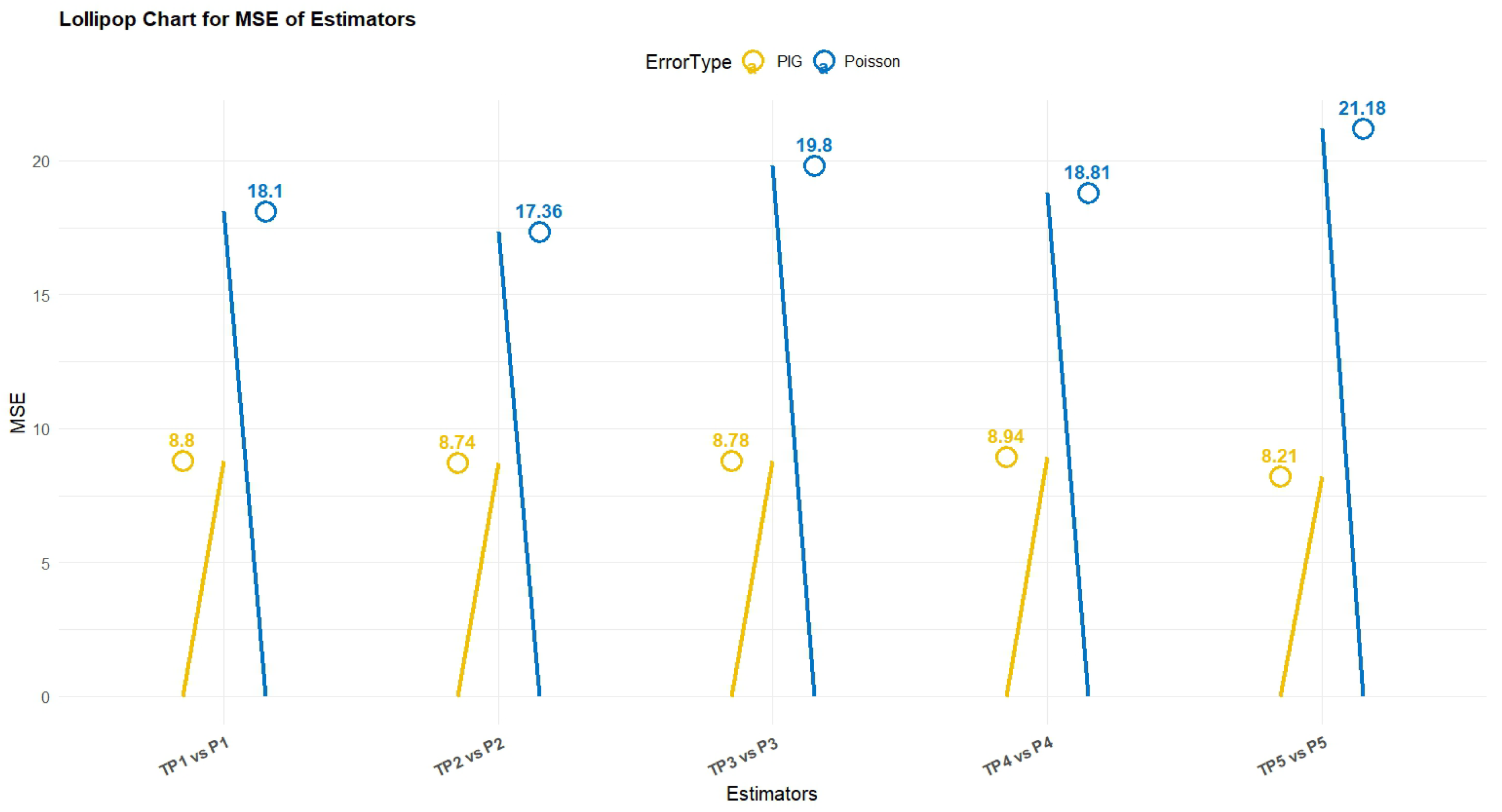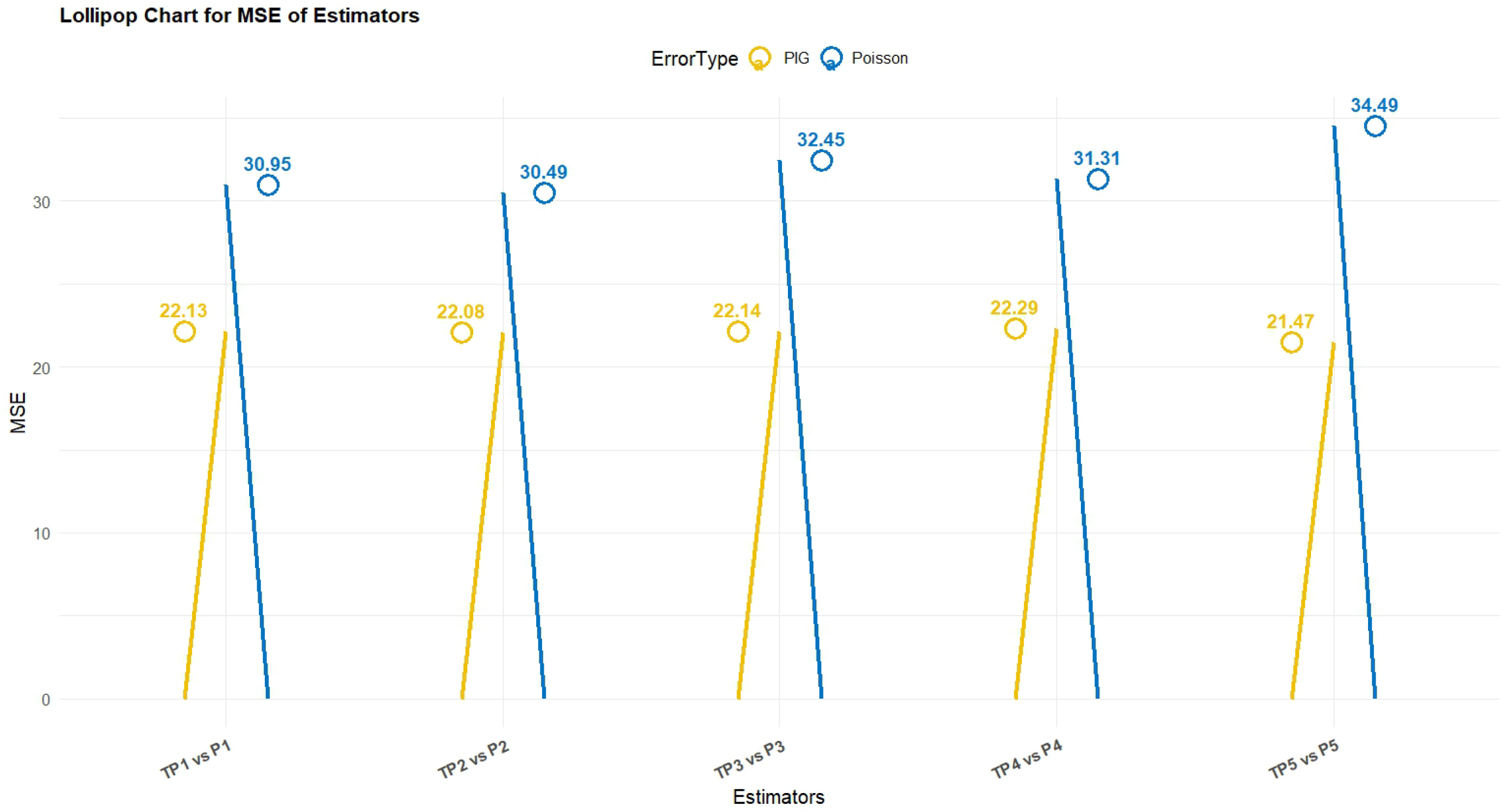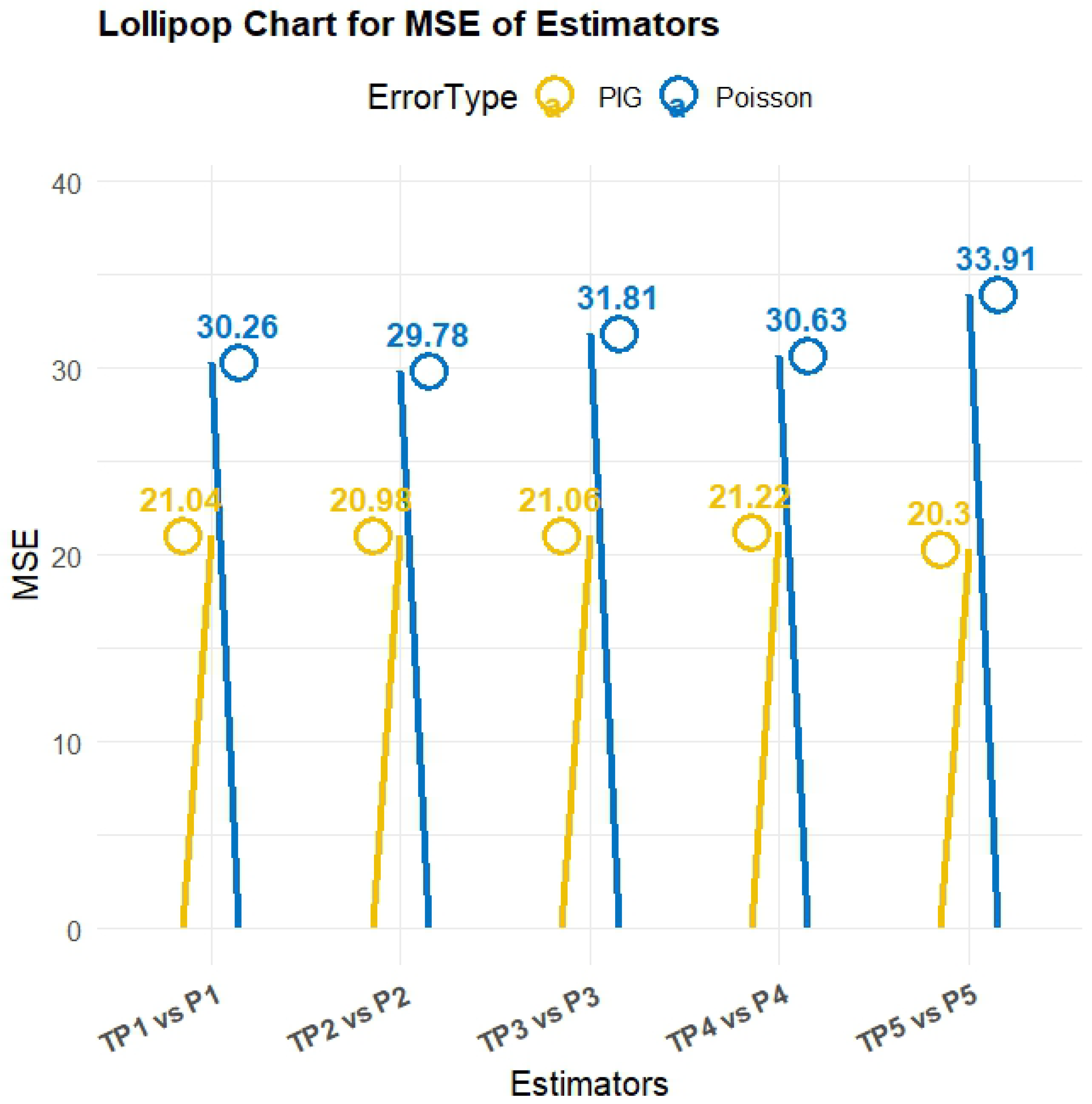Section 4 presents a critical comparison of the developed and classical ones in both simulation and empirical settings using three real-world populations of mussel data and three artificial ones generated using the P-IG distribution. Section 4.3 summarizes the findings, and excellent results of the proposed estimators are indicated. Section 5 offers the conclusion of the study.

2. Poisson Regression for Count Data

It is necessary to understand the context of the main principles of count data regression to appreciate the usefulness of traditional models and the strategic importance of more adaptive ones. Count data are non-negative integer observations that appear in a wide variety of applied situations, such as counting the number of hospital visits, insurance claims, and ecological events that are recorded. The Poisson regression model has traditionally been the preferred choice for modelling such data because it is simple and has a clear interpretive framework. It presupposes that the response variable is Poisson distributed, the average of which is linked with explanatory variables in a log-linear fashion [19,29].

One of the most popular statistical methods of the count-type data analysis is the Poisson regression model. The method can be used when the dependent variable $y_i$ for $i=0, 1, 2, \dots , n$ represents the frequency of events observed within a fixed duration or spatial domain. $y_i$ considers Poisson distribution with

$$P(y_i;{\lambda }_i)={\displaystyle \frac{e^{-{\lambda }_i}{\lambda }_i^{y_i}}{y_i!}},y_i=0,1,2,\dots$$

where

$$\mathbb{E}\left(y_i\right)=\mathrm{Var}\left(y_i\right)={\lambda }_i.$$

The respective log-likelihood of the set of observations is developed in the following way:

$$\mathcal{L}(\lambda ;\mathbf{y})=\sum _{i=1}^n\left[y_{i}log\left({\lambda }_i\right)-{\lambda }_i-log(y_i!)\right]$$

Suppose that X is a predictor matrix of dimension $n\times (p+1)$, and ${\mathbf{x}}_i$ is the ith row of $\mathbf{X}$. The model relates ${\lambda }_i$ with the predictors by use of the logarithmic link function:

$$log\left({\lambda }_i\right)={\gamma }_i={\mathbf{x}}_i^{\top }{\mathbb{R}}_{\mathrm{p}}$$

where ${\mathbb{R}}_{\mathrm{p}}={({\mathbb{R}}_{{\mathrm{p}}_0},{\mathbb{R}}_{{\mathrm{p}}_1},\dots ,{\mathbb{R}}_{{\mathrm{p}}_p})}^{\top }$ signifies regression coefficients.

The log-likelihood is differentiated with respect to the coefficient vector and equated to zero in order to estimate ${\mathbb{R}}_{\mathrm{p}}$. The maximization of the likelihood leads to the following:

$$\sum _{i=1}^n(y_i-\exp \left({\mathbf{x}}_i^{\top }{\mathbb{R}}_{\mathrm{p}}\right)){\mathbf{x}}_i=0$$

Such a set of nonlinear equations is usually solved using an iterative numerical solution algorithm like the Newton–Raphson or the Fisher scoring algorithm [19,29].

Mean Estimators Using Poisson Regression

The use of linear regression models to analyze count data is generally inappropriate because negative values of predicted results can occur, and these models do not satisfy the assumptions of constant variance. Such issues can also adversely affect mean estimation. Koc [18] attempted to address this problem by proposing ratio estimators for mean estimation that incorporate Poisson regression coefficients.

The ratio-type methods of estimation are beneficial in a survey sampling context where a strong positive correlation exists between the supplementary variable and the research variable. The method was initially introduced by Cochran in the middle of the 1900s, and since then, it has developed to form an essential part of statistical inference. Although it was initially used extensively in agricultural research, it has since been found helpful in a variety of other scientific fields. Interested readers can consult [30,31,32] to know more about ratio estimators and their different variations. Koc’s [18] class of ratio-type mean estimators is given below:

$${\overline{y}}_{koc\left(i\right)}=\left\{\begin{array}{cc}\{{\overline{Y}}_s+\widehat{\mathbb{R}}\mathrm{p}({\overline{X}}_p-{\overline{X}}_s)\}{\overline{X}}_p{\overline{x}}^{-1}\hfill & \hfill \\ \\ \{{\overline{Y}}_s+{\widehat{\mathbb{R}}}_{\mathrm{p}}({\overline{X}}_p-{\overline{X}}_s)\}{\overline{X}}_C{\overline{x}}_C^{-1}\hfill & \hfill \\ \\ \{{\overline{Y}}_s+{\widehat{\mathbb{R}}}_{\mathrm{p}}({\overline{X}}_p-{\overline{X}}_s)\}{\overline{X}}_{\mathbb{R}}{\overline{x}}_{\mathbb{R}}^{-1}\hfill & \hfill \\ \\ \{{\overline{Y}}_s+{\widehat{\mathbb{R}}}_{\mathrm{p}}({\overline{X}}_p-{\overline{X}}_s)\}{\overline{X}}_{\mathbb{R}C}{\overline{x}}_{\mathbb{R}C}^{-1}\hfill & \hfill \\ \\ \{{\overline{Y}}_s+{\widehat{\mathbb{R}}}_{\mathrm{p}}({\overline{X}}_p-{\overline{X}}_s)\}{\overline{X}}_{C\mathbb{R}}{\overline{x}}_{C\mathbb{R}}^{-1}\hfill & \hfill \\ \end{array}\right.$$

(1)

where

$$\left\{\begin{array}{cc}{\overline{X}}_C={\overline{X}}_p+C_x,{\overline{x}}_C={\overline{X}}_s+C_x,\hfill & \hfill \\ \\ {\overline{X}}_{\mathbb{R}}={\overline{X}}_p+{\mathbb{R}}_{2x},{\overline{x}}_{\mathbb{R}}={\overline{X}}_s+{\mathbb{R}}_{2x},\hfill & \hfill \\ \\ {\overline{X}}_{\mathbb{R}C}={\overline{X}}_p{\mathbb{R}}_{2x}+C_x,{\overline{x}}_{\mathbb{R}C}={\overline{X}}_s{\mathbb{R}}_{2x}+C_x,\hfill & \hfill \\ \\ {\overline{X}}_{C\mathbb{R}}={\overline{X}}_p{C}_x+{\mathbb{R}}_{2x},{\overline{x}}_{C\mathbb{R}}={\overline{X}}_s{C}_x+{\mathbb{R}}_{2x}\hfill & \hfill \\ \end{array}\right.$$

(2)

$$MSE\left({\overline{y}}_{koc\left(i\right)}\right)=\left\{\begin{array}{cc}{\psi }_{n_s,N_p}[S_y^2+w_1^2{S}_x^2+2{\mathbb{R}}_{\mathrm{p}}{w}_1{S}_x^2+{\mathbb{R}}_{\mathrm{p}}^2{S}_x^2-2w_1{S}_{xy}-2{\mathbb{R}}_{\mathrm{p}}{S}_{xy}]\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}[S_y^2+w_2^2{S}_x^2+2{\mathbb{R}}_{\mathrm{p}}{w}_2{S}_x^2+{\mathbb{R}}_{\mathrm{p}}^2{S}_x^2-2w_2{S}_{xy}-2{\mathbb{R}}_{\mathrm{p}}{S}_{xy}]\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}[S_y^2+w_3^2{S}_x^2+2{\mathbb{R}}_{\mathrm{p}}{w}_3{S}_x^2+{\mathbb{R}}_{\mathrm{p}}^2{S}_x^2-2w_3{S}_{xy}-2{\mathbb{R}}_{\mathrm{p}}{S}_{xy}]\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}[S_y^2+w_4^2{S}_x^2+2{\mathbb{R}}_{\mathrm{p}}{w}_4{S}_x^2+{\mathbb{R}}_{\mathrm{p}}^2{S}_x^2-2w_4{S}_{xy}-2{\mathbb{R}}_{\mathrm{p}}{S}_{xy}]\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}[S_y^2+w_5^2{S}_x^2+2{\mathbb{R}}_{\mathrm{p}}{w}_5{S}_x^2+{\mathbb{R}}_{\mathrm{p}}^2{S}_x^2-2w_5{S}_{xy}-2{\mathbb{R}}_{\mathrm{p}}{S}_{xy}]\hfill & \hfill \\ \end{array}\right.$$

(3)

where

$$w_i=\left\{\begin{array}{cc}\left({\overline{Y}}_p\right){\left({\overline{X}}_p\right)}^{-1}\hfill & \hfill \\ \\ \left({\overline{Y}}_p\right){({\overline{X}}_p+C_x)}^{-1}\hfill & \hfill \\ \\ \left({\overline{Y}}_p\right){({\overline{X}}_p+{\mathbb{R}}_{2x})}^{-1}\hfill & \hfill \\ \\ \left({\overline{Y}}_p{\mathbb{R}}_{2x}\right){({\overline{X}}_p{\mathbb{R}}_{2x}+C_x)}^{-1}\hfill & \hfill \\ \\ \left({\overline{Y}}_p{C}_x\right){({\overline{X}}_p{C}_x+{\mathbb{R}}_{2x})}^{-1}\hfill & \hfill \\ \end{array}\right.$$

(4)

The ${\overline{y}}_{koc\left(i\right)}$ class has an MSE in Equation (3) that depends on finite population correction (fpc) factor ${\psi }_{n_s,N_p}$ containing population and sample sizes $(N_p,n_s)$, population averages $({\overline{X}}_p,{\overline{Y}}_p)$, sample averages $({\overline{X}}_s,{\overline{Y}}_s)$, variances $(S_y^2,S_x^2)$, CV $\left(C_x\right)$, kurtosis $\left({\mathbb{R}}_{2x}\right)$, and co-variance $\left(S_{xy}\right)$.

3. Formulation of P-IG Regression and Associated Estimators

3.1. P-IG Regression

Poisson regression is widely used; however, in some cases, real data may exhibit repeated failures under the condition that the variance is significantly greater than the mean, which is known as overdispersion. In such situations, the Poisson model, which assumes equality of the mean and variance, performs poorly; the parameters are estimated with bias; the standard errors are underestimated; and, consequently, inference tends to be unreliable (Hilbe [33]). Although adjustments such as quasi-Poisson and negative binomial models partially account for overdispersion, they often do so at the expense of interpretability. They are also limited in modelling data with both continuous and discrete components. This challenge led us to consider the P-IG regression for mean estimation. It is a mixture of Poisson and inverse Gaussian distributions. The P-IG regression preserves the count data structure while allowing for overdispersion and mixed distributions, which are essential feature for robust mean estimation in complex data sets. It has a probability mass function (PMF) defined as follows:

$$P(Y=y)={\displaystyle \frac{{\mu }^y{e}^{-\lambda \mu }}{y!}}\sqrt{{\displaystyle \frac{2\lambda }{\pi }}}{\int }_0^{\infty }{t}^{y-{\displaystyle \frac{1}{2}}}\exp \left[-\lambda \left(t+{\displaystyle \frac{{\mu }^2}{2t}}\right)\right]\mathrm{d}t,y=0,1,2,\dots$$

The foregoing is indeed the mixed-Poisson formulation of the P-IG distribution [34,35,36]. There are also closed-form representations based on the modified Bessel function of the second kind, $K_{y+{\displaystyle \frac{1}{2}}}\left(\lambda \mu \right)$, and recursive probability formulae that can be expressed in a computational form [37,38]. The P-IG family extends the Poisson model by introducing a dispersion parameter $\lambda$ that inflates the variance $\mathrm{Var}\left(Y\right)=\mu +{\mu }^3/\lambda$, making it suitable for overdispersed count data. When

$$Y_i\sim \mathrm{P}\text{-}\mathrm{IG}({\mu }_i,\lambda ),$$

the mean will be ${\mu }_i$ and variance

$$\mathrm{Var}\left(Y_i\right)={\mu }_i+{\displaystyle \frac{{\mu }_i^3}{\lambda }}.$$

where $\lambda$ is parameter of dispersion. The mean ${\mu }_i$ is expressed as a log-linear model of the explanatory variables ${\mathbf{x}}_i$:

$${\mu }_i=\exp ({\mathbf{x}}_i^{\top }\Omega ),$$

$\Omega$ is the regression coefficients vector. The fact that the mean response is always positive, as ensured by the use of the log-link, is also consistent with the count data setting.

Maximum likelihood estimation (MLE) is used to determine the $\Omega$ and $\lambda$ parameters. The log-likelihood has the following form:

$$\ell (\Omega ,\lambda )=\sum _{i=1}^{n}log\left[P(Y_i=y_i\mid {\mu }_i=\exp ({\mathbf{x}}_i^{\top }\Omega ),\lambda )\right]$$

Replacing the PMF, the log-likelihood gets to

$$\ell (\Omega ,\lambda )=\sum _{i=1}^n\left[y_{i}log\left({\mu }_i\right)-log(y_i!)-\lambda {\mu }_i+\frac{1}{2}log\left(\frac{2\lambda }{\pi }\right)+log\left({\int }_0^{\infty }{t}^{y_i-\frac{1}{2}}\exp \left[-\lambda \left(t+\frac{{\mu }_i^2}{2t}\right)\right]\mathrm{d}t\right)\right].$$

The optimization over $\Omega$ and $\lambda$ is performed numerically through the application of various numerical optimization algorithms such as the Newton–Raphson or BFGS. The optimum value of $\lambda$ is then estimated and the final estimates of $\Omega$ and $\lambda$ are obtained. This estimation step enables the P-IG model to be adaptable and to accommodate a wide range of dispersion and information structures, which is beneficial in particular when the Poisson model assumptions are overly constraining.

3.2. Proposed PIG Regression-Based Estimators

Utilization of auxiliary information in statistical models is a well-known mechanism to improve both the accuracy and effectiveness of parameter estimation processes and is essential in the context of mean estimation in count data analysis. In P-IG regression-based mean estimation, supplementary variables are linked with the research variable, which can greatly reduce the MSE of the estimators. Such variables can be included in the regression model directly, or they can be used during post-estimation calibration processes. They enhance the accuracy of the predicted means ${\widehat{\mu }}_i$, especially in overdispersed or structurally heterogeneous data, whereby the standard Poisson regression is usually inadequate. The P-IG model, $\mathrm{Var}\left(Y_i\right)={\mu }_i+{\displaystyle \frac{{\mu }_i^3}{\lambda }}$, offers a flexible of variance structure that allows the maximum use of the informational worthiness of nuisance variables and could possibly fit with complex data structure. The theoretical and practical importance of the strategic use of supplementary information in the P-IG architecture lies in guaranteeing the robustness of mean estimation based on the foundations of model-assisted estimation and small-area inference (Sarndal et al. [27]; Rao [28]). We suggest the following mean estimators based on P-IG-regression with the help of auxiliary information and following Alomair and Shahzad [24]:

$${\tilde{\mu }}_j={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right)·{\displaystyle \frac{{\overline{Y}}_s+\Omega \left({\overline{X}}_p-{\overline{X}}_s\right)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}·\left({\hslash }_a{\overline{X}}_p+{\hslash }_b\right)·\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$$

(5)

Under the assumption of ${\overline{Y}}_s={\overline{Y}}_p(1+{\zeta }_0)$, ${\overline{X}}_s={\overline{X}}_p(1+{\zeta }_1)$ where $|{\zeta }_0|,|{\zeta }_1| \approx 0$, the expectations are

$$\left.\begin{array}{cc}\hfill E\left({\zeta }_k\right)& =0,\hfill \\ \hfill E\left({\zeta }_0^2\right)& ={\psi }_{n_s,N_p}{C}_Y^2,\hfill \\ \hfill E\left({\zeta }_1^2\right)& ={\psi }_{n_s,N_p}{C}_X^2,\hfill \\ \hfill E\left({\zeta }_0{\zeta }_1\right)& ={\psi }_{n_s,N_p}{C}_{YX},\hfill \\ \hfill {\psi }_{n_s,N_p}& =\left({\displaystyle \frac{1}{n_s}}-{\displaystyle \frac{1}{N_p}}\right)\hfill \end{array}\right\}$$

(6)

The simplification of Equation (5), along with its extension in terms of Equation (6), is obtained as

$$\begin{array}{c}\hfill {\tilde{\mu }}_j={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_p(1+{\zeta }_0)+\left(1-{\displaystyle \frac{n_s}{N_p}}\right)\left({\overline{Y}}_p(1+{\zeta }_0)-\Omega {\overline{X}}_p{\zeta }_1\right){(1+{\eta }_a{\zeta }_1)}^{-1}·\exp \left({\eta }_b^2{\zeta }_1^2-{\eta }_b{\zeta }_1\right)\end{array}$$

(7)

Approximated to $O\left(n_s^{-1}\right)$:

$$\begin{array}{c}\hfill {\tilde{\mu }}_j={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_p(1+{\zeta }_0)+\left(1-{\displaystyle \frac{n_s}{N_p}}\right)\left({\overline{Y}}_p(1+{\zeta }_0)-{\overline{Y}}_p({\eta }_a+{\eta }_b)+\Omega {\overline{X}}_p{\zeta }_1\right)\\ \hfill +\left({\overline{Y}}_p({\eta }_a^2+{\eta }_a{\eta }_b+1.5{\eta }_b^2)+\Omega {\overline{X}}_p({\eta }_a+{\eta }_b)\right){\zeta }_1^2-{\overline{Y}}_p({\eta }_a+{\eta }_b){\zeta }_0{\zeta }_1\end{array}$$

(8)

The bias of ${\tilde{\mu }}_j$, after eliminating ${\overline{Y}}_p$ and taking expectation, is obtained up to order $O\left(n_s^{-1}\right)$ as

$$\mathrm{Bias}\left({\tilde{\mu }}_j\right)={\psi }_{n_s,N_p}\left(1-{\displaystyle \frac{n_s}{N_p}}\right)\left[\left(\Omega {\overline{X}}_p({\eta }_a+{\eta }_b)+{\overline{Y}}_p({\eta }_a^2+{\eta }_a{\eta }_b-1.5{\eta }_b^2)\right)S_X^2-{\overline{Y}}_p({\eta }_a+{\eta }_b)C_{YX}\right]$$

(9)

where

$${\eta }_a={\displaystyle \frac{{\hslash }_a{\overline{X}}_p}{{\hslash }_a{\overline{X}}_p+{\hslash }_b}},{\eta }_b={\displaystyle \frac{{\theta }_a{\overline{X}}_p}{2({\theta }_a{\overline{X}}_p+{\theta }_b)}}$$

From Equation (8), after subtracting ${\overline{Y}}_p$, squaring and applying the expectation operator, the MSE of ${\tilde{\mu }}_j$ is obtained up to $O\left(n_s^{-1}\right)$ as given below:

$$\mathrm{MSE}\left({\tilde{\mu }}_j\right)={\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_j^2{S}_X^2-2{\delta }_j{S}_{YX}\right)$$

(10)

where

$${\delta }_j=\left(1-{\displaystyle \frac{n_s}{N_p}}\right)\left(R({\eta }_a+{\eta }_b)+\Omega \right)$$

Table 1. Variants within the proposed class ${\tilde{\mu }}_j$.

Estimators	Constant Values
	ℏa	ℏb	${\mathit{\theta }}_{\mathit{a}}$	${\mathit{\theta }}_{\mathit{b}}$
${\tilde{\mu }}_1={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right){\displaystyle \frac{{\overline{Y}}_s+\Omega ({\overline{X}}_p-{\overline{X}}_s)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}({\hslash }_a{\overline{X}}_p+{\hslash }_b)\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$	1	0	1	0
${\tilde{\mu }}_2={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right){\displaystyle \frac{{\overline{Y}}_s+\Omega ({\overline{X}}_p-{\overline{X}}_s)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}({\hslash }_a{\overline{X}}_p+{\hslash }_b)\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$	1	$C_X$	1	0
${\tilde{\mu }}_3={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right){\displaystyle \frac{{\overline{Y}}_s+\Omega ({\overline{X}}_p-{\overline{X}}_s)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}({\hslash }_a{\overline{X}}_p+{\hslash }_b)\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$	1	${\Omega }_{1X}$	1	0
${\tilde{\mu }}_4={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right){\displaystyle \frac{{\overline{Y}}_s+\Omega ({\overline{X}}_p-{\overline{X}}_s)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}({\hslash }_a{\overline{X}}_p+{\hslash }_b)\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$	1	${\Omega }_{2X}$	1	0
${\tilde{\mu }}_5={\displaystyle \frac{n_s}{N_p}}{\overline{Y}}_s+\left(1-{\displaystyle \frac{n_s}{N_p}}\right){\displaystyle \frac{{\overline{Y}}_s+\Omega ({\overline{X}}_p-{\overline{X}}_s)}{{\hslash }_a{\overline{X}}_s+{\hslash }_b}}({\hslash }_a{\overline{X}}_p+{\hslash }_b)\exp \left({\displaystyle \frac{{\theta }_a({\overline{X}}_p-{\overline{X}}_s)}{{\theta }_a({\overline{X}}_p+{\overline{X}}_s)+2{\theta }_b}}\right)$	1	$S_X$	1	0

outlines the family members associated with the suggested class ${\tilde{\mu }}_j$. MSE of ${\tilde{\mu }}_j$ estimator in the set of j = 1, 2, 3, 4, and 5, is

$$MSE\left({\tilde{\mu }}_j\right)=\left\{\begin{array}{cc}{\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_1^2{S}_X^2-2{\delta }_1{S}_{YX}\right)\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_2^2{S}_X^2-2{\delta }_2{S}_{YX}\right)\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_3^2{S}_X^2-2{\delta }_3{S}_{YX}\right)\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_4^2{S}_X^2-2{\delta }_4{S}_{YX}\right)\hfill & \hfill \\ \\ {\psi }_{n_s,N_p}\left(S_Y^2+{\delta }_5^2{S}_X^2-2{\delta }_5{S}_{YX}\right)\hfill & \hfill \\ \end{array}\right.$$

(11)

4. Numerical Illustration

This section carries out the comparative performance assessment of the average estimators based on the P-IG and Poisson regression coefficients using three empirical and three simulated datasets.

4.1. Application to Mussel Dataset

We employed the well-known mussel dataset that was initially used by Ref. [39] and later by Ref. [40] to briefly discuss the empirical performance of the suggested mean estimators derived through the P-IG regression coefficient. This dataset contains N = 44 observations and only one response variable, which is a count-based variable representing the number of species of mussels (y), along with several explanatory variables that depend on the geographical, ecological, and chemical parameters of river environments. As complementary variables among these explanatory variables, we used the river system indicators, i.e., the Alabama–Coosa (AC), Savannah (SV), and Apalachicola (AP) systems. Due to the count nature of the response, the P-IG regression coefficient is especially appropriate because it allows for the overdispersion that appears so often in ecological count data.

There are a number of reasons why this dataset as an empirical platform is suitable for our study: First, the assumptions used in the P-IG framework are satisfied by the discrete and overdispersed response (study) variable. Second, the data contains a variety of auxiliary covariates, which allow us to evaluate how extra information influences the accuracy of mean estimation.

To analyze the estimators, three populations was assumed from mussel data:

• Population 1: $Y=$ the number of mussel species and $X=$ Alabama–Coosa river system (AC).
• Population 2: $Y=$ the number of mussel species and $X=$ Savannah river system (SV).
• Population 3: $Y=$ the number of mussel species and $X=$ Apalachicola river system (AP).

4.2. Simulation Design

In order to evaluate the behavior of ${\tilde{\mu }}_j$ in diverse scenarios, we systematically generated datasets according to the P-IG distribution that represents a flexible family of models adapted for overdispersed counts and possesses the properties of both a discrete and continuous part. The generated data contain 100 observations of ($y,x$). The covariate x, which was supposed to approximate environmental or spatial gradients (e.g., distance to a source, pollution index), was produced by an integer-valued uniform random variable over the range $[1,33]$ and ordered in descending order to reflect the monotonic decreasing trend observed in actual ecological field studies. The response variable y for three artificial populations were then modeled to depend inversely on x via a linear mean functions with added stochastic noises:

$${\mu }_i=20-0.4x_i+{\varpi }_i,{\varpi }_i\sim \mathcal{N}(0,1),i=1,2,\dots ,100,$$

$${\mu }_i=18-0.5x_i+{\varpi }_i,{\varpi }_i\sim \mathcal{N}(0,1),i=1,2,\dots ,100,$$

$${\mu }_i=22-0.49x_i+{\varpi }_i,{\varpi }_i\sim \mathcal{N}(0,1),i=1,2,\dots ,100,$$

In the above expression, ${\mu }_i$ indicates conditional mean of response variable $y_i$ given covariate $x_i$, and the stochastic error component is given by ${\varpi }_i$. It was intended to make it positive, so ${\mu }_i$ values were truncated at 0.5 below. The P-IG distribution was then used to generate the outcome variable $y_i$ of each population:

• First simulated population (Population 4): 

  $$y_i\sim \mathrm{P}\text{-}\mathrm{IG}({\mu }_i,\lambda =5),$$
• Second simulated population (Population 5): 

  $$y_i\sim \mathrm{P}\text{-}\mathrm{IG}({\mu }_i,\lambda =6),$$
• Third simulated population (Population 6):  

  $$y_i\sim \mathrm{P}\text{-}\mathrm{IG}({\mu }_i,\lambda =4),$$

  where ($\lambda =5,6,4$) are the dispersion parameters, corresponding to $sigma=\sqrt{{\displaystyle \frac{1}{\lambda }}}$. It is an arrangement that reads count-like properties and overdispersion, which are common in environmental and biological data. The final values of the $y_i$ were rounded to the nearest integer to approximate them as count data, which is typically obtained during field research. In addition to yielding a simulation framework with all the essential statistical properties of real-life ecological data, (P-IG)-based simulation frameworks enable the robust testing of mean estimation procedures in complex, non-Gaussian environments.

Based on reviewer’s suggestion, we have also generated another population using negative binomial distribution (NBD). The response variable y for fourth artificial population was modeled to depend inversely on x as defined earlier via a linear mean function with added stochastic noise:

$${\mu }_i=20-0.4x_i+{\varpi }_i,{\varpi }_i\sim \mathcal{N}(0,1),i=1,2,\dots ,100.$$

The NBD was then used to generate the outcome variable $y_i$ of artificial population:

• Fourth simulated population (Population 7): 

$$y_i\sim \mathrm{NBD}({\mu }_i,\lambda =2).$$

Note that the results of real-life Populations 1–3, and artificial Populations 4–7 with replications 1000, are available in

Table 2. MSE computation with mussel data.

Estimators	Population 1	Population 2	Population 3
${\overline{y}}_{koc\left(1\right)}$	18.09802	17.93694	21.00994
${\overline{y}}_{koc\left(2\right)}$	17.35626	16.44771	19.66512
${\overline{y}}_{koc\left(3\right)}$	19.79844	18.33648	24.12391
${\overline{y}}_{koc\left(4\right)}$	18.80512	52.82268	22.25344
${\overline{y}}_{koc\left(5\right)}$	21.17745	18.56836	25.93548
${\tilde{\mu }}_1$	8.801967	8.401536	9.253721
${\tilde{\mu }}_2$	8.738982	8.289148	9.142953
${\tilde{\mu }}_3$	8.780960	8.274641	9.215744
${\tilde{\mu }}_4$	8.941959	8.430957	9.499182
${\tilde{\mu }}_5$	8.207373	7.837018	8.467741

,

Table 3. PRE analysis with mussel data from Population 1.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	205.6134	197.1862	224.9320	213.6468	240.5991
${\tilde{\mu }}_2$	207.0953	198.6074	226.5531	215.1866	242.3332
${\tilde{\mu }}_3$	206.1053	197.6580	225.4701	214.1579	241.1747
${\tilde{\mu }}_4$	202.3944	194.0991	221.4105	210.3020	236.8324
${\tilde{\mu }}_5$	220.5094	211.4716	241.2275	229.1247	258.0296

,

Table 4. PRE analysis with mussel data from Population 2.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	213.4960	195.7703	218.2515	628.7264	221.0115
${\tilde{\mu }}_2$	216.3906	198.4247	221.2107	637.2510	224.0080
${\tilde{\mu }}_3$	216.7700	198.7725	221.5985	638.3683	224.4008
${\tilde{\mu }}_4$	212.7510	195.0871	217.4899	626.5324	220.2402
${\tilde{\mu }}_5$	228.8746	209.8721	233.9727	674.0151	236.9314

,

Table 5. PRE analysis with mussel data from Population 3.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	227.0432	212.5104	260.6942	240.4810	280.2708
${\tilde{\mu }}_2$	229.7939	215.0850	263.8526	243.3945	283.6663
${\tilde{\mu }}_3$	227.9788	213.3862	261.7685	241.4720	281.4257
${\tilde{\mu }}_4$	221.1764	207.0191	253.9578	234.2669	273.0285
${\tilde{\mu }}_5$	248.1175	232.2357	284.8920	262.8026	306.2856

,

Table 6. MSE using simulation study.

Estimators	Population 4	Population 5	Population 6	Population 7
${\overline{y}}_{koc\left(1\right)}$	30.95435	19.09929	36.38091	30.25956
${\overline{y}}_{koc\left(2\right)}$	30.49407	18.82019	35.86090	29.78202
${\overline{y}}_{koc\left(3\right)}$	32.44886	19.99843	38.06561	31.80542
${\overline{y}}_{koc\left(4\right)}$	31.31463	19.31701	36.78756	30.63287
${\overline{y}}_{koc\left(5\right)}$	34.48946	21.21078	40.35775	33.90591
${\tilde{\mu }}_1$	22.12762	13.95673	26.32689	21.04035
${\tilde{\mu }}_2$	22.07544	13.91839	26.26496	20.98232
${\tilde{\mu }}_3$	22.14098	13.96653	26.34273	21.05520
${\tilde{\mu }}_4$	22.29310	14.07780	26.52301	21.22409
${\tilde{\mu }}_5$	21.46685	13.46525	25.53984	20.30167

,

Table 7. PRE analysis with simulated data from Population 4.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	139.8901	137.8100	146.6442	141.5183	155.8661
${\tilde{\mu }}_2$	140.2208	138.1358	146.9908	141.8528	156.2346
${\tilde{\mu }}_3$	139.8057	137.7269	146.5557	141.4329	155.7721
${\tilde{\mu }}_4$	138.8517	136.7871	145.5556	140.4678	154.7091
${\tilde{\mu }}_5$	144.1960	142.0519	151.1580	145.8744	160.6638

,

Table 8. PRE analysis with simulated data from Population 5.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	136.8465	134.8467	143.2888	138.4065	151.9753
${\tilde{\mu }}_2$	137.2234	135.2181	143.6835	138.7877	152.3939
${\tilde{\mu }}_3$	136.7504	134.7521	143.1883	138.3093	151.8687
${\tilde{\mu }}_4$	135.6695	133.6870	142.0565	137.2161	150.6683
${\tilde{\mu }}_5$	141.8413	139.7686	148.5188	143.4582	157.5223

,

Table 9. PRE analysis with simulated data from Population 6.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	138.1892	136.2140	144.5883	139.7338	153.2948
${\tilde{\mu }}_2$	138.5150	136.5351	144.9292	140.0632	153.6562
${\tilde{\mu }}_3$	138.1061	136.1321	144.5014	139.6497	153.2026
${\tilde{\mu }}_4$	137.1674	135.2068	143.5192	138.7005	152.1613
${\tilde{\mu }}_5$	142.4477	140.4116	149.0440	144.0399	158.0188

and

Table 10. PRE analysis with simulated data from Population 7.

n	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}1\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}2\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}3\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}4\mathbf{\right)}}$	${\overline{\mathit{y}}}_{\mathit{k}\mathit{o}\mathit{c}\mathbf{\left(}5\mathbf{\right)}}$
${\tilde{\mu }}_1$	143.8168	141.5471	151.1639	145.5910	161.1470
${\tilde{\mu }}_2$	144.2146	141.9387	151.5820	145.9938	161.5928
${\tilde{\mu }}_3$	143.7154	141.4473	151.0573	145.4884	161.0334
${\tilde{\mu }}_4$	142.5718	140.3218	149.8553	144.3307	159.7520
${\tilde{\mu }}_5$	149.0497	146.6974	156.6641	150.8885	167.0105

.

4.3. Interpretation

As illustrated across Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, the simulation-based findings and empirical-based findings of the proposed P-IG regression-based mean estimators, which are identified as ${\tilde{\mu }}_j$, show that compared to the traditional Poisson regression-based estimators, which are represented by ${\overline{y}}_{koc\left(i\right)}$, the former has a clear advantage in not only the overall MSE but also the PRE.

Table 2 displays the computed MSE values for three real-world populations based on the mussel dataset. The suggested estimators have much smaller MSEs compared to the traditional ones in all three populations. It is worth noting that in all the populations, ${\tilde{\mu }}_5$ has the minimal MSE, thus proving to be stronger under overdispersion and the presence of possible outliers. As an example in Population 3, where mussel species are estimated by taking AP as auxiliary variable, ${\tilde{\mu }}_5$ leads to an MSE of 8.467741 as opposed to 19.66512 with ${\overline{y}}_{koc\left(2\right)}$, emphasizing the practical benefit of using the P-IG-based approach. The PRE of each estimator based on the three populations considered is further expounded in Table 3, Table 4 and Table 5. In Population 1 (Table 3), ${\tilde{\mu }}_5$ attains the highest PRE (306.2856) which surpasses all of the conventional estimators. The same efficiency level can be seen in Populations 2 and 3, where ${\tilde{\mu }}_5$ was equal to PRE of 236.9314 and 258.0296, respectively (Table 4 and Table 5). These results indicate the increased efficiency of estimation that can be obtained by employing the P-IG regression framework.

Additional evidence can be found in Table 6, which gives the results of the simulation where the MSE values were calculated using three synthetic populations. Once again, the proposed estimators are better, and ${\tilde{\mu }}_5$ again has the smallest MSE. In Population 6, the MSE of ${\tilde{\mu }}_5$ is 25.53984, and it is much lower than the 36.38091 as obtained by ${\overline{y}}_{koc\left(1\right)}$. This advantage is also proved by PRE metrics in Table 7, Table 8, Table 9 and Table 10.

For summarizing all the results, visual comparisons are also provided in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. These findings, therefore, confirm the assertion that the suggested P-IG-based averaging estimators are not only conceptually sound but also empirically better. They offer an effective technique for calculating the mean, especially in environments that are overdispersed and contain misdirected values. The consistency of MSE and PRE measures favors the practical use of these estimators ${\tilde{\mu }}_j$ in survey sampling and count data analysis.

5. Conclusions

The current article introduces an event-driven family of mean estimators that utilize the P-IG regression coefficient rather than relying on traditional Poisson regression-based estimators. The proposed family is empirically better and theoretically sound due to some crucial limitations of the Poisson model, which is incapable of dealing with overdispersed and heterogeneous count data. The theoretical derivations have revealed that the use of the supplementary variable that is implicit in the P-IG architecture can provide more efficient estimation in light of both MSE and PRE. Intensive tests on real-life data and synthesized data were used to support this theoretical contribution. To be precise, it was demonstrated in both the mussel dataset and in the simulated populations that the P-IG-based estimators of the characteristic of the member of a population, namely the P-IG-based estimator ${\tilde{\mu }}_5$, were superior to the P-IG-based estimators by any of the utilized measures of estimator performance, i.e., smaller MSE and higher PRE value. The simulation studies also found these findings by applying the adaptability and robustness of the proposed estimators in complex data environments. These results reinforce the view that the mixed-type P-IG regression model offers a highly general and resilient framework for mean estimation under diverse dispersion and nonlinearity. Consequently, the integration of P-IG regression principles into the sampling theory represents a significant methodological contribution to statistical estimation.