On Robustness for Spatio-Temporal Data
Abstract
:1. Introduction
2. M-Estimators of the Spatio-Temporal Variogram
2.1. Underlying Model for Z
2.2. M-Estimators of the Spatio-Temporal Variogram
2.3. Distribution of Variables
3. Approximation to the Distribution of M-Estimators of the Spatio-Temporal Variogram
3.1. Von Mises Approximation
3.2. Saddlepoint Approximation of the TAIF
4. Independence of the Transformed Variables
5. VOM + SAD Approximation of the Distribution of the Empirical Spatio-Temporal Estimator
Accuracy of the Approximation
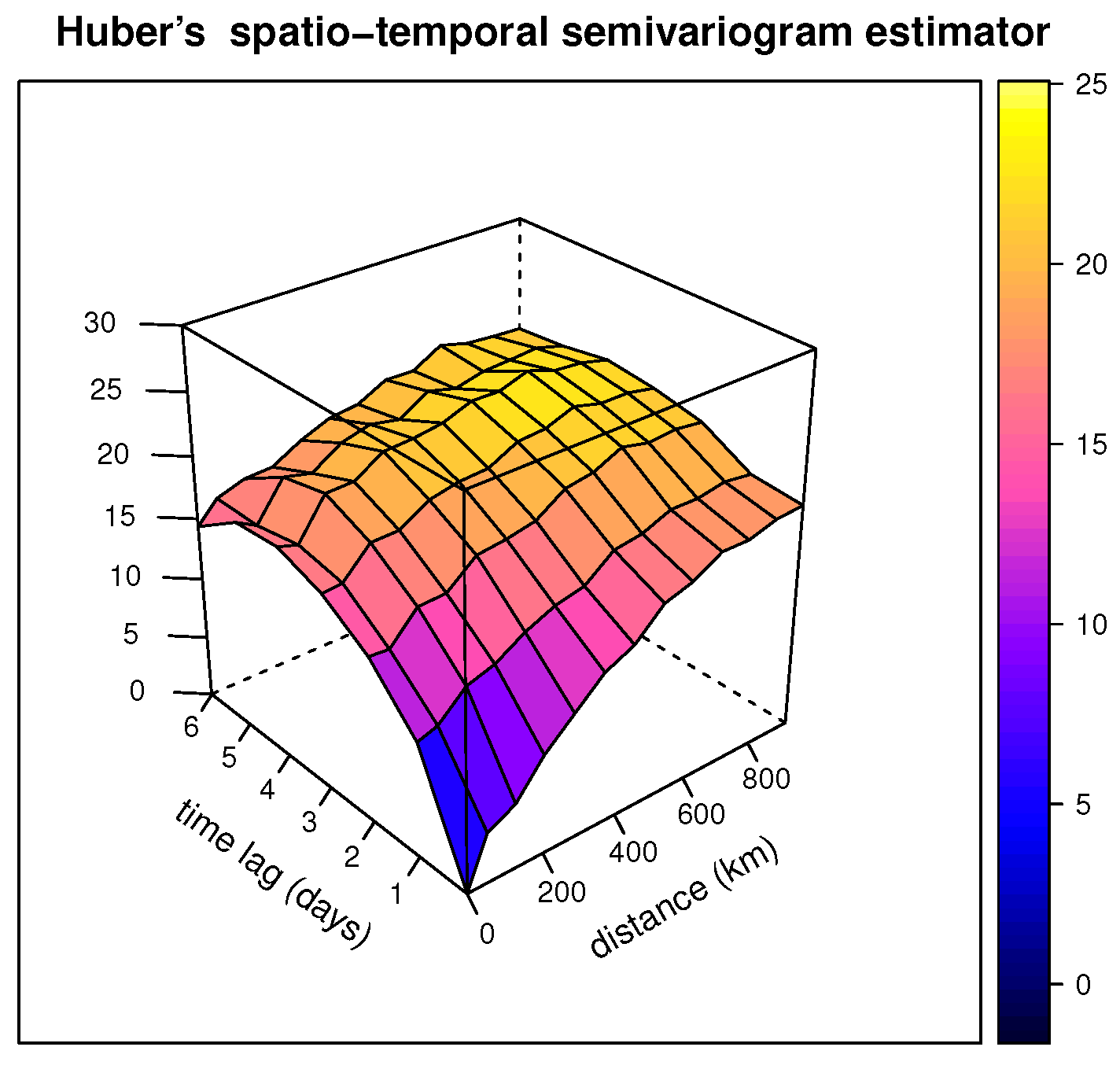
6. Huber’s Spatio-Temporal Variogram Estimator
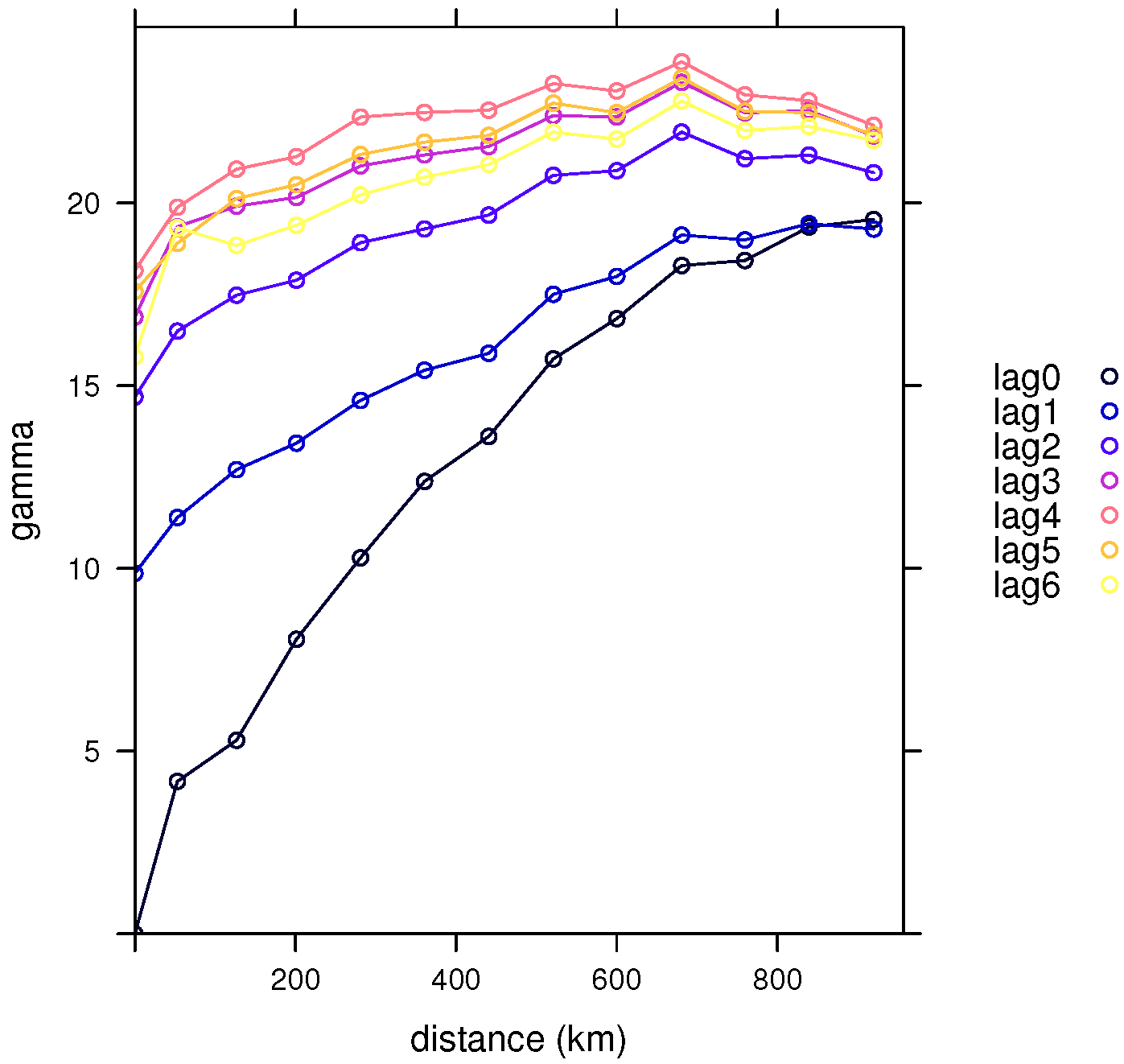
7. Example
8. Significant Time Dimension
9. Identification of Spatio-Temporal Outliers
9.1. Average M-Estimators
9.2. Identification of Spatio-Temporal Outliers
10. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christakos, G. Spatiotemporal Random Fields: Theory and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Hristopulos, D.T. Random Fields for Spatial Data Modeling: A Primer for Scientists and Engineers; Springer Nature: Berlin, Germany, 2020. [Google Scholar]
- Cressie, N.A.C. Statistics for Spatial Data; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Chilès, J.P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Wikle, C.K.; Zammit-Mangion, A.; Cressie, N. Spatio-Temporal Statistics with R; Chapman & Hall/CRC: London, UK, 2019. [Google Scholar]
- Varouchakis, E.A.; Hristopulos, D.T. Comparison of spatiotemporal variogram functions based on a sparse dataset of groundwater level variations. Spat. Stat. 2019, 34, 1–18. [Google Scholar] [CrossRef]
- García-Pérez, A. Saddlepoint approximations for the distribution of some robust estimators of the variogram. Metrika 2020, 83, 69–91. [Google Scholar] [CrossRef]
- García-Pérez, A. New robust cross-variogram estimators and approximations for their distributions based on saddlepoint techniques. Mathematics 2021, 9, 762. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Tukey, J.W. A survey of sampling from contaminated distributions. In Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling, Stanford Studies in Mathematics and Statistics; Oklin, I., Ed.; Stanford University Press: Redwood City, CA, USA, 1960; Chaper 39; pp. 448–485. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Ebner, B.; Henze, N. Tests for multivariate normality—A critical review with emphasis on weighted L2-statistics. Test 2020, 29, 845–892. [Google Scholar] [CrossRef]
- Kotz, S.; Balakrishnan, N.; Johnson, N.L. Continuous Multivariate Distributions. Volume 1: Models and Applications, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Syahel, W.A. Robust Statistics: The Approach Based on Influence Functions; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Ronchetti, E. Accurate and robust inference. Econom. Stat. 2020, 14, 74–88. [Google Scholar] [CrossRef]
- Cressie, N.; Hawkins, D.M. Robust estimation of the variogram: I. Math. Geol. 1980, 12, 115–125. [Google Scholar] [CrossRef]
- La Vecchia, D.; Ronchetti, E. Saddlepoint approximations for short and long memory time series: A frequency domain approach. J. Econom. 2019, 213, 578–592. [Google Scholar] [CrossRef]
- Von Mises, R. On the asymptotic distribution of differentiable statistical functions. Ann. Math. Stat. 1947, 18, 309–348. [Google Scholar] [CrossRef]
- Withers, C.S. Expansions for the distribution and quantiles of a regular functional of the empirical distribution with applications to nonparametric confidence intervals. Ann. Stat. 1983, 11, 577–587. [Google Scholar] [CrossRef]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Field, C.A.; Ronchetti, E. A tail area influence function and its application to testing. Sequential Anal. 1985, 4, 19–41. [Google Scholar] [CrossRef]
- Daniels, H.E. Saddlepoint approximations for estimating equations. Biometrika 1983, 70, 89–96. [Google Scholar] [CrossRef]
- Lugannani, R.; Rice, S. Saddle point approximation for the distribution of the sum of independent random variables. Adv. Appl. Probab. 1980, 12, 475–490. [Google Scholar] [CrossRef]
- García-Pérez, A. Von Mises approximation of the critical value of a test. Test 2003, 12, 385–411. [Google Scholar] [CrossRef]
- Jensen, J.L. Saddlepoint Approximations; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Viena, Austria, 2021; Available online: http://www.R-project.org (accessed on 18 April 2022).
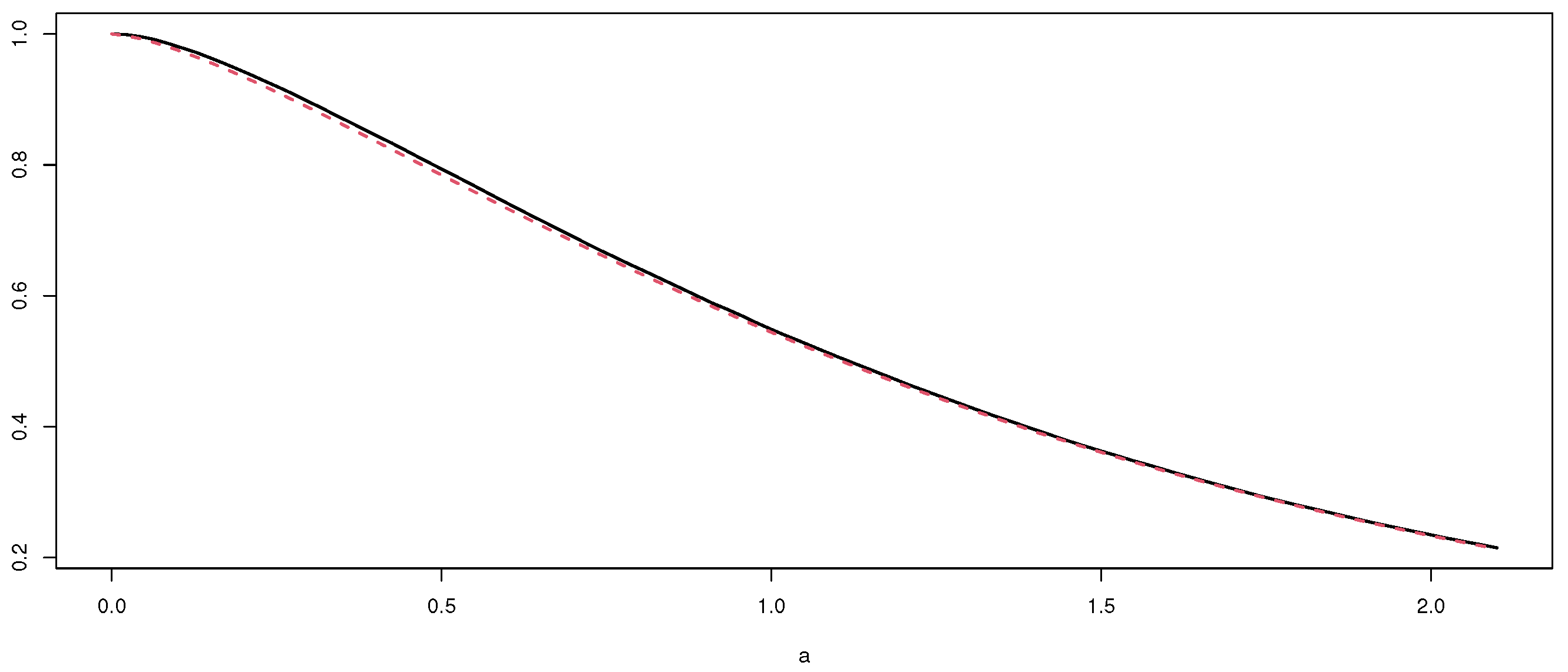
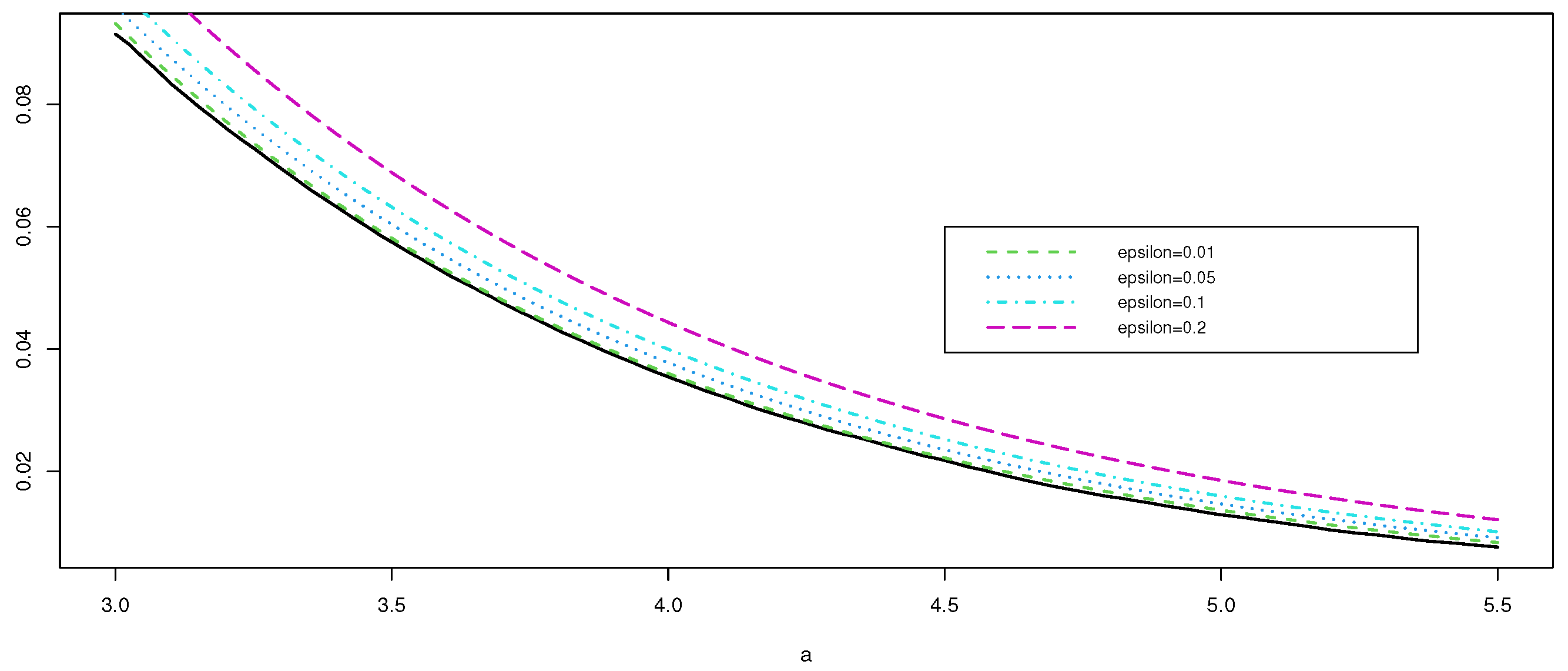
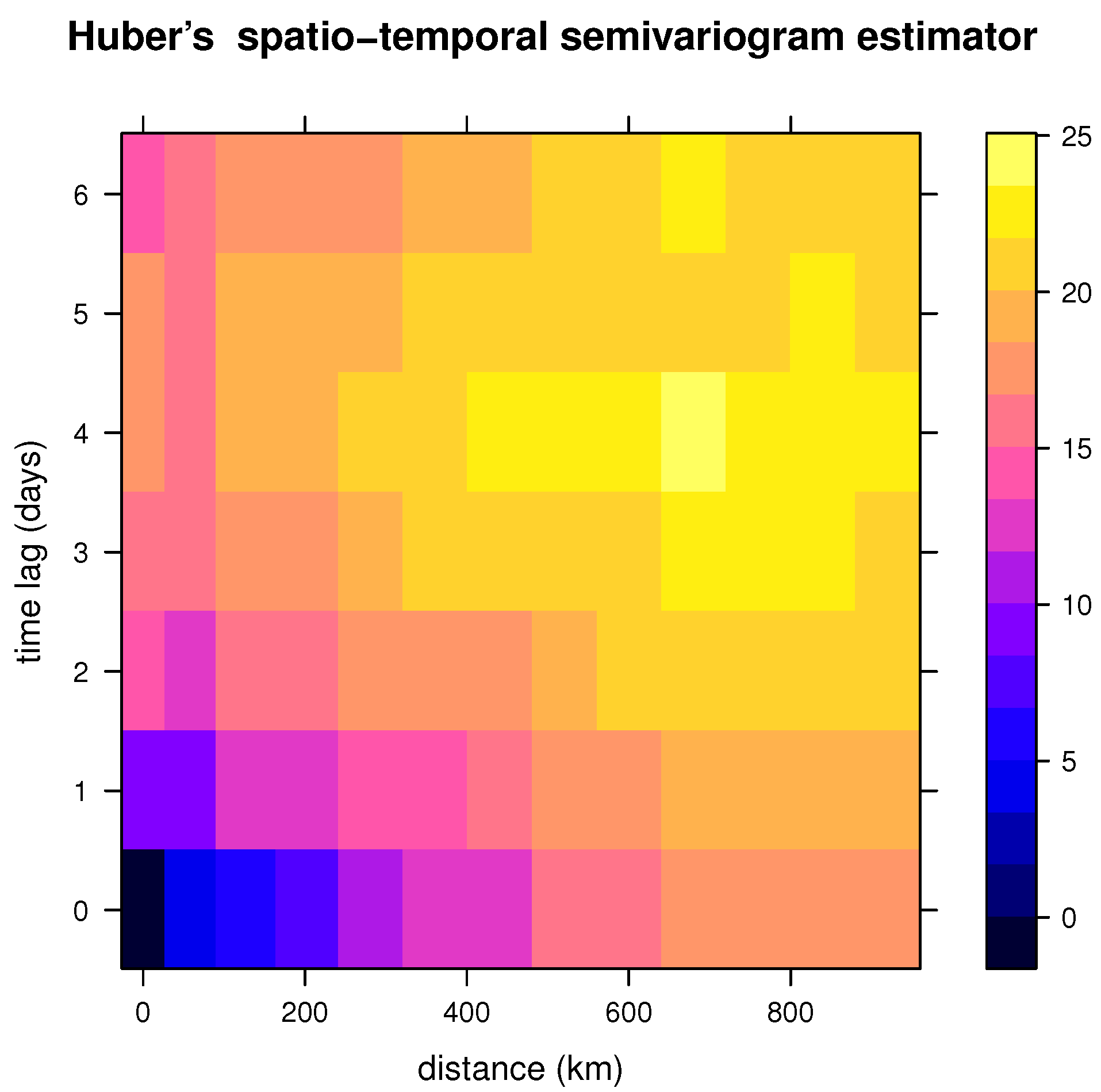
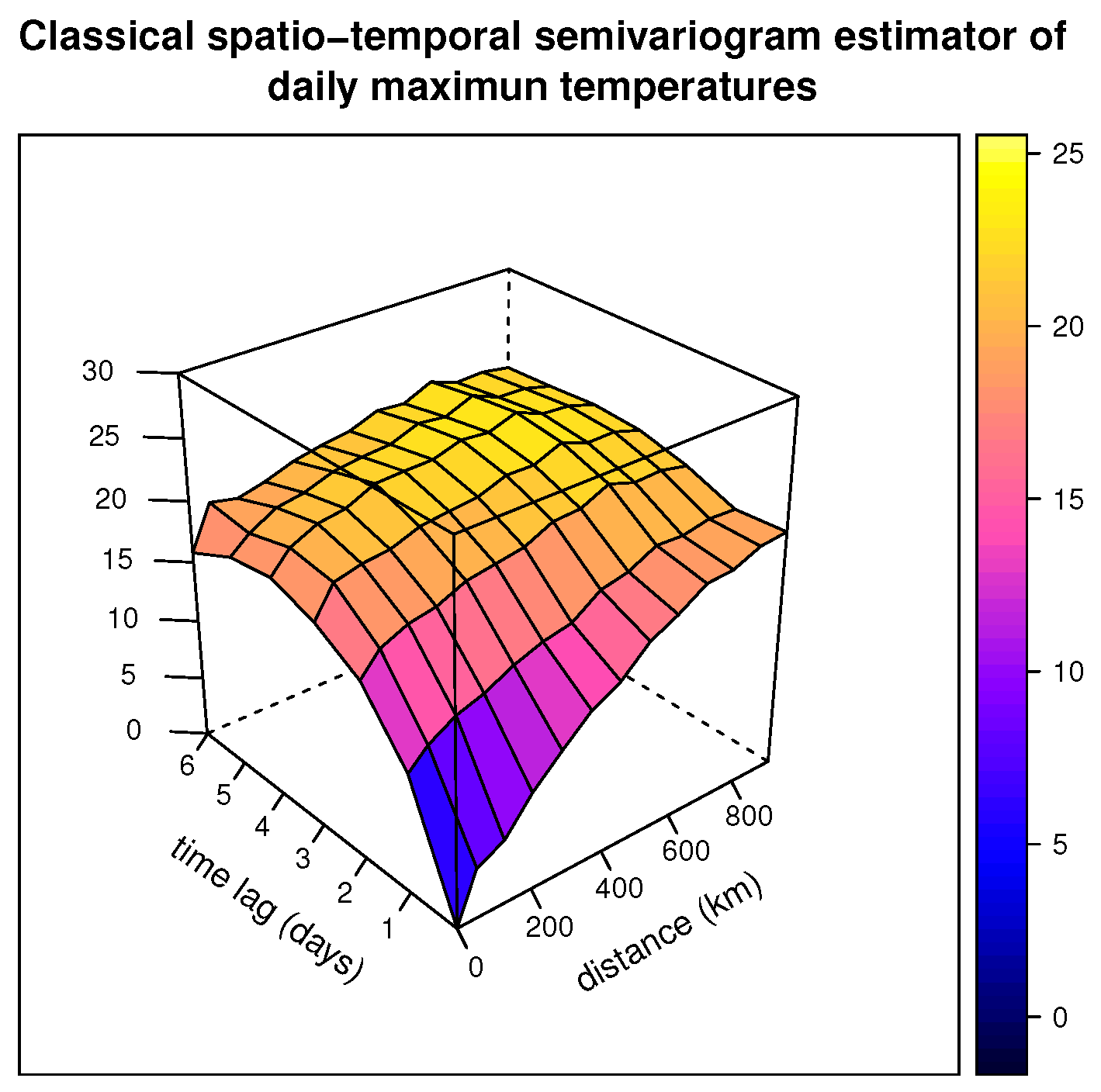

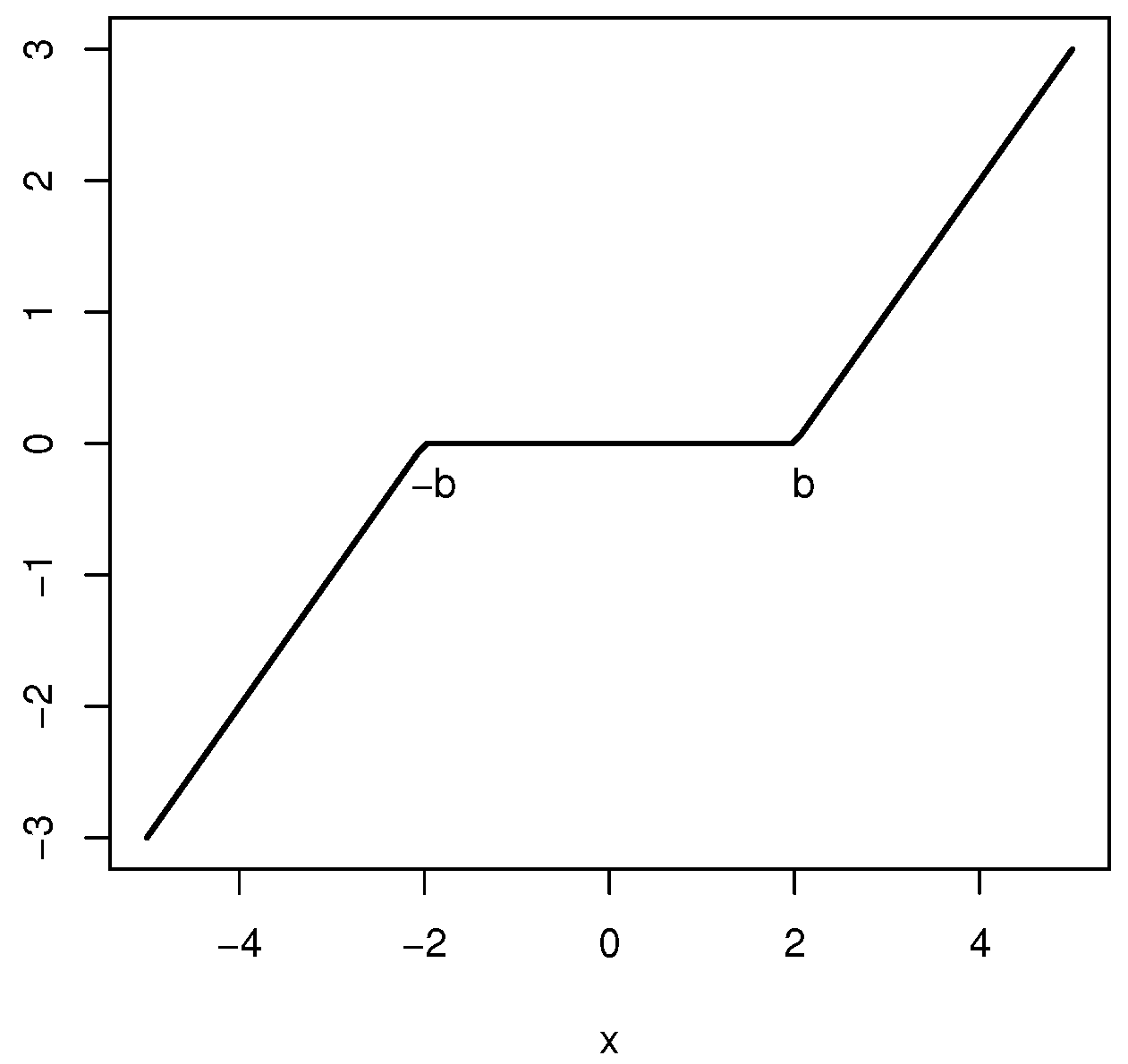

| a | Exact | Approximation |
|---|---|---|
| 2.5 | 0.14714 | 0.148299 |
| 3.0 | 0.09308 | 0.093233 |
| 3.5 | 0.05577 | 0.058124 |
| 4.0 | 0.03548 | 0.036006 |
| 4.5 | 0.02089 | 0.022196 |
| 5.0 | 0.01313 | 0.013633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Pérez, A. On Robustness for Spatio-Temporal Data. Mathematics 2022, 10, 1785. https://doi.org/10.3390/math10101785
García-Pérez A. On Robustness for Spatio-Temporal Data. Mathematics. 2022; 10(10):1785. https://doi.org/10.3390/math10101785
Chicago/Turabian StyleGarcía-Pérez, Alfonso. 2022. "On Robustness for Spatio-Temporal Data" Mathematics 10, no. 10: 1785. https://doi.org/10.3390/math10101785






