2.1. Efficient Market Hypothesis
In his Foundations of Finance (1976), Fama wrote: “An efficient capital market is a market that is efficient in processing information. The prices of securities observed at any time are based on ‘correct’ evaluation of all information available at that time. In an efficient market, prices ‘fully reflect’ available information.” (
Fama 1976, p. 134). This statement provides a central message regarding the importance of the timing of price information and market efficiency. Under this mechanism, stock prices provide an accurate signal to traders, which allows them to evaluate the value of firms. That is, firms can raise funds to finance their activities by selling securities at fair prices, and investors are able to acquire these assets at prices that fully reflect their underlying intrinsic values. In this sense, prices play a significant and effective function in allocating resources.
The essence of efficient market can be seen from its pricing process. This assumes that market participants at time
t − 1 use market information
to assess a joint distribution of security prices for time
t as of
{
, where
is the price of security
i at time
t and
i = 1, 2, …,
n. From this assessment of the distribution of prices, the market observes appropriate prices {
for individual securities, which in turn gives rise to the aggregate market price,
. Note that the information given by
includes not only the prices per se, but also the process that describes the evolution of the state of the market over time. It follows that the market price,
can be used to predict the expected price in
t given by:
The above expression can be written as:
This expression implies that errors in forecasting
using
on average approach zero. This also informs investors that if there are deviations by using
in predicting the future stock price,
the errors must be associated with random news that hits the market between time
t − 1 and
t.
2 Since price is sensitive to news, which arrives randomly in the market, the stock price can be said to wander along a random course. An analysis of an efficient market then tends to explore whether or not the market does, in fact, use available information in setting stock prices. One way to approach this issue is to explore whether the source of information for future price movements is associated with past prices. Let us consider that the one-period price evolves with a constant equilibrium rate,
, as:
Taking the natural logarithm using
=
ln(
), we obtain:
where
is the constant rate of an expected price change in the natural logarithm,
is independently and identically distributed (iid) with mean 0 and variance
and is expressed as
iid (0,
). The above expression in Equation (4) can be called a random walk with a drift, which can be alternatively expressed as:
where
=
.
Taking expectation on prices, the notion of Equation (2) then can be expressed as:
Equation (5) suggests that an expected stock return deviates from its equilibrium is expected to be zero, which implies there are no systematic excess profits that can be explored by checking the evolution of stock returns over time. To test this proposition, a linear regression function can be used and expressed as:
It follows that market efficiency, in combination with the assumption of constant expected returns over time, implies an absence of autocorrelation of the returns with s order of lags. Thus, the null hypothesis is: for s = 1, 2, …, S. A further test of market efficiency can be achieved by examining whether is orthogonal to any lagged news.
In analyzing the market efficiency, researchers opt to apply the random walk process to describe the possible correlations of information dependency.
Campbell et al. (
1997) clearly distinguish the notion of independent assumption from that of a serial correlation and note that the assumption of incremental iid is too strong (
Campbell et al. 1997), since even though Cov[
0 cannot be rejected, Cov[
,
= 0 for some
s ≠ 0 is usually rejected. This has been displayed in stock return series where large returns tend to be followed by large returns, or the volatility of stock returns appears to be highly dependent, presenting a clustering phenomenon shown in most GARCH-type conditional variance (
Ding et al. 1993;
Chen and Chiang 2016;
Chen et al. 2018).
2.2. The Model with News Information
Empirical analysis of the impact of news on stock returns follows two approaches. The first is to derive a news variable from rational expectations. Known as an efficient markets-rational expectations hypothesis (
Mishkin 1982), it posits that investors are rational, and are able to use econometric models and available information to form an optimal forecast of a state variable. Thus, the unpredicted component is nothing but the result of news hitting market. This approach has been proposed by
Mishkin (
1982);
Cornell (
1983);
Chiang (
1985);
Pearce and Roley (
1985) and
Lauterbach (
1989). Clearly, this approach simply relies on a policy/state variable, such as an unexpected change in money supply or a change in interest rates as a proxy for measuring monetary policy uncertainty, which in turn is used to test the news impact on stock returns.
The second approach is based on survey data of market participants or headline news, which forms the future economic prospects that influence stock returns. For instance,
McQueen and Roley (
1993) find that good news in an industrial production index raises stock prices.
Boyd et al. (
2005);
Leduc and Liu (
2016) and
Caggiano et al. (
2014) report that news of rising unemployment leads to contraction and lower expected earnings and hence results in lower stock prices.
Birz and Lott (
2011) choose newspaper articles as a measure of news. These authors indicate that news about GDP and unemployment affects stock returns.
Despite their success in linking macroeconomic news (
Birz and Lott 2011) to the stock returns, their choice of news variables is restricted to macroeconomic indicators and fails to include broad coverage of news, such as the political risk, changes in immigration policy, and trade wars among others, which could significantly disrupt prevailing economic conditions and therefore affect investors’ expectations and investment decisions. To alleviate the weakness arising from narrow news content, this study employs EPU indices which reflect broader news coverage as described in earlier. Further, most studies are focused on daily data; as a result, the impact of news has been treated as short lived. This approach ignores the longer-term effects on stock returns without investigating the delayed reactions to news. Finally, with the exception of
Flannery and Protopapadakis (
2002), very few studies pay attention to the issue of stock return heteroskedasticity. From an efficient market point of view, examining the dependency of volatility appears to be an integral part of analyzing investors’ behavior.
Motivated by the above empirical issues, this study employs EPU indices to serve as news variables. The literature suggests that EPU affects both stock returns (
Bansal et al. 2005;
Ozoguz 2009;
Antonakakis et al. 2013;
Lopez de Carvalho 2017) and stock variance (
Liu and Zhang 2015;
Chiang 2019). To incorporate this notion into the test equations, we write:
where Equation (7) is the mean equation,
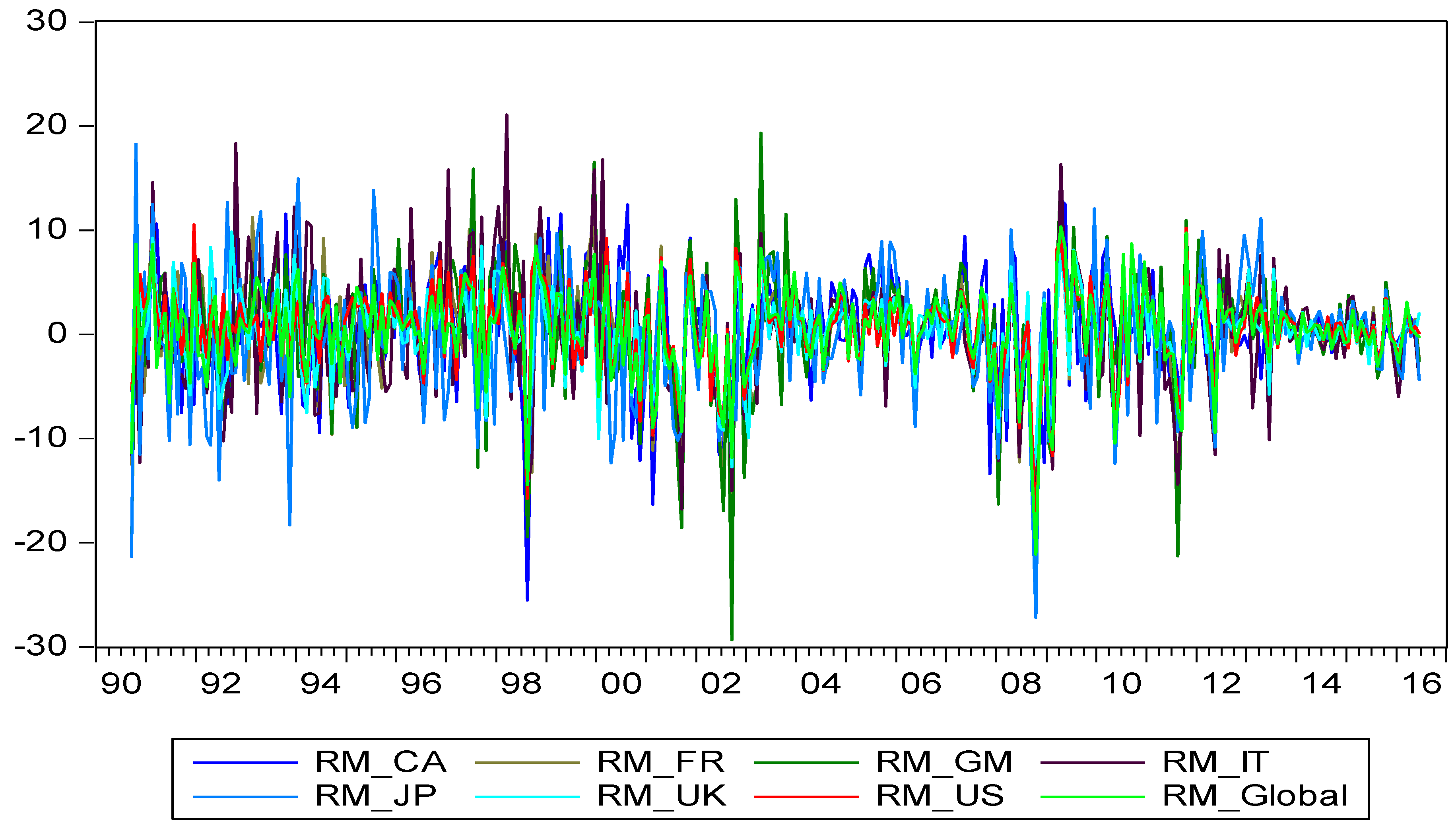
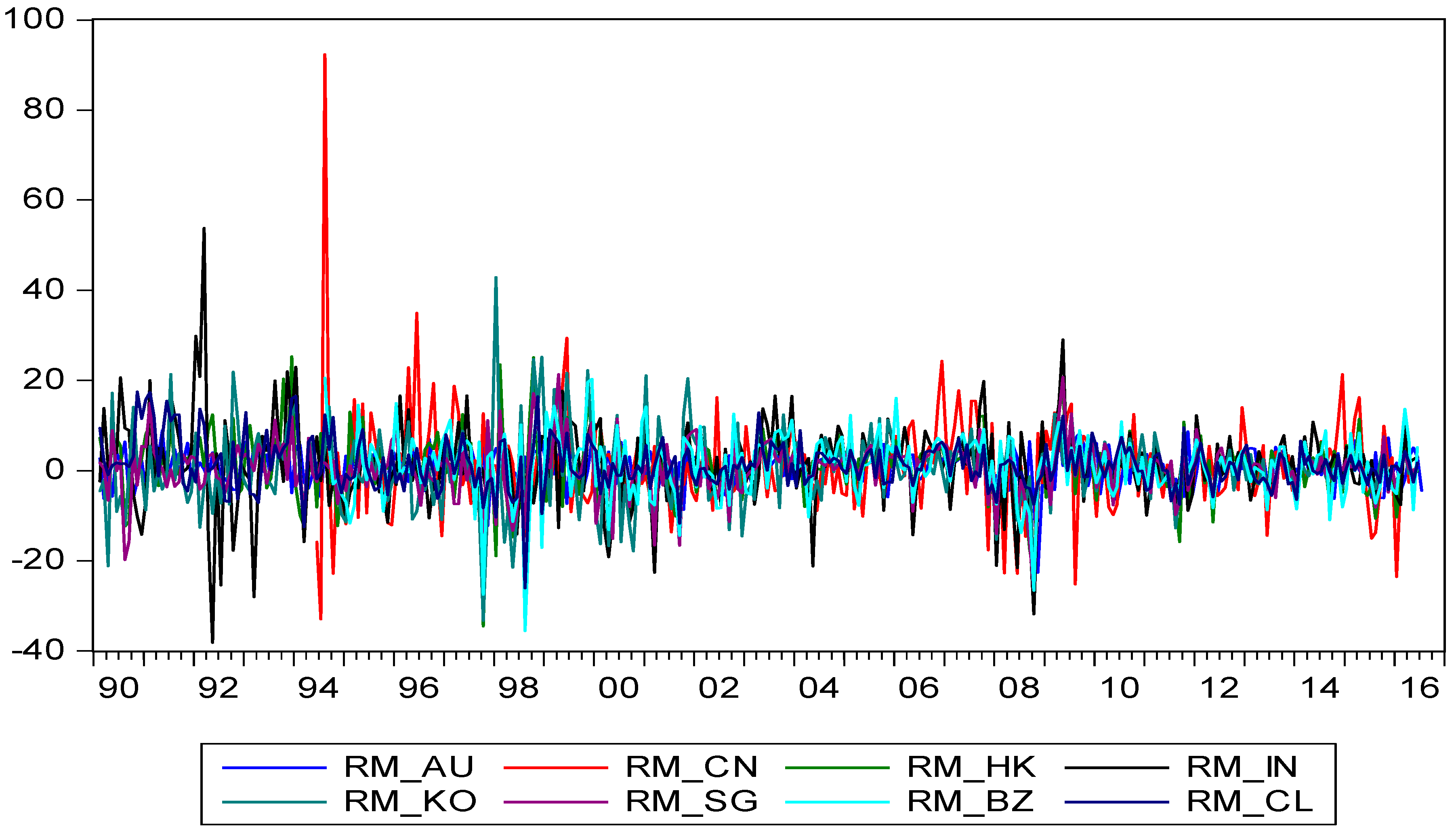
is the stock return,
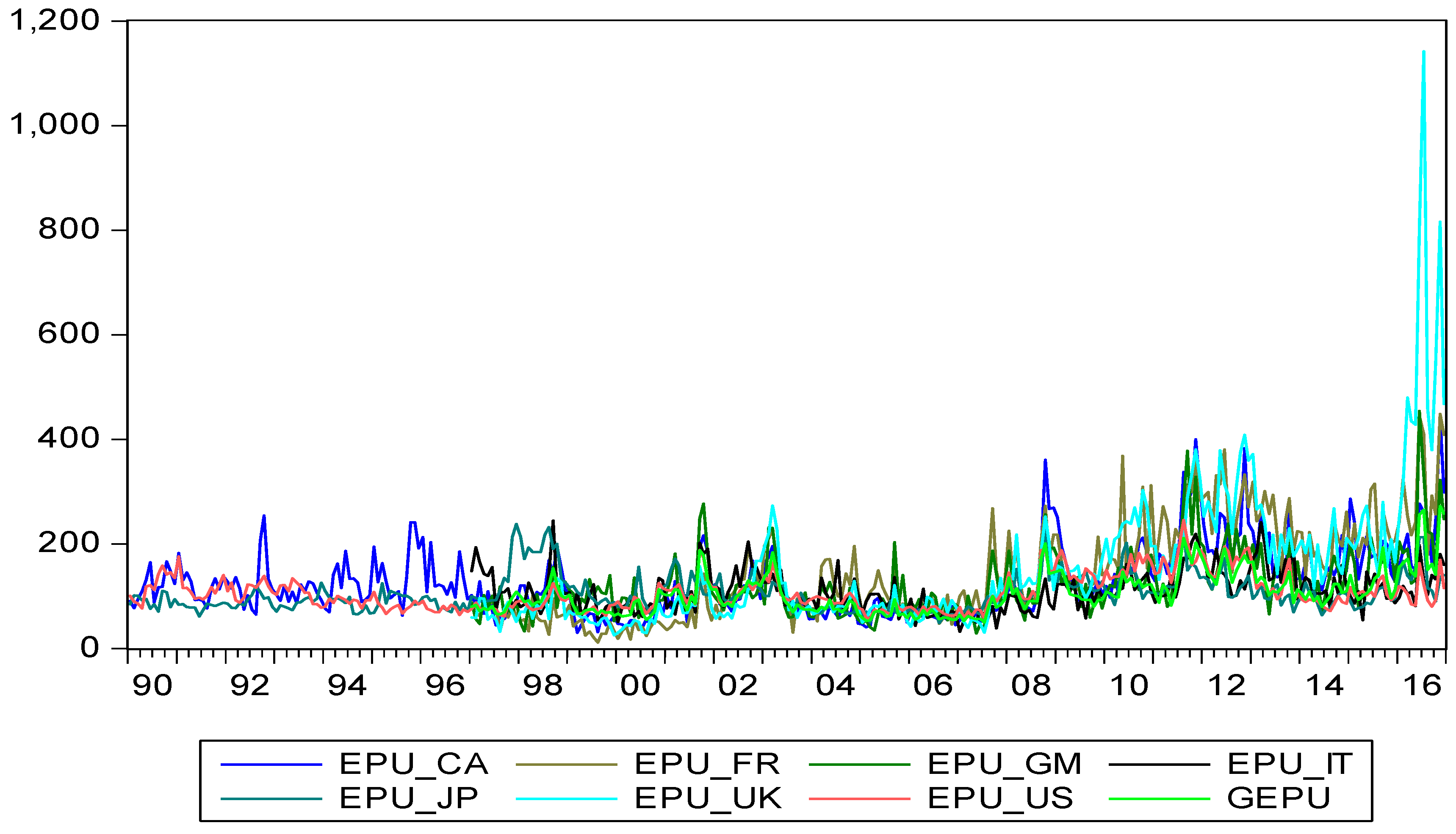
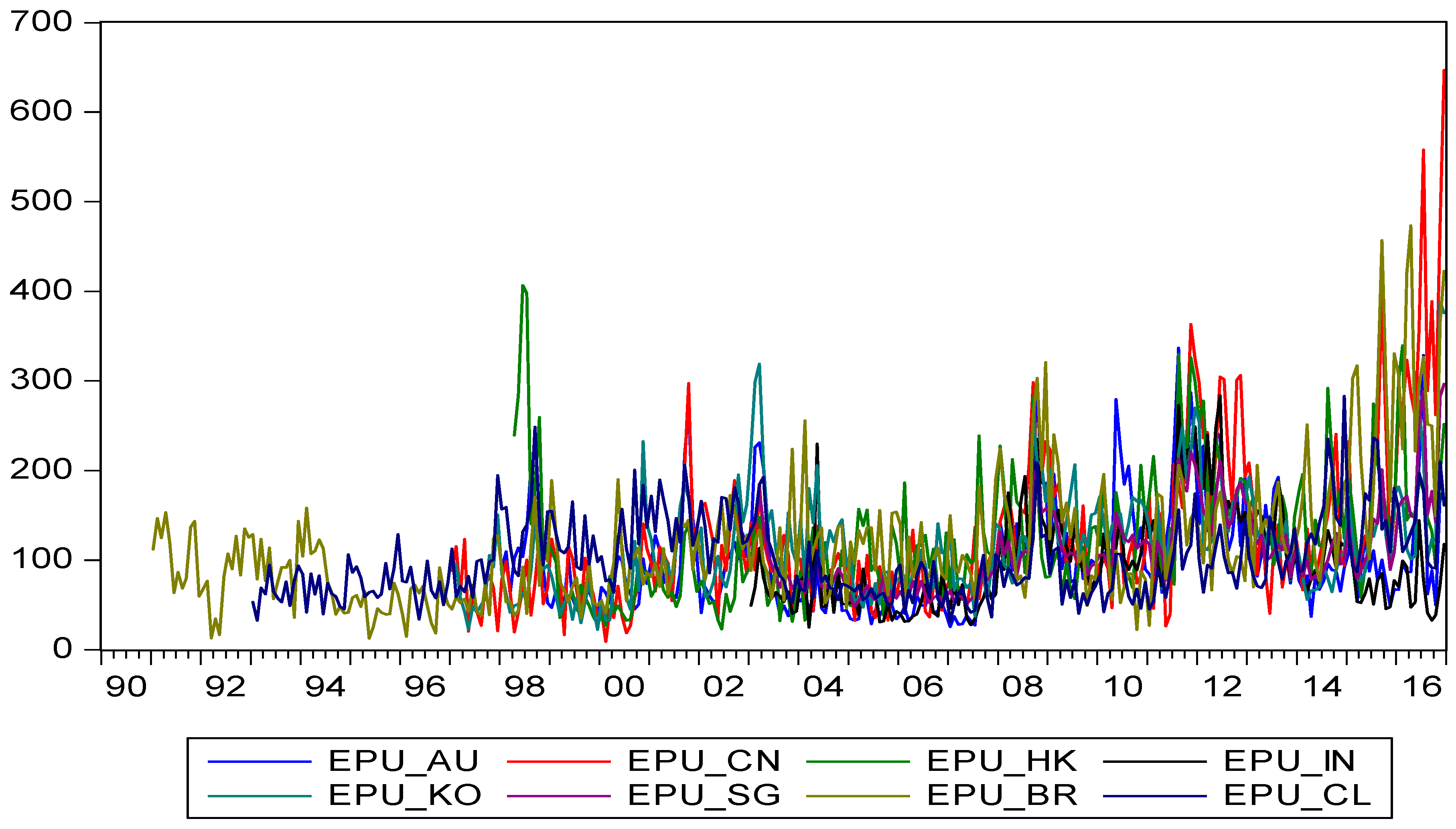
denotes the local
and
represents the global
The AR(1) term is included in Equation (7) to capture either the momentum effect resulted from a price ceiling or the positive feedback of trading. Equation (8) is the variance equation, which assumes the GARCH(1,1)
3 process. However, the EPU innovations from respective local markets and the global market are included in the variance equation to capture the local news shock and contagious effect from global markets (
Chiang et al. 2007;
Forbes 2012;
Bali and Cakici 2010). Finally, following
Nelson (
1991);
Li et al. (
2005);
Chiang and Zhang (
2018), the error series is assumed to follow the GED distribution, specified as
~ GED(0,
which accommodates the thickness of the tails of a distribution.
2.3. Uncertainty Premium Hypotheses
Equation (7) provides a dynamic regression framework pertinent to test uncertainties and stock returns, this section outlines each hypothesis as follows:
(i) Local uncertainty premium hypothesis
If a rise in
signifies a potential deterioration of economic activities that endangers future cash flows (
Bloom 2009;
Leduc and Liu 2016), it is expected that
0 would be rejected. Note a rejection of
0 is consistent with the EMH (
Li 2017;
Chen et al. 2017;
Lopez de Carvalho 2017). However, if
0 for
i ≥ 1 is rejected and there is a positive relation, then the market is inefficient and investors will be rewarded by an uncertainty premium from the local market.
(ii) Global uncertainty premium hypothesis
It is observed that an increase in uncertainty over the global market is soon learned by local investors via mass media, digital devices, trade connections or financial institution linkages, which will induce investors to reassess their portfolio positions (
Chiang et al. 2007;
Forbes 2012;
Klößner and Sekkel 2014;
Chen et al. 2018). This spillover hypothesis can be tested by examining
0. A rejection of
0 is consistent with the efficient-market hypothesis. However, if
0 is rejected, that is,
for
i ≥ 1 is rejected and
> 0, evidence would go against the EMH, and investors will be rewarded by an uncertainty premium from a rise in lagged global EPU.
(iii) Uncertainty innovation hypothesis
The literature suggests that uncertainty causes higher stock market volatility.
Liu and Zhang (
2015) show that the inclusion of EPU helps to improve forecasting ability of existing volatility models; and
Tsai (
2017) reports that EPU has a predictive ability not only to explain local stock volatility but also to describe cross market volatility. Testing these phenomena involves examining Cov[
,
= 0 and Cov[
,
= 0. In terms of Equation (8), the null hypothesis tests joint significance of
in a variance equation, which can be examined by Lagrange Multiplier (LM) test using the chi-squared distribution.