Impacts of Global Warming of 1.5, 2.0 and 3.0 °C on Hydrologic Regimes in the Northeastern U.S.
Abstract
:1. Introduction
2. Study Area
3. Dataset
3.1. GCM and Downscaled Output
3.2. Observed Meteorological and Streamflow Data
3.3. Determination of 1.5, 2.0 and 3.0 °C Time Periods
4. Methodology
4.1. Hydrological Modeling
4.2. Hydrologic Flow Conditions
4.3. Hydrological Indicators
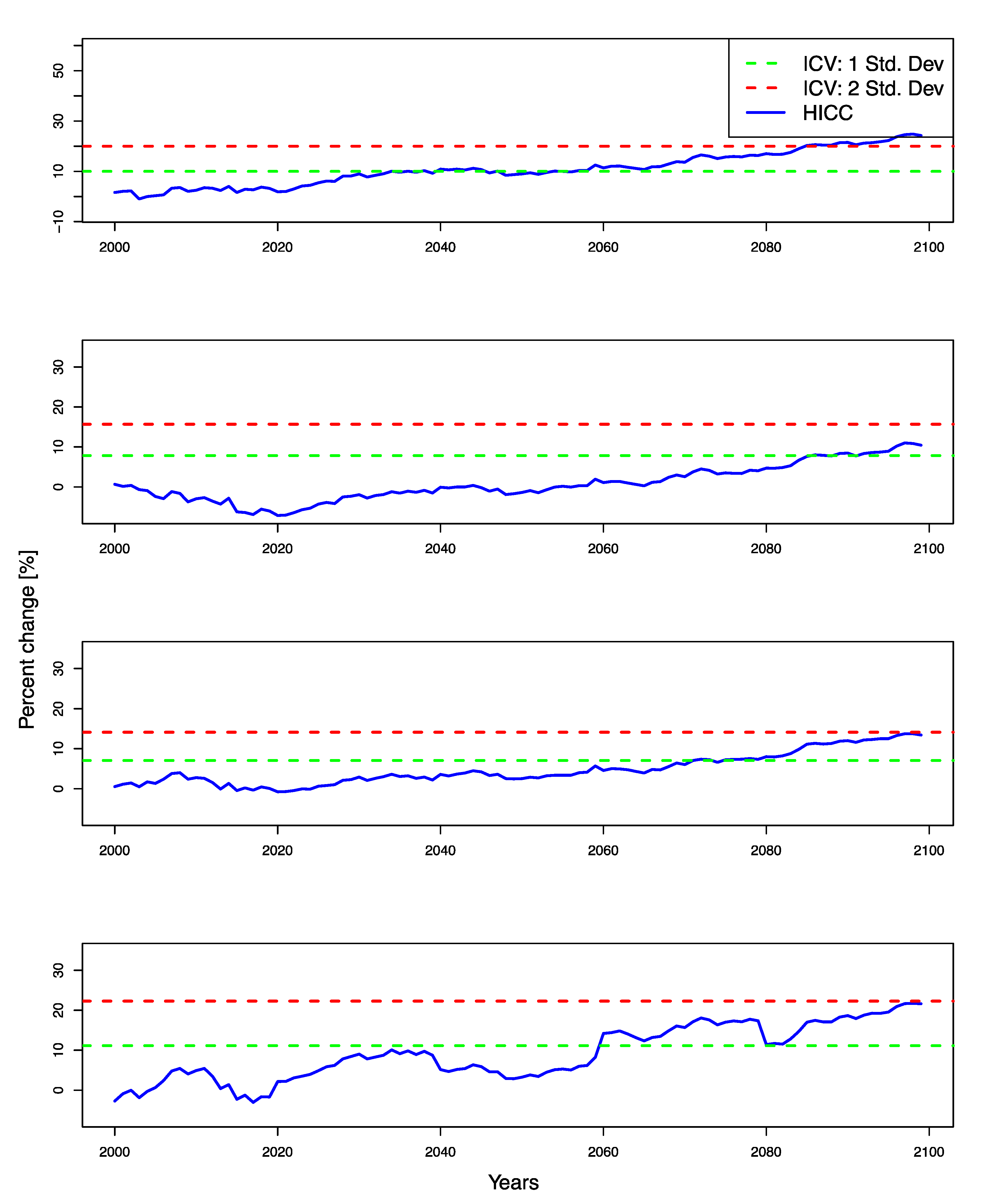
4.4. Estimation of Time of Emergence
- Using each of the 14 model simulations for the years 1980–2099, we estimated one hundred 20-year periods varying by one year, i.e., 1980–1999, 1981–2000, 1982–2001, …, 2080–2099.
- The 20-year mean value was calculated for each period. A total of 100 mean values were obtained for each climate simulation.
- The change in streamflow for each of 100 mean values relative to mean value at the reference period (1980–1999) was calculated
- The median value of these changes, which was represented by the model GISS-E2-R over 14 simulations, was defined as HICC.
- The standard deviation of the streamflow changes over members was calculated for each period and a total of 100 standard deviation values were obtained. ICV was then defined as ±2 or ±1 standard deviations of inter-member differences.
5. Results
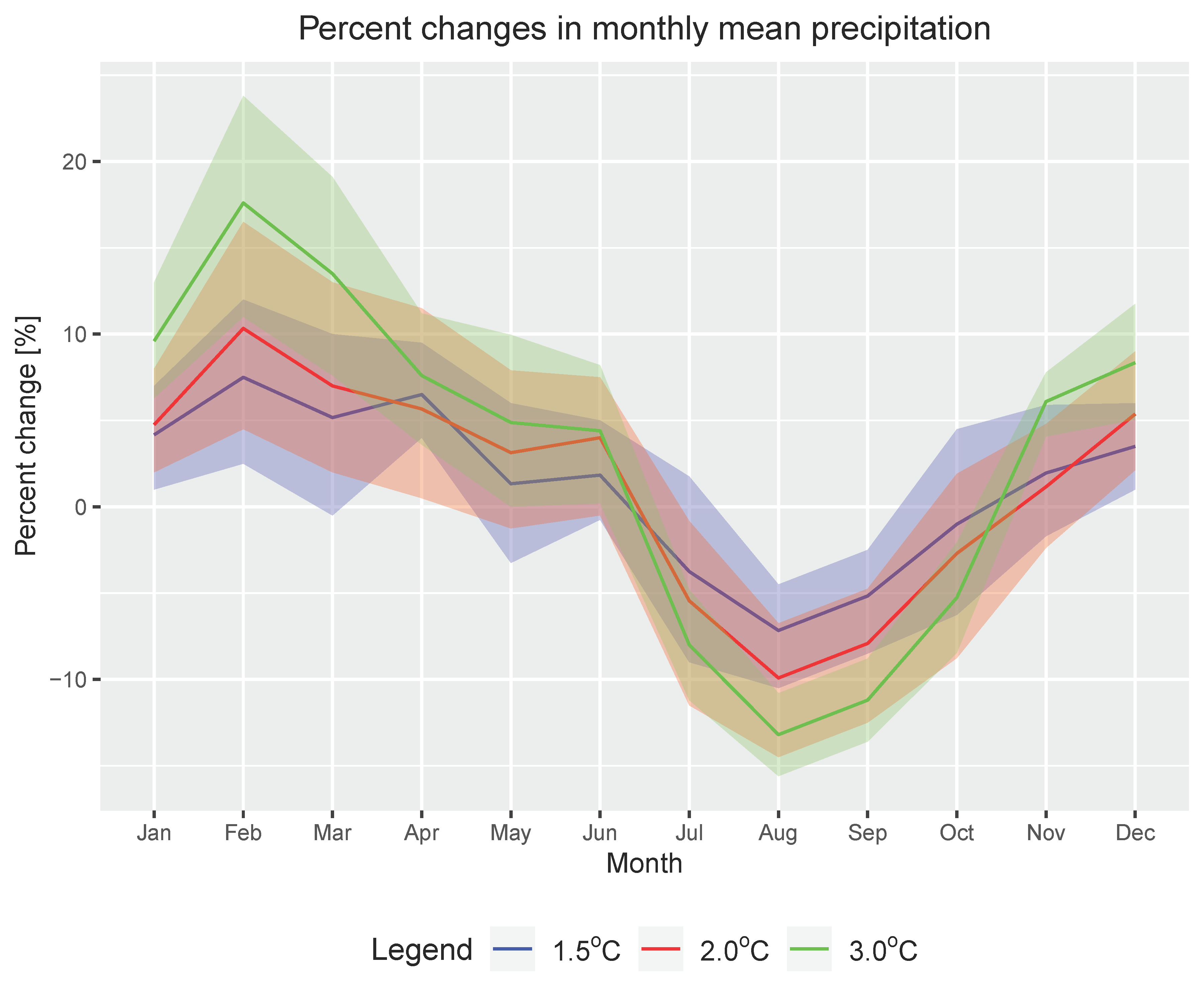
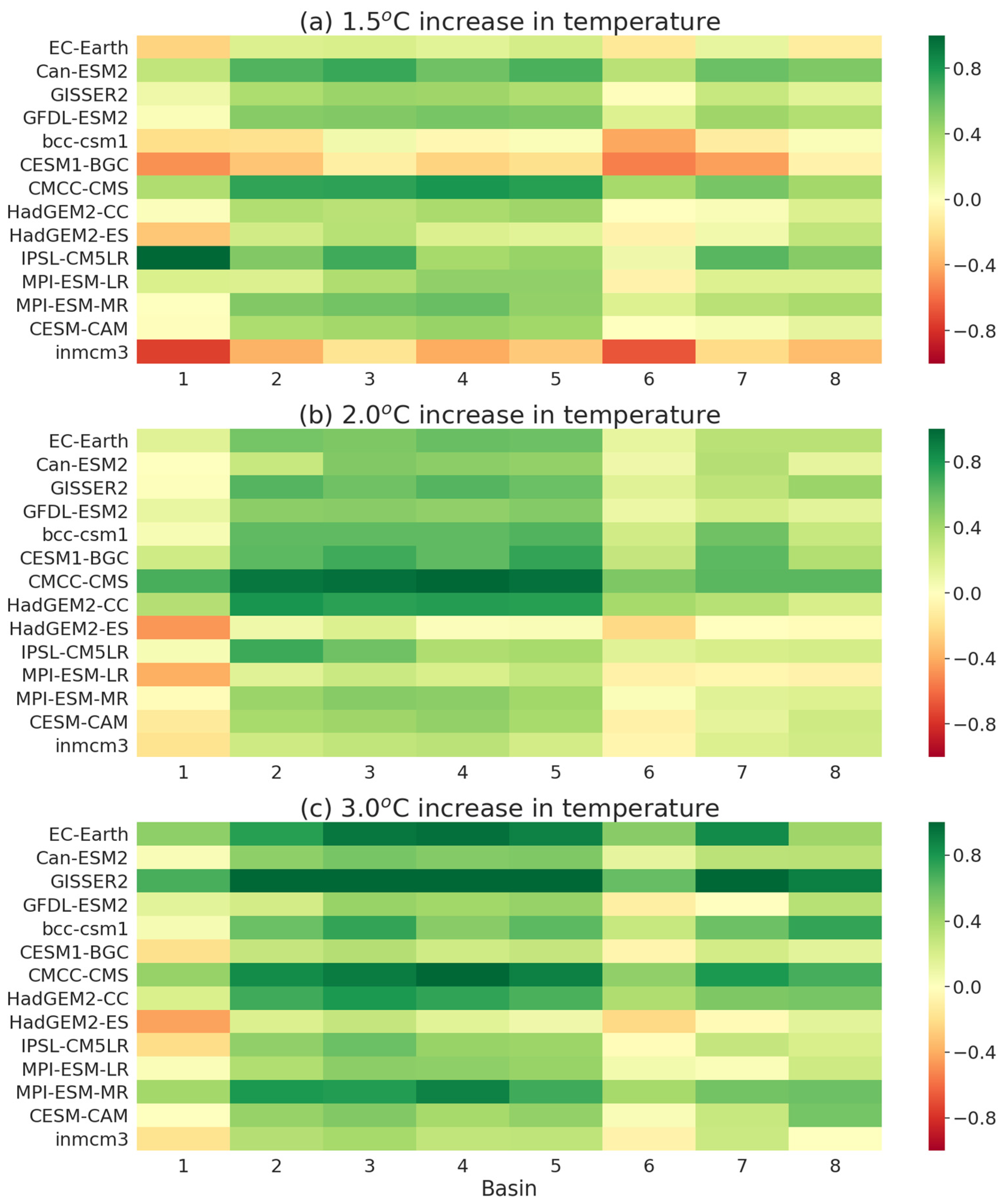
5.1. Changes in Precipitation
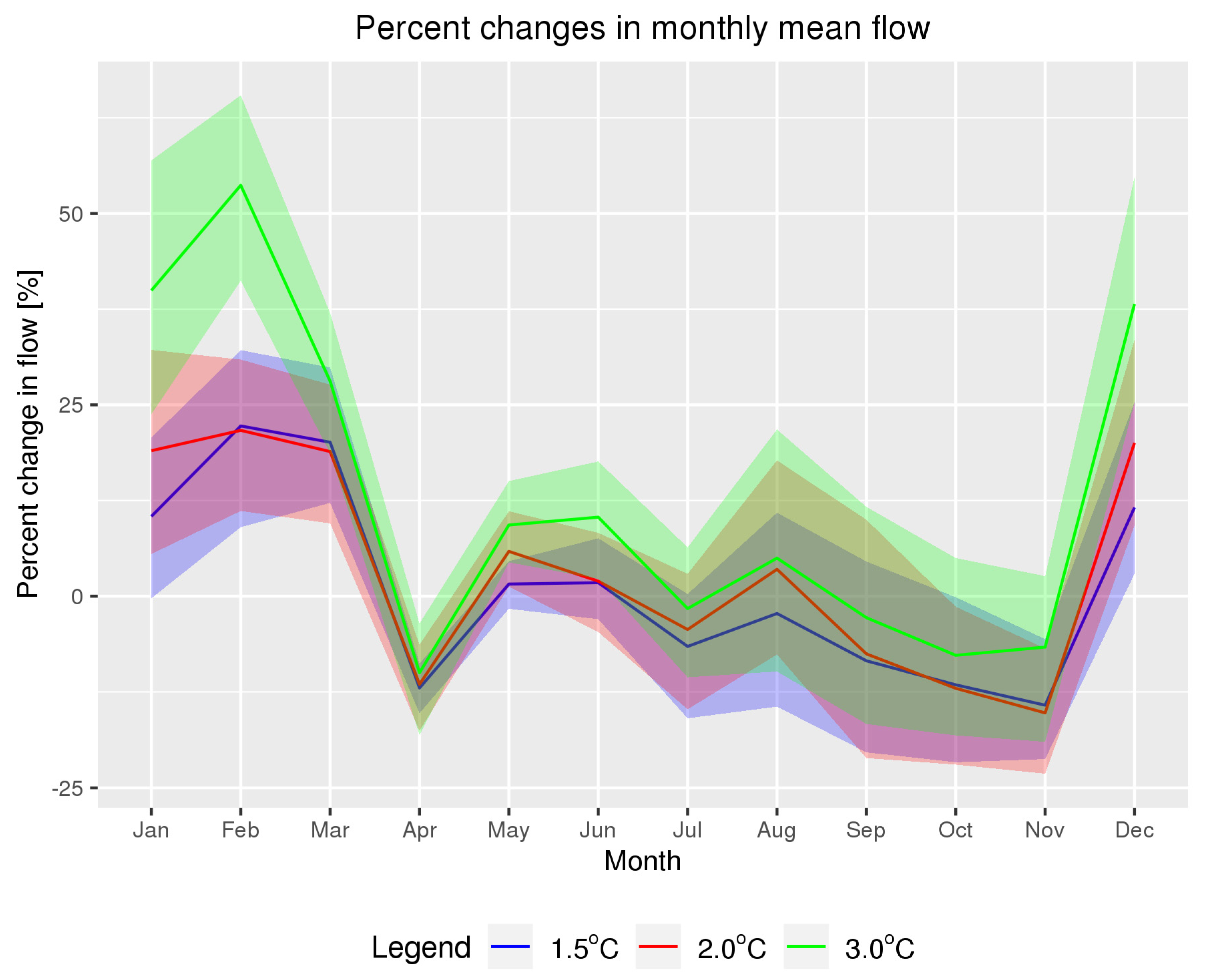
5.2. Changes in Streamflow Conditions
5.2.1. Magnitude
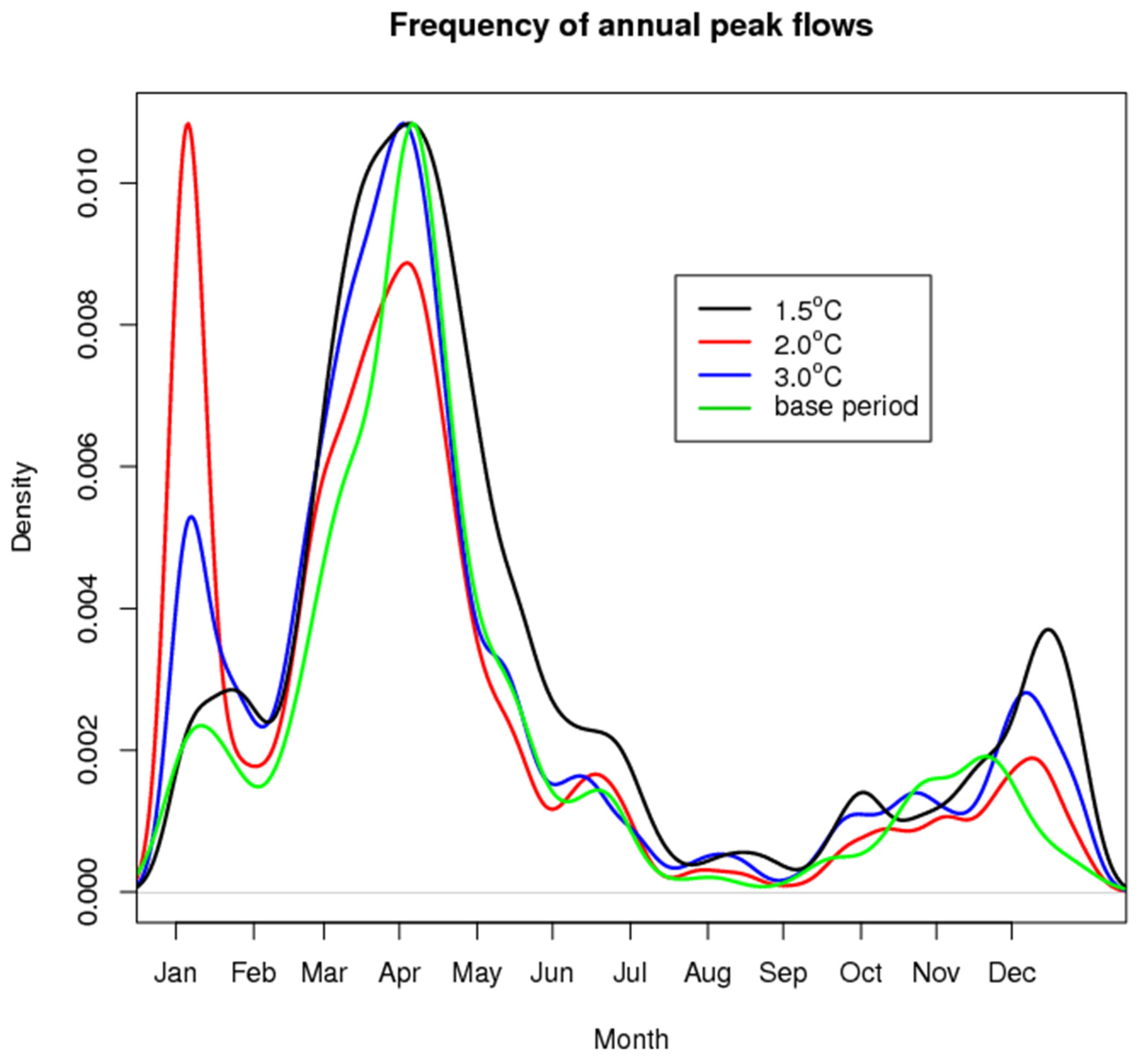
5.2.2. Frequency
5.3. Anomalies in Hydrological Flow Conditions
5.4. Alteration of Hydrologic Regimes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hirabayashi, Y.; Mahendran, R.; Koirala, S.; Konoshima, L.; Yamazaki, D.; Watanabe, S.; Kim, H.; Kanae, S. Global flood risk under climate change. Nat. Clim. Chang. 2013, 3, 816–821. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.A.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Abatzoglou, J.T.; Siebert, S.; Huning, L.S.; AghaKouchak, A.; Mankin, J.S.; Hong, C.; Tong, D.; Davis, S.J.; Mueller, N.D. Agricultural risks from changing snowmelt. Nat. Clim. Chang. 2020, 10, 459–465. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Hayhoe, K.; Wake, C.P.; Huntington, T.G.; Luo, L.; Schwartz, M.D.; Sheffield, J.; Wood, E.; Anderson, B.; Bradbury, J.; DeGaetano, A.; et al. Past and future changes in climate and hydrological indicators in the US Northeast. Clim. Dyn. 2007, 28, 381–407. [Google Scholar] [CrossRef]
- Siddique, R.; Karmalkar, A.; Fengyun., S.; Palmer, R.N. Hydrological extremes across the Commonwealth of Massachusetts. J. Hydrol. Reg. Stud. 2020. Under Review. [Google Scholar] [CrossRef]
- Siddique, R.; Palmer, R. Climate Change Impacts on Local Flood Risks in the U.S. Northeast: A Case Study on the Connecticut and Merrimack River Basins. JAWRA J. Am. Water Resour. Assoc. 2020. [Google Scholar] [CrossRef]
- Campbell, J.L.; Driscoll, C.T.; Pourmokhtarian, A.; Hayhoe, K. Streamflow responses to past and projected future changes in climate at the Hubbard Brook Experimental Forest, New Hampshire, United States. Water Resour. Res. 2011, 47, W02514. [Google Scholar] [CrossRef]
- Betsill, M.; Dubash, N.K.; Paterson, M.; van Asselt, H.; Vihma, A.; Winkler, H. Building productive links between the UNFCCC and the broader global climate governance landscape. Glob. Environ. Politics 2015, 15, 1–10. [Google Scholar] [CrossRef]
- Rogelj, J.; den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friedlingstein, P.; Andrew, R.M.; Rogelj, J.; Peters, G.P.; Canadell, J.G.; Knutti, R.; Luderer, G.; Raupach, M.R.; Schaeffer, M.; van Vuuren, D.P.; et al. Persistent growth of CO2 emissions and implications for reaching climate targets. Nat. Geosci. 2014, 7, 709. [Google Scholar] [CrossRef]
- Gosling, S.N.; Zaherpour, J.; Mount, N.J.; Hattermann, F.F.; Dankers, R.; Arheimer, B.; Breuer, L.; Ding, J.; Haddeland, I.; Kumar, R. A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 C, 2 C and 3 C. Clim. Chang. 2017, 141, 577–595. [Google Scholar] [CrossRef]
- Demaria, E.M.C.; Palmer, R.N.; Roundy, J.K. Regional climate change projections of streamflow characteristics in the Northeast and Midwest U.S. J. Hydrol. Reg. Stud. 2016, 5, 309–323. [Google Scholar] [CrossRef] [Green Version]
- Marshall, E.; Randhir, T. Effect of climate change on watershed system: A regional analysis. Clim. Chang. 2008, 89, 263–280. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G.; Ahmed, K.F. Hydrological changes in the U.S. Northeast using the Connecticut River Basin as a case study: Part 2. Projections of the future. Glob. Planet. Chang. 2015, 133, 167–175. [Google Scholar] [CrossRef]
- Parr, D.; Wang, G. Hydrological changes in the U.S. Northeast using the Connecticut River Basin as a case study: Part 1. Modeling and analysis of the past. Glob. Planet. Chang. 2014, 122, 208–222. [Google Scholar] [CrossRef]
- Mitchell, D.; James, R.; Forster, P.M.; Betts, R.A.; Shiogama, H.; Allen, M. Realizing the impacts of a 1.5 C warmer world. Nat. Clim. Chang. 2016, 6, 735. [Google Scholar] [CrossRef] [Green Version]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Voisin, N.; Zhang, X.; Asrar, G.R.; Leung, L.R. Emergence of new hydrologic regimes of surface water resources in the conterminous United States under future warming. Environ. Res. Lett. 2016, 11, 114003. [Google Scholar] [CrossRef]
- Marx, A.; Kumar, R.; Thober, S.; Rakovec, O.; Wanders, N.; Zink, M.; Wood, E.F.; Pan, M.; Sheffield, J.; Samaniego, L. Climate change alters low flows in Europe under global warming of 1.5, 2, and 3° C. Hydrol. Earth Syst. Sci. 2018, 22, 1017–1032. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213. [Google Scholar] [CrossRef] [Green Version]
- Karmalkar, A.V.; Thibeault, J.M.; Bryan, A.M.; Seth, A. Identifying credible and diverse GCMs for regional climate change studies—case study: Northeastern United States. Clim. Change 2019, 154, 367–386. [Google Scholar] [CrossRef]
- Pierce, D.W.; Cayan, D.R.; Thrasher, B.L. Statistical downscaling using localized constructed analogs (LOCA). J. Hydrometeorol. 2014, 15, 2558–2585. [Google Scholar] [CrossRef]
- Zhang, J.; Howard, K.; Langston, C.; Vasiloff, S.; Kaney, B.; Arthur, A.; Van Cooten, S.; Kelleher, K.; Kitzmiller, D.; Ding, F. National Mosaic and Multi-Sensor QPE (NMQ) system: Description, results, and future plans. Bull. Am. Meteorol. Soc. 2011, 92, 1321–1338. [Google Scholar] [CrossRef] [Green Version]
- Prat, O.P.; Nelson, B.R. Evaluation of precipitation estimates over CONUS derived from satellite, radar, and rain gauge data sets at daily to annual scales (2002–2012). Hydrol. Earth Syst. Sci. 2015, 19, 2037. [Google Scholar] [CrossRef] [Green Version]
- Seo, D.-J.; Siddique, R.; Ahnert, P. Objective reduction of rain gauge network via geostatistical analysis of uncertainty in radar-gauge precipitation estimation. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Siddique, R.; Mejia, A.; Brown, J.; Reed, S.; Ahnert, P. Verification of precipitation forecasts from two numerical weather prediction models in the Middle Atlantic Region of the USA: A precursory analysis to hydrologic forecasting. J. Hydrol. 2015, 529. [Google Scholar] [CrossRef]
- Yang, X.; Sharma, S.; Siddique, R.; Greybush, S.J.; Mejia, A. Postprocessing of GEFS precipitation ensemble reforecasts over the U.S. mid-atlantic region. Mon. Weather Rev. 2017, 145. [Google Scholar] [CrossRef] [Green Version]
- James, R.; Washington, R.; Schleussner, C.-F.; Rogelj, J.; Conway, D. Characterizing half-a-degree difference: A review of methods for identifying regional climate responses to global warming targets. WIREs Clim. Chang. 2017, 8, e457. [Google Scholar] [CrossRef] [Green Version]
- Fischer, E.M.; Knutti, R. Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat. Clim. Chang. 2015, 5, 560–564. [Google Scholar] [CrossRef]
- Swain, S.; Hayhoe, K. CMIP5 projected changes in spring and summer drought and wet conditions over North America. Clim. Dyn. 2015, 44, 2737–2750. [Google Scholar] [CrossRef]
- Karmalkar, A.V.; Bradley, R.S. Consequences of Global Warming of 1.5 °C and 2 °C for Regional Temperature and Precipitation Changes in the Contiguous United States. PLoS ONE 2017, 12, e0168697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koren, V.; Reed, S.; Smith, M.; Zhang, Z.; Seo, D.-J. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service. J. Hydrol. 2004, 291, 297–318. [Google Scholar] [CrossRef] [Green Version]
- Koren, V.; Smith, M.; Cui, Z. Physically-based modifications to the Sacramento Soil Moisture Accounting model. Part A: Modeling the effects of frozen ground on the runoff generation process. J. Hydrol. 2014, 519, 3475–3491. [Google Scholar] [CrossRef]
- Siddique, R.; Mejia, A. Ensemble Streamflow Forecasting across the US Mid-Atlantic Region with a Distributed Hydrological Model Forced by GEFS Reforecasts. J. Hydrometeorol. 2017, 18, 1905–1928. [Google Scholar] [CrossRef]
- Wood, A.W.; Hopson, T.; Newman, A.; Brekke, L.; Arnold, J.; Clark, M. Quantifying streamflow forecast skill elasticity to initial condition and climate prediction skill. J. Hydrometeorol. 2016, 17, 651–668. [Google Scholar] [CrossRef]
- Sharma, S.; Siddique, R.; Reed, S.; Ahnert, P.; Mendoza, P.; Mejia, A. Relative effects of statistical preprocessing and postprocessing on a regional hydrological ensemble prediction system. Hydrol. Earth Syst. Sci. 2018, 22. [Google Scholar] [CrossRef] [Green Version]
- Burnash, R.J.C. The NWS river forecast system-catchment modeling. Comput. Model. Watershed Hydrol. 1995, 188, 311–366. [Google Scholar]
- Armstrong, D.S.; Parker, G.W.; Richards, T.A. Characteristics and Classification of least Altered Streamflows in Massachusetts; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2008; ISBN 141132188X.
- Archfield, S.; Vogel, R.; Steeves, P.; Brandt, S.; Weiskel, P.; Garabedian, S. The Massachusetts Sustainable-Yield Estimator: A decision-support tool to assess water availability at ungaged sites in Massachusetts. US Geol. Surv. Sci. Investig. Rep. 2009, 5227, 2010. [Google Scholar]
- Kuzmin, V.; Seo, D.-J.; Koren, V. Fast and efficient optimization of hydrologic model parameters using a priori estimates and stepwise line search. J. Hydrol. 2008, 353, 109–128. [Google Scholar] [CrossRef]
- Deser, C.; Knutti, R.; Solomon, S.; Phillips, A.S. Communication of the role of natural variability in future North American climate. Nat. Clim. Chang. 2012, 2, 775–779. [Google Scholar] [CrossRef]
- Fyfe, J.C.; Gillett, N.P.; Zwiers, F.W. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in projections of regional precipitation change. Clim. Dyn. 2011, 37, 407–418. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1108. [Google Scholar] [CrossRef] [Green Version]
- Hawkins, E.; Sutton, R. Time of emergence of climate signals. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Bi, X. Time of emergence (TOE) of GHG-forced precipitation change hot-spots. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Zhuan, M.-J.; Chen, J.; Shen, M.-X.; Xu, C.-Y.; Chen, H.; Xiong, L.-H. Timing of human-induced climate change emergence from internal climate variability for hydrological impact studies. Hydrol. Res. 2018, 49, 421–437. [Google Scholar] [CrossRef]

| No. | USGS ID | Location | Area (km2) | Lat/Lon | Land Use |
|---|---|---|---|---|---|
| 1 | 01105600 | Old Swamp River, MA | 12.2 | 42°11′25″ 70°56′43″ | Forest, 41%; residential, 34% |
| 2 | 01169000 | North River at Shatteckville, MA | 230.69 | 42°38′18″ 72°43′32″ | Forested |
| 3 | 01162500 | Priest Brook near Winchedon, MA | 49.70 | 42°40′57″ 72°06′56″ | Mostly forested |
| 4 | 01176000 | Quaboag River near West Brimfield, MA | 387.16 | 42°10′56″ 72°15′51″ | Forested |
| 5 | 01096000 | Squannacook River near West Groton, MA | 173.14 | 42°38′03″ 71°39′30″ | 7.3% imperviousness, 18% permanently protected land area |
| 6 | 01095220 | Stillwater River near Sterling, MA | 78.69 | 42°24′39″ 71°47′30″ | Mostly undeveloped forest and wetlands |
| 7 | 01097380 | Nasoba Brook near Acton, MA | 33.17 | 42°30′45″ 71°24′17" | 25% protected open space, 10% impervious |
| 8 | 01100600 | Shawsheen River near Wilmington, MA | 96.42 | 42°34′05″ 71°12′55″ | 50% residential, 30% forest |
| Model | 1.5 °C | 2.0 °C | 3.0 °C |
|---|---|---|---|
| MPI-ESM-LR | 2012–2031 | 2030–2049 | 2058–2077 |
| HadGEM2-ES | 2020–2039 | 2028–2047 | 2049–2068 |
| CMCC-CMS | 2023–2042 | 2025–2044 | 2053–2072 |
| MPI-ESM-MR | 2015–2034 | 2023–2042 | 2053–2072 |
| inmcm4 | 2038–2057 | 2050–2069 | 2078–2097 |
| CanESM2 | 2009–2028 | 2022–2041 | 2043–2062 |
| GFDL-ESM2G | 2037–2056 | 2053–2072 | 2078–2097 |
| bcc-csm1-1-m | 2014–2033 | 2029–2048 | 2056–2075 |
| IPSL-CM5A-LR | 2009–2028 | 2023–2042 | 2043–2062 |
| GISS-E2-R | 2027–2046 | 2047–2066 | 2080–2099 |
| HadGEM2-CC | 2015–2034 | 2031–2050 | 2050–2069 |
| CESM1-BGC | 2009–2028 | 2025–2044 | 2051–2070 |
| bcc-csm1-1 | 2016–2035 | 2028–2047 | 2053–2072 |
| CESM1-CAM5 | 2022–2041 | 2034–2053 | 2049–2068 |
| No. | USGS ID | Location | NSE | KGE | PB |
|---|---|---|---|---|---|
| 1 | 01105600 | Old Swamp River, MA | 0.68 | 0.61 | 8.76% |
| 2 | 01169000 | North River at Shatteckville, MA | 0.72 | 0.65 | 12.30% |
| 3 | 01162500 | Priest Brook near Winchedon, MA | 0.63 | 0.57 | 13.10% |
| 4 | 01176000 | Quaboag River near West Brimfield, MA | 0.69 | 0.66 | 6.23% |
| 5 | 01096000 | Squannacook River near West Groton, MA | 0.59 | 0.62 | 10.38% |
| 6 | 01095220 | Stillwater River near Sterling, MA | 0.78 | 0.71 | 3.48% |
| 7 | 01097380 | Nasoba Brook near Acton, MA | 0.58 | 0.52 | 15.62% |
| 8 | 01100600 | Shawsheen River near Wilmington, MA | 0.56 | 0.62 | 9.72% |
| ICV: 1 Std. Dev | ICV: 2 Std. Dev | ||||||
|---|---|---|---|---|---|---|---|
| 1.5 °C | 2.0 °C | 3.0 °C | 1.5 °C | 2.0 °C | 3.0 °C | ||
| Basin 1 | Wet | Yes | Yes | Yes | No | No | No |
| Dry | No | No | No | No | No | No | |
| Annual | No | No | Yes | No | No | No | |
| Basin 2 | Wet | Yes | Yes | Yes | No | No | Yes |
| Dry | No | No | No | No | No | No | |
| Annual | No | Yes | Yes | No | No | Yes | |
| Basin 3 | Wet | Yes | Yes | Yes | No | No | Yes |
| Dry | No | No | Yes | No | No | No | |
| Annual | Yes | Yes | Yes | No | No | Yes | |
| Basin 4 | Wet | Yes | Yes | Yes | No | No | Yes |
| Dry | No | No | No | No | No | No | |
| Annual | No | Yes | Yes | No | No | Yes | |
| Basin 5 | Wet | Yes | Yes | Yes | No | No | Yes |
| Dry | No | No | No | No | No | No | |
| Annual | Yes | Yes | Yes | No | No | Yes | |
| Basin 6 | Wet | No | No | Yes | No | No | No |
| Dry | No | No | No | No | No | No | |
| Annual | No | No | Yes | No | No | No | |
| Basin 7 | Wet | Yes | Yes | Yes | No | No | Yes |
| Dry | No | No | No | No | No | No | |
| Annual | No | No | Yes | No | No | Yes | |
| Basin 8 | Wet | No | Yes | Yes | No | No | Yes |
| Dry | Yes | Yes | Yes | No | No | No | |
| Annual | No | No | Yes | No | No | Yes | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddique, R.; Mejia, A.; Mizukami, N.; Palmer, R.N. Impacts of Global Warming of 1.5, 2.0 and 3.0 °C on Hydrologic Regimes in the Northeastern U.S. Climate 2021, 9, 9. https://doi.org/10.3390/cli9010009
Siddique R, Mejia A, Mizukami N, Palmer RN. Impacts of Global Warming of 1.5, 2.0 and 3.0 °C on Hydrologic Regimes in the Northeastern U.S. Climate. 2021; 9(1):9. https://doi.org/10.3390/cli9010009
Chicago/Turabian StyleSiddique, Ridwan, Alfonso Mejia, Naoki Mizukami, and Richard N. Palmer. 2021. "Impacts of Global Warming of 1.5, 2.0 and 3.0 °C on Hydrologic Regimes in the Northeastern U.S." Climate 9, no. 1: 9. https://doi.org/10.3390/cli9010009
APA StyleSiddique, R., Mejia, A., Mizukami, N., & Palmer, R. N. (2021). Impacts of Global Warming of 1.5, 2.0 and 3.0 °C on Hydrologic Regimes in the Northeastern U.S. Climate, 9(1), 9. https://doi.org/10.3390/cli9010009




