On the Development and Optimization of an Urban Design Comfort Model (UDCM) on a Passive Solar Basis at Mid-Latitude Sites
Abstract
:1. Introduction
1.1. Urban Compactness and the Geometry Adjustment
1.2. GreenSect and Trees in Urban Microclimate
2. Methodology
2.1. Applied Urban Climate
2.2. Optimization for Urban Thermal Comfort
2.3. Case Studies
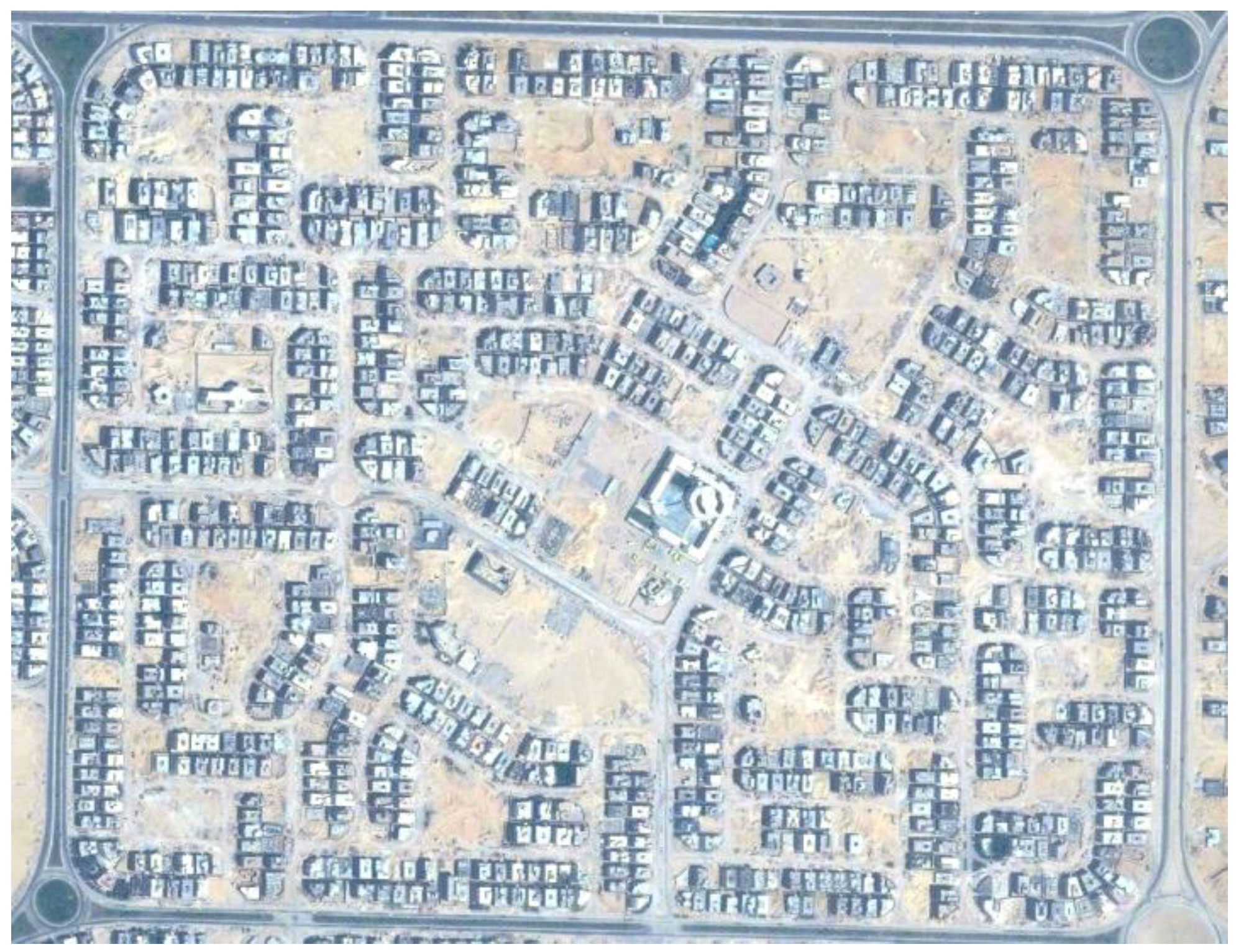
2.3.1. Case 1, the Fifth Community
2.3.2. Case 2, Misr Al-Gadida
3. Methods
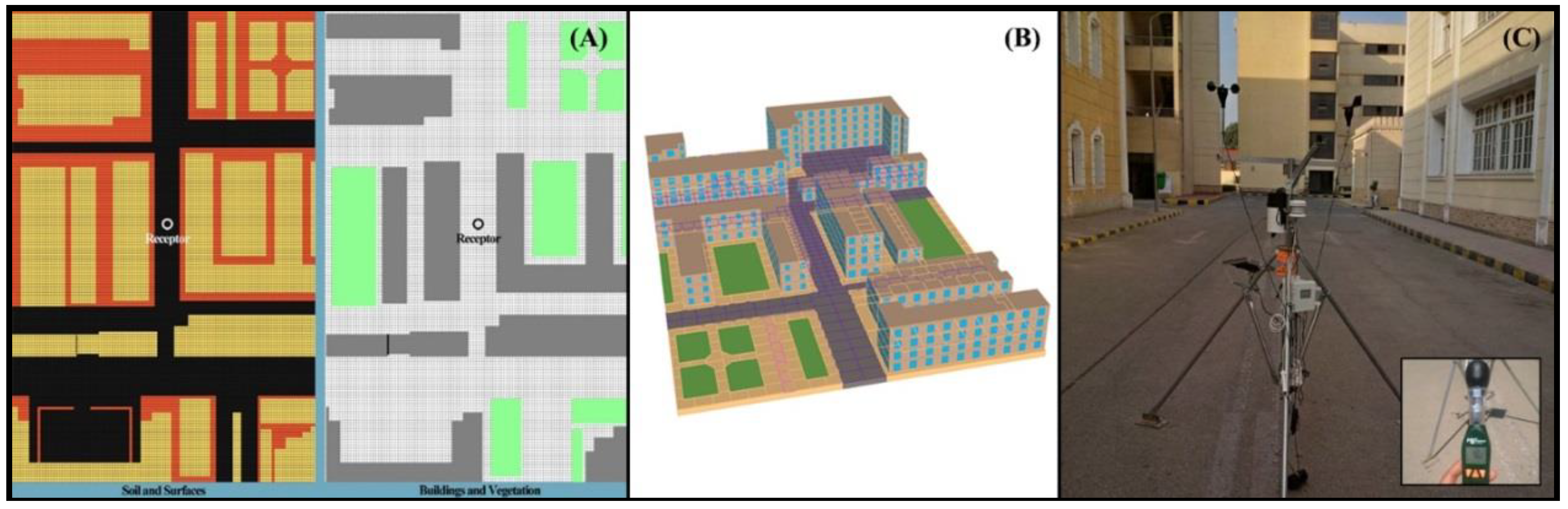
3.1. Numerical Simulation Tool
3.2. Optimization Tools
3.2.1. Optimizing Design Parameters Coefficients for Pedestrian Comfort
3.2.2. Optimizing Urban Form Geometry for Pedestrian Comfort
4. Urban Form Passive Design
4.1. Fabric
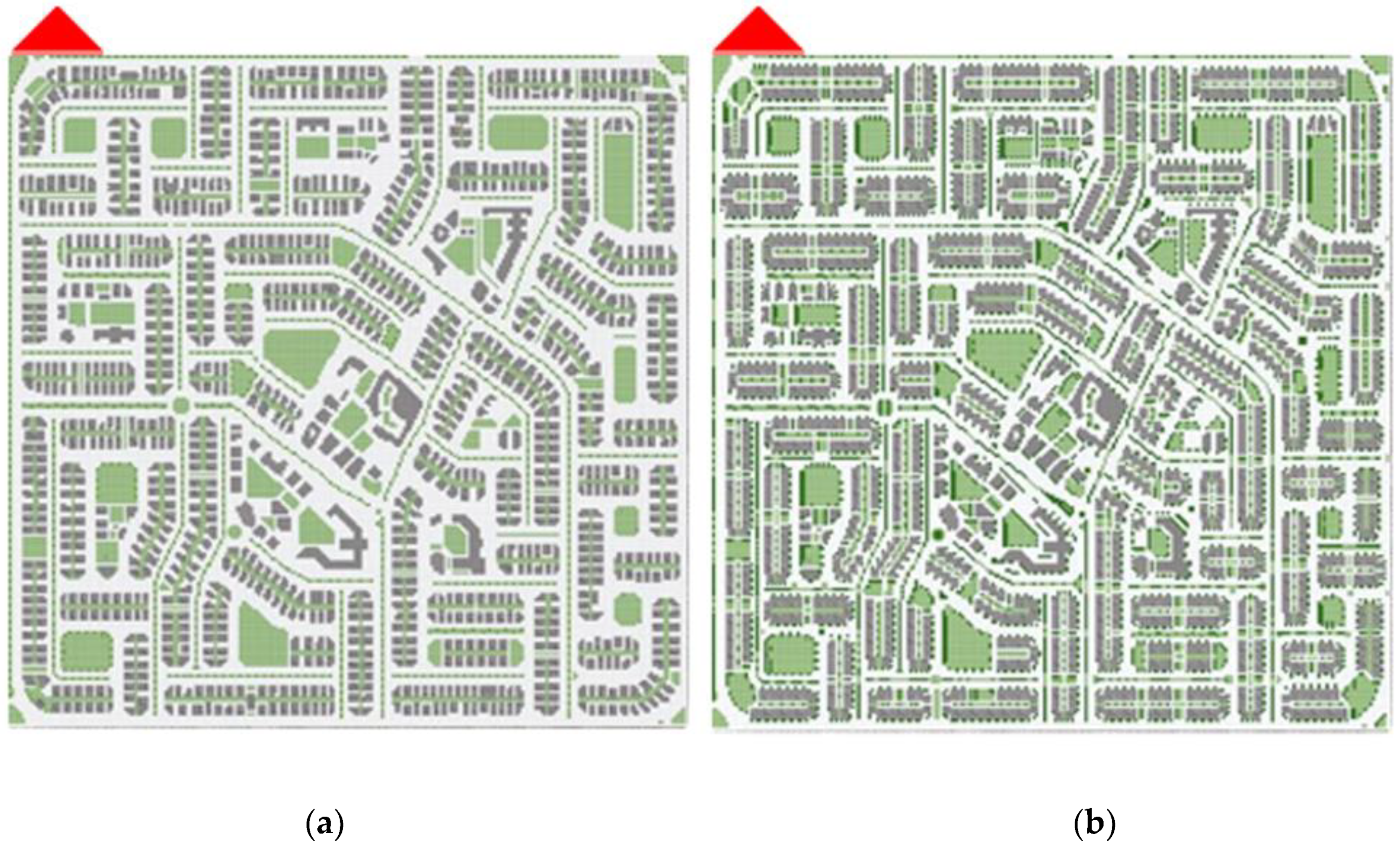
- In both cases there were two alternatives compared with the base case. Alternatives offer different housing types with more responsive clustered form, green coverage, and urban trees arrangements. This medium population-based hybrid form design resulted in different degrees of compactness (Dc). Figure 8 and Figure 9 show master plans and the clustered fabric used for the base case and the suggestions. The modifications which took place for the cases are theoretical; they have been made just for the research purposes where; DS1 is a clustered urban form planned over the same BC zoning in order to study the effect of only the clusters and; the DS2 of both cases are planned on a new zoning and network. With ground and three typical floors (G+3), all housing units are either single flat of 150 m2 or duplex of 300 m2, designed with 150 people/feddan population density limit of [75] and the 3.75 people/family of [61]. DS1 zoning and land use percentages are the same as BC whereas DS2 with completely new zoning is having merely the same land uses percentage of services.
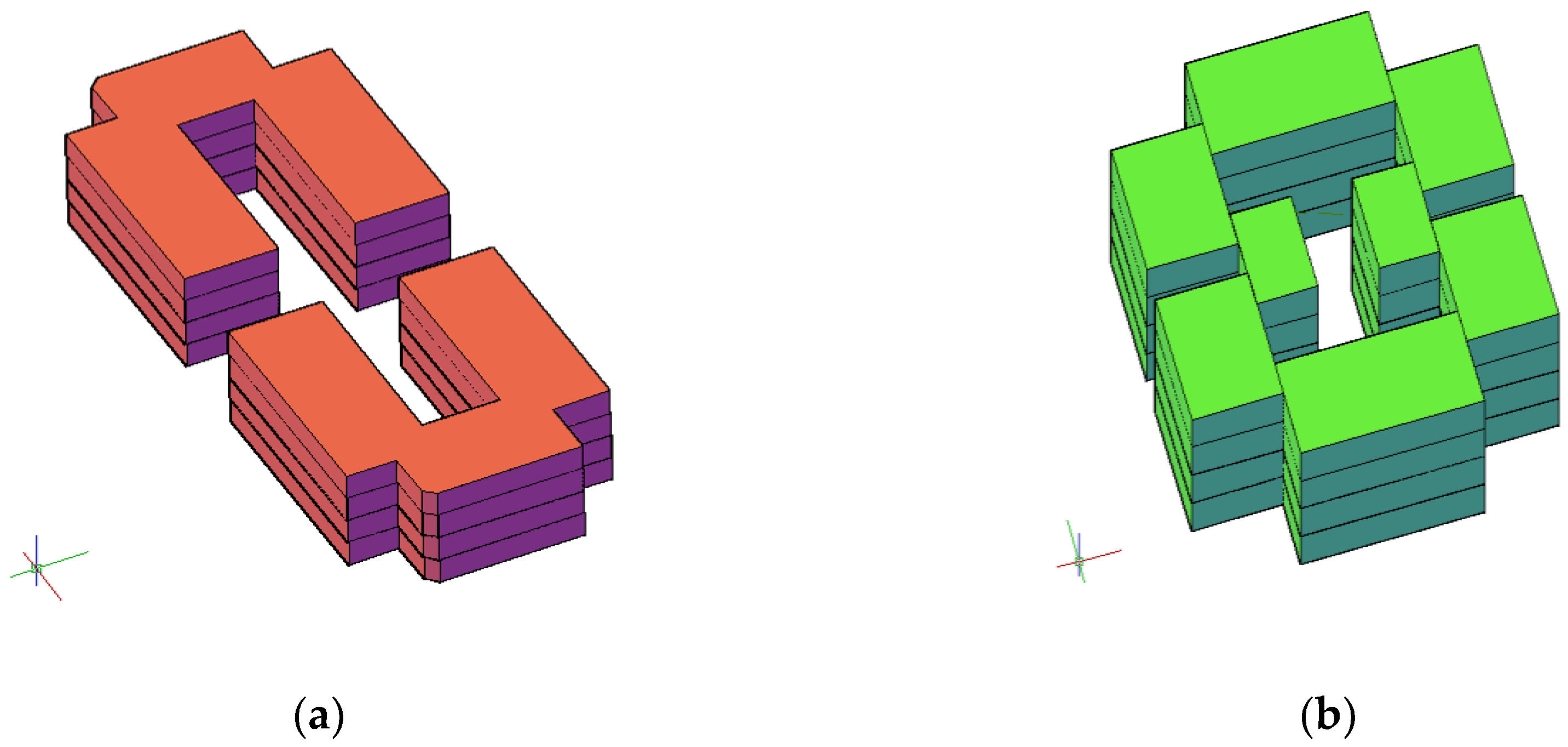
- DS2 clusters is designed to have 1:3:1.3 aspect ratio for W/L/H [76,77], and almost all clusters’ courtyards are oriented 15° from east-west axis following [20]. The canyons’ axes are either same orientation or perpendicular towards north-west to catch prevailing wind and to help the tunneling cooling effect. Figure 10 illustrates the clusters used.
- While the network patterns was hierarchical gird and hierarchical radial for BC1 and BC2 respectively, it was transformed to gird in both cases C1DS2 and C2DS2 to allow as much tunneling effect as possible.
4.2. Urban Vegetation
5. Results of UDCM Proposals
5.1. UDCM Derivation from Microclimatic Samples’ Simulations
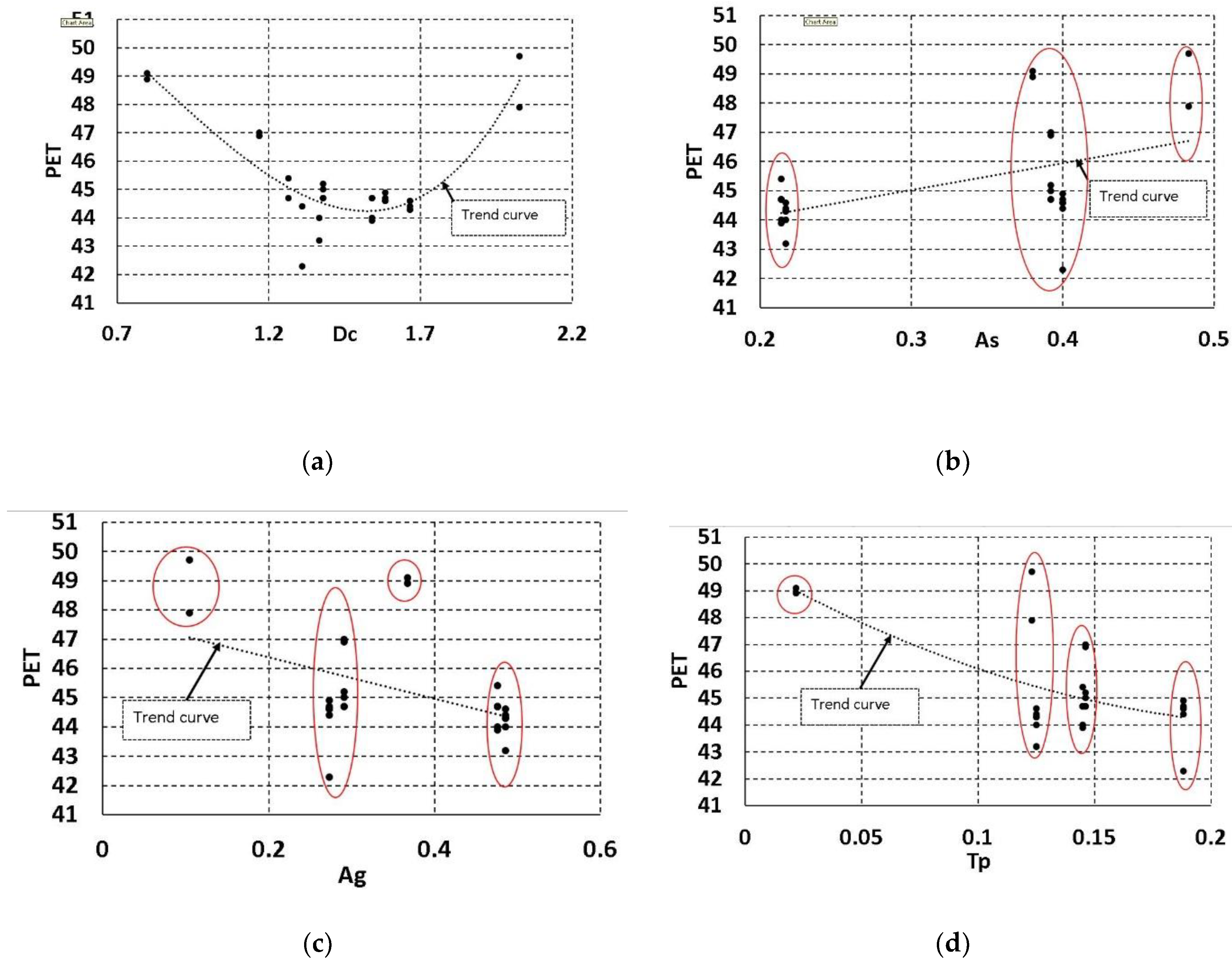
- Dc standing for fabric volume, i.e., residential construction percentage (Ac) × canopy layer height, or the number of urban floors (nf) which in turn can be calculated from the population.
- Ac is the urban site constructed area percentage.
- Ag is the green coverage area percentage.
- As is the urban asphalt network area percentage.
- Tp represents the urban trees shadow coverage with a specific tree. Tp is the trees’ grids percentage compared with the site outdoor grids built in ENVI-met model which give an indication for the urban shadow produced at peak time generated by trees.
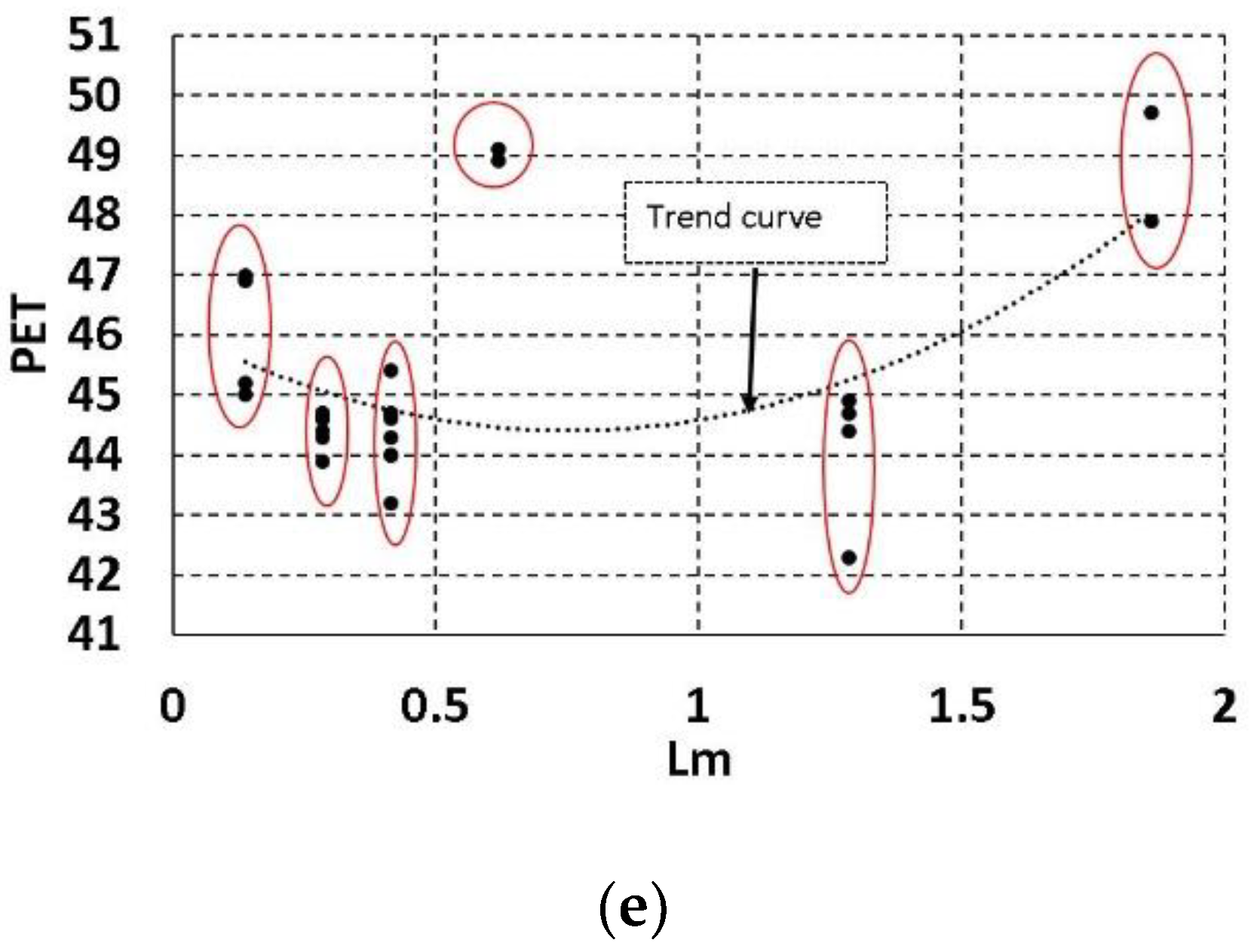
- Lm is the site mean maximum LAD of the tree—as quantification for the type of trees used in the site—to represent the effect of specific urban trees on the local comfort.
- nf is the urban site average floor number which is needed to calculate the site compactness degree.
5.1.1. MATLAB Optimization for UDCM Model
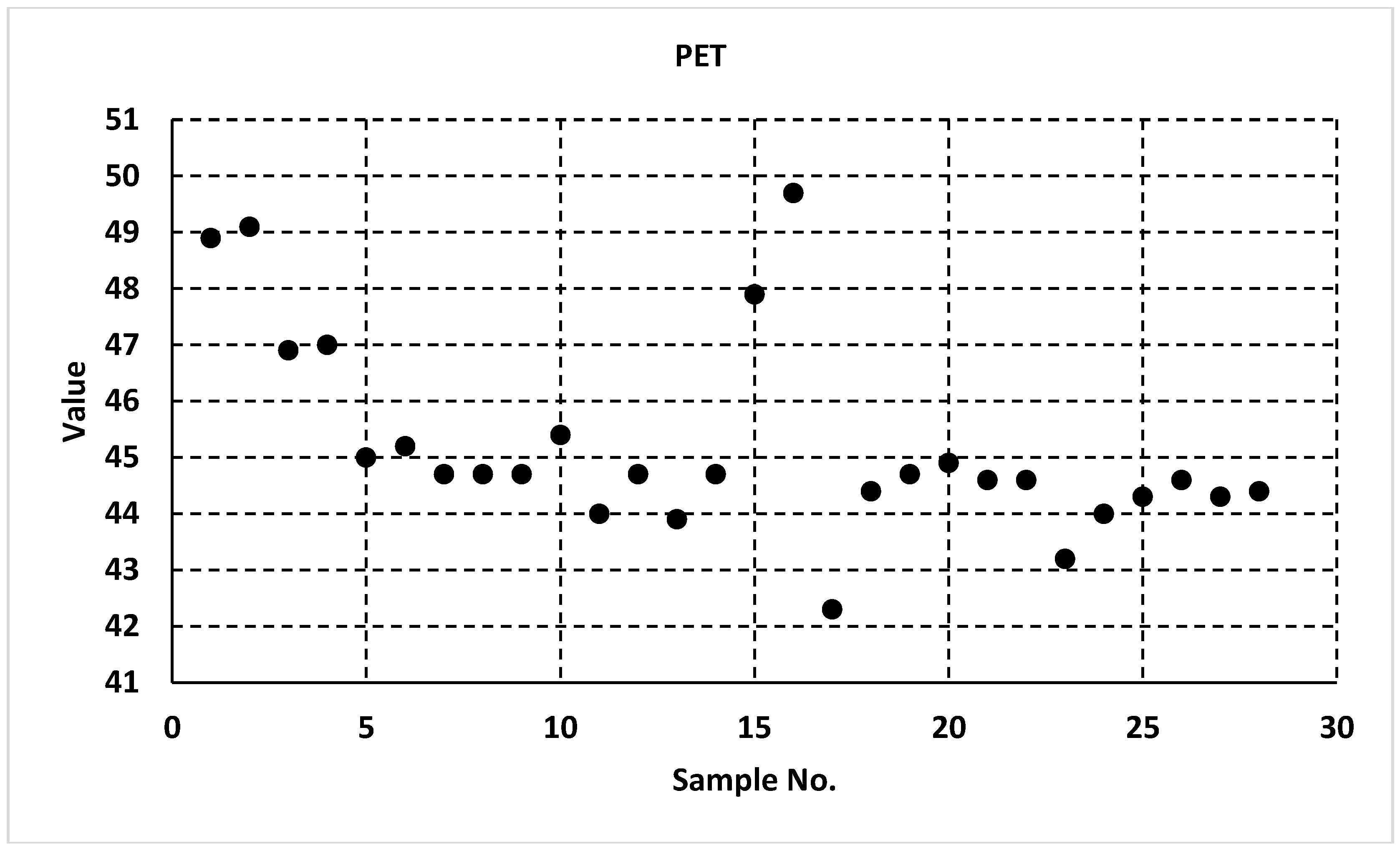
Data Inspections and Visualization
Developing UDCM
- Linear in the form of:
- Interaction in the form of: .
- Quadratic in the form of: .
- The fourth type is based on the stepwise algorithm [83], where the algorithm starts with one model form -in our case, it is linear- and iterates through adding terms in order to maximize the prediction capabilities of the final model.
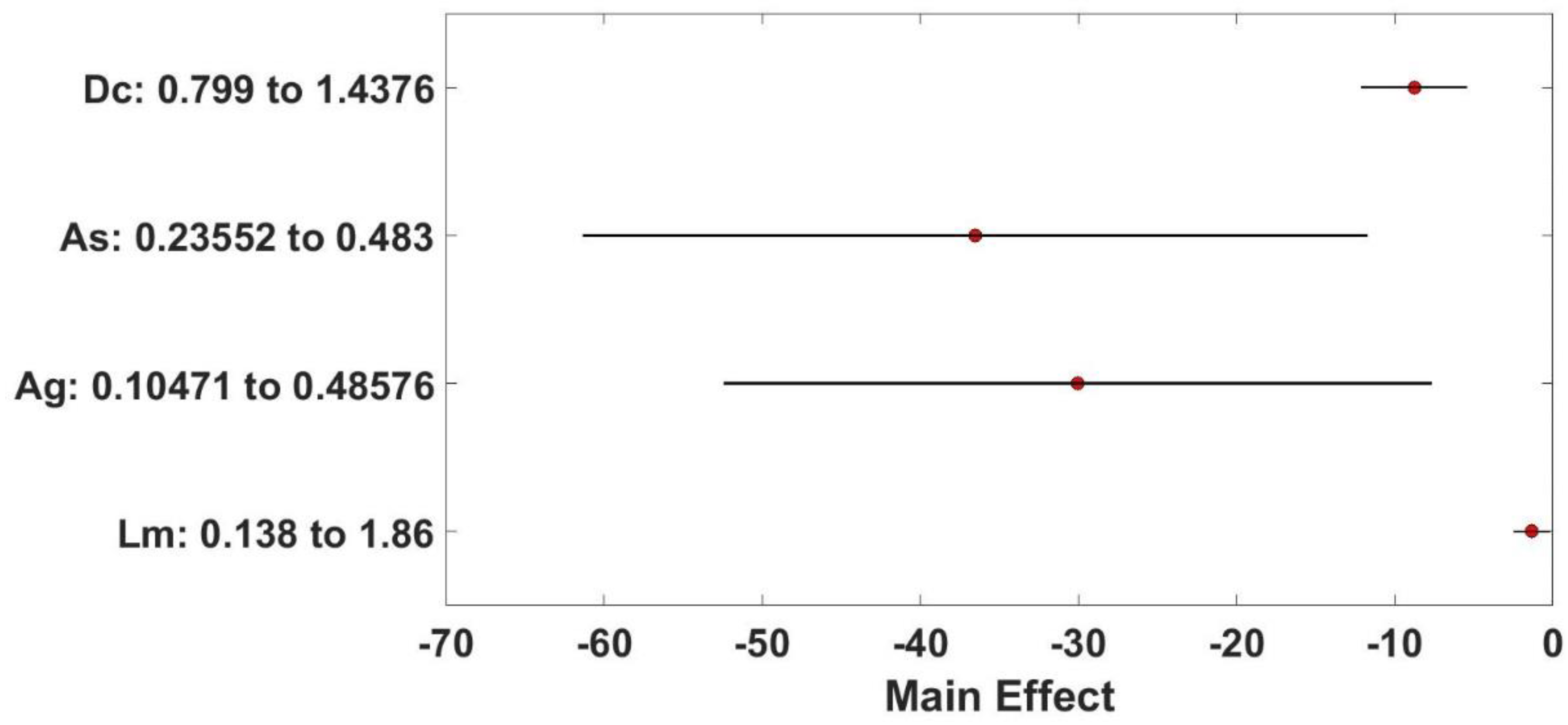
5.1.2. Optimization
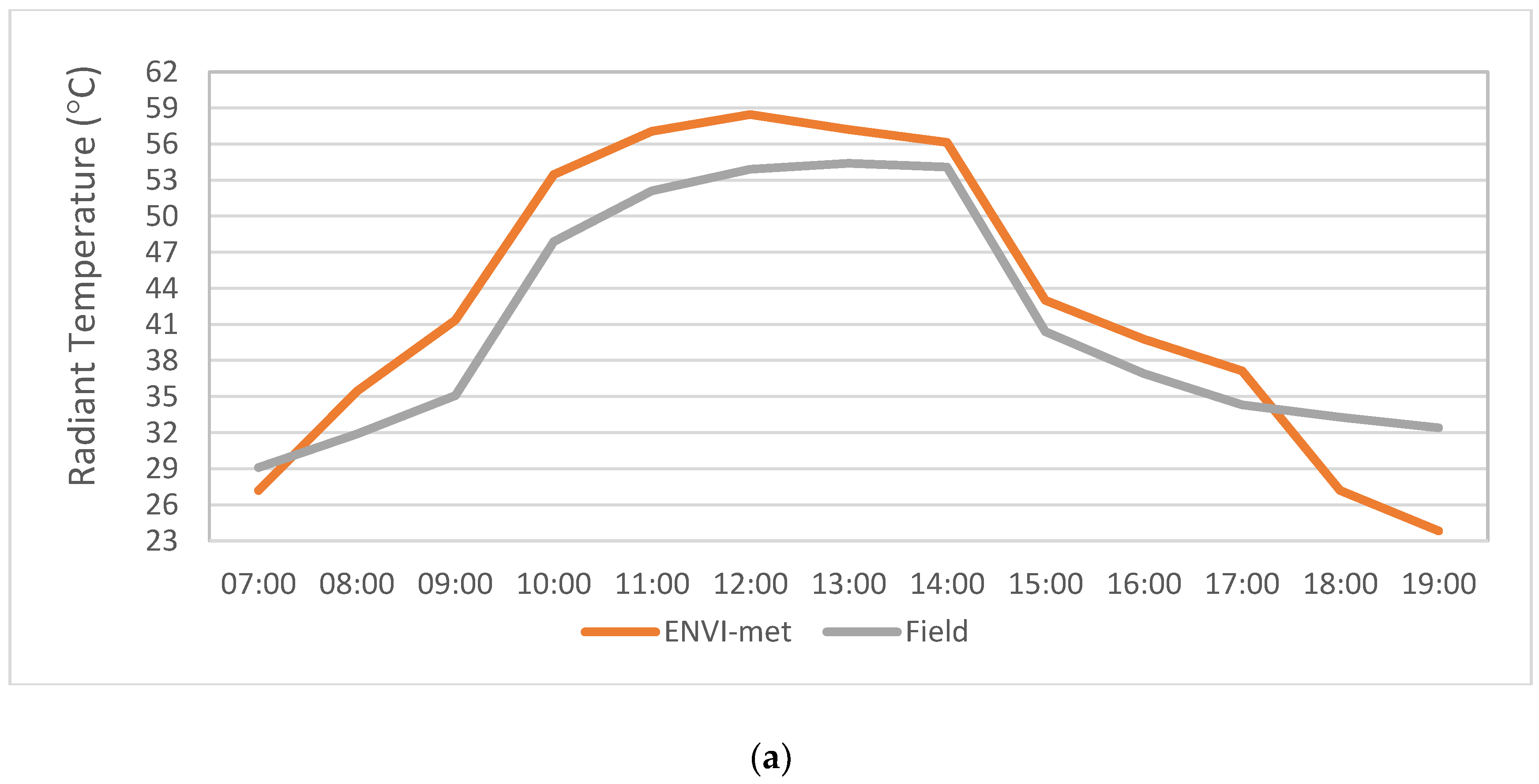
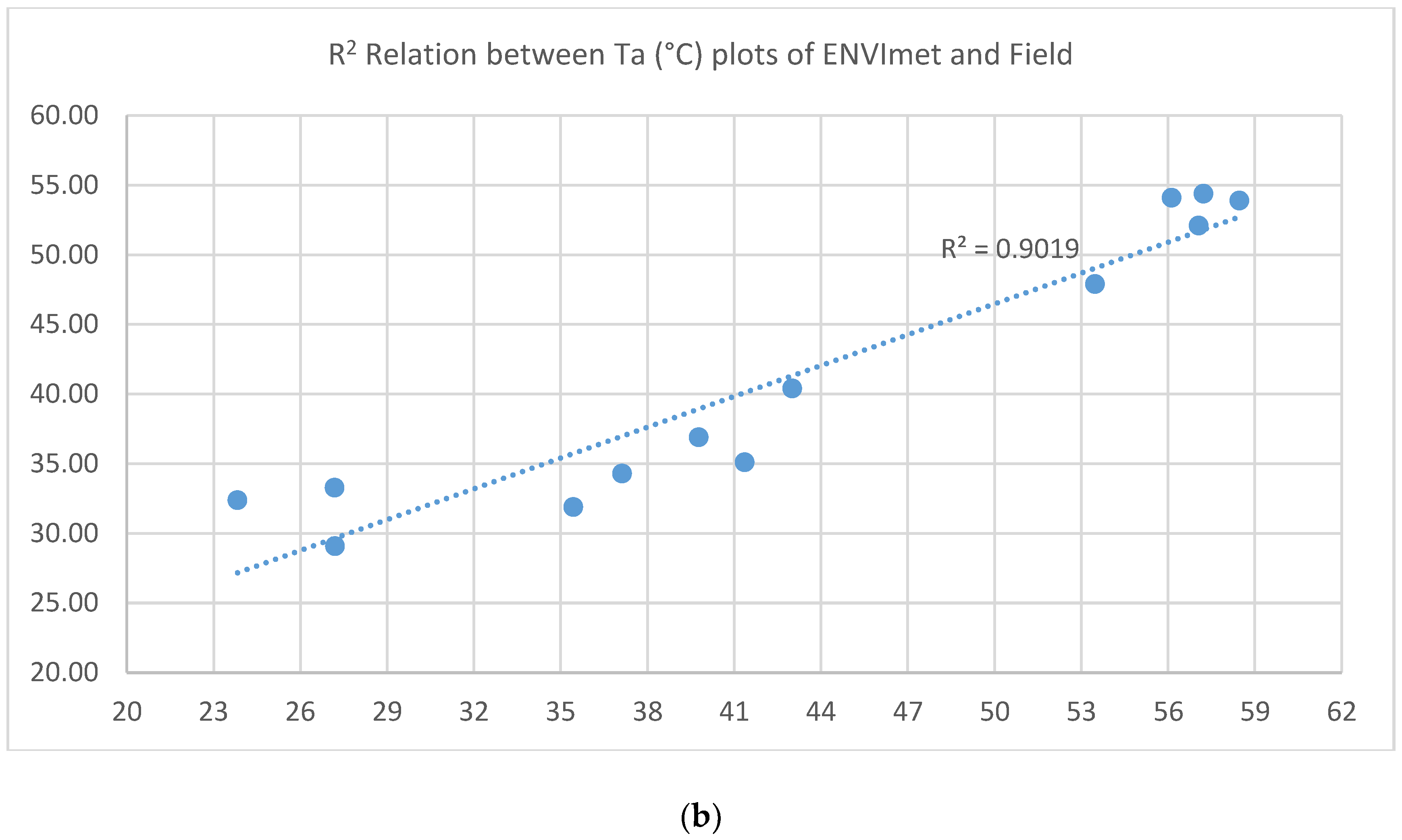
5.2. UDCM Validation
5.2.1. Grasshopper Optimization for Urban Form Geometry
5.2.2. ENVI-met Optimization Results for UDCM
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oke, T.R. Boundary Layer Climates; Methuen: London, UK, 1987. [Google Scholar]
- Pearlmutter, D.; Berliner, P.; Shaviv, E. Integrated modeling of pedestrian energy exchange and thermal comfort in urban street canyons. Build. Environ. 2007, 42. [Google Scholar] [CrossRef]
- Bruse, M.; Fleer, H. Simulating surface-plant-air interactions inside urban environments with a three dimensional numerical model. Environ. Model. Softw. 1998, 13, 373–384. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Djenane, M.; Bensalem, R.; Mayer, H. Outdoor thermal comfort in the old desert city of Beni-Isguen, Algeria. Clim. Res 2005, 28, 243–256. [Google Scholar] [CrossRef] [Green Version]
- Balling, R.C.; Brazel, S.W. Time and Space Characteristics of the Phoenix Urban Heat Island. J. Ariz.-Nev. Acad. Sci. 1987, 21, 75–81. [Google Scholar]
- Hassan, A.N.; Anthony, J.B.; Robert, C.B., Jr. Analysis of the Kuwait city urban heat island. Int. J. Climatol. 1990, 10, 401–405. [Google Scholar]
- Rosenfeld, A.H.; Akbari, H.; Bretz, S.; Fishman, B.L.; Kurn, D.M.; Sailor, D.; Taha, H. Mitigation of urban heat islands: Materials, utility programs, updates. Energy Build. 2001, 22, 255–265. [Google Scholar] [CrossRef]
- Huang, L.; Li, J.; Zhao, D.; Zhu, J. A fieldwork study on the diurnal changes of urban microclimate in four types of ground cover and urban heat island of Nanjing, China. Build. Environ. 2008, 43, 7–17. [Google Scholar] [CrossRef]
- Oke, T.R. Towards a prescription for the greater use of climatic principles in settlement planning. Energy Build. 1984, 7, 1–10. [Google Scholar] [CrossRef]
- Oke, T.R. Towards better scientific communication in urban climate. Theor. Appl. Climatol. 2006, 84, 179–190. [Google Scholar] [CrossRef]
- Arnfield, A. Two Decades of Urban Climate Research: A review of Turbulence, Exchange of Energy, Water and the urban heat islands. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Fahmy, M.; Sharples, S. Extensive review for urban climatology: Definitions, aspects and scales. In Proceedings of the THE 7th International Conference on Civil and Architecture Engineering, ICCAE-7, Military Technical Collage, Cairo, Egypt, 27–29 May 2008. [Google Scholar]
- Givoni, B. Climate Consideration in Urban and Building Design; Van Nostrand Reinhold: New York, NY, USA, 1998. [Google Scholar]
- Burton, E. Measuring urban compactness in UK towns and cities. Environ. Plan. B Plan. Des. 2002, 29, 219–250. [Google Scholar] [CrossRef]
- Tablada, A.; De Troyer, F.; Blocken, B.; Carmeliet, J.; Verschure, H. On natural ventilation and thermal comfort in compact urban environments—The Old Havana case. Build. Environ. 2009, 44, 1943–1958. [Google Scholar] [CrossRef]
- Oke, T.R. Canyon geometry and the nocturnal heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Numerical study on the effects of aspect ratio and orientation of an urban street canyon on outdoor thermal comfort in hot and dry climate. Build. Environ. 2006, 41, 94–108. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Thermal comfort in an east-west oriented street canyon in Freiburg (Germany) under hot summer conditions. Theor. Appl. Climatol 2007, 87, 223–237. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Effects of asymmetry, galleries, overhanging fac¸ades and vegetation on thermal comfort in urban street canyons. Sol. Energy 81, 742–754. [CrossRef]
- Fahmy, M.; Sharples, S. On the development of an urban passive thermal comfort system in Cairo, Egypt. Build. Environ. 2009, 44, 1907–1916. [Google Scholar] [CrossRef]
- Fahmy, M. Climate Change Adaptation for Mid-latitude Urban Developments. In Proceedings of the PLEA2012—28th Conference, Opportunities, Limits & Needs Towards an environmentally Responsible Architecture, Lima, Peru, 7–9 November 2012. [Google Scholar]
- Fahmy, M.; Elwy, I. Visual and Thermal Comfort Optimization for Arid Urban Spaces using Parametric Techniques on the Scale of Compactness Degree. In Proceedings of the PLEA2016 Los Angeles—Cities, Buildings, People: Towards Regenerative Environments, Los Angeles, CA, USA, 11–13 July 2016. [Google Scholar]
- Oke, T.R. Street Design and Urban Canopy Layer Climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Hoffman, M.E. Quantitative evaluation of passive cooling of the UCL microclimate in hot regions in summer, case study: Urban streets and courtyards with trees. Build. Environ. 2004, 39, 1087–1099. [Google Scholar] [CrossRef]
- Muhaisen, A.S. Shading simulation of the courtyard form in different climatic regions. Build. Environ. 2006, 41, 1731–1741. [Google Scholar] [CrossRef]
- Aldawoud, A.; Clark, R. Comparative analysis of energy performance between courtyard and atrium in buildings. Energy Build. 2008, 40, 209–214. [Google Scholar] [CrossRef]
- Duany, A. Introduction to the Special Issue: The Transect. J. Urban Des. 2002, 7, 251–260. [Google Scholar] [CrossRef]
- Fahmy, M.; Sharples, S.; Yahiya, M. LAI based trees selection for mid latitude urban developments: A microclimatic study in Cairo, Egypt. Build. Environ. 2010, 45, 345–357. [Google Scholar] [CrossRef] [Green Version]
- Morakinyo, T.E.; Kong, L.; Lau, K.K.-L.; Yuan, C.; Ng, E. A study on the impact of shadow-cast and tree species on in-canyon and neighborhood’s thermal comfort. Build. Environ. 2017, 115, 1–17. [Google Scholar] [CrossRef]
- Arnold, H.F. Trees in Urban Design, 1st ed.; Van Nostrand Reinhold: New York, NY, USA, 1980. [Google Scholar]
- Trowbridge, P.J.; Bassuk, N.L. Trees in the Urban Landscape; Site Assessment, Design and Installation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lam, K.C.; Leung, S.; Hui, W.C.; Chan, P.K. Environmental Quality of Urban parks and open spaces in Hong Kong. Environ. Monit. Assess. 2005, 111, 55–73. [Google Scholar] [CrossRef]
- McPherson, E.G.; Nowak, D.; Heisler, G.; Grimmond, S.; Souch, C.; Grant, R.; Rowntree, R. Quantifying urban forest structure, function, and value: The Chicago Urban Forest Climate Project. Urban Ecosyst. 1997, 1, 49–61. [Google Scholar] [CrossRef]
- Heisler, G.M. Mean wind speed below building height in residential neighborhoods with different tree densities. ASHRAE Trans. 1990, 96, 1389–1397. [Google Scholar]
- Oke, T.R.; Crowther, J.M.; McNaughton, K.G.; Monteith, J.L.; Gardiner, B. The Micrometeorology of the Urban Forest [and Discussion]. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1989, 324, 335–349. [Google Scholar] [CrossRef]
- Kurn, M.; Bretz, S.E.; Huang, B.; Akbari, H. The Potential for Reducing Urban Air Temperatures and Energy Consumption Through Vegetative Cooling; Heat Island Project Energy & Environment Division, Lawrence Berkeley Laboratory, University of California: Berkeley, CA, USA, 1994. [Google Scholar]
- Akbari, H. Shade trees reduce building energy use and CO2 emissions from power plants. Environ. Pollut. 2002, 116, S119–S126. [Google Scholar] [CrossRef]
- Huang, Y.J.; Akbari, H.; Taha, H.; Rosenfeld, A.H. The Potential of Vegetation in Reducing Summer Cooling Loads in Residential Buildings. J. Clim. Appl. Meteorol. 1987, 26, 1103–1116. [Google Scholar] [CrossRef] [Green Version]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and Shade Trees to Reduce Energy Use and Improve Air Quality in Urban Areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Ali-Toudert, F. Dependence of Out Door Thermal Comfort on the Street Design in Hot and Dry Climate. PhD. Thesis, Institute of Meteorology, Freiburg, Germany, 2005. [Google Scholar]
- Sailor, D.J.; Hutchinson, D.; Bokovoy, L. Thermal property measurements for ecoroof soils common in the western U.S. Energy Build. 2008, 40, 1246–1251. [Google Scholar] [CrossRef]
- Jacobs, A.F.G.; Ronda, R.J.; Holtslag, A.A.M. Water vapour and carbon dioxide fluxes over bog vegetation. Agric. For. Meteorol. 2003, 116, 103–112. [Google Scholar] [CrossRef]
- Dimoudi, A.; Nikolopoulou, M. Vegetation in the Urban Environments: Microclimatic Analysis and Benefits. Energy Build. 2003, 35, 69–76. [Google Scholar] [CrossRef]
- Streiling, S.; Matzarakis, A. Influence of single and small clusters of trees on the bio climate of a city: A case study. J. Arboricult. 2003, 29, 309–315. [Google Scholar]
- Shahidan, M.; Salleh, E.; Shariff, K. Effects of Tree Canopies on Solar Radiation Filtration in a Tropical Microclimatic Environment. In Proceedings of the 24th Conference on Passive and Low Energy Architecture, Singapore, 22–24 November 2007. [Google Scholar]
- Pearlmutter, D.; Bitan, A.; Berliner, P. Microclimatic analysis of compact urban canyon in an arid zone. Atmos. Environ. 1999, 33, 4143–4150. [Google Scholar] [CrossRef]
- Shashua-Bar, L.; Swaid, H.; Hoffman, M.E. On the correct specification of the analytical CTTC model for predicting the urban canopy layer temperature. Energy Build. 2004, 36, 975–978. [Google Scholar] [CrossRef]
- Thorsson, S.; Lindberg, F.; Eliasson, I.; Holmer, B. Different methods for estimating the mean radiant temperature in an outdoor urban setting. Int. J. Climatol. 2007, 27, 1983–1993. [Google Scholar] [CrossRef] [Green Version]
- Kong, F.; Yin, H.; James, P.; Hutyra, L.R.; He, H.S. Effects of spatial pattern of greenspace on urban cooling in a large metropolitan area of eastern China. Landsc. Urban Plan. 2014, 128, 35–47. [Google Scholar] [CrossRef]
- Tan, Z.; Lau, K.K.L.; Ng, E. Urban tree design approaches for mitigating daytime urban heatisland effects in a high-density urban environment. Energy Build. 2015, 114, 265–274. [Google Scholar] [CrossRef]
- Ng, E.; Chen, L.; Wang, Y.; Yuan, C. A study on the cooling effects of greening in a high-density city: An experience from Hong Kong. Build. Environ. 2012, 47, 256–271. [Google Scholar] [CrossRef]
- Kenawy, I.; Afifi, M.; Mahmoud, A. The effect of planting design on thermal comfort in outdoor spaces. In Proceedings of the First International Conference on Sustainability and the Future, Egypt, Cairo, 23–25 November 2010. [Google Scholar]
- Yin, Z.; Stewart, J.; Bullard, S.; MacLachlan, T. Changes in urban built-up surface and population distribution patterns during 1986-1999: A case study of Cairo, Egypt. Comput. Environ. Urban Syst. 2005, 29, 595–616. [Google Scholar] [CrossRef]
- EEAA. Egypt State of Environment Report; Ministery of State for Environmental Affairs: Cairo, Egypt, 2008.
- Stewart, D.J.; Yin, Z.-Y.; Bullard, S.M.; MacLachlan, J.T. Assessing the Spatial Structure of Urban and Population Growth in the Greater Cairo Area, Egypt: A GIS and Imagery Analysis Approach. Urban Stud. 2004, 41, 95–116. [Google Scholar] [CrossRef]
- Stewart, D.J. Changing Cairo: The political economy of urban form. Int. J. Urban Reg. Res. 1999, 23, 103–127. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Hand Book of Fundamentals, SI ed.; American Society of Heating, Refrigerating, and Air-Conditioning Engineers Inc.: Atlanta, GA, USA, 2005. [Google Scholar]
- El Araby, M. Urban growth and environmental degradation. The case of Cairo, Egypt. Cities 2002, 18, 135–149. [Google Scholar]
- Fahmi, W.; Sutton, K. Greater Cairo’s housing crisis: Contested spaces from inner city areas to new communities. Cities 2008, 25, 277–297. [Google Scholar] [CrossRef]
- CAPMAS. Final Report of Population Statistics for Egypt 2006; Central Agency for Public Mobilisation and Statistics: Cairo, Egypt, 2008. [Google Scholar]
- NUCA. Construction Regulations in New Cairo, in Arabic; New Urban Communities Authority; Ministry of Housing, Utilities, and Urban Communities Cairo: Cairo, Egypt, 2006.
- Heliopolis-Company. Heliopolis Company Profile; Heliopolis Company for Construction and Development: Cairo, Egypt, 2006. [Google Scholar]
- Bruse, M. ENVI-Met V3.1, a Microscale Urban Climate Model. Available online: www.envi-met.com (accessed on 18 October 2010).
- Hoppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Lau, K.K.-L.; Ren, C.; Ng, E. Performance of Hong Kong’s common trees species for outdoor temperature regulation, thermal comfort and energy saving. Build. Environ. 2018, 137, 157–170. [Google Scholar] [CrossRef]
- Salata, F.; Golasi, I.; de Lieto Vollaro, R.; de Lieto Vollaro, A. Urban microclimate and outdoor thermal comfort. A proper procedure to fit ENVI-met simulation outputs to experimental data. Sustain. Cities Soc. 2016, 26, 318–343. [Google Scholar] [CrossRef]
- Onset. HOBO U30 Data Loggers. Available online: http://www.onsetcomp.com/products/data-loggers/U30-data-loggers (accessed on 3 February 2018).
- Extech. Extech HT30: Heat Stress WBGT (Wet Bulb Globe Temperature) Meter. Available online: http://www.extech.com/ht30/ (accessed on 3 February 2018).
- Mathworks. Mathworks Web Site. Available online: https://www.mathworks.com/ (accessed on 21 December 2017).
- Moore, H. MATLAB for Engineers; Pearson: London, UK, 2017. [Google Scholar]
- Tedeschi, A.; Andreani, S.; Buono, A.; Degni, M.; Friesen, L.; Galli, A.; Lipari, F.; Lombardi, D.; Lonnbardi, L.; Mamou-Mani, A.; et al. AAD_Algorithms-Aided Design, Parametric Strategies Using Grasshopper®; Le Penseur: Brienza, Italy, 2014. [Google Scholar]
- McNeel, R. Rhinoceros (Version 5). Available online: https://www.rhino3d.com/features (accessed on 8 October 2017).
- Woodbury, R. Elements of Parametric Design; Routledge, Taylor & Francis Group: Abingdon, UK, 2010. [Google Scholar]
- Law3. Urban Planning Law and Excutive Regulations; Egyptian Ministry of Urban Planning and Housing: Cairo, Egypt, 1982. [Google Scholar]
- Waziry, Y. Application on Environmental Architecture: Solar Design Studies of Courtyard in Cairo and Toshky; Madbuli Publishing: Cairo, Egypt, 2002. (In Arabic) [Google Scholar]
- Ahmad, H.S. Desert Climate Condition Effects on the Vernacular Islamic and Contemporary Desert House Forms in Northern Africa; Hewaln University Cairo: Cairo, Egypt, 1994. [Google Scholar]
- Santamouris, M.; Papanikolaou, N.; Koronakis, I.; Livada, I.; Asimakopoulos, D. Thermal and air flow characeristics in a deep pedestrian canyon under hot weather conditions. Atmos. Environ. 1999, 33, 4503–4521. [Google Scholar] [CrossRef]
- Barbosa, O.; Tratalos, J.A.; Armsworth, P.R.; Davies, R.G.; Fuller, R.A.; Johnson, P.; Gaston, K.J. Who benefits from access to green space? A case study from Sheffield, UK. Landsc. Urban Plan. 2007, 83, 187–195. [Google Scholar] [CrossRef]
- Duany A and Talen, E. Transect Planning. J. Am. Plan. Assoc. 2002, 68, 245–266. [Google Scholar] [CrossRef]
- Matzarakis, A.; Mayer, H.; Iziomon, M.G. Applications of a universal thermal index: Physiological equivalent temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
- NOUH. The Environmental Guide for Urban Spaces; Harmoney, N.O.f.U.: Cairo, Egypt, 2012. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; J. Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fahmy, M.; El-Hady, H.; Mahdy, M. LAI and Albedo Measurements Based Methodology for Numerical Simulation of Urban Tree’s Microclimate: A Case Study in Egypt. Int. J. Sci. Eng. Res. 2016, 7, 790–797. [Google Scholar]
- Morakinyo, T.E.; Dahanayake, K.K.C.; Adegun, O.B.; Balogun, A.A. Modelling the effect of tree-shading on summer indoorand outdoor thermal condition of two similar buildings in a Nigerianuniversity. Energy Build. 2016, 130, 721–732. [Google Scholar] [CrossRef]
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments—Application of the RayMan model. Int. J. Biometeorol. 2007, 51, 323–334. [Google Scholar] [CrossRef]




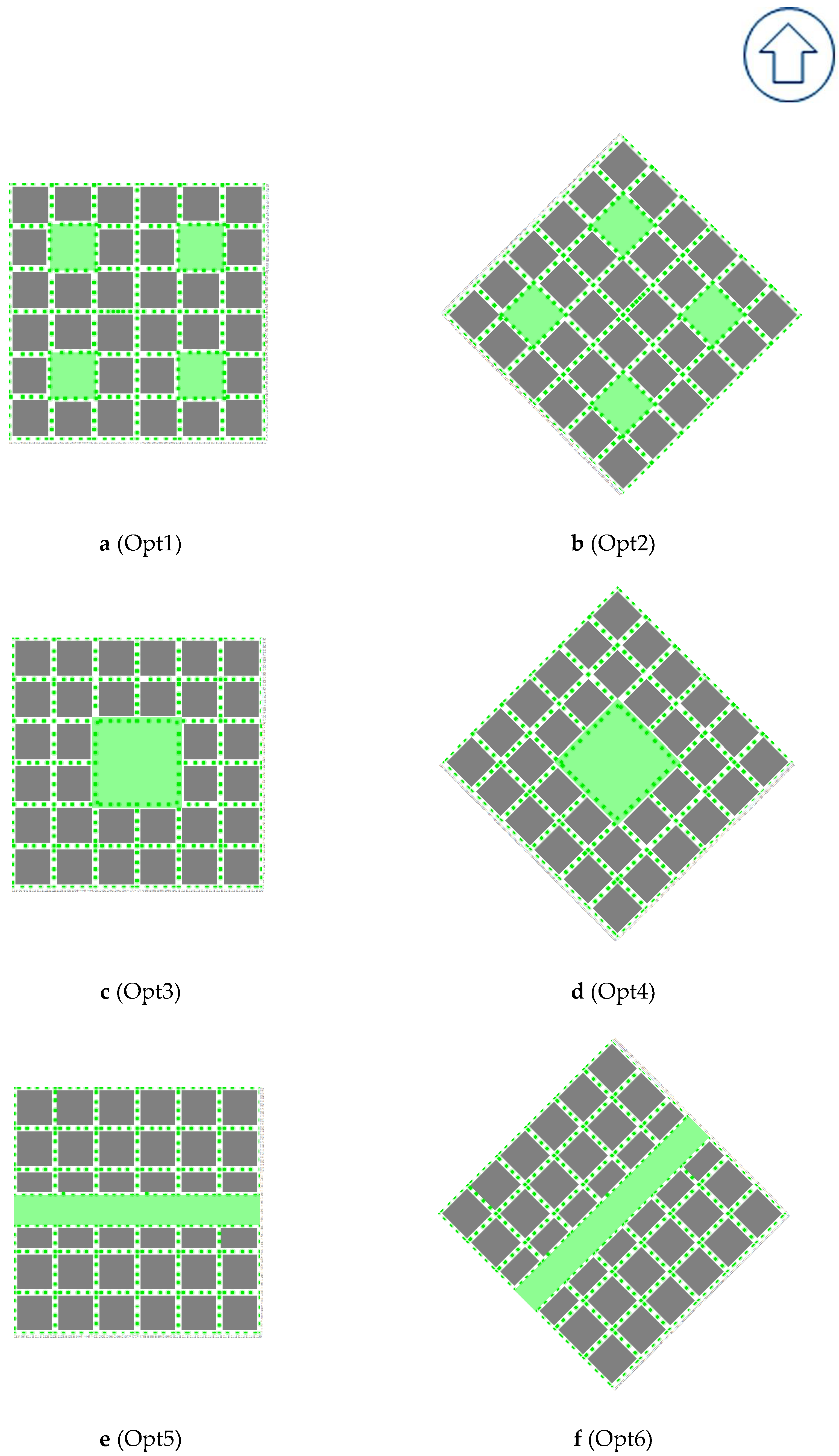
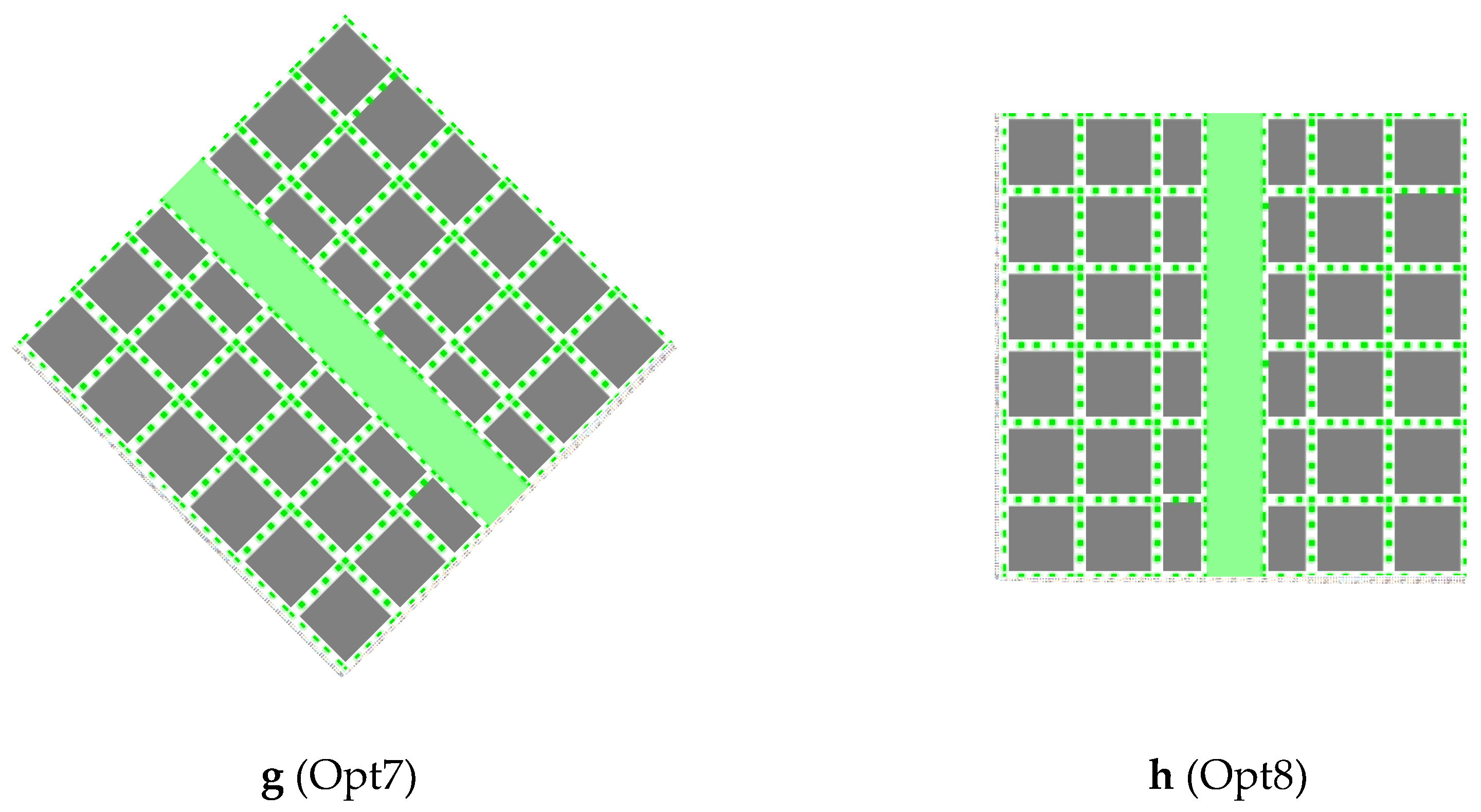
| Abbreviation | Meaning |
|---|---|
| T0 | No Trees; the base case situation of site one |
| TE1 | Ficus Elastica (Indian rubber plant), with LAI = 1. |
| TE2 | Peltophorum Pterocarpum (Yellow Poinciana), with LAI = 1. |
| TE3 | Ficus Nitida, with LAI = 1. |
| TC1 | Ficus Elastica (Indian rubber plant), with LAI = 3. |
| TC2 | Peltophorum Pterocarpum (Yellow Poinciana), with LAI = 3. |
| TC3 | Ficus Nitida, with LAI = 3. |
| Case Name | Urban Area in Feddans | Green Coverage %, Ag | Tree Type, Tp and Lm | Cluster Closure Ratio; | Cluster Aspect Ratio; H/W/L | Urban Fabric %, Ac | Average no. of Site Floors, nf | Degree of Compactness, Dc | Total Population in Persons | Population Density in p/f | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | BC1 | 380.15 | 0.368 | TE3, 0.022, 0.62 | ------ | ------ | 0.252 | 3.171 | 0.799 | 14,950 | 039 |
| 2 | C1DS1 | 0.291 | TE1, 0.146, 0.138 | various | various | 0.299 | 3.911 | 1.169 | 46,662 | 123 | |
| 3 | C1DS1_Dc | 0.291 | TE1, 0.146, 0.138 | various | various | 0.299 | 4.610 | 1.378 | 55,004 | 145 | |
| 4 | C1DS1_Lm | 0.291 | TC2, 0.146, 0.285 | various | various | 0.299 | 4.610 | 1.378 | 55,004 | 145 | |
| 5 | C1DS2 | 0.476 | TC1, 0.145, 0.414 | 3.47 | 1:1.3:3 | 0.310 | 4.077 | 1.264 | 50,448 | 133 | |
| 6 | C1DS2_Dc | 0.476 | TC1, 0.145, 0.414 | 4.27 | 1:1.6: 3 | 0.310 | 4.968 | 1.540 | 61,473 | 162 | |
| 7 | C1DS2_Lm | 0.476 | TC2, 0.145, 0.285 | 4.27 | 1:1.6: 3 | 0.310 | 4.968 | 1.540 | 61,473 | 162 | |
| 8 | BC2 | 199.0 | 0.105 | TC3, 0.123, 1.86 | ------ | ------ | 0.412 | 4.920 | 2.027 | 52,943 | 266 |
| 9 | C2DS1 | 0.273 | TC1, 0.077, 0.414 + TC3, 0.111, 1.86 | various | various | 0.327 | 4.006 | 1.310 | 27,372 | 138 | |
| 10 | C2DS1_Dc | 0.273 | TC1, 0.077, 0.414 + TC3, 0.111, 1.86 | various | various | 0.327 | 4.845 | 1.584 | 33,104 | 166 | |
| 11 | C2DS1_Lm | 0.273 | TC2, 0.188, 0.285 | various | various | 0.327 | 4.845 | 1.584 | 33,104 | 166 | |
| 12 | C2DS2 | 0.465 | TC1, 0.125, 0.414 | 3.47 | 1:1.3:3 | 0.318 | 4.296 | 1.366 | 28,545 | 143 | |
| 13 | C2DS2_Dc | 0.465 | TC1, 0.125, 0.414 | 4.27 | 1:1.6: 3 | 0.318 | 5.237 | 1.665 | 34,798 | 175 | |
| 14 | C2DS2_Lm | 0.465 | TC2, 0.125, 0.285 | 4.27 | 1:1.6: 3 | 0.318 | 5.237 | 1.665 | 34,798 | 175 |
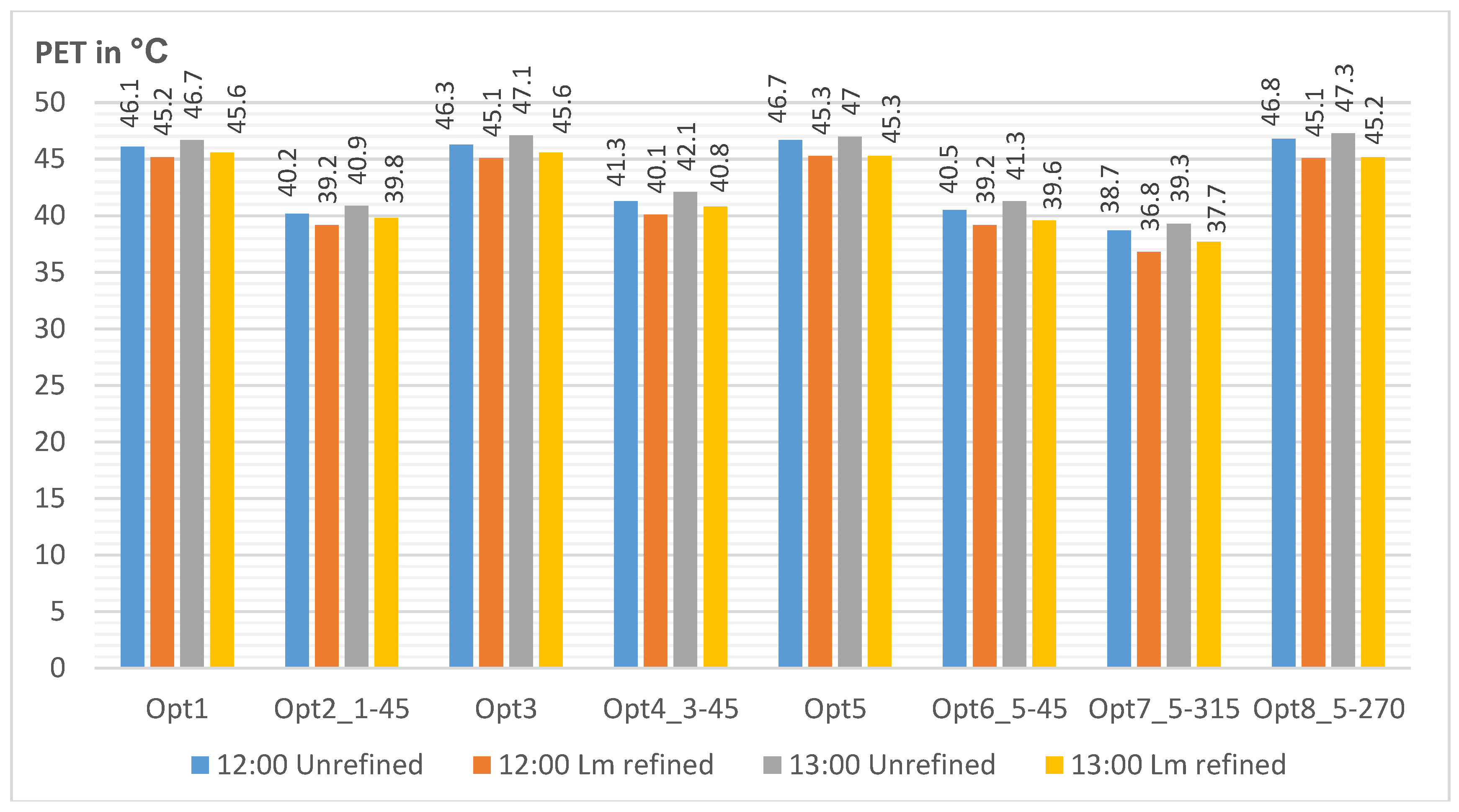
| No | Samples | Output Time (LST) | (PET) | Dc | As | Ag (%) | Tp | Lm |
|---|---|---|---|---|---|---|---|---|
| 1 | C1BC | 12:00 | 48.9 | 0.799 | 0.380 | 0.36757 | 0.022 | 0.620 |
| 2 | C1BC | 13:00 | 49.1 | 0.799 | 0.380 | 0.36757 | 0.022 | 0.620 |
| 3 | C1DS1 | 12:00 | 46.9 | 1.169 | 0.392 | 0.29117 | 0.146 | 0.138 |
| 4 | C1DS1 | 13:00 | 47.0 | 1.169 | 0.392 | 0.29117 | 0.146 | 0.138 |
| 5 | C1DS1_Dc | 12:00 | 45.0 | 1.378 | 0.392 | 0.29117 | 0.146 | 0.138 |
| 6 | C1DS1_Dc | 13:00 | 45.2 | 1.378 | 0.392 | 0.29117 | 0.146 | 0.138 |
| 7 | C1DS1_Lm | 12:00 | 44.7 | 1.378 | 0.392 | 0.29117 | 0.146 | 0.285 |
| 8 | C1DS1_Lm | 13:00 | 44.7 | 1.378 | 0.392 | 0.29117 | 0.146 | 0.285 |
| 9 | C1DS2 | 12:00 | 44.7 | 1.264 | 0.214 | 0.47620 | 0.145 | 0.414 |
| 10 | C1DS2 | 13:00 | 45.4 | 1.264 | 0.214 | 0.47620 | 0.145 | 0.414 |
| 11 | C1DS2_Dc | 12:00 | 44.0 | 1.540 | 0.214 | 0.47620 | 0.145 | 0.414 |
| 12 | C1DS2_Dc | 13:00 | 44.7 | 1.540 | 0.214 | 0.47620 | 0.145 | 0.414 |
| 13 | C1DS2_Lm | 12:00 | 43.9 | 1.540 | 0.214 | 0.47620 | 0.145 | 0.285 |
| 14 | C1DS2_Lm | 13:00 | 44.7 | 1.540 | 0.214 | 0.47620 | 0.145 | 0.285 |
| 15 | C2BC | 12:00 | 47.9 | 2.027 | 0.483 | 0.10471 | 0.123 | 1.860 |
| 16 | C2BC | 13:00 | 49.7 | 2.027 | 0.483 | 0.10471 | 0.123 | 1.860 |
| 17 | C2DS1 | 12:00 | 42.3 | 1.310 | 0.40 | 0.27299 | 0.188 | 1.267 |
| 18 | C2DS1 | 13:00 | 44.4 | 1.310 | 0.40 | 0.27299 | 0.188 | 1.267 |
| 19 | C2DS1_Dc | 12:00 | 44.7 | 1.584 | 0.40 | 0.27299 | 0.188 | 1.267 |
| 20 | C2DS1_Dc | 13:00 | 44.9 | 1.584 | 0.40 | 0.27299 | 0.188 | 1.267 |
| 21 | C2DS1_Lm | 12:00 | 44.6 | 1.584 | 0.40 | 0.27299 | 0.188 | 0.285 |
| 22 | C2DS1_Lm | 13:00 | 44.6 | 1.584 | 0.40 | 0.27299 | 0.188 | 0.285 |
| 23 | C2DS2 | 12:00 | 43.2 | 1.366 | 0.217 | 0.48576 | 0.125 | 0.414 |
| 24 | C2DS2 | 13:00 | 44.0 | 1.366 | 0.217 | 0.48576 | 0.125 | 0.414 |
| 25 | C2DS2_Dc | 12:00 | 44.3 | 1.665 | 0.217 | 0.48576 | 0.125 | 0.414 |
| 26 | C2DS2_Dc | 13:00 | 44.6 | 1.665 | 0.217 | 0.48576 | 0.125 | 0.414 |
| 27 | C2DS2_Lm | 12:00 | 44.3 | 1.665 | 0.217 | 0.48576 | 0.125 | 0.285 |
| 28 | C2DS2_Lm | 13:00 | 44.4 | 1.665 | 0.217 | 0.48576 | 0.125 | 0.285 |
| Dc | As | Ag | Tp | Lm | ||
|---|---|---|---|---|---|---|
| 1 | Urban heart | 5.0–8.0 | 0.15–0.45 | 0.10–0.30 | (0.10–0.6) of (As + Ag) | 0.10–2.0 |
| 2 | Urban center | 2.8–5.0 | ||||
| 3 | Urban core | 1.6–3.0 | ||||
| 4 | Sub urban | 0.4–1.8 | ||||
| 5 | Rural reserve | 0.3–0.5 |
| Model | R2 | AdjR2 |
|---|---|---|
| Linear | 0.81 | 0.76 |
| Interaction | 0.94 | 0.89 |
| Quadratic | 0.94 | 0.89 |
| Stepwise | 0.94 | 0.92 |
| Algorithm | Dc | As | Ag | Lm |
|---|---|---|---|---|
| SQP | 1.2083 | 0.3000 | 0.3000 | 1.9649 |
| 1.2084 | 0.1500 | 0.3000 | 1.9645 | |
| 1.2307 | 0.3000 | 0.3000 | 1.9733 | |
| interior-point | 1.2138 | 0.1500 | 0.3000 | 2.0000 |
| 1.2138 | 0.1500 | 0.3000 | 2.0000 | |
| 1.2138 | 0.1500 | 0.3000 | 2.0000 | |
| active-set | 1.2138 | 0.1500 | 0.3000 | 2.0000 |
| 1.2406 | 0.0871 | 0.3629 | 2.0608 | |
| 1.2442 | 0.3729 | 0.3729 | 2.0729 | |
| simulated annealing | 1.2603 | 0.1500 | 0.3000 | 1.7437 |
| 1.1931 | 0.1500 | 0.3000 | 2.0000 | |
| 1.1197 | 0.1662 | 0.3000 | 1.8154 | |
| GA | 0.3010 | 0.2394 | 0.1009 | 0.1015 |
| 0.3001 | 0.2354 | 0.1000 | 0.1000 | |
| 0.3000 | 0.2354 | 0.1000 | 0.1000 | |
| Average | 1.0308 | 0.1991 | 0.2691 | 1.5931 |
| PET | Thermal Perception | Physiological Stress |
|---|---|---|
| 4 °C | Very cold–cold | Extreme cold stress–strong cold stress |
| 8 °C | Cold–cool | Strong cold stress–moderate cold stress |
| 13 °C | Cool–slightly cool | Moderate cold stress–slight cold stress |
| 18 °C | Slightly cool–comfortable | Slight cold stress–no cold stress |
| 23 °C | Comfortable–slightly warm | No cold stress–slight heat stress |
| 29 °C | Slightly warm–warm | Slight heat stress–moderate heat stress |
| 35 °C | Warm–hot | Moderate heat stress–strong heat stress |
| 41 °C | Hot–very hot | Strong heat stress–extreme heat stress |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahmy, M.; Kamel, H.; Mokhtar, H.; Elwy, I.; Gimiee, A.; Ibrahim, Y.; Abdelalim, M. On the Development and Optimization of an Urban Design Comfort Model (UDCM) on a Passive Solar Basis at Mid-Latitude Sites. Climate 2019, 7, 1. https://doi.org/10.3390/cli7010001
Fahmy M, Kamel H, Mokhtar H, Elwy I, Gimiee A, Ibrahim Y, Abdelalim M. On the Development and Optimization of an Urban Design Comfort Model (UDCM) on a Passive Solar Basis at Mid-Latitude Sites. Climate. 2019; 7(1):1. https://doi.org/10.3390/cli7010001
Chicago/Turabian StyleFahmy, Mohammad, Hisham Kamel, Hany Mokhtar, Ibrahim Elwy, Ahmed Gimiee, Yasser Ibrahim, and Marwa Abdelalim. 2019. "On the Development and Optimization of an Urban Design Comfort Model (UDCM) on a Passive Solar Basis at Mid-Latitude Sites" Climate 7, no. 1: 1. https://doi.org/10.3390/cli7010001





