Trajectory Planning for Robotic Manipulators in Automated Palletizing: A Comprehensive Review

Abstract

Recent industrial production paradigms have seen the promotion of the outsourcing of low-value-added operations to robotic cells as a service, particularly end-of-line packaging. As a result, various types of research have emerged, offering different approaches to the trajectory design optimization of robotic manipulators and their applications. Over time, numerous improvements and updates have been made to the proposed methodologies, addressing the limitations and restrictions of earlier work. This survey-type article compiles research articles published in recent years that focus on the main algorithms proposed for addressing placement and minimum-time path planning for a manipulator responsible for performing pick-and-place tasks. Specifically, the research examines the construction of an automated robotic cell for the palletizing of regular heterogeneous boxes on a collision-free mixed pallet. By reviewing and synthesizing the most recent research, this article sheds light on the state-of-the-art manipulator planning algorithms for pick-and-place tasks in palletizing applications.

1. Introduction

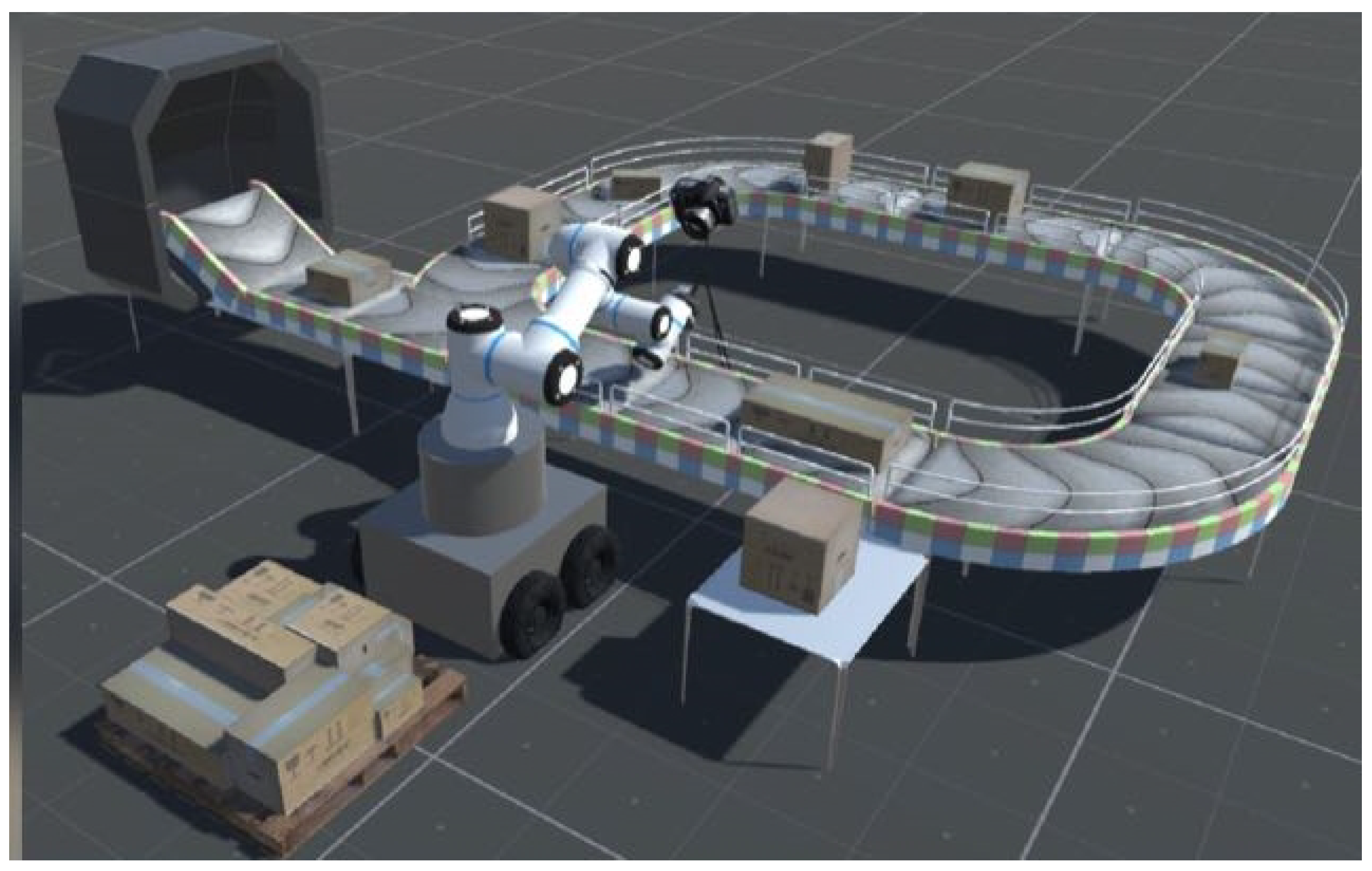
Industrial robots are increasingly used for manufacturing and packaging operations, including end-of-line palletizing. In modern production, companies often outsource such low-value-added tasks to specialized robotized cells that provide packing ’as a service’. A typical palletizing cell consists of a conveyor feeding products, a palletizing station, and a robotic manipulator that transfers products from the infeed to the pallet [1]. A possible schematic of a robotic packaging cell is shown in Figure 1.

Planning efficient trajectories for the manipulator in this context is critical to ensure high throughput and collision-free operation. Robotic trajectory planning generally involves computing a path and time schedule for a robot to move from a start to a goal configuration while satisfying kinematic and dynamic constraints. Classic objectives include minimizing motion time, distance, or energy and avoiding collisions. Over the past decades, a wide variety of algorithms has been developed to address these objectives, from early optimal control approaches in the 1980s to modern sampling-based planners and machine learning techniques. Despite significant progress, several open challenges remain. For example, in a mixed-case palletizing scenario, the robot must autonomously determine a feasible stacking sequence and trajectory on the fly, since there may be no pre-defined stacking pattern. Programming a robot to handle heterogeneous packages without a fixed pattern under real-time constraints remains difficult. Moreover, achieving high-speed motion without sacrificing precision or causing excessive wear is an ongoing concern. The manipulator operates in a semi-structured, dynamic environment—for example, boxes arriving on a conveyor in a constrained workspace—where it must reliably avoid static and moving obstacles while carrying payloads.

A number of recent works have specifically targeted palletizing applications to address these challenges. For example, researchers have proposed heuristic “stacking” algorithms for robot-based mixed-case palletizing using industrial arms [2], as well as mobile robotic systems capable of building heterogeneous pallets from homogeneous unit loads [3]. Other studies optimized palletizing operations by minimizing the robot’s travel distance via integer linear programming (ILP) [4] or by integrating visual perception and high-level planning in human–robot collaborative palletizing frameworks [5]. These efforts underscore the active interest in improving palletizing efficiency, yet a fully generalized solution that meets all performance requirements in diverse scenarios is still lacking. However, some recent studies have focused on the integrated design of complete palletizing systems, implementing specialized algorithms to address each subsystem’s challenges. For instance, Zhu et.al. [6] proposed a palletizing system combining vision-based object detection, packing arrangement computation, and collision-free trajectory planning to optimize the entire workflow. Other researchers have targeted specific subsystems for incremental improvements. For example, Boshoff et.al. [7] employed Unmanned Aerial Vehicles (UAVs) to enhance obstacle and target pose estimation, enabling more accurate dynamic environment mapping. Song et al. [8] presented a light-weight robotic system optimized for narrow cuboid spaces, introducing an adsorption-tray hybrid gripper and a time-optimal “lift-then-pick” strategy that enhances efficiency and doubles robustness. Another study integrated digital twin technology with reinforcement learning to create an adaptive motion planner that dynamically selects between geometry-based and RL-based strategies while Bayesian optimization improves reward tuning, resulting in faster training and reliable performance across tasks [9]. Additionally, Zhixiang et al. [10] proposed a new trajectory planning method based on Fourier series expansion, achieving smoother and more efficient joint motions compared to quintic polynomials, effectively reducing impact and increasing motion continuity in palletizing operations.

Industrial robotic manipulators are the most prevalent solution for palletizing tasks, with their classification typically based on functionality criteria including autonomy level, payload capacity, degrees of freedom (DOFs), and operational speed [11,12]. Collaborative manipulators (cobots) have become particularly favored in palletizing due to their flexibility and ease of integration [13], with Martín et al. [14] categorizing these systems as rigid, discrete, non-redundant, and non-actuated (as illustrated in Figure 2). Performance metrics are critical for evaluating manipulator effectiveness in palletizing applications, with Moreno et al. [15] identifying key performance indices, while Patel and Sobh [16] reviewed measurement methodologies and Hwang et al. [17] demonstrated optimization approaches for seven-DOF serial manipulators—the most common architecture for complex palletizing tasks.

Unlike prior surveys that looked broadly at manipulator kinematics or control (for instance, ref. [18] reviewed optimal trajectory planning methods, Ratiu and Prichici [19] surveyed trajectory optimization for industrial robots, and Rahimi and Nazemizadeh [20] expounded upon dynamic analysis and intelligent control techniques for flexible robot manipulators from 1970 to 2013, and Haddadin et al. [21] presented the literature on model-based algorithms for real-time collision detection), this work concentrates on the state of the art of useful algorithms for robotic placement, path planning, and trajectory optimization in the context of automated palletizing. We compile relevant research, from foundational works before 2010 to the most recent studies published in 2025, highlighting the evolution of approaches and the current state of the art. The contributions of this review are to (1) summarize the key algorithms and strategies for robot path planning and trajectory optimization; (2) analyze their applicability to palletizing scenarios, including the strengths and limitations of each method; and (3) identify open research directions for future work. This paper is a review article—all findings are synthesized from existing studies, and no new experimental results are presented. In the remainder of this paper, we first outline the problem scope and definitions. Section 2 discusses manipulator placement and related performance metrics. Section 3 then reviews trajectory planning approaches (path generation and scheduling), and Section 4 covers specific path planning methods (graph search, sampling-based, optimal control, spline-based, and learning-driven techniques). Section 5 highlights research gaps and future directions, and finally, Section 6 concludes the paper with key insights for both research and industry.

2. Manipulator Placement

The choice of a robotic manipulator’s placement (i.e., the pose of its base in the work cell) is a crucial initial decision that influences the robot’s reachable workspace and performance for a given task. The base position and orientation determine which target points are reachable by the end effector and affect metrics such as achievable speed, payload capacity, and precision in different regions of the workspace. In palletizing cells, for example, the robot base must be positioned so that all pallet locations and conveyor pickup points lie within the arm’s reachable volume. Typically, one can identify regions in the manipulator’s workspace (sometimes called “dexterous” or “high-performance” zones) where the robot can move with better kinematic or dynamic performance. The goal of base placement is to align these high-performance zones with the task requirements (e.g., the pallet locations) to optimize overall operation.

Determining the optimal robot location is challenging because there are infinitely many possible poses for the base and many task-related variables to consider. The problem is often formulated as an optimization task: given certain performance indicators, find the base pose that maximizes those performance measures. Researchers have approached this by first identifying key task properties, then selecting appropriate performance indices to include in an objective function. Common performance criteria include kinematic reachability, cycle time, energy consumption, accuracy, and manipulability.

2.1. Placement Performance Indicators

Multiple studies have proposed algorithms to optimize robot base placement for specific applications by focusing on particular performance indicators. For example, Nektarios and Aspragathos [22] formulated an algorithm to find the base location that maximizes the end effector’s achievable speed along a given reference trajectory. Schneider et al. [23] developed a method to optimize a manipulator’s location in a machining process by considering the rigidity of the robot mechanism. In another work, Malhan et al. [24] sought to position a workpiece within the robot’s workspace such that the manipulator could exert the required forces for an assembly operation.

Other authors have optimized base placement under different criteria. Tian and Collins [25] found placements that minimize the distance traveled by the end effector. Vosniakos and Matsas [26] explored optimal robot locations for milling tasks by evaluating manipulability indices and external force interactions. Similarly, Pámanes-García et al. [27] investigated base positioning using various kinematic performance indices (e.g., conditioning and manipulability) as objectives. Notably, some strategies have been proposed specifically to improve performance in palletizing tasks. For instance, Masood and Khan [28] examined different pallet pattern placement strategies and their effects on robot positioning in a palletizing cell, highlighting how the base location can influence the efficiency of stacking operations.

2.2. Optimization in Task Space vs. Joint Space

When formulating placement optimization mathematically, one can define the problem in the task (Cartesian) space or in the joint (configuration) space of the robot. An optimization in Cartesian space might aim to maximize coverage or performance over a set of task points (e.g., pallet coordinates), whereas a joint-space formulation can incorporate the robot’s kinematic and dynamic characteristics more directly. For example, Weingartshofer et al. [29] proposed an algorithm that uses the results of a joint-space trajectory planner to find the optimal location of the tool center point (and, by extension, the robot base). In their approach, the objective function is built from characteristics of trajectories in joint space, linking the placement problem with path planning outcomes. In another study, Dos Santos et al. [30] presented a strategy to locate the robot base so as to minimize energy consumption while maximizing positioning accuracy for a given trajectory. They introduced performance indices relating energy use to manipulability and optimized the base pose based on those indices.

For complex scenarios where a robot must perform multiple tasks or service multiple locations, researchers have employed reachability analysis and workspace mapping techniques. Instead of optimizing for a single trajectory, these methods consider the set of all target points and motions the robot must execute. Tools such as reachability maps or accessibility indices can evaluate how well a candidate base position allows the robot to reach the necessary points with acceptable orientations. For example, some authors have computed reachable workspace volumes or used inversion of reachability to determine good base locations for multi-task operations [31]. Techniques like the used of a reachability index and capability map [32,33] graphically represent how reachable each point in the environment is from a given base pose. By analyzing these maps, one can choose a base placement that covers all required task points. Other authors have suggested compound algorithms to solve the problem. Doan and Lin [34] presented a methodology of three algorithms; the first two algorithms solve the robot’s kinematics, including range constraints, singularity, and collision-free trajectories, and the third cycle optimizes the robot’s location based on the already obtained results.

In palletizing applications, such analyses ensure the robot can access the entire stack footprint on the pallet, as well as pick-up points on the conveyor. Additionally, each of the implemented algorithms can be adapted to optimize key parameters of interest in the palletizing task, such as total travel distance, palletizing time, and maneuverability, among others. For instance, the methodology proposed in [35] addresses optimal robot placement for the execution of diverse trajectories. This approach could be adapted to minimize the number of movements required in palletizing tasks. Overall, the literature on manipulator placement reveals that optimizing the robot’s base location—though often treated separately from trajectory planning—forms an important foundation for efficient task execution in automated packing cells.

3. Trajectory Planning

Trajectory planning is concerned with the generation of a feasible motion for the robot that moves it through a sequence of poses or via points over time. This involves determining not just the geometric path in space but also the timing (velocity and acceleration profiles) along that path [36,37,38,39]. A trajectory is typically defined in either joint space (angles of each robot joint as functions of time) or task space (position/orientation of the end effector as functions of time) or a combination of both. According to one definition proposed by Feng and Jia [40], trajectory planning specifies the values of each joint as a function of time such that the robot accomplishes the desired motion. In essence, the planner must find a collision-free path from an initial pose to a target pose, then assign a time law to move along this path while respecting the manipulator’s kinematic and dynamic limits.

For pick-and-place operations like palletizing, the robot’s overall movement can often be segmented into distinct phases: (1) moving to pick up a product (synchronizing with a moving conveyor if necessary), (2) transferring the product through free space at high speed, and (3) placing the product onto the pallet with careful positioning. Each phase can impose different constraints. For example, during pickup, the robot may need to match the conveyor speed to grasp the item; during transfer, it may accelerate to maximum speed to minimize travel time; and during placement, it must avoid collisions with previously stacked items, possibly moving more slowly to ensure accuracy.

Key considerations in trajectory planning include time optimality, energy efficiency, and obstacle avoidance. Often, there are trade-offs among these goals. A minimum-time trajectory may demand rapid accelerations and jerking (rate of acceleration change), which can excite vibrations or stress the mechanical structure. On the other hand, a trajectory optimized for smoothness or energy may not be the fastest. In industrial practice, planners typically generate a nominal geometric path (via waypoints or a continuous curve), then perform time parameterization subject to velocity, acceleration, and jerk limits. Shin and McKay’s classic work [41] is an example of time-optimal trajectory planning along a predefined path under actuator constraints. Several studies have addressed minimum-time path planning in robotics. Messay et al. [42] proposed kinematic calibration algorithms to minimize discrepancies between the manipulator’s mathematical model and its geometric representation, incorporating kinetic, dynamic, and payload constraints—where dynamics involve torque, power, and energy limits and kinematics consider joint velocity, acceleration, and vibration boundaries. Haddad et al. [43] introduced efficient schemes for time-optimal trajectory planning, while Luan et al. [44] developed a maximum-speed algorithm tailored for serial palletizing robots, emphasizing real-world applicability. Zhang et al. [45] formulated the problem as a convex optimization to generate smooth, minimum-time trajectories. Similarly, Xu and Hong [46] devised an optimal path planning algorithm to enhance efficiency and mitigate vibrations. Abu-Dakka et al. [47] advanced a parallel-population genetic algorithm to compute time-optimal trajectories for manipulators. Complementary to planning, trajectory tracking has been implemented via diverse controllers; for instance, Xiao and Yin [48] tackled tracking control under unknown dynamics and kinematics. While such optimal control formulations can yield minimum execution times, they are computationally intensive and may require simplifications (e.g., trapezoidal velocity profiles or piecewise polynomial motions) for practical use.

Polynomial trajectory laws are widely used due to their computational simplicity and guarantee of smoothness. Third-order (cubic) or fifth-order (quintic) polynomials are often employed to interpolate between waypoints with specified boundary conditions (velocities and accelerations set to zero at end points, for instance). These polynomial trajectories ensure continuous velocity and acceleration profiles. Higher-order polynomials or spline curves can further ensure continuity of jerk. For example, Piazzi and Visioli [49] presented a global trajectory optimization producing minimum-jerk motion using cubic splines, effectively controlling end-effector velocities and accelerations to reduce overall jerk. Such spline-based approaches improve motion smoothness, which is important for high-speed palletizing, where abrupt changes could tip or destabilize a carried package. B-spline curves, in particular, are powerful for trajectory planning because they offer local control (adjusting one segment does not globally affect the entire trajectory) and can enforce smoothness constraints. B-splines have been used to shape and smooth robotic paths, improving tracking performance and reducing cycle time. They can be applied in either Cartesian or joint space, and increasing the spline degree or the number of control points provides greater control over the trajectory. However, very high-degree polynomials can lead to numerical issues or trajectory oscillations, so in practice, a moderate-degree spline is chosen.

An essential aspect of trajectory planning in industrial settings is handling the robot’s dynamic limits while pushing for speed. Robots are asked to operate at ever higher velocities to shorten cycle times, yet operating at high speed can degrade precision and repeatability, in addition to increasing wear on joints and motors. Therefore, trajectory planners often incorporate constraints on acceleration and jerk to avoid exciting vibrations in the robot’s structure. A high-speed trajectory must be carefully time-scaled so as not to exceed the robot’s torque limits or cause excessive end-effector sway when carrying a load. Research by Gasparetto et al. [50] notes that advanced motion planning is needed to allow robots to achieve higher speeds without compromising mechanical integrity. In palletizing, this means the robot should move as fast as possible between picks and placements but with a motion profile that the robot can physically realize without overshooting or oscillation.

Another critical consideration is obstacle avoidance. In a palletizing scenario, obstacles may include the pallet itself, a pallet rack, and the stack of already placed items (which grows over time). The trajectory planner must ensure the manipulator does not collide with these objects at any point. This can be addressed by planning paths in the configuration space that steer clear of obstacle configurations or by adding intermediate via points above the stack. Some works have integrated collision avoidance directly into trajectory optimization. For instance, one can include potential field forces or collision penalty terms in an optimal control framework to push the trajectory away from obstacles. A recent approach proposed by Tonan et al. [51] demonstrated trajectory planning for an underactuated 2-DOF manipulator that includes via points specifically to avoid obstacles, effectively achieving collision-free motion, even with a robot that has fewer actuators than degrees of freedom. By exploiting the concept of differential flatness, they parameterized the trajectory with high-order polynomials through key via points, enabling an underactuated arm to maneuver around obstacles similarly to a fully actuated robot. This illustrates how advanced analytical methods can broaden the scope of trajectory planning (in this case, to underactuated systems) while still satisfying typical industrial constraints.

In summary, trajectory planning provides the time-parameterized reference that the robot’s control system will track. It must balance competing objectives of speed, smoothness, precision, and safety. In the next section, we review prominent path planning and trajectory generation methods from the literature, ranging from classic graph search algorithms to modern learning-based techniques, and we discuss how each can be applied to the palletizing use case.

4. Path Planning Methods

A variety of algorithmic methods has been developed to plan paths and trajectories for robotic manipulators. Here, we survey the main categories, including graph-based search algorithms, sampling-based planners, artificial potential field methods, spline interpolation techniques, and learning-based approaches. We emphasize how these methods contribute to the overall trajectory planning problem and their relevance to palletizing tasks.

Table 1. Path planning and optimization methods for robotic palletizing.

Method	Key Idea	Advantages	Limitations	Elements
A* Search	Graph search on a grid using heuristics to find the shortest path	Guaranteed optimal path on a grid; effective with good heuristics	Computational cost grows exponentially with dimensionality; grid-constrained paths	Grid map and vision sensor
PRM	Randomly samples collision-free configurations to build a roadmap graph	Fast planning in static environments; reusable for multiple queries	Trajectories may need smoothing; not suited for dynamic environments	Local planner
RRT	Incrementally grows a random tree toward unexplored space	Effective in high-dimensional spaces; good for single-query planning	Paths often suboptimal; no infeasibility proof	Random tree structure
APF	Goal as attractor and obstacles as repellers in the potential field	Computationally light; real-time reactive capability	Prone to local minima; no global optimality guarantee	Distance sensors
Neural Networks	Learn path generation or control policies from data	Fast computation after training; no explicit model needed	Require large training datasets; interpretability challenges	Training datasets
B-Spline	Piecewise polynomial curves for smooth interpolation	Continuous velocity/acceleration; local adjustability	Not standalone; struggles with singularities	High-degree polynomials
Energy-Optimal	Optimizes trajectory to minimize energy consumption	Reduces energy use and mechanical wear	Complex implementation; may increase cycle time	Simulation models

provides a comparative summary of the strengths and limitations of each method.

4.1. Graph Search Algorithms (Grid-Based Planning)

A foundational path planning approach involves discretizing the robot’s workspace or configuration space into a grid and searching for the lowest cost path, as exemplified by the ${\mathrm{A}}^{*}$ algorithm [52]. ${\mathrm{A}}^{*}$ efficiently guides the search from a start state to a goal using heuristics, guaranteeing grid-based optimality for metrics like path length and time (see Figure 3). While effective for low-dimensional spaces (e.g., planar end-effector motion), ${\mathrm{A}}^{*}$ faces scalability challenges in high-DOF manipulators due to the curse of dimensionality. Finely discretized grids exacerbate computational costs, and the resulting piecewise linear paths often require smoothing for practical execution. Despite these limitations, ${\mathrm{A}}^{*}$ remains viable for palletizing tasks reducible to lower dimensional searches (e.g., gantry crane motion or pick-and-place sequencing), sometimes integrated with sensor-updated occupancy grids. Modified versions, such as those proposed in [53,54], address computational efficiency and adaptability.

4.2. Sampling-Based Methods (Probabilistic Planning)

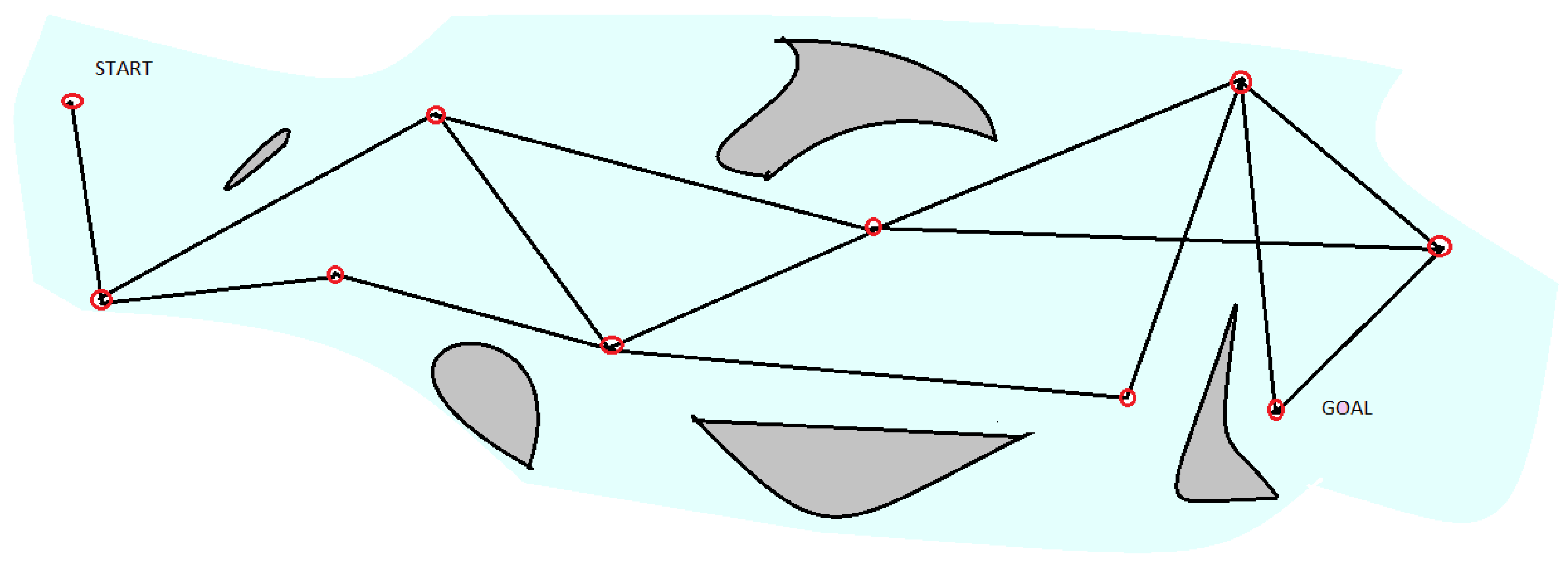
The Probabilistic Roadmap Method (PRM) and Rapidly-exploring Random Tree (RRT) algorithms offer distinct advantages for robotic palletizing tasks. The PRM constructs a collision-free roadmap through random sampling of the configuration space, which is particularly effective for palletizing in known environments where obstacle locations are predetermined. While computationally intensive for high-DOF manipulators, recent enhancements, like environment pre-learning and hybrid PRM–reinforcement learning approaches, have improved its efficiency for palletizing applications.The algorithm’s ability to find optimal paths using graph search methods (e.g., A*) makes it suitable for the optimization of palletizing sequences when combined with post-processing smoothing techniques. Conversely, RRT excels in dynamic palletizing environments through its incremental tree growth method. Its strength lies in real-time adaptability, which is particularly valuable when handling variable pallet loads or moving obstacles, although path quality may require refinement [55,56]. The algorithm’s natural bias toward unexplored regions (Voronoi bias) proves advantageous when palletizing in cluttered workspaces.

4.3. Probabilistic Roadmap Method (PRM)

The PRM constructs a collision-free roadmap through random sampling of the robot’s configuration space, which is particularly effective in known environments where pallet locations and obstacles are predetermined [57]. The method randomly generates numerous valid configurations (nodes) and connects them with feasible motions (edges) to form a graph; a graph search (e.g., Dijkstra or A*) is then employed on this roadmap to find an optimal path from the start to the goal (see Figure 4). The PRM is computationally intensive for high-DOF manipulators, but several enhancements have improved its efficiency for palletizing applications. For example, environmental pre-learning techniques can bias sampling using prior knowledge of the workspace [58], and hybrid approaches combine the PRM with reinforcement learning to guide sampling in complex pallet layouts [59]. Various other improvements and variants of the PRM have been discussed in the literature [60,61], aiming to accelerate roadmap construction and solution finding. Notably, once a roadmap is built, classical graph search algorithms can be used to find time-optimal or energy-optimal paths through it, making the PRM suitable for optimizing palletizing sequences when paired with post-processing smoothing. In practice, planners often integrate the PRM with a smoothing stage (e.g., fitting a spline through the roadmap waypoints) to ensure the piecewise path can be executed fluidly on the manipulator.

4.4. Rapidly Exploring Random Trees (RRT)

RRT algorithms excel in dynamic or unstructured palletizing environments through an incremental tree-growth strategy. RRT incrementally builds a tree in the configuration space by extending toward random samples. At each iteration, given a randomly sampled configuration ($q_{\mathrm{rand}}$), the tree finds its nearest node ($q_{\mathrm{near}}$) (according to a distance metric) and adds a new node in that direction:

$$q_{\mathrm{new}}=q_{\mathrm{near}}+ϵ{\displaystyle \frac{(q_{\mathrm{rand}}-q_{\mathrm{near}})}{|q_{\mathrm{rand}}-q_{\mathrm{near}}|}},$$

(1)

where $ϵ$ is a fixed step size (see Figure 5). By iterating this process, RRT rapidly explores the space and eventually finds a collision-free path to the goal (which can then be smoothed for execution). These examples illustrate two core paradigms—spline interpolation and sampling-based search—that underlie many palletizing trajectory planners. Starting from the initial robot state, an RRT rapidly expands by stochastically sampling the configuration space and extending toward unexplored regions. The key strength of RRT is its real-time adaptability—it can quickly find a feasible route around newly detected obstacles or changing stack geometries—which is particularly valuable when handling variable pallet loads or moving obstacles on a conveyor. The trade-off is that the raw paths produced by RRT tend to be jagged or suboptimal, often requiring refinement or smoothing before execution [55,56]. The algorithm’s natural Voronoi bias toward unexplored space is advantageous in cluttered workspaces, as it efficiently probes free regions of the palletizing cell that might be missed by deterministic planners.

In summary, these sampling-based planners address critical palletizing requirements in complementary ways. The PRM provides an offline-optimized route (ideal for repetitive tasks in static setups), while RRT offers online adaptability to dynamic conditions. Recent RRT variants, such as bidirectional RRT and RRT-Connect [62,63], and optimized sampling strategies [64] have further improved planning speed and path quality, making RRT more practical for high-speed palletizing. Moreover, combining the PRM or RRT with other techniques can yield better overall performance. For example, integrating a local artificial potential field for reactive obstacle avoidance or smoothing the final trajectory with a B-spline blend allows the planner to simultaneously optimize multiple criteria (path length, execution time, and energy use) [59]. These integrations are frequently tuned to palletizing-specific constraints (like maintaining a box’s orientation or avoiding previously stacked items), highlighting the flexibility of sampling-based methods to be customized for the palletizing domain.

4.5. Artificial Potential Field Methods

The Artificial Potential Field (APF) method provides real-time path planning by modeling robot motion as particle dynamics in a virtual force field. In this framework, attractive forces draw the robot toward palletizing targets while repulsive forces deflect it from obstacles, enabling reactive collision avoidance, which is crucial for high-speed pallet operations. The method’s computational efficiency stems from local force calculations, permitting high-frequency trajectory adjustments, which are particularly valuable when handling unexpected obstacles like fallen boxes. However, traditional APF methods suffer from local minima traps, where force equilibria halt progress, which is a significant limitation in dense pallet configurations.

Enhanced variants like the Velocity Potential Field (VPF) [65] address these shortcomings by incorporating motion dynamics to escape stagnant points. For palletizing, APF excels in fine tuning end-effector approaches between tightly packed boxes, where its fast response enables gentle, collision-free placements [66]. While insufficient for global planning due to minima issues, modern implementations combine APF with higher-level planners: global algorithms (e.g., RRT) handle overall path planning, while APF modules manage real-time obstacle avoidance and placement precision [67,68]. This hybrid approach leverages APF’s simplicity for local refinements while mitigating its topological limitations.

4.6. Learning-Based Approaches and Neural Networks

Machine learning techniques, especially neural networks and reinforcement learning, have been increasingly applied to robot path planning and control in recent years. These learning-based approaches aim to allow the robot to improve its planning performance through experience or to generalize from examples rather than relying solely on hard-coded models.

Early works on neural networks for manipulators often focused on solving sub-problems like inverse kinematics or redundancy resolution. For example, Jin et al. [69] provided a comprehensive survey of neural network approaches for robot manipulator control and planning. Neural networks have been used to learn inverse kinematic mappings or to compute joint trajectories that satisfy certain criteria. In one study, Li et al. [70] applied a primal dual neural network to solve a constrained optimization problem for motion control, effectively computing an optimal path that minimizes an $L_1$ norm-based cost in real time. Similarly, Xie et al. [71] designed a neural network-based scheme for repetitive motion planning (RMP) in redundant manipulators. Their dynamic neural network controller handles nonconvex constraints and can iteratively improve the planned trajectory for tasks that repeat, which is relevant for repetitive palletizing cycles.

Reinforcement Learning (RL) has emerged as a particularly promising approach for trajectory planning and control. In reinforcement learning, the robot (or an agent controlling the robot) learns a policy for actions (e.g., joint velocity commands) by interacting with the environment and receiving feedback in the form of rewards or penalties. Over time, the agent can learn strategies that are difficult to derive analytically. Deep reinforcement learning methods have been applied to manipulators for pick-and-place tasks with notable success. For instance, Park et al. (2007) [59] demonstrated that combining RL with a sampling-based planner yields efficient real-time planning in uncertain, dynamic environments. More recently, Iqdymat and Stamatescu (2025) [72] showed that integrating deep RL with optimal control can significantly improve both precision and energy efficiency for a six-DOF industrial manipulator in a warehouse pick-and-place scenario. This kind of result is promising for palletizing, as it suggests that learning algorithms can autonomously discover trajectories that optimize multiple objectives (time, energy, and accuracy) in ways that hand-tuned trajectories might not.

However, learning-based methods also have challenges. Training requires a large number of trials or quality data, and in robotics, that often means extensive simulation or risking trials on real hardware. Safety is a major concern—an agent exploring trajectories might collide with objects or exceed joint limits if not carefully constrained. There are ongoing developments in safe reinforcement learning to address this, such as adding safety layers or constraint handling within the learning process. Data efficiency is another issue: methods like imitation learning and the incorporation of model knowledge (e.g., using model-predictive control with learning) are being explored to reduce the amount of trial and error needed.

In the context of palletizing, one could envision a learning-based system that observes the outcomes of its packing attempts (stack stability, time per cycle, and energy used) and gradually refines its motions. Over many pallets, it might learn subtle improvements, like how to slightly adjust its approach angle to place a box without disturbing neighbors or how to sequence picks to minimize energy use. Some recent works have combined vision, planning, and learning to create intelligent palletizing robots that improve over time [1,73]. The current literature indicates that while purely learning-driven planners are still emerging, they are set to complement and enhance classical methods by handling complexity and uncertainties that are hard to model explicitly.

4.7. Spline-Based Trajectory Generation

Spline interpolation methods, including B-splines and other polynomial splines, are widely used to generate smooth trajectories for manipulators. Spline-based planning sits somewhere between pure path planning and control—it takes a coarse path or a set of waypoints and produces a refined trajectory that a robot can follow smoothly.

B-splines (basis splines) are piecewise polynomial functions defined over a sequence of control points. The trajectory of degree d can be defined by control points ($P_0,P_1,\dots ,Pn$) and basis functions ($N_{i,d}\left(u\right)$) on a normalized time parameter ($0\le u\le 1$):

$$\mathbf{x}\left(u\right)=\sum _{i=0}^n{N}_{i,d}\left(u\right)·P_i,$$

(2)

which guarantees up to $C^{d-1}$ continuity at the control points and yields a smooth path through the via points.

In trajectory planning, the control points can be chosen to guide the robot through certain positions, and the B-spline ensures a smooth curve that interpolates or approximates those points. One major benefit of B-splines is that they produce trajectories with continuous higher-order derivatives (velocity and acceleration), which is crucial for avoiding exciting vibrations in a robot. They also allow for local adjustability: moving one control point mainly affects only the neighboring segments of the trajectory, not the entire path. According to recent studies, using cubic B-splines to smooth a planned path can improve tracking performance and reduce motion time. For example, Yu et al. [74] suggested learning an environment’s layout first to generate an initial collision-free path, followed by path smoothing with a cubic B-spline for execution. This is very applicable to palletizing, where the initial path might come from a discrete algorithm or heuristic (like placing a box in a calculated position); then, a spline is fitted to ensure the motion is gentle and fast.

Spline trajectories can be generated in either joint space or task space. Joint-space splines have the advantage of inherently respecting joint limits if the control points are chosen appropriately, and they avoid singularity issues. Task-space splines (like Cartesian splines for the end effector) can directly encode straight-line moves or specific path shapes in the workspace, which might be needed to avoid obstacles or adhere to process constraints (e.g., keeping a box level). Often, planners use a hybrid: they generate a coarse collision-free Cartesian path (via waypoints around obstacles or over stacks), then time-parameterize it with a joint-space spline that achieves those waypoints.

There are also optimal spline-based approaches. We mentioned the work by Piazzi and Visioli [49], who used interval analysis to find a minimum-jerk trajectory via cubic splines. Other researchers have formulated multi-objective optimizations where control points of a spline are adjusted to minimize time and energy use or to avoid obstacles while keeping the spline smooth [75,76,77]. These approaches turn trajectory generation into an optimization problem over the spline parameters, which can be solved by techniques like sequential quadratic programming or even genetic algorithms.

In palletizing, spline methods are extremely useful in generating the final joint commands for the robot. For instance, once a sequence of pick-and-place positions is determined (the order in which boxes will be placed and their target coordinates), a spline-based trajectory planner can generate a seamless motion that connects all these points with minimal idle time and smooth accelerations. This could involve blending segments of straight-line motion (to extract and insert boxes vertically) with swift curved motions in free space. B-spline blending allows the robot to not completely stop at intermediate points, saving time by rounding off the corners of the motion, so to speak, while still passing near those important via points. The purpose of the constraint is to ensure that these blended motions do not hit any obstacles—a challenge that can be met by careful placement of control points or by imposing collision-avoidance constraints in spline optimization.

4.8. Energy-Efficient Trajectory Optimization

Energy efficiency has gained increasing attention in robotic trajectory planning, especially for operations like palletizing that involve repetitive motions. An energy-efficient trajectory is one that completes the task with minimal energy consumption, which not only reduces operating costs and environmental impact (lower electricity usage and lower ${\mathrm{CO}}_2$ emissions) but can also reduce wear on the robot. Energy consumption for a robotic manipulator is affected by factors such as the masses moved (including the payload), acceleration and deceleration profiles, and the durations of motion and idle times.

Several approaches have been explored to plan low-energy trajectories. One straightforward approach is to minimize peak accelerations and velocities, since rapid accelerations generally require high motor torques and currents. Another approach is to exploit gravity and dynamics. For example, motions can be planned to recuperate energy (through regenerative braking on motors) or avoid fighting against gravity more than necessary. In pick-and-place tasks, scheduling and trajectory go hand in hand for energy optimization, e.g., placing heavier objects lower or sooner could reduce the robot’s energy expenditure over the entire stacking process.

Numerous studies have formulated trajectory planning as an optimization problem with an energy-related cost function. Srinivas and Javed [78,79] provided a review of various optimization approaches aimed at improving the energy efficiency of serial manipulators. Specific case studies on palletizing robots show that point-to-point trajectory planning (PTP) can be tuned for energy savings. For instance, one might extend the motion duration slightly (sacrificing a bit of cycle time) if it allows motors to operate in a more efficient regime or avoid sharp accelerations, thereby using less energy overall. Techniques like iterative learning control have been used to optimize input shaping over repeated cycles to converge to lower energy usage without deviating from the required motion profile [80,81,82,83,84,85,86,87].

A practical example was provided by Paes et al. [88], who generated energy-optimal trajectories through intelligent programming of the robot’s velocity profile, achieving measurable energy reductions per cycle. Vidussi et al. [89] introduced an energy analysis framework that includes a performance index relating a robot’s energy consumption to its inertia ellipsoid (essentially capturing how the robot’s configuration affects the required effort). By evaluating such indices, a planner can choose configurations and paths that inherently favor lower energy use (for instance, avoiding configurations where the robot is stretched out and torque requirements are higher).

Another line of research combines energy optimization with other objectives. Multi-objective optimization can seek a trade-off between time and energy use. For example, using a Pareto-optimal approach or evolutionary algorithms like NSGA-II, one can obtain a set of trajectories ranging from fastest (higher energy) to most energy-efficient (slower), then select a suitable compromise [90]. In industrial settings, often, the fastest cycle that does not exceed a given energy threshold (or that stays below a temperature threshold for motors) is desired, so such a trade-off analysis is valuable.

For palletizing, energy-efficient planning might also consider the layout of tasks—not just how to move but what sequence to move in. Research has shown that even the path order (which box to place next) can affect energy usage, essentially coupling scheduling with trajectory planning. Integrating these decisions is complex but has potential for optimization.

A summary of the main aspects of the basic algorithms for planning or optimizing the trajectory of a robotic manipulator is presented in Table 1.

4.9. Experimental Setups and Performance Metrics

A number of cited studies have validated trajectory planning approaches with real or simulated palletizing experiments, emphasizing various performance metrics. Common performance indices include the cycle time per pick and place (which determines throughput in boxes per hour), energy consumption of the robot during motion, peak or average accelerations (related to mechanical stress and vibration), and precision of placement [15]. Standard methodologies for measuring and comparing these metrics in robotic systems were surveyed by Patel and Sobh [16]. Here, we summarize key experimental findings from the literature.

Moreno et al. [15] identified throughput, energy per cycle, and placement accuracy as critical metrics for palletizing robots. In their evaluations, optimized trajectories achieved faster cycle times without increasing energy usage beyond acceptable limits, illustrating the importance of smooth motion profiles. Hwang et al. [17] demonstrated that for a seven-DOF serial manipulator, carefully optimized joint trajectories can reduce energy consumption by minimizing unnecessary motions while still meeting the task’s time constraints—an important result for heavy-payload palletizing, where energy efficiency and heat buildup are concerns. Zhu et al. [6] implemented a complete palletizing system (combining vision-based detection, packing sequence optimization, and trajectory planning) and reported significant improvements in throughput over baseline methods; in their case study, the integrated approach allowed for adaptive picking and stacking of mixed boxes with virtually zero collisions, improving the palletizing rate by an order of magnitude compared to manual planning. Sakamoto et al. [91] focused on motion planner performance and, in experiments, showed that their reusable roadmap planners greatly decrease computation time on repeated palletizing tasks: in a trial of 30 pick-and-place cycles, a standard PRM failed to find a path 30% of the time in a cluttered scenario, whereas their reuse-based PRM succeeded in 100% of trials and kept planning times below 0.4 s for all subsequent picks. This translated to a higher sustained throughput, since the robot spent less time waiting for a new trajectory to be planned. Similarly, Xu and Hong [92] developed an S-curve time-optimal trajectory for a palletizing robot under kinematic constraints and verified on hardware that it significantly reduced cycle time and vibration compared to a non-optimized motion—the robot could move faster between pick-and-place positions without exciting dangerous oscillations, improving the overall palletizing speed. Across these studies, the consensus is that carefully planned trajectories (whether optimized offline or adjusted online) can dramatically enhance palletizing performance. The choice of metric often depends on the use-case: automotive and fast-moving consumer goods industries prioritize cycle time (boxes per minute), whereas contexts like food or pharmaceutical palletizing might emphasize gentle handling (lower impact forces) and energy efficiency. By examining metrics like these in experimental settings, researchers can quantitatively demonstrate the benefits of advanced trajectory planning algorithms for palletizing applications.

5. Research Gaps and Future Directions

Robotic trajectory planning methodologies have evolved greatly over the past decades, and different approaches tend to excel under different palletizing conditions. In the 1980s, classical optimal control formulations were applied to manipulator motion—for example, solving for minimum-time or minimum-energy joint trajectories along predefined paths [41]. These early methods assumed well-structured tasks (fixed start/end points and no moving obstacles) and proved effective for straightforward palletizing scenarios where a robot repeatedly moves identical objects. Under such conditions, simple time-optimal polynomial profiles or bang–bang control could minimize cycle time. By the 1990s, researchers began addressing more complex environments; techniques like artificial potential fields emerged to enable real-time obstacle avoidance, which was particularly useful as palletizing robots started to handle irregular stacking patterns in semi-structured warehouses. However, potential field planners could get stuck in local minima if a pallet configuration was densely packed, highlighting that no single method worked universally.

The late 1990s and early 2000s saw the rise of graph search and sampling-based planners. Grid-based algorithms (e.g., ${\mathrm{A}}^{*}$ variants) were adapted for robotic arms, but the high dimensionality of a six-DOF or seven-DOF palletizer made exhaustive search impractical, except for simplified sub-tasks. This led to probabilistic algorithms—notably, the PRM [57] and RRT [55]—which trade completeness for efficiency. These methods brought about significant advantages for palletizing in more unpredictable settings: a PRM could pre-compute roadmaps for a known workspace (useful if the pallet layout is static for long periods), while RRT could quickly re-plan on the fly when boxes shift or new obstacles (like a forklift intrusion) appear. During the 2010s, attention shifted to optimality and learning. Researchers introduced multi-objective optimizations that balance speed, energy, and smoothness—an important development for palletizing, since the path that is fastest may also cause wear or require excessive power. For instance, techniques were developed to adjust spline control points or time scaling to minimize both motion time and energy consumption [92]. At the same time, learning-based approaches gained traction: reinforcement learning and imitation learning have been explored to allow robots to learn palletizing strategies from experience [59]. These are promising approaches for highly unstructured scenarios (e.g., a service robot that must adapt to arbitrary pallet patterns), but they typically require many training examples and careful tuning to ensure safety and reliability on hardware.

Overall, this historical trajectory shows that no one-size-fits-all solution exists in trajectory planning; instead, each method has specific applicability conditions in palletizing. Classical polynomial and spline methods are extremely efficient for regular, repetitive palletizing tasks where the environment is known a priori—they leverage smooth motion generation and low computation time but are less adaptable to change. Sampling-based planners handle changing or uncertain environments well and are, thus, employed when the pallet contents or surroundings vary (at the cost of extra smoothing steps to improve path quality). Optimization-based planners (including modern model-predictive control and hybrid optimization algorithms) are favored when fine tuning of performance metrics is needed—for example, in high-throughput palletizing cells where even a small reduction in cycle time per pick can yield huge gains over thousands of cycles or in energy-critical operations where minimizing peak power usage prolongs robot life. Learning-based methods, while still emerging, are beginning to show value in scenarios where the robot must generalize to new pallet arrangements or collaborate with humans; in such cases, the ability to improve performance with experience can complement the fixed strategies derived from classical algorithms.

Each approach’s historical context informs its best use: what was once a theoretical optimal control solution is now a practical component (for instance, used to time-optimize a segment of an RRT path), and what was once an experimental learning algorithm might soon become a standard feature in next-generation palletizing robots. The palletizing domain continues to drive such innovations, as evidenced by the increasing integration of these diverse planning techniques in both research prototypes and industrial solutions.

However, despite the rich array of methods demonstrated in the literature for manipulator trajectory planning, several critical challenges remain, particularly in the realm of high-mix palletizing and service-oriented automation. In this section, we highlight some open issues and suggest directions for future research.

• Real-time adaptation and autonomy: Many advanced planning algorithms (e.g., optimal control or global optimization methods) are computationally intensive and run offline. In a dynamic packing environment, the system should adapt on the fly to changing conditions—such as last-minute package additions or a shifting load. Future research should focus on real-time trajectory planning frameworks that can re-plan or adjust mid-course without stopping the operation. This might involve hybrid approaches (combining fast reactive planning with slower optimal refinements) or leveraging of the speed of learning-based methods to update plans online. Ensuring stability and safety during such real-time re-planning is a key challenge.
• Integrated task and motion planning: In palletizing, deciding what to do (task planning, i.e, which item to pick next and where to place it) is tightly coupled with how to do it (motion planning, i.e., planning the trajectory to execute that pick/place). However, most current research treats these separately. There is a need for integrated planning that considers the sequence of actions and trajectories jointly for optimization. For example, an algorithm could evaluate the estimated energy or time cost of placing a box in various candidate locations and choose the plan that minimizes a global objective. This integration leads to a combinatorial explosion in complexity, but smarter heuristics or decomposition techniques (or, again, learning approaches that can approximate the solution) could make this tractable. Some initial work along these lines, particularly using ILP for sequencing, combined with motion planning, is promising but can be expanded to more complex scenarios (multiple robots, random arrival of items, etc.).
• Safety and collision avoidance in learning-based systems: As reinforcement learning and other AI-driven methods become more prevalent, ensuring safety during both training and deployment is paramount. Robots learning their own motions must be constrained so they do not damage goods or themselves. Future research might explore safe exploration techniques in RL, where the agent is guided by a baseline planner (for instance, an RRT or a spline planner) and only allowed to make modest deviations that are known to be safe. Another concept involves adding a safety layer that monitors and overrides learned policies if a potential collision or limit violation is predicted. Developing verifiably safe RL for manipulators in industrial settings is an important direction, which will likely involve interdisciplinary work between control theory and machine learning.
• Handling of uncertainties: In a packing cell, uncertainties abound—the exact weight of a box might deviate, the box’s contents may shift, sensor noise can affect perception of positions, etc. Robust trajectory planning that can tolerate or compensate for uncertainties is an open problem. Techniques such as robust optimization, stochastic trajectory planning, and feedback motion planning (where the trajectory is continually adjusted based on sensor feedback) are worth investigating. For instance, if a box’s position on the conveyor is slightly off from expectation, the trajectory to grab it should adjust in real time (perhaps using visual servoing). While basic approaches exist (many industrial arms come with vision-guided correction capabilities), the challenge is to integrate these seamlessly with higher-level planning so that the entire operation (from pick to place) is robust, not just individual sub-motions.
• Advanced control of underactuated and redundant systems: Most palletizing robots today are fairly standard six-axis articulated arms (fully actuated and typically non-redundant in their workspace). However, the push for cheaper or more flexible systems could introduce underactuated manipulators (to save cost) or mobile base manipulators (introducing redundancy). The recent work on differentially flat underactuated planning hints at the potential for using clever trajectory planning to get good performance out of cheaper hardware. Further research could extend these methods to higher-DOF systems or underactuated arms, making robotic palletizing solutions more accessible and economical. On the other end, exploiting redundancy (such as a seven-DOF arm or a robot on a sliding rail) for obstacle avoidance and singularity avoidance is an area that can be deepened. Redundancy resolution in real time, especially for time-optimal or energy-optimal criteria, remains a complex issue that future algorithms need to manage, possibly by combining search methods with instant optimization at the control level.
• Human–robot collaboration and ergonomics: Another growing trend is collaborative palletizing, where robots work alongside human workers to build pallets. In such settings, trajectory planning must also account for human safety, ergonomics, and unpredictability. The robot’s motions might need to be not just collision-free but also intuitive or predictable to the human partner. Future research could explore trajectory generation that maximizes criteria like human comfort or task division efficiency. This involves integrating human motion prediction into the planning loop and ensuring the robot’s trajectory planner can respond smoothly to human actions (slowing down, changing course safely, etc.). While this extends beyond pure trajectory planning into the domain of human–robot interaction, it is a vital frontier for “as-a-service” robots that may operate in semi-structured warehouse environments.
• Benchmarking and standardization: Given the variety of available methods, it can be difficult to determine which approach is best suited for a new palletizing application [93]. The literature would benefit from standardized benchmarks—for example, a set of palletizing scenarios of varying complexity (simple patterns, random case sizes, mixed-SKU pallets, etc.) on which different planning algorithms are tested and compared. Future research could establish such benchmarks and evaluation metrics (beyond time and energy, including maintainability, scalability, and ease of implementation). This would help translate academic results into industrial practice by clarifying the trade-offs. It would also highlight which areas (e.g., dynamic re-planning and multi-robot coordination) are least addressed by current methods and, thus, need more focus.

In conclusion, addressing these gaps will require the combination of insights from classical robotics (kinematics, dynamics, and control) with modern techniques in computation and AI. The continuing development of faster processors; cloud computing; and, perhaps, dedicated motion planning hardware could also unlock real-time capabilities that were previously infeasible. The concept of robotized as-a-service packing inherently demands flexibility, adaptability, and reliability; hence, trajectory planning research must continue to evolve to meet these demands in increasingly unstructured and challenging environments.

6. Conclusions

This review has surveyed the state of the art in manipulator trajectory planning and path optimization, with a particular focus on applications in robotic palletizing and automated packing. We summarized a broad spectrum of approaches—from classical algorithms like A* and dynamic programming to sampling-based planners such as PRM/RRT and modern techniques involving splines and machine learning. Each category of methods offers distinct strengths: graph search and sampling planners provide fundamental tools for finding feasible paths in complex spaces, polynomial and spline techniques ensure smooth and high-speed motions, and learning-based methods promise adaptive and efficient control that can improve over time.

One key finding is that there is no one-size-fits-all solution; instead, successful systems often integrate multiple planning layers. For example, a palletizing robot might use a high-level planner (or even simple heuristics) to decide the placement order and rough paths, then refine those with a spline or time-optimal segment and finally adjust in real time using a local avoidance or feedback controller. By combining approaches, the weaknesses of one method can be mitigated by the strengths of another—such hybrid strategies have been evidenced in several studies (such as by combining the PRM with RL or using vision feedback on top of pre-planned paths).

From a practical industry perspective, some insights can be drawn. First, for relatively structured palletizing tasks (e.g., uniform box sizes and known layouts), traditional motion planning methods (like precomputed trajectories or pattern-based approaches) are often sufficient and very efficient. However, as product variability increases and as service-based deployments demand quick reconfiguration, more advanced planning becomes necessary. Companies can benefit from investments in trajectory optimization: even a small reduction in cycle time or energy per pick–place cycle, when multiplied by thousands of cycles per day, can yield significant productivity and cost gains. For instance, smoothing a robot’s motion with spline interpolation can reduce wear and avoid abrupt moves, leading to less downtime for maintenance. Likewise, energy-efficient trajectories can lower operating costs and help meet sustainability targets without requiring new hardware.

Our review also highlighted that palletizing applications drive specific research needs, such as planning with increasing obstacles (as the pallet stack grows) and handling heavy payload dynamics. Solutions like continually updated RRTs for each layer of the stack and pre-emptive avoidance maneuvers have been developed to address these. Furthermore, the integration of computer vision (for item detection and localization) with motion planning is crucial in palletizing cells. Modern systems employ vision to inform the planner about the environment, essentially closing the loop from perception to action.

Finally, we identified several future research directions, including real-time adaptive planning, integrated task and motion optimization, safe learning-based control, and human–robot collaborative planning. Advancements in these areas will likely define the next generation of “smart” packing robots. Such robots would not only execute pre-programmed motions but could also learn and optimize their trajectories based on operational data, adapt to new products or layouts with minimal reprogramming, and work safely alongside humans in shared environments.

In conclusion, the field of manipulator trajectory planning is rich and continually evolving. For robotic palletizing, which sits at the intersection of logistics and automation, leveraging the latest planning algorithms can significantly enhance performance. By applying the methods reviewed in this paper, industry practitioners can design robotic cells that are faster, more efficient, and more flexible. At the same time, ongoing research—particularly on the combination of classical optimal control with artificial intelligence—is poised to unlock even greater capabilities, making robot-as-a-service palletizing an increasingly attractive and reliable option for a wide range of end-of-line packaging needs.