Open-Loop Characterisation of Soft Actuator Pressure Regulated by Pulse-Driven Solenoid Valve

Abstract

Solenoid valves are widely used for pressure regulation in soft pneumatic robots, but their inherent electromechanical nonlinearities—such as dead zones, saturation, and pressure-dependent dynamics—pose significant challenges for accurate control. Conventional pulse modulation techniques, including pulse-width modulation (PWM), often exacerbate these effects by neglecting valve-switching transients. This paper presents a physics-informed dynamic modelling framework that captures transient and pressure-dependent behaviours in solenoid valve-driven soft pneumatic systems operating under pulse modulation. The model is experimentally validated on a soft pneumatic actuator (SPA) platform using four modulation schemes: PWM, integral pulse frequency modulation (IPFM), its inverted variant (IIPFM), and $\Delta$$\Sigma$ modulation. Results demonstrate that only the IIPFM scheme produces near-linear input–pressure characteristics, in close agreement with model predictions. The proposed framework provides new physical insights into valve-induced nonlinearities and establishes a systematic basis for high-fidelity modelling and control of soft pneumatic robotic systems.

1. Introduction

The field of soft robotics aims to bridge the gap between conventional rigid machines and living organisms, enabling the development of robotic systems that are lightweight, resilient, and inherently safe for human and environmental interaction [1,2,3]. Among the various actuation strategies [4], pneumatic actuation has emerged as the dominant technology, offering a compelling combination of high power-to-weight ratio, fast response, and low manufacturing cost, which has been a major driver of innovation in the field [5,6].

Gas flow in soft robots is typically controlled using solenoid valves. A key distinction arises between high-precision proportional valves and low-cost on/off types. Although proportional valves enable continuous flow modulation and simpler control, their size, weight, and cost limit their use in systems with many actuators [7]. As a result, most applications rely on compact and inexpensive on/off solenoid valves (e.g., 2/2 or 3/2 types), shifting the complexity from hardware to control algorithms to achieve analogue-like performance from inherently binary devices. In particular, 3/2 valves are commonly preferred for the pressurisation switching process, as a single valve is sufficient to control both inflation and deflation. In contrast, a 2/2 valve configuration requires two separate valves and is, therefore, more suitable for applications where maintaining a constant pressure is of paramount importance, since it allows the exhaust pathway to be blocked [5,7].

One of the main challenges in using soft pneumatic actuators (SPAs) lies in developing effective control schemes due to their highly nonlinear behaviour. Accurate and reliable modelling can, therefore, greatly support the design and optimisation of such control systems, reducing both the time and cost associated with real-world experimentation. Moreover, improved models contribute to minimising tracking error and enhancing the overall performance of the soft pneumatic system [8,9]. Indeed, the precision of robotic motion is fundamentally linked to the effectiveness of actuator pressure control, as the precision of pressure regulation directly determines the robot’s overall accuracy [5]. Despite this, few studies have focused on the dynamic modelling of the pressurisation process itself, which is typically governed by a valve.

Pulse-width modulation (PWM) is the standard approach used to bridge this control gap. By varying the duty cycle of a high-frequency signal, PWM regulates the average pressure within the actuator [7]. However, it remains a time-triggered method poorly suited to the nonlinear, state-dependent dynamics of soft pneumatic systems. This mismatch leads to performance issues such as oscillatory pressure fluctuations (chattering), unwanted vibrations in the soft structure, and considerable energy inefficiency due to continuous valve switching, even at steady state [10].

An alternative strategy to overcome these limitations is pulse frequency modulation (PFM). Unlike PWM, PFM generates a pulse train whose frequency depends on the system state. This modulation strategy has been applied to hydraulic valves to mitigate dead-zone effects [11]. Its neuron-inspired variant, the integral PFM (IPFM), is triggered whenever the integral of the control error reaches a predefined threshold. This event-driven approach activates the actuator only when necessary, enhancing energy efficiency and robustness to noise [12,13]. In the context of soft robotics, IPFM provides a promising framework for achieving smooth, analogue-like pressure control using standard on/off solenoid valves. We proposed a variant of this modulator—the inverse IPFM (IIPFM)—in [14], which maintains the output high by default and switches it to zero whenever the integral of the control error exceeds a threshold, thereby improving linearity in pressure control of pneumatic solenoid valves.

$\Delta \Sigma$ modulation ($\Delta \Sigma$M) is well known for its ability to improve the signal-to-noise ratio by pushing quantisation error to higher frequencies. It employs a feedback loop in which the error between the modulator input and output (the $\Delta$) is sent to an integrator (the $\Sigma$), which accumulates this error to correct persistent discrepancies. A quantiser then converts the integrated signal into a discrete output. The feedback loop ensures that the average output value tracks the average input [15]. A $\Delta \Sigma$M was applied in [16,17] to drive solenoid valves in odour systems.

In summary, as the complexity of soft robotic tasks continues to increase, it becomes essential to explore pneumatic technologies that simplify pressure regulation and enable high-precision control. In this study, we propose a practical approach to modelling the pressure dynamics of solenoid valves in pneumatic systems. This approach enables the evaluation of system performance under pulse-type inputs in order to meet the diverse pressure demands of different applications. It also provides tuning guidelines to achieve the most linear behaviour possible for pressure. Specifically, the linearity achieved in pressure regulation for a representative soft pneumatic system is compared for four types of modulator: PWM, IPFM, IIPFM and $\Delta \Sigma$M. Based on these results, a tuning method for modulators is proposed to linearise valve behaviour. Open-loop experiments demonstrate that, for SPAs, IIPFM provides a superior alternative to other conventional modulators, achieving significantly more linear behaviour and mitigating the nonlinear effects typically associated with pulse modulators, such as chattering.

This work forms part of a broader research effort aimed at achieving precise and efficient control of SPAs. The overall objective can be divided into three sequential stages: (1) linearisation of the actuator behaviour through appropriate pulse modulation strategies; (2) closed-loop control of the internal pressure; and (3) outer-loop control of the actuator curvature or tip position. The present paper addresses the first stage, focusing on the characterisation and linearisation of the pressure dynamics in order to provide a solid foundation for the subsequent development of closed-loop controllers.

It is pertinent to note that the primary goal of this study is to develop a model for the dynamics of the pressurisation process and to calibrate a pulse modulator that linearises the relationship between the output pressure and the actuation signal. This study, therefore, establishes the foundations for future closed-loop analysis by facilitating the precise control of the SPA using the simplest strategies possible. In particular, the near-linear pressure response achieved with the IIPFM modulation paves the way for straightforward controller design (e.g., PID-based) and stability assessment in forthcoming work.

The contributions of this paper are as follows:

• The development of a dynamic model to describe the pressure at the output of solenoid valves;
• A comparative analysis of linearity of system behaviour when actuated by four types of pulse modulator, namely PWM, IPFM, IIPFM, and $\Delta \Sigma$M;
• A method of tuning pulse modulators by optimising the linearity of the valve;
• The validation of analytical results by means of open-loop experiments.

The remainder of the paper is organised as follows. Section 2 describes the system under consideration, which consists of a soft pneumatic bending actuator. Section 3 presents the dynamic model of the system and identification experiments. Section 4 analyses and compares the behaviour of the system in terms of linearity when actuated by the four types of pulse modulator considered. Section 5 proposed a method to tune pulse modulators to ensure maximum linearity of the valve behaviour. Section 6 deals with the experimental validation of the analytical results. Finally, Section 7 draws the main conclusions of this paper.

2. Soft Pneumatic System

Figure 1a shows the soft pneumatic system under consideration, which consists of a solenoid valve that commutes between a path that feeds the SPA with a pressure source and an exhaust path. A sensor measures the pressure at the SPA and sends the information to the controller in order to decide the state of the valve at any given time. Two groups of elements can be identified (see Figure 1b for connections among them). The first is the pneumatic system, which is composed of the following:

• A compressor (SGS SC50V), used as the source of pressurized air to the system.
• The pressure regulator (SMC ITV1030-31F2N3), that serves to achieve a desired constant pressure during the experiments.
• A 2-litre tank, utilized as an air reservoir to mitigate the small oscillations caused by the regulator and reduce the effect of momentary intense consumption of air.
• The 3/2 solenoid valve (SMC V114-5G-M5).
• The SPA (manufactured in the laboratory), consisting of a dual-cavity bellows-type bending actuator with a total internal volume of 28 ml and external dimensions of $11.9\times 1.8\times 3.7$ cm. The actuator was fabricated using Dragon Skin 20 silicone. Further details on the SPA design can be found in [18].

And the second is the control unit, which consists of the following:

• A PC with MATLAB R2020b software that serves to program the controller unit and monitor the state of the platform with data from sensors.
• A dSpace processor (MicroLabBox I), i.e., a real-time computing unit that runs the control algorithm, and also serves as digital and analogue I/O board.
• A driver (MD10C R3), that actuates on the solenoid valve by converting the pulse train containing the control signal information at the logic level to the rated voltage of the solenoid valve.
• Two pressure sensors (MPX5100DP) with an accuracy of $\pm 2.5$% of the full-scale (1 bar), placed at the entrance of the valve and at the output, respectively.

Figure 1. Pneumatic control system under consideration: (a) picture of the setup (b) connections of pneumatic (white) and control elements (blue).

Figure 1. Pneumatic control system under consideration: (a) picture of the setup (b) connections of pneumatic (white) and control elements (blue).

3. Modelling of the Soft Pneumatic System

This section presents the dynamic model of the pressurisation process of the soft pneumatic system under consideration and identification experiments. Note that such process is mainly described by the valve dynamics. However, the pressure dynamics are also influenced by the driven element. Firstly, the SPA fluid chambers act as variable-volume tanks, and secondly, the expansion and contraction of the soft walls makes pressure more susceptible to short-term fluctuations during valve switching [19].

3.1. Theoretical Model

An ideal solenoid valve could be instantaneously switched between two states: feeding the actuator or releasing the air, so that the output pressure would only depend on the pneumatic dynamics and the time spent in each state, i.e., the duty cycle of the pulse train. In real valves, however, the electromechanical part influences the pressure response severely. Switching between states depend on the transient dynamics of the electric current and the non-instantaneous displacement of the spool. The dead-zone and the saturation observed when using solenoid valves are related to these transients. For 2-position valves, the switching times are typically defined as follows: the on-time (denoted as $t_{on}$), which refers to the time required for the valve to fully transition from the initial state to the second state, and the off-time (denoted as $t_{off}$), which relates to the time required to return to the initial state.

The proposed model of the SPA pressure consists of four states: two are used to describe the charging and discharging dynamics when the valve is fully switched (ideal valve), and the other two represent the switching times and their effect on the valve dynamics.

The discharging dynamics can be described by a first-order model with a pressure-dependent time constant, i.e.,

$${\dot{P}}_1\left(t\right)={\displaystyle \frac{-P\left(t\right)}{{\tau }_1\left(P\right)}}$$

(1)

where P is the actuator pressure, ${\dot{P}}_i$ its derivative at state i, and ${\tau }_1\left(P\right)$ the time constant. In accordance with theoretical models, the dependence of ${\tau }_1$ on pressure takes the form ${\tau }_1\left(P\right)=c_1\sqrt{P\left(t\right)}$, where $c_1$ is a constant (e.g., see [10]).

The charging dynamics are described by a first-order model:

$${\dot{P}}_2\left(t\right)={\displaystyle \frac{-P\left(t\right)}{{\tau }_2}}+{\displaystyle \frac{k_2}{{\tau }_2}}$$

(2)

where ${\tau }_2$ is the time constant and $k_2$ the tank pressure. During the experiments, each valve-switching event produced short-term pressure oscillations, an effect also observed in other valve-driven pneumatic systems [20]. After this brief transient, however, the pressure consistently returned to a value very close to that at the switching instant. Based on this observation, and in agreement with the system identification results, each transition is modelled as a state that maintains the output pressure for $t_{on}$ and $t_{off}$, respectively:

$${\dot{P}}_3={\dot{P}}_4=0$$

(3)

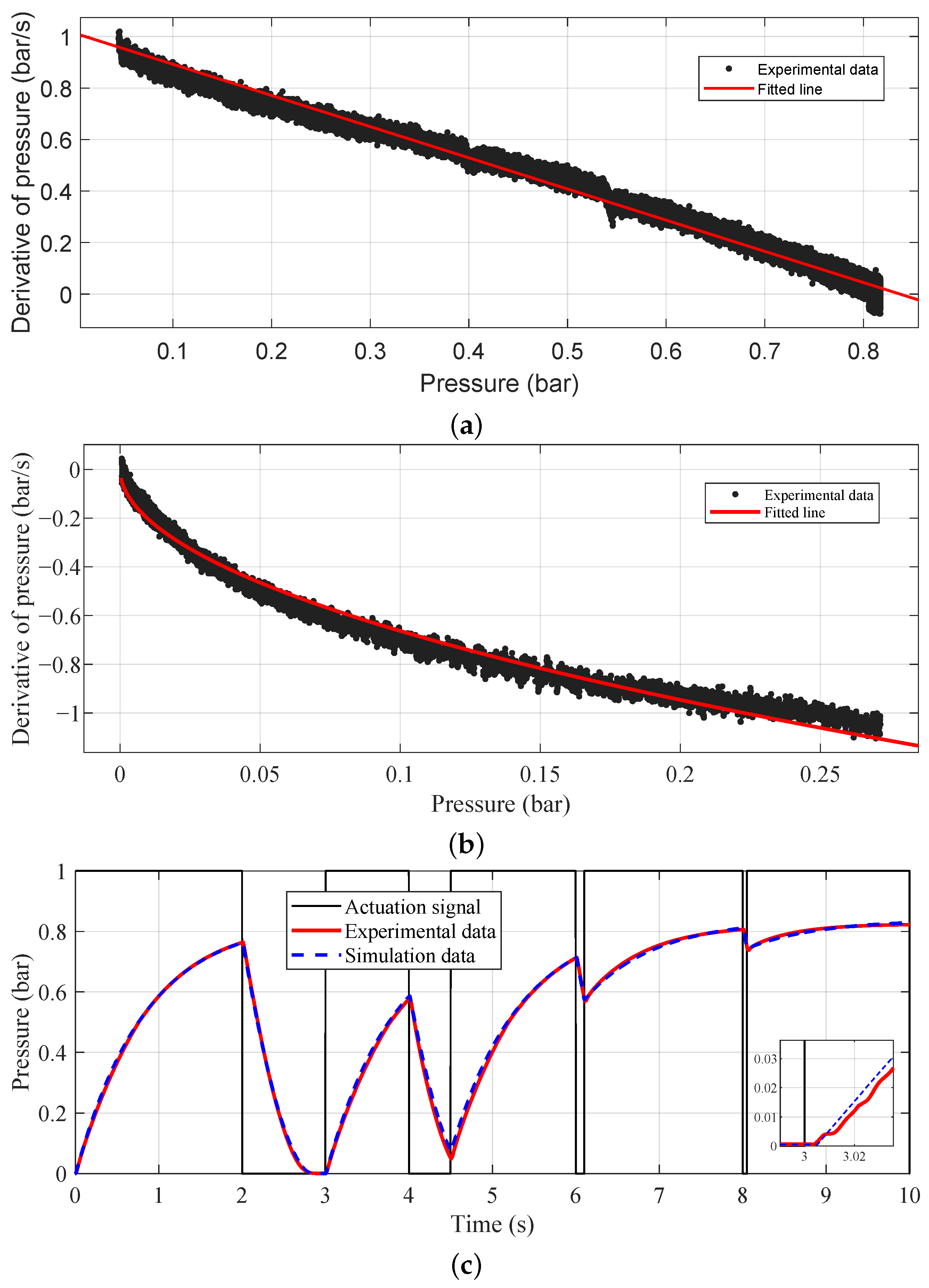
3.2. Identification Results

The dynamics of the valve were identified from three types of experiments. First, the valve was fully opened for a sufficient time for the pressure to reach its maximum value, equal to the source pressure, starting from an initial pressure of 0 bar, in order to identify the charging dynamics (state 1). The pressure readings from the output sensor exhibited a typical damped response. To identify the dynamics, the pressure time derivative was plotted against the pressure (black dots), as shown in Figure 2a. As can be observed, the experimental data were fitted by an almost straight line (red line), with a coefficient of determination of $R^2=0.97$. The identified parameters were: $k_2=0.837$ bar and ${\tau }_2=0.826$ s.

In the second experiment, the valve was fully closed and the pressure was observed to decay from the source pressure to 0 bar in order to identify the discharging dynamics (state 2). Figure 2b again shows the time derivative of the pressure plotted against the instantaneous pressure. It can be observed that, in this case, the response could not be attributed to a linear behaviour, as the pressure decay rate decreased with pressure. Particularly, the only type of function that fitted the experimental data was a power law (red line) of the form $\dot{P}=a{P}^b$, with a and b being constants. To express this law in a similar way to conventional models, it was rewritten in the form of Equation (1) as $\dot{P}=-P/\left(0.533\sqrt{P}\right)$. This gave a $R^2$ value of $0.98$ for the fitting.

The third experiment consisted of applying a pulse-based input to the valve with various low-state durations. This test was used to observe the nonlinearities that arise when using this kind of signal—such as those generated by pulse modulators—and to validate the previously identified dynamics during the charging and discharging states. These nonlinear effects were modelled as two additional states in which the pressure remains constant ($\dot{P}=0$) for a short time after switching the valve: one corresponding to the transition from closed to open (state 3), lasting $t_{on}$, and another from open to closed (state 4), lasting $t_{off}$. Figure 2c shows the input signal (solid black line) and compares the system response (solid red line) with the model response (dashed blue line). As can be seen, the four-state model accurately captures the experimental data. A zoomed-in view of the signal around 3 seconds is shown in the bottom-right corner, illustrating that although the actuation signal is switched at 3 s, the pressure begins to rise 3 ms later. The identified model parameters were $c_1=0.533 \mathrm{s}/{\mathrm{bar}}^{0.5}$, $k_2=0.837$ bar, ${\tau }_2=0.826$ s, $t_{on}=3$ ms, and $t_{off}=10$ ms.

4. System Behaviour Under Pulse-Type Inputs

This section analyses the system behaviour when actuated by four types of pulse modulators, namely PWM, IPFM, IIPFM, and $\Delta \Sigma$M. The fundamentals of these modulators are first presented. The section also examines the equilibrium pressure achieved in the SPA when a general pulse-type input is applied, as well as the time constants associated with the charging and discharging dynamics and the chattering observed in the output pressure due to transient effects during valve commutations. Finally, expressions for the system behaviour under each modulator are derived to assess the system linearity.

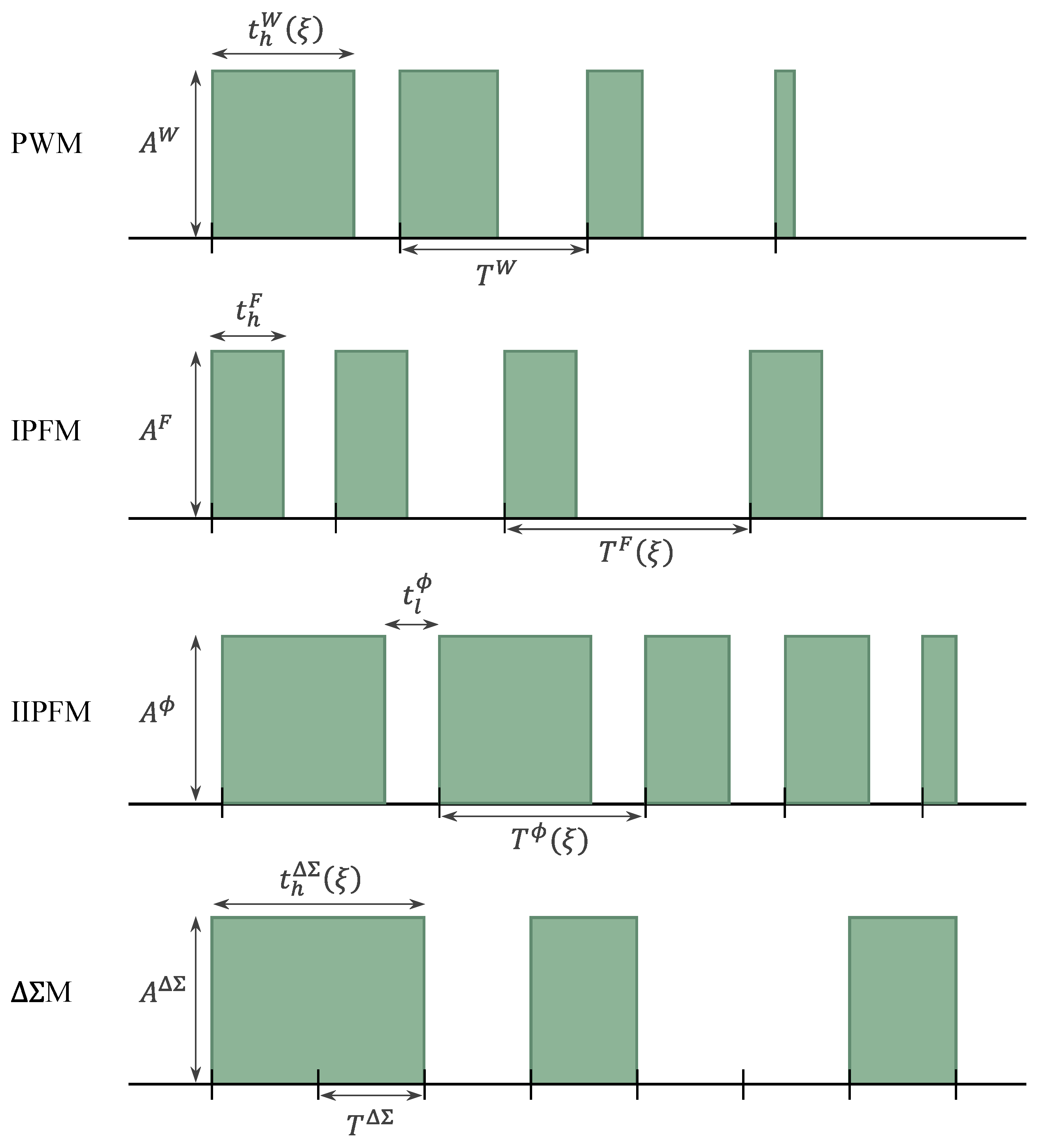
4.1. Fundamentals

Constant-amplitude pulse modulators are used to drive solenoid valves, as the analogue signal from the controller can be converted into a two-state signal compatible with their discrete nature.

The following is a summary of the four modulators’ fundamentals. PWM maintains a constant period while adjusting the duration of the high state within each cycle in response to the input signal. In contrast, IPFM generates a sequence of pulses with constant width, where the input signal is represented by the time interval between consecutive pulses; the firing frequency therefore increases with increasing input. The IIPFM variant, on the other hand, keeps the interval between pulses fixed while varying the pulse width according to the input signal, resulting in a firing frequency that decreases as the input increases. Finally, $\Delta \Sigma$M employs a reference period in which the output state is either fully low or fully high. The information is encoded within the generated sequence, such that the durations of the high and low states are integer multiples of the reference period. An apparent firing frequency is, thus, defined by the density of pulses in each state.

The parameters describing the pulse train generated by these modulators, shown in Figure 3, are as follows: pulse amplitude (A), high-state duration or pulse width ($t_h$), low-state duration or time interval between pulses ($t_l$), and firing frequency (f). The information is encoded in the duty cycle, $D=t_h/(t_h+t_l)$. For convenience, we define the term input fraction as $\xi =x/A$. From now on, the parameters pertinent to PWM, IPFM, IIPFM and $\Delta \Sigma$M are denoted by superscripts W, F, $\varphi$, and $\Delta \Sigma$, respectively. A deeper insight into the description of the modulators can be found in Appendix A.

4.2. General Analysis

Next, analytical expressions of pressure are derived for a general pulse input. The procedure is based on a modification of the averaging method reported for example in [21]. The switching times $t_{on}$ and $t_{off}$ are introduced in the expressions as they are essential to reflect the nonlinearities.

4.2.1. Equilibrium Pressure

First, let us consider the case where switching times are ideally zero (i.e., $t_{on}=t_{off}=0$). Only two states, corresponding to discharging and charging, participate. The equilibrium is found at a pressure level where the net pressure change over a period becomes zero, i.e., ${\alpha }_1{f}_1\left(P_{eq}\right)+{\alpha }_2{f}_2\left(P_{eq}\right)=0$, where $P_{eq}$ is the equilibrium pressure, ${\alpha }_i$ is the fraction of time in a period in which the system is at state i and $f_i$ is the derivative function for state i. Usually, for any pulse modulator, ${\alpha }_1=1-D$, and ${\alpha }_2=D$. Using Equations (1) and (2) results in the following:

$${\alpha }_1\left({\displaystyle \frac{-P_{eq}^{0.5}}{c_1}}\right)+{\alpha }_2\left({\displaystyle \frac{k_2-P_{eq}}{{\tau }_2}}\right)=0$$

(4)

Solving for $P_{eq}$, the equilibrium pressure is obtained as

$$P_{eq}=k_2+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\tau }_2^2{\alpha }_1^2}{c_1^2{\alpha }_2^2}}\left(1-\sqrt{1+4k_2{\displaystyle \frac{c_1^2{\alpha }_2^2}{{\tau }_2^2{\alpha }_1^2}}}\right)$$

(5)

Therefore, in the ideal case, all pulse modulators would generate the same pressure curve described by Equation (5). The differences in the real response of each pulse modulator are caused by the switching times.

Equations (4) and (5) do not change in appearance when considering states 3 and 4, because time derivatives are zero, according to Equation (3). Nonetheless, the switching times produce a variation in both the effective time on the high state ($t_h-t_{on}$) and the effective time on the low state ($t_l-t_{off}$). The novelty of the modelling approach consists of the consideration of valve transient times, generalized for any constant-amplitude pulse modulator, through the time fractions ${\alpha }_1$ and ${\alpha }_2$ that are now redefined and are different for each modulator:

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }& ={\displaystyle \frac{t_l-t_{off}}{T}}=(1-D)-{\displaystyle \frac{t_{off}}{T}}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }& ={\displaystyle \frac{t_h-t_{on}}{T}}=D-{\displaystyle \frac{t_{on}}{T}}\hfill \end{array}$$

(7)

where ${\alpha }_1^{\prime }$ and ${\alpha }_2^{\prime }$ are the redefined time fractions considering the effective low and high states, respectively. Note that the ratios $t_{on}/T$ and $t_{off}/T$ differ for each modulator because, although $t_{on}$ and $t_{off}$ are the same, T differs. Therefore, if the value of ${\alpha }_1$ is below zero, this indicates saturation, whereas if the value of ${\alpha }_2$ is below zero, this indicates that the system is in the dead-zone region.

From Equation (5), the quadratic ratio of the time fractions (${\alpha }_1^2/{\alpha }_2^2$) emerges as a key term, which will serve as the starting point for analysing the linearity of each modulator later on. Using Equations (6) and (7), pulse modulators produce the following ratio:

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{{\alpha }_2^{\prime }}^2}}={\displaystyle \frac{{\left(1-\xi -\frac{t_{off}}{T}\right)}^2}{{\left(\xi -\frac{t_{on}}{T}\right)}^2}}$$

(8)

4.2.2. Equivalent Dynamics

Charging and discharging dynamics were identified as first-order systems with different time constants (i.e., Equations (1) and (2), respectively). The equivalent dynamics observed when switching between them is modelled as a first order system with chattering, which has a time constant that is a reflection of both states, as explained next. For switched first order linear systems, the equivalent system dynamics is a first order system with a time constant given by ${\tau }_m^{-1}={\sum }_i{\alpha }_i/{\tau }_i$, where ${\tau }_i$ is the time constant at state i. In this case, a first order approximation of the discharging dynamics is used to derive the following expression:

$${\tau }_m\left(P_{eq}\right)={\displaystyle \frac{2{\tau }_2{c}_1\sqrt{P_{eq}}}{{\alpha }_1{\tau }_2+2{\alpha }_2{c}_1\sqrt{P_{eq}}}}$$

(9)

In general, the time constant of the switched system depends on the operating point ($P_{eq}$). Again, for the ideal case of instantaneous switching, all pulse modulators behave the same. The differences arise when considering the switching times by replacing ${\alpha }_1$ and ${\alpha }_2$ with ${\alpha }_1^{\prime }$ and ${\alpha }_2^{\prime }$.

The amplitude of the chattering is estimated using the product of the time spent in one state times the derivative at that state (i.e., $|t_h{\dot{P}}_2\left(P_{eq}\right)|$). Substituting Equation (5) on Equation (2) and multiplying by $t_h$, the following is obtained:

$$\Delta P_2={\displaystyle \frac{t_h{\tau }_2{\alpha }_1^2}{2c_1^2{\alpha }_2^2}}\left(\sqrt{1+4k_2{\displaystyle \frac{c_1^2{\alpha }_2^2}{{\tau }_2^2{\alpha }_1^2}}}-1\right)$$

(10)

where $\Delta P_2$ denotes the change in pressure in the pseudo-steady state, specifically during the high state. In this case, the chattering depends on the modulator being used even for the ideal case, because $t_h$ is defined differently for each modulator. This equation can be useful to further guide the tuning of modulators by imposing a maximum value of $t_h$ corresponding to a maximum acceptable chattering.

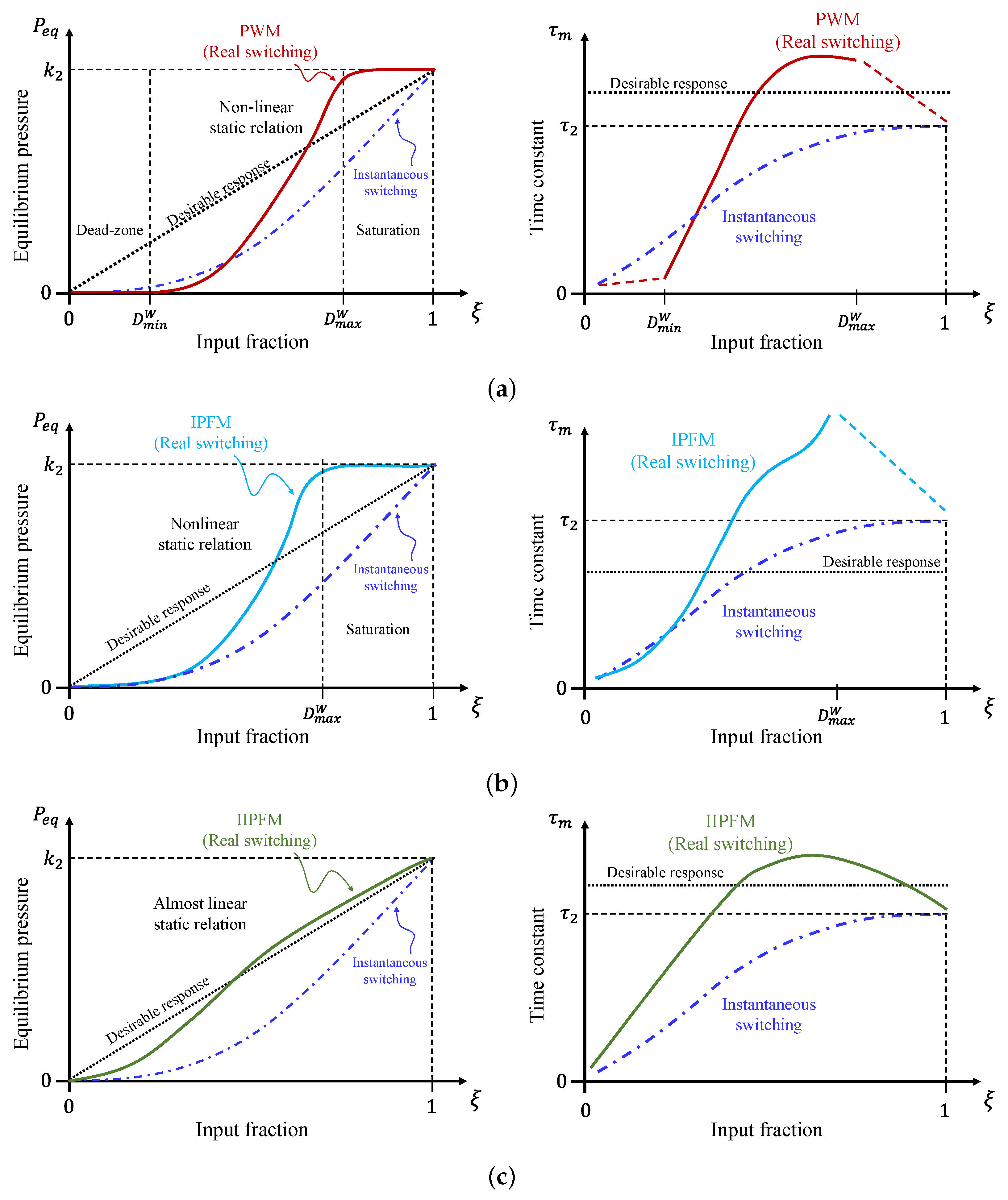
4.3. Linearity Analysis for Each Modulator

The analytical expressions for pressure derived in the previous section are now particularised for each modulator. The analysis is carried out first for the dead-zone and saturation effects, and then for the static response.

4.3.1. Dead-Zone and Saturation

The dead-zone and saturation thresholds are obtained by particularising Equations (6) and (7) for each modulator. Then, each expression is set equal to 0 and solved for the input fraction. All the solutions are shown in

Table 1. Dead-zone and saturation thresholds for the four modulators considered.

Modulator Type	Dead-Zone	Saturation
PWM	$t_{on}{f}^W$	$1-t_{off}{f}^W$
IPFM	0	${\displaystyle \frac{t_h^F}{t_h^F+t_{off}}}$
IIPFM	$1-{\displaystyle \frac{G^{\varphi }}{1+\frac{t_{on}}{t_l^{\varphi }}}}$	1
$\Delta \Sigma$M	0	1

.

For PWM, the redefined time fractions are as follows:

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }& =(1-\xi )-t_{off}{f}^W\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }& =\xi -t_{on}{f}^W\hfill \end{array}$$

(12)

While those for IPFM are given by:

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }& =1-\left(1+{\displaystyle \frac{t_{off}}{t_h^F}}\right)\xi \hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }& =\left(1-{\displaystyle \frac{t_{on}}{t_h^F}}\right)\xi \hfill \end{array}$$

(14)

For its part, the expressions for the IIPFM case are as follows:

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }& ={\displaystyle \frac{1}{G^{\varphi }}}\left(1-{\displaystyle \frac{t_{off}}{t_l^{\varphi }}}\right)\left(1-\xi \right)\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }& =1-{\displaystyle \frac{1}{G^{\varphi }}}\left(1+{\displaystyle \frac{t_{on}}{t_l^{\varphi }}}\right)\left(1-\xi \right)\hfill \end{array}$$

(16)

According to them, it is important to note that it is possible to avoid the dead-zone with IIPFM if the gain is set to

$$G^{\varphi }=1+{\displaystyle \frac{t_{on}}{t_l^{\varphi }}}$$

(17)

And the redefined time fractions corresponding for $\Delta \Sigma$M results in

$$\begin{array}{cc}\hfill {\alpha }_1^{\prime }& =1-(1+2f^{\Delta \Sigma }{t}_{off})\xi +2f^{\Delta \Sigma }{t}_{off}{\xi }^2\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\alpha }_2^{\prime }& =(1-2f^{\Delta \Sigma }{t}_{on})\xi +2f^{\Delta \Sigma }{t}_{on}{\xi }^2\hfill \end{array}$$

(19)

4.3.2. Static Response

From Equation (4), it can be stated that the linear static relationship between the equilibrium pressure and the input fraction is given by $P_{eq}=k_2\xi$. To this end, the quadratic ratio of time fractions as a function of the system parameters must be

$${\displaystyle \frac{{{\alpha }_1^{*}}^2}{{{\alpha }_2^{*}}^2}}={\displaystyle \frac{c_1^2{k}_2}{{\tau }_2^2}}{\displaystyle \frac{{(1-\xi )}^2}{\xi }}$$

(20)

Since PWM uses a constant firing frequency, Equation (8) becomes

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{\alpha }_2^{\prime 2}}}{|}_{\mathrm{PWM}}={\displaystyle \frac{{(1-\xi -t_{off}{f}^W)}^2}{{(\xi -t_{on}{f}^W)}^2}}$$

(21)

This differs significantly from Equation (20), since the products of the firing frequency and the switching times ($t_{off}{f}^W$ and $t_{on}{f}^W$) are constant. These terms produce a translation of $\xi$.

Since the firing frequency of IPFM is proportional to the input, i.e., $f^F=\xi /t_h^F$:

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{{\alpha }_2^{\prime }}^2}}{|}_{\mathrm{IPFM}}={\displaystyle \frac{{(1-(1+\frac{t_{off}}{t_h^F})\xi )}^2}{{(1-\frac{t_{on}}{t_h^F})}^2{\xi }^2}}$$

(22)

Although it is still different from the ideal ratio, it can be seen in the denominator that the translation of $\xi$ can be avoided. This suggests searching for a modulator that can also simplify the numerator.

Using above expressions, Equation (8) becomes

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{{\alpha }_2^{\prime }}^2}}{|}_{\mathrm{IIPFM}}={\displaystyle \frac{{(t_l^{\varphi }-t_{off})}^2}{{(t_l^{\varphi }+t_{on})}^2}}{\displaystyle \frac{{(1-\xi )}^2}{{\xi }^2}}$$

(23)

This expression approximates the ideal ratio, Equation (20), with high accuracy, aside from the fact that the denominator includes a squared term of $\xi$.

For $\Delta \Sigma$M, the firing frequency is $2\xi (1-\xi )/T^{\Delta \Sigma }$, which results in a time fraction ratio equal to

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{{\alpha }_2^{\prime }}^2}}{|}_{\Delta \Sigma \mathrm{M}}={\displaystyle \frac{{(1-\xi (1+2f^{\Delta \Sigma }{t}_{off})+2f^{\Delta \Sigma }{t}_{off}{\xi }^2)}^2}{{(\xi (1-2f^{\Delta \Sigma }{t}_{on})+2f^{\Delta \Sigma }{t}_{on}{\xi }^2)}^2}}$$

(24)

There is no approximation to the ideal ratio as good as with the IIPFM.

5. Pulse Modulator Tuning by Optimisation

This section presents an approach for selecting the parameters of the modulators in order to achieve the most linear valve behaviour possible, i.e., to maximise the overall linearity of the system. The proposed method is analytically validated for one of the modulators.

To ensure a fair comparison among the different modulation strategies, the parameters of each modulator will be tuned to optimise the linearity of the combined modulator–valve–SPA system. Although the switching frequency naturally varies between modulators due to their distinct operating principles, the tuning process was performed so that their overall performance could be meaningfully compared. It should be emphasised that full standardisation of the frequency is not feasible, as PWM operates at a fixed frequency, whereas IPFM, IIPFM and $\Delta \Sigma$M generate pulses whose frequency depends on the modulator state. Consequently, the comparison focuses on equivalent dynamic behaviour rather than on absolute switching rates.

5.1. Tuning Method

Once the expressions describing the equilibrium pressure for each pulse modulator have been derived, the design criteria for a pulse modulator should take into account three key considerations. First, the quadratic time fraction ratio should be as close as possible to the ideal ratio (Equation (20)), which is similar to consider a linear static relationship between the equilibrium pressure and the input fraction. Second, dead-zone and saturation effects should be mitigated by ensuring minimum switching times where possible ($t_h>t_{on}$ and $t_l>t_{off}$). Third, short periods or pulse widths lead to reduced chattering in the system response. The latter two aspects will be treated as constraints in the optimisation process.

For this purpose, an optimisation procedure was programmed to minimise the following cost function:

$$J=\sum _{i=1}^N|P_{eq}\left({\xi }_i\right)-k_2{\xi }_i|,0\le {\xi }_i\le 1,$$

(25)

Taking into account the following restrictions, i.e., for IPFM, $t_h^F>t_{on}$; for IIPFM, $t_l^{\varphi }>t_{off}$ and Equation (17); for $\Delta \Sigma$M, $T^{\Delta \Sigma }>t_{off}$ and $T^{\Delta \Sigma }>t_{on}$; and there were no restrictions for PWM.

Cost function of Equation (25) quantifies the deviations of the curve of a given modulator and parameter value in Equation (5) from the desired linear response, i.e., $P_{des}=k_2\xi$. One hundred equally spaced points ($N=100$) were evaluated for each parameter value. Optimal values were found sweeping $f^W\in [1,80]$ Hz, $t_h^F\in [0.0125,1]$ s, $t_l^{\varphi }\in [0.0125,1]$ s, and $T^{\Delta \Sigma }\in [0.0125,1]$ s with 1 ms and $0.1$ Hz steps, respectively.

Figure 4 shows the value of J for the four modulators. For a better comparison, they were plotted on the same axis: the period of PWM ($T^W$), the pulse width of IPFM ($t_h^F$), the pulse separation for IIPFM ($t_l^{\varphi }$), and the period for $\Delta \Sigma$M ($T^{\Delta \Sigma }$). The optimization gives a minimum of J for IIPFM at $t_l^{\varphi }=20$ ms and at $f^W=20$ Hz for PWM. The IIPFM minimum is almost $2.5$ times smaller, indicating that it is substantially more linear. The optimal values for the remainder modulators are given in

Table 2. Optimal values in terms of linearity for the four modulators considered.

Modulation Type	Restriction	${\mathit{J}}_{\mathbf{min}}$	Selected Parameter
PWM	$f^W>0$ Hz	10.5	20 Hz
IPFM	$t_h^F>3$ ms	12.5	20 ms
IIPFM	$t_l^{\varphi }>10$ ms	4.8	20 ms
$\Delta \Sigma$M	$T^{\Delta \Sigma }>10$ ms	9.6	20 ms

.

5.2. Validation of the Tuning Method

The analytical expression for the pulse width that minimises the deviation from the ideal (linear) case is derived next for the IIPFM. The analytical and optimised values are then compared to validate the proposed method. It should be noted that this mathematical procedure can only be applied to the IIPFM, as its ratio expression closely resembles that of the ideal case.

As shown in Section 4.3, the ideal quadratic ratio (Equation (20)) and the actual ratio for IIPFM (Equation (23)) are very similar:

$${\displaystyle \frac{{{\alpha }_1^{\prime }}^2}{{{\alpha }_2^{\prime }}^2}}{|}_{\mathrm{IIPFM}}\approx {\displaystyle \frac{{{\alpha }_1^{*}}^2}{{{\alpha }_2^{*}}^2}}$$

(26)

Because ${(1-\xi )}^2/{\xi }^2$ is a good approximation of $2{(1-\xi )}^2/\xi$ in the $[0,1]$ range:

$${\displaystyle \frac{{(t_l^{\varphi }-t_{off})}^2}{{(t_l^{\varphi }+t_{on})}^2}}{\displaystyle \frac{{(1-\xi )}^2}{{\xi }^2}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{c_1^2{k}_2}{{\tau }_2^2}}{\displaystyle \frac{{(1-\xi )}^2}{{\xi }^2}}$$

(27)

The expression can be simplified to an equality involving dynamic model parameters and the pulse separation:

$${\displaystyle \frac{{(t_l^{\varphi }-t_{off})}^2}{{(t_l^{\varphi }+t_{on})}^2}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{c_1^2{k}_2}{{\tau }_2^2}}$$

(28)

In order to maximise the linearity, the pulse width is deduced to be

$${t_l^{*}}^{\varphi }={\displaystyle \frac{t_{off}+t_{on}\frac{c_1}{{\tau }_2}\sqrt{\frac{k_2}{2}}}{1-\frac{c_1}{{\tau }_2}\sqrt{\frac{k_2}{2}}}}$$

(29)

This yields a value of ${t_l^{*}}^{\varphi }=19$ ms, which is very close to that obtained through optimisation, i.e., 20 ms, thereby validating the proposed method.

Figure 5 illustrates the dependence of the equilibrium pressure and the equivalent time constant on the input fraction and includes a comparison with the linear case, i.e., the desired response, for all modulators. The curves were obtained by numerically computing Equations (5) and (9) using the optimal parameter values.

6. Experimental Open-Loop Assessment

This section presents open-loop results obtained by using the four types of modulators to assess the system behaviour in terms of linearity for both static and dynamic characteristics of the SPA. For the experiments, the optimal values obtained in Section 5 were used as the nominal parameters for each modulator (see Table 2). The output amplitude A was set to the nominal voltage specified in the manufacturer’s datasheet for all modulators (i.e., 24 V).

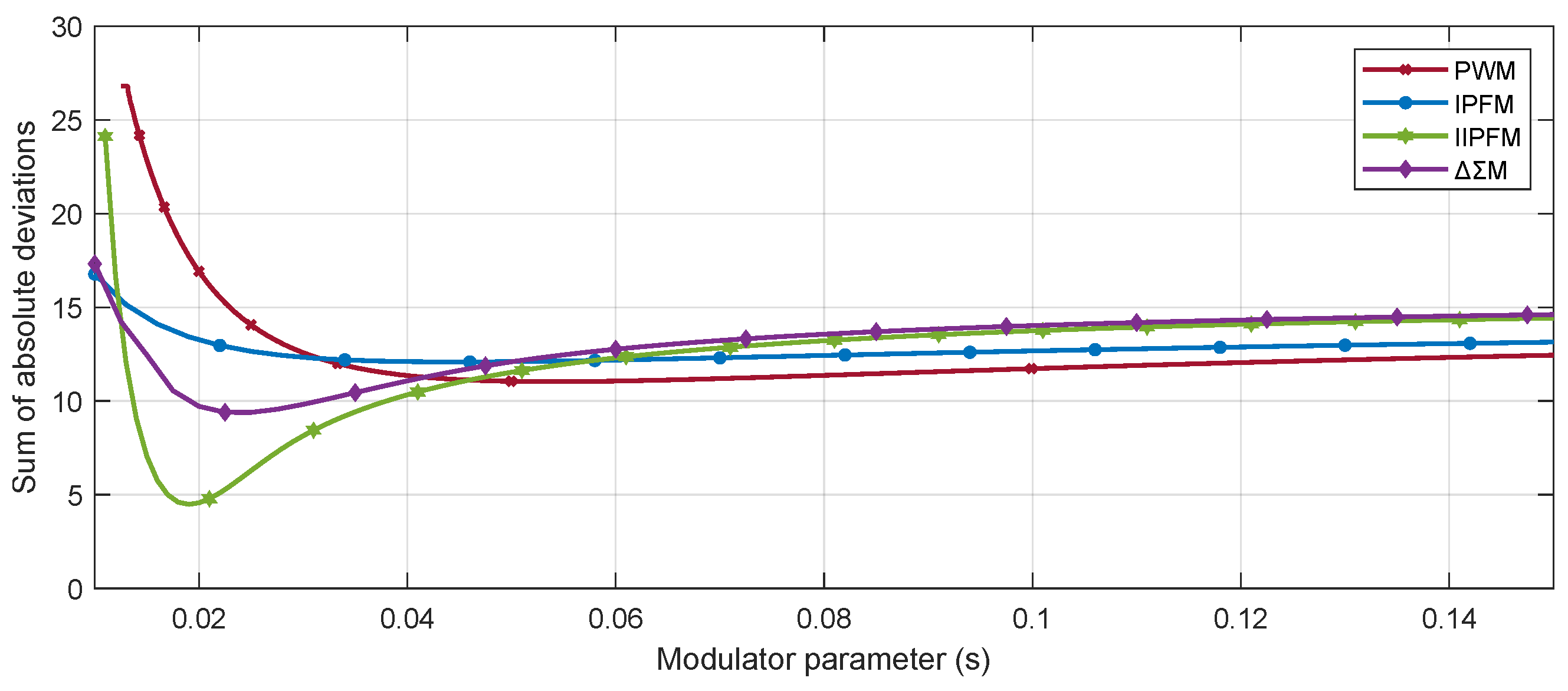
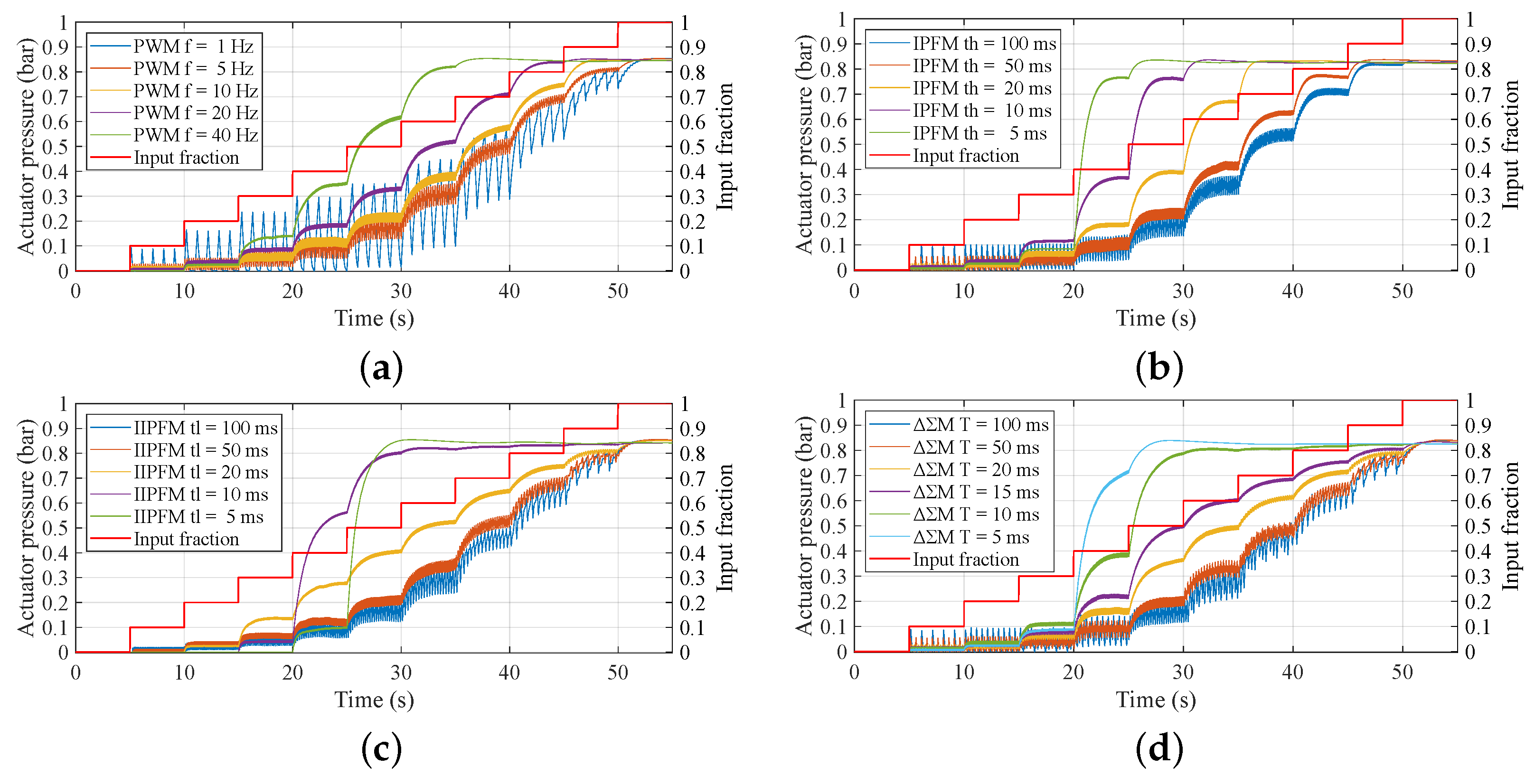
6.1. Nonlinearities Dependency on Parameter Tuning

The first set of tests aims to show the relevance of four types of nonlinearities, namely dead-zone, saturation, nonlinear static curve and chattering. This is achieved by varying the parameter associated with each of the modulators, including the following: frequency $f^W$ for PWM, pulse width $t_h^F$ for IPFM, pulse separation $t_l^{\varphi }$ for IIPFM, and period $T^{\Delta \Sigma }$ for $\Delta \Sigma$M. Refer to Appendix A for more details about fundamental equations of the modulators. The effect of the threshold, $K_{ti}^{\varphi }$, in IIPFM will be shown in Section 6.2.

Figure 6 shows the pressure curves obtained when the solenoid valve was actuated by the four types of modulators, in open loop, in response to a stepwise input fraction increasing from 0 to 1 in steps of $0.1$ every 5 s. The particularities observed for each modulator are described below:

• PWM (Figure 6a): The frequency $f^W$ varied from 1 to 40 Hz. It can be seen that in each case, the steady-state pressure value at each step is not linearly dependent on the input fraction: a change in input fraction from $0.6$ to $0.7$ produces larger changes in output pressure than an increment from $0.2$ to $0.3$. It is also observed that there is a saturation that increases with frequency, from almost no saturation at $f^W=1$ Hz to producing saturation at an input fraction of 0.6 at $f^W=40$ Hz. The dead-zone also increases with frequency, although it is not as relevant as the saturation ($t_{on}$ is almost three times smaller than $t_{off}$). Observations agree with reasonings of Section 4.3.1. Finally, chattering increases with decreasing frequency when using PWM and it is greater for intermediate values of input fractions (0.4–0.6). Although at low frequencies the dead-zone and saturation problems are minimised, the measured chattering is very high, which is not suitable for the application as it produces undesired abrupt movements in the actuator. Furthermore, the static response is still nonlinear and the saturation causes the actuator to operate incorrectly close to the tank pressure. The best compromise between reduced chattering and lower saturation is achieved at $f^W=20$ Hz.
• IPFM (Figure 6b): The pulse width $t_h^F$ was varied from 5 ms to 100 ms and $G^F=1$. As can be seen, there is no dead-zone because the pulse width is greater than the opening time. It is also observed that for small pulse widths (5 and 10 ms) there is an abrupt change in pressure for intermediate input fractions ($0.4$ and $0.5$). The saturation problem is greater than that observed in the PWM case. This is due to the fact that the elapsed time between pulses is reduced as the input increases: $t_l^F=t_h^F({\xi }^{-1}-1)$. As the pulse width increases, the saturation is reduced but still present ($D_{max}^F={(1+t_{off}/t_h^F)}^{-1}$) and chattering increases. For a given pulse width, chattering decreases as the input fraction increases because the firing frequency of the pulses increases. In summary, IPFM is good at dealing with the dead-zone, but the nonlinear static response and the saturation problem remain. The case of $t_h^F=20$ ms allows the best compromise.
• IIPFM (Figure 6c): The results were obtained for $t_l^{\varphi }\in [5,100]$ ms and $G^{\varphi }=1$. It is observed that dead-zone and saturation are significant for the smallest pulse width, but for $t_l^{\varphi }\ge 20$ ms the saturation is eliminated. The dead-zone also decreases as the pulse width increases. On the contrary, the chattering increases with pulse width. For a given pulse width, the chattering increases with the input fraction (the opposite to IPFM). The case of $t_l^{\varphi }=20$ ms (the optimal value obtained in Section 5) is of particular interest: the saturation is eliminated, there is an almost linear ratio of proportion between the input fraction and the output pressure (each increment in input fraction produces a similar increment in pressure), and a small dead-zone is observed.
• $\Delta \Sigma$M (Figure 6d): A first-order $\Delta \Sigma$M was employed, with the parameter $T^{\Delta \Sigma }$ adjusted from 5 ms to 100 ms. As can be observed, this modulator has similar problems to IPFM for the 5 and 10 ms range, but because the high and low state durations of $\Delta \Sigma$M are multiples of the period, it can be tuned to ensure that both the opening and closing times are met at the same time. With this modulation strategy, both the dead-zone and the saturation are no longer a problem, as seen for $T^{\Delta \Sigma }\ge 15$ ms. However, chattering increases with the period, while its amplitude seems to be almost uniform across all input fractions. The observed pattern in chattering is inconsistent caused by the way in which $\Delta \Sigma$M is able to encode a given input by using an irregular pattern of equal width pulses. The case corresponding to $T^{\Delta \Sigma }=20$ ms is the most linear case with a low chattering, although it is less linear than the IIPFM for small inputs (0.1–0.4).

Note that the aspect of the curves with larger pulse widths and low frequency (blue curves) is almost the same and corresponds to that of the expression derived for the case of instantaneous switching (i.e., Equation (5) with $t_{on}=t_{off}$ = 0), which correspond to cases where $t_h\gg t_{on}$ and $t_l\gg t_{off}$).

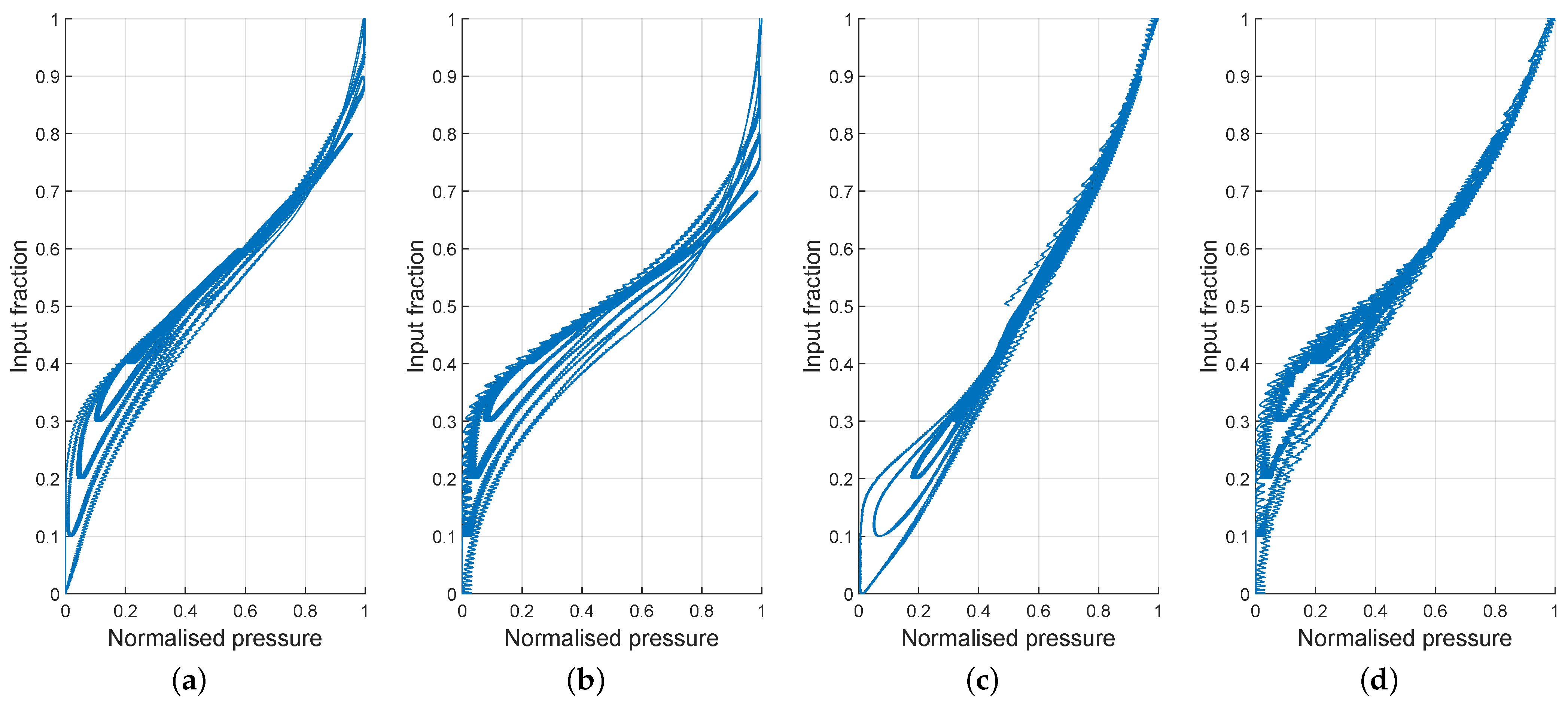
6.2. Static and Dynamic Linearity

The static and dynamic characteristics of the best-performing cases from the experiments shown in Figure 6 are compared in Figure 7, along with an IIPFM case in which the threshold was increased by $G^{\varphi }=1.15$. The specific features observed regarding the equilibrium pressure and time constants for each modulator are as follows:

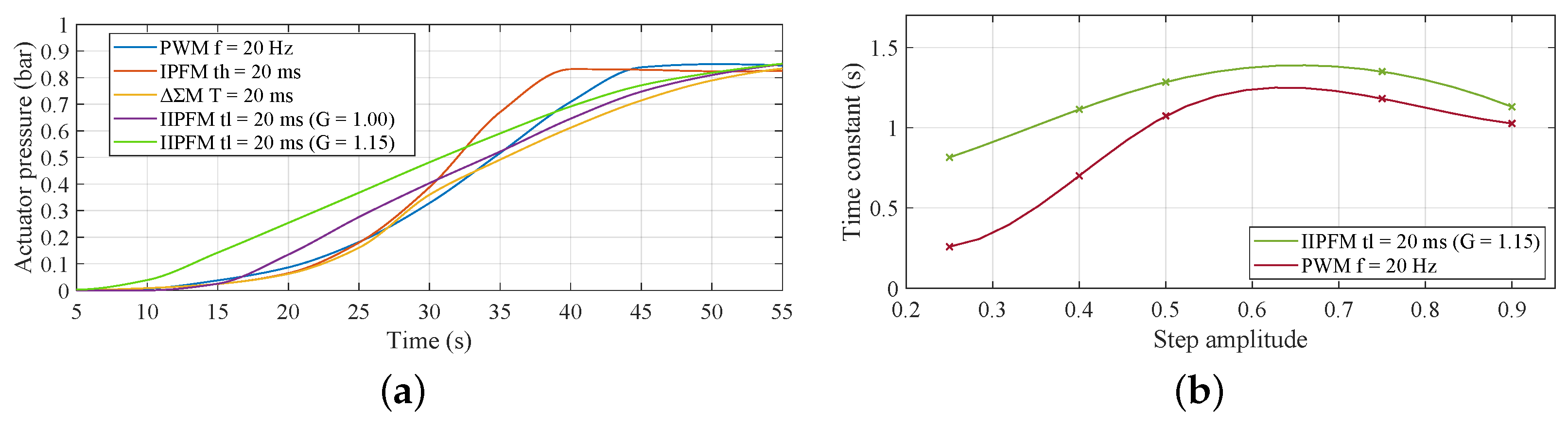
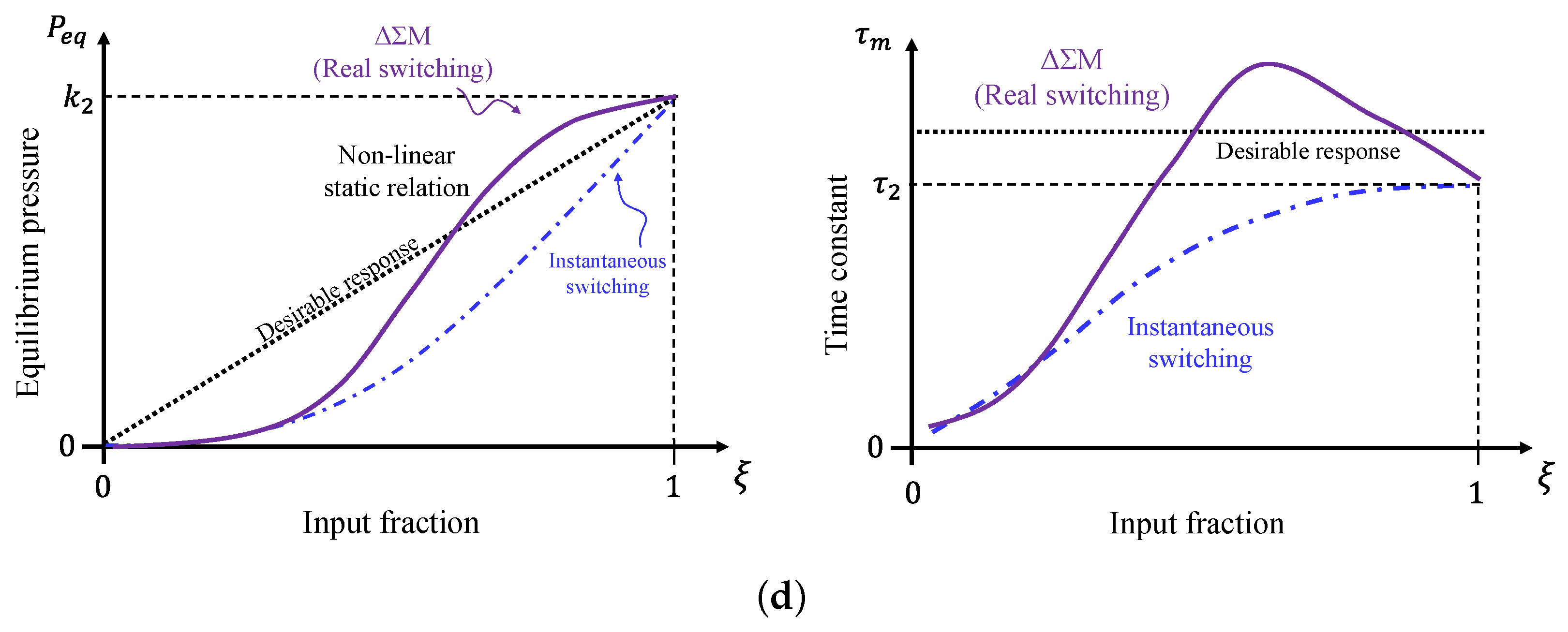
• Figure 7a shows the equilibrium pressure is plotted against the input fraction. It can be seen that both PWM and IPFM cause saturation, and the curves are far from being straight lines. In contrast, the IIPFM curves are closer to a straight line. The $\Delta \Sigma$M is an intermediate case between the IPFM and IIPFM curves. It is also observed that the IIPFM curve with $G^{\varphi }=1.15$ has no dead-zone while preserving the linearity and saturation elimination. To express the linearity of the static curve in a quantitative way, the five experiments were fitted to a line of the form $P=m\xi +n$.

  Table 3. Linear regression indices of the selected cases.

  Modulation Type	MSE ($\times {10}^{-3}$)	MD ($\times {10}^{-2}$)	FIT (%)
  PWM	7.3	7.56	75.23
  IPFM	13.0	10.02	68.23
  IIPFM ($G^{\varphi }=1.00$)	2.5	4.07	84.20
  IIPFM ($G^{\varphi }=1.15$)	1.3	3.13	87.89
  $\Delta \Sigma$M	4.5	5.55	78.82

  gives the mean square error (MSE), the maximum deviation (MD) and the goodness of fit, in percentage, for all the cases. As can be seen, the best cases in terms of the three performance indices are obtained with the IIPFM. Furthermore, the $G^{\varphi }=1.15$ case further increases the linearity of the system. By contrast, the worst cases in terms of linearity are IPFM and PWM. Note that the MSE is almost 7 times smaller with IIPFM than with PWM, and the fitness has a difference of $12.66$ % in favour of IIPFM.
• Figure 7b shows the measured time constant of the transient response measured when the valve is subjected to input steps against the amplitude of the step for PWM and IIPFM. The time constant of the measurements for IIPFM is ${\tau }_m^{\varphi }=1.139\pm 0.207$ s, while ${\tau }_m^W=0.847\pm 0.388$ s for PWM. The standard deviation of the time constant is almost halved when using IIPFM.

Figure 7. Open-loop results: static and dynamic linearity for (a) equilibrium pressure (b) time constants.

Figure 7. Open-loop results: static and dynamic linearity for (a) equilibrium pressure (b) time constants.

6.3. Frequency Analysis

A second group of tests was carried out on the pneumatic system to provide another perspective on the linearity achieved in the best cases in the frequency domain.

6.3.1. System Behaviour for Sine Inputs

The first tests consisted of applying a fixed frequency sinusoidal input to the system, with the amplitude decreasing discretely over time (piece-wise amplitude). The input fraction is plotted against the resulting pressure, normalised to the maximum value. The phase shift introduced by the system is compensated by shifting the curve until the input and output sinusoids are in phase.

Figure 8 shows the deviations from the linear case, i.e., a straight line from point $(0,0)$ to $(1,1)$, corresponding to the effect of the nonlinearities obtained with the four types of modulators. It can be seen that IPFM is the worst performing modulator, as the plot is S-shaped, which indicates that the output is influenced severely by nonlinearities. Meanwhile, the results of the IIPFM ($G^{\varphi }=1.15$) are the cases that look closer to a straight line, especially for input fractions above $0.3$. In general, all four modulators perform worse at low input fractions, but the IIPFM is again the case that is closer to a straight line even in this range. $\Delta \Sigma$M seems to be an intermediate case between IPFM and IIPFM, as it performs well for input fractions above $0.5$, similar to IIPFM, but very similar to IPFM for input fractions below $0.5$. Moreover, chattering in $\Delta \Sigma$ seems to be greater than in any other case. PWM performs worse than IIPFM and $\Delta \Sigma$M.

6.3.2. System Behaviour for Chirp-Type Inputs

The last experiments consisted of applying a chirp signal, of constant amplitude and with frequencies that range from $0.1$ to 100 Hz, as the input fraction given to each modulator. An offset of $0.5$ and an amplitude of $0.25$ were considered.

The bispectrum is a higher (third) order statistical measure that analyses the nonlinear interaction between different frequency components in a signal. Unlike the power spectrum, which describes the energy distribution as a function of frequency, the bispectrum captures the phase relationships and nonlinear interactions between trios of frequencies in a signal, allowing for the detection and quantification of nonlinear and non-Gaussian phenomena [22]. A high value on the Z-axis at a point $(f_1,f_2)$ indicates a strong nonlinear interaction between the frequencies $f_1$ and $f_2$, which generates a component at frequency $f_1+f_2$. Figure 9 shows the normalized value of bispectrum, known as bicoherence, of the valve response with the PWM (Figure 9a), the IPFM (Figure 9b), the IIPFM (Figure 9c), and the $\Delta \Sigma$M (Figure 9d). As can be seen, the colour distribution in the graph is more uniform for the IIPFM case, indicating that this modulator exhibits a more linear response than the others.

7. Conclusions

7.1. Summary and Main Findings

The present study has focused on the use of pulse modulation strategies to control a soft pneumatic actuator by means of a solenoid valve. A model of the pressure dynamics inside the soft pneumatic actuator (SPA) has been proposed to account for the nonlinearities introduced by the valve when actuated by pulse modulators. From the model, numerous expressions has been obtained to characterize the open-loop behaviour of the pressurisation process. It is possible to estimate dead-zone and saturation thresholds, chattering amplitude, nonlinear static response and pressure-dependent time constant.

A variety of known modulators, namely pulse-width modulator (PWM), $\Delta \Sigma$ modulator ($\Delta \Sigma$M), integral pulse frequency modulator (IPFM) and its inverse version (IIPFM), were applied to the valve and compared in terms of linearity. It has been demonstrated that, despite PWM is the most used modulator, it is not the best option as it introduces dead-zone and saturation that quickly increase with frequency, while other modulators are able to get rid of them, such as IIPFM and $\Delta \Sigma$M. Although IPFM is able to eliminate the dead-zone is the worst in terms of saturation and static response linearity. The primary limitation identified for IIPFM is the increase of chattering phenomena under conditions of elevated pressure. Nonetheless, this remains within a tolerable range for the majority of application scenarios.

Experimental results confirm the validity of the proposed dynamic model and its underlying assumptions. Moreover, the linearisation achieved through IIPFM is expected to facilitate the simplification of control algorithms for pressure regulation in SPAs.

7.2. Implications for Control Design and Future Work

Once the system has been effectively linearised, conventional control and system analysis techniques can be employed. In particular, linear control strategies are of primary interest. Since the neuron dynamics will be intentionally tuned to linearise the plant as much as possible, the main controller and the neuron can be treated as decoupled subsystems and therefore designed separately. This decoupling allows the controller to be developed according to standard design criteria in order to meet the desired closed-loop performance specifications.

Future work will follow the three stages outlined in this research. The next phase will focus on closed-loop pressure regulation by designing and testing controllers for the equivalent IIPFM-valve-actuator dynamics. Once pressure is properly controlled through this nearly linear dynamics, an outer loop will be implemented to regulate the actuator curvature or tip position, enabling precise motion control in soft robotic applications and completing the transition from open-loop characterisation to full closed-loop operation.