Brownian Motion at Lipid Membranes: A Comparison of Hydrodynamic Models Describing and Experiments Quantifying Diffusion within Lipid Bilayers
Abstract
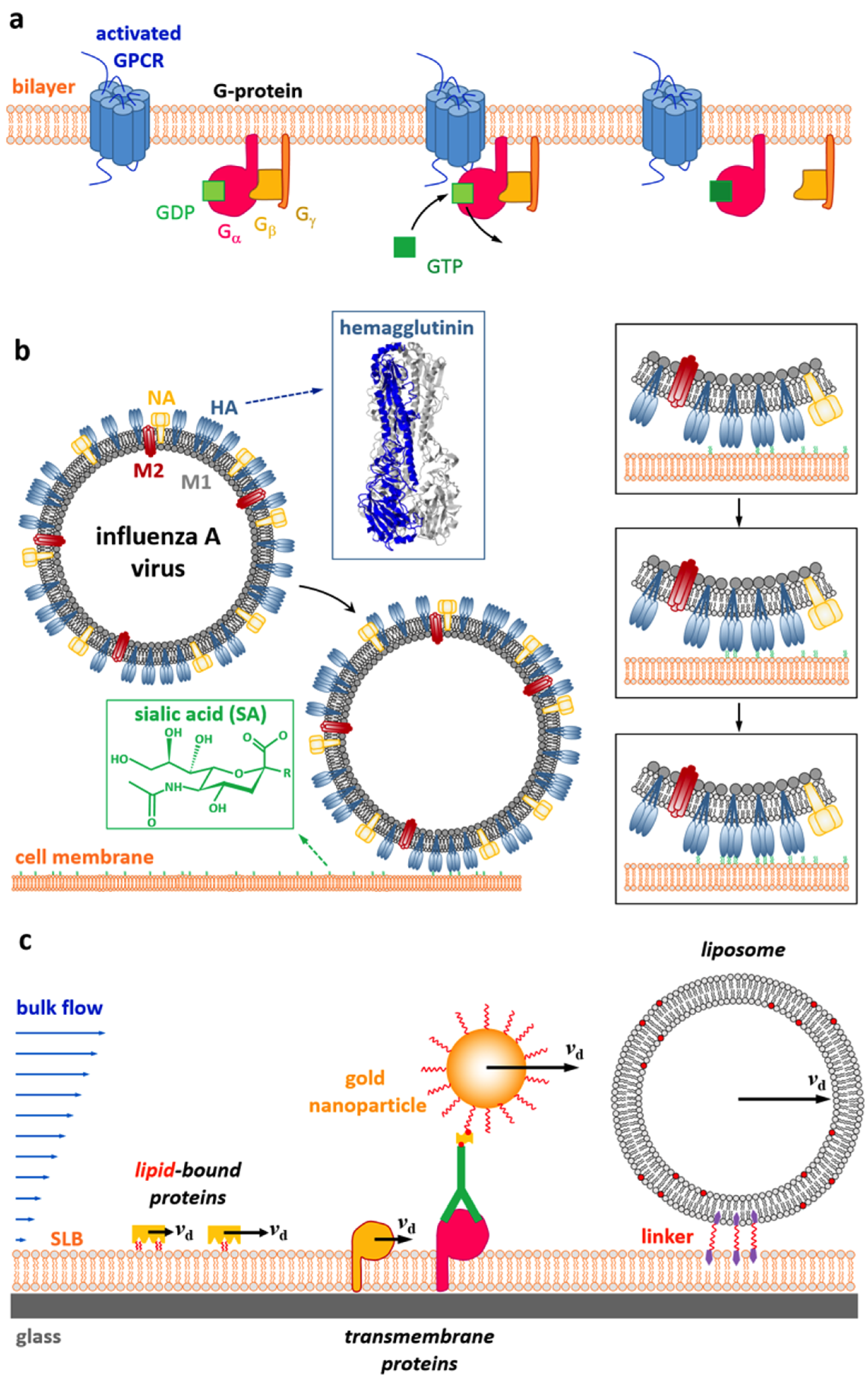
:1. Introduction
2. Models of Membrane Hydrodynamics
3. Experimental Observations
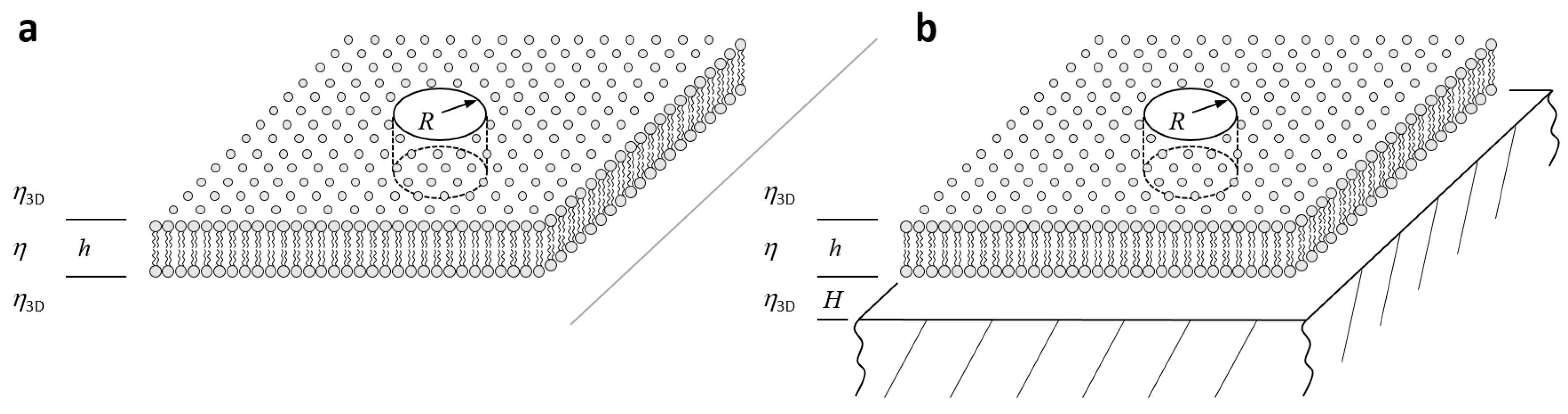
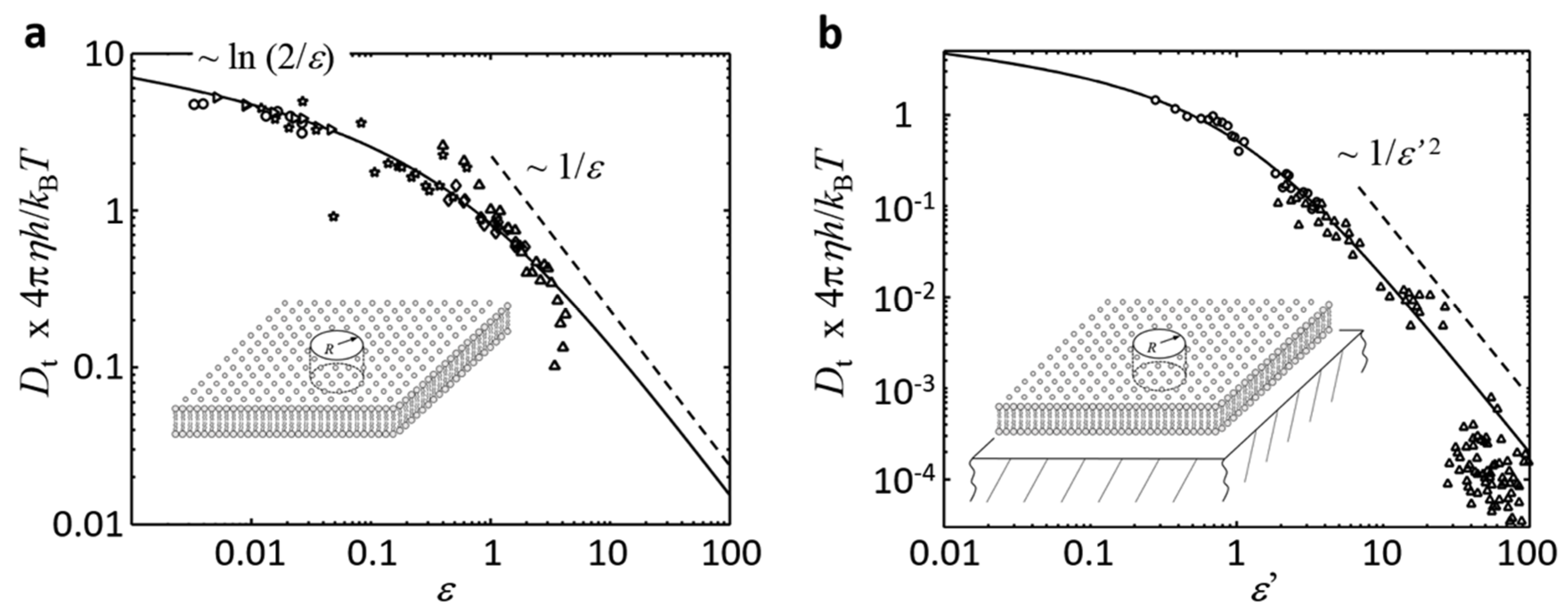
3.1. Freestanding Bilayers in the Limit of Small (, ): Saffman and Delbrück
3.2. Freestanding Bilayers in the Limit of Large (,): Hughes, Pailthorpe, and White
3.3. Lipid Bilayers Close to a Support (): Evans and Sackmann
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Tanaka, M.; Sackmann, E. Polymer-supported membranes as models of the cell surface. Nature 2005, 437, 656–663. [Google Scholar] [CrossRef] [PubMed]
- Stein, W.D.; Lieb, W.R. Transport and Diffusion across Cell Membranes, 1st ed.; Academic Press: Orlando, FL, USA, 1986; p. XVII. [Google Scholar]
- Kusumi, A.; Nakada, C.; Ritchie, K.; Murase, K.; Suzuki, K.; Murakoshi, H.; Kasai, R.S.; Kondo, J.; Fujiwara, T. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: High-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 2005, 34, 351–378. [Google Scholar] [CrossRef] [PubMed]
- Tocanne, J.F.; Dupoucezanne, L.; Lopez, A. Lateral diffusion of lipids in model and natural membranes. Prog. Lipid Res. 1994, 33, 203–237. [Google Scholar] [CrossRef]
- Irannejad, R.; von Zastrow, M. GPCR signaling along the endocytic pathway. Curr. Opin. Cell Biol. 2014, 27, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Metzger, H.; Kinet, J.P. How antibodies work—Focus on Fc-receptors. FASEB J. 1988, 2, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Mercer, J.; Schelhaas, M.; Helenius, A. Virus entry by endocytosis. Annu. Rev. Biochem. 2010, 79, 803–833. [Google Scholar] [CrossRef] [PubMed]
- Barrow, E.; Nicola, A.V.; Liu, J. Multiscale perspectives of virus entry via endocytosis. Virol. J. 2013, 10, 177. [Google Scholar] [CrossRef] [PubMed]
- Mammen, M.; Choi, S.K.; Whitesides, G.M. Polyvalent interactions in biological systems: Implications for design and use of multivalent ligands and inhibitors. Angew. Chem. Int. Ed. 1998, 37, 2755–2794. [Google Scholar] [CrossRef]
- Block, S.; Zhdanov, V.P.; Höök, F. Quantification of multivalent interactions by tracking single biological nanoparticle mobility on a lipid membrane. Nano Lett. 2016, 16, 4382–4390. [Google Scholar] [CrossRef] [PubMed]
- Bernardino de la Serna, J.; Schutz, G.J.; Eggeling, C.; Cebecauer, M. There is no simple model of the plasma membrane organization. Front. Cell Dev. Biol. 2016, 4, 106. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G. Non-brownian diffusion in lipid membranes: Experiments and simulations. Biochim. Biophys. Acta 2016, 1858, 2451–2467. [Google Scholar] [CrossRef] [PubMed]
- Saffman, P.G.; Delbruck, M. Brownian-motion in biological-membranes. Proc. Natl. Acad. Sci. USA 1975, 72, 3111–3113. [Google Scholar] [CrossRef] [PubMed]
- Iino, R.; Koyama, I.; Kusumi, A. Single molecule imaging of green fluorescent proteins in living cells: E-cadherin forms oligomers on the free cell surface. Biophys. J. 2001, 80, 2667–2677. [Google Scholar] [CrossRef]
- Dimova, R.; Aranda, S.; Bezlyepkina, N.; Nikolov, V.; Riske, K.A.; Lipowsky, R. A practical guide to giant vesicles. Probing the membrane nanoregime via optical microscopy. J. Phys. Condens. Matter 2006, 18, S1151–S1176. [Google Scholar] [CrossRef] [PubMed]
- Tien, H.T.; Diana, A.L. Bimolecular lipid membranes—A review and a summary of some recent studies. Chem. Phys. Lipids 1968, 2, 55–101. [Google Scholar] [CrossRef]
- Winterhalter, M. Black lipid membranes. Curr. Opin. Colloid Interface Sci. 2000, 5, 250–255. [Google Scholar] [CrossRef]
- Yoshina-Ishii, C.; Boxer, S.G. Controlling two-dimensional tethered vesicle motion using an electric field: Interplay of electrophoresis and electro-osmosis. Langmuir 2006, 22, 2384–2391. [Google Scholar] [CrossRef] [PubMed]
- Jönsson, P.; Gunnarsson, A.; Höök, F. Accumulation and separation of membrane-bound proteins using hydrodynamic forces. Anal. Chem. 2011, 83, 604–611. [Google Scholar] [CrossRef] [PubMed]
- Lundgren, A.; Fast, B.J.; Block, S.; Agnarsson, B.; Reimhult, E.; Gunnarsson, A.; Hook, F. Affinity purification and single-molecule analysis of integral membrane proteins from crude cell-membrane preparations. Nano Lett. 2018, 18, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Gunnarsson, A.; Nystrom, L.S.; Burazerovic, S.; Gunnarsson, J.; Snijder, A.; Geschwindner, S.; Hook, F. Affinity capturing and surface enrichment of a membrane protein embedded in a continuous supported lipid bilayer. Chemistryopen 2016, 5, 445–449. [Google Scholar] [CrossRef] [PubMed]
- Bally, M.; Gunnarsson, A.; Svensson, L.; Larson, G.; Zhdanov, V.P.; Höök, F. Interaction of single virus-like particles with vesicles containing glycosphingolipids. Phys. Rev. Lett. 2011, 107, 188103. [Google Scholar] [CrossRef] [PubMed]
- Block, S.; Fast, B.J.; Lundgren, A.; Zhdanov, V.P.; Höök, F. Two-dimensional flow nanometry of biological nanoparticles for accurate determination of their size and emission intensity. Nat. Commun. 2016, 7, 12956. [Google Scholar] [CrossRef] [PubMed]
- Tabaei, S.R.; Gillissen, J.J.J.; Block, S.; Hook, F.; Cho, N.J. Hydrodynamic propulsion of liposomes electrostatically attracted to a lipid membrane reveals size-dependent conformational changes. ACS Nano 2016, 10, 8812–8820. [Google Scholar] [CrossRef] [PubMed]
- Hughes, B.D.; Pailthorpe, B.A.; White, L.R. The translational and rotational drag on a cylinder moving in a membrane. J. Fluid Mech. 1981, 110, 349–372. [Google Scholar] [CrossRef]
- Evans, E.; Sackmann, E. Translational and rotational drag coefficients for a disk moving in a liquid membrane-associated with a rigid substrate. J. Fluid Mech. 1988, 194, 553–561. [Google Scholar] [CrossRef]
- Petrov, E.P.; Schwille, P. Translational diffusion in lipid membranes beyond the Saffman-Delbruck approximation. Biophys. J. 2008, 94, L41–L43. [Google Scholar] [CrossRef] [PubMed]
- Petrov, E.P.; Petrosyan, R.; Schwille, P. Translational and rotational diffusion of micrometer-sized solid domains in lipid membranes. Soft Matter 2012, 8, 7552–7555. [Google Scholar] [CrossRef]
- Lee, C.C.; Petersen, N.O. The lateral diffusion of selectively aggregated peptides in giant unilamellar vesicles. Biophys. J. 2003, 84, 1756–1764. [Google Scholar] [CrossRef]
- Ramadurai, S.; Holt, A.; Krasnikov, V.; van den Bogaart, G.; Killian, J.A.; Poolman, B. Lateral diffusion of membrane proteins. J. Am. Chem. Soc. 2009, 131, 12650–12656. [Google Scholar] [CrossRef] [PubMed]
- Weiss, K.; Neef, A.; Van, Q.; Kramer, S.; Gregor, I.; Enderlein, J. Quantifying the diffusion of membrane proteins and peptides in black lipid membranes with 2-focus fluorescence correlation spectroscopy. Biophys. J. 2013, 105, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Hormel, T.T.; Kurihara, S.Q.; Brennan, M.K.; Wozniak, M.C.; Parthasarathy, R. Measuring lipid membrane viscosity using rotational and translational probe diffusion. Phys. Rev. Lett. 2014, 112, 188101. [Google Scholar] [CrossRef] [PubMed]
- Cicuta, P.; Keller, S.L.; Veatch, S.L. Diffusion of liquid domains in lipid bilayer membranes. J. Phys. Chem. B 2007, 111, 3328–3331. [Google Scholar] [CrossRef] [PubMed]
- Stanich, C.A.; Honerkamp-Smith, A.R.; Putzel, G.G.; Warth, C.S.; Lamprecht, A.K.; Mandal, P.; Mann, E.; Hua, T.A.D.; Keller, S.L. Coarsening dynamics of domains in lipid membranes. Biophys. J. 2013, 105, 444–454. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.H.; Paprica, A.; Petersen, N.O. Effects of size of macrocyclic polyamides on their rate of diffusion in model membranes. Biophys. J. 1997, 73, 2580–2587. [Google Scholar] [CrossRef]
- Kaizuka, Y.; Groves, J.T. Structure and dynamics of supported intermembrane junctions. Biophys. J. 2004, 86, 905–912. [Google Scholar] [CrossRef]
- De Wit, G.; Danial, J.S.H.; Kukura, P.; Wallace, M.I. Dynamic label-free imaging of lipid nanodomains. Proc. Natl. Acad. Sci. USA 2015, 112, 12299–12303. [Google Scholar] [CrossRef] [PubMed]
- Gambin, Y.; Lopez-Esparza, R.; Reffay, M.; Sierecki, E.; Gov, N.S.; Genest, M.; Hodges, R.S.; Urbach, W. Lateral mobility of proteins in liquid membranes revisited. Proc. Natl. Acad. Sci. USA 2006, 103, 2098–2102. [Google Scholar] [CrossRef] [PubMed]
- Kriegsmann, J.; Gregor, I.; von der Hocht, I.; Klare, J.P.; Engelhard, M.; Enderlein, J.; Fitter, J. Translational diffusion and interaction of a photoreceptor and its cognate transducer observed in giant unilamellar vesicles by using dual-focus FCS. ChemBioChem 2009, 10, 1823–1829. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.A.; Ajdari, A. Hydrodynamics of particles embedded in a flat surfactant layer overlying a subphase of finite depth. J. Fluid Mech. 1998, 369, 151–173. [Google Scholar]
- Ramachandran, S.; Komura, S.; Imai, M.; Seki, K. Drag coefficient of a liquid domain in a two-dimensional membrane. Eur. Phys. J. E 2010, 31, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Levine, A.J.; Liverpool, T.B.; MacKintosh, F.C. Mobility of extended bodies in viscous films and membranes. Phys. Rev. E 2004, 69, 021503. [Google Scholar] [CrossRef] [PubMed]
- Levine, A.J.; Liverpool, T.B.; MacKintosh, F.C. Dynamics of rigid and flexible extended bodies in viscous films and membranes. Phys. Rev. Lett. 2004, 93, 038102. [Google Scholar] [CrossRef] [PubMed]
- Oppenheimer, N.; Diamant, H. Correlated diffusion of membrane proteins and their effect on membrane viscosity. Biophys. J. 2009, 96, 3041–3049. [Google Scholar] [CrossRef] [PubMed]
- Reister, E.; Seifert, U. Lateral diffusion of a protein on a fluctuating membrane. Europhys. Lett. 2005, 71, 859–865. [Google Scholar] [CrossRef]
- Gov, N.S. Diffusion in curved fluid membranes. Phys. Rev. E 2006, 73, 041918. [Google Scholar] [CrossRef] [PubMed]
- Henle, M.L.; Levine, A.J. Hydrodynamics in curved membranes: The effect of geometry on particulate mobility. Phys. Rev. E 2010, 81, 011905. [Google Scholar] [CrossRef] [PubMed]
- Naji, A.; Brown, F.L.H. Diffusion on ruffled membrane surfaces. J. Chem. Phys. 2007, 126, 235103. [Google Scholar] [CrossRef] [PubMed]
- Naji, A.; Levine, A.J.; Pincus, P.A. Corrections to the Saffman-Delbruck mobility for membrane bound proteins. Biophys. J. 2007, 93, L49–L51. [Google Scholar] [CrossRef] [PubMed]
- Criado, M.; Vaz, W.L.C.; Barrantes, F.J.; Jovin, T.M. Translational diffusion of acetylcholine-receptor (monomeric and dimeric forms) of torpedo-marmorata reconstituted into phospholipid-bilayers studied by fluorescence recovery after photobleaching. Biochemistry 1982, 21, 5750–5755. [Google Scholar] [CrossRef] [PubMed]
- Vaz, W.L.C.; Criado, M. A comparison of the translational diffusion of a monomer and an oligomer of the acetylcholine-receptor protein reconstituted into soybean lipid bilayers. Biochim. Biophys. Acta 1985, 819, 18–22. [Google Scholar] [CrossRef]
- Gambin, Y.; Reffay, M.; Sierecki, E.; Homble, F.; Hodges, R.S.; Gov, N.S.; Taulier, N.; Urbach, W. Variation of the lateral mobility of transmembrane peptides with hydrophobic mismatch. J. Phys. Chem. B 2010, 114, 3559–3566. [Google Scholar] [CrossRef] [PubMed]
- Guigas, G.; Weiss, M. Influence of hydrophobic mismatching on membrane protein diffusion. Biophys. J. 2008, 95, L25–L27. [Google Scholar] [CrossRef] [PubMed]
- Shenoy, S.; Moldovan, R.; Fitzpatrick, J.; Vanderah, D.J.; Deserno, M.; Losche, M. In-plane homogeneity and lipid dynamics in tethered bilayer lipid membranes (tBLMs). Soft Matter 2010, 6, 1263–1274. [Google Scholar] [CrossRef] [PubMed]
- Sackmann, E.; Tanaka, M. Supported membranes on soft polymer cushions: Fabrication, characterization and applications. Trends Biotechnol. 2000, 18, 58–64. [Google Scholar] [CrossRef]
- Sinner, E.K.; Knoll, W. Functional tethered membranes. Curr. Opin. Chem. Biol. 2001, 5, 705–711. [Google Scholar] [CrossRef]
- Pace, H.; Nystrom, L.S.; Gunnarsson, A.; Eck, E.; Monson, C.; Geschwindner, S.; Snijder, A.; Hook, F. Preserved transmembrane protein mobility in polymer-supported lipid bilayers derived from cell membranes. Anal. Chem. 2015, 87, 9194–9203. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.F.; Granick, S. Slaved diffusion in phospholipid bilayers. Proc. Natl. Acad. Sci. USA 2005, 102, 9118–9121. [Google Scholar] [CrossRef] [PubMed]
- Netz, R.R.; Andelman, D. Neutral and charged polymers at interfaces. Phys. Rep. 2003, 380, 1–95. [Google Scholar] [CrossRef]
- Knight, J.D.; Lerner, M.G.; Marcano-Velazquez, J.G.; Pastor, R.W.; Falke, J.J. Single molecule diffusion of membrane-bound proteins: Window into lipid contacts and bilayer dynamics. Biophys. J. 2010, 99, 2879–2887. [Google Scholar] [CrossRef] [PubMed]
- Ziemba, B.P.; Falke, J.J. Lateral diffusion of peripheral membrane proteins on supported lipid bilayers is controlled by the additive frictional drags of (1) bound lipids and (2) protein domains penetrating into the bilayer hydrocarbon core. Chem. Phys. Lipids 2013, 172, 67–77. [Google Scholar] [CrossRef] [PubMed]
- Camley, B.A.; Brown, F.L.H. Diffusion of complex objects embedded in free and supported lipid bilayer membranes: Role of shape anisotropy and leaflet structure. Soft Matter 2013, 9, 4767–4779. [Google Scholar] [CrossRef]
| Model | System | Bilayer | T/°C | Approach | ηh/(nNs/m) | Remarks | Ref. |
|---|---|---|---|---|---|---|---|
| SD | Peptides | DMPC; GUV | 35 | FRAP; Dt | 0.525 | Low dynamic range in ε | [29] |
| SD | Proteins | DOPC + DOPG; GUV | n.s. | FCS; Dt | 0.304 |  in Figure 3a in Figure 3a | [30] |
| SD | Proteins | POPC + POPE; BLM | 22 | 2fFCS; Dt | 0.15 | 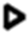 in Figure 3a in Figure 3a | [31] |
| SD, HPW | Beads | DOPC; BLM | 24 | SPT; Dt, Dr | 15.3 ± 3.4 (SD), 15.9 ± 2.3 (HPW) | Relatively high values extracted for ηh | [32] |
| SD | DOPC domains, 0.5–10 µm | DOPC + DPPC + Chol; GUV | 16–30 | SPT; Dt | 10–500 |  in Figure 3a in Figure 3a | [33] |
| SD | DPPC domains, 1–10 µm | DPhPC + DPPC + Chol; GUV | 26.2 | SPT; Dt | 3.3 ± 1.1 |  in Figure 3a in Figure 3a | [34] |
| HPW | DPPC domains, 0.7–2 µm | DPhPC + DPPC (1:1); GUV | 23.5 | SPT; Dt, Dr | 2.1–2.3 |  in Figure 3a in Figure 3a | [28] |
| HPW | DPPC domains, 0.5–10 µm | DOPC + DPPC + Chol (2:2:1); GUV | 16–30 | SPT; Dt | n.d. | [33] | |
| ES | Crosslinked C10 chains | DMPC; multi-SLB | 27–38 | FRAP; Dt | 0.13–0.08 | Low dynamic range in ε′ | [35] |
| ES | Bilayer junctions | DMPC + DOTAP + PC (88:10:2); SLB | n.s. | SPT; Dt | 0.4 | Complex bilayer geometry, in Figure 3b in Figure 3b | [36] |
| ES | SM nanodomains | DOPC + SM (1:1); DIB | n.s. | SPT; Dt | 0.87 |  in Figure 3b in Figure 3b | [37] |
| !SD | Peptides, proteins | SOPC, C12E5; GUV | 20 | FRAP; Dt | n.s. | 1/R instead ln(1/R) scaling, evanescent excitation | [38] |
| !SD | Proteins | POPC; GUV | 25 | 2fFCS; Dt | n.s. | 1/R instead ln(1/R) scaling | [39] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Block, S. Brownian Motion at Lipid Membranes: A Comparison of Hydrodynamic Models Describing and Experiments Quantifying Diffusion within Lipid Bilayers. Biomolecules 2018, 8, 30. https://doi.org/10.3390/biom8020030
Block S. Brownian Motion at Lipid Membranes: A Comparison of Hydrodynamic Models Describing and Experiments Quantifying Diffusion within Lipid Bilayers. Biomolecules. 2018; 8(2):30. https://doi.org/10.3390/biom8020030
Chicago/Turabian StyleBlock, Stephan. 2018. "Brownian Motion at Lipid Membranes: A Comparison of Hydrodynamic Models Describing and Experiments Quantifying Diffusion within Lipid Bilayers" Biomolecules 8, no. 2: 30. https://doi.org/10.3390/biom8020030
APA StyleBlock, S. (2018). Brownian Motion at Lipid Membranes: A Comparison of Hydrodynamic Models Describing and Experiments Quantifying Diffusion within Lipid Bilayers. Biomolecules, 8(2), 30. https://doi.org/10.3390/biom8020030





