δ Gravity: Dark Sector, Post-Newtonian Limit and Schwarzschild Solution
Abstract
:1. Introduction
2. Gravity
2.1. Theories Formalism and Modified Action
2.2. Gravity Action and Equations of Motion
2.3. Test Particle
2.3.1. Massive Particles
2.3.2. Massless Particles
3. Cosmological Case
3.1. Photon Trajectory and Luminosity Distance
3.2. Solution of the Equations of Motion
3.3. Analysis and Results
- GR: and with ,
- Gravity with Matter: and with .
3.4. Introduction to Inflation
4. Non-Relativistic Case
4.1. Newtonian and Post-Newtonian Limit
4.2. Trajectory of a Particle:
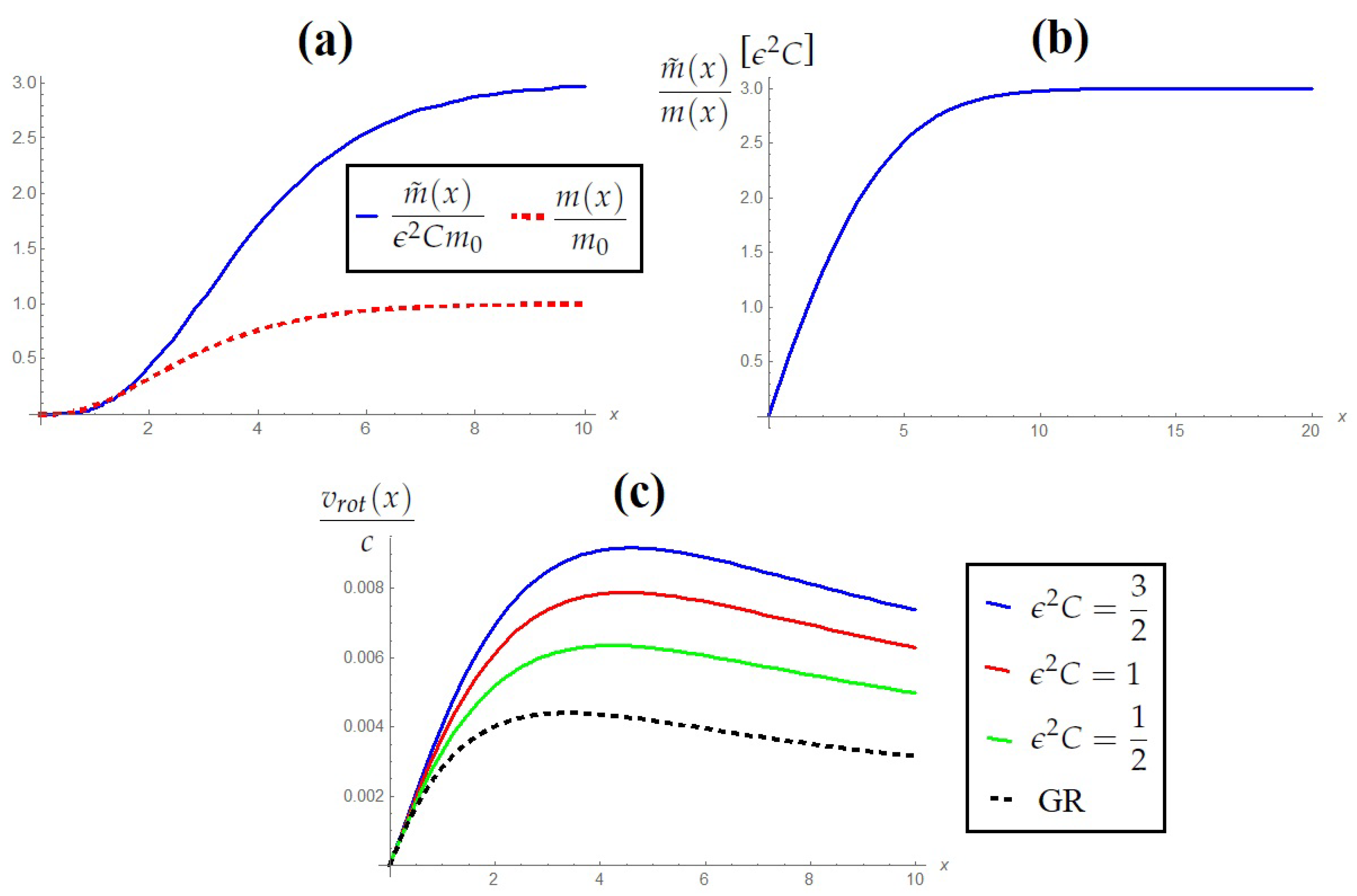
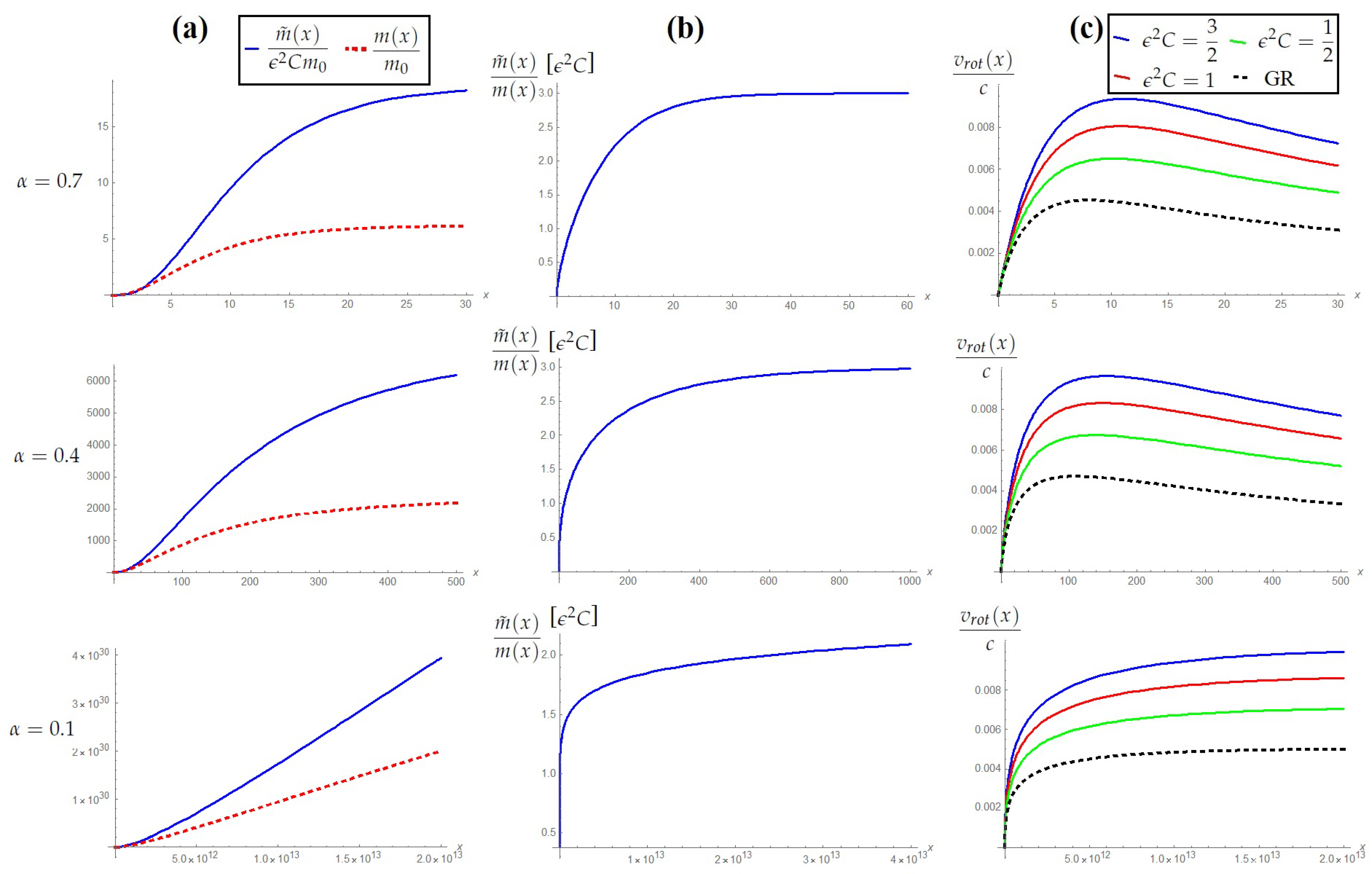
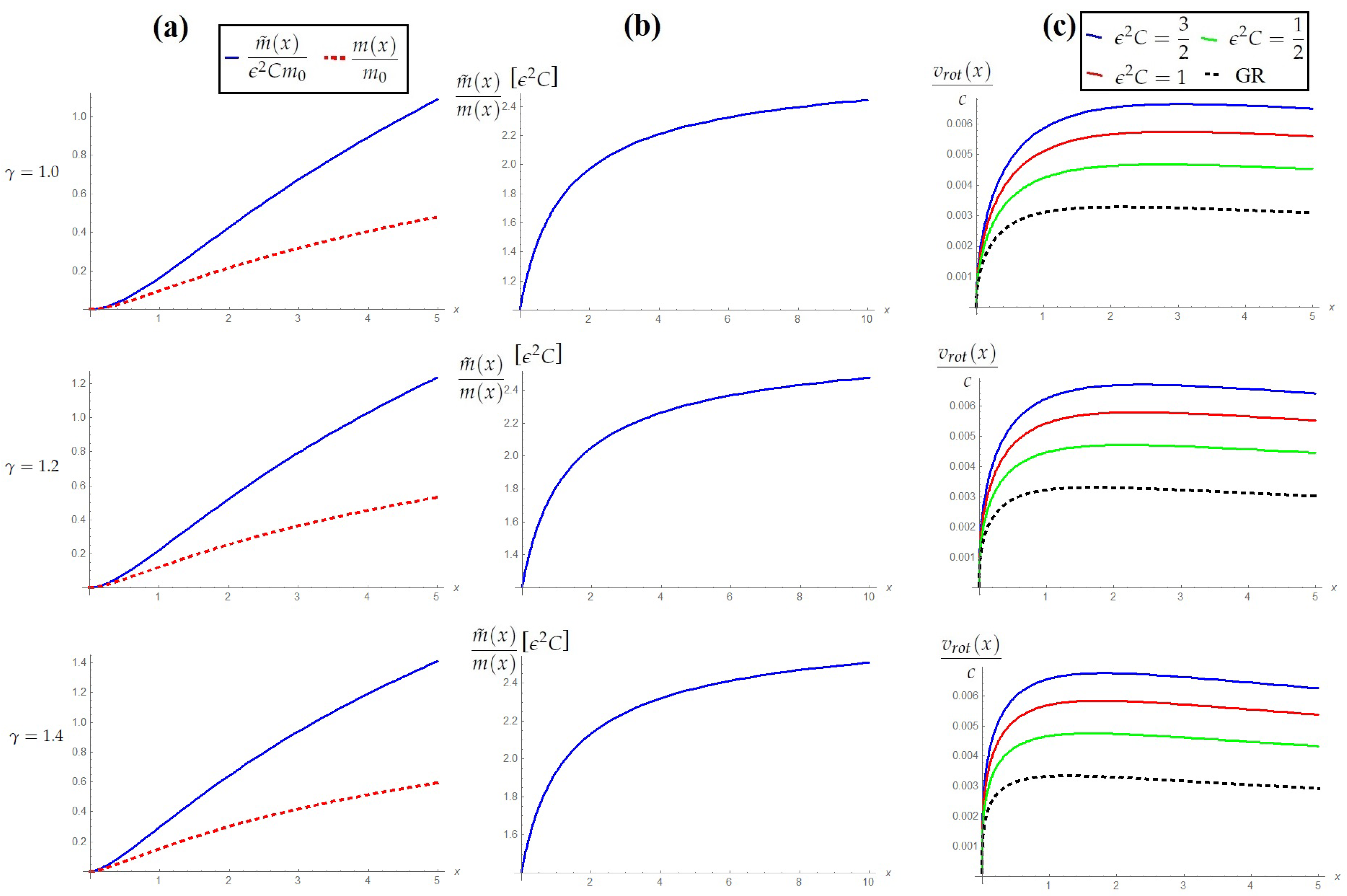
4.3. Density Profiles
4.3.1. Spherically Homogeneous Profile
4.3.2. Exponential Profile
4.3.3. Einasto Profile
4.3.4. Navarro–Frenk–White Profile
5. Schwarzschild Case
5.1. Schwarzschild Solution
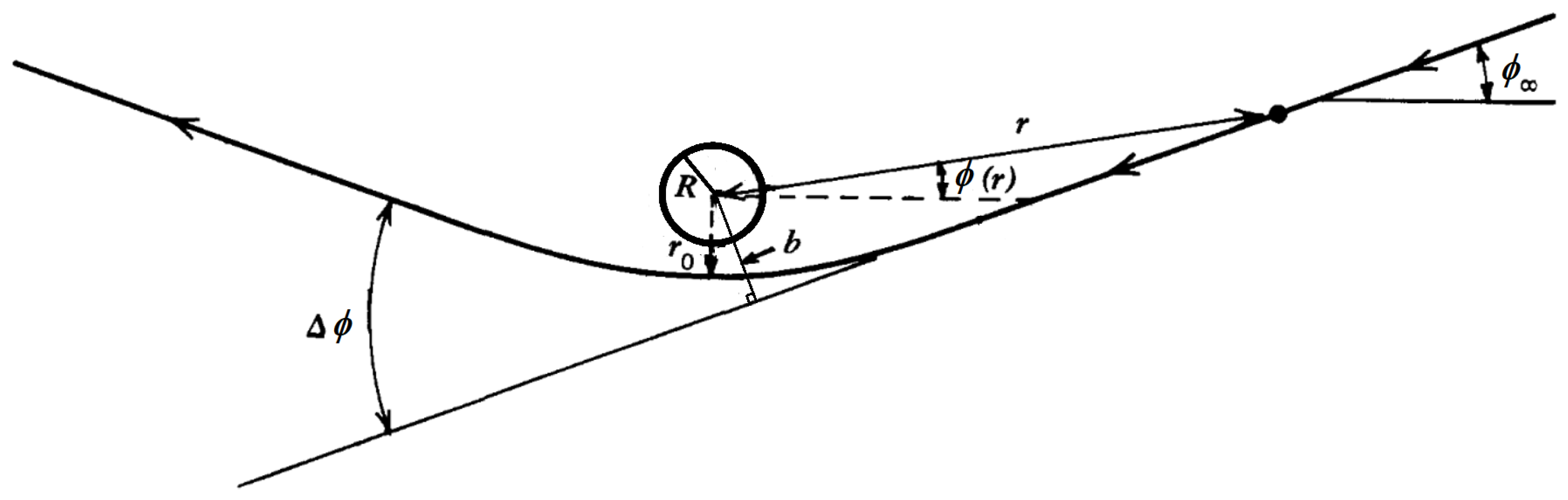
5.2. Gravitational Lensing
5.3. Perihelion Precession
5.4. Black Holes
- If and , we have ,
- If and , we have .
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DM | Dark Matter |
| DE | Dark Energy |
| GR | General Relativity |
| DGT | Gauge Theories |
| GCT | General Coordinates Transformation |
| ExGCT | Extended General Coordinates Transformation |
| NFW | Navarro–Frenk–White |
| FLRW | Friedmann–Lemaître–Robertson–Walker |
Appendix A. Perfect Fluid
Appendix B. Harmonic Gauge
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. [The Supernova Cosmology Project] Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Ann. Rev. Nucl. Part. Sci. 2009, 59, 397–429. [Google Scholar] [CrossRef]
- Hooper, D.; Baltz, E.A. Strategies for Determining the Nature of Dark Matter. Annu. Rev. Nucl. Part. Sci. 2008, 58, 293–314. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark Energy and the Accelerating Universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Bosma, A.; van der Kruit, P.C. The local mass-to-light ratio in spiral galaxies. Astron. Astrophys. 1979, 79, 281–286. [Google Scholar]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 /R = 4kpc/ to UGC 2885 /R = 122 kpc/. Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Salucci, P.; Gentile, G. Comment on Scalar-tensor gravity coupled to a global monopole and flat rotation curves. Phys. Rev. D 2006, 73, 128501. [Google Scholar] [CrossRef]
- Salucci, P.; Lapi, A.; Tonini, C.; Gentile, G.; Yegorova, I.A.; Klein, U. The universal rotation curve of spiral galaxies—II. The dark matter distribution out to the virial radius. Mon. Not. R. Astron. Soc. 2007, 378, 41–47. [Google Scholar] [CrossRef]
- Persic, M.; Salucci, P. The universal galaxy rotation curve. Astrophys. J. 1991, 368, 60–65. [Google Scholar] [CrossRef]
- Persic, M.; Salucci, P. Dark and visible matter in spiral galaxies. Mon. Not. R. Astron. Soc. 1988, 234, 131–154. [Google Scholar] [CrossRef]
- Ashman, K.M. Dark matter in galaxies. Astron. Soc. Pac. 1992, 104, 1109–1138. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Bekenstein, J. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Martin, J. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). C. R. Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Albrecht, A.; Bernstein, G.; Cahn, R.; Freedman, W.L.; Hewitt, J.; Hu, W.; Huth, J.; Kamionkowski, M.; Kolb, E.W.; Knox, L.; et al. Report of the Dark Energy Task Force. arXiv 2006, arXiv:astro-ph/0609591. [Google Scholar]
- Peacock, J.A.; Schneider, P.; Efstathiou, G.; Ellis, J.R.; Leibundgut, B.; Lilly, S.J.; Mellier, Y. Report by the ESA-ESO Working Group on Fundamental Cosmology, ESA-ESO Working Groups Report No. 3. arXiv 2006, arXiv:astro-ph/0610906. [Google Scholar]
- Tsujikawa, S. Modified Gravity Models of Dark Energy. Lect. Notes Phys. 2010, 800, 99–145. [Google Scholar]
- Alfaro, J.; González, P.; Ávila, R. A finite quantum gravity field theory model. Class. Quantum Gravity 2011, 28, 215020. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. One-loop divergencies in the theory of gravitation. Annales de l’institut Henri Poincaré 1974, 20, 69–94. Available online: http://www.numdam.org/item?id=AIHPA_1974__20_1_69_0 (accessed on 1 January 2011).
- Alfaro, J. Bv Gauge Theories. arXiv 1997, arXiv:hep-th/9702060. [Google Scholar]
- Alfaro, J.; Labraña, P. Semiclassical gauge theories. Phys. Rev. D 2002, 65, 045002. [Google Scholar] [CrossRef]
- Alfaro, J. Delta-gravity and dark energy. Phys. Lett. B 2012, 709, 101–105. [Google Scholar] [CrossRef]
- Alfaro, J.; González, P. Cosmology in delta-gravity. Class. Quantum Gravity 2013, 30, 085002. [Google Scholar] [CrossRef]
- Alfaro, J.; González, P. δ Gravity, δ Matter and the Accelerated Expansion of the Universe. arXiv 2017, arXiv:1704.02888. [Google Scholar]
- Caldwell, R.R.; Kamionkowski, M.; Weinberg, N.N. Phantom Energy: Dark Energy with ω < −1 Causes a Cosmic Doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [PubMed]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Cline, J.M.; Jeon, S.; Moore, G.D. The phantom menaced: Constraints on low-energy effective ghosts. Phys. Rev. D 2004, 70, 043543. [Google Scholar] [CrossRef]
- Hao, J.; Li, X. Attractor solution of phantom field. Phys. Rev. D 2017, 67, 107303. [Google Scholar] [CrossRef]
- Einasto, J. On Galactic Descriptive Functions. Astron. Nachr. 1969, 291, 97–109. [Google Scholar] [CrossRef]
- Dhar, B.K.; Williams, L.L.R. Surface brightness and intrinsic luminosity of ellipticals. Mon. Not. R. Astron. Soc. 2012, 427, 204–244. [Google Scholar] [CrossRef]
- Retana-Montenegro, E.; Van Hese, E.; Gentile, G.; Baes, M.; Frutos-Alfaro, F. Analytical properties of Einasto Dark Matter haloes. Astron. Astrophys. 2012, 540, A70. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter. Astrophys. J. 1996, 462, 563–575. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Daylan, T.; Finkbeiner, D.P.; Hooper, D.; Linden, T.; Portillo, S.K.N.; Rodd, N.L.; Slatyer, T.R. The Characterization of the Gamma-Ray Signal from the Central Milky Way: A Compelling Case for Annihilating Dark Matter, FERMILAB-PUB-14-032-A, MIT-CTP-4533. arXiv 2014, arXiv:1402.6703. [Google Scholar]
- Formalont, E.B.; Sramek, R.A. Measurements of the Solar Gravitational Deflection of Radio Waves in Agreement with General Relativity. Phys. Rev. Lett. 1976, 36, 1475–1478. [Google Scholar] [CrossRef]
- Boulanger, N. Inconsistency of interacting, multi-graviton theories. Nucl. Phys. B 2001, 597, 127–171. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical aspects of massive gravity. Rev. Mod. Phys. 2012, 84, 671–710. [Google Scholar] [CrossRef]
- de Rham, C. Massive Gravity. Living Rev. Relat. 2014, 17, 7. [Google Scholar] [CrossRef]
- de Rham, C.; Matas, A.; Tolley, A.J. New Kinetic Interactions for Massive Gravity? Class. Quantum Gravity 2014, 31, 16. [Google Scholar]
- Lee, T.D.; Wick, G.C. Negative metric and the unitarity of the S-matrix. Nucl. Phys. B 1969, 9, 209–243. [Google Scholar] [CrossRef]
- Lee, T.D.; Wick, G.C. Finite Theory of Quantum Electrodynamics. Phys. Rev. D 1972, 6, 2721. [Google Scholar]
- Bender, C.M. Introduction to PT-symmetric quantum theory. Contemp. Phys. 2005, 46, 277–292. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Schmelzer, I. Are Boulware-Deser ghosts really the death penalty for massive gravity? arXiv 2017, arXiv:1711.09009. [Google Scholar]
- Alfaro, J. Delta-gravity, Dark Energy and the accelerated expansion of the Universe (Appendix A). J. Phys. Conf. Ser. 2012, 384, 012027. [Google Scholar] [CrossRef]
- Siegel, W. Fields, Section IIIB. arXiv 2005, arXiv:hep-th/9912205. [Google Scholar]
- Weinberg, S. Section 1.4: Luminosity distances. In Cosmology; Oxford University Press Inc.: New York, NY, USA, 2008; pp. 31–34. ISBN 978-0-19-852682-7. [Google Scholar]
- Holanda, R.F.L.; Goncalves, R.S.; Alcaniz, J.S. A test for cosmic distance duality. J. Cosmol. Astropart. Phys. 2012, 2012, 6. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. [The Supernova Cosmology Project] The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-energy Constraints above z > 1 and Building an Early-type-hosted Supernova Sample. Astrophys. J. 2012, 746, 1–24. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. arXiv 2015, arXiv:1502.01589. [Google Scholar]
- González, P. Inflation in Gravity. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1043, 012017. [Google Scholar] [CrossRef]
- Weinberg, S. Chapter 7: Einstein’s Field Equations, Chapter 8: Classic Tests of Einstein’s Theory and Chapter 9: Post-Newtonian Celestial Mechanics. In Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons, Inc.: New York, NY, USA; London, UK; Sydney, Australia; Toronto, ON, Canada, 1972; pp. 151–249. ISBN 0-471-92567-5. [Google Scholar]
- Conroy, C.; Loeb, A.; Spergel, D.N. Evidence against Dark Matter Halos Surrounding the Globular Clusters MGC1 and NGC 2419. Astrophys. J. 2011, 741, 1–5. [Google Scholar] [CrossRef]
- Jihye, S.; Sungsoo, K.; Young-Wook, L. Dark Matter Content in Globular Cluster NGC 6397. J. Korean Astron. Soc. 2013, 46, 173–181. [Google Scholar]
- Pitjev, N.P.; Pitjeva, E.V. Constraints on Dark Matter in the Solar System. Astron. Lett. 2013, 39, 141–149. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Chapter 10: Particle in a Gravitational Field. In The Classical Theory of Fields, Fourth Revised English Edition. Course of Theoretical Physics, Vol. 2; Institute for Physical Problems, Academy of Sciences of the U.S.S.R. Translated from the Russian by Morton Hamermesh, University of Minnesota; Butterworth-Heinenann: Oxford, UK, 1996; pp. 226–258. ISBN 0-7506-2768-9. [Google Scholar]
- Ray, J.R. Lagrangian Density for Perfect Fluids in General Relativity. J. Math. Phys. 1972, 13, 1451–1453. [Google Scholar] [CrossRef]
| 1 | To obtain the best combination of parameters, we used NonLinearModelFit from Mathematica 11.0. Then, we used these parameters to minimize Equation (71). For more details, see the Mathematica 11.0 help. |
| 2 | The age of the universe of Planck was calculated using the cosmological parameters obtained in [52]. That is, and km/s/Mpc. |
| 3 | The only constant that we can not fix is . Fortunately, this constant is irrelevant to find . This is true for an NFW profile too. |
| 4 |

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfaro, J.; González, P. δ Gravity: Dark Sector, Post-Newtonian Limit and Schwarzschild Solution. Universe 2019, 5, 96. https://doi.org/10.3390/universe5050096
Alfaro J, González P. δ Gravity: Dark Sector, Post-Newtonian Limit and Schwarzschild Solution. Universe. 2019; 5(5):96. https://doi.org/10.3390/universe5050096
Chicago/Turabian StyleAlfaro, Jorge, and Pablo González. 2019. "δ Gravity: Dark Sector, Post-Newtonian Limit and Schwarzschild Solution" Universe 5, no. 5: 96. https://doi.org/10.3390/universe5050096




