Joint Optimization for UAV-Assisted Communications with Spatiotemporal Traffic Forecasting
Abstract
1. Introduction
- A holistic closed-loop forward-looking optimization framework is proposed. This framework tightly couples the spatiotemporal traffic prediction module with the communication resource optimization module, enabling the genuine predeployment of unmanned aerial vehicles;
- An integrated traffic-forecasting model. We introduce a GMM-ML model based on Gaussian mixture models for cellular network traffic prediction. This model excels in handling task heterogeneity and few-shot learning scenarios, achieving highly accurate and robust forecasting of future traffic hotspots by extracting frequency-domain meta-features;
- Formulation of a long-term performance optimization problem and design of an efficient solution algorithm. We model the active UAV deployment problem as a long-term discounted mixed-integer non-convex optimization problem. To address this complexity, we designed the P-IALO algorithm, which decomposes the problem effectively and employs iterative BCD and SCA solutions to ensure convergence and practicality;
- Comprehensive simulation validation and analysis were conducted. Through extensive simulations calibrated with real-world data, we validated the significant advantages of our approach over existing reactive and predictive benchmark schemes. The study reveals performance improvements in throughput, quality of service, and system stability, alongside critical analysis of the framework’s robustness under predictive uncertainty.
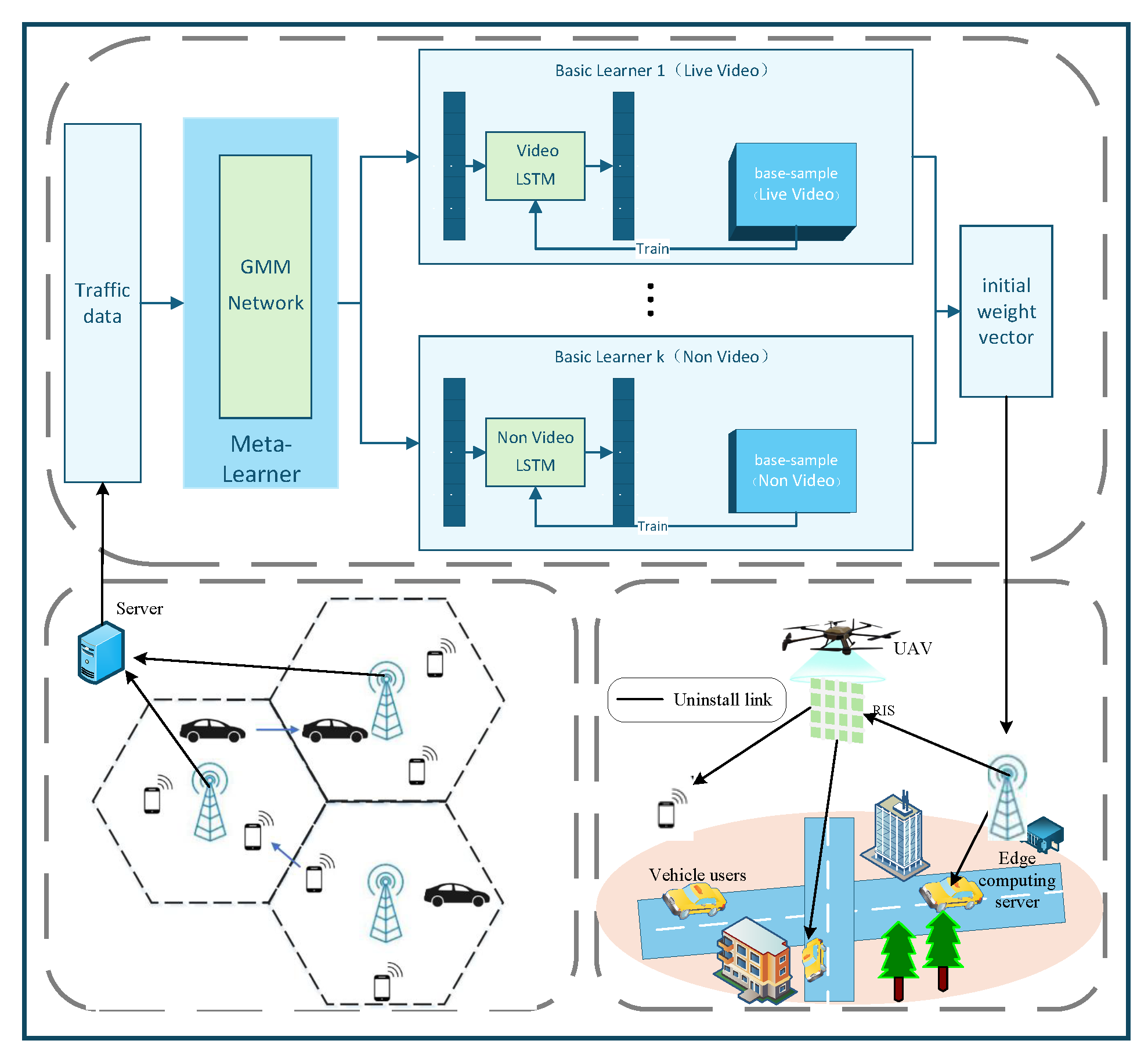
2. Related Work
3. System Model
3.1. Network Scenario Description
3.2. Traffic-Forecasting Model
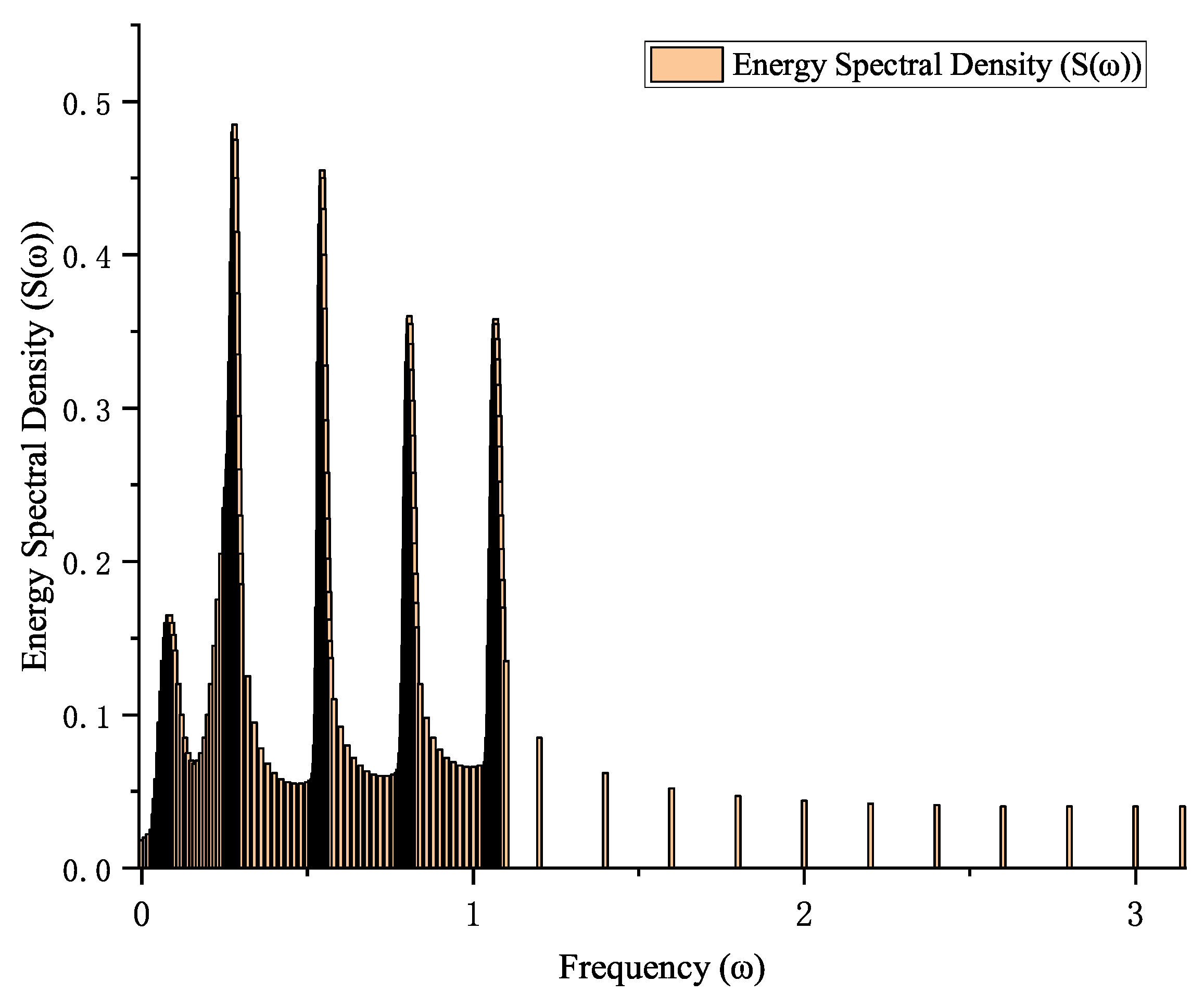
3.2.1. Generation of a Feature Candidate Pool Based on the Global Energy Spectrum
3.2.2. Theoretical Analysis of Non-Gaussian Multimodal Distributions
3.3. Communication and Channel Modeling
3.4. User Association and the Quality-of-Service (QoS) Model
4. Problem Formulation
4.1. Decision Variables
4.2. Objective Function
- User Association Constraint: Each user can be associated with at most one access point (UAV) in any time slot slot
- UAV Service Capacity Constraint: The number of users served by a single UAV cannot exceed its maximum service capacity
- Quality-of-Service (QoS) Constraint: The achievable data rate for an associated user must satisfy its minimum requirement
- UAV Mobility Constraint: The position change of a UAV between consecutive time slots is constrained by its maximum velocity
- UAV Initial Position Constraint:
5. Solution Algorithm: Proactive Iterative Optimization Algorithm
5.1. Detailed Explanation of the Key Steps
| Algorithm 1 Predictive iterative association and location optimization (P-IALO) |
|
Input: Initial drone position , Prediction model , Total time slots T, Prediction window , Discount factor , Reward weight . Output: Optimal trajectory and associated policy .
|
5.1.1. User Association Subproblem
5.1.2. UAV Location Subproblem
- Non-convexity analysis: The objective function () is a nested composite function. The inner function () is a convex function with respect to , which second derivatives are positive. However, the outer function () is concave. The convexity of the composite of a concave and convex function cannot be guaranteed; hence, the entire objective function is non-convex.
- Continuously convex approximation (SCA): For a non-convex function, at a given local point (), construct a globally convex approximation function that serves as an upper or lower bound, and iteratively optimize this approximation. Here, we opt to construct a differentiable global lower bound; by maximizing this bound, we ensure the original objective function is non-decreasing at each iteration.
- Constructing a lower bound approximation: xml-ph-0000@deepl.internal, which is a concave function.Let , which is a concave function.Let . As previously stated, is a convex function with respect to .For the concave function (), its first-order Taylor expansion constitutes its global upper bound as follows:However, here, we require a lower bound. Although itself is not concave, we may approximate itself with a linear lower bound and then utilize ’s monotonicity. Specifically, for a convex function (), its first-order Taylor expansion at a given point () constitutes a global lower bound as follows:Since is a monotonically increasing function, we obtainTherefore, constitutes a global lower bound for the original objective function term ().
- Calculate the derivativeWe now require .Let .Since , by the chain ruleAt the point , this derivative is constant, denoted as (taking the negative sign yields )Simultaneously, let
- Constructing the convex approximation problem: Substituting the above derivation yields that for the unmanned aerial vehicle (j), the lower bound of its optimization objective isLet . Note that is a concave function with respect to , while is a linear function with respect to since is convex but prefixed with a negative sign. The composition of a concave function with a linear function remains concave. Hence, is a concave function with respect to . Maximizing a concave function constitutes a convex optimization problem.
- Adding a trust region: Since Taylor series expansions are only accurate near local points, it is necessary to ensure that the new solution () does not deviate too far from the current point (); otherwise, the approximation becomes inaccurate, potentially causing algorithmic divergence. Therefore, we introduce a trust region constraint as follows:where is the trust region radius for the (r)th iteration, which can be adaptively adjusted. This constraint is a convex constraint (quadratic convex constraint).
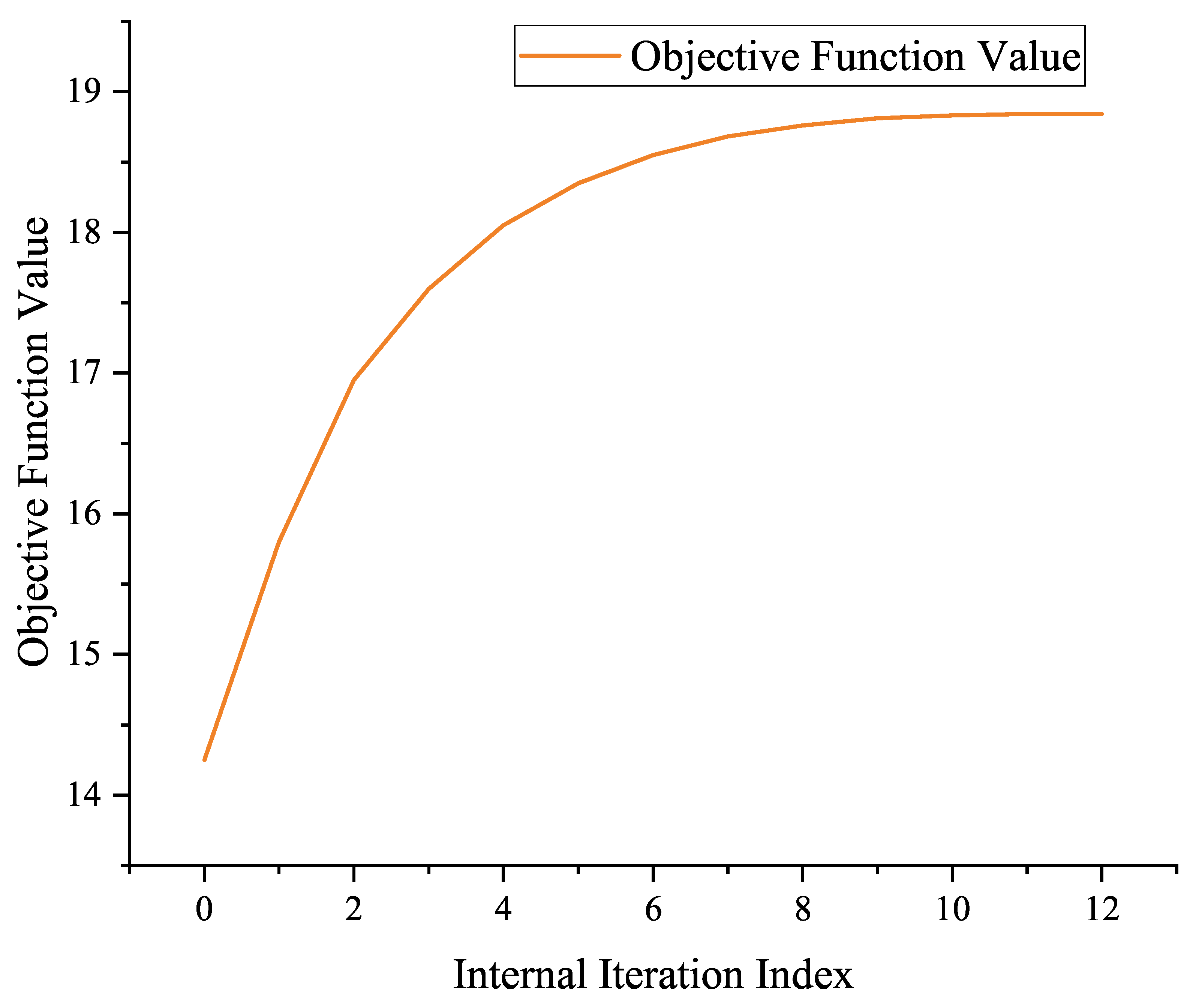
- The final convex formulation: For each drone (j), the convex optimization problem to be solved at the (r + 1)th iteration isThis is a constrained convex optimization problem. The objective function is concave, and the constraint set is convex. This paper opts to utilize MATLAB (R2024a)’s fmincon toolbox for direct solutions. The new position obtained from the solution () will be employed for the next iteration.By alternately executing these two sub-steps, the value of the original objective function improves (or remains unchanged) with each iteration. As the objective function has an upper bound, the algorithm ultimately converges to a local optimum.
5.2. Lyapunov-Based Convergence Analysis
6. Experiments and Analysis
6.1. Experimental Objectives
Datasets and Preliminary Analysis
- (1)
- Spatial Gridding and Cell DefinitionThe traffic prediction section employs a mobile network dataset provided by Telecom Italia’s Big Data Challenge program. The dataset comprises approximately 3 million traffic records collected in Milan between 1 November 2013 and 1 January 2014. The city area was divided into 10,000 grids, each representing a square region with a side length of 235 m, serving as the fundamental spatial unit for this study. Each record contains a timestamp, a grid ID, and a mobile traffic load (i.e., a traffic payload). Given that the grid size approximates the coverage area of a 50-base station, each grid is defined herein as a “cell”.
- (2)
- Time Series ConstructionFor analytical convenience, the entire dataset’s temporal span is divided into consecutive one-hour intervals, denoted asAssume there are N time intervals, where r denotes the traffic record index, represents the cell ID for record r, indicates the timestamp for record r, and signifies the traffic load for record r. The time series for the pth cell traffic load is represented by the vector .
- (3)
- Meta-feature extractionWithin each cell, although traffic load variations differ daily, they exhibit fixed periodic patterns weekly. To quantify the temporal correlation of the cellular traffic load, the autocorrelation coefficient of the normalized traffic load vector for cell P can be calculated as follows:This paper selects five specific frequency components: , , , , and , corresponding to periods of 1 week, 1 day, 12 h, 8 h, and 6 h, respectively (as sinusoidal signals) as the meta-features for the cellular network. This selection is based on a systematic analysis of the frequency-domain energy distribution across all the cellular traffic sequences in the dataset.The real and imaginary parts of the five principal frequency components may form a 10-dimensional principal frequency component vector, i.e., the cellular principal feature, as follows:where and represent the real and imaginary parts of the complex number, respectively.
6.2. Comparison Algorithms
6.3. Evaluation Metrics
6.4. Results and Analysis
6.4.1. Fundamental Performance Analysis
6.4.2. Robustness Analysis
6.4.3. Impacts of Different Forecasting Models on P-IALO Performance
6.4.4. Impact of the Prediction Time Horizon on the System Performance
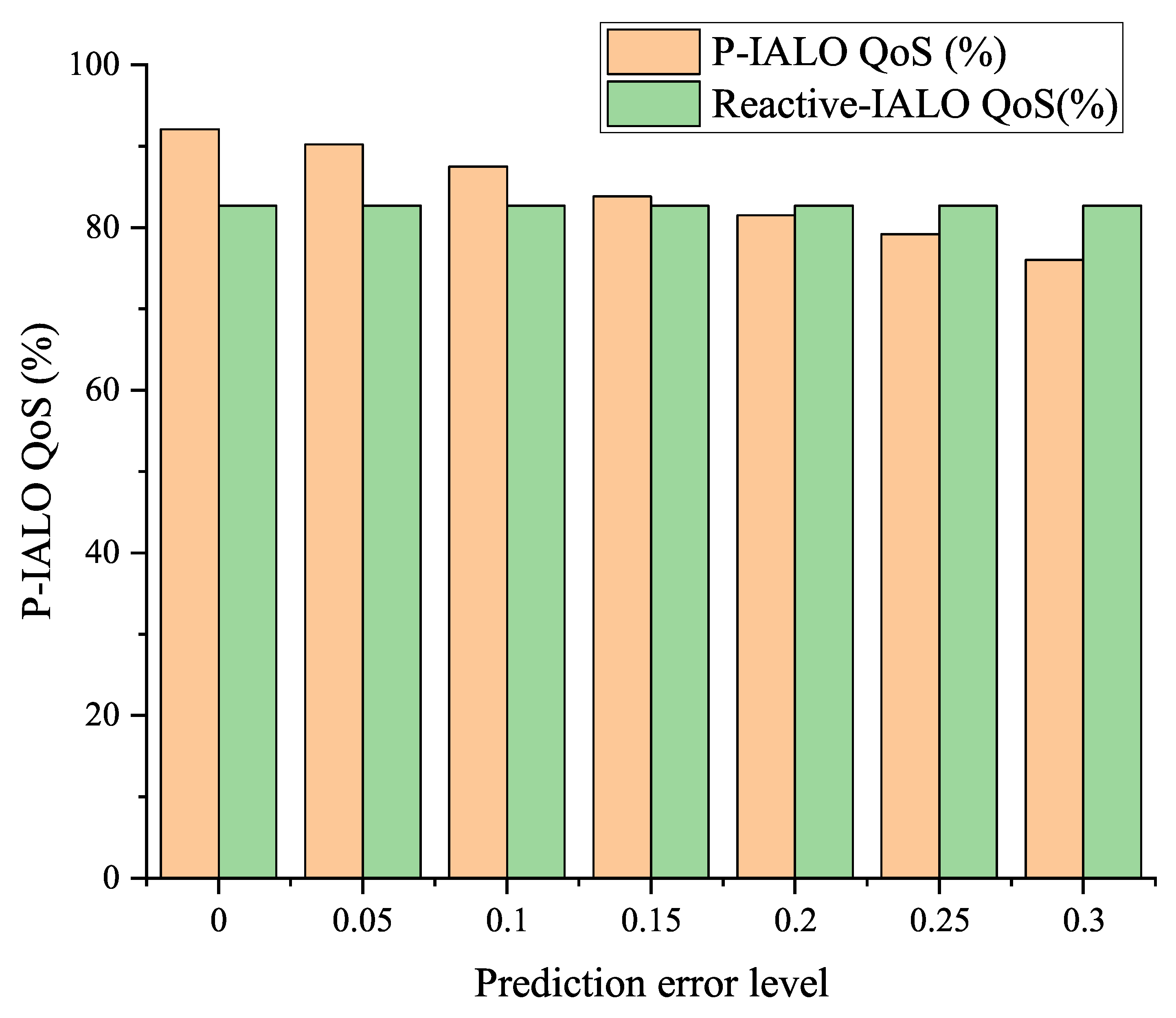
6.4.5. Quantitative Analysis of the Relationship Between the Prediction Error and System Performance
Error Propagation Model and Theoretical Analysis
Empirical Analysis of the Error–Performance Quantitative Relationship
6.4.6. Hyperparameter Sensitivity Analysis
- Fine-tuning critical parameters: and require a grid search or a Bayesian optimization;
- Empirical configuration of secondary parameters: K and may be set according to scenario characteristics;
- Default values for secondary parameters: and employ recommended default values.
| Hyperparameter | First-Order Sensitivity Index | Total Sensitivity Index | Sensitivity Level | Recommended Range | Performance Variance Explained (%) |
|---|---|---|---|---|---|
| Discount factor | 0.28 | 0.35 | High | [0.85, 0.92] | 32.5 |
| Reward weight | 0.22 | 0.27 | High | [0.25, 0.35] | 25.8 |
| Number of GMM components K | 0.15 | 0.19 | Medium | [5, 7] | 17.3 |
| Prediction window | 0.12 | 0.16 | Medium | [5, 7] | 13.5 |
| Learning rate | 0.06 | 0.09 | Low | [0.01, 0.05] | 5.9 |
| Trust domain value | 0.08 | 0.11 | Low | [40, 60] | 9.1 |
6.4.7. System Scalability Analysis
Computational Complexity Analysis
- Association subproblem: Employing a greedy algorithm to sort and match N users and U drones, with complexity ;
- Position subproblem: Each drone independently solves a convex optimization problem. Using an interior-point method yields , where n is the variable dimension;
- Forecasting module: Performs -step forecasting for M base stations using a GMM meta-learning framework, with complexity .
Multi-UAV Scalability Verification
6.4.8. Robustness Analysis of Channel Models
Impacts of Altitude Disturbances on the Communication Model
Impacts of Motion Disturbances on the Communication Quality
6.4.9. Limitations and Practical Deployment Challenges
Limitations at the Algorithmic Level
Technical Challenges in Practical Deployment
7. Conclusions
- (1)
- The introduction of a closed-loop, forward-looking optimization framework: We introduce a framework that for the first time, tightly integrates traffic forecasting into the UAV decision-making cycle, establishing an integrated “forecast–optimize–execute” architecture. This endows UAVs with the capacity to anticipate future network conditions, achieving a fundamental shift from reactive response to proactive scheduling;
- (2)
- The design of a high-performance traffic prediction model: We design a prediction model by incorporating a meta-learning approach based on Gaussian mixture models (GMM-ML). This model effectively addresses challenges in scenarios with small samples and heterogeneity, significantly enhancing both prediction accuracy and generalization to provide reliable inputs for subsequent optimization;
- (3)
- The formulation of a long-term optimization model: We establish a long-term optimization problem that innovatively incorporates a “service readiness reward” into the objective function. This incentivizes drones to predeploy to forecast hotspot areas, balancing immediate utility with future gains and enhancing the overall system performance;
- (4)
- The development of the P-IALO solution algorithm: We develop the P-IALO algorithm, which leverages techniques such as rolling optimization, block coordinate descent, and continuous convex approximation. It decomposes the complex MINLP problem to efficiently solvable subproblems, ensuring both convergence and real-time performance suitable for practical deployment;
- (5)
- A comprehensive simulation validation: In a real-data-driven simulation environment, the proposed framework demonstrates superiority across multiple dimensions—including throughput, QoS satisfaction, interruption frequency, convergence speed, and robustness. It exhibits particular stability under prediction errors and small-sample conditions, confirming its strong practical value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the Road to 6G: Visions, Requirements, Key Technologies, and Testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Pandey, G.K.; Gurjar, D.S.; Yadav, S.; Jiang, Y.; Yuen, C. UAV-Assisted Communications With RF Energy Harvesting: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2025, 27, 782–838. [Google Scholar] [CrossRef]
- Mao, K.; Zhu, Q.; Wang, C.X.; Ye, X.; Gomez-Ponce, J.; Cai, X.; Miao, Y.; Cui, Z.; Wu, Q.; Fan, W. A Survey on Channel Sounding Technologies and Measurements for UAV-Assisted Communications. IEEE Trans. Instrum. Meas. 2024, 73, 1–24. [Google Scholar] [CrossRef]
- Bithas, P.S.; Ropokis, G.A.; Karagiannidis, G.K.; Nistazakis, H.E. UAV-Assisted Communications With RIS: A Shadowing-Based Stochastic Analysis. IEEE Trans. Veh. Technol. 2024, 73, 10000–10010. [Google Scholar] [CrossRef]
- He, Z.; Chow, C.Y.; Zhang, J.D. STNN: A Spatio-Temporal Neural Network for Traffic Predictions. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7642–7651. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Xiao, F.; Xing, K.; Yang, Z.; Liu, Y.; Peng, C. Spatio-Temporal Analysis and Prediction of Cellular Traffic in Metropolis. IEEE Trans. Mob. Comput. 2019, 18, 2190–2202. [Google Scholar] [CrossRef]
- Yu, J.; Wu, J.; Jiang, H. Spatio-Temporal Trajectory Design for UAVs: Enhancing URLLC and LoS Transmission in Communications. IEEE Wirel. Commun. Lett. 2024, 13, 2417–2421. [Google Scholar] [CrossRef]
- Pang, Y.; Zhao, X.; Hu, J.; Yan, H.; Liu, Y. Bayesian Spatio-Temporal grAph tRansformer network (B-STAR) for multi-aircraft trajectory prediction. Knowl.-Based Syst. 2022, 249, 108998. [Google Scholar] [CrossRef]
- Shao, Z.; Peng, X.; Zhang, P.; Liu, Z.; Chen, Y.; Yang, R.; Xiang, P. An intelligent GNN seismic response prediction and computation framework adhering to meshless principles: A case study for high-speed railway bridges. Eng. Anal. Bound. Elem. 2025, 179, 106359. [Google Scholar] [CrossRef]
- Li, Q.; Wu, C.; Chen, J.; Zhang, Z.; He, K.; Du, R.; Wang, X.; Zhao, Q.; Liu, Y. Privacy-Preserving Universal Adversarial Defense for Black-Box Models. IEEE Trans. Inf. Forensics Secur. 2025, 20, 11503–11515. [Google Scholar] [CrossRef]
- Wu, C.; Sun, J.; Chen, J.; Alazab, M.; Liu, Y.; Xiang, Y. TCG-IDS: Robust Network Intrusion Detection via Temporal Contrastive Graph Learning. IEEE Trans. Inf. Forensics Secur. 2025, 20, 1475–1486. [Google Scholar] [CrossRef]
- Ge, X.; Yu, S.; Yoon, W.S.; Kim, Y.D. A new prediction method of alpha-stable processes for self-similar traffic. In Proceedings of the IEEE Global Telecommunications Conference, Dallas, TX, USA, 29 November–3 December 2004. [Google Scholar]
- Tedjopurnomo, D.A.; Bao, Z.; Zheng, B.; Choudhury, F.M.; Qin, A.K. A Survey on Modern Deep Neural Network for Traffic Prediction: Trends, Methods and Challenges. IEEE Trans. Knowl. Data Eng. 2022, 34, 1544–1561. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Zhang, J.; Feng, J.; Wang, W.; Xin, K. An approach for spatial-temporal traffic modelling in mobile cellular networks. In Proceedings of the IEEE International Teletraffic Congress, Ghent, Belgium, 8–10 September 2015. [Google Scholar]
- Xu, F.; Lin, Y.; Huang, J.; Wu, D.; Shi, H.; Song, J.; Li, Y. Big data driven mobile traffic understanding and forecasting: A time series approach. IEEE Trans. Serv. Comput. 2016, 9, 796–805. [Google Scholar] [CrossRef]
- Shu, Y.; Yu, M.; Yang, O.; Liu, J.; Feng, H. Wireless traffic modelling and prediction using seasonal ARIMA models. IEICE Trans. Commun. 2005, 88, 3992–3999. [Google Scholar] [CrossRef]
- Li, R.; Zhao, Z.; Zhou, X.; Palicot, J.; Zhang, H. The prediction analysis of cellular radio access network traffic: From entropy theory to networking practice. IEEE Commun. Mag. 2014, 52, 234–240. [Google Scholar] [CrossRef]
- Tikunov, D.; Nishimura, T. Traffic prediction for mobile networks using Holt-Winter’s exponential smoothing. In Proceedings of the IEEE International Conference on Software, Telecommunications and Computer Networks, Split, Croatia, 27–29 September 2007. [Google Scholar]
- Ju, F.; Yang, J.; Liu, H. Analysis of self-similar traffic based on the on/off model. In Proceedings of the IEEE International Workshop on Chaos-Fractals Theories and Applications, Shenyang, China, 6–8 November 2009. [Google Scholar]
- Chen, X.; Jin, Y.; Qiang, S.; Hu, W.; Jiang, K. Analysing and modelling spatio-temporal dependence of cellular traffic at city scale. In Proceedings of the IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015. [Google Scholar]
- Sun, H.; Liu, H.X.; Xiao, H.; Ran, B. Short-term traffic forecasting using the local linear regression model. In Proceedings of the Annual Meeting of the Transportation Research Board, Washington, DC, USA, 21–23 March 2002. [Google Scholar]
- Zhang, Y.; Roughan, M.; Willinger, W.; Qiu, L. Spatio-temporal compressive sensing and internet traffic matrices. In Proceedings of the ACM SIGCOMM 2009 Conference on Data Communication, Barcelona, Spain, 16–21 August 2009. [Google Scholar]
- Li, R.; Zhao, Z.; Zhou, X.; Zhang, H. Energy savings scheme in radio access networks via compressive sensing-based traffic load prediction. Trans. Emerg. Telecommun. Technol. 2014, 25, 468–478. [Google Scholar] [CrossRef]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Filho, R.H.; Maia, J.E.B. Network traffic prediction using PCA and K-means. In Proceedings of the IEEE Network Operations and Management Symposium (NOMS), Osaka, Japan, 19–23 April 2010. [Google Scholar]
- Falvo, M.; Gastaldi, M.; Nardecchia, A.; Prudenzi, A. Kalman filter for short-term load forecasting: An hourly predictor of municipal load. In Proceedings of the IASTED International Conference on ASM, Palma de Mallorca, Spain, 29–31 August 2007. [Google Scholar]
- Xu, Y.; Yin, F.; Xu, W.; Lin, J.; Cui, S. Wireless traffic prediction with scalable Gaussian process: Framework, algorithms, and verification. IEEE J. Sel. Areas Commun. 2019, 37, 1291–1306. [Google Scholar] [CrossRef]
- Nie, L.; Jiang, D.; Yu, S.; Song, H. Network traffic prediction based on deep belief network in wireless mesh backbone networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017. [Google Scholar]
- Tian, Y.; Pan, L. Predicting short-term traffic flow by long short-term memory recurrent neural network. In Proceedings of the IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015. [Google Scholar]
- Cai, L.; Janowicz, K.; Mai, G.; Yan, B.; Zhu, R. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Trans. GIS 2020, 24, 736–755. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, Y.; Feng, Z.; Zhang, P.; Cui, S. Spatio-temporal wireless traffic prediction with recurrent neural network. IEEE Wirel. Commun. Lett. 2018, 7, 554–557. [Google Scholar] [CrossRef]
- Hua, Y.; Zhao, Z.; Liu, Z.; Chen, X.; Li, R.; Zhang, H. Traffic prediction based on random connectivity in deep learning with long short-term memory. In Proceedings of the IEEE Vehicular Technology Conference (VTC-Fall), Chicago, IL, USA, 27–30 August 2018. [Google Scholar]
- Wang, J.; Tang, J.; Xu, Z.; Wang, Y.; Xue, G.; Zhang, X.; Yang, D. Spatiotemporal modelling and prediction in cellular networks: A big data enabled deep learning approach. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef]
- Huang, D.Y.; Yang, B.; Wu, Z.H.; Kuang, J.Y.; Yan, Z.M. Spatiotemporal fully connected convolutional networks for city-wide cellular traffic prediction. Comput. Eng. Appl. 2021, 57, 168–175. [Google Scholar]
- Lin, J.; Chen, Y.; Zheng, H.; Ding, M.; Cheng, P.; Hanzo, L. A data-driven base station sleeping strategy based on traffic prediction. IEEE Trans. Netw. Sci. Eng. 2021, 11, 5627–5643. [Google Scholar] [CrossRef]
- Zeng, Q.; Sun, Q.; Chen, G.; Duan, H. Attention-based multi-component spatiotemporal cross-domain neural network model for wireless cellular network traffic prediction. EURASIP J. Adv. Signal Process. 2021, 2021, 46. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Wang, Z.; Zheng, H. A deep learning method based on an attention mechanism for wireless network traffic prediction. Ad Hoc Netw. 2020, 107, 102258. [Google Scholar] [CrossRef]
- Li, F.; Zhang, Z.; Chu, X.; Zhang, J.; Qiu, S.; Zhang, J. A Meta-Learning Based Framework for Cell-Level Mobile Network Traffic Prediction. IEEE Trans. Wirel. Commun. 2023, 22, 4264–4280. [Google Scholar] [CrossRef]
- Li, Y.; Bi, Y.; Wang, J.; Li, Z.; Zhang, H.; Zhang, P. Unmanned aerial vehicle assisted communication: Applications, challenges, and future outlook. Clust. Comput. 2024, 27, 13187–13202. [Google Scholar] [CrossRef]
- Das, S.; Kumar, N.; Dixit, D. Unmanned Aerial Vehicle Assisted Wireless Communications: Enabling Connectivity and Applications. In Next-Generation Wireless Systems: Fundamentals and Applications; Springer Nature: Singapore, 2025; pp. 265–307. [Google Scholar]
- Yang, B.; Xiong, X.; Liu, H.; Jia, Y.; Gao, Y.; Tolba, A.; Zhang, X. Unmanned aerial vehicle assisted post-disaster communication coverage optimisation based on internet of things big data analysis. Sensors 2023, 23, 6795. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, P.; Boukerche, A. Unmanned aerial vehicle-assisted energy-efficient data collection scheme for sustainable wireless sensor networks. Comput. Netw. 2019, 165, 106927. [Google Scholar] [CrossRef]
- Tang, J.; Huang, J.; Wang, B.; Song, Y.; Yu, G. Resource optimisation for multi-UAV-assisted communication systems based on user scheduling. J. Beihang Univ. 2025, 51, 1143–1151. [Google Scholar]
- Wang, Z.; Hu, Y.; Fan, Z.; Wan, X.; Xu, Y. Max-min rate optimisation algorithm for UAV-assisted non-orthogonal multiple access backscatter communication systems. Trans. Chin. Inst. Electron. Inf. Technol. 2023, 45, 2358–2365. [Google Scholar]
- Pan, Y.; Hu, H.; Jin, H.; Lei, Y.; Feng, H.; Jiang, L.; Zhang, M. Optimisation of Trajectory and Resource Allocation for UAV-Assisted Communications in Unlicensed Bands. Chin. J. Electron. Inf. Technol. 2024, 46, 4287–4294. [Google Scholar]
- Ha, D.; Jeong, S.; Kang, J.; Kang, J. Secrecy Energy Efficiency Maximisation for Secure Unmanned Aerial Vehicle-Assisted Simultaneous Wireless Information and Power Transfer Systems. Drones 2023, 7, 672. [Google Scholar] [CrossRef]

| Distribution Type | Feature Description | GMM-ML (RMSE) | LSTM (RMSE) | Performance Retention (%) |
|---|---|---|---|---|
| Single-peak Gaussian | Stationary periodic | 0.062 | 0.089 | 100.0 |
| Bimodal hybrid | Weekday/Weekend pattern | 0.071 | 0.102 | 87.3 |
| Heavy-tailed distribution | Sudden traffic events | 0.085 | 0.118 | 72.9 |
| Multimodal asymmetric | Complex urban pattern | 0.078 | 0.125 | 79.5 |
| Time-varying distribution | Distribution drift | 0.092 | 0.142 | 67.4 |
| Channel Condition | Number of Convergence Slots | Objective Function Variance | Lyapunov Function Terminal Value | Stability Metric |
|---|---|---|---|---|
| Steady-state channel | 15.2 | 0.32 | 0.08 | 0.95 |
| Slow-fading channel | 18.7 | 0.45 | 0.12 | 0.89 |
| Fast-fading channel | 25.3 | 0.78 | 0.21 | 0.76 |
| Burst interference | 32.8 | 1.25 | 0.35 | 0.63 |
| Category | Parameter | Value | Description |
|---|---|---|---|
| Scene Settings | Coverage area | Urban hotspot areas | |
| Number of ground-based stations (M) | 9 | Distributed uniformly in a grid | |
| Number of users (N) | 60 | Random initial distribution | |
| Number of drones (U) | 3 | Initial positions are random | |
| Simulation time (T) | 100 time slots | Each time slot ( | |
| Communication Model | UAV altitude () | 100 m | |
| UAV transmission power () | 20 dBm | ||
| Noise power spectral density | −174 dBm/Hz | ||
| System bandwidth (W) | 20 MHz | Assumed to be equally distributed among associated users | |
| Carrier frequency () | 2.4 GHz | ||
| Antenna gain () | 0 dBi | Omnidirectional antenna | |
| User QoS requirements () | [5, 20] Mbps | Uniform random allocation | |
| UAV service capacity (K) | 10 | A maximum of 10 users per drone | |
| Mobility Model | User mobility model | Random waypoint model | Speed: [0, 1.5] m/s (walking) |
| The maximum drone speed () | 30 m/s | ||
| Prediction Model | Prediction window () | 5 time slots | Forecasts for the next 5 min |
| Hotspot threshold () | 0.7 | Traffic normalized above 0.7 constitutes a hotspot | |
| Number of GMM components () | 5 | Automatic selection | |
| Algorithm Parameters | P-IALO discount factor () | 0.9 | |
| P-IALO reward weighting () | 0.3 | Determined via a grid search | |
| SCA trust domain initial radius () | 50 m | ||
| Internal iteration convergence threshold () | |||
| Maximum internal iterations () | 20 |
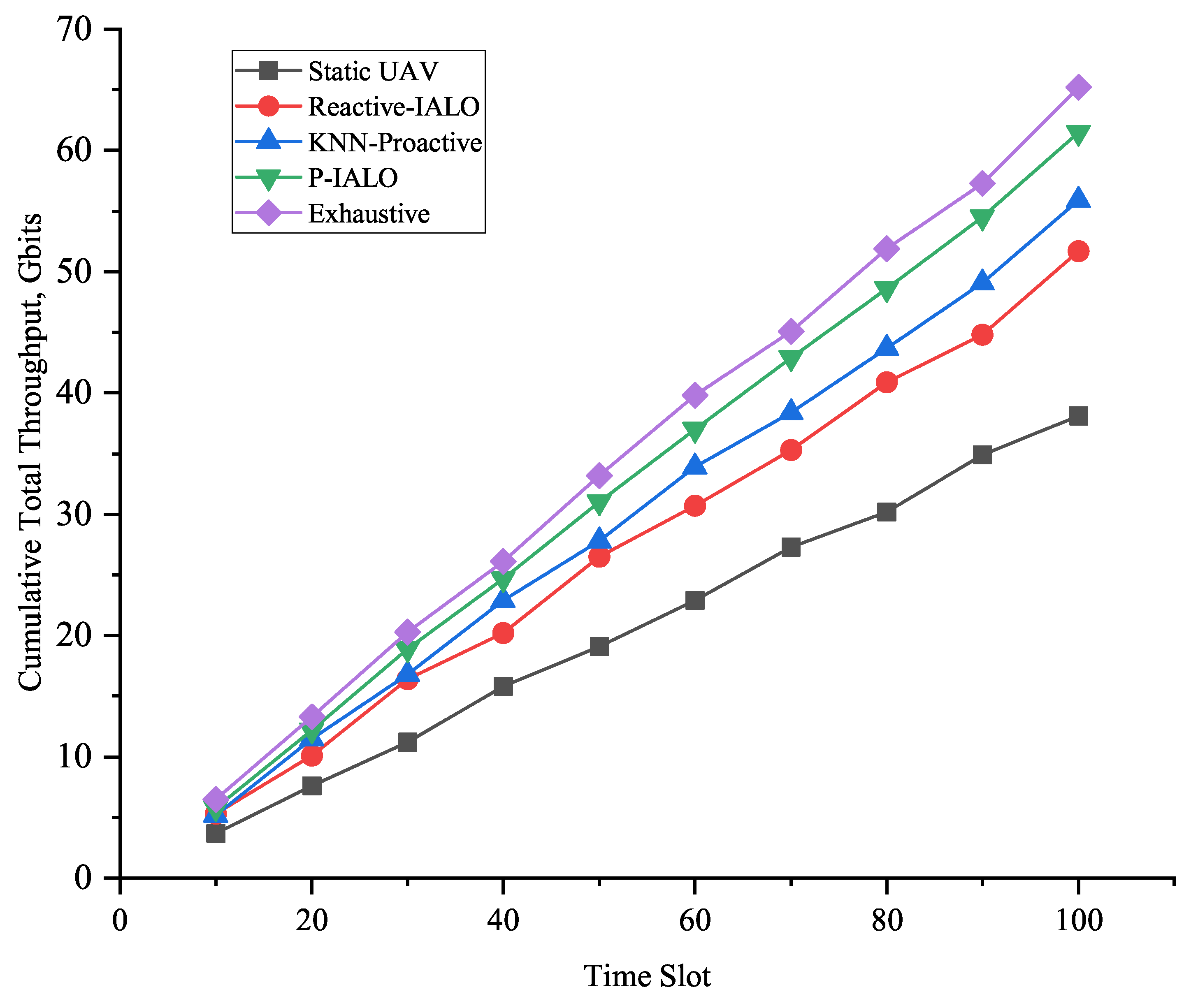
| Algorithm | Total Throughput (Gbits) | QoS Satisfaction (%) Mean | Average Interrupt Count |
|---|---|---|---|
| Mean ± Std. | ± Std. | Mean ± Std. | |
| Static UAV | 38.1 ± 2.5 | 65.2 ± 8.1 | 0.0 ± 0.0 |
| Reactive-IALO | 51.7 ± 4.8 | 82.7 ± 5.3 | 3.8 ± 1.2 |
| KNN-Proactive | 55.9 ± 3.9 | 86.5 ± 4.5 | 3.2 ± 0.9 |
| P-IALO | 61.5 ± 3.1 | 92.1 ± 3.2 | 2.5 ± 0.7 |
| Exhaustive Search | 65.2 ± 2.0 | 95.0 ± 2.5 | - |
| Training Data Proportion | GMM-ML Prediction RMSE | LSTM Prediction RMSE | GMM-ML Training Time (min) | LSTM Training Time (min) |
|---|---|---|---|---|
| 10% | 0.095 | 0.152 | 8.5 | 25.3 |
| 30% | 0.078 | 0.115 | 12.3 | 38.7 |
| 50% | 0.068 | 0.095 | 18.9 | 52.4 |
| 70% | 0.063 | 0.082 | 25.6 | 65.8 |
| 100% | 0.062 | 0.075 | 35.2 | 82.5 |
| Training Data Proportion | P-IALO (GMM-ML) Throughput | P-IALO (LSTM) Throughput | Performance Retention Rate |
|---|---|---|---|
| 10% | 56.3 | 50.2 | 89.6% |
| 30% | 59.8 | 55.7 | 95.2% |
| 50% | 61.5 | 58.9 | 97.9% |
| 70% | 62.3 | 60.8 | 99.2% |
| 100% | 62.8 | 62.1 | 100% |
| Prediction Model | RMSE (Normalized) | MAE (Normalized) | R2 |
|---|---|---|---|
| ARIMA | 0.125 | 0.098 | 0.763 |
| LSTM | 0.089 | 0.072 | 0.845 |
| GRU | 0.085 | 0.069 | 0.862 |
| KNN | 0.078 | 0.063 | 0.885 |
| GMM-ML | 0.062 ± 0.007 | 0.051 ± 0.006 | 0.918 |
| Prediction Model | Total Throughput (Gbits) | QoS Satisfaction (%) | Number of Service Interruptions |
|---|---|---|---|
| ARIMA | 55.3 | 85.2 | 3.5 |
| LSTM | 58.7 | 88.9 | 3.0 |
| GRU | 59.2 | 89.3 | 2.9 |
| KNN | 60.1 | 90.5 | 2.7 |
| GMM-ML | 62.8 | 92.1 | 2.5 |
| Prediction Span () | Prediction Accuracy (%) | System Utility Value | Average Drone Travel Distance (m) | |
|---|---|---|---|---|
| 1 | 94.5 ± 2.1 | 58.3 ± 3.3 | 125.6 ± 15.2 | 0.1 |
| 3 | 92.8 ± 2.5 | 60.7 ± 3.2 | 142.3 ± 16.8 | 0.2 |
| 5 | 90.1 ± 2.8 | 62.8 ± 3.1 | 156.7 ± 17.5 | 0.3 |
| 7 | 86.3 ± 3.2 | 61.2 ± 3.4 | 168.9 ± 18.3 | 0.4 |
| 10 | 81.7 ± 3.8 | 58.9 ± 3.6 | 185.4 ± 19.7 | 0.5 |
| Prediction Error (RMSE) | Throughput Loss (%) | QoS Satisfaction Decline (%) | Spectrum Efficiency Loss (bps/Hz) | Service Readiness Loss (%) |
|---|---|---|---|---|
| 0.05 | 3.2 | 2.1 | 0.15 | 5.3 |
| 0.08 | 6.5 | 4.7 | 0.31 | 11.8 |
| 0.10 | 8.7 | 6.5 | 0.42 | 14.2 |
| 0.15 | 16.3 | 12.8 | 0.78 | 26.8 |
| 0.20 | 25.9 | 20.5 | 1.25 | 41.3 |
| 0.25 | 37.4 | 30.2 | 1.81 | 58.7 |
| Number of UAVs (U) | Total Throughput (Gbps) | QoS Satisfaction (%) | Average Computation Time (seconds) | Convergence Iteration Count |
|---|---|---|---|---|
| 1 | 45.2 | 78.3 | 8.5 | 12.3 |
| 2 | 58.7 | 87.6 | 12.3 | 14.2 |
| 3 | 61.5 | 92.1 | 15.7 | 15.8 |
| 4 | 65.3 | 93.8 | 21.4 | 17.5 |
| 5 | 67.2 | 94.5 | 28.9 | 19.2 |
| Number of UAVs | Theoretical Overhead (Kbps) | Measured Overhead (Kbps) | Percentage of the Total Cost (%) |
|---|---|---|---|
| 2 | 8.2 | 0.47 | |
| 3 | 24.6 | 1.42 | |
| 4 | 49.2 | 2.84 | |
| 5 | 81.9 | 4.71 |
| Flight Condition | Standard Deviation of the Altitude | Vibration Intensity | Rate Loss (%) | QoS Compliance Rate Variation (%) |
|---|---|---|---|---|
| Steady flight | ||||
| Moderate turbulence | ||||
| Strong turbulence |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tai, X.; Liu, X.; Li, Y.; Zhu, J. Joint Optimization for UAV-Assisted Communications with Spatiotemporal Traffic Forecasting. Electronics 2025, 14, 4681. https://doi.org/10.3390/electronics14234681
Tai X, Liu X, Li Y, Zhu J. Joint Optimization for UAV-Assisted Communications with Spatiotemporal Traffic Forecasting. Electronics. 2025; 14(23):4681. https://doi.org/10.3390/electronics14234681
Chicago/Turabian StyleTai, Xing, Xiangyu Liu, Yuxuan Li, and Jiao Zhu. 2025. "Joint Optimization for UAV-Assisted Communications with Spatiotemporal Traffic Forecasting" Electronics 14, no. 23: 4681. https://doi.org/10.3390/electronics14234681
APA StyleTai, X., Liu, X., Li, Y., & Zhu, J. (2025). Joint Optimization for UAV-Assisted Communications with Spatiotemporal Traffic Forecasting. Electronics, 14(23), 4681. https://doi.org/10.3390/electronics14234681





