Support-Vector-Regression-Based Kinematics Solution and Finite-Time Tracking Control Framework for Uncertain Gough–Stewart Platform
Abstract
1. Introduction
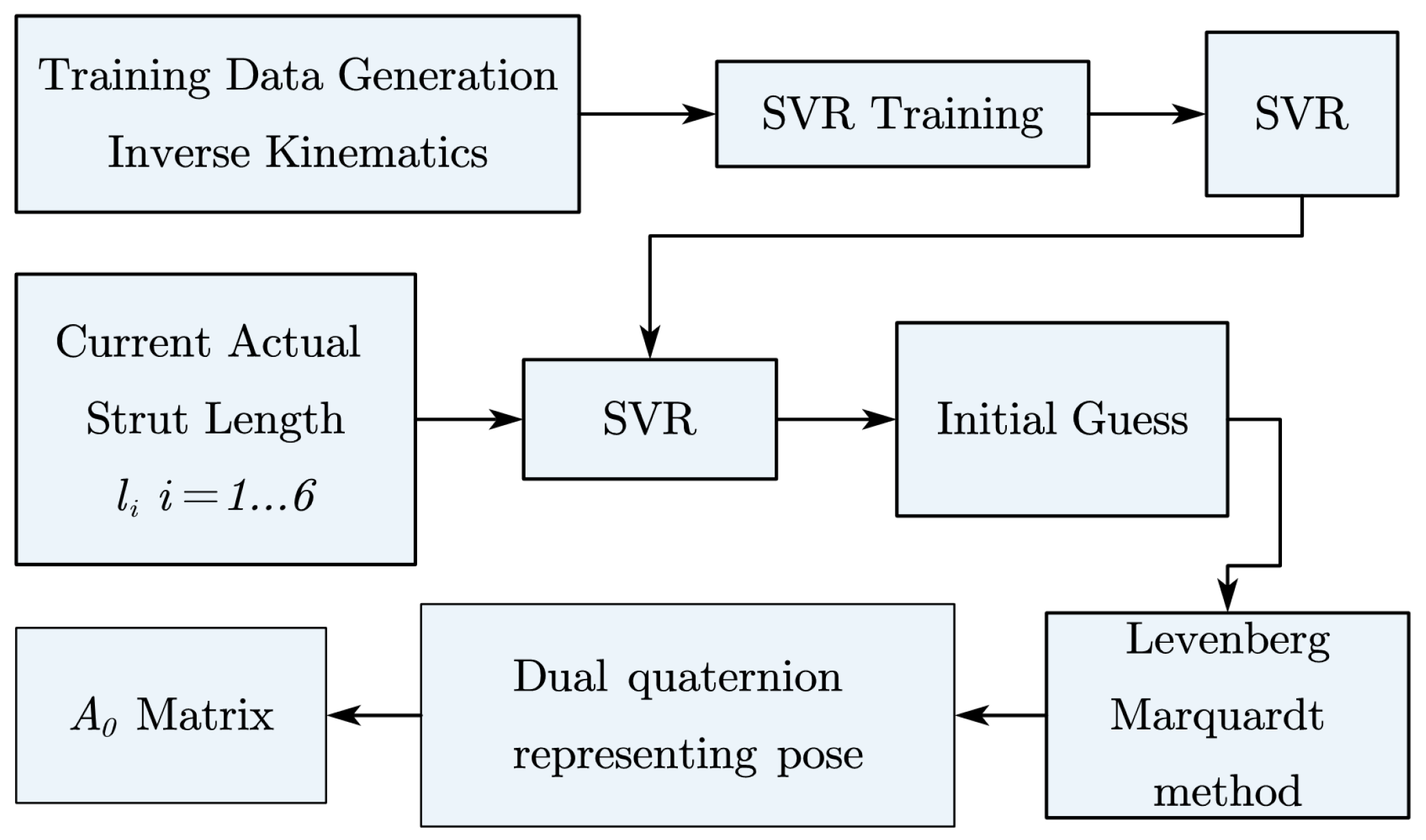
- Novel Kinematics Solution Based on SVR: This paper proposes an innovative kinematics solution for Generalized Spatial Mechanisms (GSP) by integrating Support Vector Regression (SVR) with the Levenberg–Marquardt method. Unlike traditional iterative algorithms, this hybrid approach ensures computational accuracy through iteration while leveraging SVR for efficient inference of the initial iterative values. This not only prevents the iteration from getting trapped in local optima but also improves overall computational efficiency. The proposed method accelerates convergence and reduces sensitivity to initial conditions, making it a highly effective alternative for solving complex spatial mechanism problems.
- Finite-Time Convergent Precise Trajectory Tracking: A significant advancement of this study is the introduction of a finite-time convergent sliding mode control (SMC) strategy, specifically designed for the precise and rapid trajectory tracking of Generalized Spatial Mechanisms (GSP). Compared to traditional SMC methods, the proposed approach guarantees finite-time convergence, ensuring deterministic control performance within a predefined time horizon. Furthermore, in comparison with the widely used PID control method, this approach exhibits smaller tracking errors and faster convergence speed, making it particularly suitable for scenarios that demand high responsiveness and control precision.
- Enhanced Robustness Against Uncertainties and Disturbances: The proposed control framework explicitly considers model uncertainties and external disturbances, thereby significantly enhancing system robustness. Unlike conventional control schemes, which often suffer from degraded performance under varying conditions, our method ensures sustained precision and stability. Extensive simulations validate the effectiveness of our approach, achieving superior tracking performance and robustness even when subject to unknown disturbances and model mismatches.
2. Problem Statement
3. Control Development
3.1. Kinematic Solution of the GSP
3.1.1. Inverse Kinematics of the GSP
3.1.2. Forward Kinematics of the GSP
3.2. Controller Design
- 1.
- If there exists a function , a function , a real number , and , such that for an open neighborhood containing the origin, the following conditions hold:the solution of system is finite-time stable.
- 2.
3.3. Stability Proof
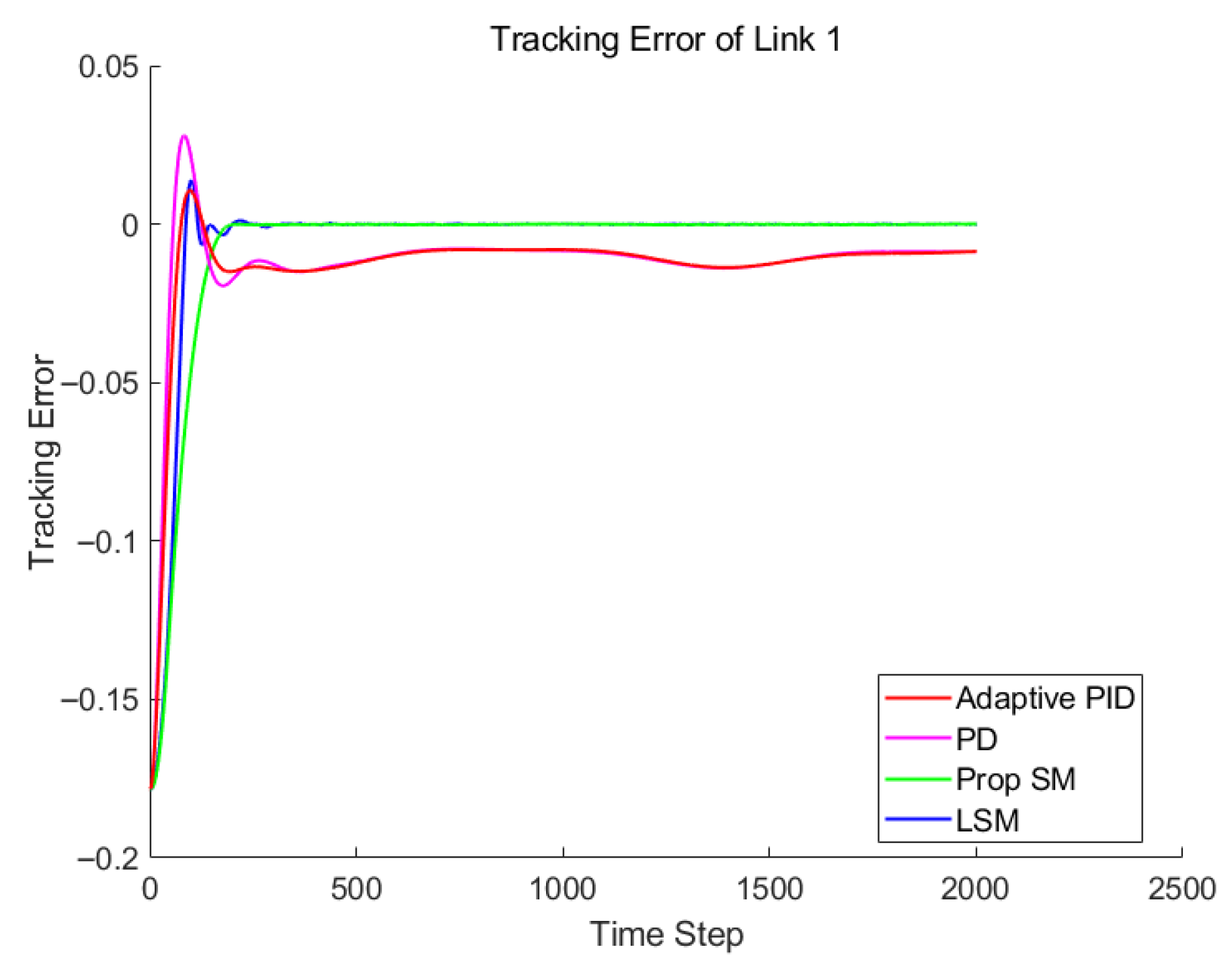
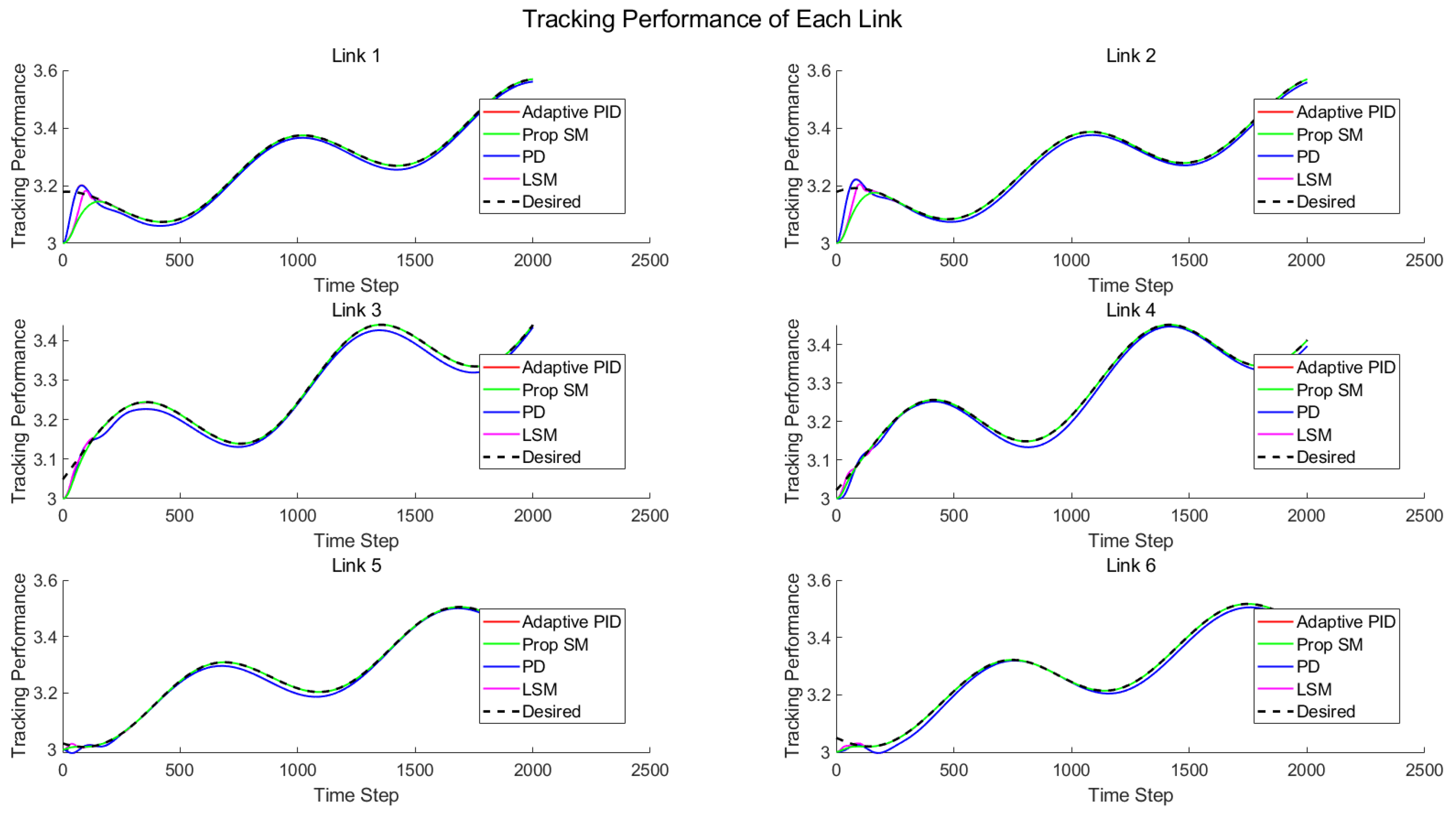
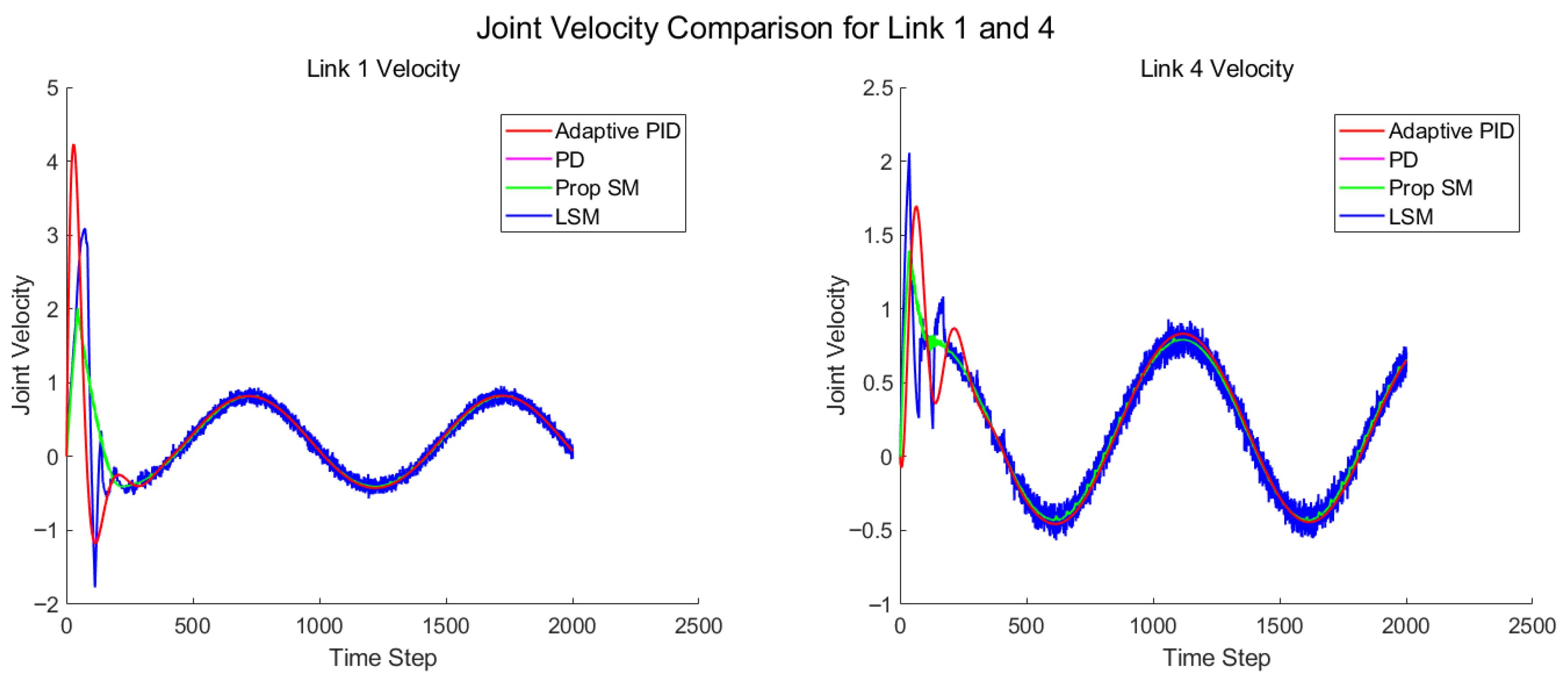
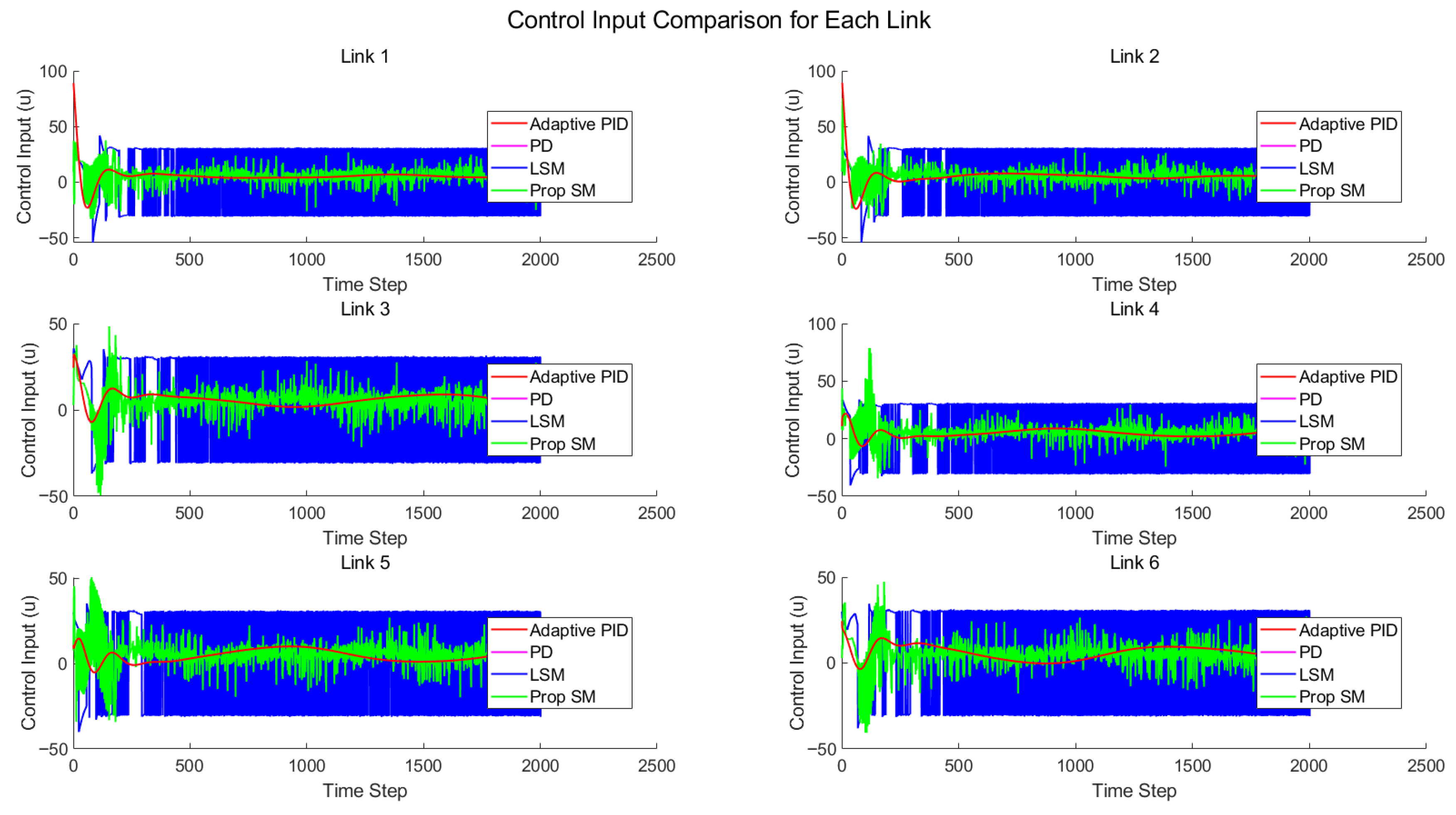
4. Simulation Results
- Set the desired motion trajectory of the moving platform and obtain the corresponding joint space trajectory using inverse kinematics.
- Measure the current lengths and velocities of the legs and use forward kinematics to solve the dynamic model of the moving platform at this time step.
- Calculate the control forces for the six legs by combining the position and velocity errors with the A matrix in the dynamic model.
- Substitute the control forces into the dynamic equations and, considering external disturbances, solve for the strut lengths at the next time step using a differential approach. This process then repeats in a new cycle.
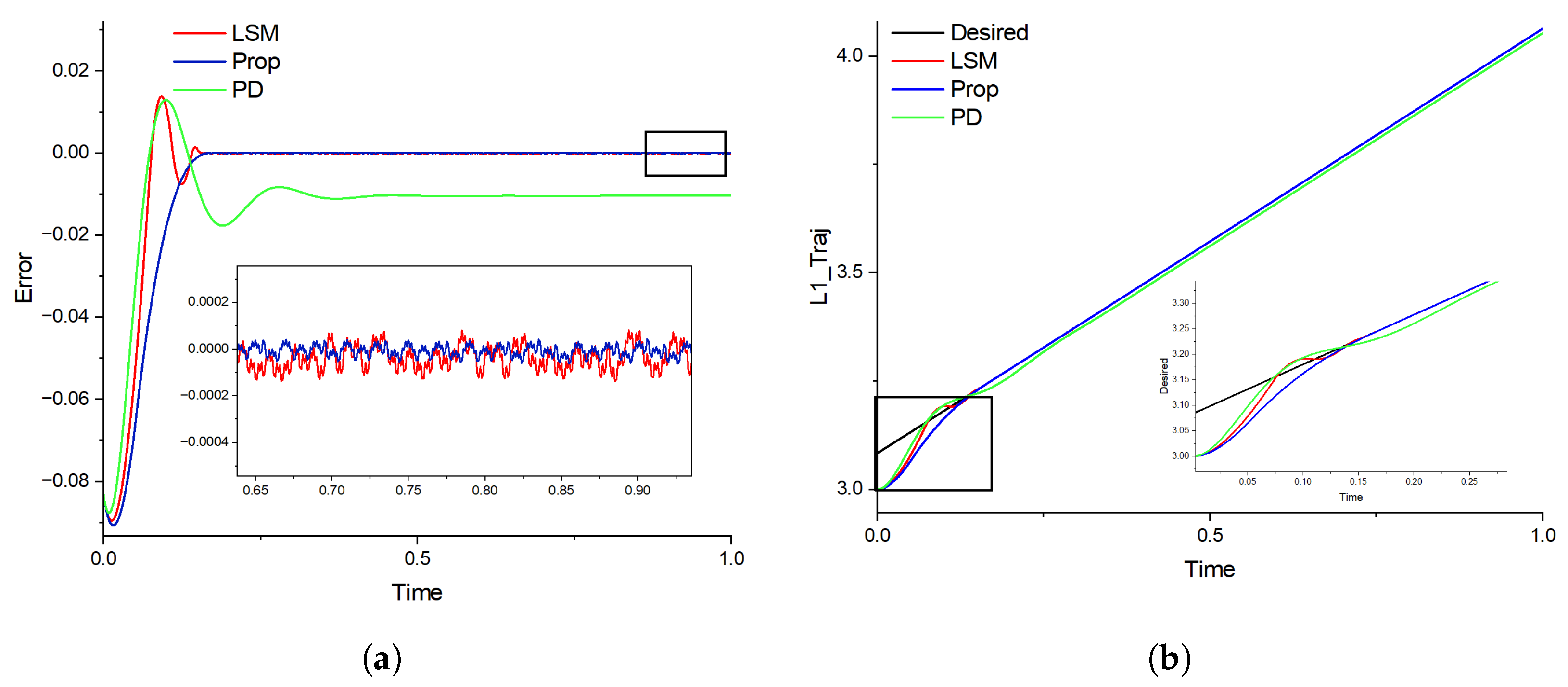
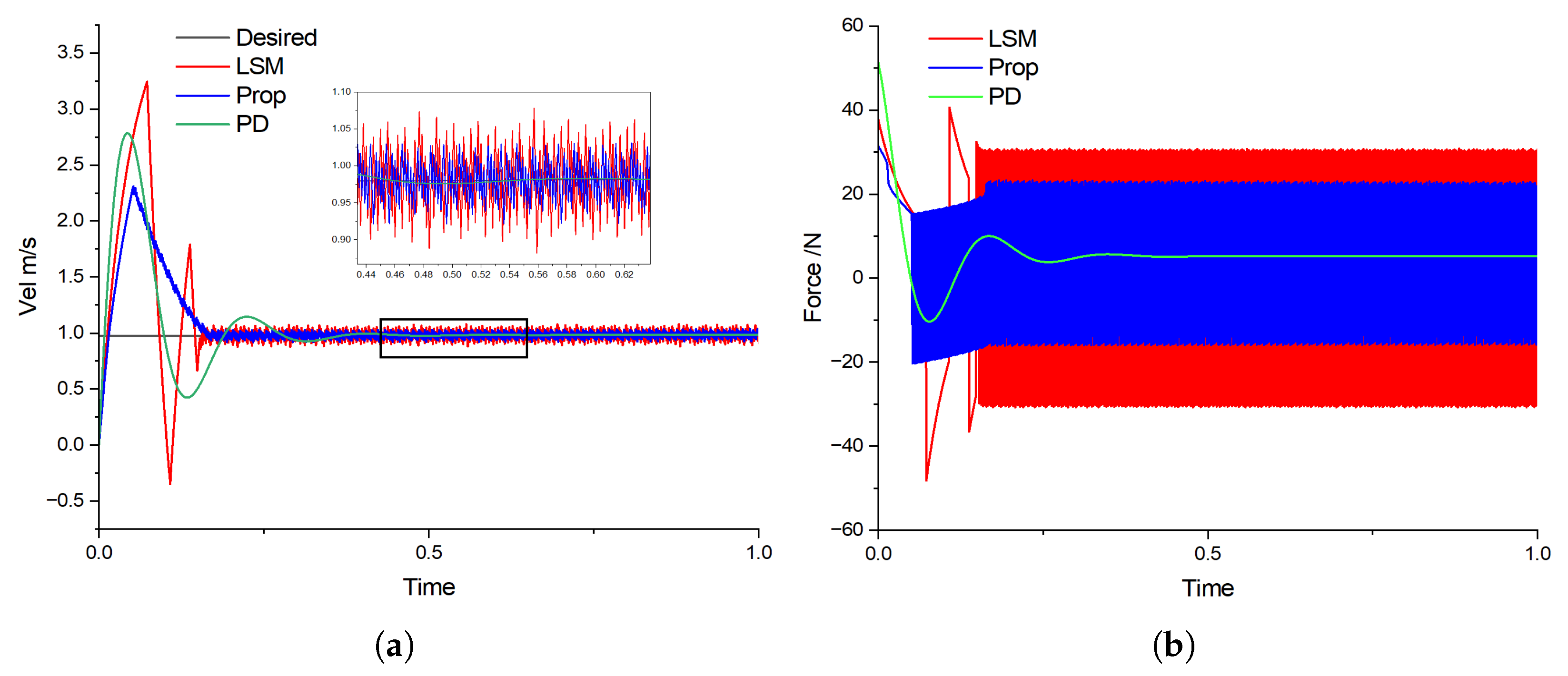
4.1. Case1: Vertical Lifting
4.2. Case2: Complex Trajectory Tracking
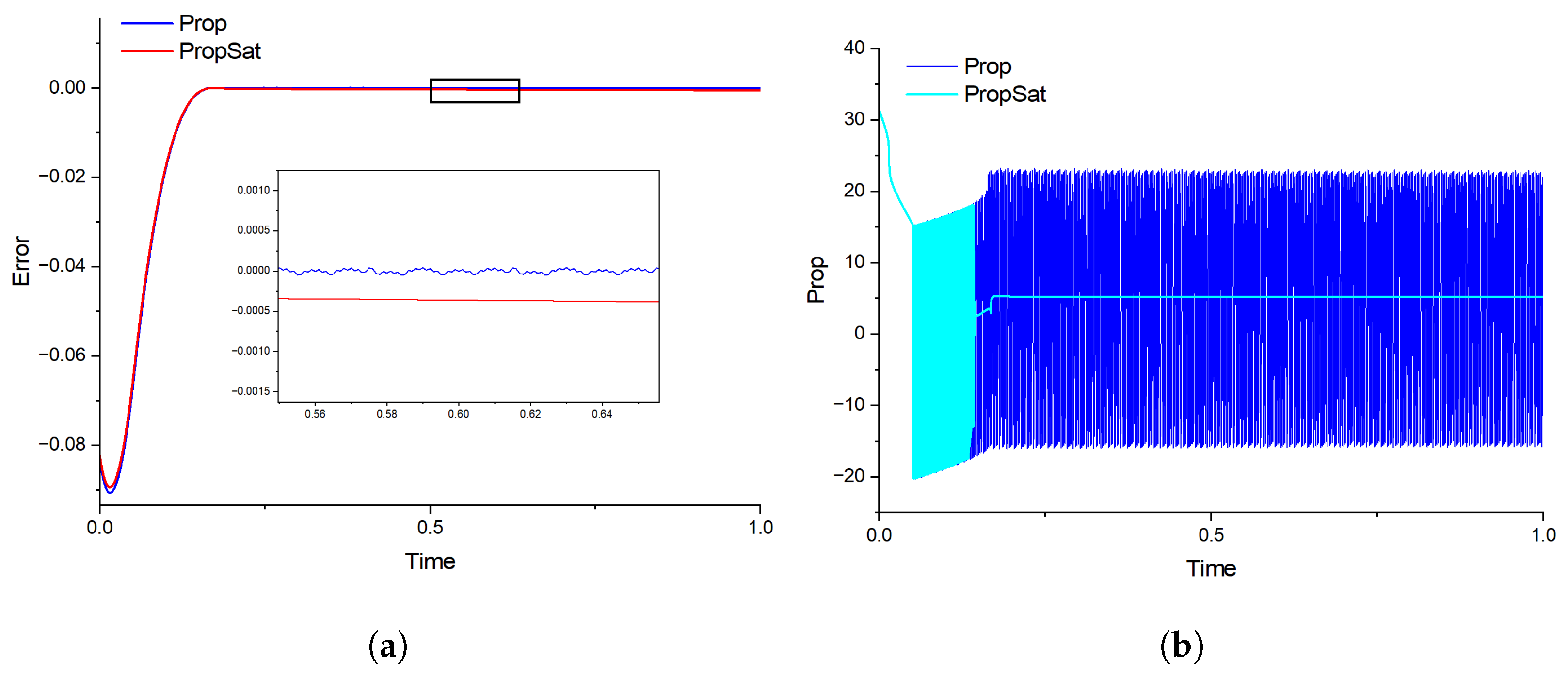
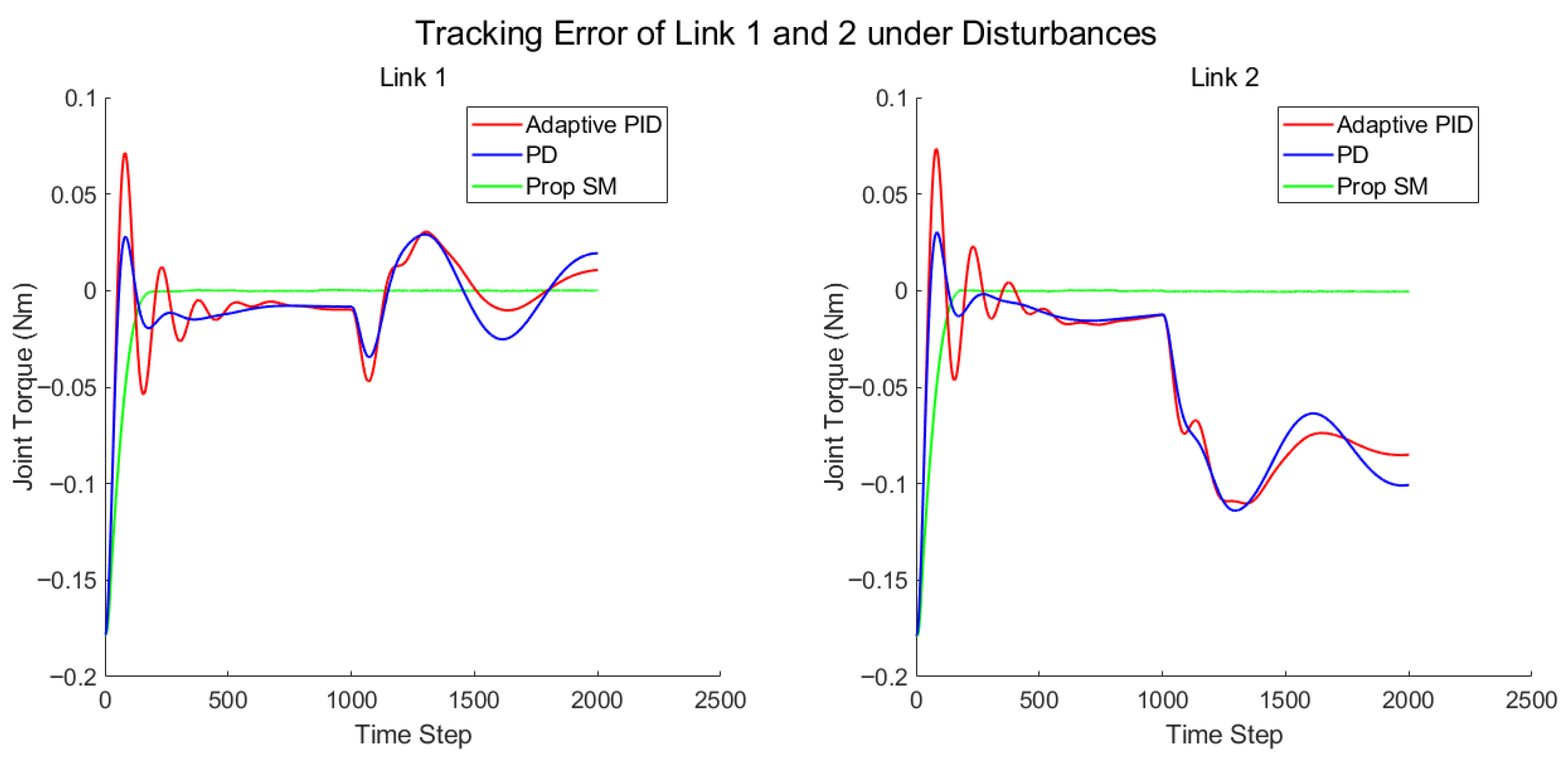
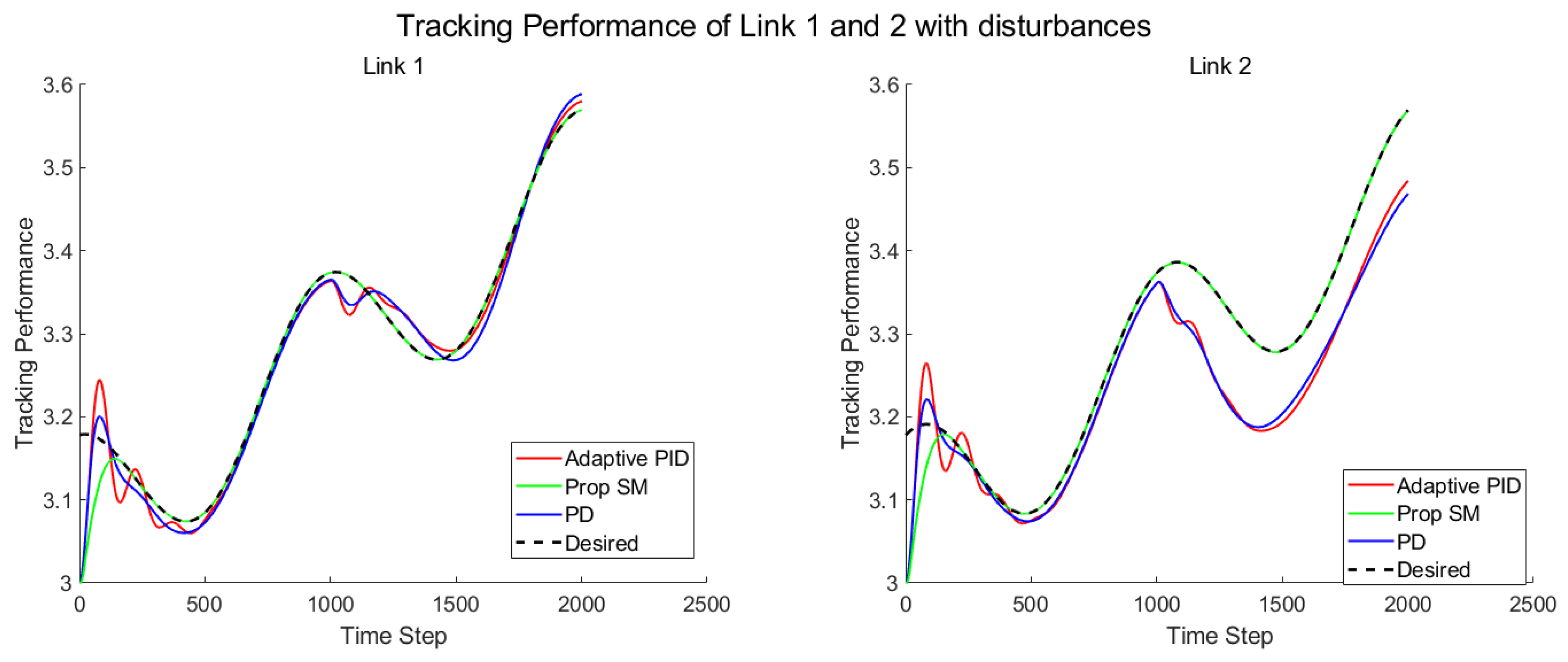
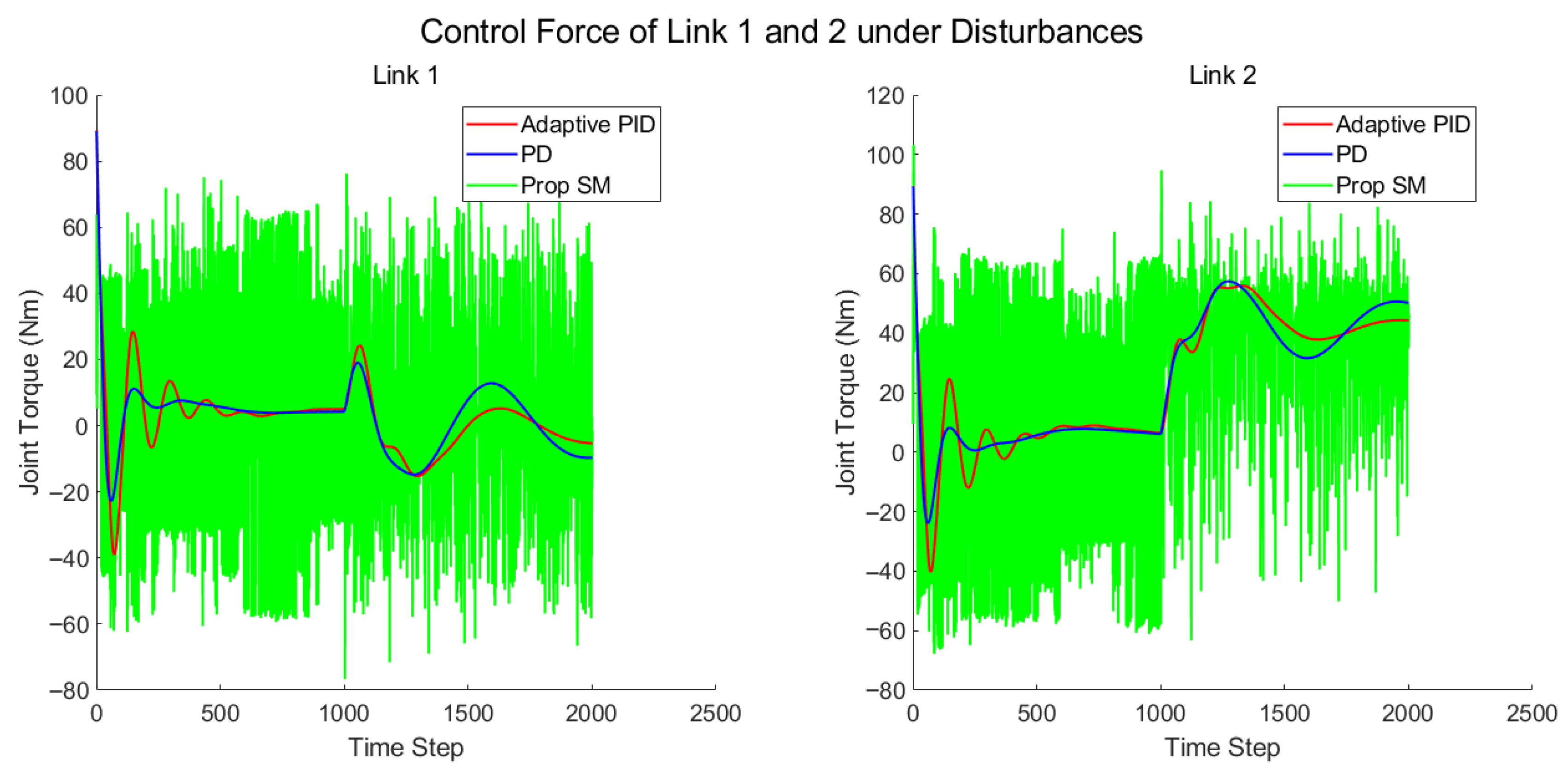
4.3. Case3: Tracking with Disturbances
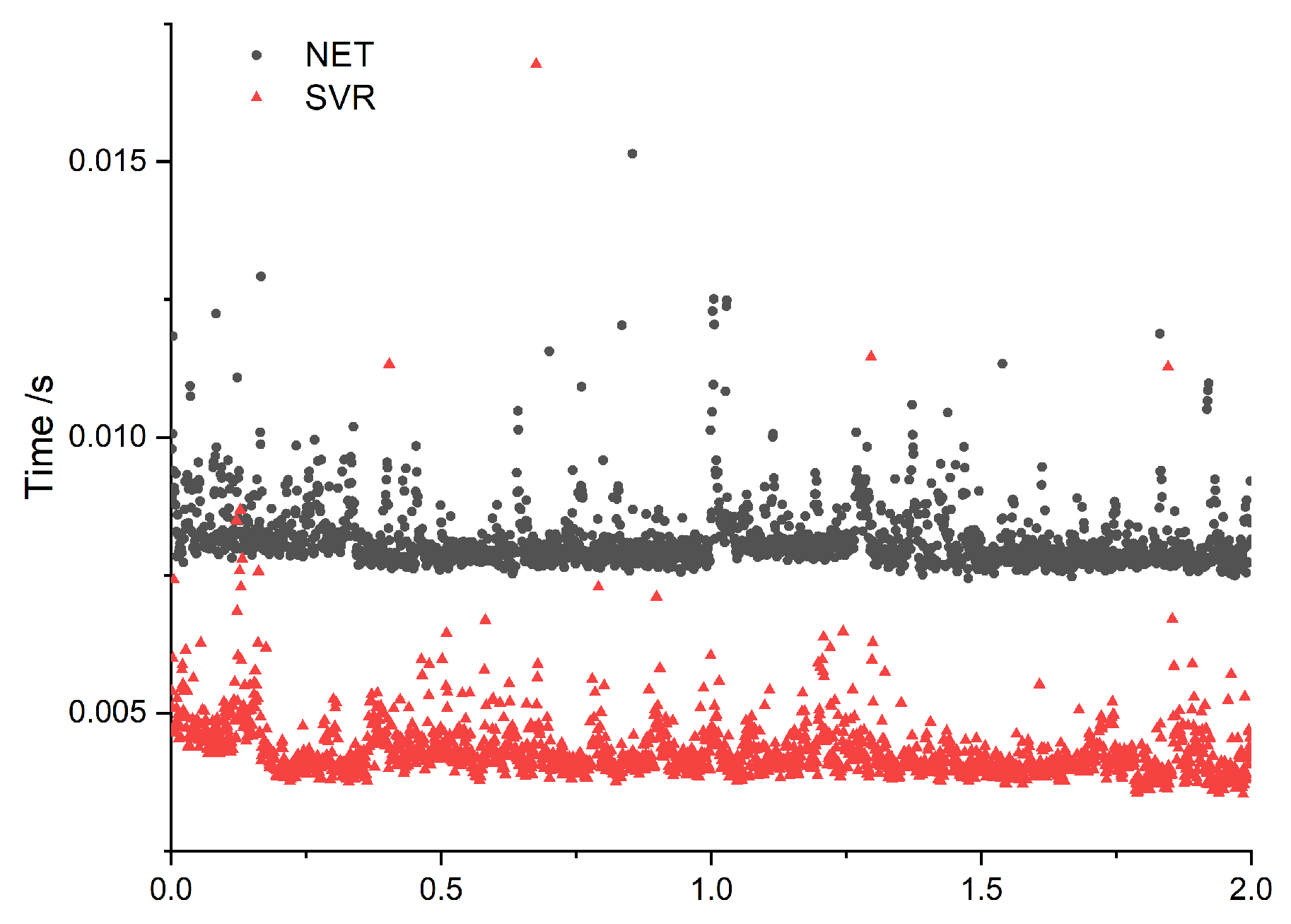
4.4. Case4: Efficient Forward Kinematics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duong, T.T.C.; Nguyen, C.C.; Tran, T.D. Experimental Investigation of Motion Control of a Closed-Kinematic Chain Robot Manipulator Using Synchronization Sliding Mode Method with Time Delay Estimation. Appl. Sci. 2025, 15, 5206. [Google Scholar] [CrossRef]
- Vu, M.T.; Alattas, K.A.; Bouteraa, Y.; Rahmani, R.; Fekih, A.; Mobayen, S.; Assawinchaichote, W. Optimized Fuzzy Enhanced Robust Control Design for a Stewart Parallel Robot. Mathematics 2022, 10, 1917. [Google Scholar] [CrossRef]
- Xie, B.; Dai, S. Robust Terminal Sliding Mode Control on SE(3) for Gough–Stewart Flight Simulator Motion Platform with Payload Uncertainty. Electronics 2022, 11, 814. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, C.C.; Nguyen, T.M.; Duong, T.T.C.; Ngo, H.T.T.; Sun, L. Decentralized Adaptive Control of Closed-Kinematic Chain Mechanism Manipulators. Machines 2025, 13, 331. [Google Scholar] [CrossRef]
- Jing, X.; Li, C. Dynamic Modeling and Solution of 6-DOF Parallel Mechanism. IEEE Access 2022, 10, 33695–33703. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, F.; Liu, Y.; Liu, H.; Huang, T.; Qiu, J. Reduced-Order Observer-Based Preassigned Finite-Time Control of Nonlinear Systems and Its Applications. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4205–4215. [Google Scholar] [CrossRef]
- Huang, X.; Liao, Q.; Wei, S.; Qiang, X.; Huang, S. Forward Kinematics of the 6-6 Stewart Platform with Planar Base and Platform Using Algebraic Elimination. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 2655–2659. [Google Scholar] [CrossRef]
- Sheng, L.; Wan-long, L.; Yan-chun, D.; Liang, F. Forward kinematics of the Stewart platform using hybrid immune genetic algorithm. In Proceedings of the 2006 International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 2330–2335. [Google Scholar] [CrossRef]
- Tarokh, M. Real Time Forward Kinematics Solutions for General Stewart Platforms. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 901–906. [Google Scholar] [CrossRef]
- Yang, X.; Wu, H.; Chen, B.; Li, Y.; Jiang, S. A dual quaternion approach to efficient determination of the maximal singularity-free joint space and workspace of six-DOF parallel robots. Mech. Mach. Theory 2018, 129, 279–292. [Google Scholar] [CrossRef]
- Chen, S.H.; Fu, L.C. The Forward Kinematics of the 6-6 Stewart Platform Using Extra Sensors. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006; Volume 6, pp. 4671–4676. [Google Scholar] [CrossRef]
- Sang, L.H.; Han, M.C. The estimation for forward kinematic solution of Stewart platform using the neural network. In Proceedings of the 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human and Environment Friendly Robots with High Intelligence and Emotional Quotients (Cat. No.99CH36289), Kyongju, Republic of Korea, 17–21 October 1999; Volume 1, pp. 501–506. [Google Scholar] [CrossRef]
- Chauhan, D.K.S.; Vundavilli, P.R. Forward kinematics of the Stewart parallel manipulator using machine learning. Int. J. Comput. Methods 2022, 19, 2142009. [Google Scholar] [CrossRef]
- Huang, T.; Wang, J.; Pan, H. Adaptive bioinspired preview suspension control with constrained velocity planning for autonomous vehicles. IEEE Trans. Intell. Veh. 2023, 8, 3925–3935. [Google Scholar] [CrossRef]
- Sosa-Méndez, D.; Lugo-González, E.; Arias-Montiel, M.; Garcia-Garcia, R.A. ADAMS-MATLAB co-simulation for kinematics, dynamics, and control of the Stewart–Gough platform. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417719824. [Google Scholar] [CrossRef]
- Huang, C.I.; Wang, R.S. Hybrid control based on type-2 fuzzy-iterative learning control strategies with stewart platform for repetitive trajectories. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Zhou, Y.; She, J.; Wang, F.; Iwasaki, M. Disturbance Rejection for Stewart Platform Based on Integration of Equivalent-Input- Disturbance and Sliding-Mode Control Methods. IEEE/ASME Trans. Mechatronics 2023, 28, 2364–2374. [Google Scholar] [CrossRef]
- Dai, X.; Song, S.; Xu, W.; Huang, Z.; Gong, D. Modal space neural network compensation control for Gough-Stewart robot with uncertain load. Neurocomputing 2021, 449, 245–257. [Google Scholar] [CrossRef]
- Lafmejani, A.S.; Masouleh, M.T.; Kalhor, A. Trajectory tracking control of a pneumatically actuated 6-DOF Gough–Stewart parallel robot using Backstepping-Sliding Mode controller and geometry-based quasi forward kinematic method. Robot. Comput.-Integr. Manuf. 2018, 54, 96–114. [Google Scholar] [CrossRef]
- Kalani, H.; Rezaei, A.; Akbarzadeh, A. Improved general solution for the dynamic modeling of Gough–Stewart platform based on principle of virtual work. Nonlinear Dyn. 2016, 83, 2393–2418. [Google Scholar] [CrossRef]
- Gallardo, J.; Rico, J.; Frisoli, A.; Checcacci, D.; Bergamasco, M. Dynamics of parallel manipulators by means of screw theory. Mech. Mach. Theory 2003, 38, 1113–1131. [Google Scholar] [CrossRef]
- Liu, M.J.; Li, C.X.; Li, C.N. Dynamics analysis of the Gough-Stewart platform manipulator. IEEE Trans. Robot. Autom. 2000, 16, 94–98. [Google Scholar] [CrossRef]
- Khalil, W.; Guegan, S. Inverse and direct dynamic modeling of Gough-Stewart robots. IEEE Trans. Robot. 2004, 20, 754–761. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Jing, Y.; Chen, X.; Qiu, J. Direct adaptive preassigned finite-time control with time-delay and quantized input using neural network. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1222–1231. [Google Scholar] [CrossRef]
- Chen, X.; Hu, S.; Xie, X.; Qiu, J. Consensus-Based Distributed Secondary Control of Microgrids: A Pre-Assigned Time Sliding Mode Approach. IEEE/CAA J. Autom. Sin. 2024, 11, 2525–2527. [Google Scholar] [CrossRef]
- Chen, X.; Huang, T.; Cao, J.; Park, J.H.; Qiu, J. Finite-time multi-switching sliding mode synchronisation for multiple uncertain complex chaotic systems with network transmission mode. IET Control. Theory Appl. 2019, 13, 1246–1257. [Google Scholar] [CrossRef]
- Gu, Y.; Shen, M.; Park, J.H.; Wang, Q.G.; Zhu, Z.H. Dynamic Guaranteed Cost Event-Triggered-Based Anti-Disturbance Control of T-S Fuzzy Wind-Turbine Systems Subject to External Disturbances. IEEE Trans. Fuzzy Syst. 2024, 32, 7063–7072. [Google Scholar] [CrossRef]
- Tian, Y.; Shi, Y.; Shao, X.; Hu, Q.; Yang, H.; Zhu, Z.H. Spacecraft Proximity Operations Under Motion and Input Constraints: A Learning-Based Robust Optimal Control Approach. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 7838–7852. [Google Scholar] [CrossRef]
- Zhou, W.; Cheng, H.; Chen, Z.; Hua, M. Adaptive Sliding Mode Fault-Tolerant Tracking Control for Underactuated Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2025, 13, 712. [Google Scholar] [CrossRef]
- Ahn, H.; Kim, S.; Park, J.; Chung, Y.; Hu, M.; You, K. Adaptive Quick Sliding Mode Reaching Law and Disturbance Observer for Robust PMSM Control Systems. Actuators 2024, 13, 136. [Google Scholar] [CrossRef]
- Huang, T.; Pan, H.; Sun, W.; Gao, H. Sine resistance network-based motion planning approach for autonomous electric vehicles in dynamic environments. IEEE Trans. Transp. Electrif. 2022, 8, 2862–2873. [Google Scholar] [CrossRef]
- Keshavan, J.; Belgaonkar, S.; Murali, S. Adaptive Control of a Constrained First Order Sliding Mode for Visual Formation Convergence Applications. IEEE Access 2023, 11, 112263–112275. [Google Scholar] [CrossRef]
- Huang, T.; Wang, J.; Pan, H.; Sun, W. Finite-time fault-tolerant integrated motion control for autonomous vehicles with prescribed performance. IEEE Trans. Transp. Electrif. 2022, 9, 4255–4265. [Google Scholar] [CrossRef]
- Kamal, S.; Chalanga, A.; Bandyopadhyay, B. Multivariable continuous integral sliding mode control. In Proceedings of the 2015 International Workshop on Recent Advances in Sliding Modes (RASM), Istanbul, Turkey, 9–11 April 2015; IEEE: Piscatway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Amirkhani, S.; Mobayen, S.; Iliaee, N.; Boubaker, O.; Hosseinnia, S.H. Fast terminal sliding mode tracking control of nonlinear uncertain mass–spring system with experimental verifications. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419828176. [Google Scholar] [CrossRef]
- Huang, T.; Wang, J.; Pan, H. Approximation-Free Prespecified Time Bionic Reliable Control for Vehicle Suspension. IEEE Trans. Autom. Sci. Eng. 2024, 21, 5333–5343. [Google Scholar] [CrossRef]
- Zhai, J.; Xu, G. A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 391–395. [Google Scholar] [CrossRef]



| Position vectors of U-joints and S-joints | |
| = [0.0868, 0.4924, 0]T | = [0.7818, 0.6235, 0]T |
| = [−0.0868, 0.4924, 0]T | = [−0.7818, 0.6235, 0]T |
| = [−0.4698, −0.1710, 0]T | = [−0.9309, 0.3654, 0]T |
| = [−0.3830, −0.3214, 0]T | = [−0.1490, −0.9888, 0]T |
| = [0.3830, −0.3214, 0]T | = [0.1490, −0.9888, 0]T |
| = [0.4698, −0.1710, 0]T | = [0.9309, 0.3654, 0]T |
| Center of mass of the upper and lower sections of each link | |
| c1 = 0.5 | c2 = 0.5 |
| Mass of the moving platform and each link section | |
| m = 1.5 kg | m1 = 0.1 kg, m2 = 0.1 kg |
| Inertia matrices | |
| Method | Link 1 | Link 2 | Link 3 | Link 4 | Link 5 | Link 6 |
|---|---|---|---|---|---|---|
| Average Tracking Error | ||||||
| APID | 0.0105 | 0.0100 | 0.0112 | 0.0099 | 0.0096 | 0.0114 |
| PD | 0.0105 | 0.0098 | 0.0122 | 0.0092 | 0.0086 | 0.0125 |
| Prop SM | 9.89 × 10−4 | 9.33 × 10−4 | 1.06 × 10−3 | 8.84 × 10−4 | 1.07 × 10−3 | 7.87 × 10−4 |
| LSM | 7.70 × 10−4 | 8.03 × 10−4 | 7.17 × 10−4 | 7.69 × 10−4 | 7.41 × 10−4 | 7.26 × 10−4 |
| Convergence Time (time step = 1 ms) | ||||||
| APID | 63 | 64 | 61 | 66 | 59 | 54 |
| PD | 101 | 107 | 53 | 63 | 60 | 44 |
| Prop SM | 198 | 191 | 186 | 139 | 166 | 325 |
| LSM | 490 | 264 | 608 | 485 | 566 | 513 |
| Method | Leg 1 | Leg 2 | Leg 3 | Leg 4 | Leg 5 | Leg 6 |
|---|---|---|---|---|---|---|
| APID | 157.83 | 164.24 | 105.09 | 70.81 | 68.54 | 104.82 |
| PD | 157.05 | 163.37 | 104.25 | 70.62 | 68.10 | 103.77 |
| Prop SM | 180.68 | 182.88 | 186.74 | 195.37 | 195.14 | 185.32 |
| LSM | 1.81 × 103 | 1.81 × 103 | 1.83 × 103 | 1.84 × 103 | 1.85 × 103 | 1.83 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, X.; Yu, W. Support-Vector-Regression-Based Kinematics Solution and Finite-Time Tracking Control Framework for Uncertain Gough–Stewart Platform. Electronics 2025, 14, 2872. https://doi.org/10.3390/electronics14142872
Jing X, Yu W. Support-Vector-Regression-Based Kinematics Solution and Finite-Time Tracking Control Framework for Uncertain Gough–Stewart Platform. Electronics. 2025; 14(14):2872. https://doi.org/10.3390/electronics14142872
Chicago/Turabian StyleJing, Xuedong, and Wenjia Yu. 2025. "Support-Vector-Regression-Based Kinematics Solution and Finite-Time Tracking Control Framework for Uncertain Gough–Stewart Platform" Electronics 14, no. 14: 2872. https://doi.org/10.3390/electronics14142872
APA StyleJing, X., & Yu, W. (2025). Support-Vector-Regression-Based Kinematics Solution and Finite-Time Tracking Control Framework for Uncertain Gough–Stewart Platform. Electronics, 14(14), 2872. https://doi.org/10.3390/electronics14142872






