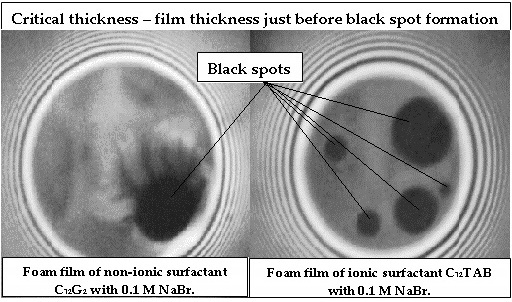
Influence of the Hamaker Constant on the Value of the Critical Thickness of Foam Films
Abstract
:1. Introduction
- Experimental data of the critical thickness (in the place of the black spot formation) for films stabilized by nonionic surfactant n-dodecyl-β-D-maltoside (C12G2) and cationic surfactant n-dodecyl trimethylammonium bromide (C12ТАВ) in the presence of 0.1M NaBr;
- Values of the Hamaker constant calculated by means of different equations for film thicknesses from 15 to 70 nm;
- Values of critical thickness calculated by Vrij approach and Radoev-Scheludko-Manev (RShM) formula, using the measured drainage coefficients and the calculated values of the Hamaker constant.
2. Materials and Methods
2.1. Materials
2.2. Experimental Conditions
2.3. Methods
Interferometric Method for Thin Liquid Films Investigation
2.4. Calculations
2.4.1. Film Drainage
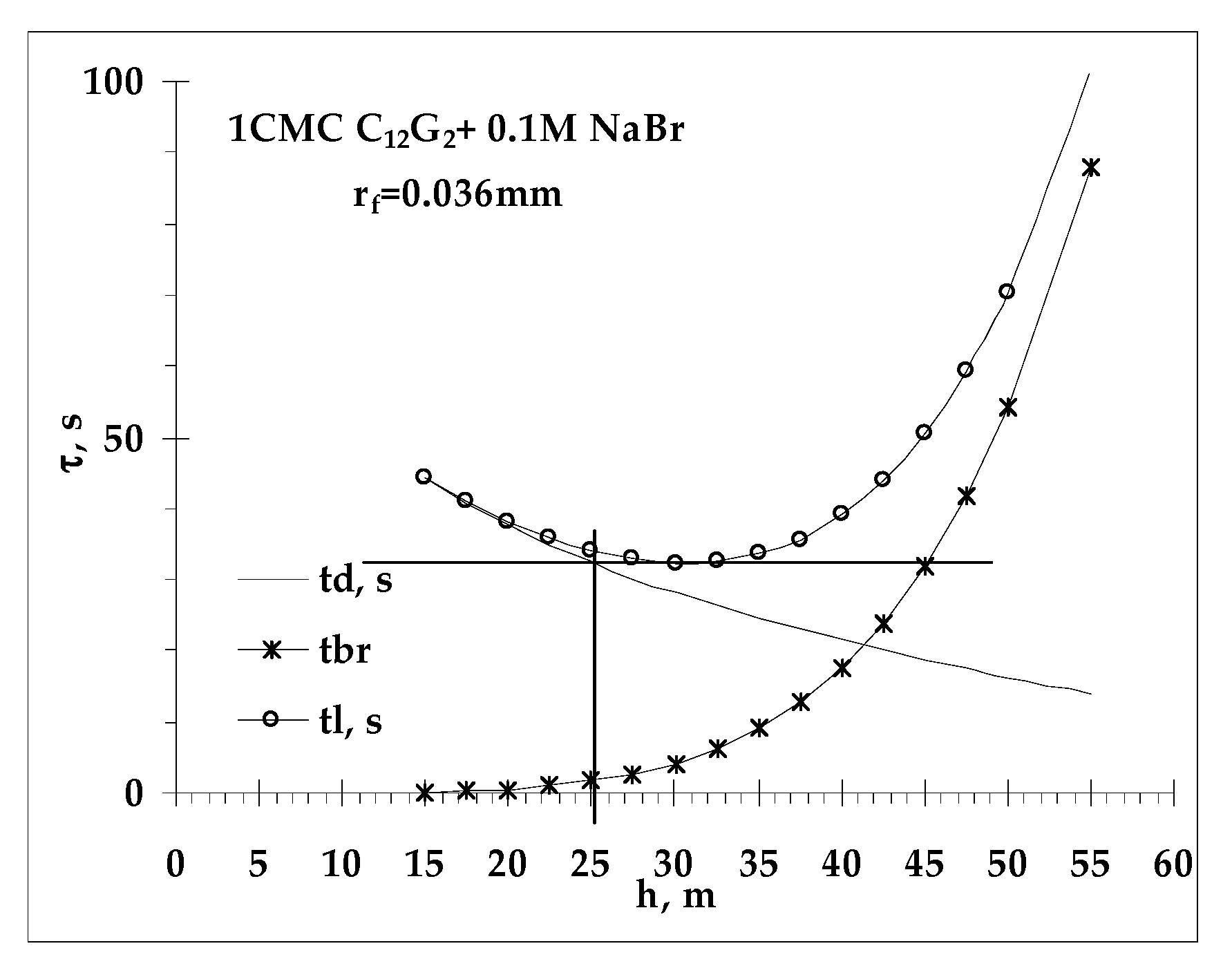
2.4.2. Critical Thickness
2.4.3. Hamaker Constant
3. Results and Discussion
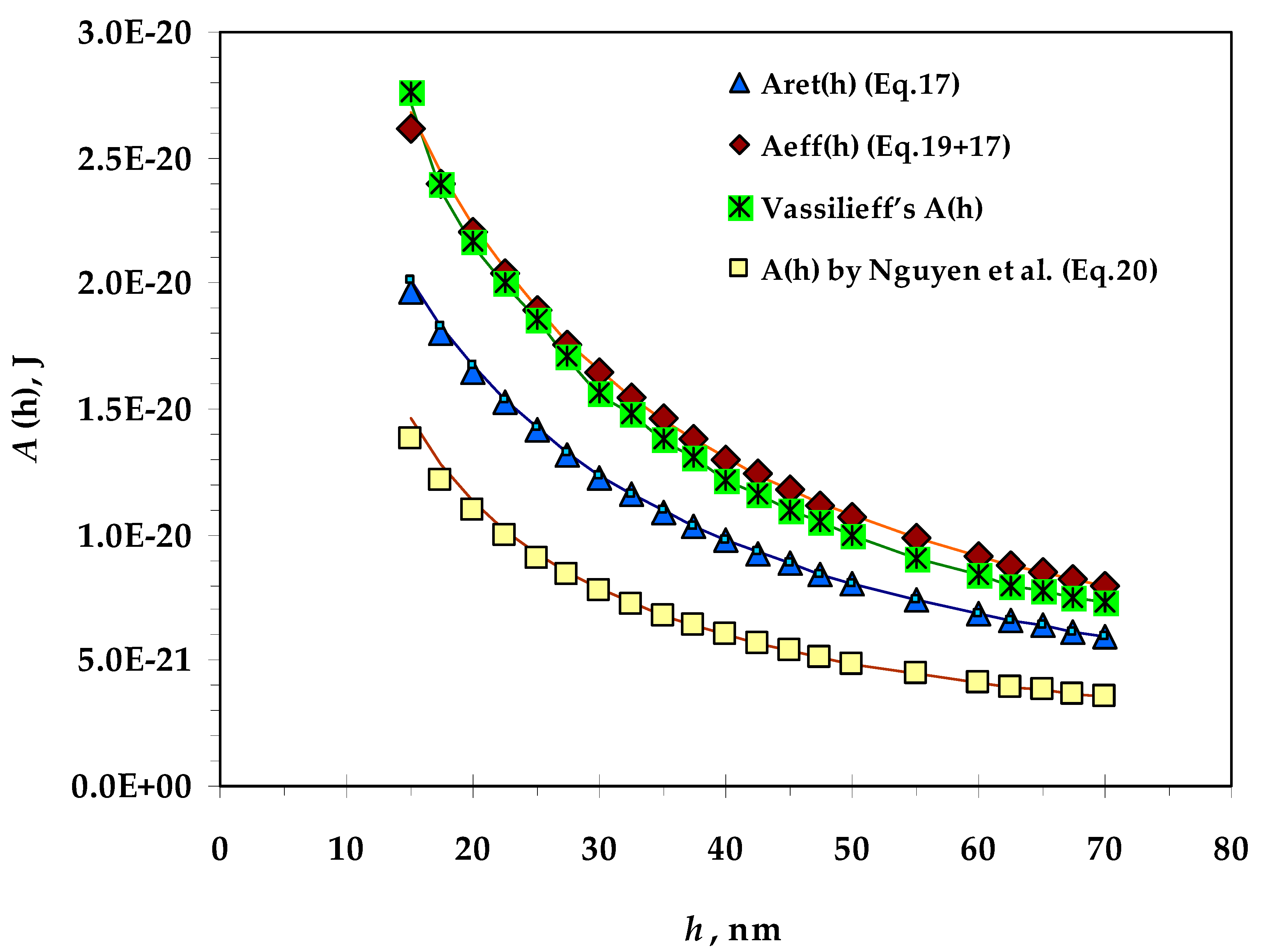
3.1. Hamaker Constant
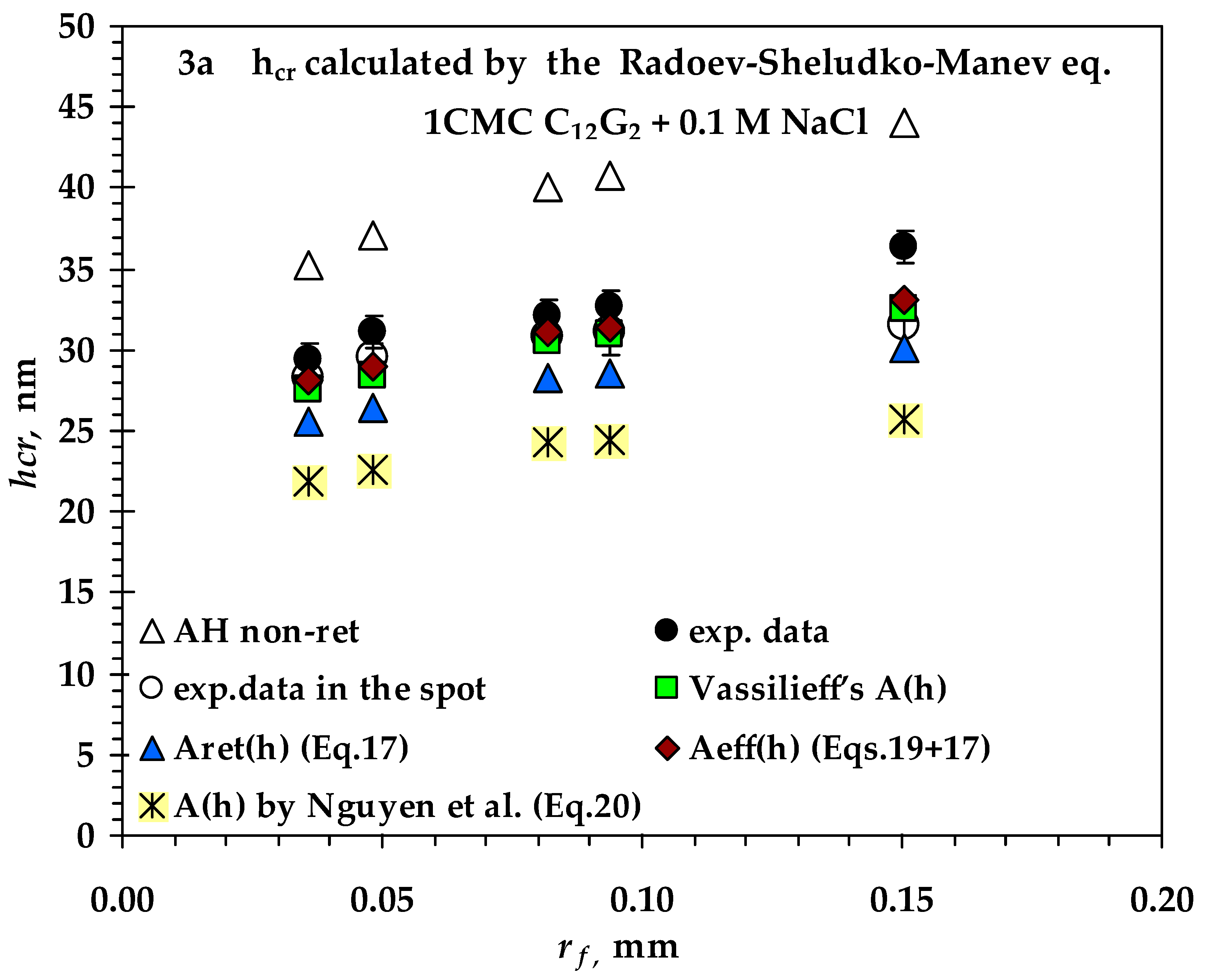
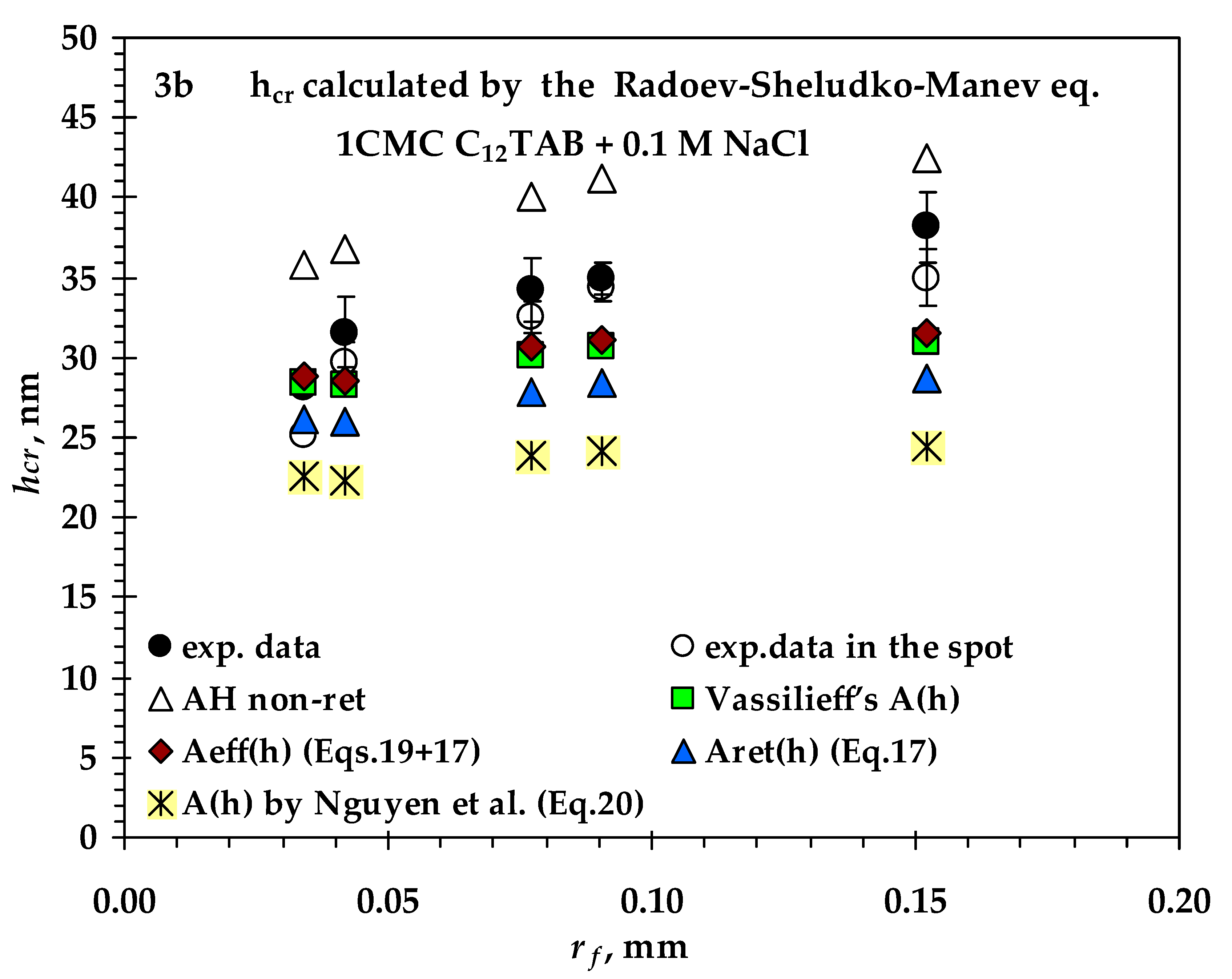
- Vassilieff’s values of the Hamaker constant are very close to the values of Aeff (h) (introduced by Coons et al.);
- The calculated values of the Hamaker constant by Nguyen are the lowest, probably because the authors model an expression for the bubble–particle system and introduce fitting coefficients for this system;
- There is no significant difference between the calculated values of A(h) at the two ionic strengths.
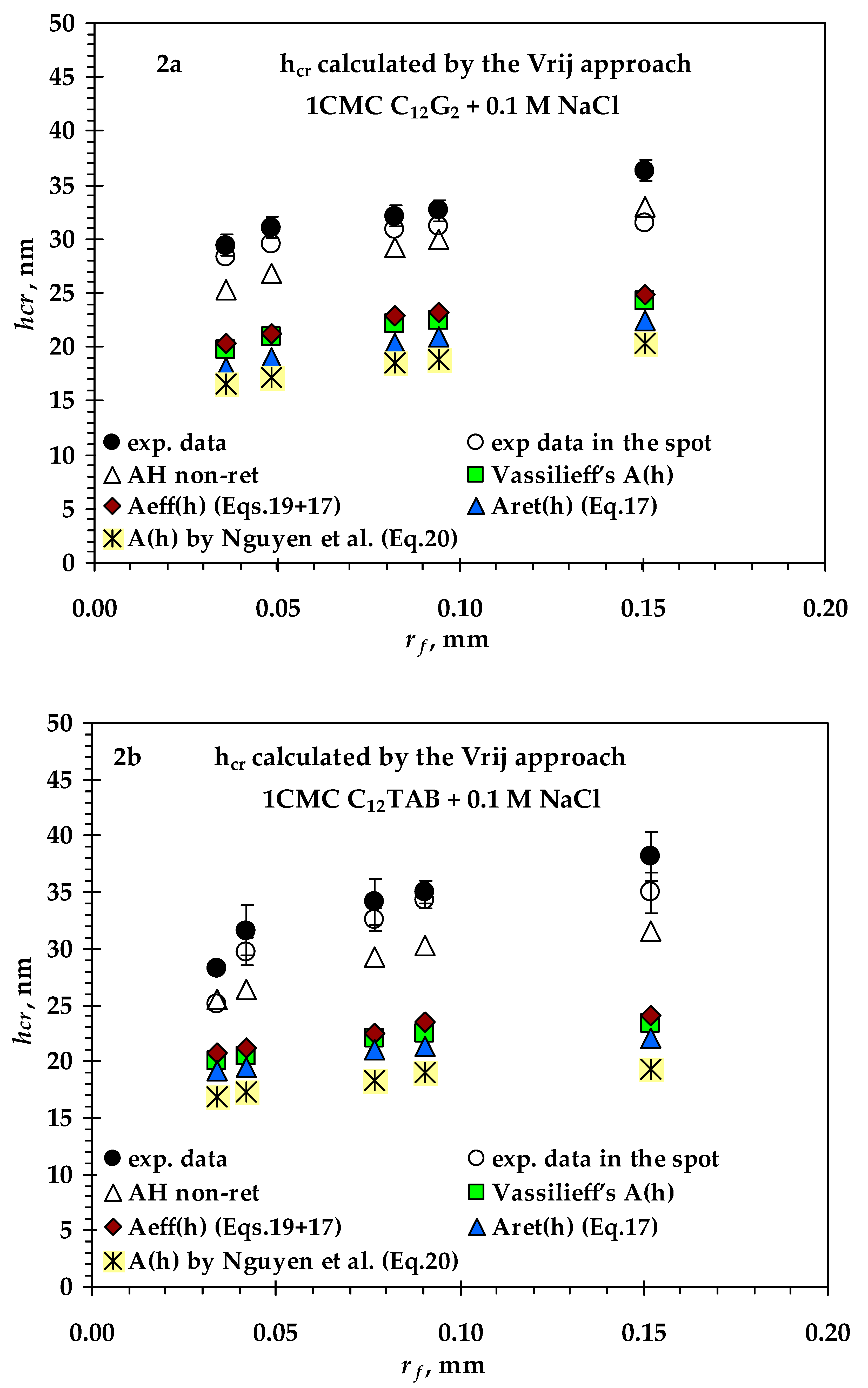
3.2. Comparison between Measured and Calculated Critical Thickness Values for Foam Films Stabilized by Nonionic n-Dodecyl-β-D-maltoside (C12G2) and by Cationic Surfactant n-Dodecyl Trimethyl Ammonium Bromide (C12TAB)
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| h, nm | AH Retarded × 1020, J | |||
|---|---|---|---|---|
| Vassilieff’s A(h) | Aret(h) (by Equation (17)) | Aeff (h) (by Equation (19) + (17)) | A(h) by Nguyen et al. (Equation (20)) | |
| 70.0 | 0.73 | 0.59 | 0.79 | 0.36 |
| 67.5 | 0.75 | 0.62 | 0.82 | 0.37 |
| 65.0 | 0.78 | 0.64 | 0.85 | 0.38 |
| 62.5 | 0.80 | 0.66 | 0.88 | 0.40 |
| 60.0 | 0.84 | 0.68 | 0.91 | 0.41 |
| 55.0 | 0.91 | 0.74 | 0.99 | 0.45 |
| 50.0 | 1.00 | 0.80 | 1.07 | 0.49 |
| 47.5 | 1.05 | 0.84 | 1.12 | 0.51 |
| 45.0 | 1.10 | 0.88 | 1.18 | 0.54 |
| 42.5 | 1.16 | 0.93 | 1.24 | 0.57 |
| 40.0 | 1.22 | 0.98 | 1.30 | 0.60 |
| 37.5 | 1.31 | 1.03 | 1.38 | 0.64 |
| 35.0 | 1.38 | 1.09 | 1.46 | 0.68 |
| 32.5 | 1.48 | 1.16 | 1.55 | 0.72 |
| 30.0 | 1.56 | 1.23 | 1.65 | 0.78 |
| 27.5 | 1.71 | 1.32 | 1.76 | 0.84 |
| 25.0 | 1.86 | 1.42 | 1.89 | 0.91 |
| 22.5 | 2.00 | 1.53 | 2.04 | 1.00 |
| 20.0 | 2.17 | 1.65 | 2.20 | 1.10 |
| 17.5 | 2.40 | 1.80 | 2.40 | 1.22 |
| 15.0 | 2.76 | 1.97 | 2.62 | 1.38 |
Appendix B
| 1.5 × 10-4 M C12G2 + 0.1 M NaBr | 4.2 × 10−3 M C12TAB + 0.1 M NaBr | ||
|---|---|---|---|
| Radius, mm | α, s−1 | Radius, mm | α, s−1 |
| 0.036 | 0.0430 | 0.034 | 0.0390 |
| 0.048 | 0.0320 | 0.042 | 0.0334 |
| 0.082 | 0.0200 | 0.077 | 0.0199 |
| 0.094 | 0.0180 | 0.090 | 0.0171 |
| 0.151 | 0.0113 | 0.152 | 0.0140 |
Appendix C
References
- Stubenrauch, C.; Schlarmann, J.; Strey, R. A disjoining pressure study of n-dodecyl-b-D-maltoside foam films. Phys. Chem. Chem. Phys. 2002, 4, 4504–4513. [Google Scholar] [CrossRef]
- Muruganathan, R.M.; Krustev, R.; Müller, H.J.; Möhwald, H.; Kolaric, B.; Klitzing, R.V. Foam films stabilized by dodecyl maltoside. 1. Film thickness and free energy of film formation. Langmuir 2004, 20, 6352–6358. [Google Scholar] [CrossRef] [PubMed]
- Cristobal, R. (Ed.) Sugar-Based Surfactants; Surfactant Science Series; CRC Press: Boca Raton, FL, USA, 2009; Volume 143. [Google Scholar]
- Stubenrauch, C.; Khristov, K. Foams and foam films stabilized by CnTAB: Influence of the chain length and of impurities. J. Colloid Interface Sci. 2005, 286, 710–718. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Buchavzov, N.; Carey, E.; Stubenrauch, C. Binary mixtures of β-dodecylmaltoside (β-C12G2) with cationic and non-ionic surfactants: Micelleand surface compositions. Soft Matter 2008, 4, 840–848. [Google Scholar] [CrossRef]
- Buchavzov, N.; Stubenrauch, C. A disjoining pressure study of foam films stabilized by mixtures of nonionic and ionic surfactants. Langmuir 2007, 23, 5315–5323. [Google Scholar] [CrossRef] [PubMed]
- Petkova, R.; Tcholakovaand, N.S.; Denkov, D. Foamingand Foam Stability for Mixed Polymer−Surfactant Solutions: Effects of Surfactant Typeand Polymer Charge. Langmuir 2012, 28, 4996–5009. [Google Scholar] [CrossRef] [PubMed]
- Manev, E.; Scheludko, A.; Exerowa, D. Effect of surfactant concentration on the critical thicknesses of liquid films. Colloid Polym. Sci. 1974, 252, 586–593. [Google Scholar] [CrossRef]
- Exerowa, D.; Kruglyakov, P.M. (Eds.) Foam, Foam Films: Theory, Experiment, Application; Marcel Dekker: New York, NY, USA, 1997. [Google Scholar]
- Vrij, A. Posible mehanism for spontaneous rupture of thin, free liquid films. Discuss. Faraday Soc. 1966, 42, 23–33. [Google Scholar] [CrossRef]
- Radoev, B.; Scheludko, A.; Manev, E. Critical thickness of thin liquid films. Theory and experiment. J. Colloid Interface Sci. 1983, 95, 254–265. [Google Scholar] [CrossRef]
- Coons, J.E.; Halley, P.J.; Mc Glashan, S.A.; Tran-Cong, T. Scaling laws for the critical rupture thickness of common thin films. Colloids Surf. A Physicochem. Eng. Asp. 2005, 263, 258–266. [Google Scholar] [CrossRef] [Green Version]
- Manev, E.D.; Angarska, J.K. Critical thickness of thin liquid films: Comparison of theory and experiment. Colloids Surf. A Physicochem. Eng. Asp. 2005, 263, 250–257. [Google Scholar] [CrossRef]
- Ivanova, D.S.; Angarska, J.K. Drainage and critical thickness of foam films stabilized by n-dodecyl-β-D-maltoside. Colloids Surf. A Physicochem. Eng. Asp. 2013, 438, 93–103. [Google Scholar] [CrossRef]
- Ivanova, D.; Angarska, J.; Manev, E.; Tachev, K. Critical thickness of foam films stabilized by nonionic or ionic surfactants and their mixtures. Colloids Surf. A Physicochem. Eng. Asp. 2017, 519, 34–45. [Google Scholar] [CrossRef]
- Ivanova, D.S.; Angarska, Z.K.; Karakashev, S.I.; Manev, E.D. Drainage of foam films stabilized by n-dodecyl-β-d-maltoside or dodecyl trimethylammonium bromide and their mixtures. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 93–101. [Google Scholar] [CrossRef]
- Angarska, J.K.; Manev, E.D. Effect of tetrapentyl ammonium bromide adsorption on the electrostatic interactions in aqueous octaethyleneglycol decylether foam films. Colloids Surf. A Physicochem. Eng. Asp. 2003, 223, 73–82. [Google Scholar] [CrossRef]
- Manev, E.; Tsekov, R.; Radoev, B. Effect of thickness non-homogeneity on the kinetic behaviour of microscopic foam films. J. Dispers. Sci. Technol. 1997, 18, 769–788. [Google Scholar] [CrossRef]
- Vassilieff, C. On the approximate calculation of the disjoining pressure from the Lifshitz theory. Annu. Sofia Univ. 1977/1978, 72, 5–10. [Google Scholar]
- Nir, S.; Vassilieff, C. Vander Waals Interactionsin Thin Films. In Thin Liquid Films; Ivanov, M., Dekker, N.Y., Eds.; CRC Press: New York, NY, USA, 1988; pp. 250–256. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Kralchevsky, P.A.; Nagayama, K. Chapter 5: Liquid Films and Interactions between Particle and Surface. In Particles at Fluid Interfaces and Membranes; Kralchevsky, P., Nagayama, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; Volume 10, pp. 183–247. [Google Scholar]
- Russel, W.B.; Saville, D.A.; Schowalter, W.R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Nguyen, A.V.; Evans, G.M.; Schulze, H.J. Prediction of van der Waalsinteractioninbubble–particleattachmentinflotation. Int. J. Miner. Process. 2001, 61, 155–169. [Google Scholar] [CrossRef]
- Karakashev, S.I.; Nguyen, A.V. Effect of sodium dodecyl sulphate and dodecanol mixtures on foam film drainage: Examining influence of surface rheology and intermolecular forces. Colloids Surf. A Physicochem. Eng. Asp. 2007, 293, 229–240. [Google Scholar] [CrossRef]
- Tsekov, R.; Ivanova, D.; Slavchov, R.; Radoev, B.; Manev, E.; Nguyen, A.; Karakashev, S. Streaming potential effect on the drainage of thin liquid films stabilized by ionic surfactants. Langmuir 2010, 26, 4703–4708. [Google Scholar] [CrossRef]
- Angarska, J.K.; Ivanova, D.S.; Manev, E.D. Drainage of foam films stabilized by nonionic, ionic surfactants and their mixtures. Colloids Surf. A Physicochem. Eng. Asp. 2015, 481, 87–99. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanova-Stancheva, D. Influence of the Hamaker Constant on the Value of the Critical Thickness of Foam Films. Coatings 2019, 9, 576. https://doi.org/10.3390/coatings9090576
Ivanova-Stancheva D. Influence of the Hamaker Constant on the Value of the Critical Thickness of Foam Films. Coatings. 2019; 9(9):576. https://doi.org/10.3390/coatings9090576
Chicago/Turabian StyleIvanova-Stancheva, Dilyana. 2019. "Influence of the Hamaker Constant on the Value of the Critical Thickness of Foam Films" Coatings 9, no. 9: 576. https://doi.org/10.3390/coatings9090576