Interconnections between Electronic Structure and Optical Properties of Multilayer Nanolaminate TiAlN/Ag and Al2O3/Ag Coatings
Abstract
:1. Introduction
2. Materials and Methods
2.1. Parameters of Multilayer Coatings
2.2. Parameters of Electron Spectroscopy Experiments
2.3. Modelling of Optical Properties
3. Results and Discussion
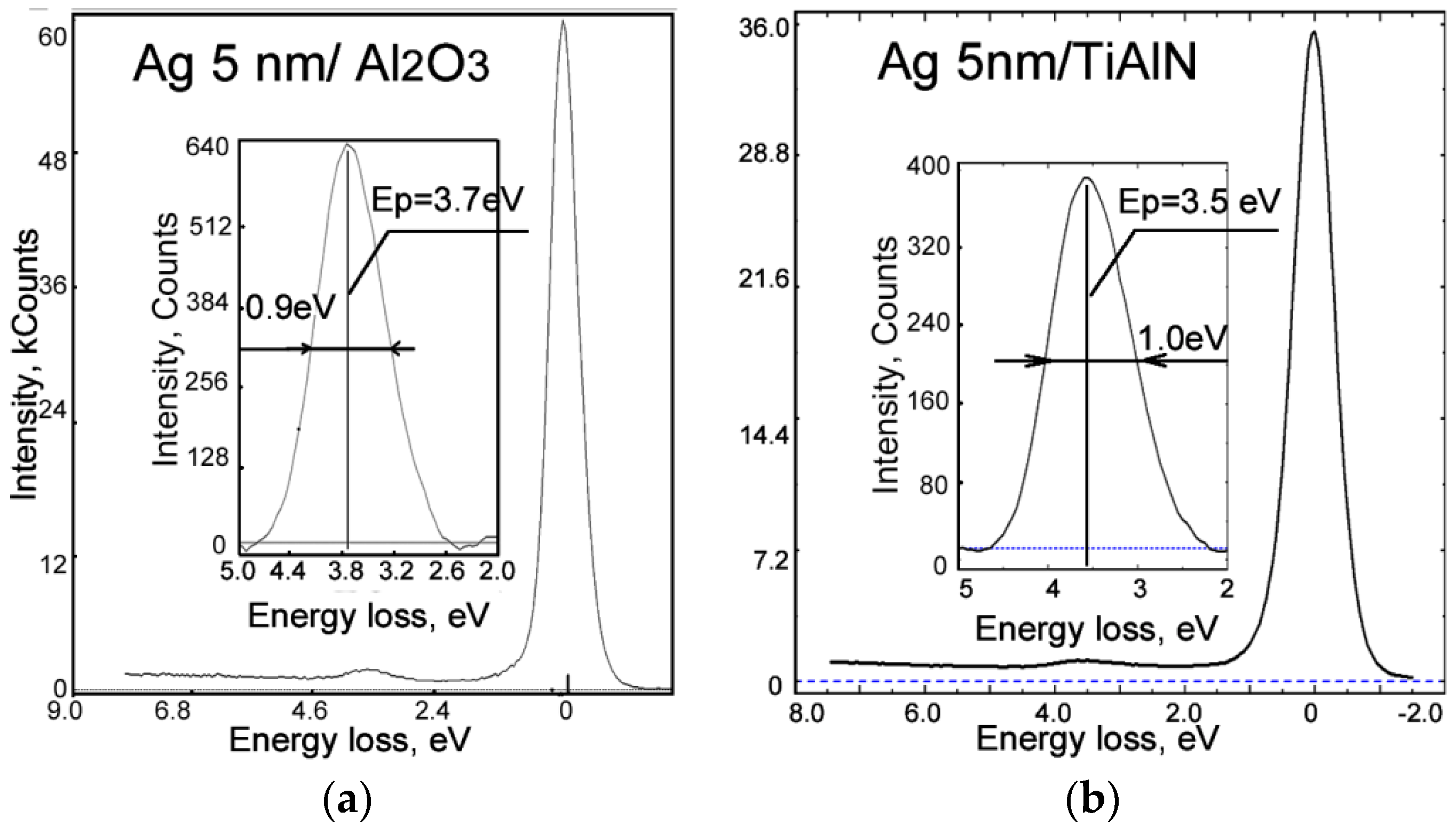
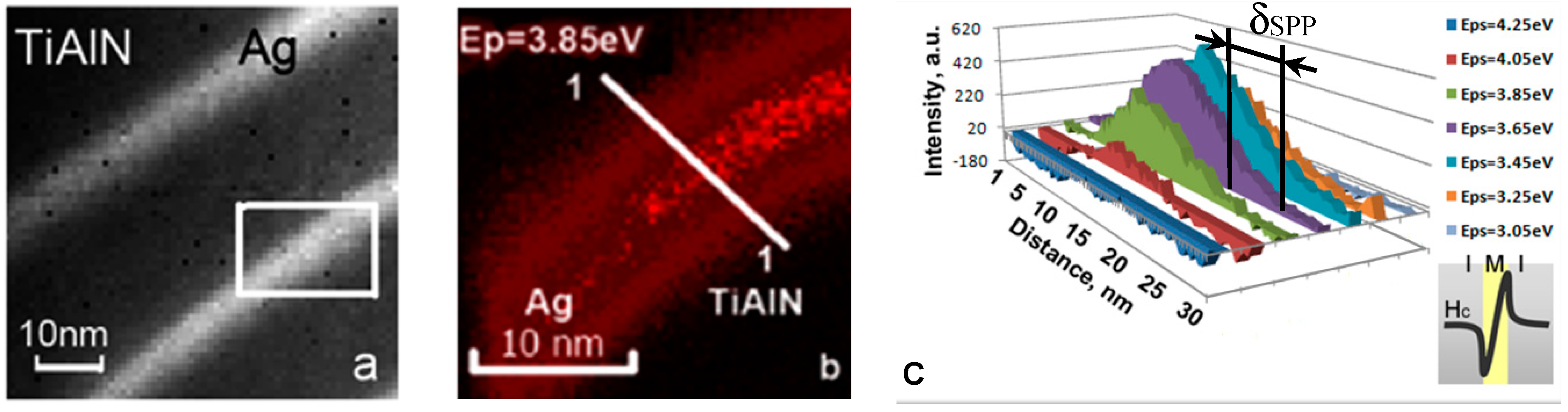
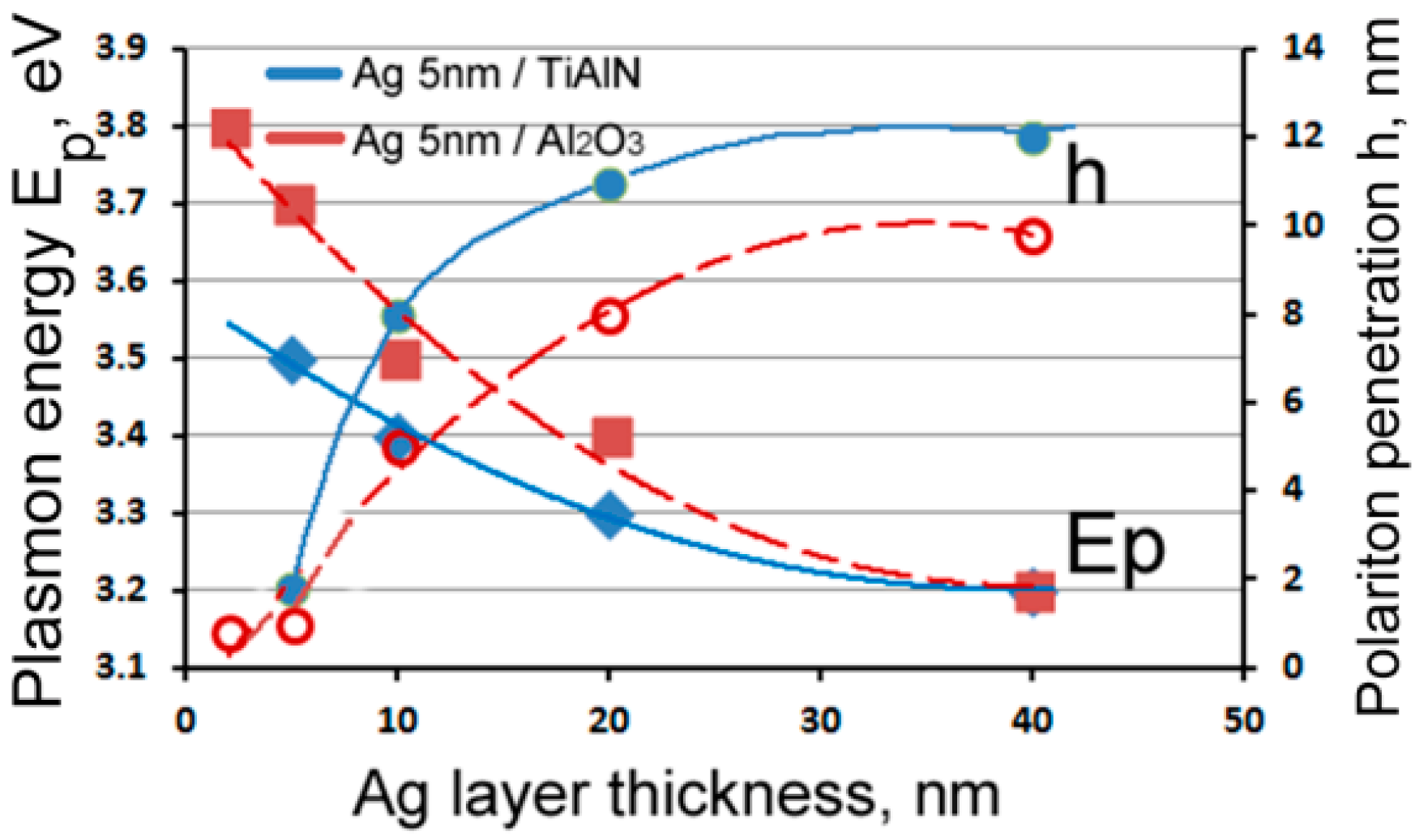
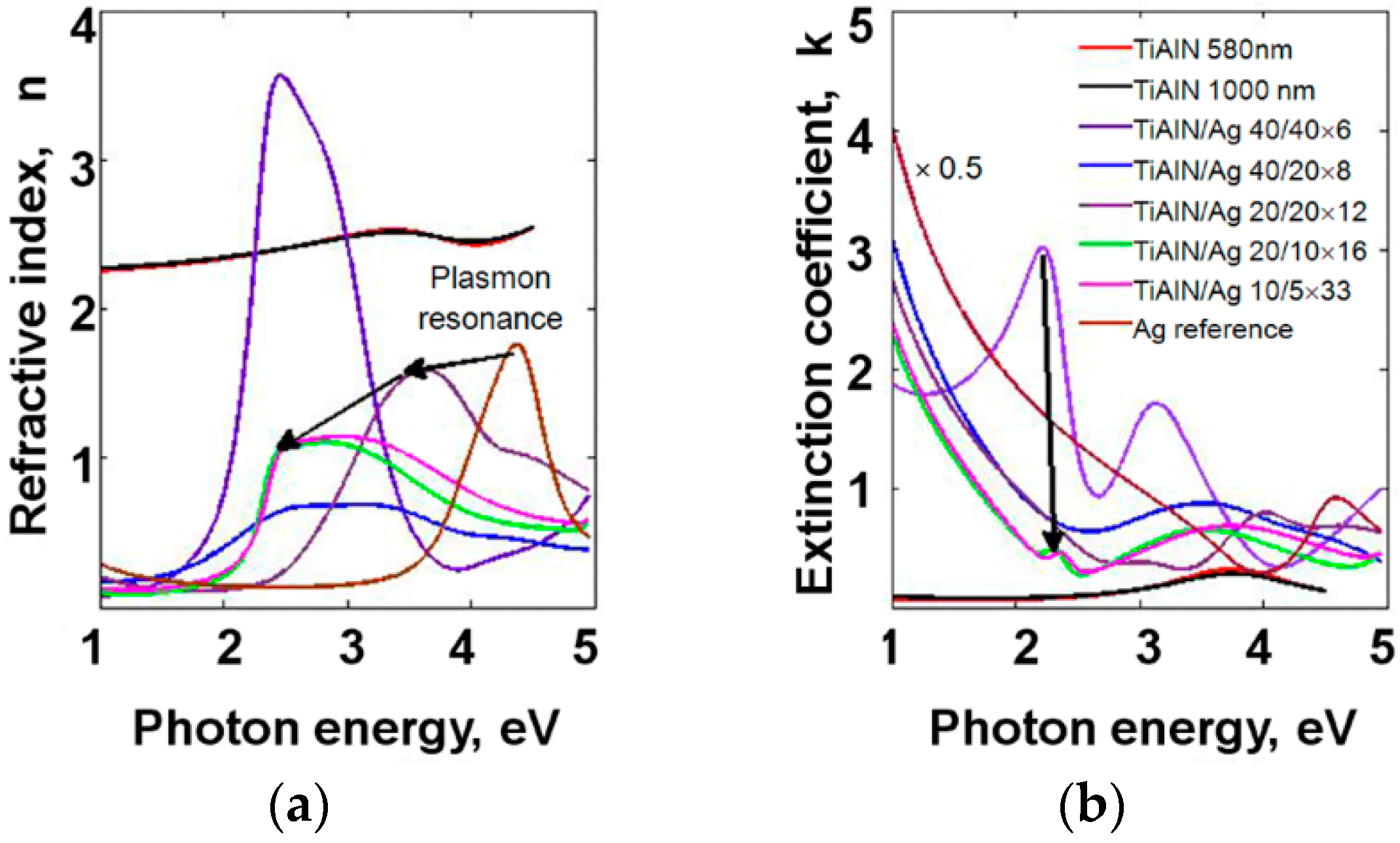
3.1. Experimental Studies of Plasmon Losses
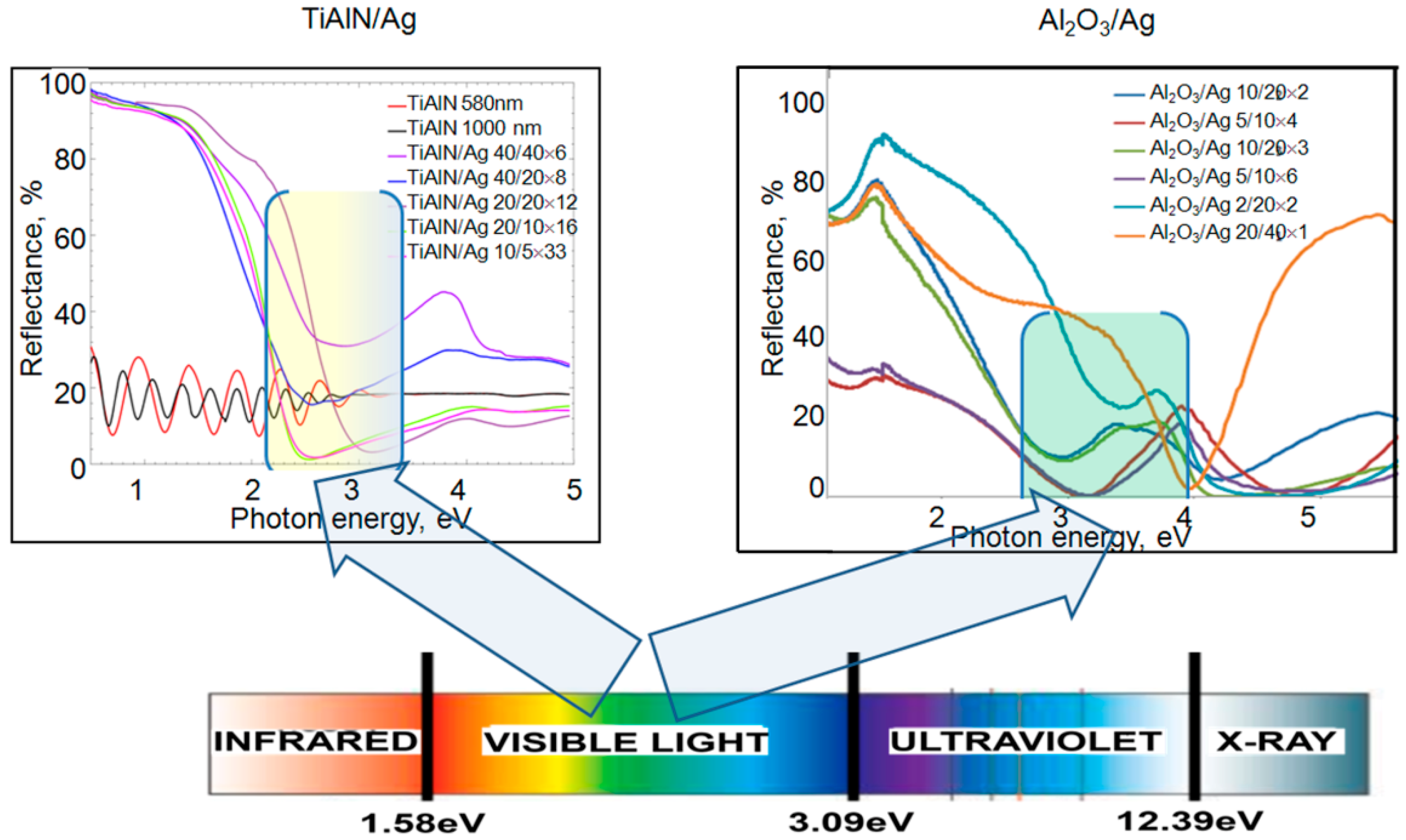
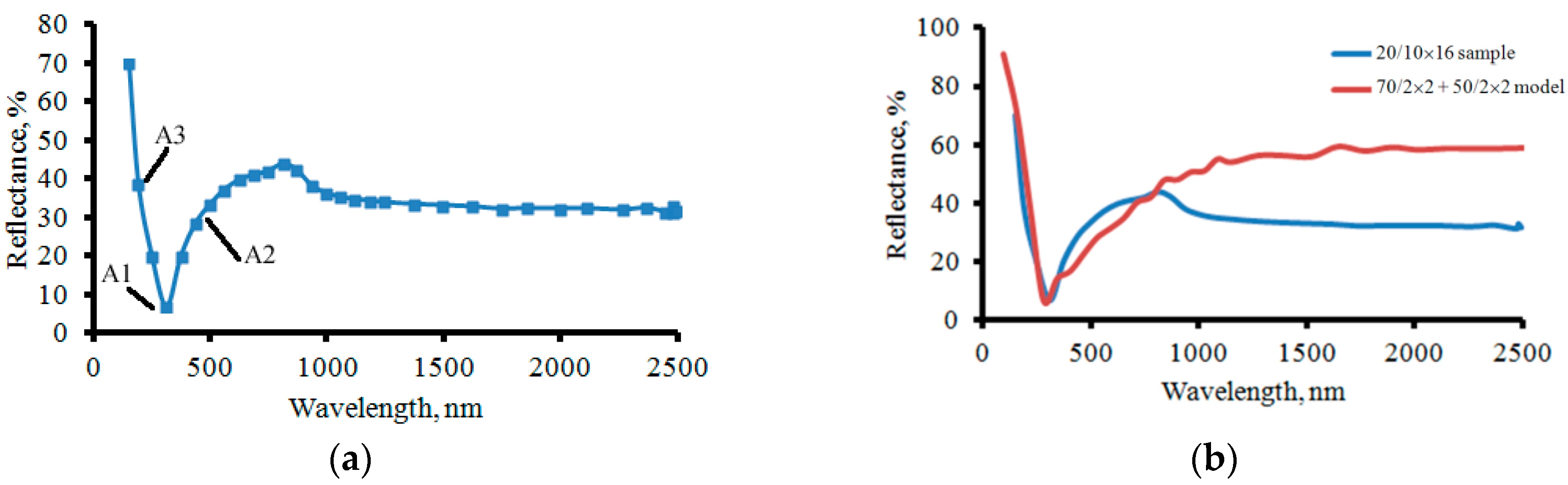
3.2. Features of Light Reflection Spectra
3.3. Architectural Design of MIM Multilayer Coatings based on Ag/Al2O3
4. Conclusions
- Surface plasmon-polariton interactions on “metal-dielectric” interfaces are increasing the effective thickness of metal nanolayers.
- IR and UV cut-off positions are shifted through the electromagnetic spectrum depending on the plasmonic system parameters, namely thickness and the number of layers in the system.
- Ag/TiAlN and Ag/Al2O3 nanocomposite systems could be used as broadband optical coatings with high light transmission and low reflection at a selected wavelength range of electromagnetic spectrum with nearly total IR reflection and relatively high (60%) reflection of UV. The total thickness of such coatings could be one or two orders smaller than a light wavelength.
- Their transmittance and reflectance bands could be tuned by the selection of individual layers thicknesses for a metal and a dielectric, the number of bilayers, as well as by the selection of the dielectric. These light filtering coatings could be fabricated using different metals and dielectrics.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Abbrevation | Expansion | |
| MIM | metal-insulator-metal | |
| SP | surface plasmon | |
| SPP | surface plasmon-polariton | |
| DOS | density of states | |
| MEMS | microelectromechanical system(s) | |
| IR | infrared | |
| UV | ultraviolet | |
| DL | Drude–Lorenz | |
| DC | direct current | |
| FWHM | full width at half maximum (half-width) | |
| HREELS | high-resolution electron energy loss spectroscopy | |
| EELS | electrons energy losses spectroscopy | |
| REELS | reflection electrons energy losses spectroscopy | |
| SEM | scanning electron microscopy | |
| AEM | (scanning) Auger electron microscopy | |
| TMM | Transfer Matrix Method | |
| Variable | Meaning | Dimension |
| R | surface reflectivity coefficient | – |
| n | reflective index | – |
| k | extinction coefficient | – |
| ω | angular frequency | 1/s |
| ωp | angular frequency of the plasmon | 1/s |
| νm | scattering rate | 1/s |
| Ne | density of conducting electrons | 1/m3 |
| ε | dielectric permittivity | – |
| me | mass of the electron | kg |
| meff | effective mass of the conduction electrons | kg |
| E0 | primary energy | eV |
| Hy | magnitude of the magnetic field | A/m |
| ΔE | energy losses | eV |
| δSPP | transboundary penetration depth of the plasmon | m |
| c | light velocity | m/s |
| Ep | plasmon resonance energy | eV |
| real part of the relative permittivity of a metal | – | |
| imaginary part of the relative permittivity of the metal | – | |
| εd | relative permittivity of the dielectric | – |
| λ | wavelength | m |
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin, Germany, 2007. [Google Scholar]
- Boriskina, S.V.; Tong, J.K.; Huang, Y.; Zhou, J.; Chiloyan, V.; Chen, G. Enhancement and tunability of near-field radiative heat transfer mediated by surface plasmon polaritons in thin plasmonic films. In Photonics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2015; Volume 2, pp. 659–683. [Google Scholar]
- Li, M.; Huang, L. Perspective on resonances of metamaterials. Opt. Express 2015, 23, 19022–19033. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224–227. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Rho, J. Metamaterials and imaging. Nano Converg. 2015, 2, 22. [Google Scholar] [CrossRef] [PubMed]
- Kanamori, Y.; Hokari, R.; Hane, K. MEMS for plasmon control of optical metamaterials. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 137–146. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, T.; Paudel, T.; Zhang, Y.; Ren, Z.F.; Kempa, K. Metamaterial-plasmonic absorber structure for high efficiency amorphous silicon solar cells. Nano Lett. 2012, 12, 440–445. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Pillai, S. Harnessing plasmonics for solar cells. Nat. Photonics 2012, 6, 130–132. [Google Scholar] [CrossRef]
- Kovalev, A.I.; Wainstein, D.L.; Vakhrushev, V.O.; Gago, R.; Soldera, F.; Endrino, J.L.; Fox-Rabinovich, G.S.; Veldhuis, S. Features of electronic and lattice mechanisms of transboundary heat transfer in multilayer nanolaminate TiAlN/Ag coatings. Sci. Rep. 2017, 7, 17078. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovalev, A.I.; Wainstein, D.L.; Rashkovskiy, A.Y.; Gago, R.; Soldera, F.; Endrino, J.L. The confinement of phonon propagation in TiAlN/Ag multilayer coatings with anomalously low heat conductivity. Appl. Phys. Lett. 2016, 108, 223106. [Google Scholar] [CrossRef]
- Wainstein, D.L.; Vakhrushev, V.O.; Kovalev, A.I. Control of optical properties of metal-dielectric planar plasmonic nanostructures by adjusting their architecture in the case of TiAlN/Ag system. J. Phys. Conf. Ser. 2017, 857, 012054. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Li, J.; Xiao, G. Significantly increased surface plasmon polariton mode excitation using a multilayer insulation structure in a metal–insulator–metal plasmonic waveguide. Appl. Opt. 2014, 53, 3642–3646. [Google Scholar] [CrossRef] [PubMed]
- Babicheva, V.E.; Malureanu, R.; Lavrinenko, A.V. Plasmonic finitethickness metal-semiconductor-metal waveguide as ultracompact modulator. Photonic Nanostruct. Fundam. Appl. 2013, 11, 323–334. [Google Scholar] [CrossRef]
- Mosquera, A.; Horvat, D.; Rashkovskiy, A.; Kovalev, A.; Miska, P.; Wainstein, D.; Allbella, J.; Endrino, J.L. Exciton and core-level electron confinement effects in transparent ZnO thin films. Sci. Rep. 2013, 3, 1714. [Google Scholar] [CrossRef]
- Wainstein, D.L.; Kovalev, A.I. Regularities of electronic structure transformations in nanomaterials with decreasing their characteristic size. J. Phys. Conf. Ser. 2017, 857, 012055. [Google Scholar] [CrossRef] [Green Version]
- Bosman, M.; Ye, E.; Tan, S.F.; Nijhuis, C.A.; Yang, J.K.W.; Marty, R. Surface plasmon damping quantified with an electron nanoprobe. Sci. Rep. 2013, 3, 1312. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, A.I.; Wainstein, D.L.; Rashkovskiy, A.Y.; Gago, R.; Soldera, F.; Endrino, J.L.; Fox-Rabinovich, G.S. Interface-induced plasmon nonhomogeneity in nanostructured metal-dielectric planar metamaterial. J. Nanomater. 2015, 16, 110. [Google Scholar] [CrossRef]
- Kovalev, A.I.; Rashkovskiy, A.Y.; Wainstein, D.L.; Gago, R.; Soldera, F.; Endrino, J.L. Influence of electronic structure, plasmon-phonon and plasmon-polariton excitations on anomalously low heat conductivity in TiAlN/Ag nanoscale multilayer coatings. Curr. Appl. Phys. 2016, 16, 459–468. [Google Scholar] [CrossRef]
- Mayer, M. SIMNRA User’s Guide 6.05; Max-Planck-Institut für Plasmaphysik: Garching, Germany, 2009. [Google Scholar]
- Wolff, P. Theory of plasma waves in metals. Phys. Rev. 1953, 92, 18–23. [Google Scholar] [CrossRef]
- Lee, W.-J.; Kim, J.-E.; Park, H.Y.; Lee, M.-H. Silver superlens using antisymmetric surface plasmon modes. Opt. Express 2010, 18, 5459–5465. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Barnes, W.L. Surface plasmon–polariton length scales: A route to sub-wavelength optics. J. Opt. A Pure Appl. Opt. 2006, 8, S87–S93. [Google Scholar] [CrossRef]
- Ealet, B.; Elyakhloufi, M.H.; Gillet, E.; Ricci, M. Electronic and crystallographic structure of γ-alumina thin films. Thin Solid Films 1994, 250, 92–100. [Google Scholar] [CrossRef]
- Tiggesbiumker, J.; Koeller, L.; Meiweis-Broer, K.H.; Liebsch, A. Blue shift of the Mie plasma frequency in Ag clusters and particles. Phys. Rev. A 1993, 48, R1749. [Google Scholar] [CrossRef]
- Naik, G.V.; Schroeder, J.L.; Ni, X.; Kildishev, A.V.; Sands, T.D.; Boltasseva, A. Titanium nitride as a plasmonic material for visible and near-infrared wavelengths. Opt. Mater. Express 2012, 2, 478–489. [Google Scholar] [CrossRef]
- Robertson, J. High dielectric constant oxides. Eur. Phys. J. Appl. Phys. 2004, 28, 265–291. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Sridhar, V.; Guo, S.; Talebi, N.; Miguel-López, A.; Hahn, K.; van Aken, P.A.; Sánchez, S. Fuel-free nanocap-like motors actuated under visible light. Adv. Funct. Mater. 2018, 28, 1705862. [Google Scholar] [CrossRef]

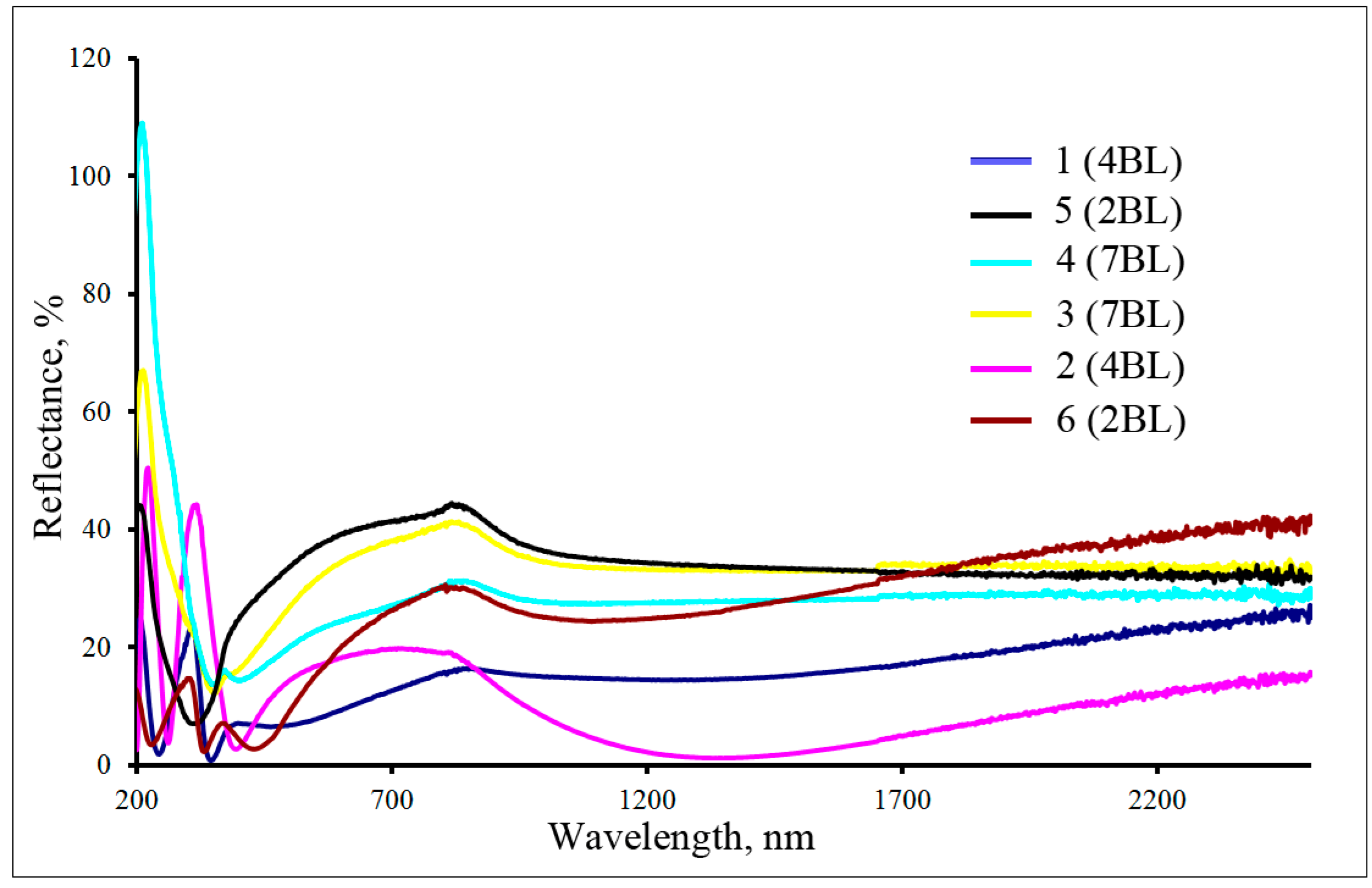
| Dielectric | Sample No. | Dielectric Layer Thickness, nm | Ag Layer Thickness, nm | No. of Dielectric/Ag Bilayers | Total Thickness, nm |
|---|---|---|---|---|---|
| Al2O3 | 1 (4 BL) | 40 | 5 | 4 | 180 |
| 2 (4 BL) | 40 | 2 | 4 | 168 | |
| 3 (7 BL) | 20 | 4 | 7 | 168 | |
| 4 (7 BL) | 8 | 1 | 7 | 63 | |
| 5 (2 BL) | 24 | 2 | 2 | 52 | |
| 6 (2 BL) | 24 | 5 | 2 | 58 | |
| Al2O3 ref | 200 | 0 | 1 | 200 | |
| TiAlN | 1 (6 BL) | 40 | 40 | 6 | 480 |
| 2 (3 BL) | 150 | 150 | 3 | 900 | |
| 3 (33 BL) | 20 | 5 | 33 | 825 | |
| 4 (16 BL) | 20 | 10 | 16 | 480 | |
| 5 (6 BL) | 150 | 20 | 6 | 1020 | |
| 6 (8 BL) | 30 | 30 | 8 | 480 | |
| 7(33 BL) | 10 | 5 | 33 | 495 | |
| TiAlN ref. | 900 | 0 | 1 | 900 |
| Point A2, nm | Point A3, nm | Min. Reflection, % | Al2O3 Layer, nm (Band Gap) | Ag Layer, nm (ωp) | Bilayer Thickness, nm | Total Thickness, nm (Attenuation Time τ) | Number of Bilayers | |
|---|---|---|---|---|---|---|---|---|
| Point A1, nm | 0.0359 | 0.181 | 0.136 | 0.0333 | −0.766 | 0.0998 | 0.0892 | 0.0126 |
| Point A2, nm | – | 0.766 | 0.233 | 0.0139 | 0.253 | 0.306 | 0.542 | 0.442 |
| Point A3, nm | – | – | 0.852 | 0.34 | −0.0126 | 0.0547 | 0.402 | 0.0023 |
| Min. reflection, % | – | – | – | 0.527 | 0.157 | 0.157 | 0.0203 | 0.783 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wainstein, D.; Kovalev, A.; Vakhrushev, V.; Gago, R.; Endrino, J.L. Interconnections between Electronic Structure and Optical Properties of Multilayer Nanolaminate TiAlN/Ag and Al2O3/Ag Coatings. Coatings 2018, 8, 290. https://doi.org/10.3390/coatings8080290
Wainstein D, Kovalev A, Vakhrushev V, Gago R, Endrino JL. Interconnections between Electronic Structure and Optical Properties of Multilayer Nanolaminate TiAlN/Ag and Al2O3/Ag Coatings. Coatings. 2018; 8(8):290. https://doi.org/10.3390/coatings8080290
Chicago/Turabian StyleWainstein, Dmitry, Anatoly Kovalev, Vladimir Vakhrushev, Raul Gago, and Jose L. Endrino. 2018. "Interconnections between Electronic Structure and Optical Properties of Multilayer Nanolaminate TiAlN/Ag and Al2O3/Ag Coatings" Coatings 8, no. 8: 290. https://doi.org/10.3390/coatings8080290





