Ab Initio Predicted Alloying Effects on the Elastic Properties of AlxHf1−xNbTaTiZr High Entropy Alloys
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Equilibrium Volume
| M | wt | Bt | we | Be | VE | x | wt | we | Δ | δt | δe | VEC | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Al | 2.965 | 84 | 2.991 | 73 | 3 | 0 | 3.216 | 3.168 a | 1.52 a | 3.216 | 3.169 | 5.0 | 4.3 | 4.40 |
| Hf | 3.402 | 142 | 3.301 | 108 | 4 | – | – | 3.178 b | 1.20 b | – | – | – | – | – |
| Nb | 3.119 | 178 | 3.071 | 169 | 5 | 0.1 | 3.208 | – | – | 3.206 | 3.163 | 5.0 | – | 4.38 |
| Ta | 3.113 | 223 | 3.073 | 191 | 5 | 0.2 | 3.199 | – | – | 3.196 | 3.157 | 5.0 | – | 4.36 |
| Ti | 3.030 | 133 | 3.053 | 106 | 4 | 0.3 | 3.190 | – | – | 3.186 | 3.150 | 5.0 | – | 4.34 |
| Zr | 3.368 | 74 | 3.347 | 95 | 4 | 0.4 | 3.181 | 3.134 | 1.50 | 3.176 | 3.144 | 5.0 | 4.3 | 4.32 |
| – | – | – | – | – | – | 0.5 | 3.172 | – | – | 3.166 | 3.138 | 5.0 | – | 4.30 |
| – | – | – | – | – | – | 0.6 | 3.163 | – | – | 3.156 | 3.132 | 4.9 | – | 4.28 |
| – | – | – | – | – | – | 0.7 | 3.154 | – | – | 3.146 | 3.126 | 4.8 | – | 4.26 |
| – | – | – | – | – | – | 1.0 | 3.127 | – | – | 3.116 | 3.107 | 4.4 | – | 4.20 |
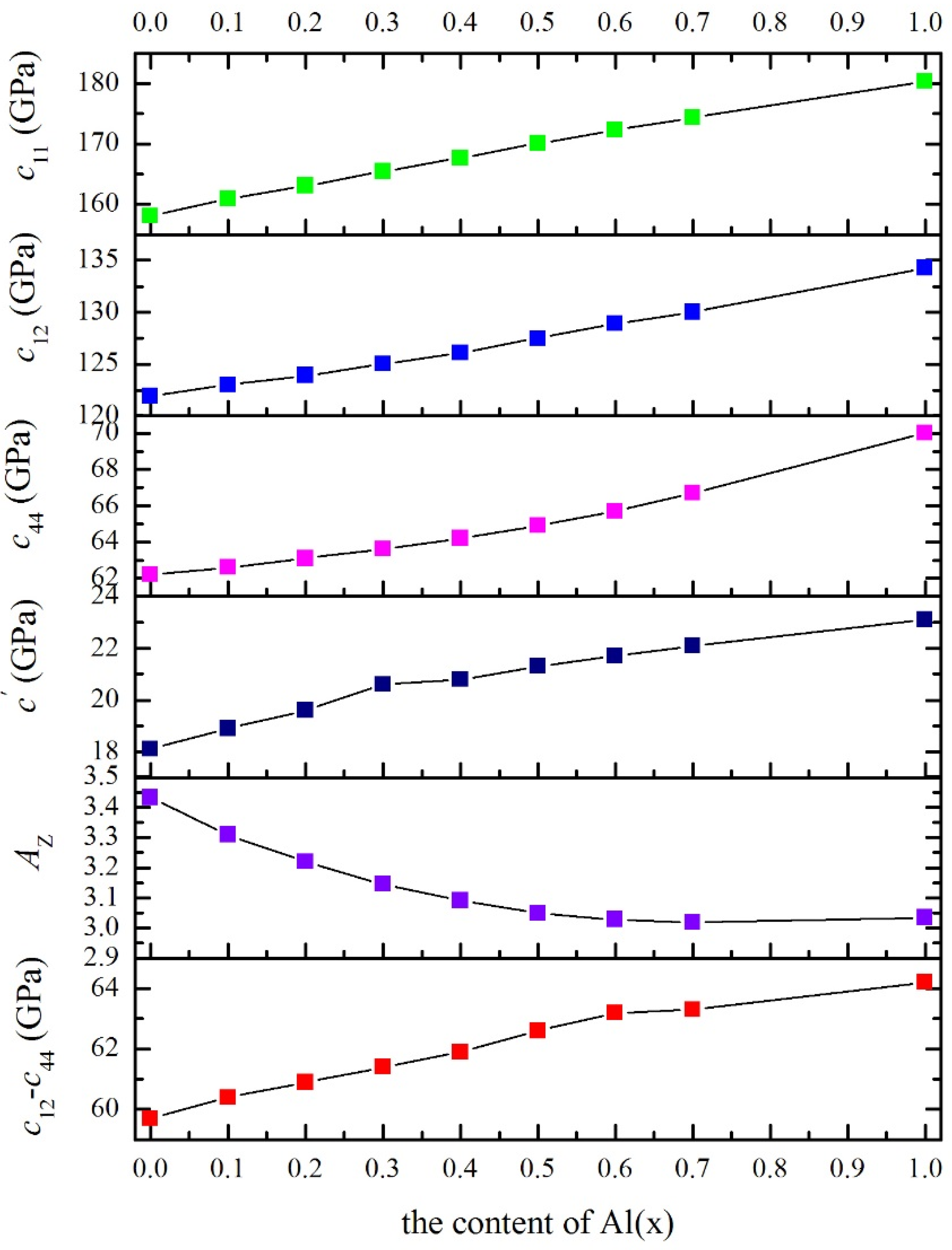
3.2. Cubic Elastic Constants
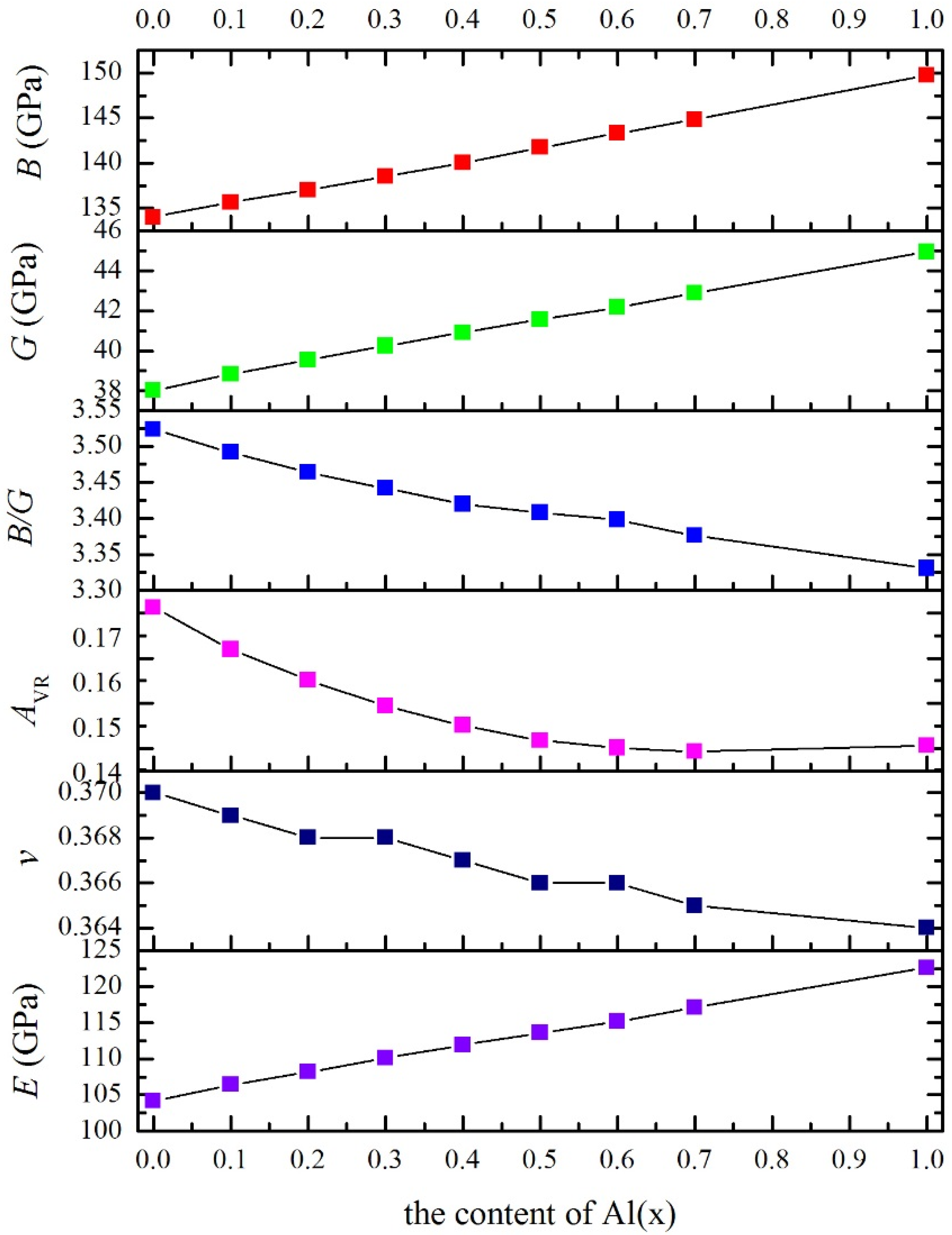
| x | B | c11 | c12 | c44 | G | B/G | E | v | cʹ | c12–c44 | AVR | AZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 134.0 | 158.1 | 121.9 | 62.2 | 38.03 | 3.523 | 104.2 | 0.370 | 18.1 | 59.7 | 0.1713 | 3.431 |
| 0.1 | 135.6 | 160.9 | 123.0 | 62.6 | 38.84 | 3.492 | 106.4 | 0.369 | 18.9 | 60.4 | 0.1620 | 3.309 |
| 0.2 | 137.0 | 163.1 | 123.9 | 63.1 | 39.55 | 3.464 | 108.2 | 0.368 | 19.6 | 60.8 | 0.1552 | 3.220 |
| 0.3 | 138.5 | 165.5 | 125.0 | 63.6 | 40.25 | 3.442 | 110.1 | 0.368 | 20.2 | 61.4 | 0.1494 | 3.146 |
| 0.4 | 140.0 | 167.7 | 126.1 | 64.2 | 40.92 | 3.420 | 111.9 | 0.367 | 20.8 | 61.9 | 0.1451 | 3.091 |
| 0.5 | 141.7 | 170.1 | 127.5 | 64.9 | 41.57 | 3.408 | 113.6 | 0.366 | 21.3 | 62.6 | 0.1418 | 3.049 |
| 0.6 | 143.3 | 172.3 | 128.9 | 65.7 | 42.18 | 3.398 | 115.2 | 0.366 | 21.7 | 63.2 | 0.1401 | 3.028 |
| 0.7 | 144.8 | 174.3 | 130.0 | 66.7 | 42.89 | 3.376 | 117.1 | 0.365 | 22.1 | 63.3 | 0.1394 | 3.019 |
| 1.0 | 149.7 | 180.4 | 134.3 | 70.0 | 44.94 | 3.331 | 122.6 | 0.364 | 23.1 | 64.3 | 0.1407 | 3.035 |
3.3. Polycrystalline Elastic Moduli
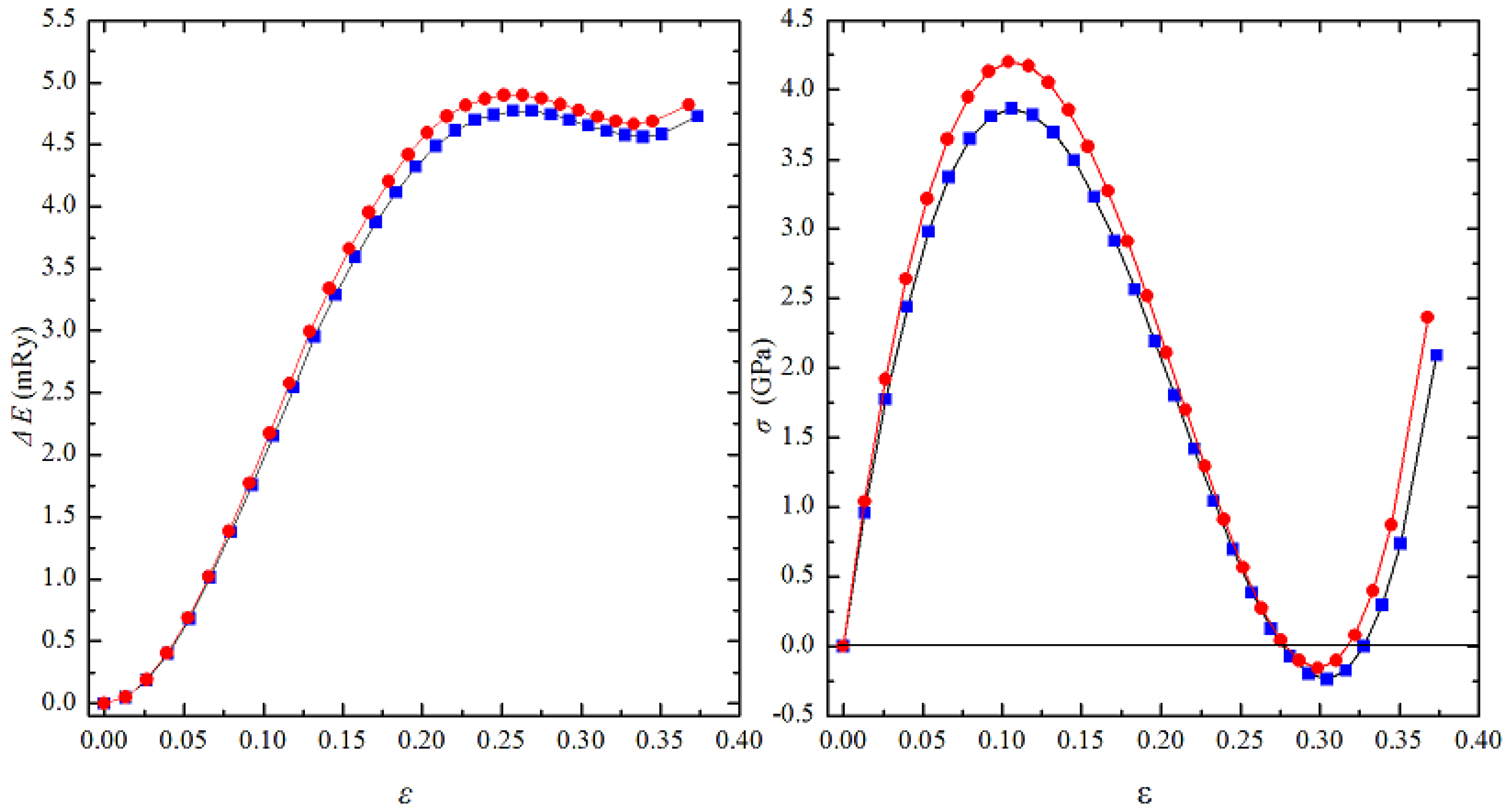
3.4. The Ideal Tensile Strength of Al0.4Hf0.6NbTaTiZr
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomi multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Chen, N.; Shen, J.; Vitos, L. Empirical design of single phase high-entropy alloys with high hardness. Intermetallics 2015, 58, 1–6. [Google Scholar] [CrossRef]
- Takeuchi, A.; Amiya, K.; Wada, T.; Yubuta, K.; Zhang, W. High-entropy alloys with a hexagonal close-packed structure designed by equi-atomic alloy strategy and binary phase diagrams. JOM 2014, 66, 1984–1992. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 2011, 509, 6043–6048. [Google Scholar] [CrossRef]
- Guo, W.; Dmowski, W.; Noh, J.-Y.; Rack, P.; Liaw, P.K.; Egami, T. Local atomic structure of a high-entropy alloy: An X-ray and neutron scattering study. Metall. Mater. Trans. A 2012, 44, 1994–1997. [Google Scholar] [CrossRef]
- Fazakas, É.; Zadorozhnyy, V.; Varga, L.K.; Inoue, A.; Louzguine-Luzgin, D.V.; Tian, F.; Vitos, L. Experimental and theoretical study of Ti20Zr20Hf20Nb20X20 (X = V or Cr) refractory high-entropy alloys. Int. J. Refract. Met. Hard Mater. 2014, 47, 131–138. [Google Scholar] [CrossRef]
- Wu, Y.D.; Cai, Y.H.; Wang, T.; Si, J.J.; Zhu, J.; Wang, Y.D. A refractory Hf25Nb25Ti25Zr25 high-entropy alloy with excellent structural stability and tensile properties. Mater. Lett. 2014, 130, 277–280. [Google Scholar] [CrossRef]
- Chen, S.; Yang, X.; Dahmen, K.; Liaw, P.; Zhang, Y. Microstructures and crackling noise of AlxNbTiMoV high entropy alloys. Entropy 2014, 16, 870–884. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Shaysultanov, D.G.; Salishchev, G.A.; Tikhonovsky, M.A. Structure and mechanical properties of a light-weight AlNbTiV high entropy alloy. Mater. Lett. 2015, 142, 153–155. [Google Scholar] [CrossRef]
- Senkov, O.N.; Senkova, S.V.; Woodward, C. Effect of aluminum on the microstructure and properties of two refractory high-entropy alloys. Acta Mater. 2014, 68, 214–228. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Chen, N.; Delczeg, L.; Vitos, L. Ab initio investigation of high-entropy alloys of 3D elements. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Tian, F.; Delczeg, L.; Chen, N.; Varga, L.K.; Shen, J.; Vitos, L. Structural stability of NiCoFeCrAlx high-entropy alloy from ab initio theory. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Tian, F.; Varga, L.K.; Chen, N.; Shen, J.; Vitos, L. Ab initio design of elastically isotropic TiZrNbMoVx high-entropy alloys. J. Alloys Compd. 2014, 599, 19–25. [Google Scholar] [CrossRef]
- Černý, M.; Šob, M.; Pokluda, J.; Šandera, P. Ab initio calculations of ideal tensile strength and mechanical stability in copper. J. Phys. Condens. Matter. 2004, 16. [Google Scholar] [CrossRef]
- Nagasako, N.; Jahn´atek, M.; Asahi, R.; Hafner, J. Anomalies in the response of V, Nb, and Ta to tensile and shear loading: Ab initio density functional theory calculations. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Wang, Y.J.; Wang, C.Y. A comparison of the ideal strength between L12Co3(Al,W) and Ni3Al under tension and shear from first-principles calculations. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Zhou, H.B.; Zhang, Y.; Liu, Y.L.; Kohyama, M.; Yin, P.G.; Lu, G.H. First-principles characterization of the anisotropy of theoretical strength and the stress-strain relation for a TiAl intermetallic compound. J. Phys. Condens. Matter. 2009, 21. [Google Scholar] [CrossRef] [PubMed]
- Černý, M.; Pokluda, J. Ideal tensile strength of cubic crystals under superimposed transverse biaxial stresses from first principles. Phys. Rev. B 2010, 82. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Vitos, L. Total-energy method based on the exact muffin-tin orbitals theory. Phys. Rev. B 2001, 64. [Google Scholar] [CrossRef]
- Kollár, J.; Vitos, L.; Skriver, H.L. Surface energy and work function of the light actinides. Phys. Rev. B 1994, 49. [Google Scholar] [CrossRef]
- Vitos, L.; Kollár, J.; Skriver, H.L. Full charge-density calculation of the surface energy of metals. Phys. Rev. B 1994, 49. [Google Scholar] [CrossRef]
- Stocks, G.M.; Temmerman, W.M.; Gyorffy, B.L. Complete solution of the korringa-kohn-rostoker coherent-potential-approximation equations: Cu-Ni alloys. Phys. Rev. Lett. 1978, 41, 339–343. [Google Scholar] [CrossRef]
- Johnson, D.D.; Nicholson, D.M.; Pinski, F.J.; Gyorffy, B.L.; Stocks, G.M. Density-functional theory for random alloys: Total energy within the coherent-potential approximation. Phys .Rev. Lett. 1986, 56, 2088–2091. [Google Scholar] [CrossRef] [PubMed]
- Vitos, L.; Abrikosov, I.A.; Johansson, B. Anisotropic lattice distortions in random alloys from first-principles theory. Phys. Rev. Lett. 2001, 87. [Google Scholar] [CrossRef]
- Gyorffy, B.L. Coherent-potential approximation for a non-overlapping-muffin-tin-potential model of random substitutional alloys. Phys. Rev. B 1972, 5, 2382–2384. [Google Scholar] [CrossRef]
- Vitos, L. The Emto Method and Applications in Computational Quantum Mechanics for Materials Engineers; Springer-Verlag: London, UK, 2007. [Google Scholar]
- Vitos, L.; Korzhavyi, P.A.; Johansson, B. Elastic property maps of austenitic stainless steels. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef]
- Taga, A.; Vitos, L.; Johansson, B.; Grimvall, G. Ab initio calculation of the elastic properties of Al1−xLix(x ≤ 0.20) random alloys. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Huang, L.; Vitos, L.; Kwon, S.K.; Johansson, B.; Ahuja, R. Thermoelastic properties of random alloys from first-principles theory. Phys. Rev. B 2006, 73, 104203–104207. [Google Scholar] [CrossRef]
- Vitos, L.; Korzhavyi, P.A.; Johansson, B. Evidence of large magnetostructural effects in austenitic stainless steels. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef]
- Vitos, L.; Johansson, B. Large magnetoelastic effects in paramagnetic stainless steels from first principles. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Zhang, H.; Punkkinen, M.P.J.; Johansson, B.; Hertzman, S.; Vitos, L. Single-crystal elastic constants of ferromagnetic bcc Fe-based random alloys from first-principles theory. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Korzhavyi, P.A.; Ruban, A.V.; Abrikosov, I.A.; Skriver, H.L. Madelung energy for random metallic alloys in the coherent potential approximation. Phys. Rev. B 1995, 51, 5773–5780. [Google Scholar] [CrossRef]
- Grimvall, G. Thermophysical Properties of Materials; North-Holland: Amsterdam, The Netherland, 1999. [Google Scholar]
- Roundy, D.; Krenn, C.R.; Cohen, M.L.; Morris, J.W. The ideal strength of tungsten. Philos. Mag. A 2001, 81, 1725–1747. [Google Scholar] [CrossRef]
- Lin, C.M.; Juan, C.C.; Chang, C.H.; Tsai, C.W.; Yeh, J.W. Effect of Al addition on mechanical properties and microstructure of refractory AlxHfNbTaTiZr alloys. J. Alloys Compd. 2015, 624, 100–107. [Google Scholar] [CrossRef]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. Mater. Int. 2011, 21, 433–446. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Nguyen-Manh, D.; Mrovec, M.; Fitzgerald, S.P. Dislocation driven problems in atomistic modelling of materials. Mater. Trans. 2008, 49, 2497–2506. [Google Scholar] [CrossRef]
- Pugh, S.F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Gu, X.J.; McDermott, A.G.; Poon, S.J.; Shiflet, G.J. Critical Poisson’s ratio for plasticity in Fe-Mo-C-B-Ln bulk amorphous steel. Appl. Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
- Clatterbuck, D.M.; Chrzan, D.C.; Morris, J.W. The ideal strength of iron in tension and shear. Acta. Mater. 2003, 51, 2271–2283. [Google Scholar] [CrossRef]
- Craievich, P.J.; Weinert, M.; Sanchez, J.M.; Watson, R.E. Local stability of nonequilibrium phases. Phys. Rev. Lett. 1994, 72, 3076–3079. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Ni, X.; Tian, F. Ab Initio Predicted Alloying Effects on the Elastic Properties of AlxHf1−xNbTaTiZr High Entropy Alloys. Coatings 2015, 5, 366-377. https://doi.org/10.3390/coatings5030366
Li S, Ni X, Tian F. Ab Initio Predicted Alloying Effects on the Elastic Properties of AlxHf1−xNbTaTiZr High Entropy Alloys. Coatings. 2015; 5(3):366-377. https://doi.org/10.3390/coatings5030366
Chicago/Turabian StyleLi, Shaohui, Xiaodong Ni, and Fuyang Tian. 2015. "Ab Initio Predicted Alloying Effects on the Elastic Properties of AlxHf1−xNbTaTiZr High Entropy Alloys" Coatings 5, no. 3: 366-377. https://doi.org/10.3390/coatings5030366





