Study on Erosion Wear of Wind Turbine Blades Dominated by Stokes Numbers

Abstract

Erosion of the leading edge of blades in windy and sandy environments can cause wind turbines to lose up to 25% of their annual power generation. Traditional studies have mostly focused on the impact of single factors on erosion rates, but the effects of multiple parameters on erosion rates within the framework of the Stokes number (Stk) of dust particles have not yet been clarified. This study employs a numerical approach based on the Euler–Lagrange framework, integrating the SST k-ω turbulence model with a discrete phase model (DPM) to simulate the unsteady gas–solid two-phase flow around a NACA 0012 airfoil. The computational model was rigorously validated through grid independence tests and comparison with experimental aerodynamic data from the database, showing strong agreement under steady conditions. Systematic simulations were conducted with particle diameters ranging from 10 to 360 μm, densities from 2650 to 3580 kg/m³, and inflow velocities from 1.5 to 21 m/s, comprehensively covering Stokes number regimes from Stk << 1 to Stk >> 1. Through parametric analysis, we quantify the control effect of Stk on erosion rate and erosion hot spots. Simulation results indicate that Stk has a zone-specific control effect on airfoil erosion: erosion hot spots in low-Stk zones migrate from the mid-to-rear edge to the leading edge. Erosion rate peaks when Stk ≈ 0.8. Inertial impact in the high-Stk zone dominates surface damage propagation. Based on the simulation results, an erosion model with an error of ≤3.6% was established for the E = K∙Stk^a∙d_p^b∙v^c zone, providing a quantitative physical basis to inform wind turbine blade protection strategies.

1. Introduction

Driven by increased awareness of climate change and the deployment of renewable energy, wind energy utilization continues to grow globally [1]. Data shows that global wind power generation exceeded 2100 terawatt hours in 2022, with an annual growth rate of 14%. It is expected to reach 7400 terawatt hours by 2050 [2]. The worldwide-installed wind power capacity has experienced substantial growth, with China playing a significant role in driving this expansion [3]. Many wind turbines are deployed in deserts or arid regions prone to sandstorms, where their performance and lifespan face severe challenges. Research has shown that the erosion effects of particles such as gravel can effectively reduce the aerodynamic performance and service life of airfoils [4]. Sandstorms and dusty weather conditions pose significant challenges to wind turbine operation. They have been shown to reduce turbine lifespan and affect power output characteristics [5], resulting in an annual power generation loss of approximately 25% [6]. Simultaneously, the accumulation of dust within the cooling system can greatly diminish the thermal efficiency of wind turbines, thereby further exacerbating power generation losses [7]. Leading edge erosion is the most prevalent form of damage to wind turbine blades. This type of wear can be caused by exposure to rain, sandstorms, and hail [8,9,10]. Recent studies have shown that the NACA 0012 airfoil also experiences significant lift loss and increased flow separation under icing conditions. This is similar to the flow instability mechanism caused by boundary layer unsteadiness due to wind and sand erosion [11]. The damage evolution shows obvious stages: In the initial stage, it manifests as small, randomly distributed micro-pits. As time passes, the damage accumulates and develops into more significant gully-like defects [6]. The size and density of these defects keep increasing over time, ultimately resulting in the delamination and failure of the surface’s protective coating. This deterioration of the leading edge shape directly causes a reduction in the blade’s lift coefficient, which in turn leads to a decline in power production [12,13,14]. It is particularly noteworthy that there is a significant coupling mechanism between wind and sand particles and the flow characteristics around the wing profile: On the one hand, particles interfere with the boundary layer structure, inducing unsteady flow separation. On the other hand, the physical damage to the leading edge caused by particle impact further exacerbates flow instability [6,15,16]. The mechanism of material spalling is similar to the evolution of gradient damage in artillery barrels under high-temperature, high-speed impact [17]. This strong coupling effect between aerodynamics and material damage further exacerbates the deterioration of blade performance.

Therefore, research on gas–solid two-phase flow in wind turbines under wind and sand environments is becoming increasingly important. The mechanism by which wind and sand affect wind turbines mainly involves two aspects: Initially, in numerical simulations based on one-way coupling regimes, the momentum exchange from sand particles can modify the flow-field structure surrounding the blades, potentially decreasing the wind-energy harvesting efficiency of wind turbines. However, it is noted that in dense sandstorms with higher loadings, more complex two-way and four-way coupling effects would further amplify this modulation [18]. Secondly, sand particles induce persistent erosion on the blade surfaces, resulting in diminished aerodynamic efficiency and, consequently, reduced operational stability of the turbine. The aerodynamic modifications resulting from wind turbine blade erosion have become a central topic of current research [19,20]. In-depth analysis of the regulatory mechanisms of particle parameters (particle size, density, velocity) on aerodynamic performance and erosion patterns through the Stokes number (Stk) is of significant engineering importance for the erosion-resistant design and operational optimization of wind turbines. The flow regime and resulting erosion patterns are governed by the interplay of these two parameters: Stk controls the inertial response and trajectory of individual particles, while particle volume fraction determines the collective two-phase coupling mechanism, ranging from one-way to four-way coupling [21]. This study focuses on the dilute regime, employing a one-way coupling approach to fundamentally isolate and elucidate the role of particle inertia (Stk). Current research mainly focuses on analyzing the impact of single factors on erosion rates. Tabakoff et al. [22] experimentally validated that the erosion rate follows a power-law dependence on the kinetic energy of the impacting particles, but they did not correlate it with the evolution of the flow field structure. Zhang et al. [23] found through numerical simulation that particles ranging from 20 to 50 μm exacerbate dynamic stall of airfoils; however, quantitative studies on the partitioning effect have been limited. Hamed et al. [24] pointed out that high-Stk particles cause concentrated erosion at the leading edge, but they did not clarify the interaction mechanism between streamline curvature and particle inertia. Recent studies have further revealed that Balachandar and Eaton [21] systematically summarized the research progress of turbulent dispersed multiphase flow. The discussion on “turbulent modulation” covers the key influence of Stk on the modulation effect, as well as its performance and physical mechanisms in different flows. Messa, G. V. et al. [25] explored particle–fluid interactions, particularly their behavior at low Stk numbers. They emphasize that when Stk << 1, particles closely follow fluid streamlines, and their motion is primarily dominated by fluid drag. Marchioli, C et al. [26] carried out an in-depth investigation into the transport mechanisms of various Stk particles within turbulent boundary layers. It was clearly found that particles with Stk ≈ 1 exhibited significant enrichment in the near-wall region and the outer region away from the wall. Furthermore, experimental investigations into the interaction between turbine wakes and inertial particles have provided valuable insights. For instance, Smith et al. [27] demonstrated the modulation of particle dispersion in wind turbine wakes under varying Stk conditions, while Ma et al. [28] quantitatively analyzed the preferential concentration and erosion potential of particles in the near-wake region. Wind tunnel experiments conducted by Wang et al. [29] confirmed that the matching relationship between the leading edge curvature radius and Stk determines the migration of erosion hot spots. However, the following key issues still need to be studied in depth: Particle size through Stk on the scale effect of unsteady characteristics of flow around objects; differentiated control laws of erosion spatial distribution and damage patterns in Stk partitions; the coupling effect weight of density and particle size in the cross-Stk interval.

Furthermore, beyond the inertia of individual particles, the collective behavior of particles in turbulence plays a crucial role in erosion patterns. As demonstrated in turbulent dispersed multiphase flows, particles exhibit preferential concentration or clustering depending on their Stokes number. This phenomenon, where particles accumulate in specific regions of the flow field, can lead to localized increases in impact frequency and thus exacerbate erosion in a non-uniform manner. The interplay between Stk-dependent clustering and the complex flow structures around an airfoil is expected to be a key factor governing the spatial distribution of erosion. However, a systematic investigation linking erosion hotspot migration to these underlying clustering mechanisms across different Stk regimes is still lacking.

This research is founded on the Euler–Lagrange approach and employs the SST k-ω turbulence model along with the discrete phase model. Numerical investigation into the degradation of aerodynamic performance and erosion behavior of the NACA 0012 airfoil under wind-sand flow conditions. The innovation lies in the following: 1. Revealing the control mechanism of particle size on flow separation. 2. Establishing a predictive model for the migration patterns of erosion space in Stk partitions. 3. Investigating the decay pattern of sensitivity in physical parameters, including particle size and density, across the cross-Stk interval.

2. Numerical Simulation Methods

2.1. Control Equation

The unsteady incompressible Navier–Stokes (N-S) equations consist of two fundamental conservation principles: mass conservation and momentum conservation. These principles are mathematically described by Equations (1) and (2), respectively:

$${\displaystyle \frac{\partial }{\partial x_i}}\left(u_i\right)=0$$

(1)

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho u_i\right)+{\displaystyle \frac{\partial }{\partial x_j}}\left(\rho u_i{u}_j\right)=-{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left[u\left({\displaystyle \frac{\partial u_i}{\partial x_i}}+{\displaystyle \frac{\partial u_j}{\partial x_j}}\right)\right]+{\displaystyle \frac{\partial }{\partial x_j}}\left(-\overline{\rho u_i^{\prime }{u}_j^{\prime }}\right)-f_{i,drag}$$

(2)

To ensure closure of the Navier–Stokes (N-S) equations, the Reynolds stress tensor appearing in the momentum equation is commonly modeled using a turbulence model rooted in the Boussinesq hypothesis. Popular approaches include the Spalart–Allmaras model, the k-ε model, and the SST k-ω model. Among the available models, the SST k-ω model is especially effective for simulating dynamic stall behavior, owing to its superior accuracy in near-wall regions and strong computational stability [30]. This conclusion is consistent with a comparative study of two-equation turbulence models in radiator channels [31]. Therefore, this study adopted the SST k-ω model [32]. The differential forms of turbulent specific dissipation and kinetic energy are shown:

$${\displaystyle \frac{Dk}{Dt}}=P_k-{\beta }^{*}\omega k+{\displaystyle \frac{\partial }{\partial x_j}}\left(\left(v+{\sigma }_k{v}_t\right){\displaystyle \frac{{\partial }_k}{\partial x_j}}\right)$$

(3)

$${\displaystyle \frac{D\omega }{D\mathrm{t}}}=\gamma {\displaystyle \frac{\omega }{k}}{P}_k-\beta {\omega }^2+{\displaystyle \frac{\partial }{\partial x_j}}\left(\left(v+{\sigma }_{\omega }{v}_t\right){\displaystyle \frac{\partial \omega }{\partial x_j}}\right)+2\left(1-F_1\right){\sigma }_{{\omega }^2}{\displaystyle \frac{1}{\omega }}{\displaystyle \frac{\partial k}{\partial x_j}}{\displaystyle \frac{\partial \omega }{\partial x_j}}$$

(4)

In this equation, k represents the turbulent kinetic energy, ω denotes the specific dissipation rate, and P_k is the turbulence production term. The symbols t and υ correspond to the eddy viscosity coefficient and turbulent viscosity, respectively. The parameter β* is a constant, while γ, σ_k, β, σ_ω, and F₁ are variables that depend on the flow conditions.

Turbulent eddy viscosity is defined as

$${\mu }_t=\frac{a_1\rho k}{\max \left(a_1\omega ,f_2{‖curlV‖}_2\right)}$$

(5)

2.2. DPM and Particle Injection Scheme

This study employs the discrete phase model (DPM)—applicable to low-volume-fraction, dilute particle flows—to simulate the transport of sand particles by airflow, as governed by the Euler–Lagrange framework [33]. This model does not consider the interactions between solid particles [34] and stipulates that the solid volume fraction must be strictly less than 10% [35]. This modeling choice allows for a focused investigation into the effects governed primarily by particle inertia (Stk). This modeling approach is predicated on a one-way coupling regime, wherein the fluid phase governs particle trajectories, while the reciprocal feedback from particles to the continuous fluid—encompassing momentum exchange and turbulence modulation—is either neglected or approximated via a simplified source term within the momentum equations. This assumption remains valid for the dilute particle flows that are the focus of the present investigation. It is, however, acknowledged that under severe sandstorm conditions characterized by significantly higher mass loadings, the flow regime would transition to two-way coupling, marked by substantial momentum feedback, or even to four-way coupling, which additionally accounts for inter-particle collisions. Such dense-phase interactions are known to induce more profound alterations to the flow field, including phenomena such as turbulence attenuation [18]. The investigation of these dense-phase coupling effects is beyond the scope of the current work but represents an important direction for future research. This simplified strategy is consistent with the loosely coupled analysis of molten ablation in supersonic particle erosion [36]. This study involves dust flow, which is a rarefied flow, so a discrete phase model was selected for sand simulation. In the present simulations, a uniform particle mass flow rate of 0.1 g/s was specified at the injection surface. Based on the inflow conditions and the injection area, this results in a global particle volume fraction on the order of 10⁻⁶, which is three orders of magnitude below the critical threshold for one-way coupling. This configuration firmly ensures that the influence of the particle phase on the continuous fluid turbulence is negligible, and the one-way coupling approach is therefore justified. The motion trajectories of discrete phase particles are obtained by numerically integrating their force equilibrium equations using ANSYS Fluent 2023 R1 software. The resulting particle phase’s kinematic equation in the x direction of the rectangular coordinate system:

$${\displaystyle \frac{d{u}_p}{dt}}=F_{drag}+{\displaystyle \frac{g_x\left({\rho }_p-\rho \right)}{{\rho }_p}}$$

(6)

In this equation, F_drag in Equation (6) represents the drag force acting on a particle per unit mass, which is formulated as

$$F_{\mathrm{drag}}={\displaystyle \frac{18\mu }{{\rho }_p{d}_p^2}}{\displaystyle \frac{C_D{\mathrm{Re}}_p}{24}}\left(u-u_p\right)$$

(7)

In this expression, u denotes the fluid phase velocity, up represents the particle velocity, and C_D is the drag coefficient. The relative Reynolds number is given by

$${\mathrm{Re}}_p={\displaystyle \frac{\rho d_p\left|u_p-u\right|}{\mu }}$$

(8)

The drag C_D coefficient in Equation (7) is not a constant but is dynamically computed based on the local particle Reynolds number (Re_p) using a widely validated spherical drag law [37]. This model applies a non-linear correction to account for finite-inertia effects across different flow regimes. The correlation is given as follows:

$$C_D=a_1+{\displaystyle \frac{a_2}{{\mathrm{Re}}_p}}+{\displaystyle \frac{a_3}{{\mathrm{Re}}_p^2}}$$

(9)

where the coefficients a₁, a₂, a₃ are piecewise constants that are automatically selected by the solver over specific ranges of Re_p, effectively covering the Stokes, transition, and Newton’s regimes. This ensures an accurate prediction of the drag force for particles ranging from 10 to 360 μm under various inflow velocities.

To simulate gas–solid momentum exchange, a source term is added to the control Equation (2) $f_{i,drag}={\displaystyle \frac{1}{\Delta V}}{\displaystyle \sum F_{drag}}$, where ΔV is the volume of the numerical grid. Particle incidence is implemented using file import, with initial concentration and diameter configured by adjusting the contents of the injection file. The geometric parameters of the incident surface are as follows: distance from the leading edge of the airfoil 5 c (c is the chord length of the airfoil, which is 1 m long), and the length of the incident surface is 6 m.

2.3. Wing Erosion Model Settings

The particle Stk represents the ratio of particle relaxation time to the characteristic flow time. A smaller Stk value indicates a shorter response time for particles to adapt to changes in the flow field. In contrast, particles with a higher Stk require more time to adjust to variations in the flow field. Stk of sand particles:

$$Stk={\displaystyle \frac{{\tau }_p}{T_f}}$$

(10)

The particle Stk represents the ratio of particle relaxation time to the characteristic flow time. A smaller Stk value indicates a shorter response time for particles to adapt to changes in the flow field. In contrast, particles with a higher Stk require more time to adjust to variations in the flow field. The Stokes number Stk in this study is defined using the integral length scale and the freestream velocity. This large-scale Stokes number is the primary parameter of interest, as it governs the inertial impaction of particles on the airfoil surface, which is the dominant mechanism for erosion hotspot formation.

Τ_p denotes the particle relaxation time, while T_f represents the flow’s characteristic time scale.

$${\tau }_p={\displaystyle \frac{{\rho }_p{d}_p^2}{18\mu }}$$

(11)

The particle relaxation time τ_p in Equation (10) is defined under the Stokes flow assumption. To account for finite particle Reynolds number effects prevalent in our simulations, an effective relaxation time τ_p is used in the analysis of results, defined as

$${\tau }_p={\displaystyle \frac{{\rho }_p{d}_p^2}{18\mu }}\times {\left({\displaystyle \frac{C_D{\mathrm{Re}}_p}{24}}\right)}^{-1}$$

(12)

where C_D is the non-linear drag coefficient calculated by the Morsi & Alexander model [37]. This correction ensures a more physically accurate calculation of the particle Stokes number.

Where ρ_p is the particle density, d_p is the particle diameter, and μ is the fluid viscosity.

$$T_f={\displaystyle \frac{L}{U}}$$

(13)

where L is the integral length scale and U is the characteristic velocity.

$$E={\displaystyle \sum _{p=1}^{N_{particles}}\frac{m_{p}C(d)f(\alpha )v^{b(v)}}{A_f}}$$

(14)

Among these, m_p is the mass flow rate of particles; C(d) is the particle diameter function, with C = 1.8 × 10⁻⁹, as determined by Eisenberg et al. for the relevant range of particle diameters from 10 to 400 μm. F(α) is the impact angle function. Ν is the relative velocity of the particle impacting the wall surface. B(ν) is the velocity exponent, where b = 2.6. At present, polyurethane-based derivatives are the most widely utilized materials for coatings on wind turbine blade surfaces [38]. This value, which indicates that the erosion rate scales with velocity raised to the power of 2.6, is adopted from the study by Eisenberg et al. on wind turbine blade coatings and is applicable in the velocity range of 1.5 to 25 m/s covered by our simulations. The erosion calculations in this study are based precisely on such typical polyurethane-based coating materials. The erosion wear of this material mainly exhibits plastic erosion characteristics. As reported in Reference [39], the peak erosion wear rate is observed at an impact angle of 30°. This profile, which exhibits a maximum erosion rate at an impact angle of 30°, is characteristic of ductile materials like polyurethane and is sourced from the experimental work of Sundararajan, valid for impact angles from 0° to 90°. Importantly, all the functional components in the equation are influenced by both the properties of the eroded material and the characteristics of the impacting particles. After reviewing a large number of literature sources, the control parameters in the above equation are set as shown in

Table 1. Parameter Settings related to the erosion wear model (Based on polyurethane-based coating materials).

α	0°	20°	30°	45°	90°
f(α)	0	0.8	1	0.5	0.4

[40,41]:

2.4. Computational Domain and Mesh Partitioning

This research develops a geometric model of the NACA 0012 airfoil, featuring a chord length of 1 m. The computational domain adopts a C-type topology structure: in the x direction, it extends forward from the leading edge to 6 c and backward from the trailing edge to c. In the y-direction, it extends 16 c in both the positive and negative directions (see Figure 1 for the calculation domain and mesh diagram).

As illustrated in Figure 1, the four outer boundaries of the computational domain are defined as velocity inlet boundaries, while the outlet boundary is specified as a pressure outlet boundary. The computational domain extends a substantial distance of six chord lengths upstream and sixteen chord lengths in the vertical direction from the airfoil. This configuration provides an ample isolation zone to minimize boundary effects on the near-body flow and to prevent the upstream propagation of disturbances. To ensure solution stability and prevent the unphysical backflow of fluid and particles, which is critical for the accuracy of the discrete phase model, the pressure outlet was configured with backflow prevention enabled. Additionally, the radial equilibrium pressure distribution model was applied at the outlet to provide a more realistic pressure profile for the curved streamlines in the wake, further suppressing numerical instabilities. The computational grid employs a hybrid grid strategy: both C-shaped and rectangular regions use a quadrilateral structured grid, while boundary layer grids are arranged in the wing-shaped near-wall region to accurately capture wall flow. The total number of grids is 2.5 × 10⁵. Numerical simulation is performed by solving the Reynolds-averaged SST k-ω equations. Pressure-velocity coupling uses the Coupled algorithm, and the governing equations are discretized through the application of the finite volume method. Both spatial and temporal discretization use a second-order upwind scheme, and a pressure-based coupled implicit solver is selected.

2.5. Verification

To validate the effectiveness of the numerical method presented in this paper, a steady flow condition was selected for verification using the NACA 0012 airfoil at v = 15 m/s, an angle of attack of 6°, and a Reynolds number Re = 1.6 × 10⁵ (Figure 2). The calculation uses a coupled algorithm based on a second-order upwind scheme. The experimental data were obtained from the aerodynamic database [42]. The tests were conducted in a low-speed, closed-return wind tunnel. The test section dimensions were 1.0 m × 0.75 m × 0.5 m. A NACA 0012 airfoil model with a chord length c = 1 m and a span of 0.75 m was employed. The model was equipped with pressure taps distributed around the airfoil profile at the mid-span section to measure the surface pressure distribution. The pressure taps were distributed around the airfoil profile to capture the entire pressure field accurately. Although a schematic is not available in [42], the report’s textual description indicates a non-uniform distribution, with a higher density of taps near the leading edge where pressure gradients are steepest.

The Reynolds number Re for the experimental validation is defined as

$$\mathrm{Re}={\displaystyle \frac{\rho U_{\infty }c}{\mu }}$$

(15)

where ρ = 1.225 kg/m³ is the air density, U_∞ = 15 m/s is the freestream velocity, c = 1 m is the airfoil chord length, and μ is the dynamic viscosity of air. This yields a Reynolds number of 1.6 × 10⁵, matching the simulation conditions.

The comparison results show that, under steady-state conditions, the CFD simulation results show strong consistency with the experimental measurements, as illustrated in Figure 2.

Given that grid resolution has a decisive impact on the accuracy of aerodynamic numerical simulations, this study systematically conducted grid independence verification. Figure 3 shows a comparison of the calculation results for the NACA 0012 airfoil under three different grid scales. The grid refinement strategy follows a strategy of gradually doubling the number of nodes along the tangent and normal directions. The numerical simulation conditions are set as follows: angle of attack α = 6°. The inlet boundary conditions use a velocity inlet with an inflow velocity of 15 m/s.

Figure 3 shows that the calculation results for the upper surface of the airfoil are consistent for all three mesh densities, with minimal error. However, there were significant differences in the calculation results for the leading edge and lower wing surface areas. The results of the coarsest grid calculations deviate significantly from those of the fine grid. Grid refinement significantly improved computational accuracy, and the simulation results gradually converged to the experimental values. However, a sharp increase in grid scale will significantly increase the demand for computing resources. As shown in Figure 3, the medium-density grid is highly consistent with the results of the finer grid in predicting the key aerodynamic characteristics of the airfoil, while maintaining good computational efficiency. Therefore, in order to balance computational accuracy and efficiency, this study selected a grid containing a total of 2.5 × 10⁵ grid cells for simulation.

To evaluate the impact of turbulence models on the accuracy of dynamic stall simulations, Figure 4 illustrates the simulation data from various turbulence models against experimental data. Analysis indicates that the SST k-ω turbulence model can simulate aerodynamic conditions more accurately than the k-epsilon model and is more consistent with experimental data [43]. Due to the fact that NACA0012 exhibits a boundary layer transition position that is extremely forward under high Reynolds number and small angle of attack conditions, the flow is nearly fully turbulent, and the transition process has a negligible impact. However, the additional transition equations introduced by Transition SST significantly increase the complexity, convergence difficulty, and sensitivity to the grid in steady-state calculations, which may introduce unnecessary sources of error or numerical instability. Therefore, the standard SST k-ω model often yields more accurate and stable aerodynamic results than the Transition SST k-ω model due to its focus on fully developed turbulent boundary layer prediction and strong numerical robustness. Based on the above comparative analysis, this study ultimately selected the SST k-ω turbulence model for subsequent calculations.

3. Analyses and Discussions

3.1. The Effect of Particle Size on the Flow Characteristics and Aerodynamic Performance of Airfoils

3.1.1. The Influence of Particle Size on Wing Flow

This section investigates the influence of particle size on the flow field around the NAC0012 airfoil in a sandstorm environment with particles of different diameters at two angles of attack, designed to be 6° and 12°.

Figure 5 shows the pressure distribution cloud map of the wing section in clean air and in environments with particles of different diameters at an angle of attack of 6°. The analysis results show that, compared with clean air conditions, the high-pressure zone range at the leading edge and trailing edge of the airfoil pressure face shows a slight contraction trend after the introduction of 10 µm particle diameter particles. However, when the particle size increases to 100 µm, the range of the high-pressure zone expands again. At this point, the overall pressure distribution of the flow field tends to be consistent with the clean air condition. This indicates that the presence of a particulate phase modulates the pressure field, with the magnitude and spatial extent of this modulation being a function of particle inertia, which is quantitatively represented by the Stokes number. The above phenomenon indicates that, under conditions of smaller attack angles and no flow separation, the presence of particles has a limited effect on the macro-scale flow structure around the airfoil. However, it will still have a measurable impact on the local pressure distribution and overall aerodynamic characteristics.

Figure 6 shows the vortex distribution diagram of a two-dimensional airfoil, comparing the flow field structure around the airfoil under clean air conditions and conditions with particles of different diameters. Analysis indicates that, under smaller angle of attack conditions, the presence of the particulate phase has no significant effect on the overall structure of the vortex field in the near-body region and wake region of the airfoil. Specifically, the flow pattern in the wake zone remained stable, with vortex distribution characteristics consistent with those of the clean air reference condition. No significant particle disturbance effects were observed.

A detailed investigation was conducted on the effect of particle diameter on the vortex distribution around the airfoil at an angle of attack of 12°. Based on previous studies, when the Reynolds number is between 1 × 10⁵ and 5 × 10⁵, the angle of attack at which vortex shedding begins is approximately 8–10°, and the angle of attack at which complete stall occurs is approximately 11–13°. Therefore, when the angle of attack is 12°, under clean air conditions, flow separation occurs on the suction surface of the NACA0012 airfoil, and an attached vortex structure forms downstream of the separation point. Figure 7 compares and analyzes the flow field characteristics of different particle diameters under the same angle of attack. The results show that when particles with a diameter of 10 μm are introduced, the wake vortex structure expands significantly, forming a distinct separation bubble, and the flow field exhibits strong unsteady characteristics. This phenomenon is typically associated with high angle of attack flow, highlighting the complexity of gas–solid two-phase interactions. When the particle diameter increases to 20 μm, the wake vortices show no significant changes, and distinct separation bubbles are still present. The flow field exhibits strong unsteady characteristics. As the particle diameter continues to increase to 30 μm, strong unsteady characteristics still exist. Further increasing the particle diameter to 50 μm, the wake vortex structure began to recover, forming a relatively regular and stable quasi-steady vortex shedding pattern. As the particle trajectory increases to 100 μm, the wake vortex scale shows a decreasing trend, and the flow stability continues to strengthen. When the particle diameter reaches 150 μm, the structural morphology of the wake vortex has basically recovered.

The analysis shows that under clean air conditions and at smaller angles of attack, the presence of particles has a relatively weak effect on the flow field, causing only slight disturbances in the pressure field and velocity field. However, under larger angle of attack conditions, the influence of particles on the airflow field around the airfoil significantly increases, and the degree of influence exhibits certain characteristics with changes in particle size. Specifically, particles in the low-to-moderate Stokes number range (dp < 50 μm) cause the upper surface flow separation point to move forward significantly, resulting in earlier separation, accompanied by significant tangential flow and an increase in the scale of the wake zone. At the same time, a large number of particles are sucked into the tail vortex area. As the Stokes number increases into a higher regime (dp ≥ 150 μm), the inertial particles suppress the flow separation, and their impact on the large-scale flow field weakens, causing it to approach the clean air reference state. The flow characteristics are close to the reference state under clean air conditions.

The primary reason for vortex shedding in the NACA 0012 airfoil is the development of a significant adverse pressure gradient on the airfoil’s upper surface at elevated angles of attack, leading to boundary layer separation. This results in the instability of the separated shear layer, which subsequently transforms into a periodic pattern of vortex shedding. This phenomenon has a similar dynamic mechanism to the instability phenomenon in turbine thermal shock tests [44]. A large angle of attack causes the airflow to undergo significant deceleration and pressure recovery after passing the point of minimum pressure on the upper surface of the airfoil. Due to kinetic energy dissipation, fluid elements in the viscous-dominated boundary layer cannot overcome the reverse pressure gradient and thus undergo flow separation near the trailing edge. However, the free shear layer formed by separation is inherently unstable and quickly curls up to form discrete concentrated vortices. As these vortices develop downstream, their self-induced velocity field interferes with and ultimately causes mature vortices to periodically detach from the trailing edge of the airfoil, forming a characteristic vortex shedding field accompanied by strong unsteady pressure fluctuations.

3.1.2. The Effect of Particle Size on the Aerodynamic Structure of Airfoils

In northwestern China, sand and dust particles with diameters from 10 μm to 150 μm account for a significant proportion of typical sandstorms [45]. This study investigated the effect of particle inertia on airfoil aerodynamics by comparing the clean air condition to two laden flows with differing Stokes numbers, achieved using 90 μm and 150 μm particles. In the simulation, the angle of attack was 6° and the Reynolds number was Re = 1.6 × 10⁵, both of which remained consistent with the verified operating conditions.

The simulation results are shown in Figure 8. It can be seen that under a 6° angle of attack, when the particle diameter is small, the particles have little effect on the pressure on the wing surface. Its surface pressure curve basically coincides with the surface pressure curve of clean air. However, at the higher Stokes number associated with the 150 μm particles, the pressure coefficient on the airfoil pressure surface is lower than in clean air and the corresponding value of 90 μm. The pressure coefficient of the suction surface is higher than that of clean air and the corresponding value of 90 μm. At the wing tip, under 150 μm conditions, the surface pressure on both the pressure side and suction side is lower than that under clean air and 90 μm conditions.

This phenomenon occurs because an increase in the Stokes number intensifies the inertial effect of the particles, leading to increased momentum exchange between the particles and the fluid. On the pressure side, larger particles deviate from the streamline trajectory due to inertia and directly collide with the wall surface, resulting in local momentum loss. This weakens the boundary layer acceleration effect, causing the static pressure value to be lower than that of clean air conditions. On the suction side, particle inertia inhibits the tendency of fluid to separate under a reverse pressure gradient, maintaining a higher energy boundary layer through enhanced turbulent mixing. This raises the local static pressure value. This discrepancy arises due to the interaction between the pressure gradient direction on the wing surface and the inertial behavior of the particles: Under pressure, the high-pressure zone at the leading edge causes particles to move outward, exacerbating wall collision losses. The reverse pressure gradient on the suction side causes particles to migrate toward the wall, enhancing energy transport near the wall. This causes a pressure reduction effect on the pressure side and a pressure increase effect on the suction side for 150 μm particles.

3.2. Erosion Rate Analysis Considering Stokes Numbers

The introduction of the Stokes number can deepen our understanding of the nature of erosion and improve the reliability and accuracy of predictions. The erosion simulation study of Stk can provide key scientific basis for the erosion-resistant design, material selection, and protection of airfoils, ensuring the durability and operational economy of equipment [46]. Therefore, it is very meaningful to introduce Stk into the wing erosion process.

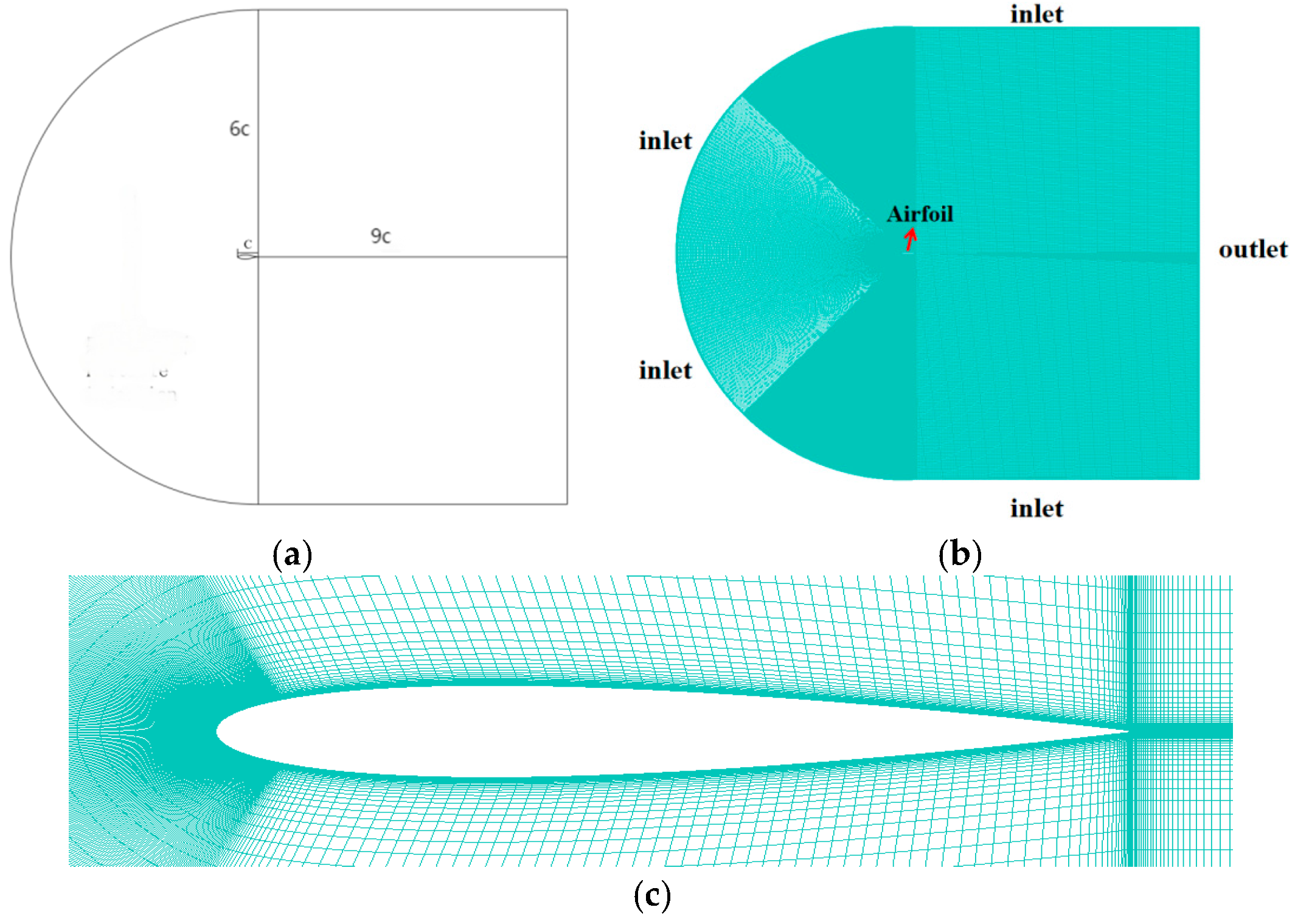
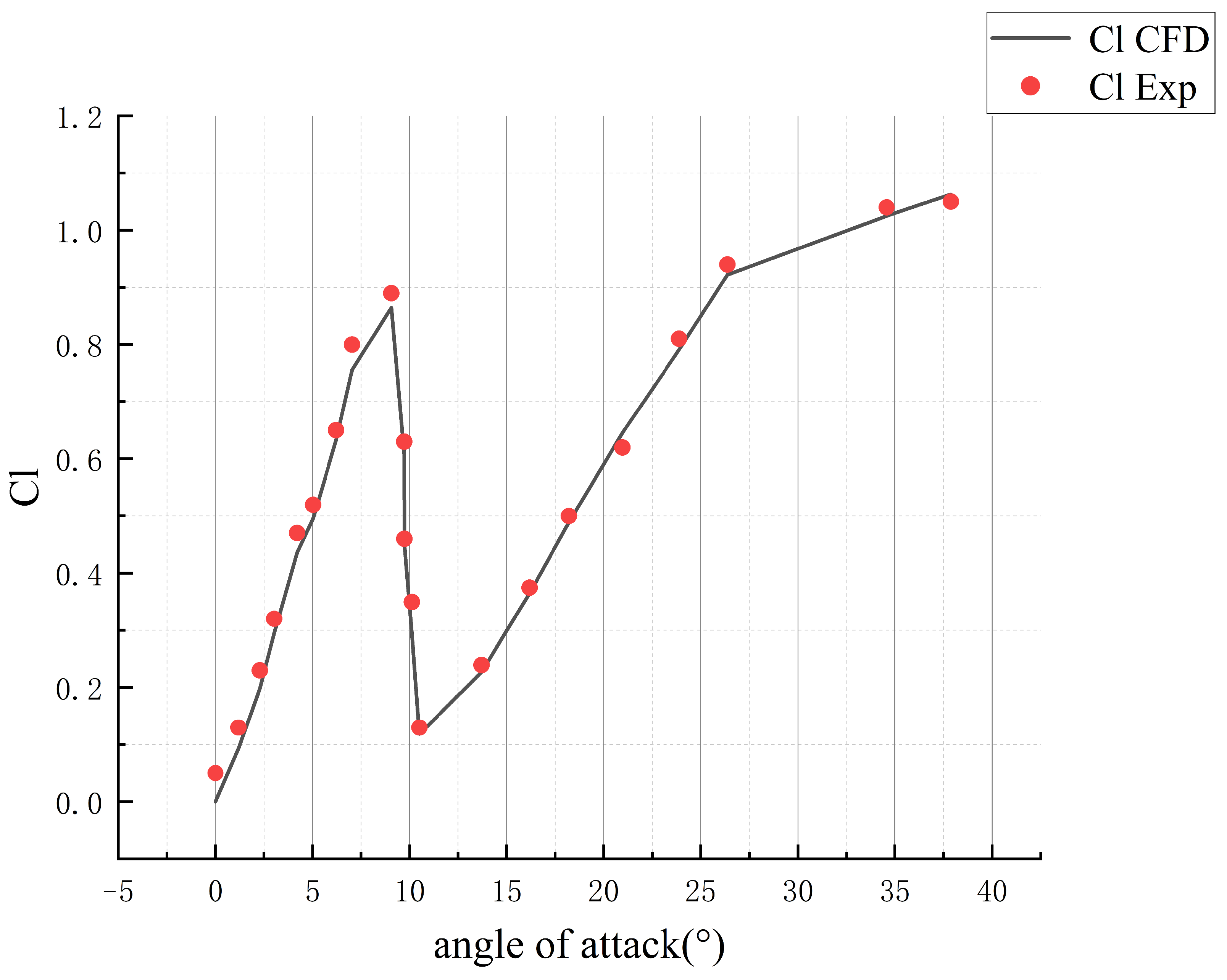
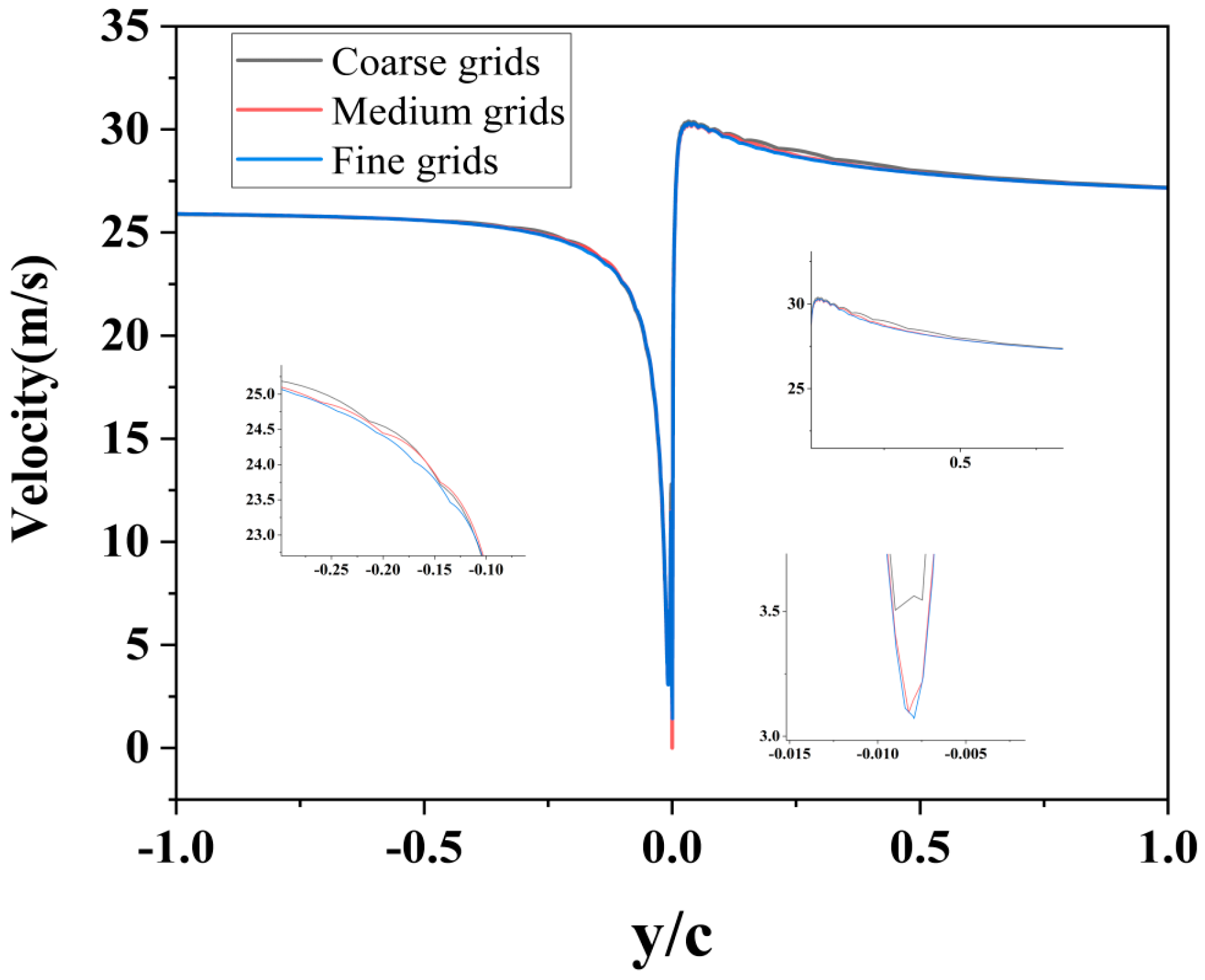
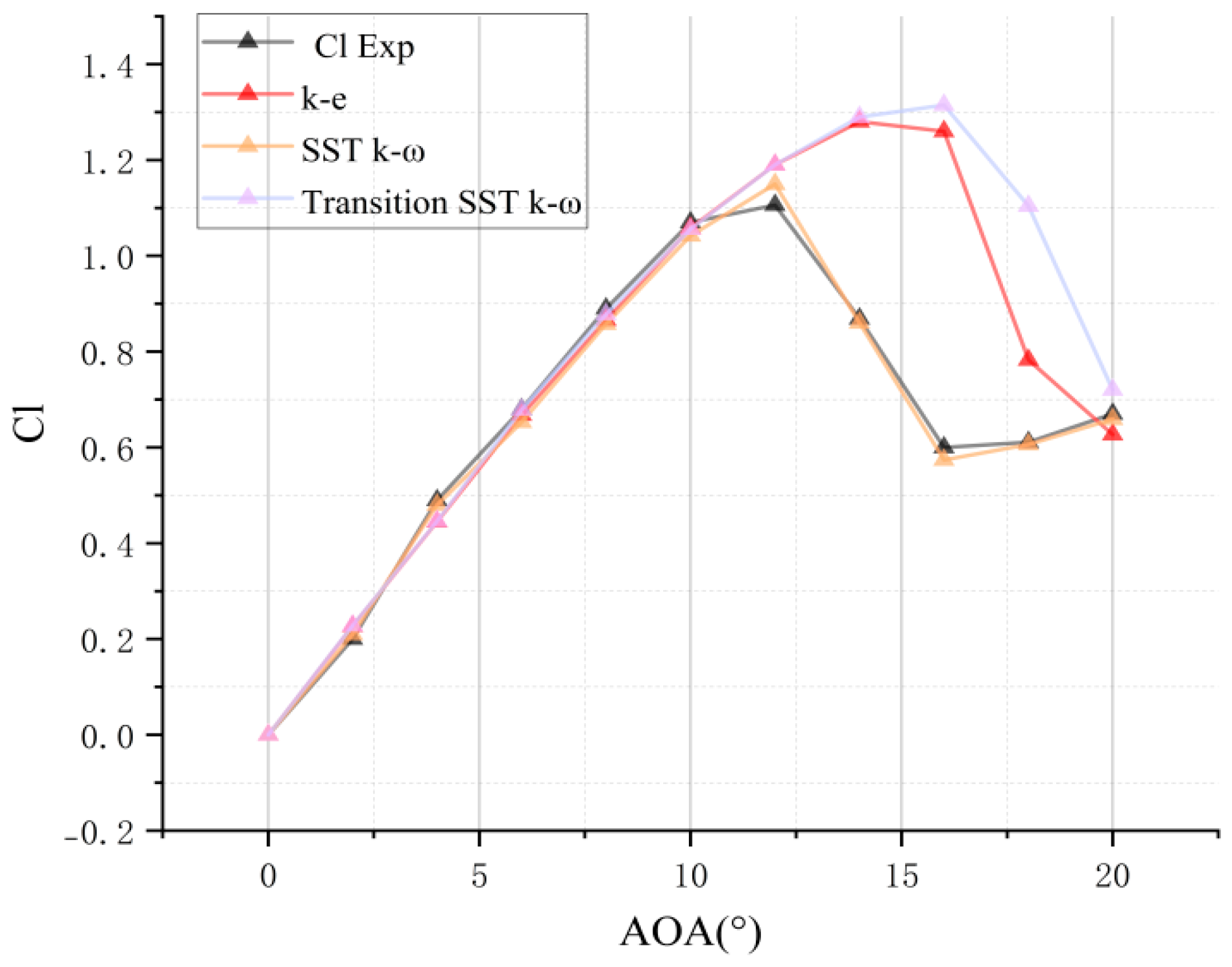
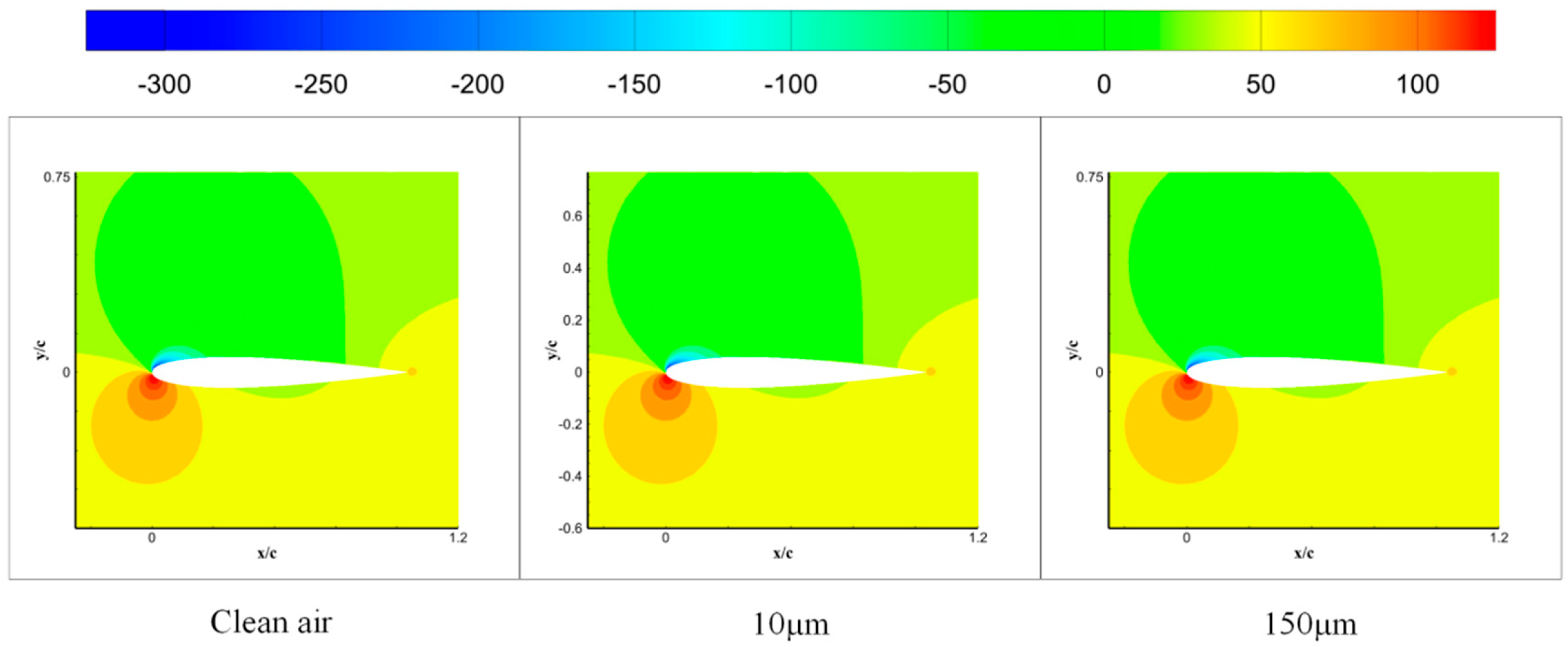
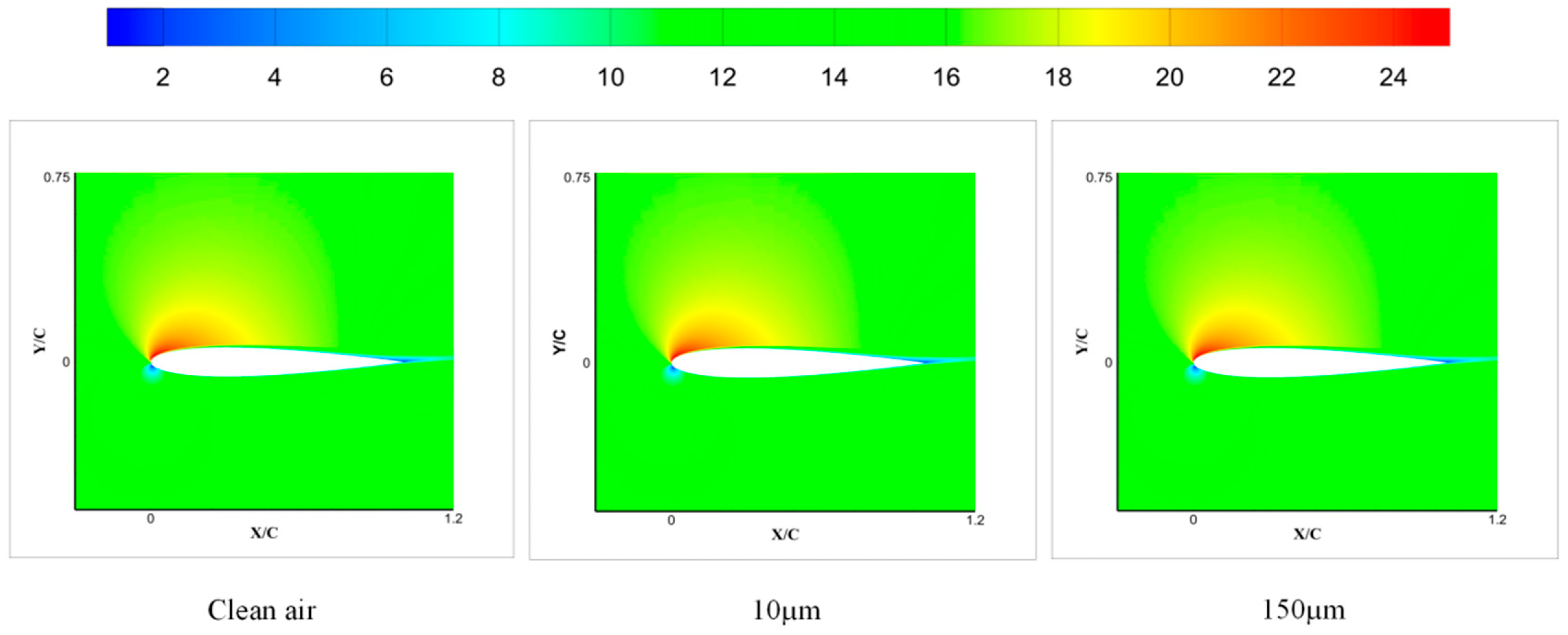
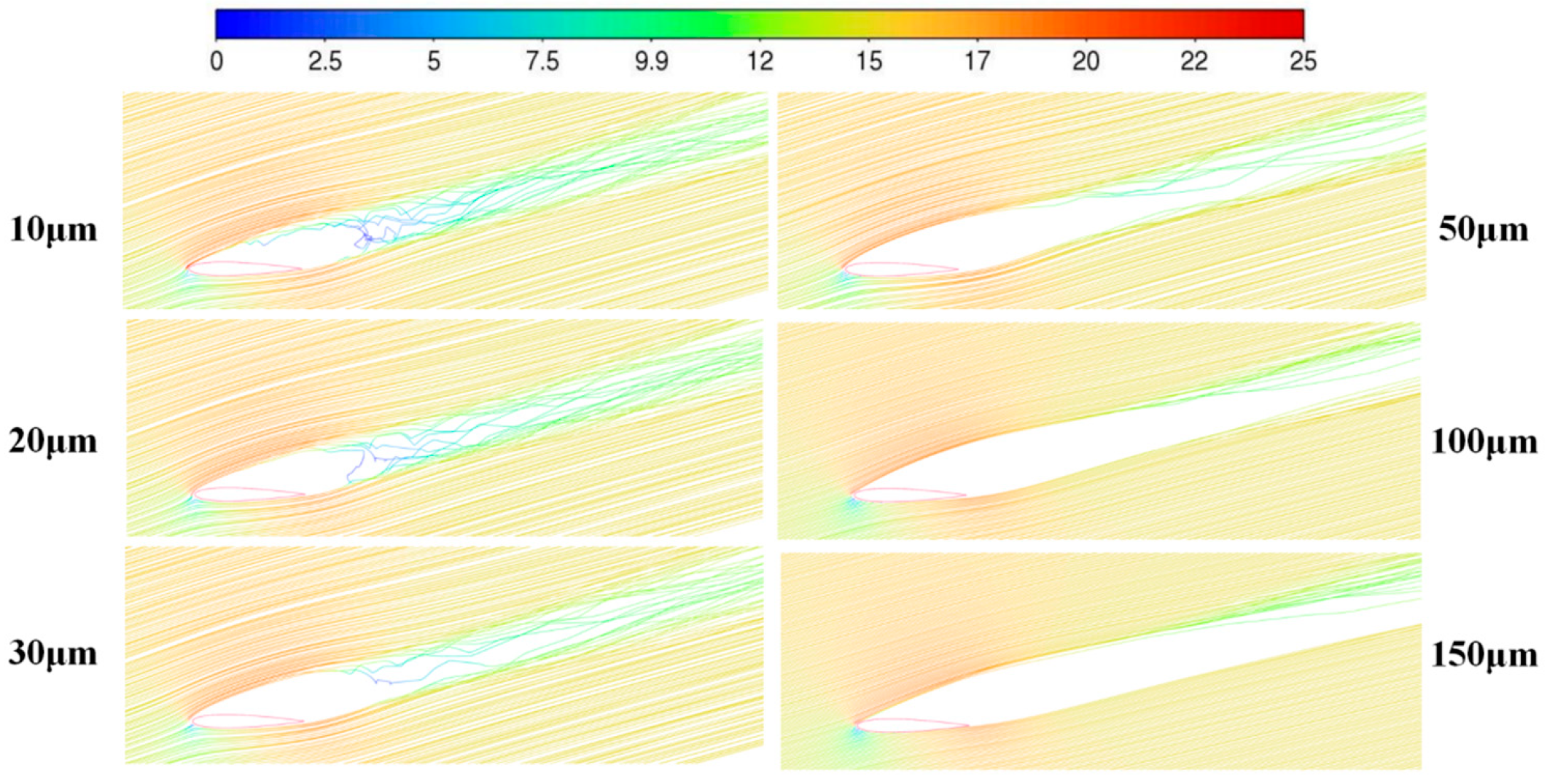
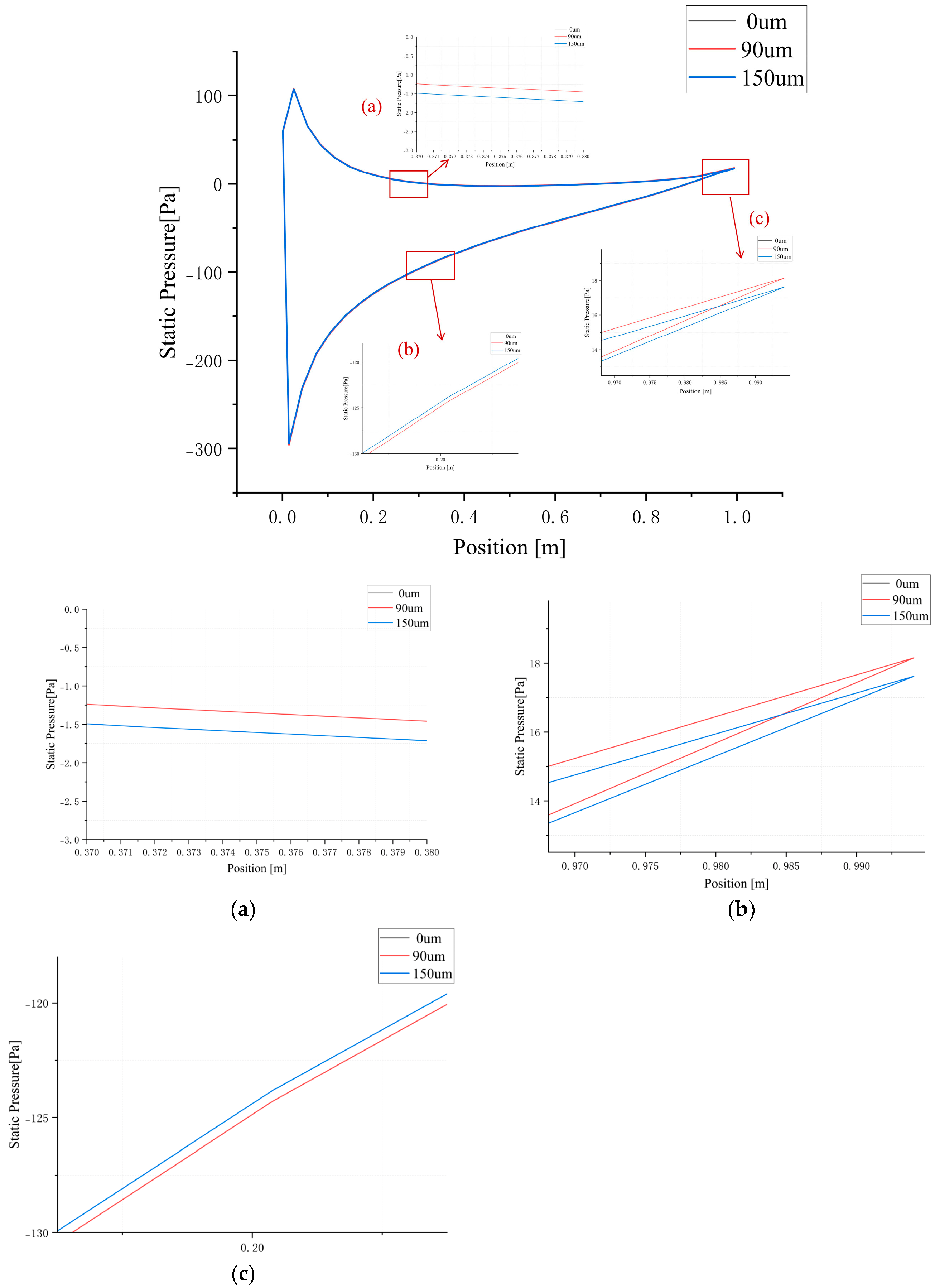
3.2.1. Consider the Velocity Erosion Analysis of the Stokes Number

Onshore wind turbines generate electricity at wind speeds ranging from approximately 3–4 m/s to 20–25 m/s. The maximum power output range starts at a rated wind speed of approximately 12–15 m/s and ends at a cut-out wind speed of approximately 20–25 m/s [47]. Therefore, the speed settings in subsequent simulations will basically follow the actual conditions in industry.

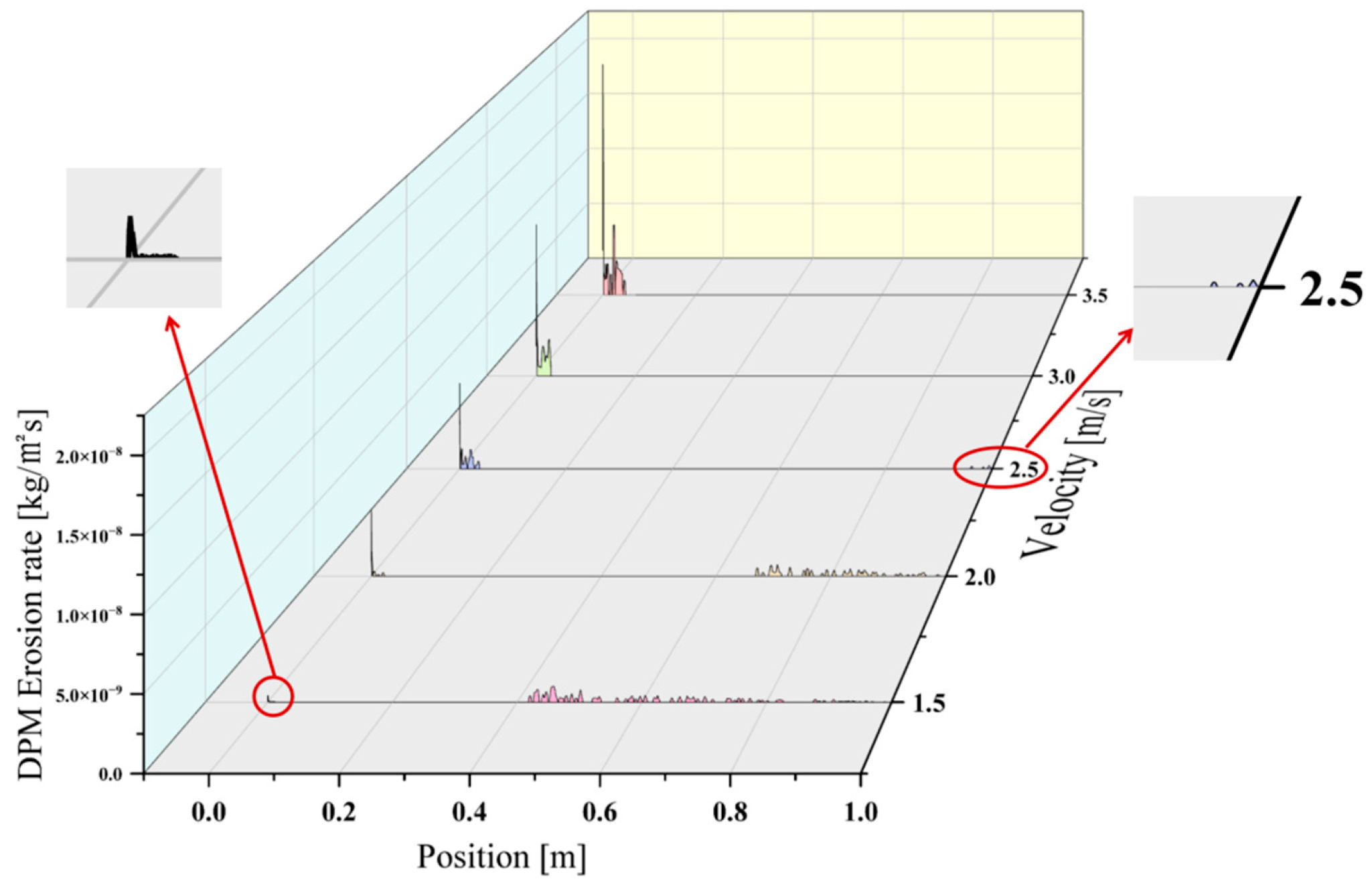
Figure 9 shows the erosion rate distribution of particles with a density of 2800 kg/m³ and a diameter of 50 μm under conditions of 1.5 m/s, 2 m/s, 2.5 m/s, 3 m/s, and 3.5 m/s, respectively, under the condition of Stk << 1. As shown in the figure, at a speed of 1.5 m/s, the peak erosion rate reaches a value of 1.03 × 10⁻⁹ kg/m²s. Erosion occurs 0.45 m from the leading edge. The average erosion rate across the wing is 2.43 × 10⁻¹⁰ kg/m²s. As the speed increases, when the speed reaches 2 m/s, the peak erosion rate reaches a value of 4.81 × 10⁻⁹ kg/m²s. Erosion occurs 0.0001 m from the leading edge. The average erosion rate across the wing is 4.32 × 10⁻¹⁰ kg/m²s. When the speed increases to 2.5 m/s, the peak erosion rate reaches a value of 6.59 × 10⁻⁹ kg/m²s. The average erosion rate across the wing is 1.03 × 10⁻⁹ kg/m²s. Erosion occurs 0.0001 m from the leading edge. When the speed increases to 3 m/s, the peak erosion rate reaches a value of 1.25 × 10⁻⁸ kg/m²s. Erosion occurs 0.0005 m from the leading edge. The average erosion rate across the wing is 2.74 × 10⁻⁹ kg/m²s. When the speed was increased to 3.5 m/s, the peak erosion rate reaches a value of 2.04 × 10⁻⁸ kg/m²s. Erosion occurs 0.0005 m from the leading edge. The average erosion rate across the wing surface is 3.98 × 10⁻⁹ kg/m²s.

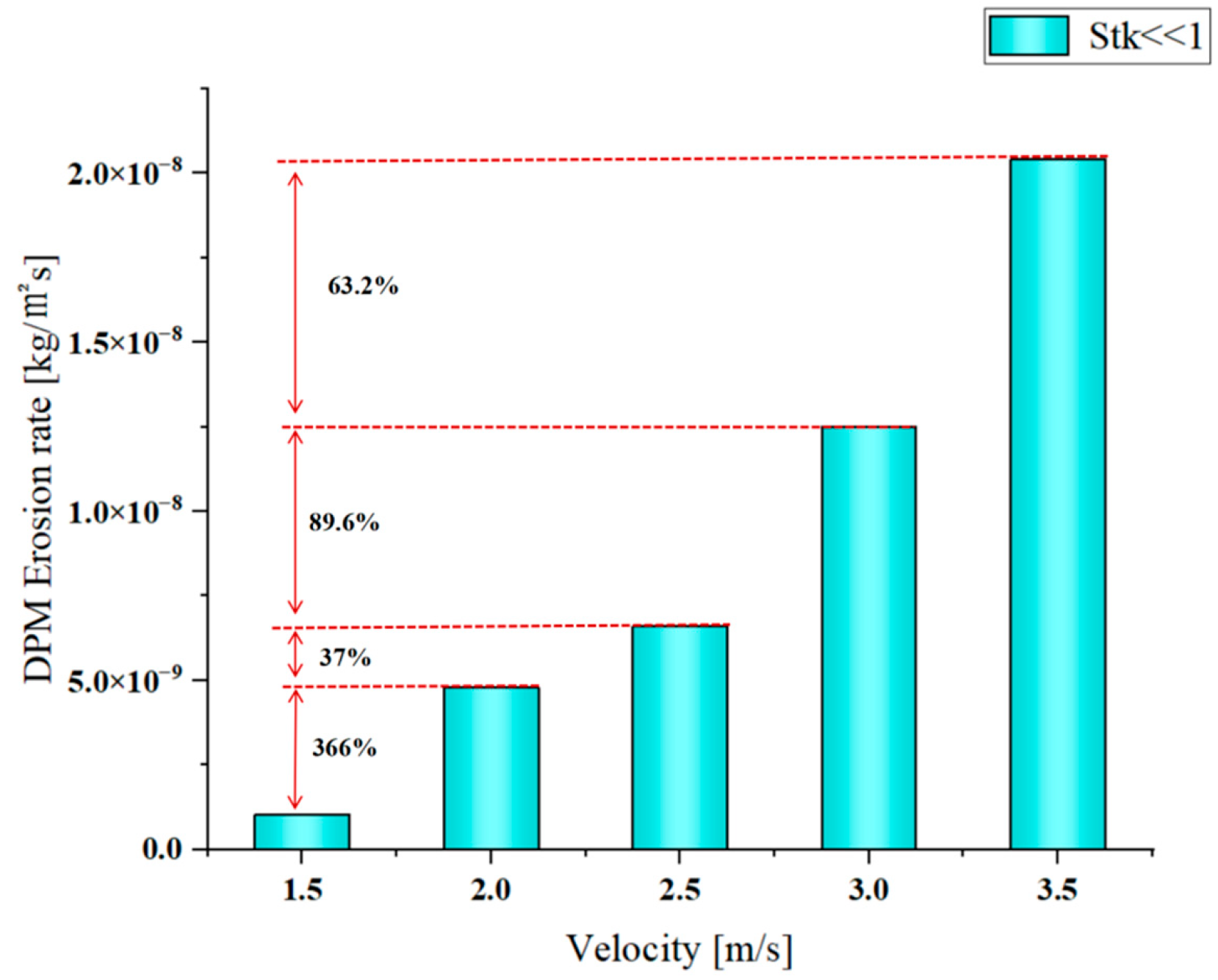
As shown in Figure 10, when Stk << 1, both the maximum erosion rate of the airfoil and the average erosion rate of the airfoil as a whole show a trend of increasing erosion rate with increasing speed. Therefore, the highest erosion rate occurs at a speed of 3.5 m/s. Taking a speed of 1.5 m/s as the baseline, when the speed is increased to 3.5 m/s, the maximum erosion rate increases to 19.4 times the baseline, and the average erosion rate on the wing surface increases to 15.4 times the baseline. The main reason for this situation is the combined effect of the Stokes number, Reynolds number, and particle kinetic energy. Particles can move well along streamlines at low Stk, but Stk increases with increasing velocity, indicating that the inertial effect of particles gradually increases, and more particles may collide with the wing surface. At a speed of 1.5 m/s, the boundary layer is relatively thick at approximately 3.12 mm, and the flow tends to be laminar. Particles can penetrate the boundary layer, but their inertia is low, so most particles follow the streamlines around the airfoil, resulting in a low collision rate. As the speed increases, the flow enters the transition zone, where laminar separation bubbles or partial turbulence occur. The boundary layer thins to approximately 2.4 mm, increasing particle inertia and causing more particles to collide with the surface, thereby increasing the erosion rate. As the speed continues to increase, turbulence effects intensify, and turbulent separation occurs at the trailing edge of the upper surface of the airfoil. The separation zone causes a reduction in local flow velocity and a shallower impact angle, thereby reducing the probability of particles colliding with the trailing edge of the airfoil.

As shown in Figure 11, as the speed increases from 1.5 m/s, the location of erosion also changes significantly. When the speed is 1.5 m/s, erosion mainly occurs in the rear part of the airfoil, at approximately 45% to 100% of the chord length. As speed increases, the area of erosion in the middle of the wing profile gradually decreases. When the speed increases to 2.5 m/s, erosion mainly occurs at the 5% chord length position before the leading edge of the airfoil and the 90% chord length position after the trailing edge. As the speed continues to increase, the collision between the rear edge particles and the airfoil gradually disappears, and erosion no longer occurs at the rear edge of the airfoil. Only erosion occurs at the leading edge. The reason for this phenomenon is that when the speed is 1.5 m/s, the flow field is in the laminar flow dominant zone, and NACA 0012 undergoes long laminar separation bubbles at an angle of attack of 6°. While particles in this regime closely follow the mean streamlines, they can still exhibit weak preferential accumulation in the high-strain-rate region near the flow reattachment point. The point of separation occurs roughly between 5% and 10% from the leading edge, while the reattachment location is situated approximately between 40% and 60% of the chord length from the leading edge. The flow velocity in the reattachment zone increases dramatically, accelerating particles and causing them to collide with the surface. The low-speed flow in the separation zone at the trailing edge causes the particles to settle, greatly increasing the probability of collision between the particles and the airfoil. This localized concentration enhancement, combined with particle acceleration upon reattachment, gives rise to the distinct erosion band observed at 45%–100% chord length.

When the speed reaches 2.5 m/s, the flow field enters the critical transition zone, with the separation point moving forward to 2%–5% of the chord length at the leading edge, and the reattachment point moving forward to 20%–30% of the chord length, while the separation bubble shortens. The shortening of the separation bubble causes an increase in the curvature of the leading edge streamline, while the increase in Stk causes the particles to collide with the leading edge due to inertia, resulting in erosion of the leading edge. Due to the forward shift in the reattachment point, the central particles flow close to the surface without any violent acceleration or diffusion collision phenomena occurring. The trailing edge is located in the turbulent separation zone, causing particles to be sucked in and collide with the wing surface, resulting in erosion. Concurrently, the effective Stk of the particles increases. For particles with Stk on the order of 0.1–1, the mechanism of clustering becomes most effective in the high-strain regions generated by the strong curvature of the flow around the leading edge. Consequently, the particle impacts become concentrated in the stagnation region and immediately downstream on the upper and lower surfaces, causing the erosion hotspot to shift decisively to the leading edge. When the speed increases to 3.5 m/s, the flow field becomes turbulent, the separation point moves forward significantly, and the separation bubble disappears. The streamlines bend sharply at the leading edge, and as Stk continues to increase, the particles cannot follow the streamlines and collide with the leading edge. The separation resistance of the rear edge turbulent boundary layer is enhanced, and the separation point disappears. As particles move along the surface to the trailing edge, their velocity decreases, and there is no separation zone to capture the particles, thus preventing erosion from occurring.

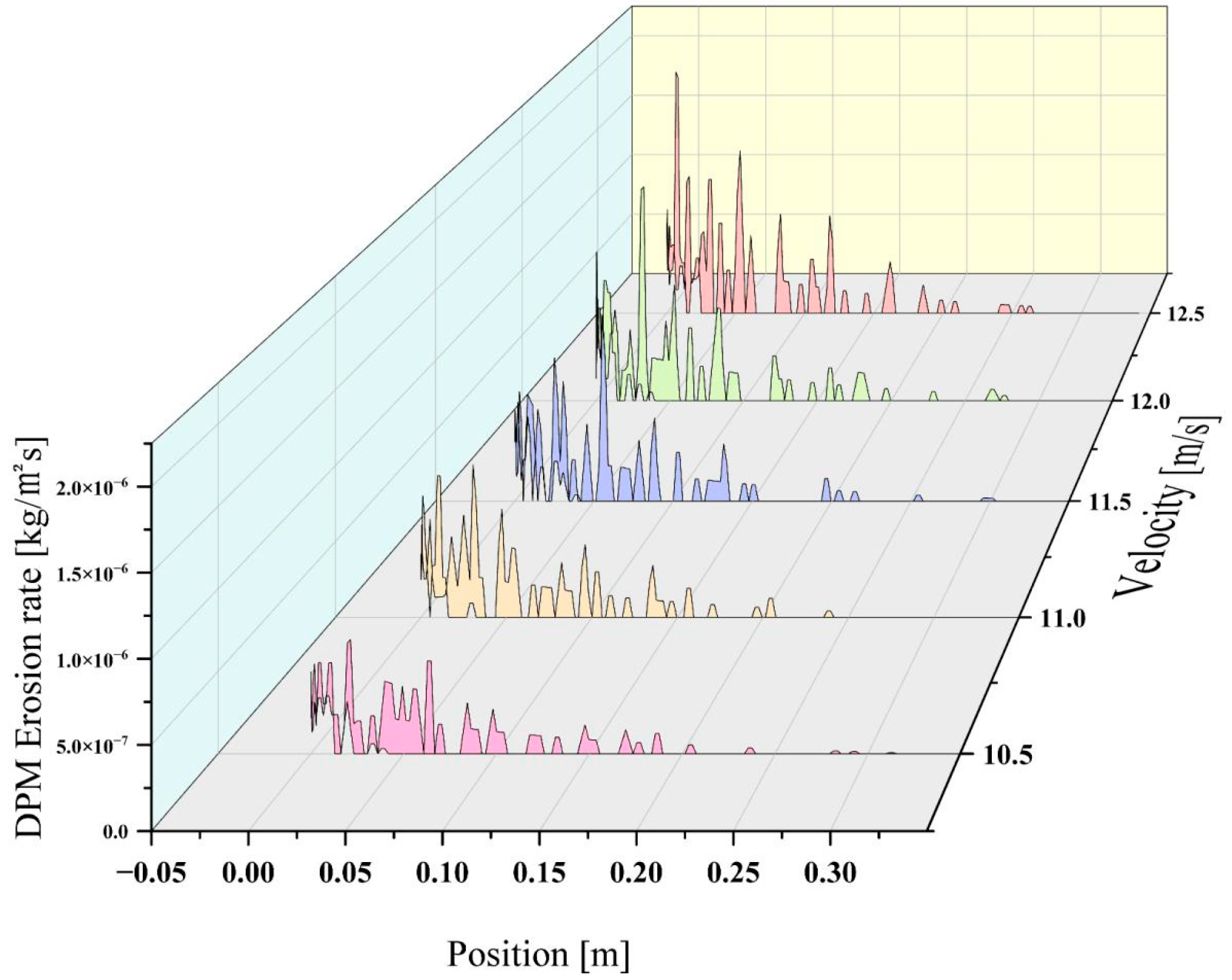
Figure 12 shows the erosion rate distribution of particles with a density of 2800 kg/m³ and a diameter of 100 μm under conditions of 10.5 m/s, 11 m/s, 11.5 m/s, 12 m/s, and 12.5 m/s, respectively, under Stk ≈ 1 conditions. At this point, the Stk ranges from 0.91 to 1.09. At a speed of 10.5 m/s, the peak erosion rate reaches a value of 6.93 × 10⁻⁷ kg/m²s, and the average erosion rate across the wing is 2.19 × 10⁻⁷ kg/m²s. Erosion occurs 0.021 m from the leading edge. At a speed of 11 m/s, erosion occurs 0.03 m from the leading edge. The peak erosion rate reaches a value of 1.01 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 2.98 × 10⁻⁷ kg/m²s. When the speed reaches 11.5 m/s, the highest erosion point occurs at a distance of 0.05 m from the leading edge, the peak erosion rate reaches a value of 1.28 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 3.27 × 10⁻⁷ kg/m²s. When the speed reaches a maximum of 12.5 m/s, the peak erosion rate reaches a value of 1.97 × 10⁻⁶ kg/m²s. The average erosion rate across the wing surface is 4.33 × 10⁻⁷ kg/m²s. Erosion occurs 0.006 m from the leading edge.

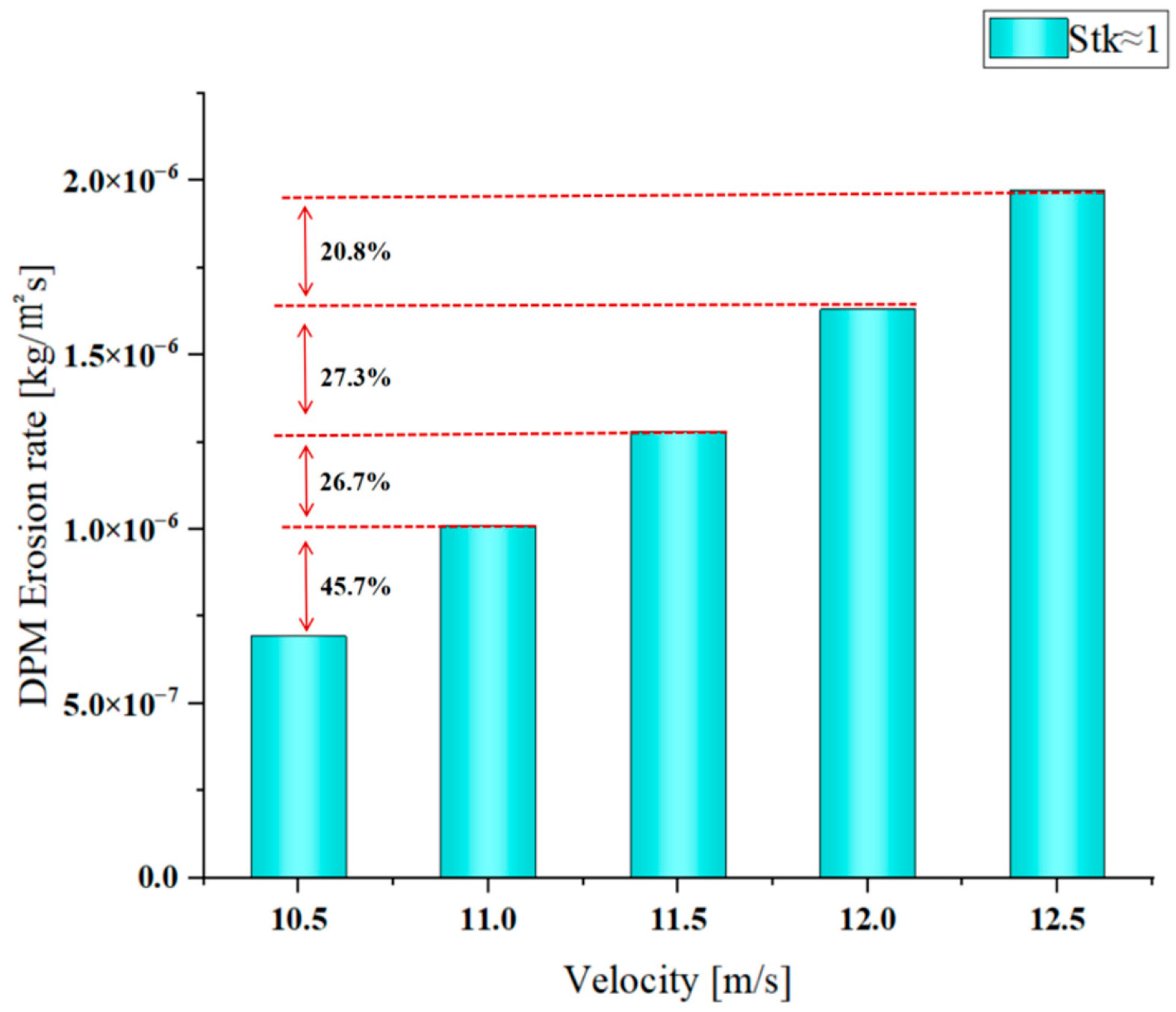
As shown in Figure 13, with the speed gradually increasing from 10.5 m/s, the maximum erosion rate and the erosion rate of the airfoil surface show a clear trend of increasing with speed. When the speed increased from 10.5 m/s to 12.5 m/s, the maximum erosion rate increased by 180% and the average erosion rate increased by 97%. The reasons for this phenomenon are as follows: From the perspective of particle characteristics, Stk ≈ 1 indicates that the particles partially follow the fluid, but compared to Stk << 1, the inertial effect is significant, causing the particles to collide with the surface at a higher energy. As speed increases, particle inertia increases, increasing the frequency and kinetic energy of collisions, thereby increasing the erosion rate. Under a small attack angle, the particles collide in a “sliding” manner, increasing the cutting effect. As the velocity increases, the ability of particles to penetrate the surface boundary layer is enhanced, resulting in more particles effectively impacting the surface and increasing the overall erosion rate.

As shown in Figure 12 and Figure 14, erosion occurs at the leading edge of the airfoil under all speed conditions. However, as speed increases, there is a tendency for erosion to gradually concentrate toward the leading edge. This situation occurs because particles are more likely to follow curved streamlines at a speed of 10.5 m/s. Some particles bypass the leading edge, resulting in fewer impacts in the stagnation zone and relatively divergent erosion locations. As particle velocity increases, the Stokes number gradually increases, and the particle inertia becomes greater, making it difficult to deflect along the streamline. This situation leads to more particles colliding with the surface, with impacts concentrated in the landing zone and higher energy, while the area of the high-damage core zone shrinks slightly. The “impact width” near the stagnation point increases, and erosion extends to both sides of the leading edge and part of the downstream area. At the leading edge of the wing profile, the streamline curvature is most pronounced. As speed increases, fluid acceleration increases and streamline curvature increases. The erosion cloud map shows that the location of the highest erosion rate has changed from the leading edge of the lower surface to the leading edge of the upper surface. The reason for this phenomenon is that as speed increases, the inertial separation of the high curvature area on the upper surface becomes more intense, and the impact on the upper surface becomes more concentrated, resulting in an increase in the erosion rate at a single location on the leading edge of the upper surface. The flat streamlined lower surface allows particles to slide easily and disperse energy, while the erosion rate at a single position at the leading edge of the lower surface decreases. Under these conditions, collision position transition occurs.

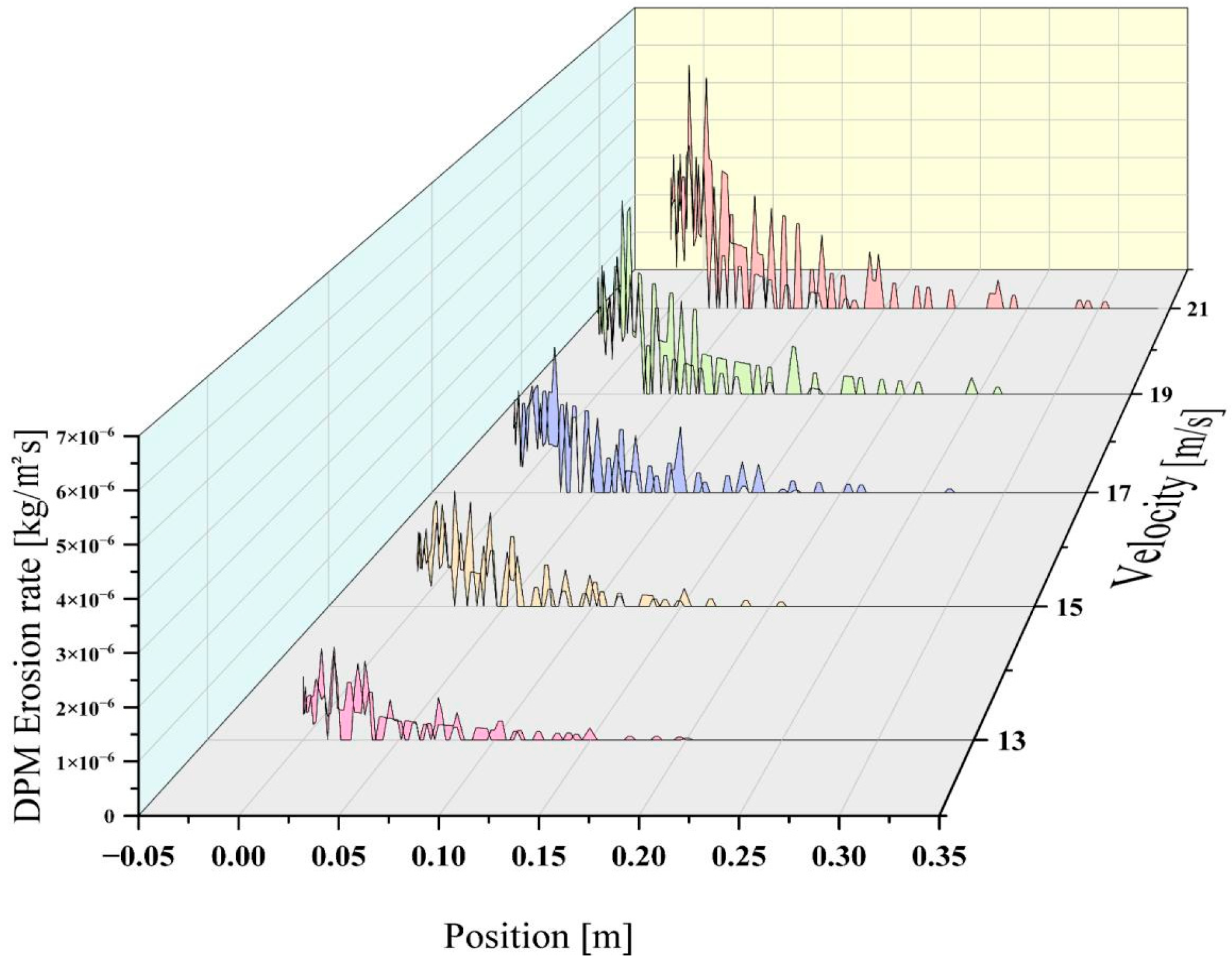
Figure 15 shows the erosion rate distribution of particles with a density of 2800 kg/m³ and a diameter of 300 μm under conditions of 13 m/s, 15 m/s, 17 m/s, 19 m/s, and 21 m/s, respectively, under conditions of Stk >> 1. As shown in the figure, at a velocity of 13 m/s, the peak erosion rate reaches a value of 1.79 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 5.17 × 10⁻⁷ kg/m²s. Erosion occurs 0.016 m from the leading edge. As the velocity rises to 15 m/s, the peak erosion rate reaches a value of 2.42 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 7.86 × 10⁻⁷ kg/m²s. Erosion occurs 0.02 m from the leading edge. As the velocity rises to 17 m/s, the peak erosion rate reaches a value of 3.29 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 1.08 × 10⁻⁶ kg/m²s. Erosion occurs 0.025 m from the leading edge. As the velocity rises to 19 m/s, the peak erosion rate reaches a value of 4.7 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 1.32 × 10⁻⁶ kg/m²s. Erosion occurs 0.0016 m from the leading edge. When the speed was increased to 21 m/s, the peak erosion rate reaches a value of 6.31 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 1.74 × 10⁻⁶ kg/m²s. Erosion occurs 0.0012 m from the leading edge.

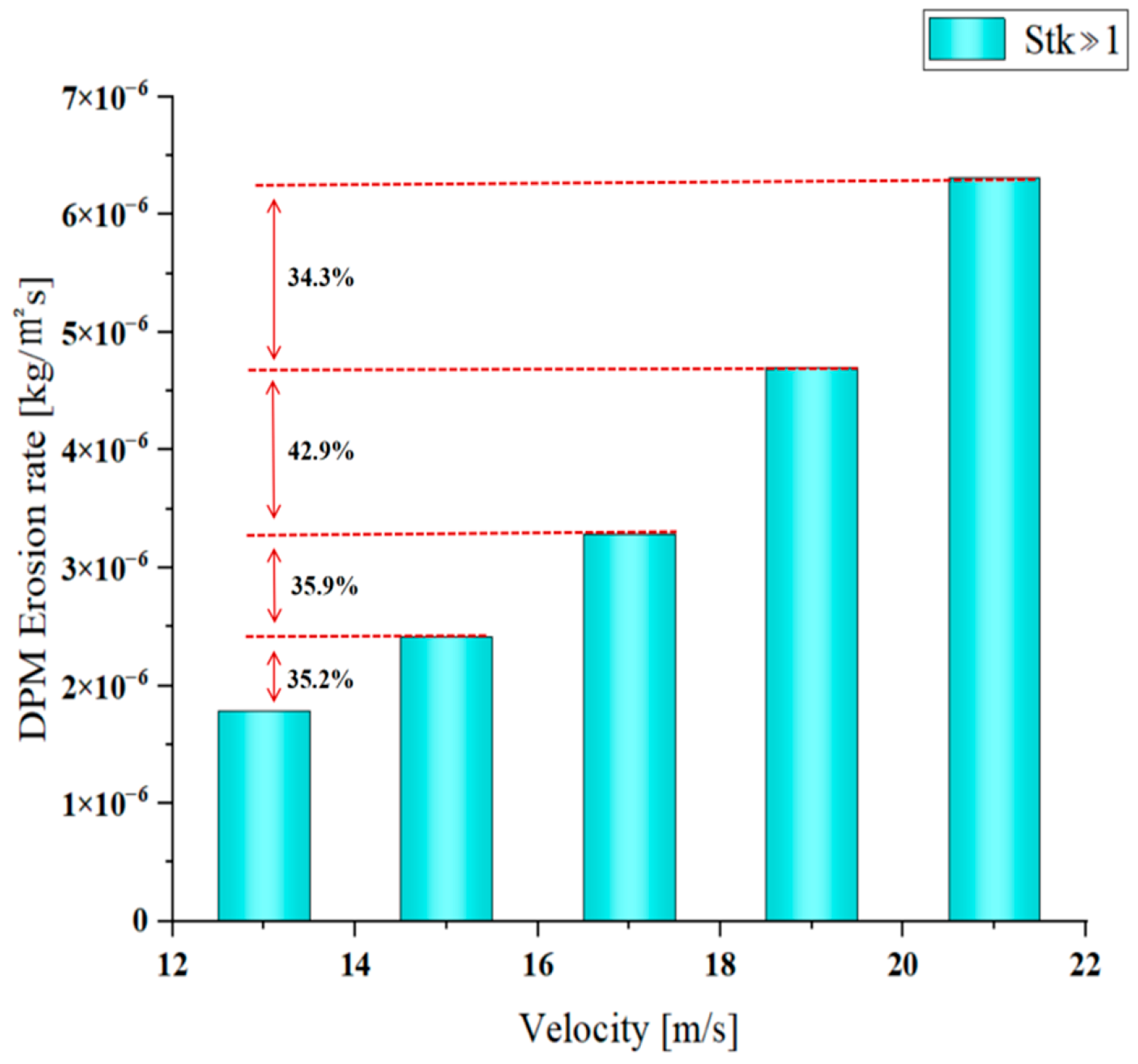
As shown in Figure 16, when Stk >> 1, both the maximum erosion rate of the airfoil and the average erosion rate of the airfoil as a whole show a trend of increasing erosion rate with increasing speed. Therefore, the highest erosion rate occurs at a speed of 21 m/s. Based on a speed of 13 m/s, when the speed is increased to 21 m/s, the maximum erosion rate increases by 252%, and the average erosion rate of the airfoil surface increases by 234%. From the perspective of particle characteristics, when Stk >> 1, it indicates that the particles cannot completely follow the airflow streamlines but tend to collide with the wing surface. Especially at an angle of attack of 6 degrees, the leading edge and upper surface are susceptible to impact. As the speed increases, the Stk increases accordingly, improving collision efficiency and intensifying erosion. At small attack angles, shallow-angle impacts tend to produce micro-cutting effects, which can easily cause noticeable collision effects. At the same time, an increase in the tangential momentum of the particles amplifies this cutting effect, resulting in a higher erosion rate. Given that air serves as a fluid medium, when exposed to high-inertia particles such as gravel, the fluid’s drag force acting on these particles is relatively weak, causing their motion to be predominantly governed by inertia. Therefore, when the speed increases, the change in particle kinetic energy is more directly converted into impact energy rather than being dissipated by the fluid. Three factors combined to cause an increase in erosion rates.

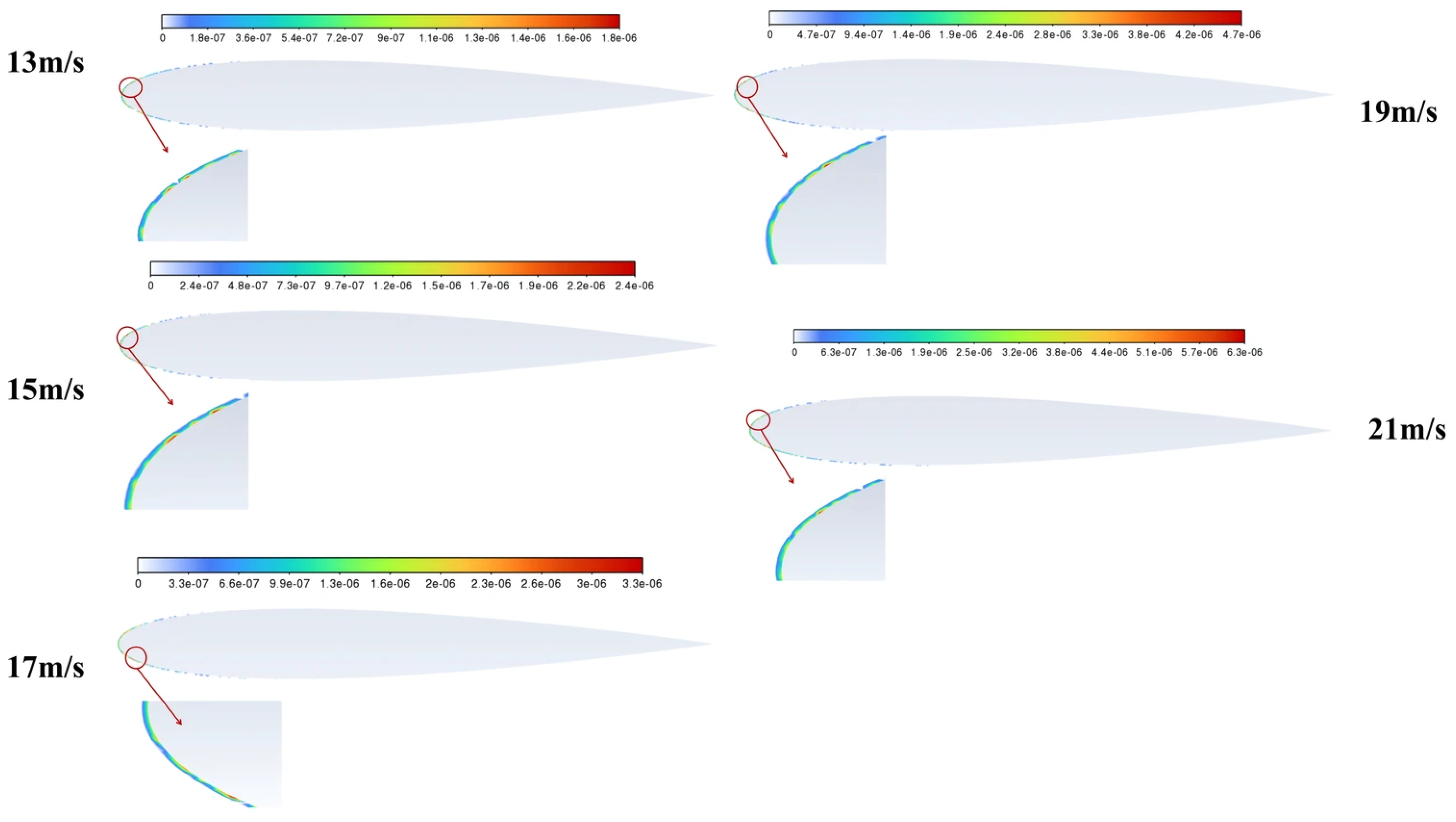
As can be seen from Figure 15 and Figure 17, with the increase in speed, the erosion area on the fan blade surface expands progressively. Combining the erosion cloud diagrams at different speeds in Figure 17, it becomes evident that erosion spread across the wing surface is predominantly concentrated on the wing’s lower side, while the erosion area on the upper surface remains basically unchanged. When Stk >> 1, particle inertia dominates, and particles cannot completely follow the airflow streamlines. As speed increases, Stk increases, particle inertia becomes stronger, and particles are more likely to deviate from the streamlines and collide with surfaces. At an angle of attack of 6°, for a symmetrical airfoil such as NACA0012, the airflow on the upper surface accelerates, and the streamline curvature is small, especially in the middle of the chord length to the trailing edge. Particles tend to maintain linear motion under the influence of inertia, but due to the straight streamlines, the impact location is concentrated near the leading edge. In the middle and rear sections, the streamlines are straight, and the particles are easily carried away by the airflow, with no significant change in the impact range. The airflow slows down on the lower surface, and the streamlines have a large curvature, making it difficult for particles to follow the curved airflow due to inertia. Some small inertial particles can follow the airflow around the surface. As the speed increases, it becomes more difficult for the particles to follow the airflow, and they are more likely to collide, causing the erosion area to expand toward the middle and rear edges.

3.2.2. Particle Density Erosion Analysis Considering the Stokes Number

To explore the impact of particle density on wind turbine blade erosion in real-world conditions, dust samples were collected from the airfoils of a wind farm in a certain region of Xinjiang and subjected to physical property analysis. The composition of the particles was analyzed using XRD, and by comparing with standard PDF cards, it was determined that the dust mainly consisted of quartz, magnesite, and limestone. Therefore, these three substances will be used as materials for analyzing the effect of particle density on wind turbine erosion in subsequent studies. Among them, the density distribution of silicon dioxide, calcium carbonate, and magnesium oxide is set at 2650 kg/m³, 2800 kg/m³, and 3580 kg/m³, respectively. Bagnold [48] explicitly adopted 2650 kg/m³ as the standard density value for sand particles in his classic wind tunnel experiments and theoretical derivations. Shao [49] clearly pointed out that the typical density of sand grains is 2650 kg/m³ when discussing particle kinetic parameters.

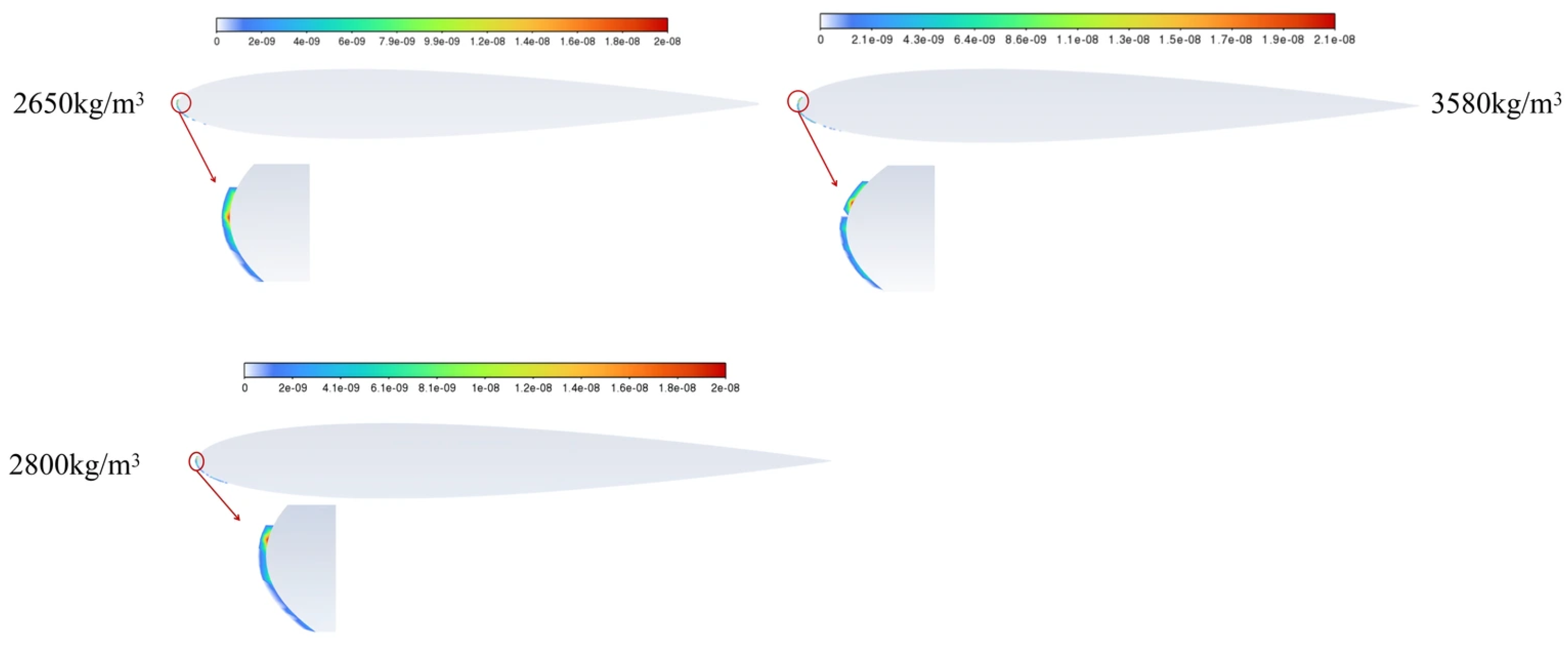
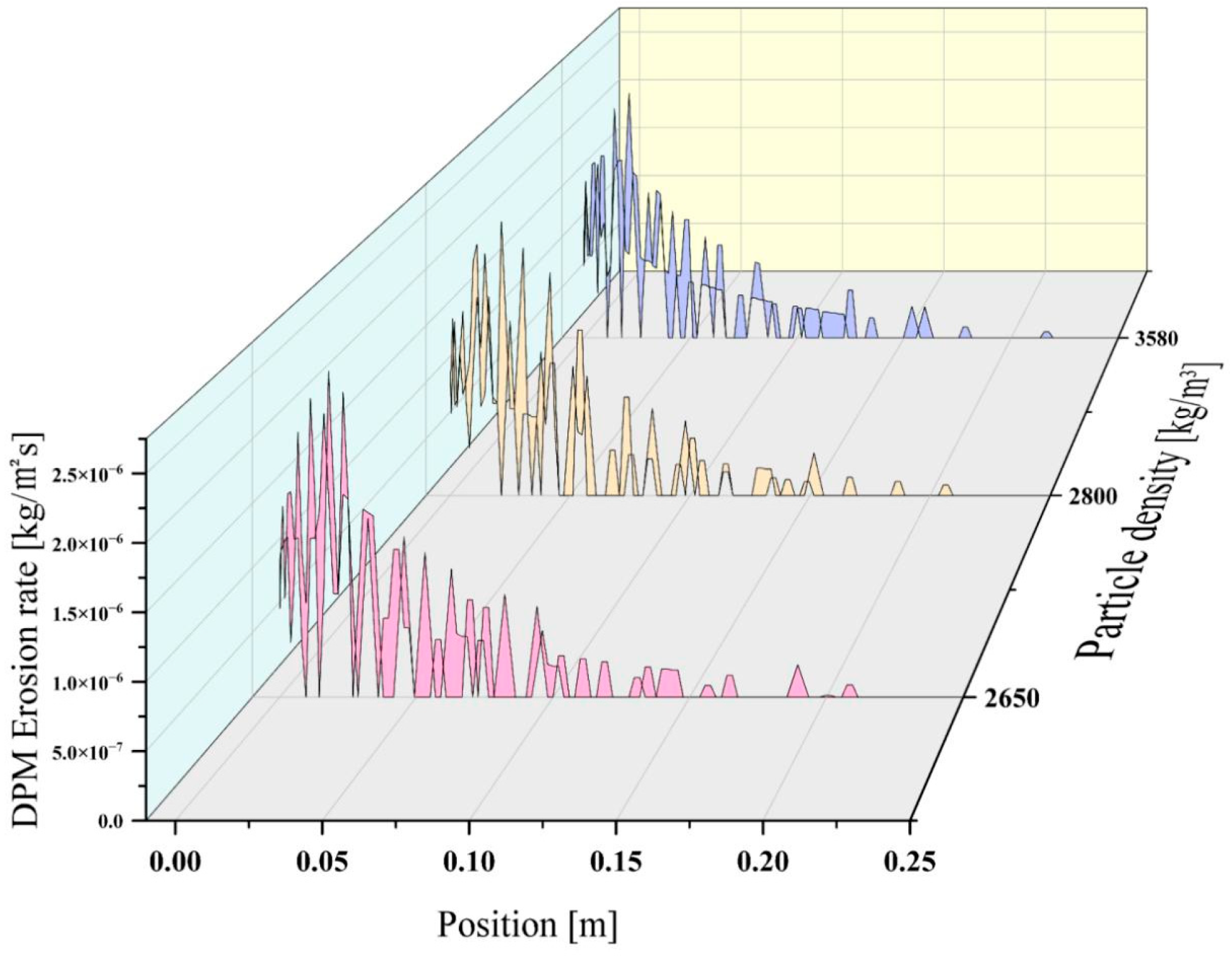
Figure 18 and Figure 19 show the erosion rate distribution and erosion cloud map for particles with densities of 2650 kg/m³, 2800 kg/m³, and 3580 kg/m³, respectively, and a particle size of 50 μm, when the incident velocity is 3.5 m/s and Stk << 1. Erosion occurs within the first 1% of the chord length of the airfoil under all three particle density conditions. As shown in the figure, when the particle density is 2650 kg/m³,the peak erosion rate reaches a value of 1.26 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 3.98 × 10⁻¹⁰ kg/m²s. Erosion occurs 0.0001 m from the leading edge. As the particle density increases, when the density reaches 2800 kg/m³, the peak erosion rate reaches a value of 2.04 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 4.32 × 10⁻⁹ kg/m²s. Erosion occurs 0.0005 m from the leading edge. When the particle density increases to 3580 kg/m³, the peak erosion rate reaches a value of 2.14 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 4.53 × 10⁻⁹ kg/m²s. Erosion occurs 0.0019 m from the leading edge.

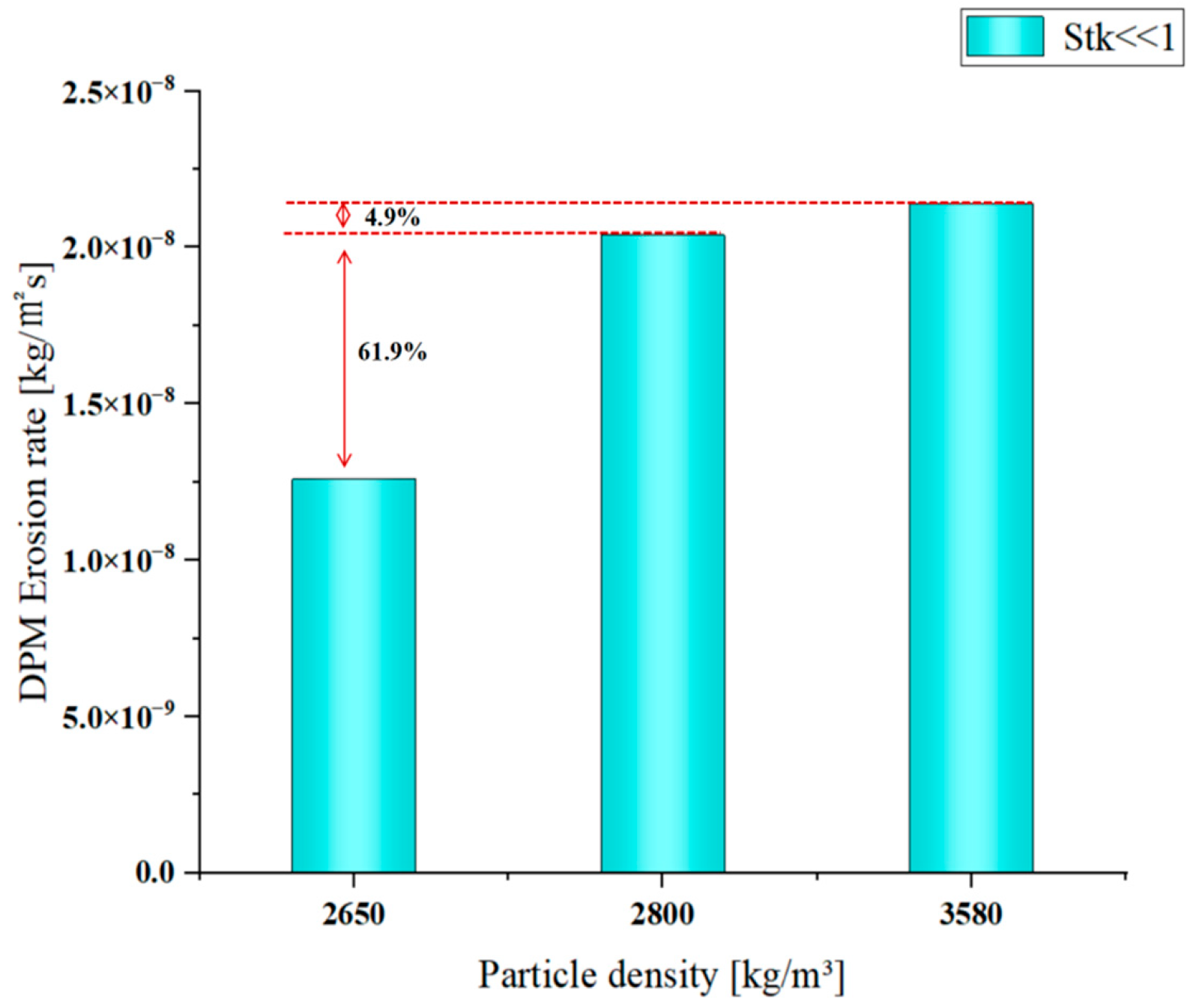
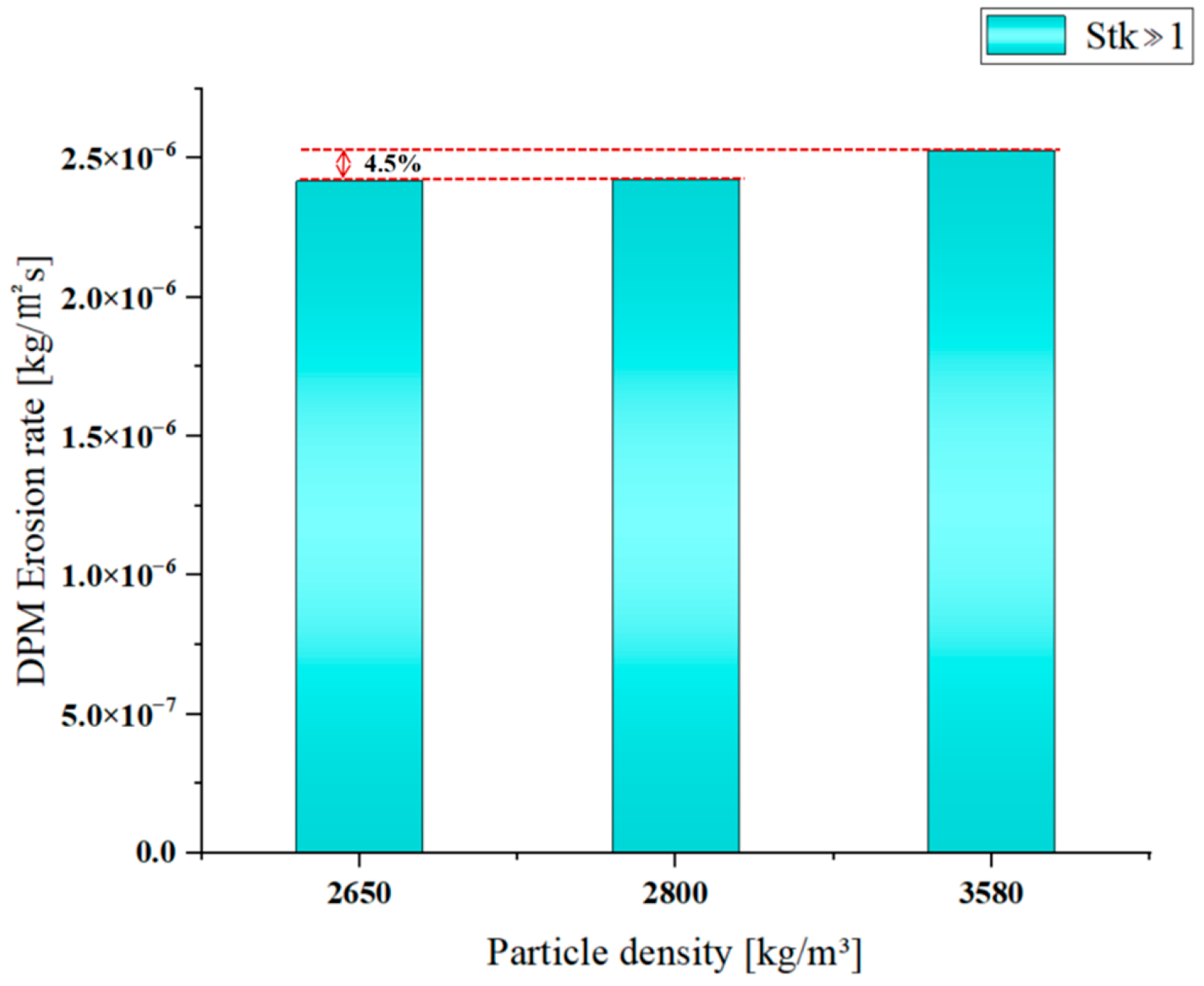
Based on particles with a density of 2650 kg/m³, when the particle density increases to 3580 kg/m³, the maximum erosion rate increases by only 69.8%. As shown in Figure 18 and Figure 20, with increasing particle density, both the peak and the average erosion rate on the airfoil surface increase. As shown in Figure 20, the location of the highest erosion rate tends to shift slightly backward as density increases. The erosion rate mainly depends on the kinetic energy of the particles hitting the surface and the frequency of impact. When the particle density increases from 2650 kg/m³ to 3580 kg/m³, the particle mass increases, resulting in a significant increase in the kinetic energy of the particles impacting the wing. Each impact transfers more energy to the wing surface, resulting in more significant erosion. In addition, because the particle concentration, fluid velocity, and flow field structure did not change, the collision frequency remained unchanged. Therefore, the increase in erosion rate is mainly driven by the increase in kinetic energy. The rearward shift in the maximum erosion rate position is related to the inertial behavior of particles and can be explained by the Stokes number. When Stk << 1, the particles follow the streamlines, but inertia cannot be ignored. An increase in Stk indicates that the particles have greater inertia and it is more difficult to follow the curvature of the fluid streamlines. In the flow field of an airfoil with an angle of attack of 6°, the fluid streamlines bend near the leading edge. When the particle density is low, it is easier to follow the streamline, and the impact points are concentrated at the leading edge or slightly forward. When the particle density is high, inertia is stronger, and particles tend to move in a straight line, causing the point of impact to move toward the rear. Therefore, there is a tendency for the location of the highest erosion rate to move backward, while the area of erosion on the wing surface also increases slightly.

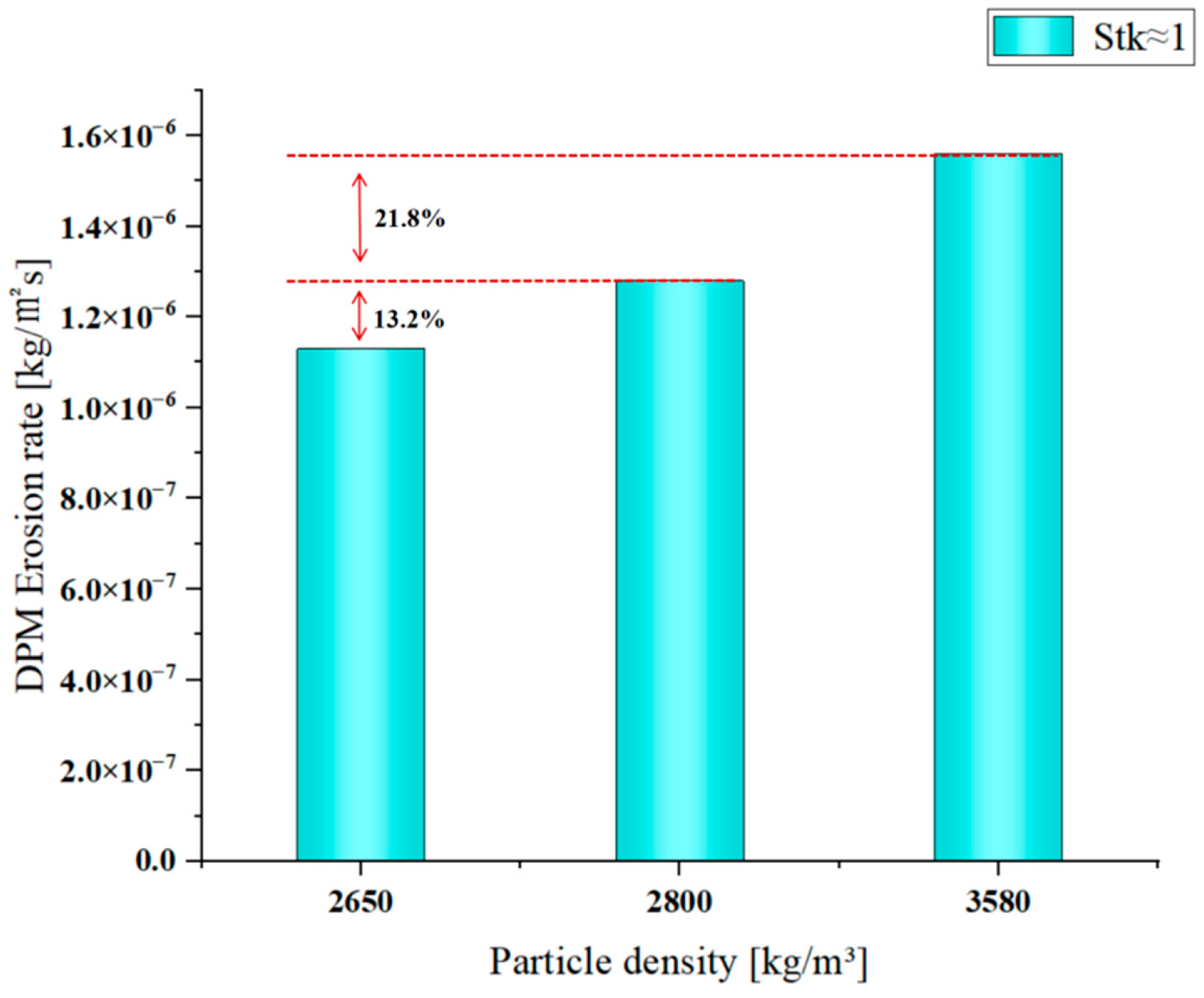
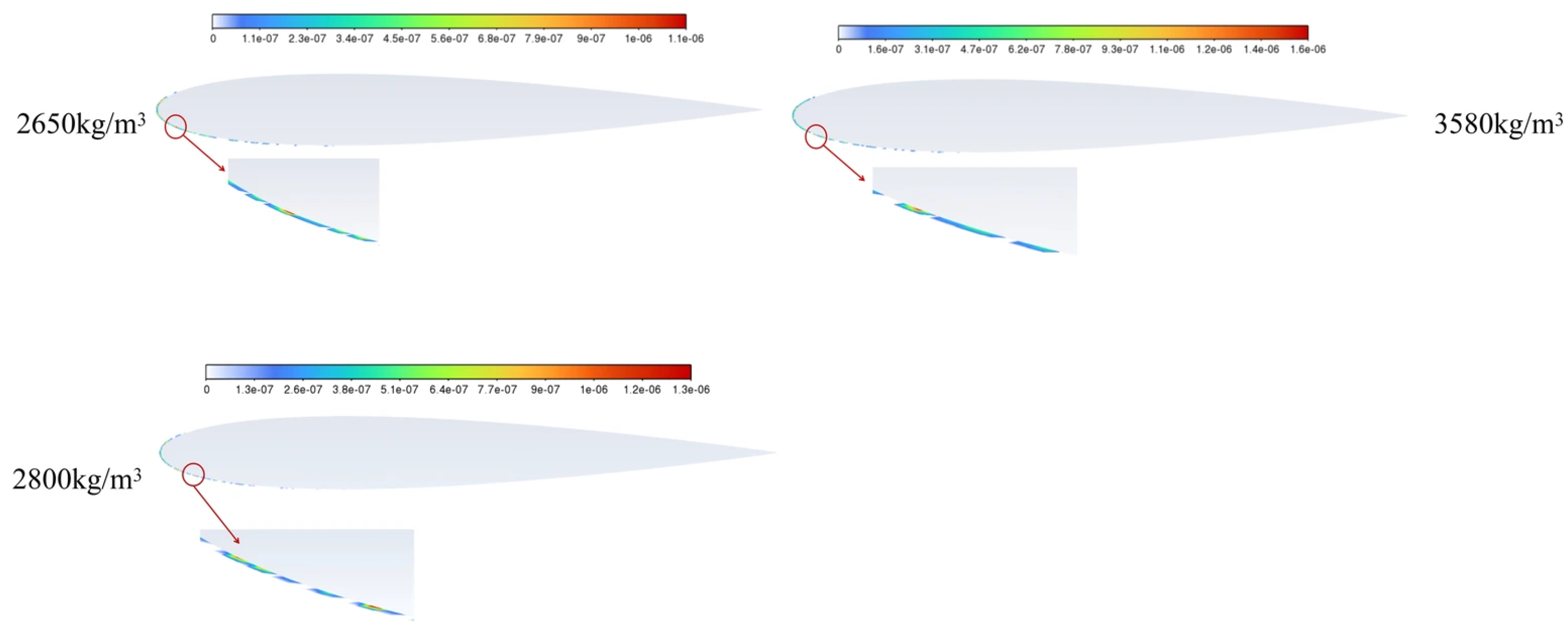
Figure 21, Figure 22 and Figure 23 show the erosion rate distribution diagrams, the highest erosion rate bar charts, and the erosion cloud diagrams for particles with densities of 2650 kg/m³, 2800 kg/m³, and 3580 kg/m³, respectively, as well as a particle size of 100 μm, when the incident velocity is 11.5 m/s and Stk ≈ 1. As illustrated in the figure, compared with particle erosion at low speeds, erosion range of the three types of particles expanded under conditions of increased speed and particle size. The erosion area has expanded to within the first 30% of the chord length of the airfoil. As shown in the figure, when the particle density is 2650 kg/m³, the peak erosion rate reaches a value of 1.13 × 10⁻⁶ kg/m²s. The average erosion rate across the wing surface is 4.53 × 10⁻⁹ kg/m²s. Erosion occurs 0.03 m from the leading edge. As the particle density increases, when the density reaches 2800 kg/m³, the peak erosion rate reaches a value of 1.28 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 3.31 × 10⁻⁷ kg/m²s. Erosion occurs 0.055 m from the leading edge. When the particle density increases to 3580 kg/m³ the peak erosion rate reaches a value of 1.56 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 3.36 × 10⁻⁷ kg/m²s. Erosion occurs 0.03 m from the leading edge. It can be seen that as the particle density increases, both the peak and the average erosion rate on the wing surface increase. The location of the highest erosion rate tends to shift slightly backward as density increases. Based on particles with a density of 2650 kg/m³, when the particle density increases to 3580 kg/m³, the maximum erosion rate increases by only 38%.

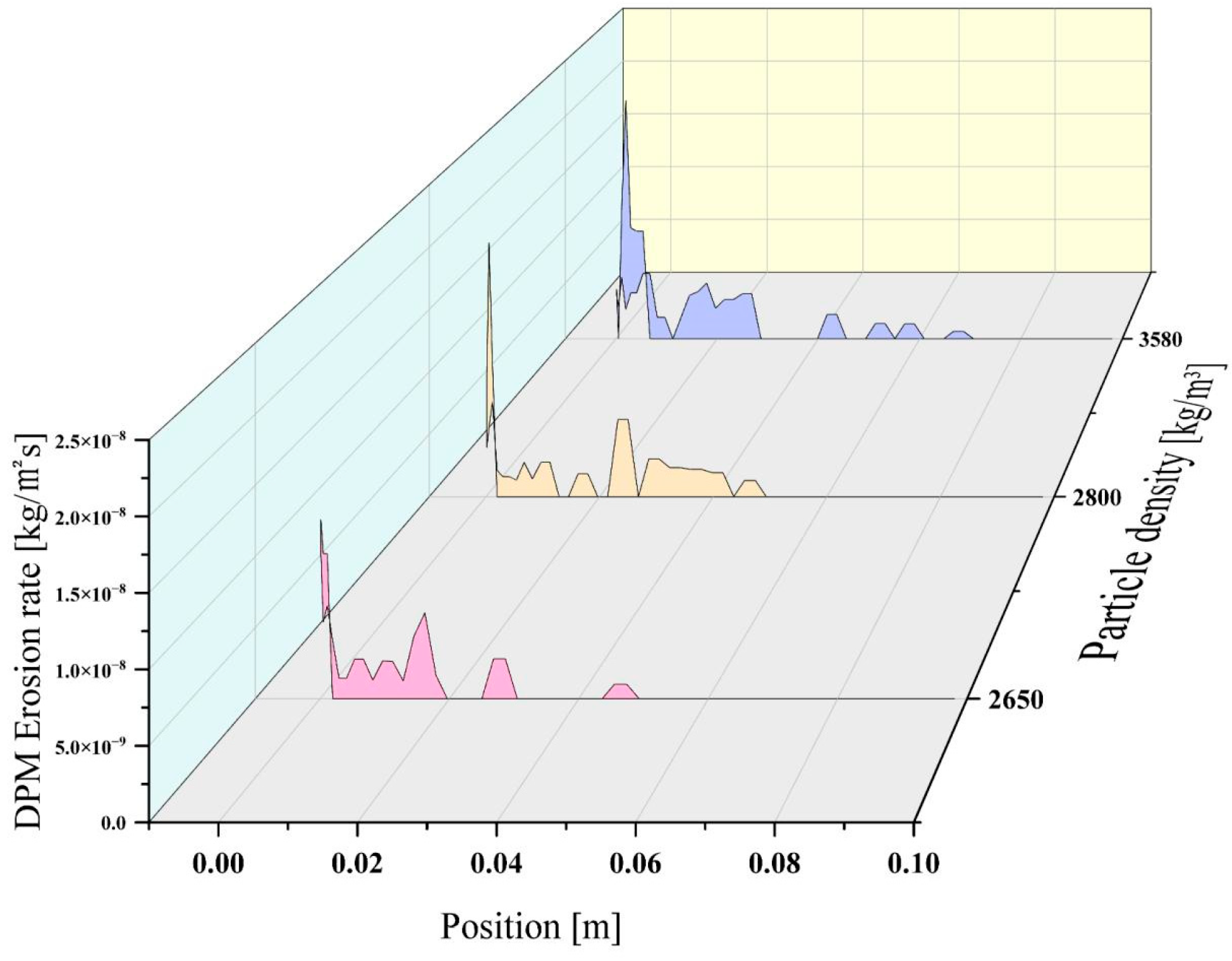
Figure 24, Figure 25 and Figure 26 show the erosion rate distribution, the highest erosion rate bar chart, and the erosion cloud chart for particles with densities of 2650 kg/m³, 2800 kg/m³, and 3580 kg/m³, respectively, and a particle size of 300 μm, when the incident velocity is 15 m/s and Stk >> 1. As shown in the figure, when the particle density is 2650 kg/m³, the peak erosion rate reaches a value of 2.417 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 7.69 × 10⁻⁷ kg/m²s. Erosion occurs 0.017 m from the leading edge. As the particle density increases, when the density reaches 2800 kg/m³, the peak erosion rate reaches a value of 2.424 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 7.86 × 10⁻⁷ kg/m²s. Erosion occurs 0.021 m from the leading edge. When the particle density increases to 3580 kg/m³, the peak erosion rate reaches a value of 2.53 × 10⁻⁶ kg/m²s. The average erosion rate across the wing is 7.78 × 10⁻⁷ kg/m²s. Erosion occurs 0.21 m from the leading edge. It can be seen that as the particle density increases, both the maximum erosion rate and the average erosion rate on the wing surface change very little. The location of the highest erosion rate tends to shift slightly backward as density increases. Based on particles with a density of 2650 kg/m³, when the particle density increases to 3580 kg/m³, the maximum erosion rate increases by only 4.5%.

The simulation results show that as particle size and impact velocity increase, the effect of particle density on erosion rate significantly weakens. From the perspective of particle characteristics, the Stokes number effect dominates the motion trajectory: when the particle size and velocity are small, Stk is low, and the particles mainly move along the streamlines, with a limited number of particles colliding with the wall surface. At this point, increasing the particle density significantly increases Stk, causing more particles to deviate from the streamline and collide with the wall surface, thereby significantly increasing the erosion rate. However, when the particle size and velocity increase to Stk >> 1, the inertia of the particles dominates their motion, and almost all particles deviate from the streamline control and collide with the wall surface in an approximately straight trajectory. Under these conditions, further increasing the density continues to increase Stk, but the effect on the particle-wall collision probability is negligible. The impact frequency mainly depends on the particle flux rather than the density. Impact kinetic energy dominates the degree of damage: when particle size and velocity are small, particle impact kinetic energy is low, and erosion rate is also low. At this point, increasing the particle density can proportionally increase the impact kinetic energy, thereby significantly improving the erosion rate. However, when the particle size and velocity are sufficiently large, the impact kinetic energy increases dramatically, with kinetic energy ∝ρd³v², and the damage caused by a single collision is significantly enhanced. In this high-kinetic energy region, the relative change in kinetic energy caused by density changes (Δρ/ρ) is insignificant compared to the enormous kinetic energy base effect caused by changes in particle size (d³) and velocity (v²). At the same time, the sensitivity of erosion rates to changes in kinetic energy may tend to saturate at high kinetic energy levels. Therefore, the relative influence of particle density on erosion rate is more significant under conditions of low particle size and low velocity. However, under conditions of high particle size and high velocity, this effect weakens, and the erosion rate is mainly determined by particle flux, particle size, and velocity, with density becoming a secondary parameter

3.2.3. Particle Size Erosion Analysis Considering the Stokes Number

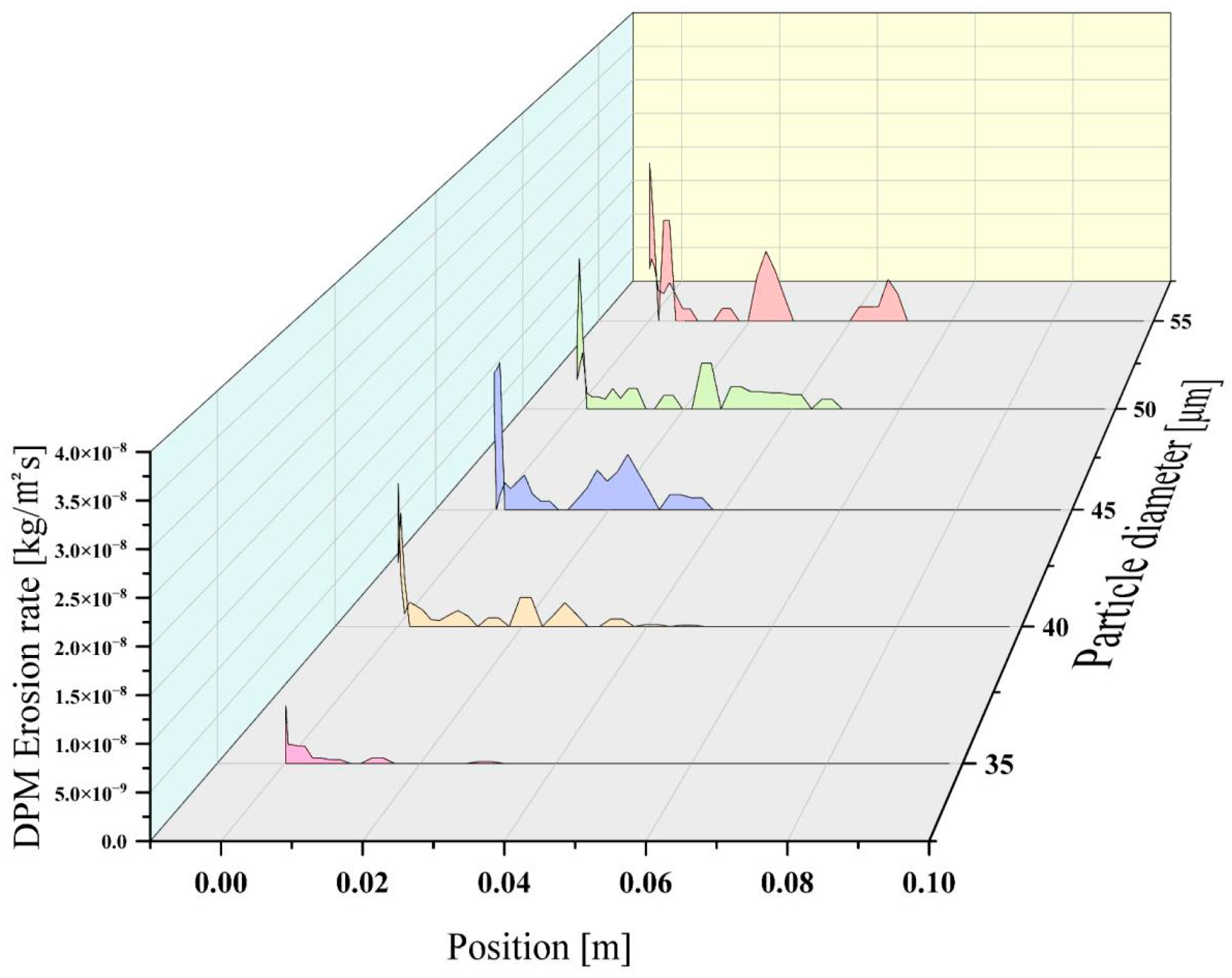
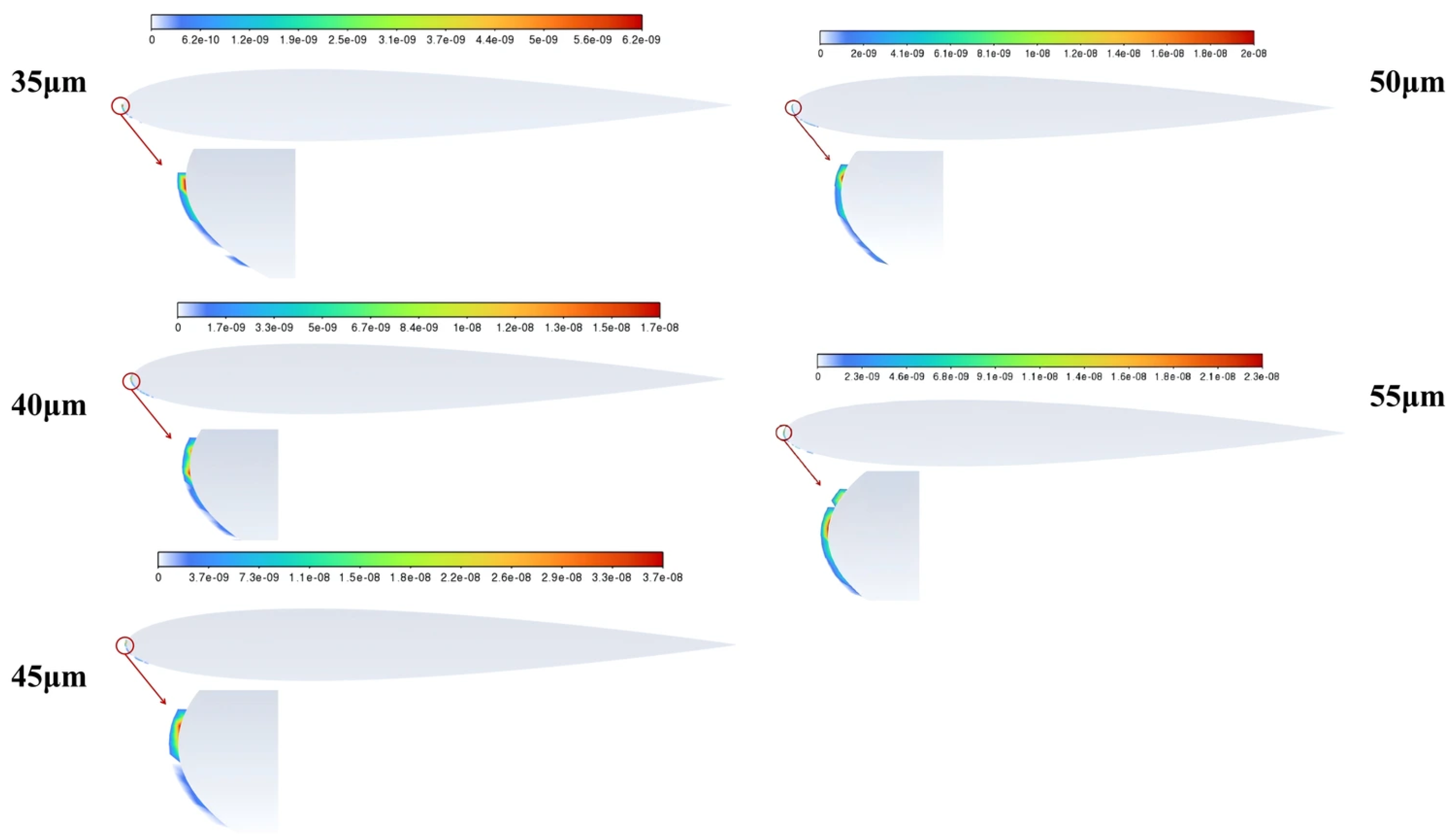
Figure 27 shows the evolution of erosion within the low Stokes number regime (Stk << 1), investigated using particles of 35, 40, 45, 50, and 55 μm in diameter. These particle sizes were selected to systematically vary the Stokes number while remaining within the low-inertia regime. As shown in the figure, when the particle size is 35 μm, the peak erosion rate reaches a value of 6.23 × 10⁻⁹ kg/m²s, and the average erosion rate across the wing surface is 1.35 × 10⁻⁹ kg/m²s. The erosion occurs at a distance of 0.0001 m from the leading edge of the airfoil. As the particle size increases, the peak erosion rate reaches a value of 1.67 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 2.99 × 10⁻⁹ kg/m²s. Erosion occurs 0.0001 m from the leading edge. When the diameter grows to 45 μm, the peak erosion rate reaches a value of 1.78 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 3.45 × 10⁻⁹ kg/m²s. Erosion occurs 0.0005 m from the leading edge. When the diameter grows to 50 μm, the peak erosion rate reaches a value of 2.04 × 10⁻⁸ kg/m²s. The average erosion rate across the wing is 3.93 × 10⁻⁹ kg/m²s. Erosion occurs 0.0005 m from the leading edge. When the diameter grows to 55 μm, the peak erosion rate reaches a value of 2.28 × 10⁻⁸ kg/m²s, the average erosion rate of the wing is 4.72 × 10⁻⁹ kg/m²s. The erosion occurs at a distance of 0.0005 m from the leading edge of the airfoil. 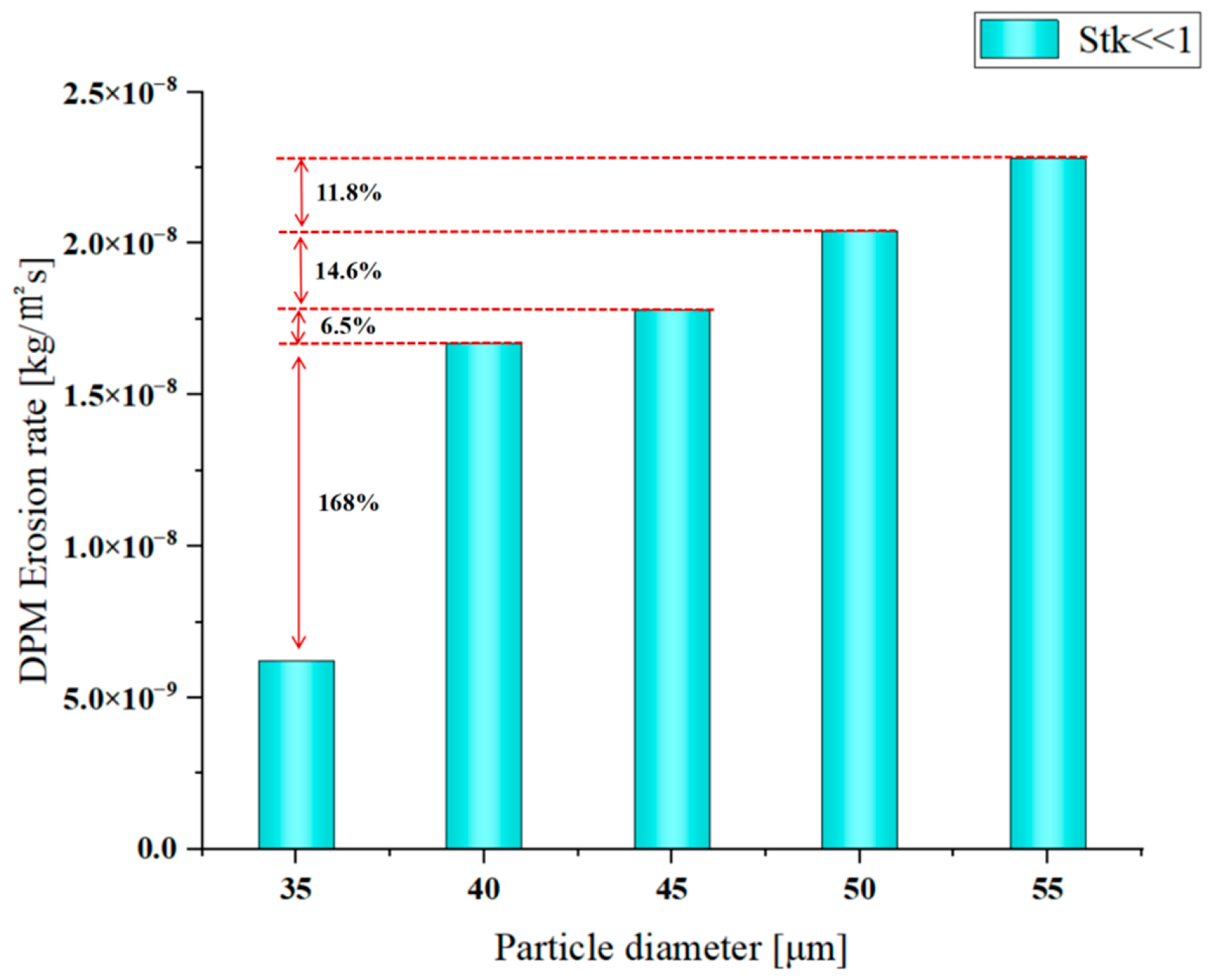As shown in Figure 27 and Figure 28, within the low Stokes number regime (Stk << 1), both the maximum and the average erosion rate exhibit a strong positive correlation with the Stokes number. Since the Stokes number scales with the square of the particle diameter, this trend manifests as a significant increase in erosion with increasing particle size. The highest erosion rate occurs when the particle size attains 55 μm. This translates to a 265% increase in the maximum erosion rate when the particle size increases from 35 μm to 55 μm, which corresponds to a 2.47 increase in the Stokes number, and the average erosion rate on the wing surface increases by 249%. An increase in particle size from 35 μm to 55 μm significantly exacerbated erosion damage to the surface of the NACA 0012 airfoil. The main manifestations are increased material removal rates and increased depth and severity of damage morphology at the leading edge of the airfoil. This change is mainly driven by the cubic increase in single-particle collision kinetic energy, while also being influenced by the collision efficiency caused by particle inertia. At this point, although the absolute value of Stk is still much less than 1, the particles can still follow the fluid streamlines relatively well, but the increased Stk causes the particles to be slightly more sensitive to local flow field disturbances. The streamline curvature is relatively large in the stagnation zone at the leading edge of the airfoil and in the reverse pressure gradient zone on the upper surface. Larger Stk causes particles to deviate slightly from the streamline due to limited inertia, increasing the probability of collision with the airfoil surface. As the particle size increases, the particle mass increases. When the impact velocity remains unchanged, the kinetic energy transmitted to the material surface by a single impact is greatly increased. Higher impact energy is more likely to cause increased erosion.

As shown in Figure 29, the erosion area expands slightly as the particle size increases. The minor enlargement of the erosion region results from the growth in particle dimensions. Essentially, it is the non-linear manifestation in space of the local streamline deviation effect caused by the increase in particle relaxation time. Although the global Stk is still small, in specific high-gradient flow field regions induced by airfoil geometry and angle of attack, increased inertia enhances the sensitivity of particle trajectories to local disturbances, resulting in a slight broadening of the spatial distribution function of collision efficiency. This is particularly evident in areas with high streamline curvature or weak separation at the boundary. It shows that even under low Stokes number conditions, particle size changes can still have a certain impact on the spatial distribution of collisions by modulating the interaction between particles and shear layers.

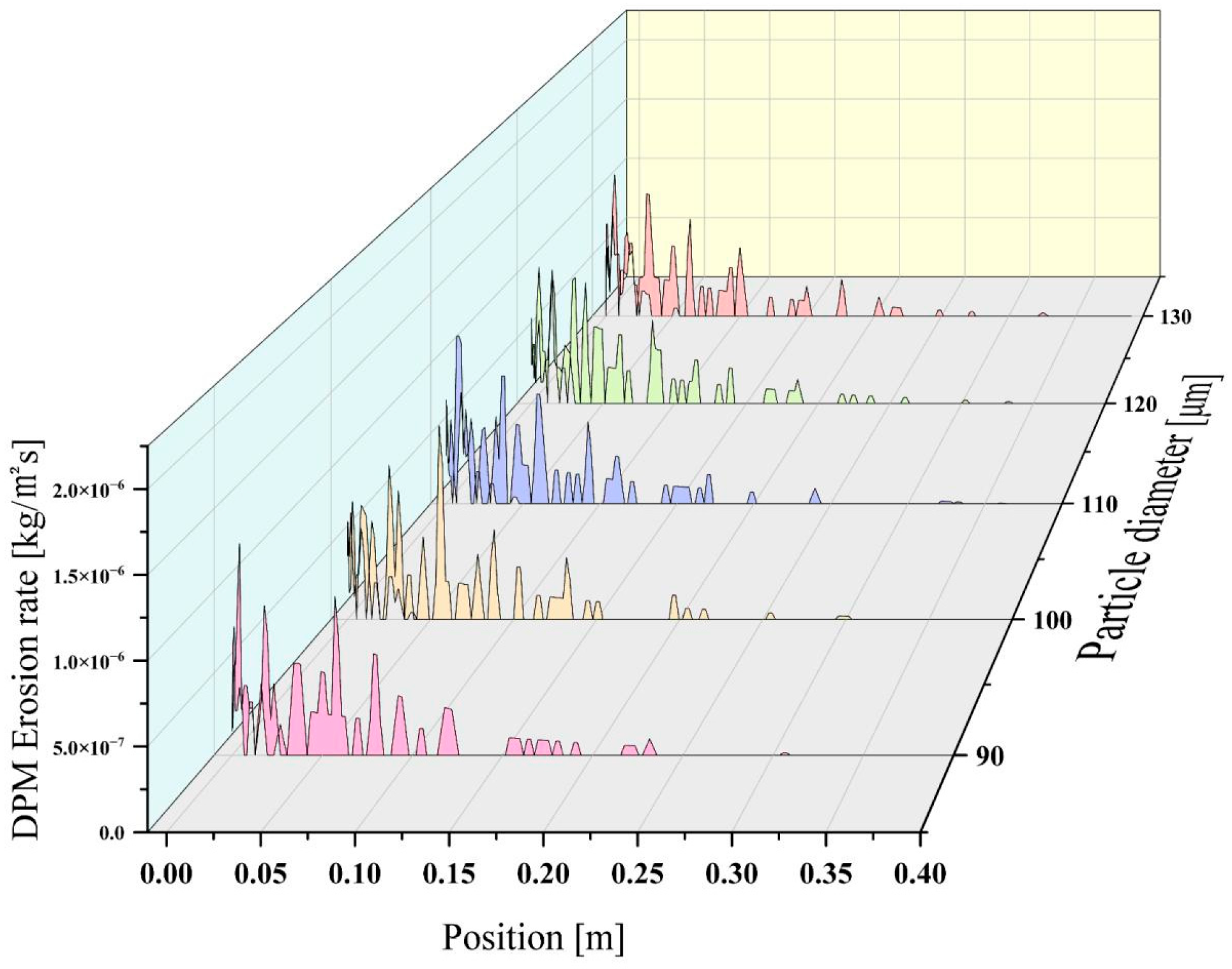
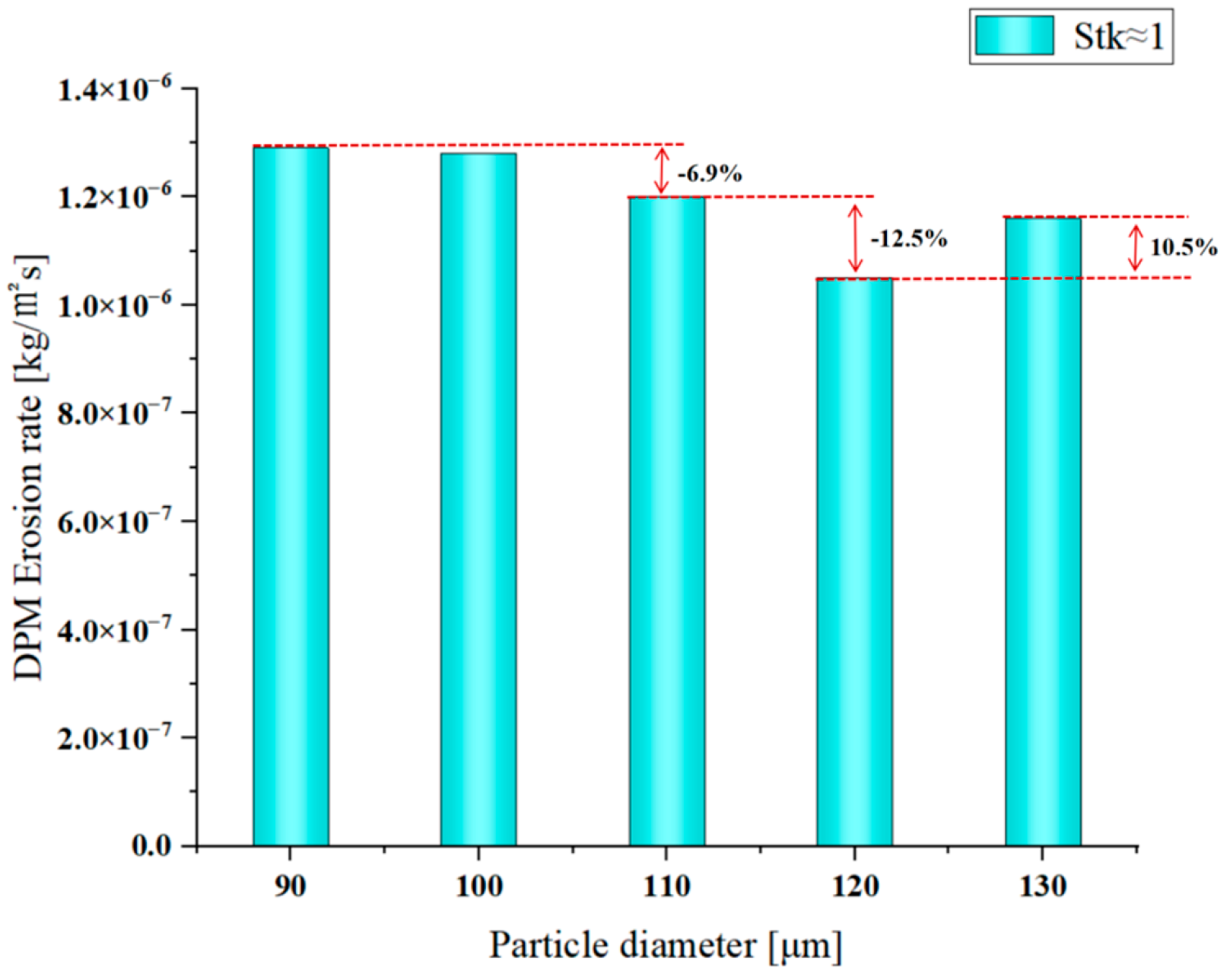
Figure 30, Figure 31 and Figure 32 show the erosion rate distribution diagrams, maximum erosion rate bar charts, and erosion cloud diagrams for particles with particle sizes of 90 μm, 100 μm, 110 μm, 120 μm, and 130 μm, respectively, under conditions of a particle density of 2800 kg/m³ and an incident velocity of 11.5 m/s, with Stk ≈ 1. As shown in the figure, when the particle size is 90 μm, the highest erosion rate is 1.29 × 10⁻⁶ kg/m²s. The average erosion rate on the airfoil is 2.95 × 10⁻⁷ kg/m²s. Erosion occurs 0.005 m from the leading edge. As the particle size increases, when the diameter grows to 100 μm, the peak erosion rate reaches a value of 1.28 × 10⁻⁶ kg/m²s. The average erosion rate on the surface is 3.27 × 10⁻⁹ kg/m²s. Erosion occurs 0.005 m from the leading edge. When the diameter grows to 110 μm, the peak erosion rate reaches a value of 1.2 × 10⁻⁶ kg/m²s. The average erosion rate on the airfoil is 3.27 × 10⁻⁷ kg/m²s. Erosion occurs 0.008 m from the leading edge. When the diameter grows to 120 μm, the peak erosion rate reaches a value of 1.05 × 10⁻⁶ kg/m²s. The average erosion rate on the airfoil is 3.4 × 10⁻⁷ kg/m²s. Erosion occurs 0.005 m from the leading edge. When the diameter grows to 130 μm, the peak erosion rate reaches a value of 1.16 × 10⁻⁶ kg/m²s. The average erosion rate on the airfoil is 3.41 × 10⁻⁷ kg/m²s. Erosion occurs 0.006 m from the leading edge. It is evident that the maximum erosion rate in the transition regime (Stk ≈ 1) peaks at a critical Stokes number of Stk ≈ 0.8. This peak effect is demonstrated by comparing different particle sizes: the erosion rate for 90 μm particles (Stk = 0.8) is 21% higher than that for 120 μm particles (Stk = 1.4). This conclusively shows that the erosion peak is intrinsically governed by the Stokes number itself. The mean erosion rate on the wing surface rises as the particle size increases, with the highest erosion rate occurring at a particle size of 130 μm. This phenomenon originates from the peak effect of collision efficiency in the Stokes number range of 0.5–1.0. When the particle size is 90 μm, Stk = 0.81, and the inertia of the particles causes them to deviate significantly from the streamlines and collide with the wall surface. This phenomenon originates from the peak effect of collision efficiency coupled with intense preferential concentration in the Stokes number range of 0.5–1.0. It is well-established that particles with Stk ≈ 1 exhibit the strongest clustering in turbulent flows because their response time matches the characteristic time of the most energetic turbulent eddies. In the context of our airfoil flow, this means that 90 μm particles (Stk = 0.8) are not only inertially likely to impact the surface but are also actively ‘focused’ into regions like the leading edge stagnation zone and the separated shear layer at higher angles of attack. This dramatic increase in local particle concentration significantly amplifies the impact frequency on specific surface areas, leading to the observed peak in erosion rate.

When the particle size increases to 120 μm, Stk = 1.44. An increase in the Stokes number leads to a decrease in collision efficiency due to excessive inertia of the particles. Owing to the reduced curvature radius at the leading edge of the NACA 0012 airfoil, the characteristic flow scale is diminished, leading to the formation of small-scale vortices that trap solid particles and thereby intensify localized erosion effects. At the same time, the flow separation effect induced by the angle of attack is enhanced, and the separation vortex generated can significantly enrich particles with Stk < 1 and intensify local collisions. At the leading edge and separation zone of the NACA0012 airfoil, the erosion rate at Stk = 0.8 was 21% higher than at Stk = 1.4, a finding that is highly consistent with the peak erosion behavior reported in the literature [50], further validating the Stokes number as the governing parameter. These findings further validate the impact of Stk on the erosion peak behavior of the airfoil.

The data shows that as particle size increases, leading to a higher Stokes number, the average erosion rate tends to increase due to enhanced inertial impaction. The essence lies in the fact that an increase in particle size leads to a significant increase in the Stokes number, thereby weakening the streamline following ability of particles and enhancing the inertial collision effect. An increase in particle size increases the relaxation time of particles, leading to a significant increase in the Stokes number. Particles are more likely to detach from the streamline in areas where the curvature of the wing profile changes, increasing the probability of collision with the wall surface. Increasing the particle size not only enhances the single-impact destruction strength but also increases the effective impact particle flux due to the convergence of particle trajectories toward the windward side, thereby improving particle collision efficiency. In the critical region where Stk ≈ 1, particle motion is in a transitional state between streamline following and inertia domination. At this point, even slight changes in particle size significantly alter the interaction between particles and vortex structures, enhancing the centrifugal effect of particles in the separation shear layer and further promoting particle transport toward the wall. Therefore, under the combined effects of multiple factors, the probability of collisions between the wing surface and particles increases, and the collision effects become more pronounced, leading to an increase in the average erosion rate.

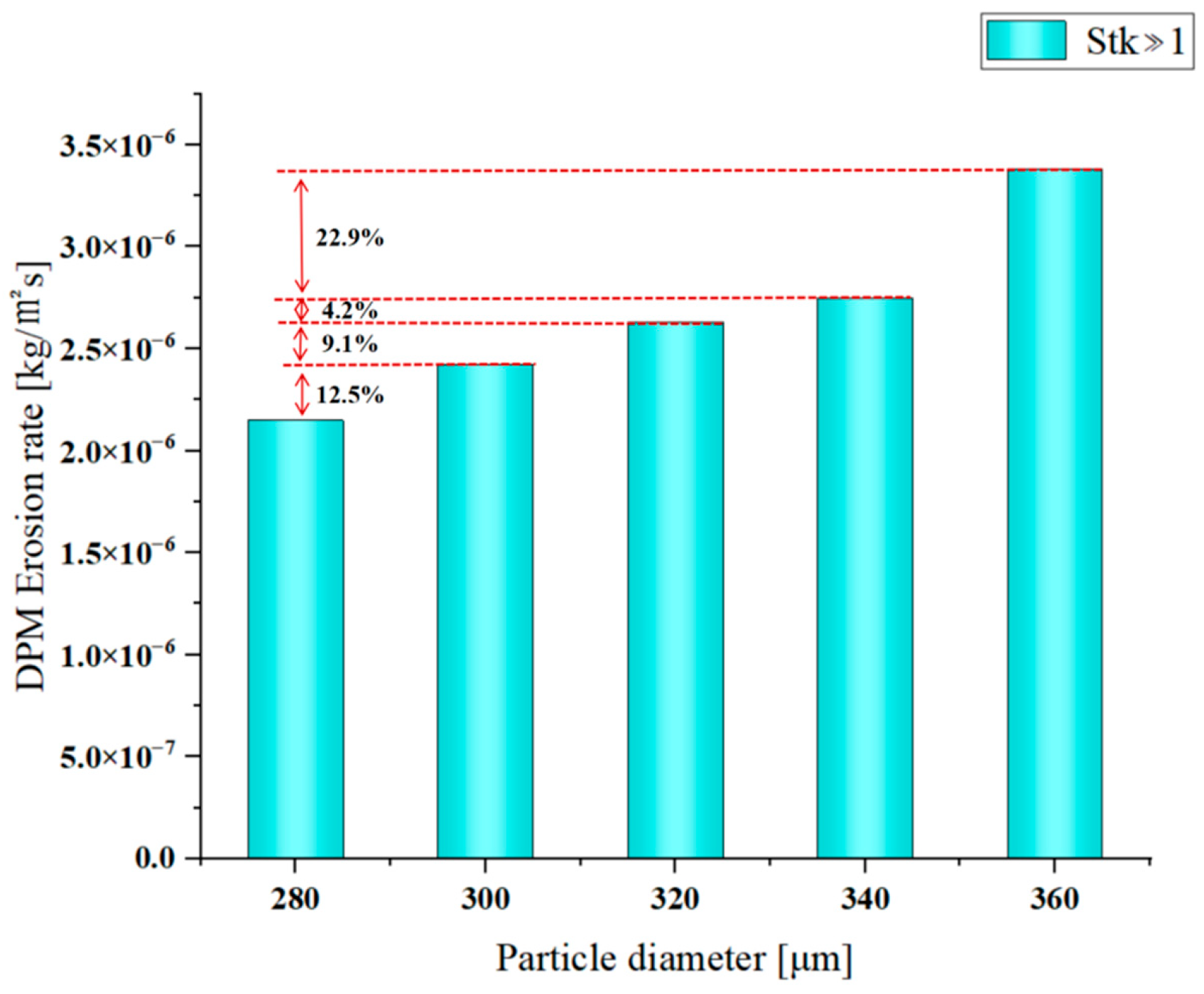
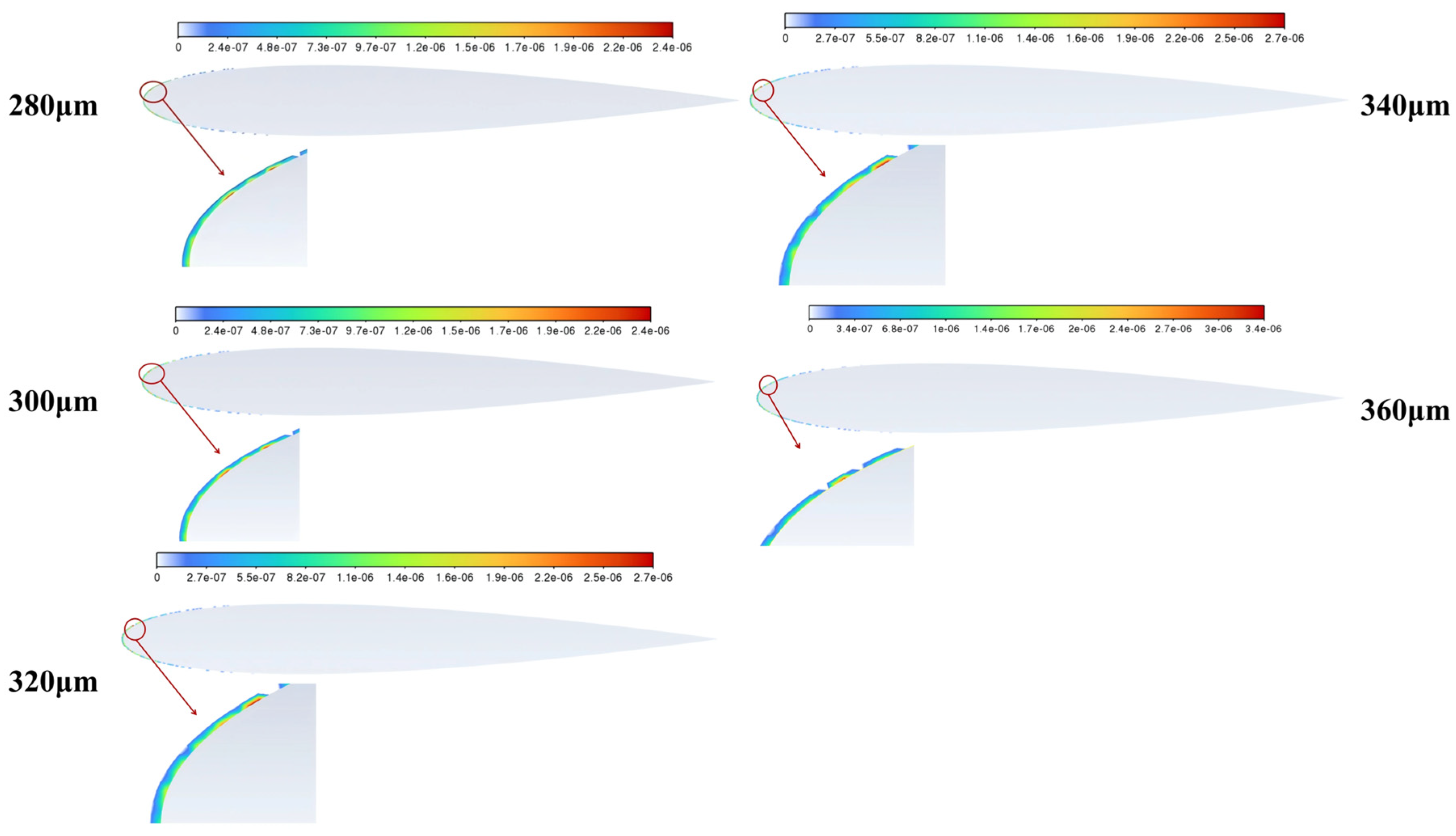
Figure 33, Figure 34 and Figure 35 show the erosion rate distribution diagrams, maximum erosion rate bar charts, and erosion cloud diagrams for particles with particle sizes of 280 μm, 300 μm, 320 μm, 340 μm, and 360 μm, respectively, under conditions of a particle density of 2800 kg/m³ and an incident velocity of 15 m/s, with Stk >> 1. As shown in the figure, when the particle size is 280 μm, the highest erosion rate is 2.15 × 10⁻⁶ kg/m²s. Erosion occurs 0.017 m from the leading edge. As the particle size increases, when it reaches 300 μm, the peak erosion rate reaches a value of 2.42 × 10⁻⁶ kg/m²s. Erosion occurs 0.021 m from the leading edge. When it reaches 320 μm, the peak erosion rate reaches a value of 2.64 × 10⁻⁶ kg/m²s. Erosion occurs 0.011 m from the leading edge. When it reaches 340 μm, the peak erosion rate reaches a value of 2.75 × 10⁻⁶ kg/m²s. Erosion occurs 0.012 m from the leading edge. When it reaches 360 μm, the peak erosion rate reaches a value of 3.38 × 10⁻⁶ kg/m²s. Erosion occurs 0.014 m from the leading edge. It is evident that when Stk >> 1, the peak erosion rate on the airfoil rises as the particle size becomes larger. Under these conditions, the highest erosion rate occurs when the particle size is 360 μm. This corresponds to a 57% increase in erosion rate when the particle size increases from 280 μm to 360 μm, which is driven by a 65.3% increase in Stokes number and a 112.5% increase in particle kinetic energy. At this point, surface erosion of the NACA0012 airfoil significantly intensifies at an angle of attack of 6°. The depth of erosion pits and material loss rate in the leading edge and approximately 10%–30% of the chord length of the upper surface significantly increase, and the erosion distribution area expands in the chord direction. As the particle size increases from 280 μm to 360 μm, the Stokes number increases by 66%. The inertial effect of the particles is enhanced, and the probability of them deviating from the streamline and colliding with the wall surface is significantly increased. The collision efficiency increases from 60% to 85%, representing a significant increase in collision efficiency. Particle kinetic energy increases cubically, with 360 μm particles having 2.12 times the kinetic energy of 280 μm particles, exacerbating plastic deformation and erosion of the material. Enhanced boundary layer penetration capability allows larger particles to more easily break through the airflow barrier and collide with the surface, especially at an angle of attack of 6°, where a high-speed low-pressure zone forms at the front end of the upper surface, creating a concentrated erosion hot spot. In summary, under the combined effects of particle inertia, increased kinetic energy, and improved boundary layer penetration, an increase in particle size will lead to a significant deterioration in erosion damage to the surface of the NACA 0012 airfoil.

3.3. Establishment of an Erosion Prediction Model Considering the Stokes Number

In order to establish a quantitative relationship between the Stk and erosion rate, this study proposes an interval-based erosion rate prediction model based on dimensional analysis and non-linear regression theory:

$$E=K•S{\mathrm{tk}}^{\mathrm{a}}•d_p^b•v^c$$

(16)

Experiments have confirmed that the erosion rate is proportional to the kinetic energy of the particles according to a power law relationship [22], where the kinetic energy is proportional to d_p³v². However, in practice, due to the effects of flow field modulation, such as boundary layer penetration and changes in the impact angle, the exponents b and c need to be corrected for different zones.

K, a, b, and c are fitting parameters. The Levenberg–Marquardt algorithm is used to optimize the parameters, with the objective function being to minimize the sum of squared relative errors.

$$\min {{\displaystyle \sum _{i=1}^N\left(\frac{E_{sim,i}-E_{pred,i}}{E_{sim,i}}\right)}}^2$$

(17)

Three intervals are divided according to the inertial characteristics of the particles and fitted independently:

Low inertia zone (Stk < 0.3): laminar separation bubbles dominate particle motion;

Transition zone (0.8 ≤ Stk ≤ 1.2): vortex enrichment effect is significant;

High inertia zone (Stk > 10): kinetic collision mechanism dominates.

The proposed empirical model E = K∙Stk^a∙d_p^b∙v^c is dimensionally non-homogeneous. The constant K therefore carries a physical dimension that ensures the overall equation is dimensionally consistent. The dimension of K is derived as K = kg∙m^−2−b−c∙s^c−1, where the exponents b and c are specific to each Stokes number regime. The numerical values and corresponding units of K are provided in

Table 2. Erosion rate model fitting parameters.

Stk Range	K (Value & Units)	a	b	c
Stk << 1	2.1 × 10−10 kg∙m−5.5∙s1.4	0.85	1.1	2.4
Stk ≈ 1	5.3 × 10−9 kg∙m−0.9∙s−0.9	−0.7	0.2	2.1
Stk >> 1	1.8 × 10−10 kg∙m−3.9∙s1.6	0.4	1.3	2.6

.

Based on the above simulation parameters, the erosion rate model fitting parameters for the three intervals are shown in the table below:

This model was developed and validated for the flow physics around stationary NACA 00XX series symmetrical airfoils with chord lengths ranging from 0.5 to 2.0 m. For asymmetrical airfoils, a thickness correction factor must be added [6]:

$$C_t={\left({\displaystyle \frac{t}{c}}\right)}^{0.3}$$

(18)

Due to Stk limitations, the prediction model is only applicable to spherical particles. When the density is less than 2650 kg/m³ or greater than 3580 kg/m³, the density needs to be appropriately corrected. The density correction formula is as follows [47]:

$$C_{\rho }={\left({\displaystyle \frac{{\rho }_p}{2650}}\right)}^{0.8}$$

(19)

The angle of attack is limited to ≤12°. When the angle of attack is too large, it will cause the separation vortex intensity to increase and the particle concentration to rise. Therefore, appropriate corrections must be made. The correction formula is as follows [47,51]:

$$C_{\alpha }=\min \left[1,1+0.05{(\alpha -12)}^{1.2}\right]$$

(20)

To ensure the fitting accuracy, the “coefficient of determination” will be employed as a measure to assess how well the model fits the data.

The regression sum of squares (SSR) in the regression equation reflects the total squared deviations between the predicted values and the mean of the original data, as expressed in Equation (21):

$$SSR={\displaystyle \sum _{i=1}^n{w}_i(}{\widehat{y}}_i-\overline{y_i}{)}^2$$

(21)

The total sum of squares (SST) indicates the sum of squared deviations between the observed data points and their overall mean, as illustrated in Equation (22):

$$SST={\displaystyle \sum _{i=1}^n{w}_i(y_i-\overline{y_i}}{)}^2$$

(22)

The “coefficient of determination” is calculated as the ratio of the regression sum of squares (SSR) to the total sum of squares (SST), as presented in Equation (23):

$$R^2={\displaystyle \frac{SSR}{SST}}$$

(23)

Based on the R² calculation method, simulation data, and fitted data, the following can be calculated: In the Stk << 1 interval (Stk < 0.3), R² = 0.96. In the Stk ≈ 1 interval (0.8 < Stk < 1.2), R² = 0.94. In the Stk >> 1 interval (Stk > 10), R² = 0.95.

To verify the accuracy of the model, the predicted values were compared with the simulation data in this paper and the results of independent experiments, as shown in

Table 3. Verification of erosion rate model.

Stk Range	Operating Conditions	Rep	Stk	φ(×10−6)	Model Prediction	Documentary Evidence	Error	Literature Sources
Stk << 1	d = 50 μm, v = 1.5 m/s	4.1	0.028	0.86	1.05 × 10−9	1.08 × 10−9	−2.7%	Tabakoff [22]
	d = 35 μm, v = 3.5 m/s	6.7	0.032	0.42	6.23 × 10−9	6.15 × 10−9	1.3%	Gabriele [52]
Stk ≈ 1	d = 130 μm, v = 11.5 m/s	86.3	1.42	0.29	1.21 × 10−6	1.18 × 10−6	2.5%	Zhang et al. [23]
Stk >> 1	d = 300 μm, v = 13 m/s	221.5	8.5	0.16	1.85 × 10−6	1.92 × 10−6	−3.6%	Hamed et al. [24]
	d = 300 μm, v = 21 m/s	358.2	13.7	0.10	6.52 × 10−6	6.75 × 10−6	−3.4%	Finnie model [53]

:

This verification proves that the model is consistent with previous experiments and simulations in terms of parameter trends and quantitative predictions, thereby enhancing the credibility of the erosion model.

4. Conclusions

This study is based on the Euler–Lagrange framework and uses numerical simulation to investigate the aerodynamic performance evolution and erosion characteristics of the NACA0012 airfoil in a wind and sand environment. It systematically reveals the coupled interaction mechanism between particle size, Stokes number, and flow parameters on the flow structure and surface damage. The main conclusions are as follows:

• The mechanism by which particle inertia, quantified by the Stokes number, affects flow characteristics and aerodynamic performance: Under a 6° small angle of attack condition, the presence of particles does not significantly alter the flow separation structure, but it does disturb the local pressure distribution: the high-pressure zone on the pressure side exhibits a trend of first contracting and then expanding as particle size increases, with 150 μm particles causing a decrease in static pressure on the pressure side and an increase in static pressure on the suction side. At a large angle of attack of 12°, small-particle-size particles induce the flow separation point to move forward, with an increase in wake vortex scale and enhanced unsteadiness; large-particle-size particles gradually weaken flow disturbances, and when the particle size is ≥150 μm, the flow field characteristics approach the clean air reference state. This phenomenon stems from the fact that small particles are easily drawn into the separation vortex region, exacerbating flow instability, while the inertial effects of large particles suppress boundary layer separation.
• The dominant role of Stokes number partitioning in erosion patterns is governed by the transition from turbulence-modulated clustering to pure inertial impaction. The spatial distribution and intensity of erosion are not solely determined by whether a single particle can hit the surface, but by how the Stk value dictates the collective behavior of the particle cloud through preferential concentration.

In the low-inertia region (Stk << 1), while particles generally follow streamlines, weak clustering in the high-strain reattachment region of the laminar separation bubble explains the initial erosion band at the mid-chord. The subsequent migration of the erosion hotspot to the leading edge with increasing velocity is a direct result of the shifting locus of the strongest flow curvature and strain, which attracts and focuses particles in this Stk range. The erosion location shifts from the mid-to-rear edge of the airfoil (45%–100% chord length) to the leading edge (<5% chord length) as the flow velocity increases.

In the critical transition region (Stk ≈ 1), erosion concentration occurs in the leading edge stagnation zone, and the highest erosion location shifts from the upper/lower leading edge as velocity increases; the erosion rate peaks at Stk = 0.8. This is attributed to a powerful synergy: particles possess sufficient inertia to deviate towards the surface, and they experience the strongest preferential concentration, dramatically increasing the local impact frequency in the leading edge region. This dual mechanism of inertial targeting and turbulent focusing creates the most severe erosion condition. At Stk = 0.8, the erosion rate reaches its peak, with the erosion rate for particles of 90 μm (Stk = 0.8) being 21% higher than that for 120 μm (Stk = 1.4).

In the high-inertia region (Stk >> 1), particle motion is dominated by inertia, and their response to turbulent structures is weak. The erosion pattern is thus characterized by pure inertial impaction. The expansion of the erosion area on the lower surface with increasing velocity occurs because higher inertia allows particles to better maintain their trajectory and impact regions of the surface with less streamline following, overwhelming any subtle clustering effects.

3.

Differential effects of particle properties on erosion rates: In low-Stk regions, erosion rates are sensitive to changes in particle size and density: the maximum erosion rate increases by 265% when the particle size is 55 μm compared to 35 μm, and by 69.8% when the density is 3580 kg/m³ compared to 2650 kg/m³. In the high-Stk region, density has little effect, and particle size dominates the erosion pattern. The fundamental reason is that under high-Stk conditions, the probability of inertial collisions between particles approaches saturation, and the increase in kinetic energy is primarily driven by the cube of particle size and the square of velocity, resulting in a significant weakening of the marginal effects of physical parameters.

4.

Establishment and validation of a regional erosion prediction model: An empirical erosion rate model was constructed based on Stokes number zones. The fitted parameters indicate that there are significant differences in the dominant mechanisms in different Stk intervals. Model validation shows that the prediction values have an error of ≤3.6% compared to independent experimental data, confirming the reliability of the model in quantitatively predicting erosion of airfoils in wind and sand environments.

The research results provide a fundamental theoretical and modeling framework to guide the erosion-resistant design of wind turbines. In sandstorm environments, the protective materials at the leading edge need to be reinforced, and the flow stability of the separation zone needs to be closely monitored under high angle of attack conditions. In terms of operating strategies, it is recommended to limit the rotational speed in areas with high sand concentration to reduce the flow velocity, which can effectively inhibit the rate of material loss.

5. Limitations and Future Work

The findings of this study are based on a two-dimensional, non-rotating airfoil model. While it successfully reveals the fundamental control mechanism of the Stokes number on erosion patterns, direct extrapolation to a full-scale, rotating wind turbine blade requires consideration of additional factors. These include centrifugal and Coriolis forces, which can alter particle trajectories, the spanwise variation in the angle of attack and chord length, and the complex, three-dimensional flow structures near the hub and tip. Future research should aim to incorporate these rotational and three-dimensional effects to develop a comprehensive erosion prediction model for operational wind turbines.