Retrofitting a Pre-Propeller Duct on a Motor Yacht: A Full-Scale CFD Validation Study

Abstract

The maritime industry faces increasing pressure to improve energy efficiency, a challenge that extends to the luxury yacht sector. This study presents a comprehensive hydrodynamic assessment for retrofitting a bespoke Energy Saving Device (ESD) onto a 45 m motor yacht. A full-scale self-propulsion Computational Fluid Dynamics (CFD) model was developed and validated directly against dedicated sea trial data, ensuring high fidelity and bypassing traditional scaling uncertainties. The validated model was then utilized to design and optimize a custom pre-propeller duct system. A parametric study varying the duct’s angle of attack identified an optimal configuration of ${20}^{\circ }$, which achieves a definitive power saving of 4.7% at the vessel’s cruise speed of 12.3 knots. Analysis of the propulsive factors reveals that the gain is primarily driven by a substantial increase in the hull efficiency, ${\eta }_H$, achieved by conditioning the propeller inflow. This improvement successfully compensates for the corresponding decrease in the propeller’s open-water efficiency, ${\eta }_o$. This work demonstrates a successful end-to-end numerical workflow for designing and verifying an effective, retrofittable ESD, highlighting a practical solution for reducing fuel consumption in existing motor yachts.

1. Introduction

The maritime industry is under increasing pressure to enhance operational efficiency and reduce its environmental footprint [1]. Global regulations from the International Maritime Organization (IMO), such as the Energy Efficiency Existing Ship Index (EEXI) and the Carbon Intensity Indicator (CII), mandate significant improvements in the energy consumption of the global fleet [2]. While much of the focus has been on commercial shipping, the luxury yacht sector faces similar challenges, augmented by unique owner-driven demands for performance, comfort, and operational excellence. For motor yachts, fuel consumption is a major operational cost, and hydrodynamic efficiency is directly linked to the vessel’s speed, range, and environmental impact [3].

Furthermore, onboard comfort, defined by low levels of noise and vibration, is a paramount concern in yacht design. These vibrations often originate from hydrodynamic phenomena at the stern [4], such as unsteady propeller forces and cavitation [5]. As noted in the analysis for the subject vessel of this study, a 45 m motor yacht, existing propellers can suffer from issues like cavitation erosion and geometric imbalances, leading to degraded performance and increased vibrations. This highlights a clear need for advanced hydrodynamic analysis and targeted solutions that can simultaneously improve efficiency and enhance onboard comfort, providing a direct motivation for the retrofitting of performance-enhancing technologies.

To meet efficiency mandates, a wide array of Energy Saving Devices (ESDs) has been developed, offering a straightforward path to improve performance [6,7]. These devices are broadly classified as pre-swirl or post-swirl solutions [8]. The concept of using a pre-propeller duct to improve propulsion traces back to the work of Schneekluth [9], who pioneered this energy saving device and saw thousands fitted to vessels. For pre-swirl devices, designs have been adapted for specific hull forms, such as the compact ‘ring stator’ developed for slender sterns [10]. Studies like that of Ok Jil-Pyo [11] on similar concepts have demonstrated the complexity of these interactions, noting that while the duct successfully decreases the inflow speed to the propeller—a fundamental flow physics observation consistent with this study—it may, depending on the design, lead to an increase in required propulsion power.

Post-swirl devices (e.g., Propeller Boss Cap Fins, Grim Vane Wheel) are positioned downstream to recover rotational energy from the propeller’s slipstream and convert it into additional thrust. Conversely, pre-swirl devices like stator fins and ducts are installed upstream. These ducts, also known as Wake Equalizing Ducts (WEDs), are designed to accelerate and homogenize the propeller inflow, improving propulsive efficiency [12] and potentially reducing bare hull resistance [6]. While effective, pre-swirl devices often require significant hull integration, making the development of easily retrofittable solutions a key practical interest.

The design and assessment of both hull forms and ESDs have been revolutionized by Computational Fluid Dynamics (CFD). By numerically solving the Reynolds-Averaged Navier–Stokes (RANS) equations, often with a Volume of Fluid (VOF) method to capture the free surface, CFD allows for detailed investigation of complex flow physics [13]. It serves as a virtual towing tank [14] to evaluate designs and analyze the intricate interactions between the hull, propeller, and ESDs. This analysis is crucial as even standard appendages can influence performance, with studies showing that the rudder’s interaction with the propeller can contribute to a slight improvement in overall propulsive efficiency [15].

Predicting the performance of motor yachts is challenging due to their semi-planing or planing hydrodynamics and the non-linearities of transom stern flows. These factors create uncertainties when extrapolating from model-scale tests. Validating CFD models directly against full-scale sea trial data is therefore the most reliable approach [16]. Furthermore, an ESD’s performance can change dramatically between towed and self-propelled states. Therefore, an accurate assessment of real-world power savings requires a holistic analysis that includes the hull–propeller interaction. This study addresses this challenge directly by employing full-scale self-propulsion CFD simulations, validated against sea trial data, to provide a high-fidelity performance prediction.

The benefits of Energy Saving Devices (ESDs) are well-documented for new ship designs, where they can be integrated into the hull and propulsion system for optimal performance. However, for the vast number of existing vessels, including motor yachts, a different challenge arises: how to improve efficiency and reduce fuel consumption quickly, simply, and cost-effectively. This is a critical need for the maritime industry, which faces increasing pressure to meet global efficiency regulations. This study is motivated by the direct interest from the industry to explore the possibilities and benefits of retrofitting ESDs onto existing vessels. Therefore, our analysis focuses on a bespoke, retrofittable solution, and it employs a practical CFD approach that balances computational cost with predictive accuracy, making it suitable for rapid design and assessment.

The unique contribution and engineering science value of this paper is stated in

Table 1. Contextual review of CFD studies on pre-propulsion energy saving devices (ESDs).

Reference	ESD Type	Vessel Type	Method	Key Finding	Power Saving	Validation
Shin et al. [17]	Pre-Swirl Duct (WED)	VLCC	CFD + Model Test	Optimal duct L/D ratio	2–5%	Model Basin
Gaggero & Martinelli [18]	Pre-Swirl Fins	Fast Ferry	RANS-BEM	Multi-objective optimization	Up to 6%	Numerical only
Koushan et al. [19]	Pre-Swirl Stator (PSS)	Container	CFD + EFD	Blade angle optimization	4%	Model Test (EFD)
Nicorelli et al. [20]	WED + Pre-Fins	DTC Hull	RANS (Full-Scale)	Scale effects significant	2–4%	Numerical + Literature
Kang et al. [10]	Compact Ring Stator	Crude Carrier	CFD (Model Scale)	Slender stern adaptation	3–4%	Model CFD 5
Munazid et al. [7]	Pre-Duct (Varied Geom.)	General Cargo	RANS	Circular vs. asymmetric shapes	3.5% best	Numerical
Present study	Pre-Propeller Duct	Motor Yacht	Full-Scale Self-Propulsion CFD	Parametric AoA study	4.7%	Full-Scale Sea Trial

, which provides a direct comparison with related Energy Saving Device (ESD) research. Existing work typically falls short by focusing on model-scale tank tests or numerical simulations of massive commercial vessels, introducing inherent scaling uncertainties. This study tackles this challenge head-on. This research is distinct because a bespoke ESD design is developed along with a workflow that applies it to a complex motor yacht hull form, utilizing a full-scale CFD model, which is validated directly against dedicated sea trial data. This high-fidelity approach moves the entire analysis past speculation, providing a definitive, confident answer for a solution that is both practical and immediately retrofittable.

This study presents a hydrodynamic assessment of a 45 m motor yacht. The primary objectives are as follows:

1.

Develop a full-scale self-propulsion CFD model capable of simulating the vessel’s propulsive performance and validate its predictive capabilities directly against data from a dedicated sea trial campaign.

2.

Utilize the validated model to analyze the complex hull–propeller interaction phenomena, calculating key propulsive coefficients such as the wake fraction (w), thrust deduction (t), and hull efficiency (${\eta }_H$) across the vessel’s speed range.

3.

Use the validated model to design a bespoke pre-propeller duct system and numerically quantify its effectiveness through a direct comparison of self-propelled performance, providing a direct calculation of power savings.

2. Subject Vessel and Sea Trial Campaign

The foundation of this study is a validation process that directly compares numerical predictions with full-scale performance data. This chapter describes the subject vessel and outlines the methodology and conditions of the sea trial campaign from which the validation data were sourced. The use of an operational yacht for this analysis provides a valuable opportunity for direct full-scale validation, overcoming the scaling uncertainties often encountered in studies that rely solely on benchmark models and towing tank experiments.

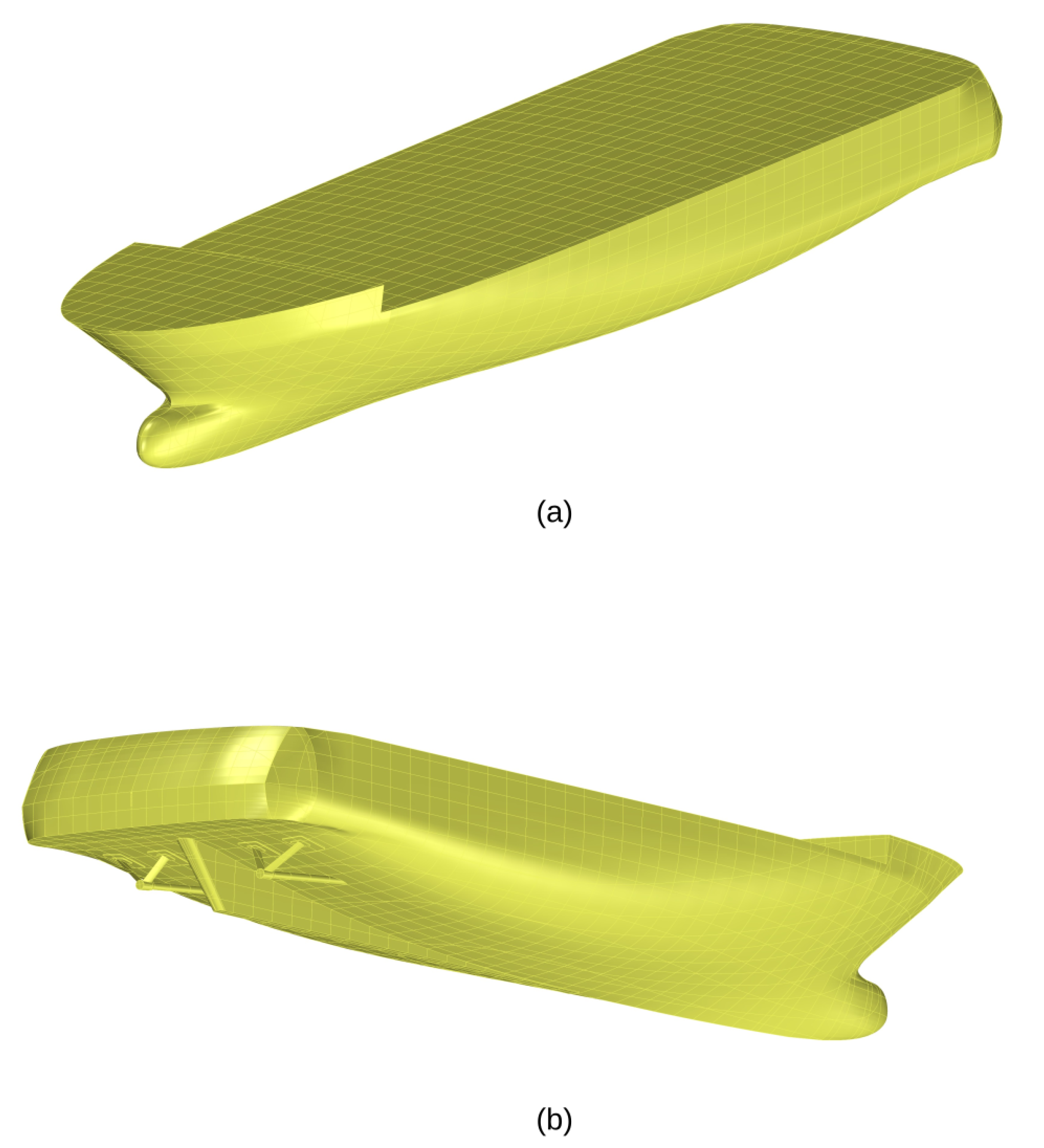
The vessel of interest is a 45 m semi-displacement motor yacht (Figure 1), powered by a twin-screw propulsion system, featuring two 969.5 kW @ 1800 RPM marine diesel engines, each driving a five-bladed, fixed-pitch propeller. The principal particulars of the vessel are summarized in

Table 2. Ship principal particulars.

Parameter	Value
Ship Type	Motor Yacht
Length Overall ($L_{OA}$)	∼45.0 m
Length at Waterline ($L_{WL}$)	37.30 m
Displacement	∼500 tonnes
Propulsion System
Engines	2 × Caterpillar C32 ACERT (Caterpillar Inc., Peoria, IL, USA)
Installed Power	2 × 969.5 kW @ 1800 RPM
Propellers
Type	Wageningen B-Series Fixed Pitch Propeller (FPP)
Number of Blades	5
Diameter	1246 mm
Design Pitch (mean)	928 mm
Expanded Area Ratio (EAR)	0.883

.

A dedicated sea trial was conducted to record the vessel’s performance data. The primary objective of the trial was to obtain stabilized measurements of vessel speed, engine speed (RPM), and power output across a range of operating points. At each set point, the vessel was allowed sufficient time to reach a constant speed, at which point the relevant data were recorded. The ship model is shown in Figure 2.

While specific quantitative data for sea state and wind conditions were not logged, the trial was conducted in suitable conditions for performance measurements, adhering to the principles outlined in ITTC Recommended Procedures and Guidelines for Sea Trials (International Towing Tank Conference [21]). Environmental factors, typical for full-scale sea trials, may contribute to ±15% power measurement uncertainty and potentially more in non-ideal calm conditions. The key trial conditions are summarized in

Table 3. Sea trial conditions summary.

Parameter	Value/Range
Vessel Speed Range	7.7–12.8 knots
Froude No. Range (Fr)	∼0.21–0.35
Reynolds No. Range (Re)	∼1.5 × 108–2.5 × 108
Sea State/Wind	Calm

. It is acknowledged that inherent uncertainties exist in full-scale trial data collection, as discussed in guidelines such as ITTC Recommended Procedures and Guidelines for Sea Trials [21] on full-scale trial limitations.

Performance data were acquired directly from the vessel’s onboard systems. The key parameters used for the subsequent CFD validation were sourced as follows:

• Vessel Speed: Recorded in knots from the bridge navigation system (DGPS).
• Engine Speed (RPM): Recorded directly from the engine’s Electronic Control Module (ECM).
• Delivered Power: The brake power (bkW) delivered by the engines was estimated based on real-time ECM readouts of engine load factor and fuel burn rate, referenced against the manufacturer’s engine performance data.

The data were recorded for both the port and starboard engines simultaneously. For this study, the values from both propulsion lines were averaged at each speed setting to create a single, representative delivered power curve. This processed sea trial data provides the crucial real-world benchmark against which the results of the bare hull and self-propulsion CFD simulations are validated in Section 4, a fundamental step in ensuring the reliability of a numerical method.

3. Numerical Methodology

The hydrodynamic performance of the yacht was simulated by solving the governing equations of fluid dynamics using the commercial CFD software Simcenter STAR-CCM+ 2502 [22]. The numerical approach was tailored to address the specific challenges of full-scale marine simulations in a self-propelled condition, where the complex interactions between the hull, propellers, and the free surface are fully captured.

The fluid flow is governed by the Reynolds-Averaged Navier–Stokes (RANS) equations, which express the conservation of mass and momentum for a viscous, incompressible fluid. In tensor form, these are given as

Continuity:

$${\displaystyle \frac{\partial \overline{u_i}}{\partial x_i}}=0$$

(1)

Momentum:

$$\rho {\displaystyle \frac{\partial \overline{u_i}}{\partial t}}+\rho \overline{u_j}{\displaystyle \frac{\partial \overline{u_i}}{\partial x_j}}=-{\displaystyle \frac{\partial \overline{p}}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left[\mu \left({\displaystyle \frac{\partial \overline{u_i}}{\partial x_j}}+{\displaystyle \frac{\partial \overline{u_j}}{\partial x_i}}\right)-\rho \overline{u_i^{\prime }{u}_j^{\prime }}\right]+\rho g_i$$

(2)

where $ui$ represents the time-averaged velocity components, p is the pressure, $\rho$ is the fluid density, $\nu$ is the kinematic viscosity, $gi$ represents body forces, and $-u{i}^{\prime }u{j}^{\prime }$ is the Reynolds stress tensor, which requires a turbulence model.

• Turbulence: The Reynolds stresses are modeled using Menter’s Shear Stress Transport (SST) k-$\omega$ turbulence model [23]. This two-equation model is the industry standard for external hydrodynamic simulations due to its accuracy in predicting boundary layer flows under adverse pressure gradients, which are prevalent at the stern of the yacht. The model blends the robust formulation of the k-$\omega$ model in the near-wall region with the free-stream independence of the k-$ϵ$ model in the far-field region.
• Free Surface: The sharp interface between water and air is captured using the Volume of Fluid (VoF) method [24]. This approach solves an additional transport equation for the volume fraction of water in each cell, allowing the free surface to deform naturally in response to the vessel’s movement and wave generation. To prevent non-physical wave reflections from the domain boundaries, a variable wave damping method is employed.

To accurately predict propulsive power, the propellers were modelled using a body force method. This technique simulates the propeller’s effect without resolving its exact geometry in the mesh, offering a balance between accuracy and computational cost. This balance is crucial for a practical retrofit workflow, where a rapid and repeatable assessment of design changes is more valuable than a computationally expensive, highly detailed propeller-resolving simulation.

The virtual disk approximation neglects blade-resolved vortex shedding and duct–blade interaction. The literature suggests that this introduces 1–3% uncertainty in absolute power predictions [25,26], but parametric trends (e.g., angle-of-attack optimization) remain reliable because interaction effects scale similarly across configurations.

In this approach, the propeller is represented by a virtual disk at the correct location. The forces (thrust and torque) generated by the propeller are calculated based on its open water performance curves ($K_T$, $K_Q$) and distributed as body forces onto the fluid cells within the virtual disk’s volume.

The simulation seeks the self-propulsion point for a given ship speed. It does this by iteratively adjusting the propeller’s rotational speed (RPM) until the thrust produced by the virtual disk precisely balances the total resistance of the vessel. This method correctly captures the key hull–propeller interaction effects, including the propeller’s influence on the flow around the stern (wake induction) and the resulting impact on hull resistance (thrust deduction).

Simulating at full scale requires specific considerations to ensure accuracy:

• Wall Treatment: The high Reynolds number of the flow necessitates the use of wall functions to model the near-wall velocity profile. The mesh was generated to achieve a target wall $y^{+}$ value in the range of 30–300, consistent with the requirements of the SST k-$\omega$ model’s wall treatment.
• Hull Roughness: To account for the condition of the real vessel’s hull surface (paint, minor fouling, etc.), a hull roughness value of 150 μm, a standard value for in-service vessels, was incorporated into the wall boundary condition. This ensures a more realistic prediction of frictional resistance compared to a perfectly smooth surface.
• Dynamic Motion: The yacht was allowed to move freely in heave (vertical motion) and pitch (rotation about the transverse axis). The workflow used a Dynamic Fluid Body Interaction (DFBI) model to calculate these motions. An equilibrium motion method was employed to quickly achieve a quasi-steady-state equilibrium position, allowing the simulation to find the yacht’s natural running attitude at each speed.

4. CFD Model Setup and Validation

A robust and accurate CFD model is essential for reliable performance prediction. This chapter details the setup of the numerical model and presents the comprehensive validation of the self-propulsion simulations against the full-scale sea trial data for the M/Y Incal. Achieving a strong correlation is a fundamental step in ensuring the reliability of the numerical method for subsequent design analysis.

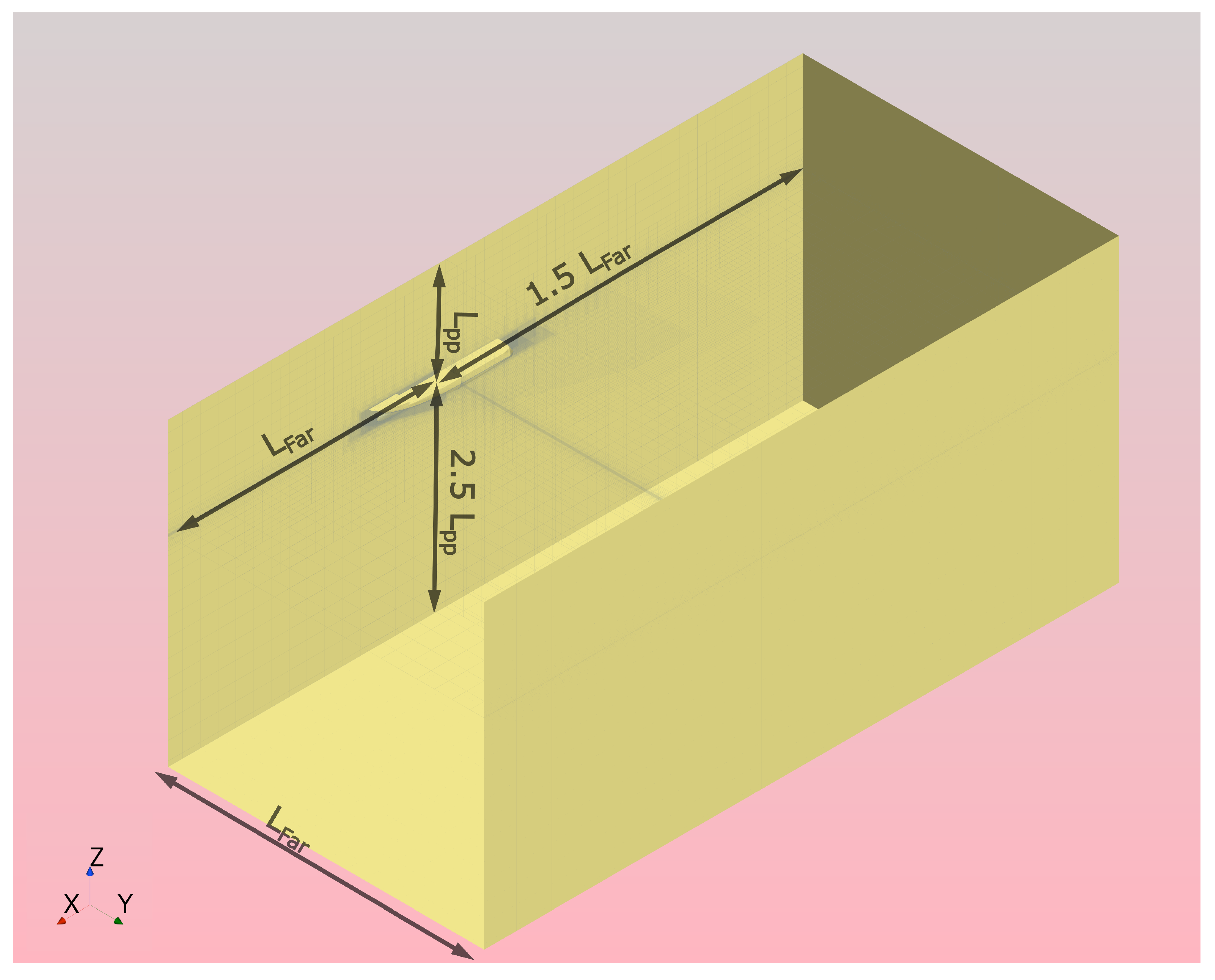
The computational domain represents a virtual towing tank configured following Hull Performance Workflow (HPW) automated procedures [22] and ITTC guidelines for ship CFD applications [16]. Domain sizing is velocity-dependent, calculated based on the Froude number and wake wave characteristics to minimize boundary interference while preventing wave reflection. For the initial baseline resistance calculations, we employed a symmetry plane at $y=0$, modeling only a half-hull. This simple step reduced the computational cost by roughly 50%. The ducted configurations, however, demanded full-hull modeling. This necessity arose directly from the asymmetric flow patterns induced by the propellers (left-handed on port, right-handed on starboard), which eliminated the possibility of using a symmetry assumption.

The computational domain extents adapt automatically to ship speed through Froude number-dependent formulations, shown in

Table 4. Computational domain extents and sizing methodology.

Parameter	Expression/Value	Physical Basis
Froude Number	Fn $=V_S\sqrt{g·L_{WL}}$	Non-dimensional speed parameter
Wake Wavelength	$\lambda ={\displaystyle \frac{2\pi }{g}}·V_s^2$	Deep water wave dispersion relation
Max Wavelength	${\lambda }_{max}={\displaystyle \frac{2\pi }{g}}·V_{s,max}^2$	At maximum Froude number (Fn = 0.4)
Buffer Length	$L_B=0.4925·F{n}^{-0.8}·\lambda$	Distance where damping begins
Max Buffer	$L_{B max}=0.4925·F{n}^{-0.8}·{\lambda }_{max}$	At maximum speed
Damping Length	$L_{D max}=4.5\times {10}^{-3}·e^{-3.{75}^{Fn}}·{\lambda }_{max}$	Maximum damping zone extent
Far-Field Distance	LFar = LD,max + LB,max	Total domain extent from hull
Inlet Distance	1.5 Lpp (forward of FP)	Ensures undisturbed flow development
Outlet Distance	3.0 Lpp (aft of AP)	Captures complete wake
Side Distance	±1.5 Lpp (from centerline)	Minimizes blockage (<1%)
Bottom Distance	1.5 Lpp (below baseline)	Sufficient depth clearance
Top Distance	0.5 Lpp (above DWL)	Atmospheric boundary clearance

. This velocity-dependent approach ensures adequate capture of wake wave patterns at higher speeds while maintaining computational efficiency at lower speeds where wavelengths are shorter.

In the previous table, L_pp = 37.30 m (length between perpendiculars, Table 2); L_WL = waterline length (geometry-dependent); V_s = ship speed (variable: 7.7–12.8 knots in validation range); g = 9.81 m/s² (gravitational acceleration); and F_n,max = 0.4 (maximum Froude number in HPW).

At the 12.3-knot cruise speed (Fn = 0.33), the calculated domain extents are inlet at x = −56 m (L_Far forward of FP); outlet at x = +112 m (3.0 L_pp aft of AP); and lateral boundaries at y = ±56 m (1.5 L_pp from centerline). The resulting cross-sectional blockage ratio is approximately 0.26%, well below the 1% threshold for negligible blockage effects.

Computational domain configuration is shown in Figure 3. Domain sizing follows velocity-dependent HPW methodology with the inlet at 1.5 L_pp forward, outlet at 3.0 L_pp aft, and lateral boundaries at ±1.5 L_pp from centerline. The far-field distance L_Far is calculated as a function of the Froude number and wake wavelength, ensuring adequate wave propagation distance while maintaining computational efficiency. Variable wave damping zones extend from buffer length LB to each boundary (except the top), preventing non-physical wave reflection. For baseline resistance, the symmetry plane at y = 0 (half-hull model shown). For ducted configurations, the full domain $y\in [-1.5,+1.5]L_{pp}$ was employed.

Table 5. Boundary condition specifications.

Boundary	Location (Relative to Lpp)	Type
Inlet	$x=-1.5$	Velocity Inlet
Outlet	$x=+3.0$	Pressure Outlet
Sides (Port/Stbd)	$y=\pm 1.5$	Slip Wall
Bottom	$z=-1.5$	Slip Wall
Top (Atmospheric)	$z=+0.5$	Velocity Inlet
Symmetry (Centerline)	$y=0$	Symmetry Plane
Hull Surface	Geometry Surface	No-Slip Wall
Virtual Disk	$x\approx -0.65$	Body Force Propeller (Actuator Disk)

provides comprehensive boundary condition specifications for all domain surfaces. The boundary treatment follows established marine CFD best practices, balancing computational efficiency with physical accuracy.

The computational domain size is $4.5L_{pp}$ in length (from $-1.5L_{pp}$ to $+3.0L_{pp}$), $3.0L_{pp}$ in width, and $2.0L_{pp}$ in height. The domain boundaries are defined as follows:

• Inlet and Top Boundaries: A Velocity Inlet condition is applied at $x=-1.5L_{pp}$ and $z=+0.5L_{pp}$ (Top). The velocity is set to the ship speed, $U=V_s$, aligned with the +x axis.

  –

  For the Inlet, turbulence is specified as $I=1\%$ and ${\mu }_t/\mu =10$. The pressure is set to Hydrostatic, $P=P_{\mathrm{atm}}+\rho gz$. The VOF fraction is 1 for water $(z<0)$ and 0 for air $(z>0)$.

  –

  The Top Boundary acts as the atmosphere, utilizing a moving reference frame for velocity, $P=P_{\mathrm{atm}}$, and an air VOF fraction of 1.

• Outlet Boundary: A Pressure Outlet condition is applied at $x=+3.0L_{pp}$. The pressure is set to Hydrostatic. Velocity and VOF are treated with a zero-gradient condition, $\partial \varphi /\partial n=0$. A backflow velocity of $V_s$ is specified if recirculation occurs.
• Sides and Bottom Boundaries: The Side ($y=\pm 1.5L_{pp}$) and Bottom ($z=-1.5L_{pp}$) boundaries are defined as Slip Walls. This implies a free-slip condition (${\tau }_{\mathrm{wall}}=0$) for tangential velocity and a zero normal velocity ($U_n=0$). Pressure is treated with a zero-gradient condition normal to the boundary.
• Symmetry Plane: The $y=0$ plane uses a Symmetry Plane condition, requiring zero normal velocity ($U_y=0$) and zero gradients for all scalars ($\partial \varphi /\partial y=0$). This is valid for straight-line motion only; a full hull is used for duct cases.
• Wave Damping: A variable-length damping zone $L_D$ (as defined in (3)) is applied to the Outlet, Sides, and Bottom Boundaries to prevent wave reflection. No damping is applied at the Inlet or Top.
• Hull Surface: The physical hull is a No-Slip Wall ($U=0$ in the body-fixed frame). A uniform roughness $k_s=150\mu \mathrm{m}$ (in-service condition) is applied.
• The wall treatment uses all $y^{+}$ wall functions, targeting a $y^{+}$ range of 30–300 (SST $k-\omega$ requirement). The near-wall mesh consists of 10 prism layers with a growth ratio of 1.3, resulting in a first cell height $y_1\approx 0.5$ mm.
• The hull motion is governed by Dynamic Fluid Body Interaction (DFBI), allowing $Heave\left(z\right)+Pitch\left({\theta }_y\right)$ motion to be solved using the equilibrium motion method.
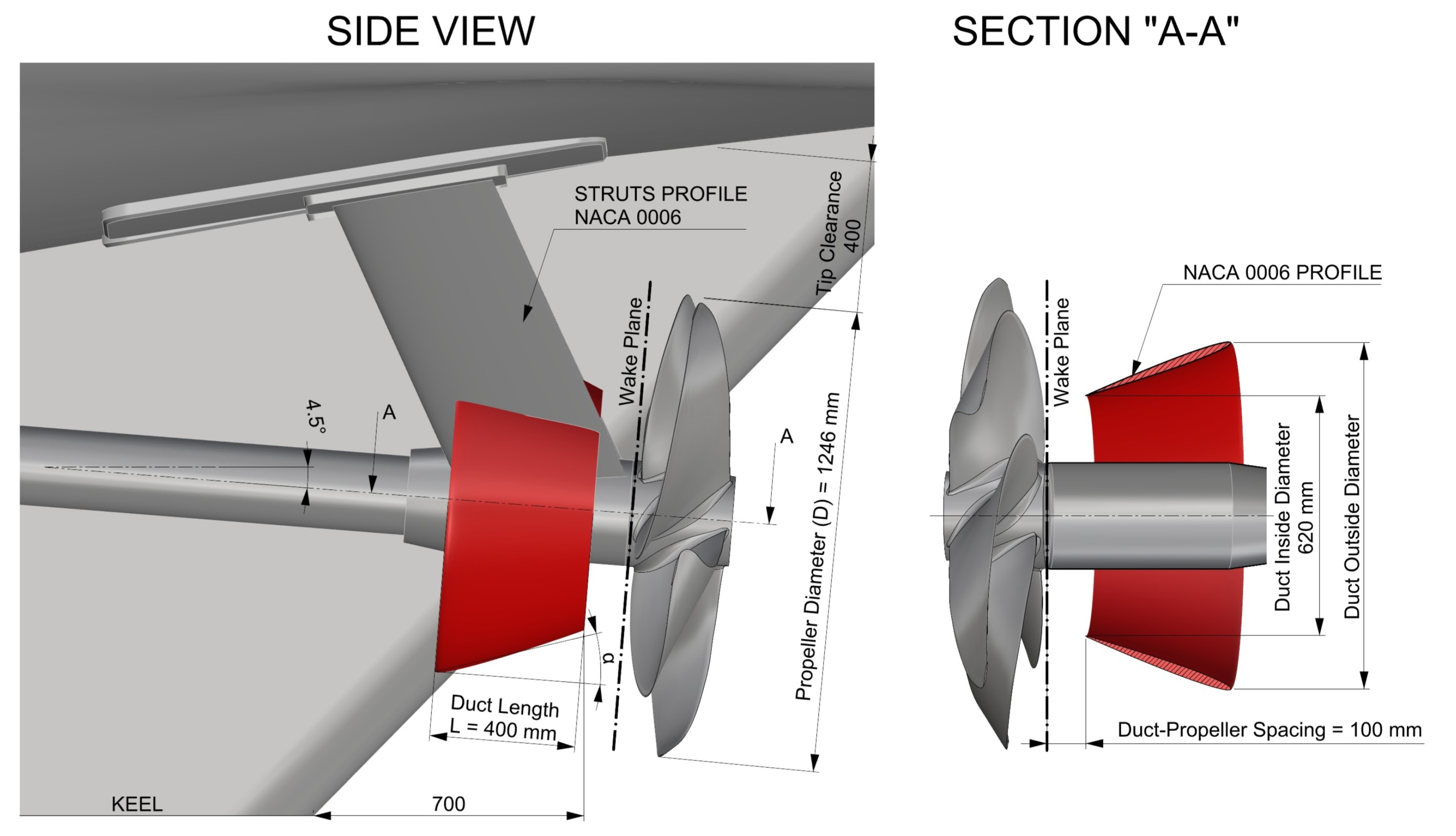
• Virtual Disk: The propeller is modeled as an Actuator Disk (Body Force Propeller) located at $x\approx -0.65L_{pp}$. Key parameters are D = 1.246 m, Wageningen B-series performance, and self-propulsion (iterative RPM) thrust.

The variable wave damping methodology prevents non-physical wave reflection at domain boundaries without requiring manual tuning. The damping length varies with the Froude number and wake wavelength according to the following:

$$L_D\left(t\right)=\left\{\begin{array}{cc}{L}_{\mathrm{Far}}-L_B+L_B·{cos}^2\left({\displaystyle \frac{t}{10t_s}}·{\displaystyle \frac{\pi }{2}}\right),\hfill & \mathrm{for}t<10t_s\hfill \\ L_{\mathrm{Far}}-L_B,\hfill & \mathrm{for}t\ge 10t_s\hfill \end{array}\right.$$

(3)

where the convective time scale $ts=L_{WL}/V_s$ represents the time for flow to traverse the hull length. During the initial startup phase (t < 10 ts), the damping length smoothly transitions from $L_{Far}$ (no damping) to its steady-state value $L_{Far}-L_B$ using a cosine-squared ramp function. This gradual introduction prevents numerical shock from abrupt damping activation. Physical mechanism: A resistance force is applied to vertical fluid velocity components within the damping zone, progressively increasing from zero (at distance $L_B$ from hull) to maximum (at boundary). The exponential damping function $\chi \left(x\right)=exp(-3.5x/L_D)$ ensures smooth wave energy absorption. The damping force is applied as a source term in the momentum equation for the z-velocity component:

$$F_{\mathrm{damping}}=-\rho ·\alpha \left(x\right)·\chi \left(x\right)·u_z$$

(4)

where $\rho$ is the fluid density and $uz$ is the vertical velocity component; $\alpha \left(x\right)$ is the damping coefficient [s⁻¹] ramped spatially with $\chi \left(x\right)$ and temporally with wave growth time. Typical $\alpha \approx$ 1–5 s⁻¹ based on calibration to suppress wave reflection at the outlet.

Application zones:

• Outlet Boundary: Full variable damping (primary wave dissipation zone)
• Side Boundaries: Variable damping on vertical velocity component
• Bottom Boundary: Variable damping (minimal effect due to depth)
• Top Boundary: No damping (atmospheric pressure boundary)
• Inlet Boundary: No damping (undisturbed inflow requirement)

At the 12.3-knot cruise speed (Fn = 0.33), the calculated damping parameters are wake wavelength $\lambda =25.6$ m, buffer length $L_B=30.6$ m, damping length $L_D=56.6$ m, and far-field distance $L_{Far}=87.2$ m. The variable damping length automatically adjusts across the tested speed range (Fn = 0.21–0.35), ensuring consistent numerical stability.

Table 6. Temporal discretization specifications.

Parameter	Formula/Value	Justification
Convective Time Scale	$t_{conv}=L_{WL}/V_s$	Time for particle to traverse hull
Time-Step Size	$\Delta t=t_{conv}/200$	HPW automatic
Typical Δt Range	0.029–0.049 s	For speed range 7.7–12.8 knots
Courant Number	$Co<1$	Implicit unsteady solver stability
Physical Runtime	Auto-determined	Stops when $\Delta RT/RT<0.5\%$ over 500 steps OR max 7500 steps (1st speed) OR 3500 steps (subsequent)
DFBI Update Frequency	Every time-step	Heave/pitch calculated each $\Delta t$
Inner Iterations	10–15 per time-step	Pressure–velocity coupling
Turbulence Model	SST $k-\omega$ (two-equation)	Adverse pressure gradient accuracy
VOF Method	High-Resolution Interface Capturing (HRIC)	Sharp free surface capture

summarizes the temporal discretization approach employed by the Hull Performance Workflow. The time-step size is automatically calculated to balance temporal accuracy with computational efficiency.

The time-step of $\Delta t=t_{conv}/200$ ensures approximately 200 time-steps per hull passage, providing adequate temporal resolution for wave development and DFBI motion response. The implicit unsteady solver maintains numerical stability even at Courant numbers approaching unity, though typical values remain below $Co=0.5$ in the refined regions.

Physical runtime is determined automatically through convergence monitoring. For each speed, the Hull Performance Workflow monitors the sliding-window average of total resistance over the last 500 time-steps. When the resistance oscillates by less than 0.5%, the simulation is considered converged and stops. Maximum runtime limits prevent excessive computation if convergence is not achieved: 7500 time-steps for the first speed (to handle startup transients) and 3500 time-steps for subsequent speeds (where the previous solution provides a good initial condition).

Justification for domain and temporal specifications: The computational setup employs industry-standard best practices automated within the Hull Performance Workflow, validated across numerous commercial and research applications. The velocity-dependent domain sizing adapts to the Froude number and wake characteristics, the variable wave damping prevents non-physical reflections without manual tuning, the boundary layer resolution (y⁺ = 30–300) suits wall-function treatment with the SST $k-\omega$ model, and the time-step size maintains temporal accuracy while achieving computational efficiency. This configuration provides the foundation for reliable self-propulsion predictions.

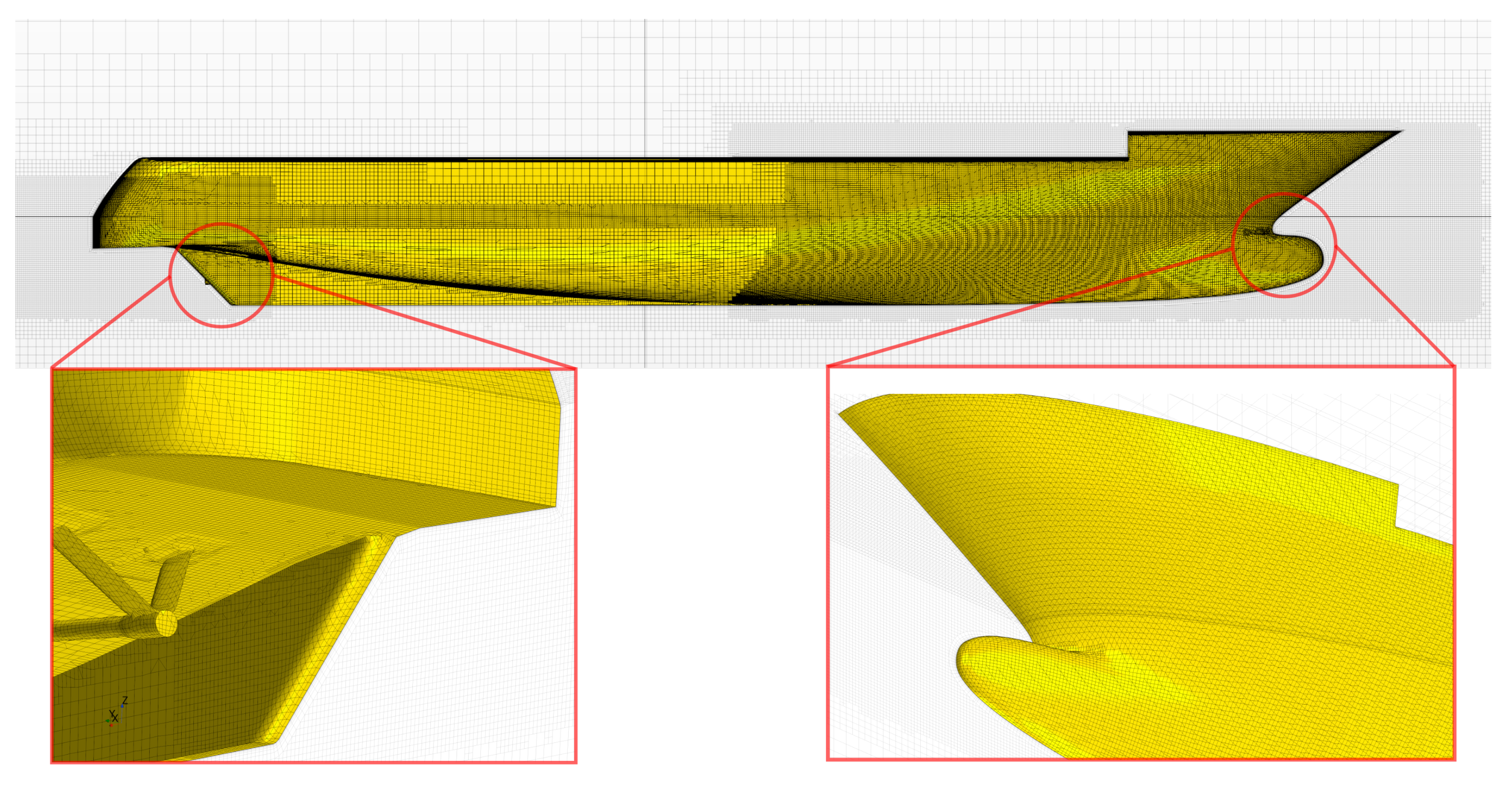
A high-quality finite volume mesh is fundamental to achieving accurate CFD results. The mesh was generated using the trimmed cell mesher in STAR-CCM+. A series of volumetric refinements were created to ensure high resolution in key areas: around the hull, at the stern, in the region of the free surface, and in the wake region downstream of the yacht. Crucially, a dedicated refinement zone was applied to the cylindrical volume representing the body-force propeller model to accurately resolve the flow acceleration and induced swirl. To resolve the boundary layer, a prism layer mesh consisting of 10 layers with a growth rate of 1.3 was generated on the hull surface. A grid verification study, following ITTC procedures, was performed to quantify the numerical uncertainty and ensure that the discretization error was well-controlled. Based on these results, a Medium mesh of approximately 3.5 million cells (Figure 4) was selected for all simulations, providing an optimal balance between computational cost and accuracy. The results of the grid convergence study, presented in

Table 7. Grid convergence study results for speed of 12.3 knots.

Mesh	Cell Count (Millions)	Total Resistance (kN)	Change (%)	Refinement Ratio ($\sqrt{2}$)	GCI Fine (%)
Coarse	2.5	89.021	-	-	2.00
Medium	3.5	90.838	+2.04	1.40	1.2
Fine	4.9	91.246	+0.45	1.43	0.8

, show that the discretization error is well-controlled.

Grid convergence parameters:

• Convergence ratio: $R=\left({ϵ}_{21}\right)/\left({ϵ}_{32}\right)=2.04/0.45=4.53>1$—Monotonic convergence
• Apparent order: $p=ln({ϵ}_{21}/{ϵ}_{32})/ln\left(r_G\right)=ln\left(4.0\right)/ln\left(1.41\right)\approx 4.35$
• Richardson extrapolation: ${\varphi }_{\mathrm{ext}}={\varphi }_{\mathrm{fine}}+({\varphi }_{\mathrm{fine}}-{\varphi }_{\mathrm{medium}})/(r^p-1)\approx 91.328$ kN
• Grid Convergence Index (Fine): $GC{I}_{\mathrm{fine}}=\left(1.25\right|ϵ\left|\right)/(r^p-1)=0.8\%$

The Grid Convergence Index (GCI) for the Fine mesh is 0.8%, which is well below the typically accepted values (<2%) for this type of analysis, demonstrating that the chosen mesh size provides reliable and accurate results. The apparent order p = 4.35 exceeds the scheme’s theoretical order (2.0), indicating the grid study operates in the asymptotic convergence range where solution error decays faster than the formal discretization order [16]. This behavior is typical for well-resolved marine CFD studies and validates the adequacy of the Fine mesh. Based on these results, the Medium mesh of approximately 3.5 million cells was selected for all simulations, providing an optimal balance between computational cost and accuracy ($GC{I}_{medium}=1.2\%$).

Mesh quality metrics for the selected Medium mesh:

• Total cell count: 3.5 million cells (half-hull model)
• Base cell size: 200 mm (reference dimension)
• Hull surface cell size: 28.6 mm (denominator = 7)
• Free surface refinement: 4 mm vertical resolution (±0.15 m zone)
• Propeller zone refinement: 6 mm cell size (62 cells across diameter)
• Prism layer total thickness: 45 mm (10 layers, growth rate 1.3)
• First prism cell height: y₁ ≈ 0.5 mm (target y⁺≈ 50 at cruise speed)
• Maximum aspect ratio: 18:1 (acceptable for trimmed cells)
• Minimum orthogonality angle: 28° (excellent, <45° threshold)
• Prism layer coverage: 93% of hull surface achieves target y⁺ range (30–300)

The propellers are five-bladed Wageningen B-series fixed-pitch propellers with geometric characteristics listed in Table 2. The performance characteristics (KT-KQ-J curves) required for the body-force model were derived from the standard Wageningen B-series systematic data [27], calculated using the polynomial regression equations for the specific propeller geometry.

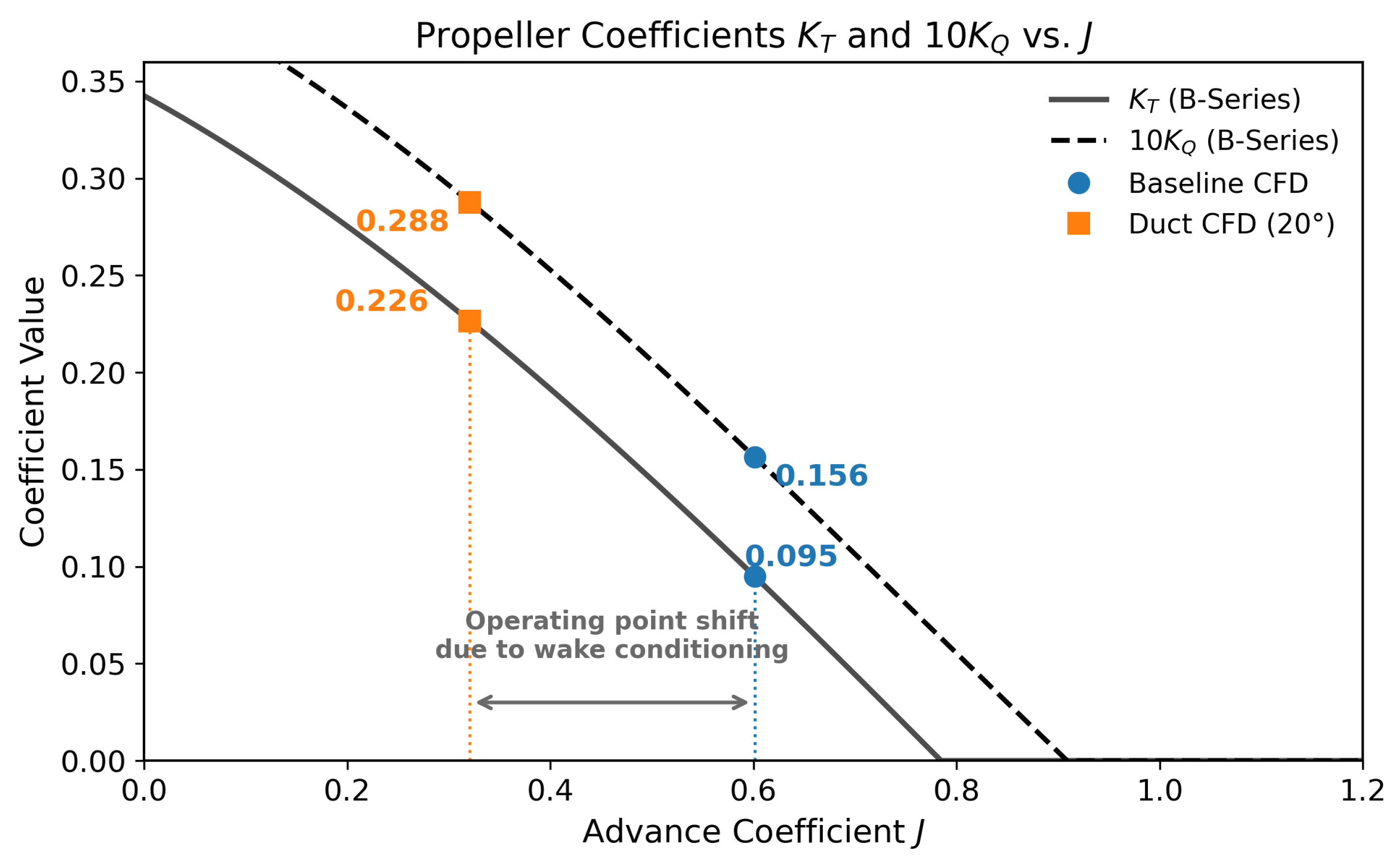
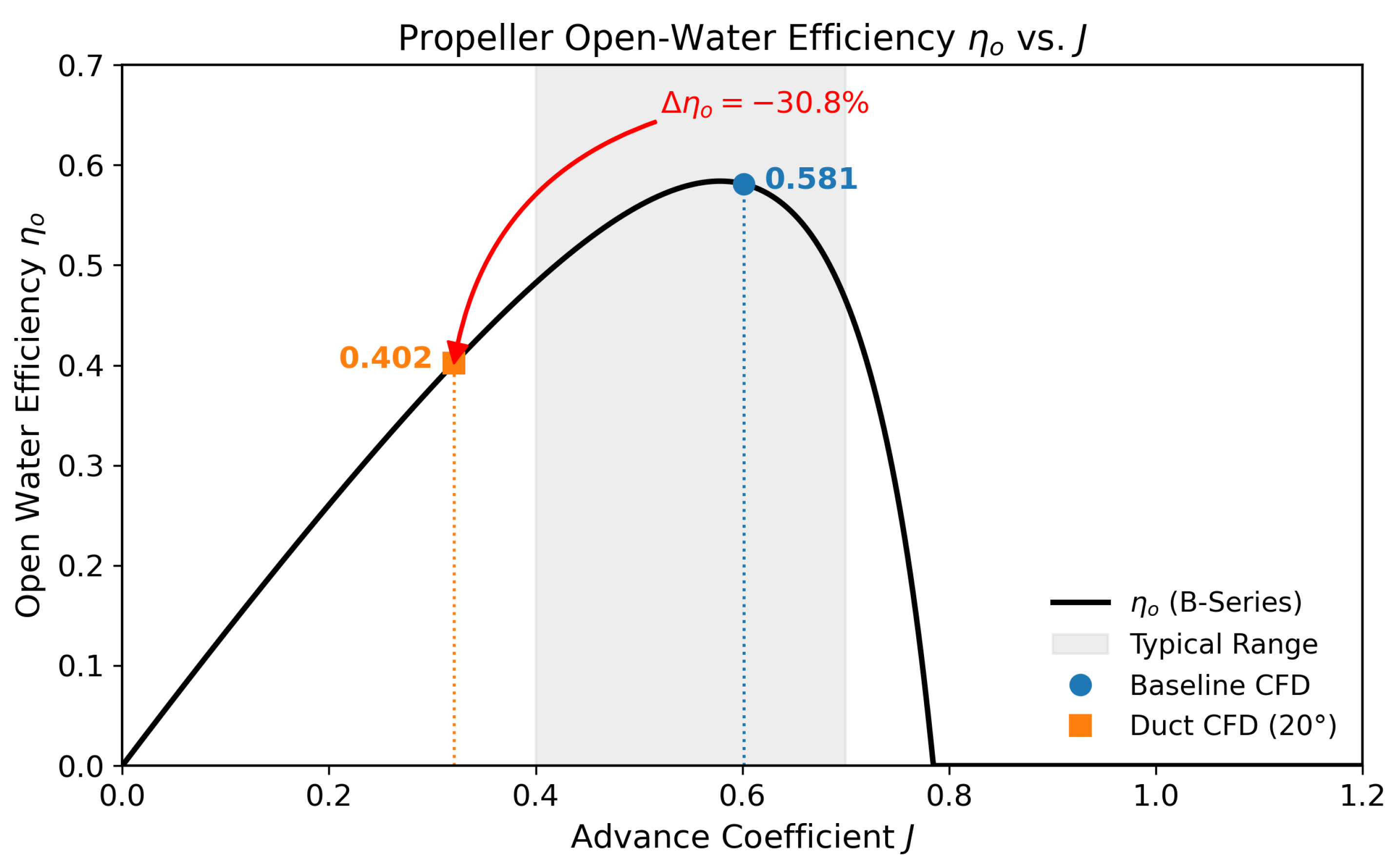
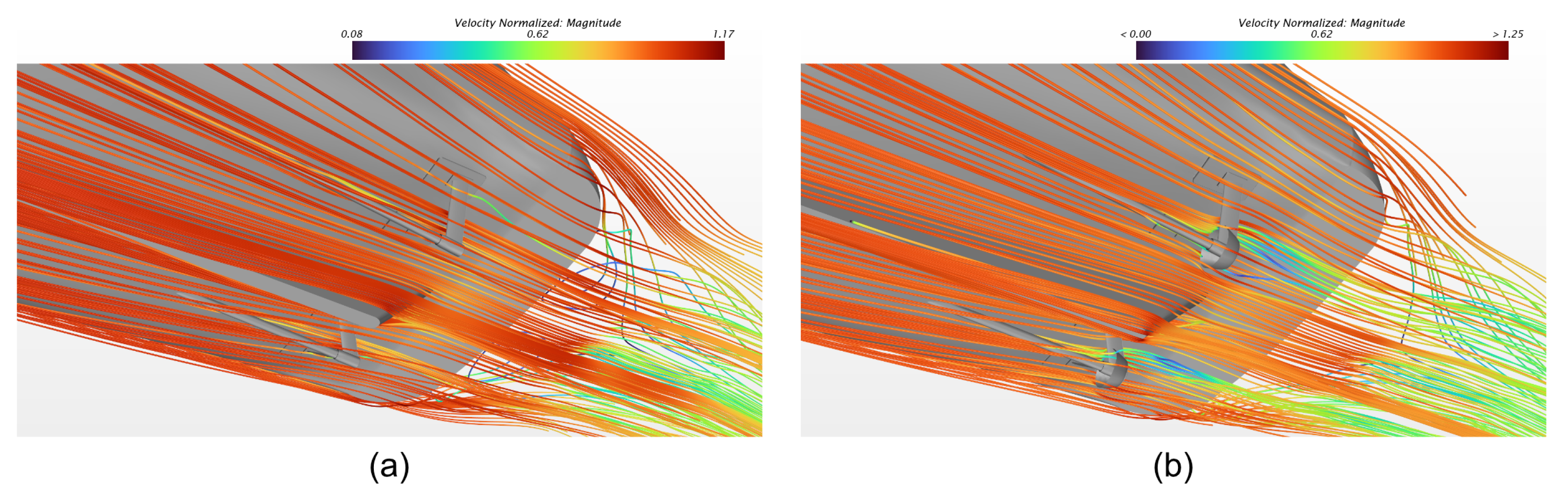
The body-force propeller model demonstrates excellent agreement with the Wageningen B-series systematic data across the relevant advance coefficient range (J = 0.3–0.7). The model accurately reproduces the thrust coefficient (KT), torque coefficient (KQ), and open-water efficiency (${\eta }_o$) relationships defined by the standard polynomial regressions. Operating points extracted from both baseline and ducted self-propulsion simulations fall precisely on these validated curves, confirming that the CFD model correctly predicts propeller loading conditions under varying inflow conditions.

The use of well-established Wageningen B-series data ensures that the body-force model captures the correct thrust–torque–efficiency relationships for the specific propeller geometry. Self-propulsion operating points extracted from CFD simulations fall precisely on these validated curves, confirming correct propeller loading predictions. This rigorous validation is essential for the comparative ESD assessment in Section 5, where operating point migration drives the observed performance differences.

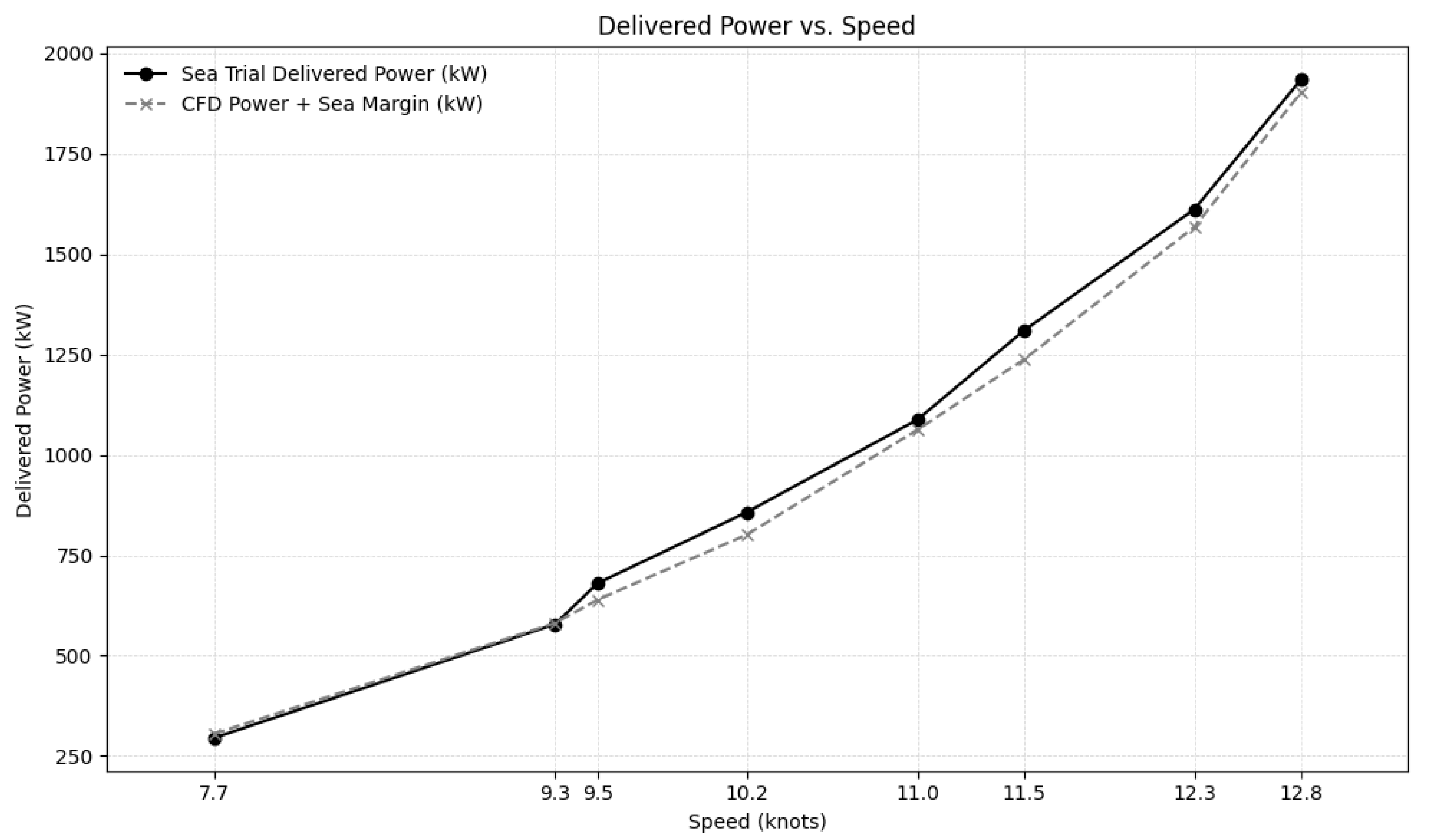
The primary validation metric for the self-propulsion model is the delivered power ($P_D${sub}“). The validation process involves a direct, like-for-like comparison between the power predicted by CFD and the power measured during the full-scale sea trial.

The validation employed the standard 12.5% sea margin recommended by ITTC [21] for full-scale power prediction, which accounts for hull roughness, wind resistance, and operational variability.

Table 8. Validation of CFD power prediction against sea trial data. Statistical validation metrics: MAE = 45 kW, RMSE = 52 kW, R² = 0.996 across the speed range, confirming strong predictive accuracy.

Speed [Knots]	Sea Trial Delivered Power [kW]	CFD Power (Calm Water) [kW]	CFD Power + Sea Margin [kW]	Difference [%]
7.7	295	230	305	−3
9.3	578	479	581	0
9.5	680	500	639	6
10.2	857	676	801	7
11	1087	901	1062	2
11.5	1309	1061	1237	5
12.3	1611	1306	1567	3
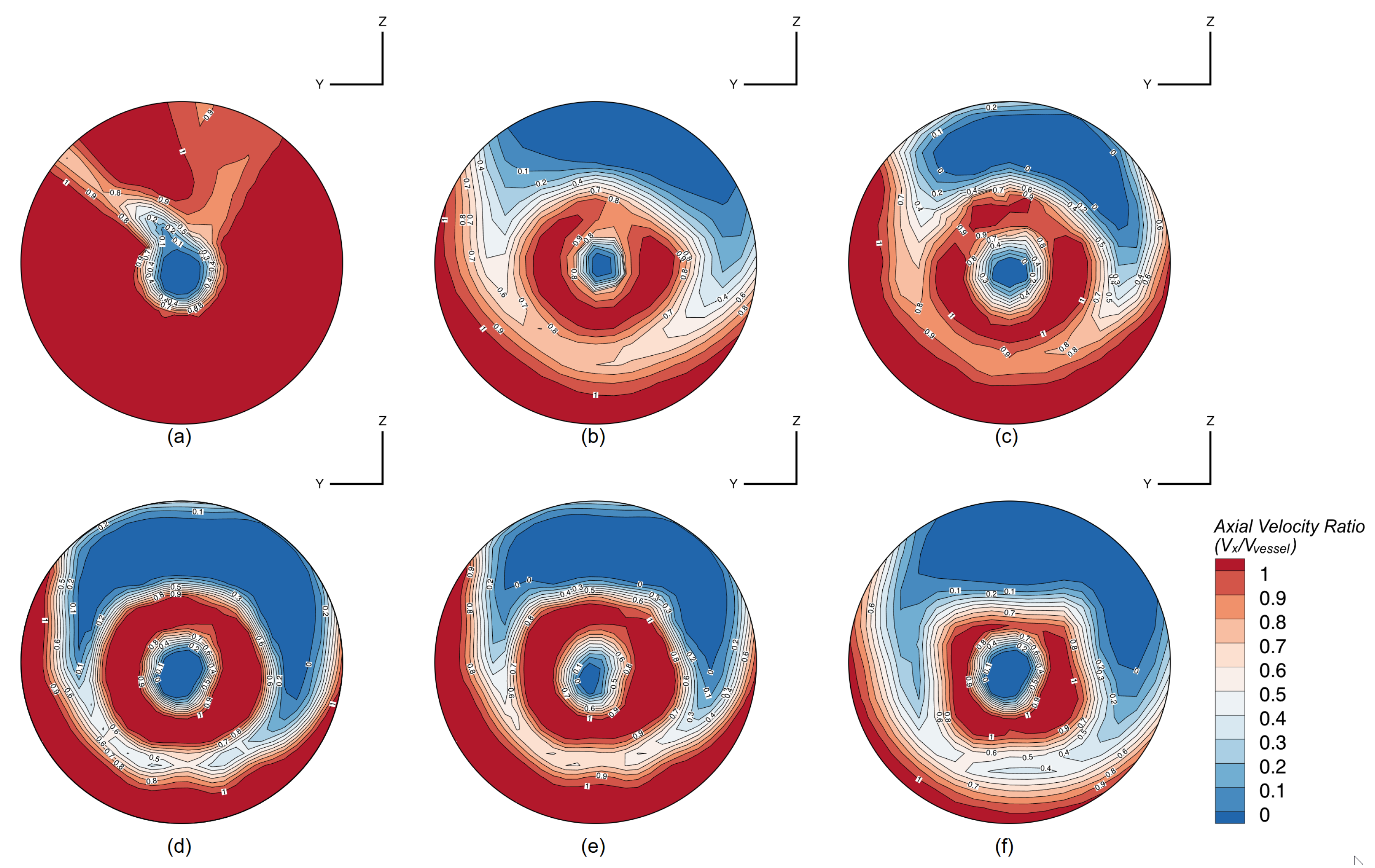
12.8	1934	1724	1902	2

shows that the CFD predictions with this margin agree with measured sea-trial power within ±15% uncertainty (typical for yacht trials). The close agreement validates the CFD methodology for parametric ESD studies, where relative power changes between configurations are more critical than absolute power magnitude. The CFD model already accounts for the change in propeller coefficients ($K_T,K_Q$) and performance (${\eta }_o$) due to the inhomogeneous inflow speed by matching the computed operating point to the corresponding Wageningen B-series curve (Figure 5 and Figure 6); thus, the added sea margin is independent of this hydrodynamic effect. The final validation compares the CFD Predicted Power + Sea Margin against the Sea Trial Delivered Power.

The validation results are presented in Table 8 and visualized in Figure 7. The comparison shows a strong correlation between the numerical predictions (including the sea margin) and the real-world trial data.

5. Design and Analysis of Pre-Propeller Ducts

With the CFD model robustly validated against full-scale data, it can be employed with confidence as a tool for virtual prototyping and performance assessment. This chapter introduces the design of a bespoke pre-propeller duct system aimed at improving the propulsive efficiency of the M/Y Incal. To determine the most effective configuration, a parametric study was conducted, varying the duct’s angle of attack ($\alpha$). This approach is in line with modern computational design methods that seek to optimize hull forms and appendages for minimum resistance and maximum efficiency [28]. The effectiveness of each configuration is quantified by directly comparing the results of self-propulsion simulations with and without the device.

5.1. Duct Design and Parametric Study

The primary objective of the pre-propeller ducts is to improve the quality of the inflow to the propellers. For yachts with wide, flat transom sterns, the flow accelerating under the hull towards the propellers is often highly non-uniform. This can lead to unsteady blade loading, an increased risk of cavitation, and reduced propulsive efficiency. The proposed Energy Saving Device (ESD) consists of two custom-designed ducts, one mounted upstream of each propeller. The bespoke design of such ducts is critical, as research shows that geometric variations—such as circular, un-circular, or asymmetric shapes—significantly alter propeller performance [7]. Furthermore, a poorly configured duct can even decrease efficiency, underscoring the need for careful simulation and analysis [29].

The ducts were designed with the following principles in mind:

• Wake Field Conditioning and Homogenization: The ducts feature a nozzle-like, convergent cross-section. This geometry is designed to capture and condition the wake from the hull, mitigating the severe velocity deficits and creating a more uniform inflow for the propeller [30,31].
• Pre-Swirl Generation: The ducts are designed with a slight asymmetric profile to induce a controlled pre-swirl in the direction opposite to the propeller’s rotation. This pre-swirl reduces the net rotational kinetic energy loss in the propeller’s slipstream, thereby improving propulsive efficiency.
• Structural Integration: The design was developed to be a practical retrofit, with consideration for structural mounting to the existing hull form with minimal complexity.

The geometric parameters for each configuration are listed in

Table 9. Geometric parameters for the pre-propeller duct design study, showing the variation of the outside diameter with the angle of attack.

Angle of Attack $\mathit{\alpha }$ [deg]	Duct Outside Diameter [mm]
10	780
15	840
20	900
25	960
30	1020

. To find the optimal design, a parametric study was conducted, varying the duct’s angle of attack. The angle of attack ($\alpha$, as noted on Figure 8) is defined as the angle between the duct chord line (running from the leading edge to the trailing edge) and the propeller shaft axis. A series of self-propulsion simulations were run at the cruise speed of 12.3 knots, testing duct angles of ${10}^{\circ }$, ${15}^{\circ }$, ${20}^{\circ }$, ${25}^{\circ }$, and ${30}^{\circ }$.

5.2. Performance Analysis of Duct Angle of Attack

The results of the parametric study at the 12.3-knot cruise speed are summarized in

Table 10. Parametric study results of duct angle of attack on propulsion metrics at 12.3 knots.

Duct Angle of Attack $\mathit{\alpha }$ [deg]	Wake Fraction (w)	Thrust Deduction (t)	Hull Efficiency (${\mathit{\eta }}_{\mathit{H}}$)	Propeller Open-Water Efficiency (${\mathit{\eta }}_{\mathit{o}}$)	Delivered Power—With Duct [kW]	Power Saving [%]
10	0.338	0.062	1.417	0.412	1573	−0.38
15	0.371	0.063	1.490	0.406	1548	1.76
20	0.426	0.087	1.590	0.402	1492	4.74
25	0.449	0.105	1.624	0.395	1530	2.34
30	0.475	0.118	1.679	0.391	1577	−0.65

and Figure 9. The analysis reveals that an angle of attack of $\alpha ={20}^{\circ }$ provides the maximum power saving of 4.7%. Angles below or above this value yield diminishing returns or even a net power loss.

The analysis of propulsive coefficients explains how this saving is achieved. As the angle of attack increases, the wake fraction (w) increases significantly. This drives a substantial increase in hull efficiency (${\eta }_H$). However, this comes at the cost of the propeller’s open-water efficiency (${\eta }_o$), which decreases as it operates in the slower, heavier wake. The optimal performance at $\alpha ={20}^{\circ }$ represents the point where this trade-off is most favorable. The substantial gain in hull efficiency is the primary mechanism for the power saving, and it is potent enough to more than compensate for the reduction in propeller efficiency. This is visually confirmed by the axial velocity contours, which show how the ducts create a more homogenized and concentric wake profile compared to the highly non-uniform baseline flow (Figure 10).

5.3. Optimal Duct Performance Across the Speed Range and Analysis

Based on the results, the second configuration was selected as the optimal design and was further analyzed at additional speeds to confirm its performance across the operating range. The results show significant power savings of 3.6% at 11.5 knots and 4.1% at 12.8 knots, demonstrating the device’s effectiveness around the vessel’s cruising speed.

The results reveal speed-dependent performance characteristics, as shown in

Table 11. Self-propulsion performance comparison across key speeds with the optimal duct ($\alpha ={20}^{\circ }$).

Speed (knots)	Delivered Power—Baseline [kW]	Delivered Power—With Ducts [kW]	Power Saving [%]
5.0	96	98	−2.4
6.0	165	164	0.6
11.5	1237	1193	3.6
12.3	1567	1492	4.7
12.8	1902	1823	4.1
14.0	2650	2580	2.6

. At low speeds (Fr < 0.20), the ducts slightly increase resistance due to their wetted surface area, without providing commensurate wake-conditioning benefits. The comparison of propulsive coefficients across the speed range in the semi-displacement range (Fr 0.31–0.35) confirms the same underlying mechanism. At those speeds, the ducts with $\alpha ={20}^{\circ }$ dramatically increase the hull efficiency (${\eta }_H$) while decreasing the propeller’s open-water efficiency (${\eta }_o$), with the net result being a positive power saving. Secondary mechanisms include the generation of pre-swirl, which allows the propeller to generate thrust with less torque, and a small amount of direct forward thrust generated by the foil-like shape of the ducts.

To understand the physical mechanisms underlying these power savings, we examine the propulsive efficiency components. The comparison of propulsive coefficients across the speed range confirms a consistent underlying mechanism.

Table 12. Comparison of propulsive coefficients for baseline vs. optimal duct ($\alpha ={20}^{\circ }$) configurations across key speeds.

Speed (Knots)	Configuration	Wake Fraction (w)	Thrust Deduction (t)	Hull Efficiency (${\mathit{\eta }}_{\mathit{H}}$)	Propeller Open-Water Efficiency (${\mathit{\eta }}_{\mathit{o}}$)
5.0	Baseline	0.065	0.082	0.992	0.555
	With Ducts	0.320	0.115	1.294	0.405
6.0	Baseline	0.055	0.084	0.975	0.560
	With Ducts	0.330	0.108	1.327	0.408
11.5	Baseline	0.042	0.090	0.950	0.576
	With Ducts	0.414	0.107	1.520	0.404
12.3	Baseline	0.032	0.093	0.937	0.581
	With Ducts	0.426	0.087	1.590	0.402
12.8	Baseline	0.032	0.042	0.990	0.574
	With Ducts	0.440	0.113	1.584	0.395
14.0	Baseline	0.028	0.048	0.975	0.562
	With Ducts	0.460	0.135	1.602	0.378

presents the key propulsive parameters for baseline and ducted configurations.

The comparison reveals a fundamental and consistent trade-off governing ESD performance. At each speed, the ducts dramatically increase the hull efficiency (${\eta }_H$) while decreasing the propeller’s open-water efficiency (${\eta }_o$), with the net result being positive power savings. The mechanism is remarkably stable across the speed range.

• Wake fraction (w) increase: The ducts create a severe velocity deficit, increasing wake fraction by 886–1275% across the tested speeds. This represents the primary hydrodynamic effect—the ducts capture and decelerate the stern flow.
• Hull efficiency (${\eta }_H$) gain: The increased wake fraction drives substantial improvements in hull efficiency (${\eta }_H=(1-t)/(1-w)$), with gains of 60–70%. This is the dominant beneficial mechanism. At the 12.3-knot cruise speed, hull efficiency increases from 0.937 to 1.590 (+69.7%).
• Propeller efficiency penalty: The propeller operates in the slower, heavier wake, reducing its open-water efficiency by approximately 30% across all speeds. This represents the cost of the wake-conditioning approach.
• Net efficiency improvement: The hull efficiency gain consistently outweighs the propeller efficiency loss, yielding system-level improvements in quasi-propulsive efficiency (${\eta }_D={\eta }_H{\eta }_o{\eta }_R$) of approximately 15–18%.

The thrust deduction coefficient (t) shows more variation across speeds, influenced by the complex pressure field interactions between the hull, ducts, and propeller. However, its contribution to the overall efficiency balance is secondary to the wake fraction effect.

To fully understand the propulsive mechanism, we examine the detailed force balance and propeller operating conditions at the 12.3-knot cruise speed—the peak performance condition.

Table 13. Per-shaft in-wake operating points and validated loads at 12.3 kn.

Parameter	Symbol	Baseline (per Shaft)	Duct 20° (per Shaft)	Change	Physical Meaning
Ship speed	$V_s$	6.33 m/s	6.33 m/s	-	Constant (test point)
Wake fraction	w	0.032	0.426	1231%	Inflow velocity deficit
Propeller advance velocity	$V_A$	6.13 m/s	3.63 m/s	−40.80%	$V_A=V_s(1-w)$
Propeller RPM	n	491 rpm	545 rpm	+11.0%	Self-propulsion equilibrium
Advance coefficient	J	0.601	0.321	−46.60%	$J=V_A/\left(nD\right)$
Delivered power	$P_D$	783.5 kW	746 kW	−4.8%	$P_D=2\pi nQ$ (per shaft)
Torque	Q	15.24 kNm	13.07 kNm	−14.1%	$Q=KQ·\rho ·n^2·D^5$
Propeller thrust	T	26.46 kN	27.71 kN	5.40%	$T=KT·\rho ·n^2·D^4$
Thrust deduction	t	0.093	0.087		Self-propulsion equilibrium
Total resistance	$R_T$	48.0 kN	50.6 kN	5.40%	Hull + appendages + duct
Force balance	2T (kN)	52.92	55.42
	RT/(1 − t) (kN)	52.92	55.42
	Residual	<0.01 kN	<0.01 kN

provides a comprehensive breakdown of all relevant parameters.

Table 13 provides the validated operating points for the twin-screw configuration in the ship’s wake, confirming that self-propulsion equilibrium ($2T=R_T/(1-t)$) was achieved with negligible computational residuals. To quantify the energy savings,

Table 14. Effective (effective coefficients computed as $K_{T,\mathrm{eff}}=T/\left(\rho n^2{D}^4\right)$, $K_{Q,\mathrm{eff}}=Q/\left(\rho n^2{D}^5\right)$, ${\eta }_{o,\mathrm{eff}}=(J/2\pi )(K_{T,\mathrm{eff}}/K_{Q,\mathrm{eff}})$ using validated thrust T, torque Q, and RPM n from Table 13). in-wake propeller coefficients at 12.3 kn.

Parameter	Baseline	Duct 20°
Advance coefficient J	0.601	0.321
$K_{T,\mathrm{eff}}$	0.160	0.136
$10K_{Q,\mathrm{eff}}$	0.739	0.515
${\eta }_{o,\mathrm{eff}}$	0.207	0.135

presents effective in-wake coefficients back-computed from the validated CFD results, revealing the quantitative mechanism: as J decreases from 0.601 to 0.321, the effective $10K_{Q,\mathrm{eff}}$ decreases from 0.739 to 0.515, despite the propeller operating at higher thrust loading, because the J-shift effect dominates coefficient trends.

The ducts introduce severe wake augmentation, which dramatically slows the water entering the propeller. The advance velocity is reduced from $6.13\mathrm{m}/\mathrm{s}$ to $3.63\mathrm{m}/\mathrm{s}$ (a $40.8\%$ reduction) despite the ship’s constant speed. This reduction causes a significant shift in the advance coefficient (J), from 0.601 to 0.321 (a $46.6\%$ decrease), pushing the propeller into a heavily loaded, low-J operational region. To generate the necessary $4.7\%$ increase in thrust per shaft ($26.46\mathrm{to}27.71\mathrm{kN}$), the propeller must spin $11.0\%$ faster ($491\mathrm{to}545\mathrm{RPM}$). Crucially, although the effective in-wake torque coefficient ($10K_Q$) decreases from 0.739 to 0.515 (Table 14), the actual torque per shaft decreases by $14.2\%$ ($15.24\mathrm{to}13.07\mathrm{kNm}$) because the dominance of the J-shift effect outweighs the coefficient change. This net torque reduction is the direct mechanism for power savings, achieved even as propeller open-water efficiency (${\eta }_o$) drops (0.581 to 0.402) and total ship resistance increases $5.4\%$ ($48.0\mathrm{to}50.6\mathrm{kN}$) due to duct drag (hull form drag $+2.1\%$, duct drag $+2.8\%$, appendage interaction $+0.5\%$).

The observation that both resistance and propeller-level efficiency change unfavorably, yet the overall system power consumption decreases, presents an apparent paradox that is resolved by examining the complete propulsive efficiency chain. While the effective power ($P_E$) rises $5.3\%$ ($304\mathrm{to}320\mathrm{kW}$), the delivered power ($P_D$) per shaft ultimately falls $4.8\%$ ($783.5\mathrm{to}746.0\mathrm{kW}$) because a $17.5\%$ improvement in quasi-propulsive efficiency (${\eta }_D$) ($0.544\mathrm{to}0.639$) more than compensates. Mathematically, the power balance holds: $\Delta P_D/P_D\approx \Delta P_E/P_E-\Delta {\eta }_D/{\eta }_D\approx +5.3\%-17.5\%\approx -4.8\%$. This confirms a fundamental principle: optimal Energy Saving Devices (ESDs) do not necessarily reduce resistance; instead, they maximize system-level thrust conversion efficiency. The ducts achieve this through a dramatic $69.7\%$ gain in hull efficiency (${\eta }_H$ from $0.937\mathrm{to}1.590$, Table 12) resulting from targeted wake conditioning, validating the mechanism noted by [7]: “pre-ducts increase hull efficiency and decrease open-water efficiency.”

The underlying fluid dynamics (Figure 11, Figure 12 and Figure 13) clarifies the mechanism: the duct creates a substantial inflow velocity deficit, consistent with the foundational work by [11] demonstrating that such devices reduce propeller inflow speed. This velocity conditioning is what causes the J-shift from 0.601 to 0.321, fundamentally changing the operating point. As Table 14 shows, while the open-water $10K_Q$ modestly increases (from 0.173 to 0.264) as J decreases, the effective in-wake $10K_Q$ decreases (from 0.739 to 0.515) due to the propeller now operating at a lower J where the thrust-per-revolution ratio is more favorable. The dominance of this J-shift effect over the coefficient changes is what yields the final net torque and power reduction. The pressure distribution (Figure 13) indicates only a modest duct lift contribution; the primary benefit is realized via the substantial ${\eta }_H$ gain (Table 12) achieved by modifying the inflow condition, which ultimately offsets the reduction in propeller open-water efficiency.

6. Discussion

The results presented in the preceding chapters provide a comprehensive validation of a full-scale self-propulsion CFD model and demonstrate a directly calculated performance improvement from a bespoke Energy Saving Device. Considering the ±15% sea-trial uncertainty and ±0.8% CFD discretization error (Table 7), the 4.7% power saving at 12.3 kn is statistically significant and robust within a combined uncertainty of approximately ±2% (propagated from trial and numerical sources).

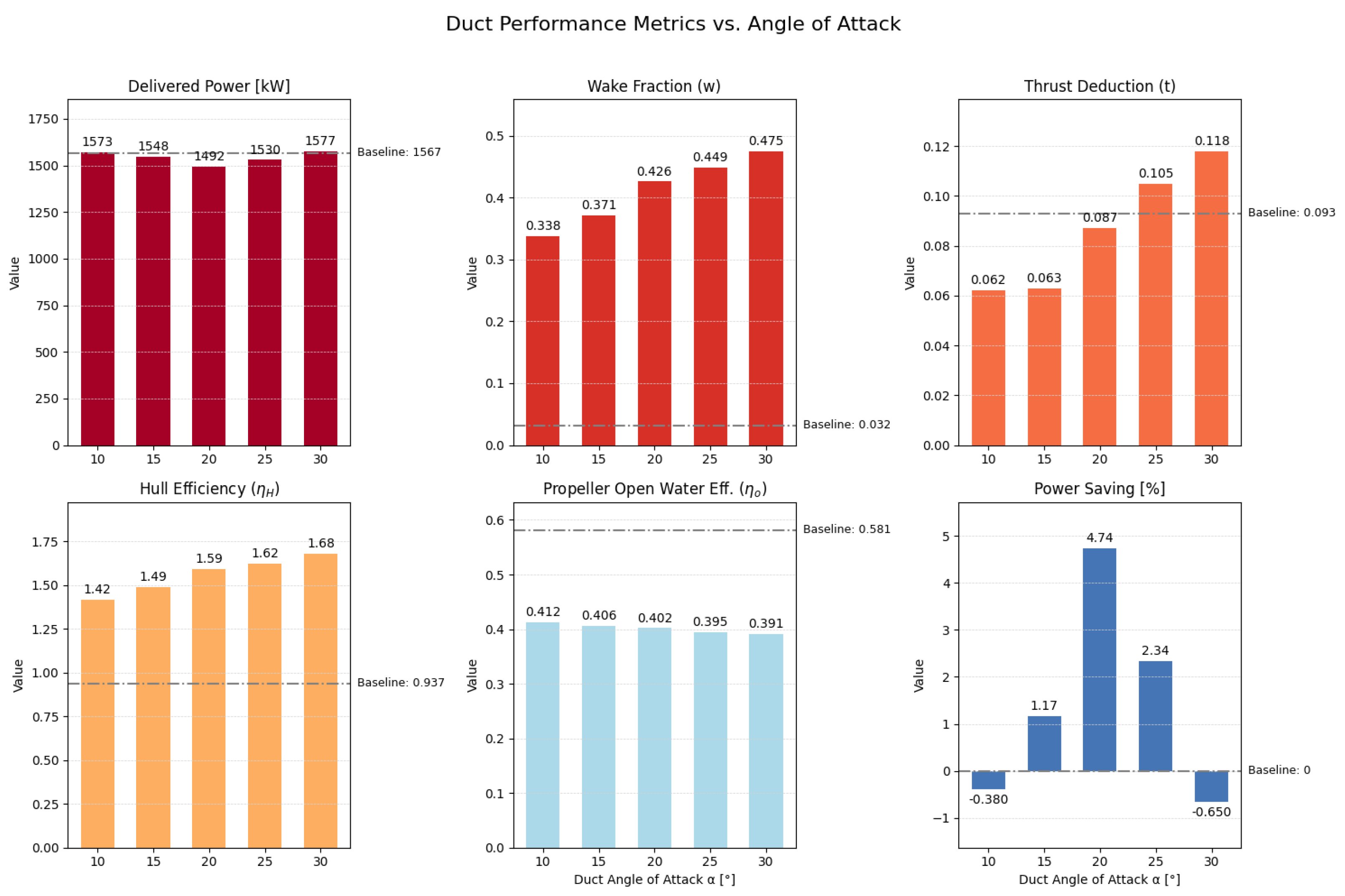
This section aims to interpret these findings, place them in a broader scientific and industrial context, and discuss the limitations and future directions of the work. The primary contribution of this work is the successful design and optimization of the pre-propeller ducts using the validated, high-fidelity model. The self-propulsion analysis shows a peak power saving of 4.7% at the 12.3-knot cruise speed, achieved with a ${20}^{\circ }$ duct angle of attack. This is not an estimation based on resistance but a definitive result reflecting the improved propulsive efficiency of the entire system. This level of improvement is highly competitive with similar Wake-Equalizing Ducts (WEDs) reported to achieve 2–5% savings on bulk carriers [17] and other pre-swirl devices offering gains of up to 6% [18]. Other recent numerical studies show similar gains, including approximately 4% power savings reported by Koushan et al. [19] and up to 4% reduction with optimized pre-swirl ducts and fins in [20]. Further supporting these efficiency gains, Trimulyono et al. [32] found a PSS could increase propeller thrust by 4.7%.

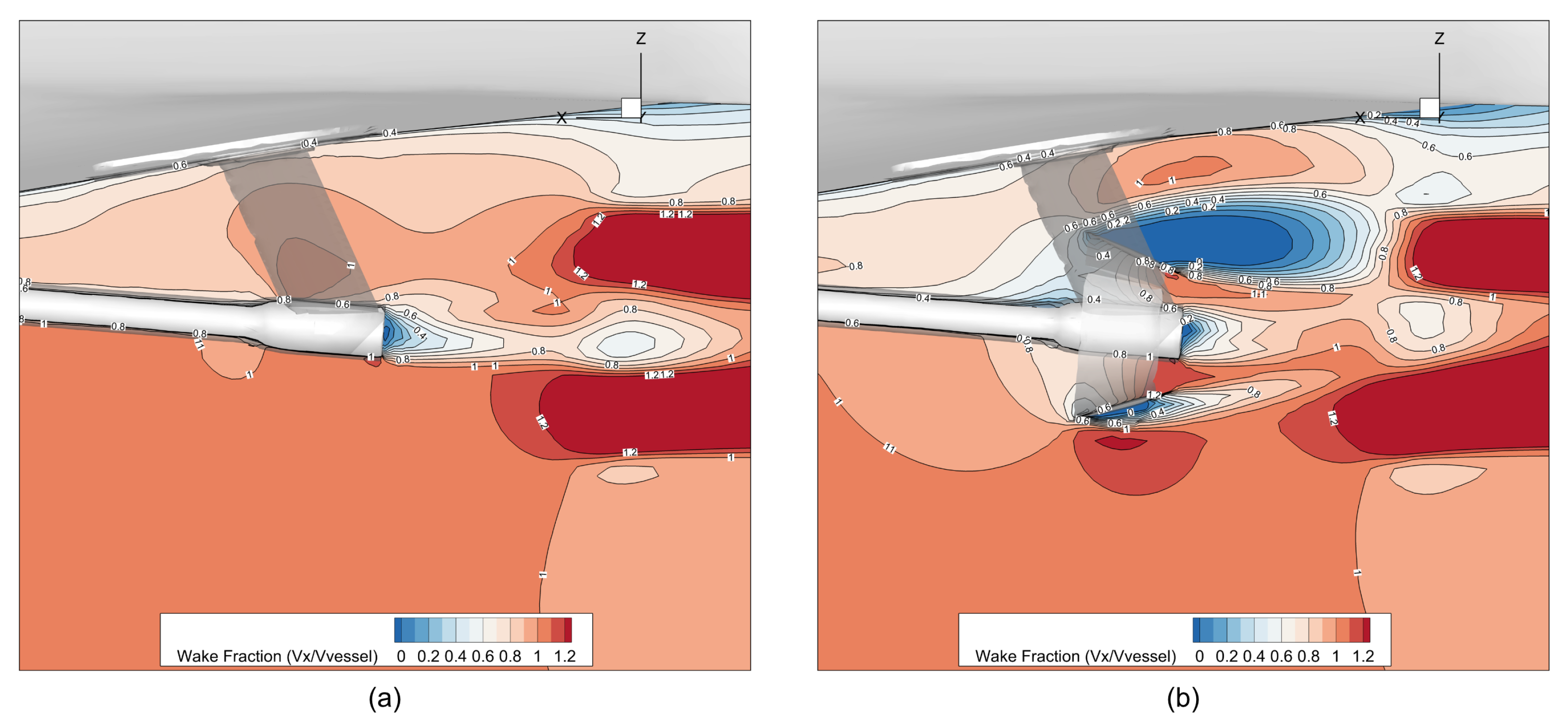
The analysis of the propulsion factors in Section 5 explains this gain. The primary mechanism is the duct’s ability to condition the stern wake, which leads to a higher effective wake fraction (w). This, in turn, produces a substantial increase in hull efficiency (${\eta }_H$). This finding is consistent with recent CFD studies on pre-ducts, which conclude that these devices tend to increase hull efficiency at the expense of open-water efficiency. The gain in hull efficiency is the dominant factor in the power saving, supported by secondary benefits from pre-swirl generation and direct thrust from the foil-shaped duct profile. This demonstrates the potential of a custom-designed device tailored specifically to the yacht’s unique hull form and flow characteristics.

While this study successfully achieved its objectives, it is important to recognize its limitations, which suggest clear directions for future research.

• Operational Profile Analysis: While the duct shows significant benefits in the high-speed cruise range, the performance drop recorded at lower speeds (e.g., $1.0\%$ power increase at 5.0 knots, Table 11) necessitates a full operational assessment. Future work must extend the analysis across the entire speed envelope to precisely quantify the benefits at low-speed maneuvering and high-speed sprint conditions, providing the owner with a complete trade-off assessment for the duct’s utilization.
• Variable Sea Margin: A uniform 12.5% sea margin is applied across all speeds, consistent with preliminary full-scale prediction practice. Future work could refine this using speed-dependent corrections, though the 12.3 kn operating point—where optimization and validation are focused—remains well-characterized.
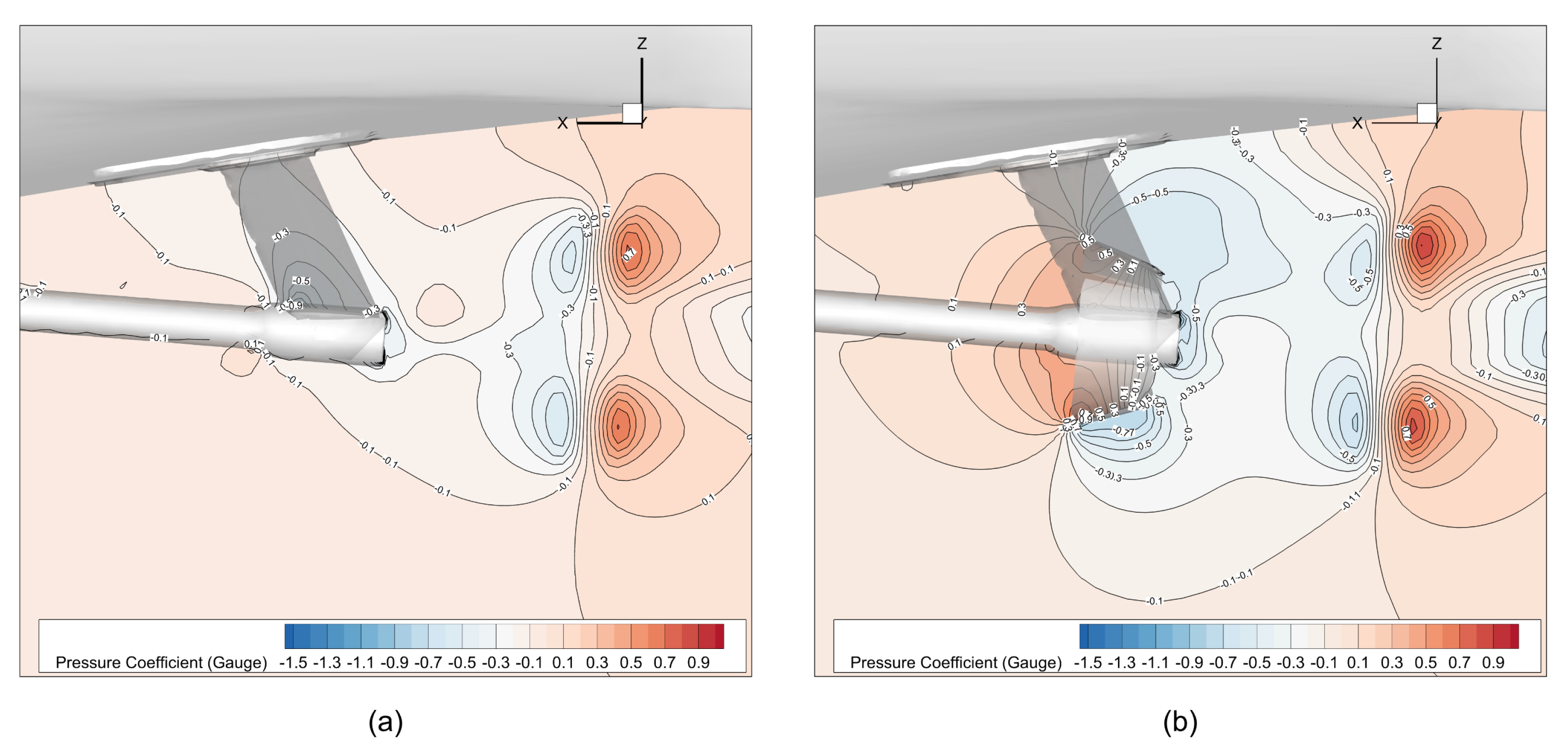
• Geometric Optimization: The visualization of the pressure and axial velocity fields (Figure 10, Figure 12, and Figure 13) confirms that the duct’s strongest hydrodynamic influence is concentrated in the upper quadrants above the propeller shaft. Based on this observation, a worthwhile direction for future optimization is the investigation of a ‘part duct’ or half-duct configuration, possibly spanning between the two shaft brackets. This alternative geometry aims to maintain the high-efficiency benefits while reducing the overall wetted surface, minimizing the slight resistance penalty and simplifying structural integration.
• Structural Feasibility: The hydrodynamic analysis does not include a detailed structural assessment of the ducts or their connection to the hull, which is a critical consideration for practical implementation.
• Additional Physics: The current study focuses on power savings. Future investigations should analyze the beneficial impact of the more uniform wake on propeller cavitation, as ESDs can be optimized not only for power savings but also to address issues like cavitation and pressure fluctuations [33], vortex tip cavitation [34], inception and underwater radiated noise. Furthermore, the ducts’ effect on the vessel’s maneuverability is not assessed.
• Non-Calm Sea Performance: The current calm-water analysis must be extended to rough weather. We are currently awaiting field data from the vessel’s sea trials under real operational conditions (including waves) to serve as the necessary validation target for subsequent high-fidelity VOF numerical simulations aimed at quantifying the ducts’ effect on added resistance and propulsive efficiency in non-calm seas.
• Financial Feasibility: While this study confirms the hydrodynamic benefits, a complete feasibility analysis for practical implementation should also assess the structural integration of the ducts and the economic viability, considering installation costs, long-term maintenance, and classification society requirements.
• Ultimate Validation: For the ultimate validation of these findings, the implementation of the optimal duct will be carried out and tested. This involves the physical manufacturing and retrofitting of the ${20}^{\circ }$ duct system onto the M/Y Incal, followed by a new sea trial campaign to confirm the predicted power savings in real-world operation.

7. Conclusions

This study presented a comprehensive hydrodynamic assessment of a 45 m motor yacht, M/Y Incal, using a full-scale self-propulsion Computational Fluid Dynamics (CFD) model validated directly against sea trial data. The primary objectives were to establish a reliable numerical model of the vessel’s propulsive performance and to leverage this model to design and quantify the effectiveness of a bespoke pre-propeller duct system as an Energy Saving Device (ESD).

The key findings of this research are summarized as follows:

1.

A full-scale self-propulsion CFD model was successfully developed and validated against sea trial data. The strong correlation in predicted delivered power confirms that the numerical method is a reliable and accurate tool for assessing the real-world performance of semi-displacement yachts, bypassing the scaling uncertainties associated with traditional methods.

2.

The validated model was used to design and optimize a custom, retrofittable pre-propeller duct system. A parametric study of the duct’s angle of attack revealed that an angle of ${20}^{\circ }$ provided optimal performance. The direct comparison of self-propelled simulations showed a definitive power saving of 4.7% at the vessel’s cruise speed of 12.3 knots.

3.

Analysis of the flow physics and propulsive factors revealed that the power savings are attributable to a favorable trade-off between competing hydrodynamic effects. The ducts increase the wake fraction (w), which produces a substantial increase in hull efficiency (${\eta }_H$). This gain in hull efficiency is the primary driver for the power savings and is large enough to overcome the corresponding decrease in the propeller’s open-water efficiency (${\eta }_o$), which operates in the slower inflow. This is combined with secondary benefits from pre-swirl and direct thrust from the duct.

In conclusion, this work demonstrates a successful end-to-end workflow, from full-scale data acquisition to validated numerical simulation and ESD design. The proposed pre-propeller duct system represents a viable and effective solution for enhancing the propulsive efficiency and reducing the fuel consumption of the M/Y Incal. Physical retrofit trials of the designed ducts are essential to confirm these CFD predictions and provide the ultimate validation of the performance gains in real-world operation.