Cycling Segments Multimodal Analysis and Classification Using Neural Networks
Abstract
:1. Introduction
2. Methods
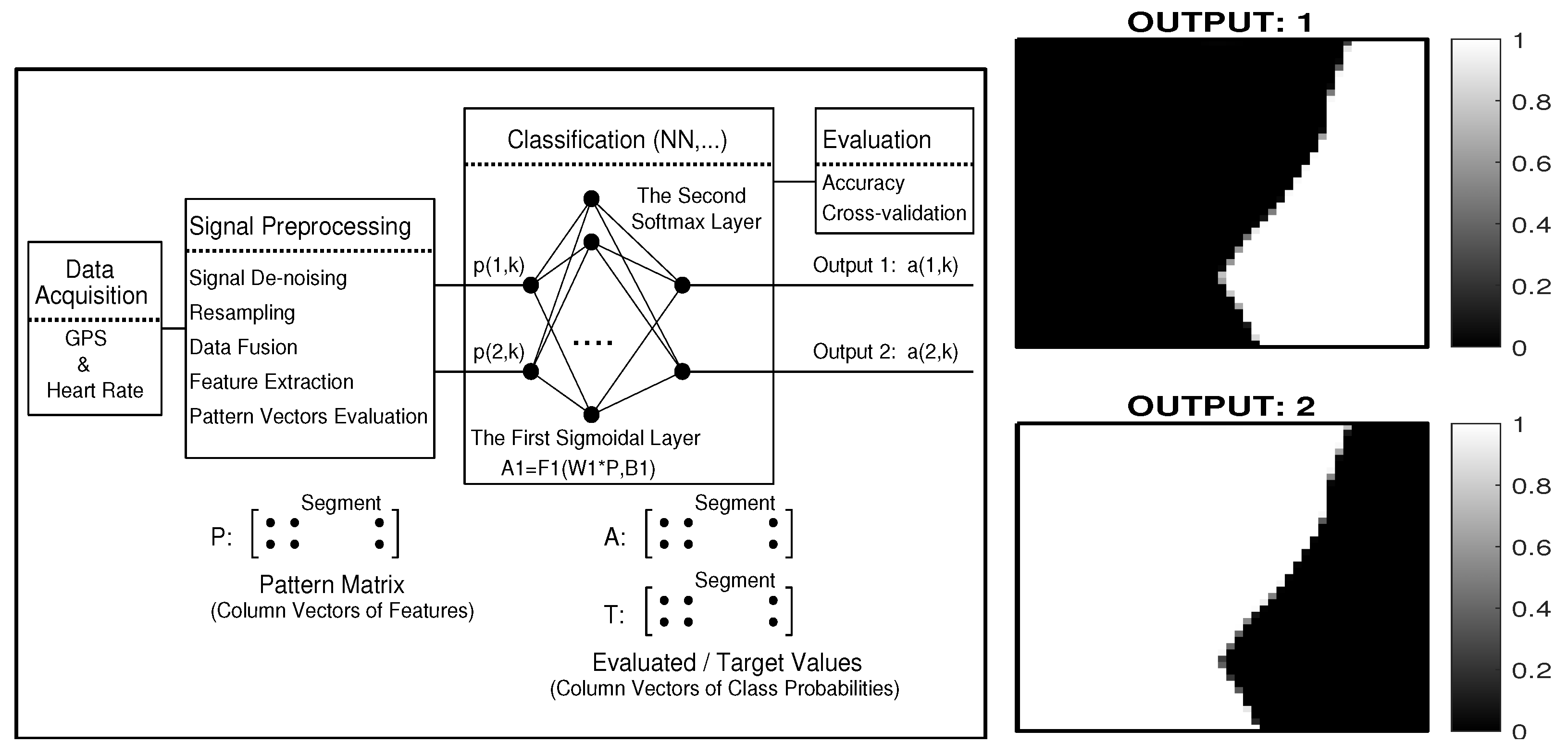
2.1. Data Acquisition
2.2. Data Processing
- transformation of the data recorded in GPX format into the CSV format and their export to the appropriate (MATLAB) computational and visualization environment;
- interconnection of all data segments and exclusion of all stops longer than a selected threshold;
- rejection of gross errors, de-noising of all recorded signals, and their resampling with uniform sampling period, allowing data fusion for the following mathematical processing;
- interconnection of recorded GPS data with the Google map region;
- data segmentation using windows of the selected length.
- selection of windows fulfilling chosen criteria (altitude gradient within given limits for uphill, downhill, or flat cycling);
- detection of relations between individual signals;
- classification of selected segment features and evaluation of the accuracy of the classification, together with cross-validation of the model;
- evaluation of the results from a biomedical point of view.
3. Results
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FIR | finite impulse response |
| GPS | global positioning system |
| GUI | graphical user interface |
| HR | heart rate |
| SVM | support vector machine |
| avg. | average |
| bpm | beats per minute |
| elev. | elevation |
| km/h | km per hour |
References
- Fister, I., Jr.; Ljubic, K.; Suganthan, P.N.; Fister, I. Computational intelligence in sports: Challenges and opportunities within a new research domain. Appl. Math. Comput. 2015, 262, 178–186. [Google Scholar] [CrossRef]
- Arduini, A.; Gomez-Cabrera, M.C.; Romagnoli, M. Reliability of different models to assess heart rate recovery after submaximal bicycle exercise. J. Sci. Med. Sport 2011, 14, 352–357. [Google Scholar] [CrossRef] [PubMed]
- Charvátová, H.; Procházka, A.; Vaseghi, S.; Vyšata, O.; Janáčová, D.; Líška, O. Physiological and GPS Data Fusion. In Proceedings of the International Workshop on Computational Intelligence for Multimedia Understanding (IWCIM), Prague, Czech Republic, 29–30 October 2015; pp. 1–4. [Google Scholar]
- Fasel, B.; Sporri, J.; Gilgien, M.; Boffi, G.; Chardonnens, J.; Muller, E.; Aminian, K. Three-Dimensional Body and Centre of Mass Kinematics in Alpine Ski Racing Using Differential GNSS and Inertial Sensors. Remote Sens. 2016, 8, 671. [Google Scholar] [CrossRef]
- Bucher, S.S.; Supej, M.; Sandbakk, O.; Holmberg, H.C. Downhill turn techniques and associated physical characteristics in cross-country skiers. Scand. J. Med. Sci. Sports 2014, 24, 708–716. [Google Scholar] [CrossRef] [PubMed]
- Hurst, H.T.; Swarén, M.; Hébert-Losier, K.; Ericsson, F.; Sinclair, J.; Atkins, S.; Homlberg, H.C. GPS-Based Evaluation of Activity Profiles in Elite Downhill Mountain Biking and the Influence of Course Type. J. Sci. Cycl. 2013, 2, 25–32. [Google Scholar]
- Formenti, D.; Trecroci, A.; Cavaggioni, L. Heart rate response to a marathon cross-country skiing race: A case study. Sport Sci. Health 2014, 11, 125–128. [Google Scholar] [CrossRef]
- Mekik, C.; Arslanoglu, M. Investigation on Accuracies of Real Time Kinematic GPS for GIS Applications. Remote Sens. 2009, 1, 22–35. [Google Scholar] [CrossRef]
- Gilgien, M.; Sporri, J.; Limpach, P.; Geiger, A.; Müller, E. The Effect of Different Global Navigation Satellite System Methods on Positioning Accuracy in Elite Alpine Skiing. Sensors 2014, 14, 18433–18453. [Google Scholar] [CrossRef] [PubMed]
- Erden, F.; Velipasalar, S.; Alkar, A.Z.; Cetin, A.E. Sensors in Assisted Living: A survey of signal and image processing methods. IEEE Signal Process. Mag. 2016, 33, 36–44. [Google Scholar] [CrossRef]
- Ahmad, F.; Cetin, A.E.; Ho, K.C.; Nelson, J. Signal Processing for Assisted Living: Developments and Open Problems. IEEE Signal Process. Mag. 2016, 33, 25–26. [Google Scholar] [CrossRef]
- Bang, Y.; Kim, J.; Yu, K. An Improved Map-Matching Technique Based on the Fréchet Distance Approach for Pedestrian Navigation Services. Sensors 2016, 16, 1768. [Google Scholar] [CrossRef] [PubMed]
- Maddison, R.; Ni Mhurchu, C.; Cavaggioni, L. Global Positioning System: A new opportunity in physical acivity measurement. Int. J. Behav. Nutr. Phys. Act. 2009, 6, 73. [Google Scholar] [CrossRef] [PubMed]
- Damani, A.; Shah, H.; Shah, K.; Vala, M. Global Positioning System for Object Tracking. Int. J. Comput. Appl. 2015, 109, 40–45. [Google Scholar] [CrossRef]
- Drawil, N.M.; Amar, H.M.; Basir, O.A. GPS localization accuracy classification: A context-based approach. IEEE Trans. Intell. Transp. Syst. 2013, 14, 262–273. [Google Scholar] [CrossRef]
- Schmid, A. Positioning Accuracy Improvement with Differential Correlation. IEEE J. Sel. Top. Signal Process. 2009, 3, 587–598. [Google Scholar] [CrossRef]
- Wang, H.; Ou, J.; Yuan, Y. Strategy of Data Processing for GPS Rover and Reference Receivers Using Different Sampling Rates. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1144–1149. [Google Scholar] [CrossRef]
- Whyte, G.P.; George, K.; Shave, R.; Middleton, N.; Nevill, A.M. Training Induced Changes in Maximum Heart Rate. Int. J. Sports Med. 2008, 29, 129–133. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vaseghi, S.; Yadollahi, M.; Ťupa, O.; Mareš, J.; Vyšata, O. Remote Physiological and GPS Data Processing in Evaluation of Physical Activities. Med. Biol. Eng. Comput. 2013, 52, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Charvátová, H.; Procházka, A.; Vaseghi, S.; Vyšata, O.; Vališ, M. GPS-based Analysis of Physical Activities Using Positioning and Heart Rate Cycling Data. Signal Image Video Process. 2016, 1–8. [Google Scholar] [CrossRef]
- Procházka, A.; Vyšata, O.; Vališ, M.; Ťupa, O.; Schatz, M.; Mařík, V. Use of Image and Depth Sensors of the Microsoft Kinect for the Detection of Gait Disorders. Neural Comput. Appl. 2015, 26, 1621–1629. [Google Scholar] [CrossRef]
- Muro-de-la-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef] [PubMed]
- Procházka, A.; Vyšata, O.; Vališ, M.; Ťupa, O.; Schatz, M.; Mařík, V. Bayesian Classification and Analysis of Gait Disorders Using Image and Depth Sensors of Microsoft Kinect. Digit. Signal Process. 2015, 47, 169–177. [Google Scholar] [CrossRef]
- Shi, G.; Wang, Y.; Li, S. Human Motion Capture System and its Sensor Analysis. Sens. Transducers 2014, 172, 206–212. [Google Scholar]
- Ťupa, O.; Procházka, A.; Vyšata, O.; Schatz, M.; Mareš, J.; Vališ, M.; Mařík, V. Motion tracking and gait feature estimation for recognising Parkinson’s disease using MS Kinect. Biomed. Eng. Online 2015, 14, 97. [Google Scholar] [CrossRef] [PubMed]
- Hostalkova, E.; Vysata, O.; Prochazka, A. Multi-dimensional biomedical image de-noising using Haar transform. In Proceedings of the 15th International Conference on Digital Signal Processing, Cardiff, UK, 1–4 July 2007; Sanei, S., Chambers, J., Eds.; Cardifff University: Cardiff, UK, 2007; pp. 175–178. [Google Scholar]
- Jerhotová, E.; Švihlík, J.; Procházka, A. Biomedical Image Volumes Denoising via the Wavelet Transform. In Applied Biomedical Engineering; Gargiulo, G.D., McEwan, A., Eds.; INTECH: Rijeka, Croatia, 2011; pp. 435–458. [Google Scholar]
- Vaseghi, S. Advanced Signal Processing and Digital Noise Reduction; Wiley & Teubner: West Sussex, UK, 2000. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Cambridge, UK, 2006. [Google Scholar]
- Procházka, A.; Vyšata, O.; Ťupa, O.; Mareš, J.; Vališ, M. Discrimination of Axonal Neuropathy Using Sensitivity and Specificity Statistical Measures. Neural Comput. Appl. 2014, 25, 1349–1358. [Google Scholar] [CrossRef]
- Lin, I.-C.; Peng, J.-Y.; Lin, C.-C.; Tsai, M.-H. Adaptive Motion Data Representation with Repeated Motion Analysis. IEEE Trans. Vis. Comput. Graph. 2011, 17, 527–538. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Bouboulis, P.; Theodoridis, S.; Mavroforakis, C.; Evaggelatou-Dalla, L. Complex Support Vector Machines for Regression and Quaternary Classification. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1260–1274. [Google Scholar] [CrossRef] [PubMed]
- Kataria, A.; Singh, M.D. A Review of Data Classification Using k-Nearest Neighbour Algorithm. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 354–360. [Google Scholar]
- Chen, H.; Wang, G.; Xue, J.H.; He, L. A novel hierarchical framework for human action recognition. Pattern Recognit. 2016, 55, 148–159. [Google Scholar] [CrossRef]
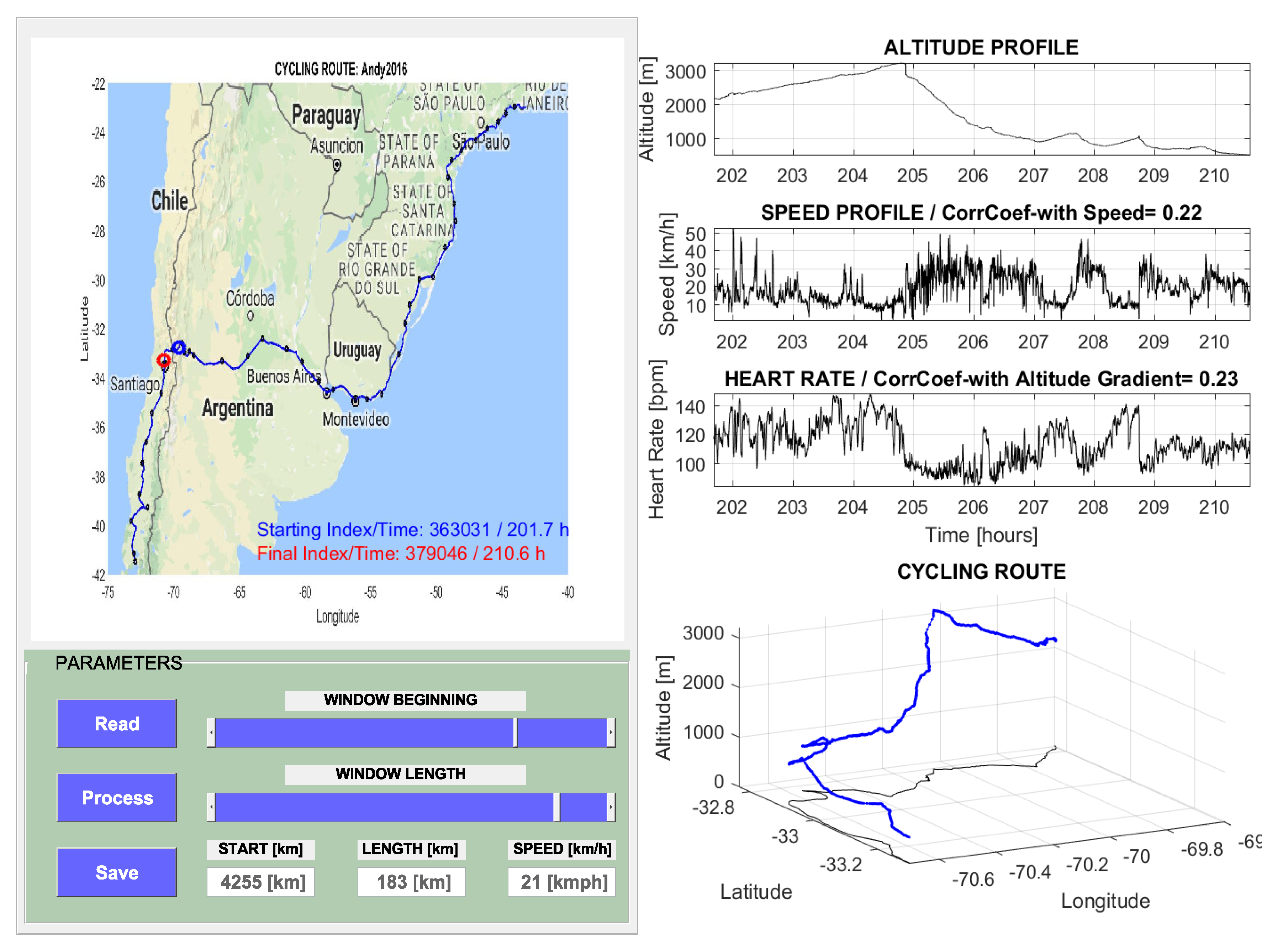
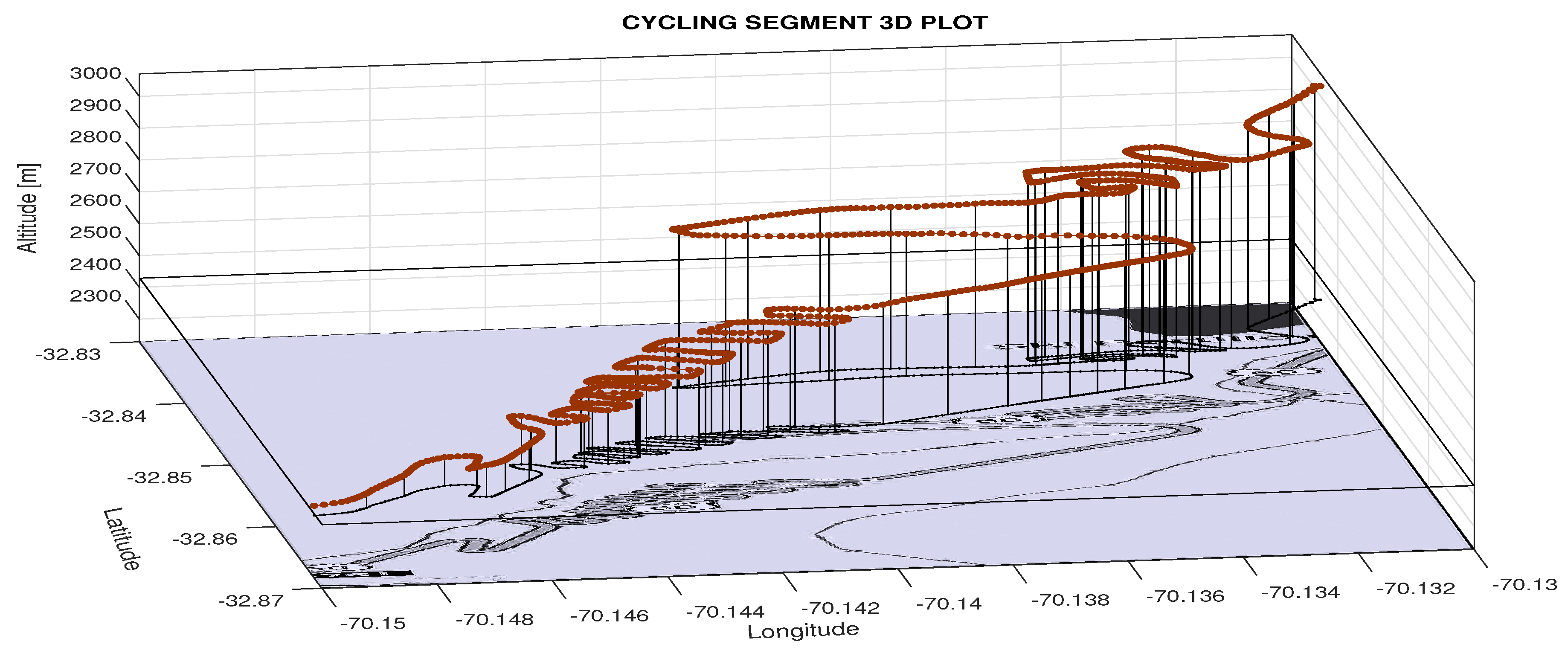

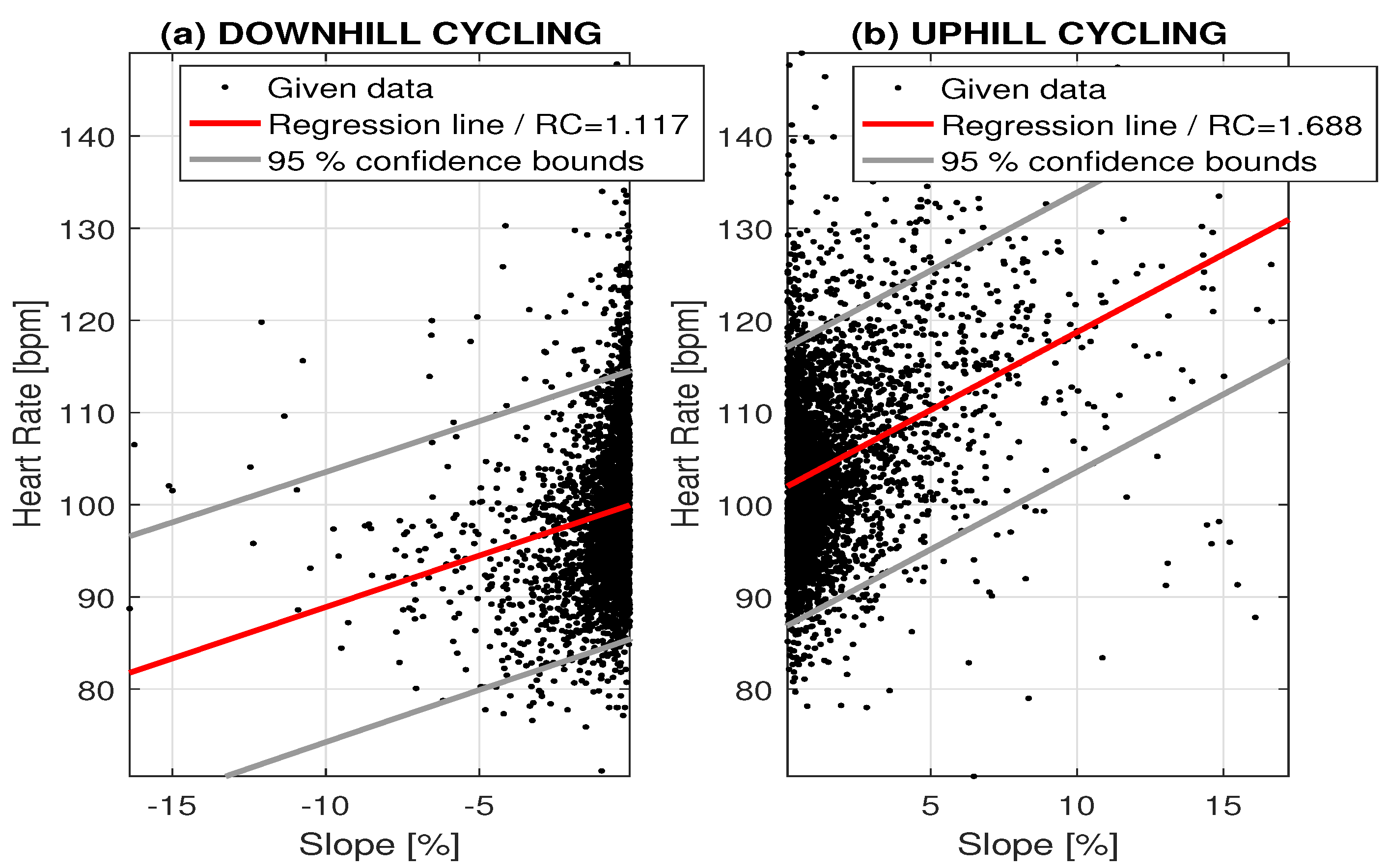
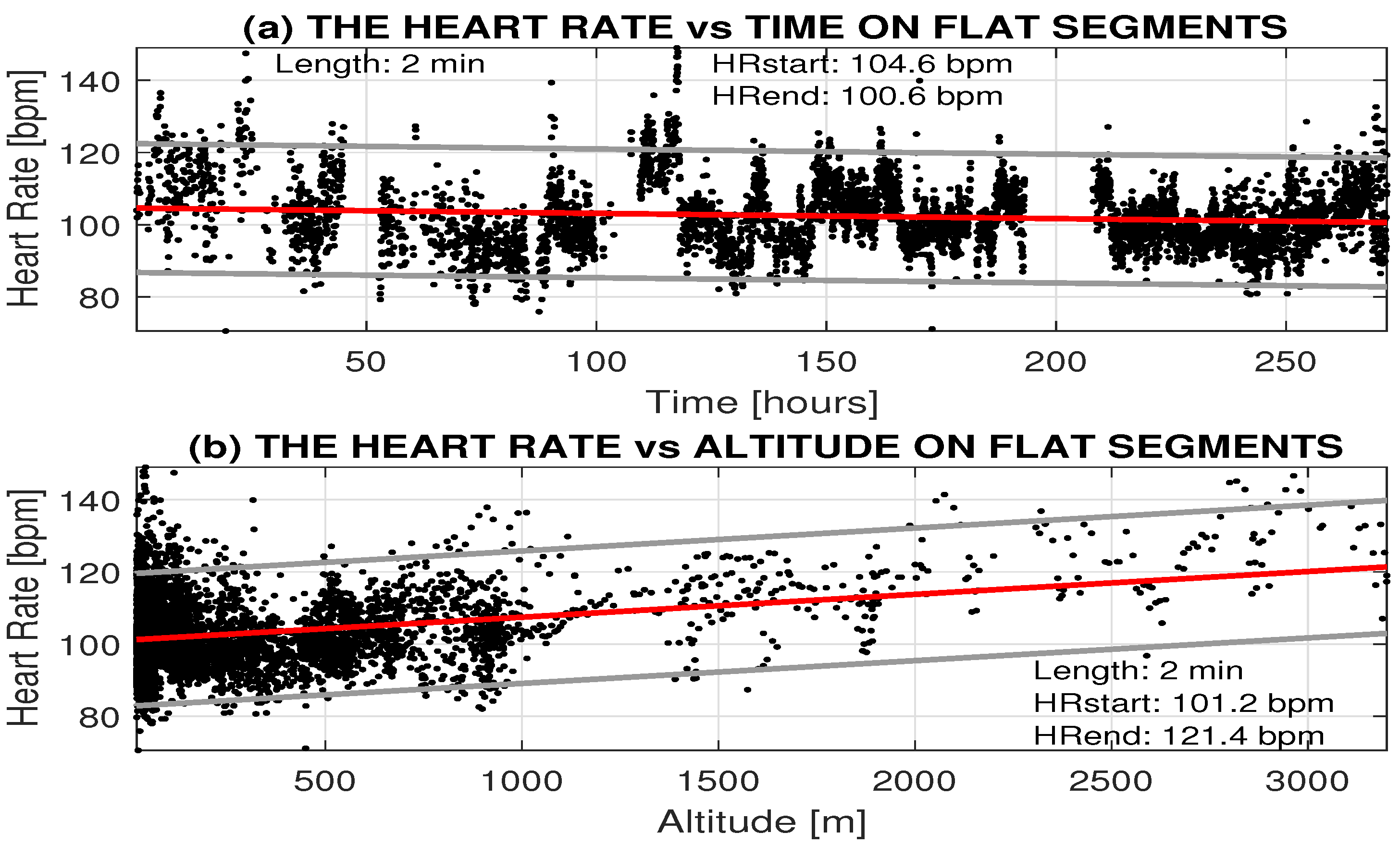

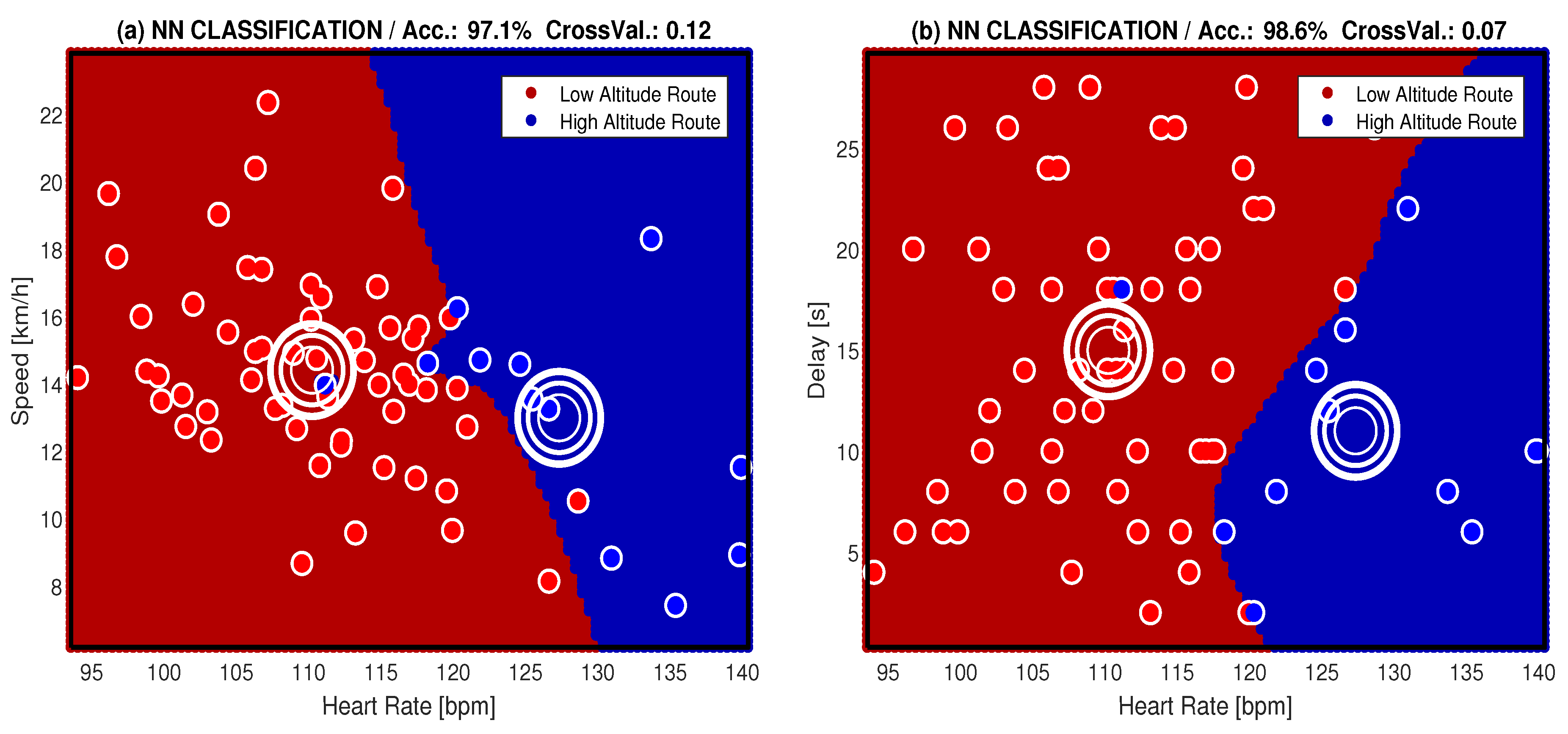
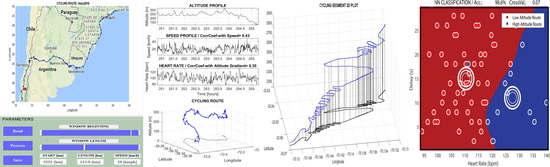
| Cycling route length | 5694 km |
| Total cycling time | 272.2 h |
| Average speed (km/h) | 20.9 km/h |
| Number of cycling segments | 48 |
| Average segment length | 118.6 km |
| Feature | Class 1 | Class 2 | ||
|---|---|---|---|---|
| Mean | STD | Mean | STD | |
| HR (bpm) | 110.3 | 7.6 | 127.4 | 8.9 |
| Speed (km/h) | 14.4 | 2.8 | 13.0 | 3.2 |
| Delay [s] | 15.0 | 7.5 | 11.0 | 5.6 |
| Speed vs. HR | Delay vs. HR | |||
|---|---|---|---|---|
| Method | Accuracy | CrossVal | Accuracy | CrossVal |
| (%) | (%) | |||
| NN | 97.1 | 0.12 | 98.6 | 0.07 |
| SVM | 95.7 | 0.12 | 92.8 | 0.10 |
| 5-NN | 92.8 | 0.10 | 92.8 | 0.10 |
| 7-NN | 92.8 | 0.09 | 91.3 | 0.13 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Procházka, A.; Vaseghi, S.; Charvátová, H.; Ťupa, O.; Vyšata, O. Cycling Segments Multimodal Analysis and Classification Using Neural Networks. Appl. Sci. 2017, 7, 581. https://doi.org/10.3390/app7060581
Procházka A, Vaseghi S, Charvátová H, Ťupa O, Vyšata O. Cycling Segments Multimodal Analysis and Classification Using Neural Networks. Applied Sciences. 2017; 7(6):581. https://doi.org/10.3390/app7060581
Chicago/Turabian StyleProcházka, Aleš, Saeed Vaseghi, Hana Charvátová, Ondřej Ťupa, and Oldřich Vyšata. 2017. "Cycling Segments Multimodal Analysis and Classification Using Neural Networks" Applied Sciences 7, no. 6: 581. https://doi.org/10.3390/app7060581