AI-Enhanced Nonlinear Predictive Control for Smart Greenhouses: A Performance Comparison of Forecast and Warm-Start Strategies
Abstract
1. Introduction
2. Related Work
2.1. NMPC Strategies for Greenhouse Climate Control
2.2. Approaches to Disturbance Handling and Prediction in Greenhouse Control
2.3. Techniques for Improving the Computational Performance of NMPC
3. Lettuce Greenhouse Model
4. NMPC Formulation
4.1. Control Objectives and Constraints
4.2. Disturbance Handling Approaches
- Feedback-Only Control (NMPC-C): This approach incorporates the currently measured disturbance and assumes it remains constant over the entire prediction horizon : for . This represents a reactive control strategy with no foresight.
- ML-Based Preview (NMPC-P): This controller utilizes current disturbance measurements for the initial control step (). For the remainder of the prediction horizon (), it integrates multivariate disturbance forecasts generated by an LSTM neural network. Thus, the combined sequence matches the full NMPC prediction horizon.The LSTM leverages a sequence of recent historical disturbance measurements (defined by a lookback window of steps) to predict the future evolution of key weather variables () over the subsequent steps.At each control interval, the NMPC controller collects the most recent measurements of all disturbance variables, feeds them to the LSTM, receives a multi-step forecast of length , and concatenates this forecast with the current measured disturbance to form the disturbance trajectory of length used in the NMPC optimization problem:Here, is the current measured disturbance, and () are the LSTM-generated forecasts. Details on the LSTM architecture, input features, and training data are provided in Section 5.1.
- Ideal Preview (NMPC-I): This ideal scenario assumes perfect, error-free knowledge of future disturbances over the prediction horizon. This serves as an upper-bound benchmark for the potential benefits of disturbance prediction.
4.3. Warm-Start Initialization
5. Simulation Setup
5.1. Disturbance Generation and Pre-Processing
5.2. Controller Comparison Approaches
5.3. Performance Metrics
5.4. Simulation Parameters
6. Results and Discussion
6.1. Short-Term (3-Day) Performance
6.2. Full Horizon (40-Day) Performance
6.2.1. Disturbance Handling Strategy Performance
6.2.2. Warm-Start Initialization Performance
6.3. Discussion of Trade-Offs and Controller Selection
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Findeisen, R.; Allgöwer, F. An Introduction to Nonlinear Model Predictive Control. In Proceedings of the 21st Benelux Meeting on Systems and Control, Veldhoven, The Netherlands, 19–21 March 2002; pp. 119–141. [Google Scholar]
- Kouvaritakis, B.; Cannon, M. Model Predictive Control: Classical, Robust and Stochastic; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- García-Mañas, F.; Rodríguez, F.; Berenguel, M.; Maestre, J.M. Multi-Scenario Model Predictive Control for Greenhouse Crop Production Considering Market Price Uncertainty. IEEE Trans. Autom. Sci. Eng. 2024, 21, 2936–2948. [Google Scholar] [CrossRef]
- Esparza-Gómez, J.M.; Guerrero-Osuna, H.A.; Ornelas-Vargas, G.; Luque-Vega, L.F. RNN-LSTM Applied in a Temperature Prediction Model for Greenhouses. Res. Comput. Sci. 2021, 150, 31–41. [Google Scholar]
- Chen, L.; Han, B.; Wang, X.; Zhao, J.; Yang, W.; Yang, Z. Machine Learning Methods in Weather and Climate Applications: A Survey. Appl. Sci. 2023, 13, 12019. [Google Scholar] [CrossRef]
- Diehl, M.; Bock, H.G.; Schlöder, J.P. A Real-Time Iteration Scheme for Nonlinear Optimization in Optimal Feedback Control. SIAM J. Control Optim. 2005, 43, 1714–1736. [Google Scholar] [CrossRef]
- Van Henten, E.J. Greenhouse Climate Management: An Optimal Control Approach; Landbouwuniversiteit Wageningen: Wageningen, The Netherlands, 1994. [Google Scholar]
- Van Henten, E.J. Sensitivity Analysis of an Optimal Control Problem in Greenhouse Climate Management. Biosyst. Eng. 2003, 85, 355–364. [Google Scholar] [CrossRef]
- Van Henten, E.J.; Bontsema, J. Time-Scale Decomposition of an Optimal Control Problem in Greenhouse Climate Management. Control Eng. Pract. 2009, 17, 88–96. [Google Scholar] [CrossRef]
- Blasco, X.; Martinez, M.; Herrero, J.M.; Ramos, C.; Sanchis, J. Model-Based Predictive Control of Greenhouse Climate for Reducing Energy and Water Consumption. Comput. Electron. Agric. 2007, 55, 49–70. [Google Scholar] [CrossRef]
- Mahmood, F.; Govindan, R.; Bermak, A.; Yang, D.; Al-Ansari, T. Data-Driven Robust Model Predictive Control for Greenhouse Temperature Control and Energy Utilisation Assessment. Appl. Energy 2023, 343, 121190. [Google Scholar] [CrossRef]
- Hu, G.; You, F. AI-Enabled Cyber-Physical-Biological Systems for Smart Energy Management and Sustainable Food Production in a Plant Factory. Appl. Energy 2024, 356, 122334. [Google Scholar] [CrossRef]
- Gruber, J.K.; Guzmán, J.L.; Rodríguez, F.; Bordons, C.; Berenguel, M.; Sánchez, J.A. Nonlinear MPC Based on a Volterra Series Model for Greenhouse Temperature Control Using Natural Ventilation. Control Eng. Pract. 2011, 19, 354–366. [Google Scholar] [CrossRef]
- Boersma, S.; Sun, C.; Van Mourik, S. Robust Sample-Based Model Predictive Control of a Greenhouse System with Parametric Uncertainty. In Proceedings of the IFAC AGRICONTROL 2022, Munich, Germany, 14–16 September 2022. [Google Scholar]
- Svensen, J.L.; Cheng, X.; Boersma, S.; Sun, C. Chance-Constrained Stochastic MPC of Greenhouse Production Systems with Parametric Uncertainty. Comput. Electron. Agric. 2024, 217, 108578. [Google Scholar] [CrossRef]
- Zavala, V.M.; Biegler, L.T. The Advanced-Step NMPC Controller: Optimality, Stability and Robustness. Automatica 2009, 45, 86–93. [Google Scholar] [CrossRef]
- Gros, S.; Zanon, M. Data-Driven Economic NMPC Using Reinforcement Learning. IEEE Trans. Automat. Control 2020, 65, 636–648. [Google Scholar] [CrossRef]
- Mallick, S.; Airaldi, F.; Dabiri, A.; Sun, C.; De Schutter, B. Reinforcement Learning-Based Model Predictive Control for Greenhouse Climate Control. Smart Agric. Technol. 2025, 10, 100751. [Google Scholar] [CrossRef]
- Mallick, S.; Airaldi, F.; Dabiri, A.; Sun, C.; De Schutter, B. Deep Neural Network Based Optimal Control of Greenhouses. In Proceedings of the 2024 European Control Conference (ECC), Stockholm, Sweden, 25–28 June 2024. [Google Scholar] [CrossRef]
- Morcego, B.; Yin, W.; Boersma, S.; Van Henten, E.; Puig, V.; Sun, C. Reinforcement Learning Versus Model Predictive Control on Greenhouse Climate Control. Comput. Electron. Agric. 2023, 215, 108372. [Google Scholar] [CrossRef]
- Jansen, Y.T.G. Optimal Control of Lettuce Greenhouse Horticulture Using Model-Free Reinforcement Learning: An Investigation on the Effect of Short-Term Weather Forecast Horizons. Master’s Thesis, Utrecht University, Utrecht, The Netherlands, 2022. [Google Scholar]
- Kuijpers, W.J.P.; Antunes, D.J.; Van Mourik, S.; Van Henten, E.J.; Van De Molengraft, M.J.G. Weather Forecast Error Modelling and Performance Analysis of Automatic Greenhouse Climate Control. Biosyst. Eng. 2022, 214, 207–229. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Zhang, C.; Li, N. Machine Learning Methods for Weather Forecasting: A Survey. Atmosphere 2025, 16, 82. [Google Scholar] [CrossRef]
- Boersma, S.; Cheng, X. A Bayesian Neural ODE for a Lettuce Greenhouse. In Proceedings of the 2024 IEEE Conference on Control Technology and Applications (CCTA), Newcastle upon Tyne, UK, 21–23 August 2024; pp. 782–786. [Google Scholar] [CrossRef]
- Zavala, V.M.; Anitescu, M. Real-Time Nonlinear Optimization as a Generalized Equation. SIAM J. Control Optim. 2010, 48, 5444–5467. [Google Scholar] [CrossRef]
- Quirynen, R.; Vukov, M.; Zanon, M.; Diehl, M. Autogenerating Microsecond Solvers for Nonlinear MPC: A Tutorial Using ACADO Integrators. Optim. Control Appl. Methods 2014, 36, 685–704. [Google Scholar] [CrossRef]
- Kirches, C.; Wirsching, L.; Bock, H.G.; Schlöder, J.P. Efficient Direct Multiple Shooting for Nonlinear Model Predictive Control on Long Horizons. J. Process. Control 2012, 22, 540–550. [Google Scholar] [CrossRef]
- Gros, S.; Mario, Z.; Rien, Q.; Alberto, B.; Diehl, M. From Linear to Nonlinear MPC: Bridging the Gap via the Real-time Iteration. Int. J. Control 2016, 93, 62–80. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Yu-Xin, T.; Qi-Changa, Y. Optimal Control of Environmental Conditions Affecting Lettuce Plant Growth in a Controlled Environment with Artificial Lighting: A Review. S. Afr. J. Bot. 2020, 130, 75–89. [Google Scholar] [CrossRef]
- Brechner, M.; Both, A.J.; Staff, C.E.A. Hydroponic Lettuce Handbook; Cornell University CEA Program: Ithaca, NY, USA, 2013. [Google Scholar]
- Dai, M.; Tan, X.; Ye, Z.; Ren, J.; Chen, X.; Kong, D. Optimal Light Intensity for Lettuce Growth, Quality, and Photosynthesis in Plant Factories. Plants 2024, 13, 2616. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Chandler, W.S.; Hoell, J.M.; Westberg, D.; Whitlock, C.H.; Stackhouse, P.W. A Global Perspective on Renewable Energy Resources: Nasa’s Prediction of Worldwide Energy Resources (Power) Project. In Proceedings of the Proceedings of ISES World Congress 2007 (Vol. I–Vol. V), Beijing, China, 8–21 September 2007; Goswami, D.Y., Zhao, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 2636–2640. [Google Scholar]
- Brad Weir, L.O. and O.-2 S.T. OCO-2 GEOS Level 3 Daily, 0.5×0.625 Assimilated CO2 V10r. Available online: https://oco2.gesdisc.eosdis.nasa.gov/ (accessed on 15 April 2025).
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A Software Framework for Nonlinear Optimization and Optimal Control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
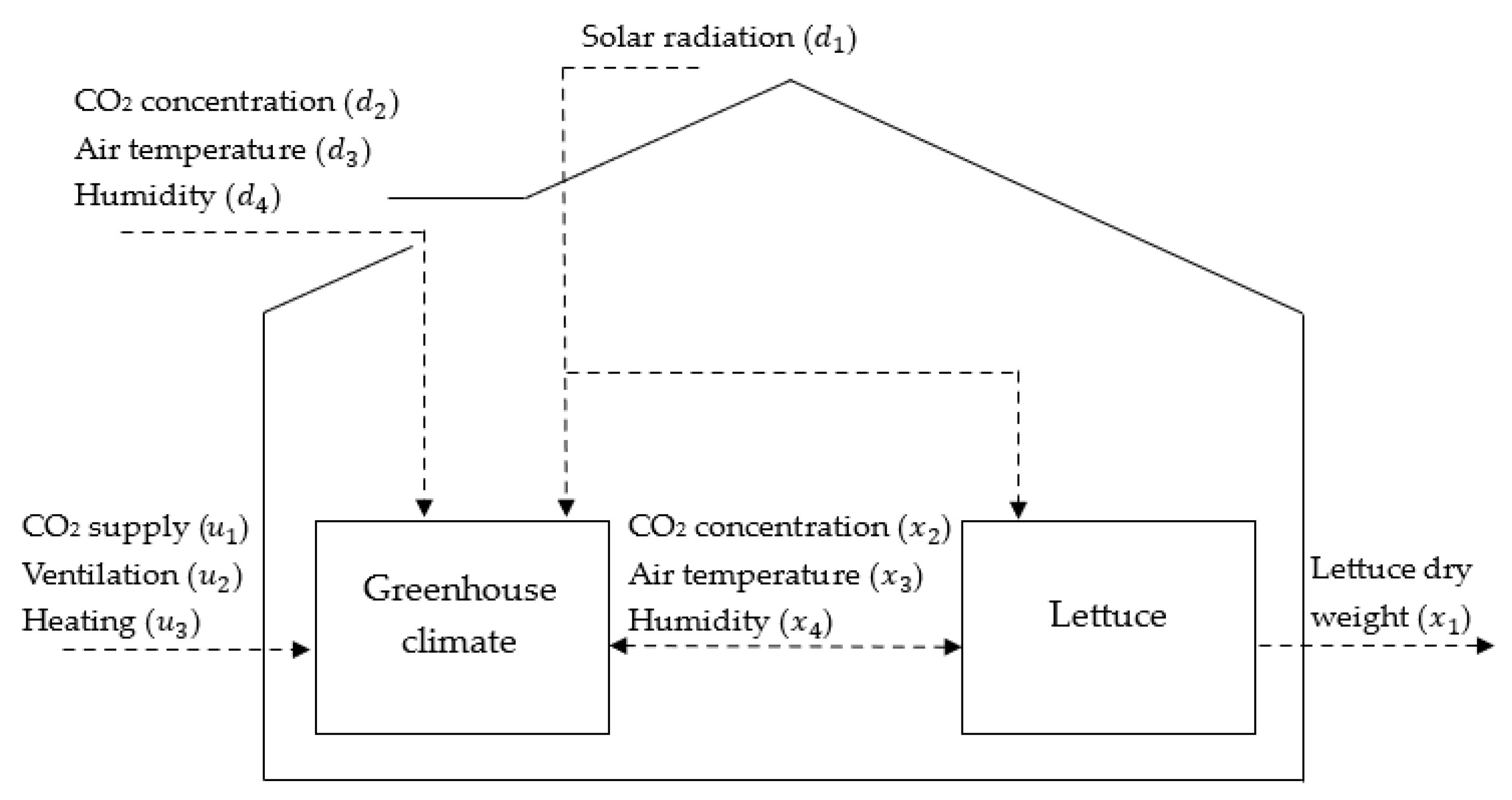
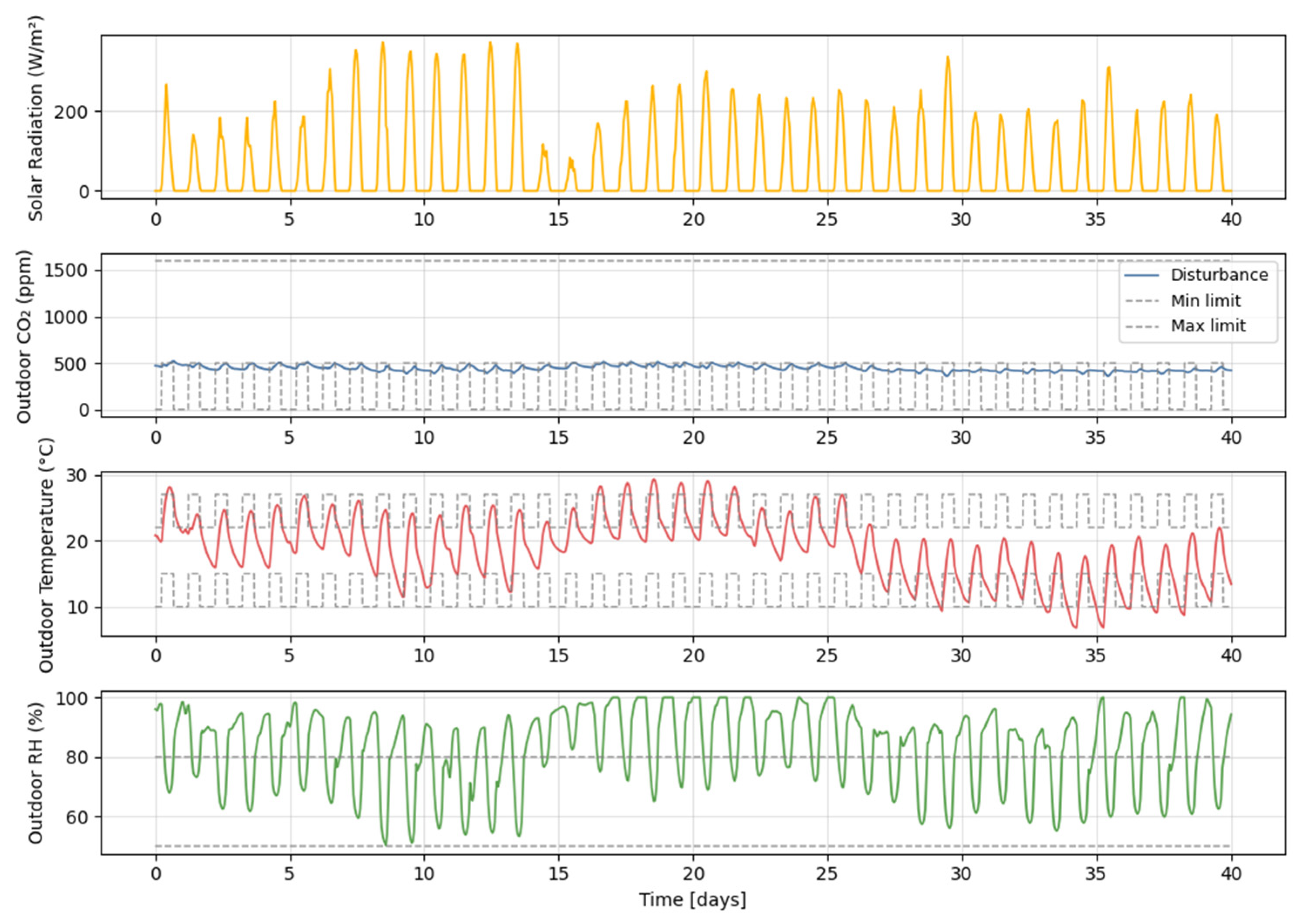
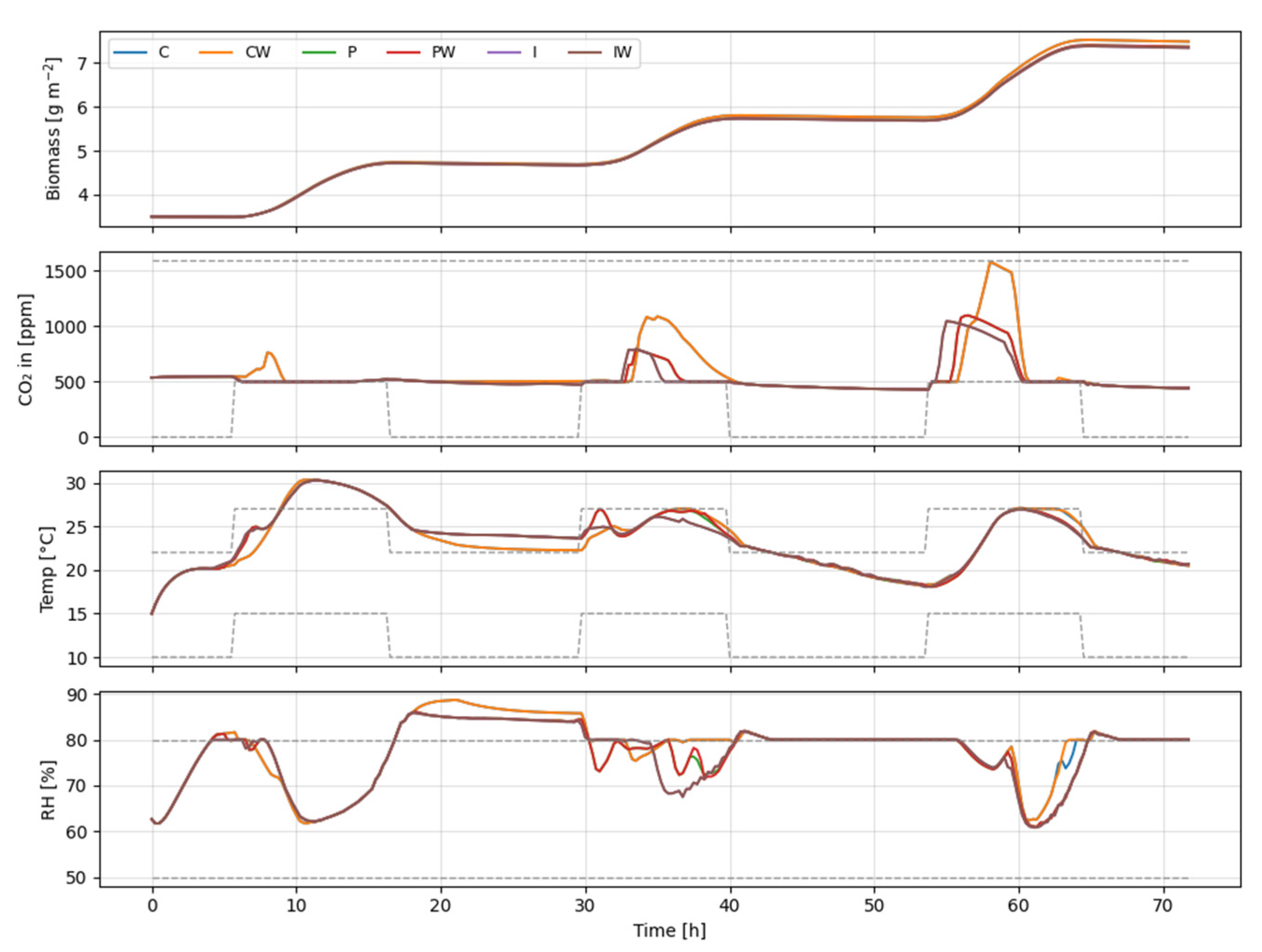

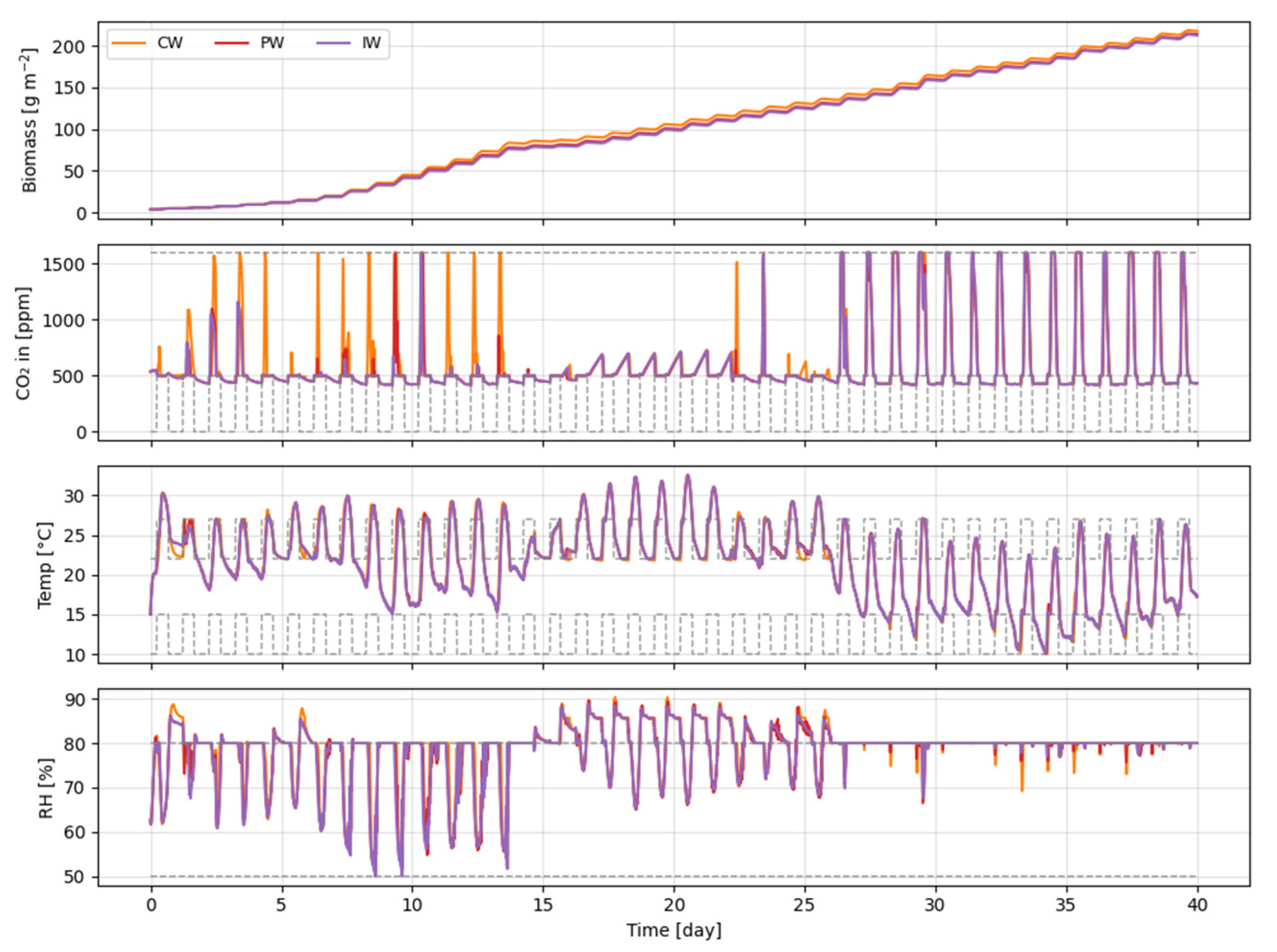


| Category | Symbol | Description | Unit |
|---|---|---|---|
| State variables | Lettuce dry weight | kg/m2 | |
| Indoor CO2 concentration | kg/m3 | ||
| Indoor Air temperature | °C | ||
| Indoor Humidity | kg/m3 | ||
| Measurement variables | Lettuce dry weight | g/m2 | |
| Indoor CO2 concentration | ppm | ||
| Indoor Air temperature | °C | ||
| Indoor Humidity | % | ||
| Disturbances | Solar radiation | W/m2 | |
| Outdoor CO2 concentration | kg/m3 | ||
| Outdoor Air temperature | °C | ||
| Outdoor Humidity | kg/m3 | ||
| Control inputs | CO2 supply | mg/m2/s | |
| Ventilation | mm/s | ||
| Heating | W/m2 |
| Symbol | Value | Unit | Explanation |
|---|---|---|---|
| p1 | 0.544 | – | Yield Factor |
| p2 | 2.65 × 10−7 | s−1 | Maintenance Respiration |
| p3 | 53 | m2·kg−1 | Effective Canopy Area |
| p4 | 3.55 × 10−9 | kg·J−1 | PAR to total radiation conversion |
| p5 | 5.11 × 10−6 | m·s−1·°C−2 | Temp effect CO2, 2nd order |
| p6 | 2.3 × 10−4 | m·s−1·°C−1 | Temp effect CO2, 1st order |
| p7 | 6.29 × 10−4 | m·s−1 | Temp effect CO2, 0th order |
| p8 | 5.2 × 10−5 | kg·m−3 | CO2 compensation point |
| p9 | 4.1 | m | Volumetric Capacity (CO2) |
| p10 | 4.87 × 10−7 | s−1 | Maintenance Respiration Weighted |
| p11 | 7.45 × 10−6 | m·s−1 | Leakage Greenhouse Cover |
| p12 | 8.314 | J·K−1·mol−1 | Gas Constant |
| p13 | 273.15 | K | Absolute Temperature |
| p14 | 10,1325 | Pa | Standard Atmospheric Pressure |
| p15 | 0.044 | kg·mol−1 | Molar Mass of CO2 |
| p16 | 3 × 104 | J·m−3·°C−1 | Heat Capacity Greenhouse Air |
| p17 | 1290 | J·m−3·°C−1 | Heat Capacity Volume |
| p18 | 6.1 | W·m−2·°C−1 | Heat Transfer Coefficient |
| p19 | 0.2 | – | Sun Heat Load Coefficient |
| p20 | 4.1 | m | Volumetric Capacity (Humidity) |
| p21 | 0.0036 | m·s−1 | Canopy Transpiration Coefficient |
| p22 | 9348 | J·kg−1·m−3·K−1 | Water Molar Value (for transpiration) |
| p23 | 8314 | J·K−1·mol−1 | Gas Constant (water vapor) |
| p24 | 273.15 | K | Absolute Temperature (humidity) |
| p25 | 17.4 | – | Saturation Vapor Pressure (Canopy Transpiration) |
| p26 | 239 | °C | Saturation Vapor Temp (Canopy Transpiration) |
| p27 | 17.269 | – | Saturation Vapor Pressure (Humidity) |
| p28 | 238.3 | °C | Saturation Vapor Temp (Humidity) |
| Variable | MAE (Train) | RMSE (Train) | MAE (Valid) | RMSE (Valid) | MAE (Test) | RMSE (Test) |
|---|---|---|---|---|---|---|
| Solar Radiation (W/m2) | 13.75 | 28.50 | 17.77 | 35.57 | 16.10 | 34.41 |
| CO2 (ppm) | 4.85 | 7.76 | 6.09 | 9.81 | 4.97 | 7.30 |
| Temperature (°C) | 0.58 | 0.93 | 0.62 | 1.01 | 0.70 | 1.17 |
| Humidity (% RH) | 2.23 | 3.54 | 2.45 | 3.99 | 2.92 | 4.61 |
| Model | Disturbance Handling | Solver Initialization |
|---|---|---|
| NMPC-C | Frozen current disturbance | Cold-start |
| NMPC-CW | Frozen current disturbance | Warm-start |
| NMPC-P | LSTM-based disturbance prediction | Cold-start |
| NMPC-PW | LSTM-based disturbance prediction | Warm-start |
| NMPC-I | Ideal disturbance | Cold-start |
| NMPC-IW | Ideal disturbance | Warm-start |
| Parameter | Symbol | Value |
|---|---|---|
| 1. Time-related parameters | ||
| Sampling time | 15 min (900 s) | |
| NMPC Prediction horizon | 24 steps (6 h) | |
| NMPC Control horizon | 24 steps (6 h) | |
| Simulation duration | 40 days (3840 control steps) | |
| 2. Model/Controller parameters | ||
| Numerical solver | - | IPOPT (via CasADi) |
| Initial crop dry weight | 0.0035 kg/m2 (3.5 g/m2) | |
| Initial indoor CO2 concentration | 0.001 kg/m3 (~400 ppm at 15 °C) | |
| Initial indoor temperature | 15 °C | |
| Initial indoor humidity | 0.008 kg/m3 (~65% RH) | |
| Initial state of control inputs | (0, 0, 0)T | |
| Economic weight: Biomass | 2800 | |
| Economic weight: CO2 input | 66 | |
| Economic weight: Heating input | 1 | |
| Slack variable penalty: Biomass | 105 | |
| Slack variable penalty: CO2 | 103 | |
| Slack variable penalty: Temp. | 105 | |
| Slack variable penalty: Humid. | 104 | |
| Lower bounds for control inputs | (0, 0, 0)T | |
| Upper bounds for control inputs | (12 mg/m2/s, 75 mm/s, 150 W/m2)T | |
| Max. rate of change inputs | (1.2, 7.5, 15)T (units/step) | |
| 3. Economic cost coefficients | ||
| Lettuce price | 1.6 Hfl kg−1 | |
| Heating energy cost | Hfl J−1 | |
| CO2 cost | 0.42 Hfl kg−1 |
| Model | (g m−2) | (%) | (%) | (%) | (%) | (Hfl/kg) | (Hfl m−2) | (s) |
|---|---|---|---|---|---|---|---|---|
| NMPC-C | 7.489 | 8.710 | 0.022 | 4.328 | 4.360 | 5.533 | 0.098 | 0.489 |
| NMPC-CW | 7.490 | 8.707 | 0.022 | 4.323 | 4.362 | 5.534 | 0.098 | 0.299 |
| NMPC-P | 7.369 | 8.785 | 0.030 | 5.688 | 3.067 | 7.931 | 0.087 | 1.188 |
| NMPC-PW | 7.369 | 8.785 | 0.030 | 5.689 | 3.066 | 7.952 | 0.087 | 0.404 |
| NMPC-I | 7.347 | 8.661 | 0.030 | 5.683 | 2.948 | 8.321 | 0.086 | 0.897 |
| NMPC-IW | 7.348 | 8.661 | 0.030 | 5.683 | 2.948 | 8.322 | 0.086 | 0.302 |
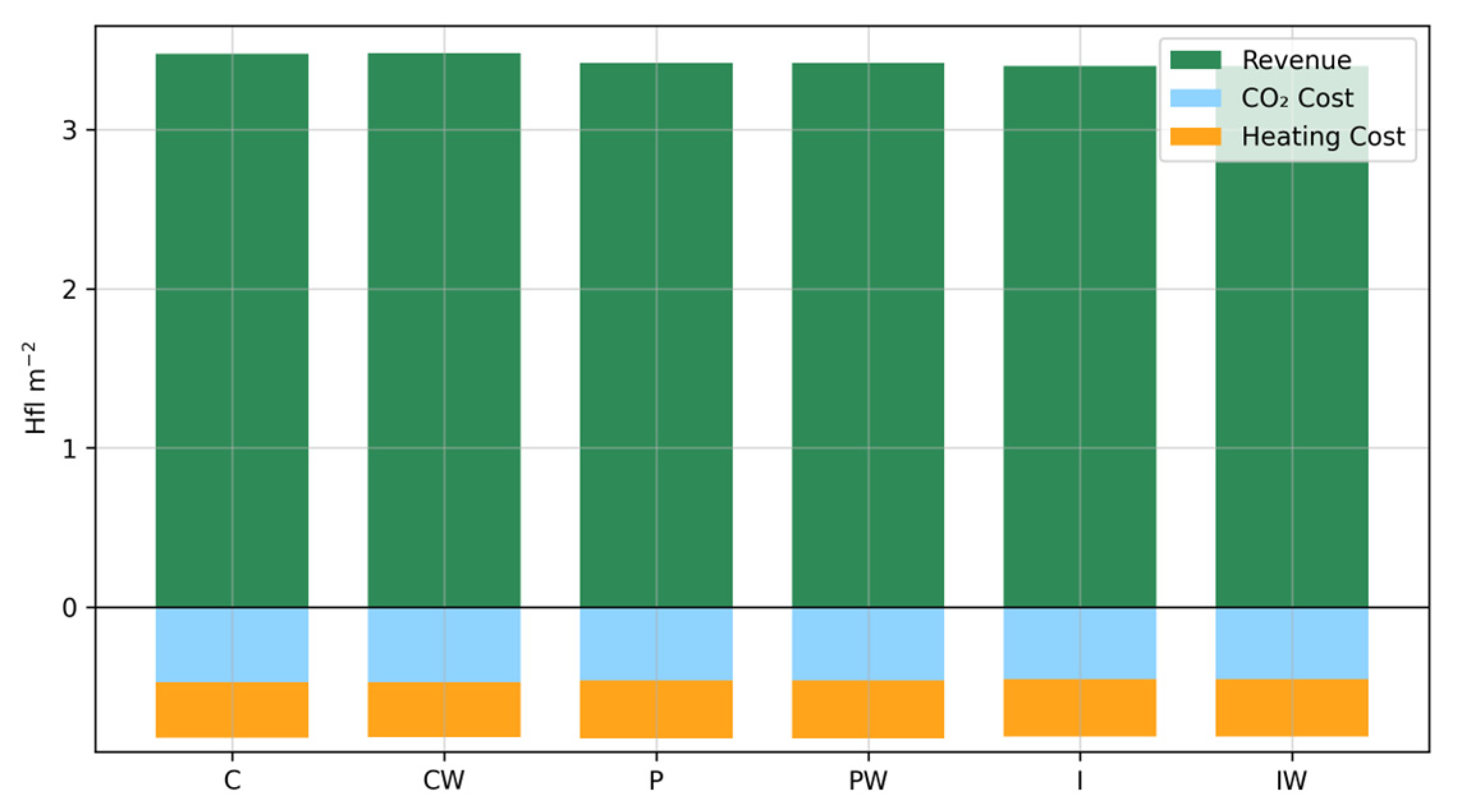
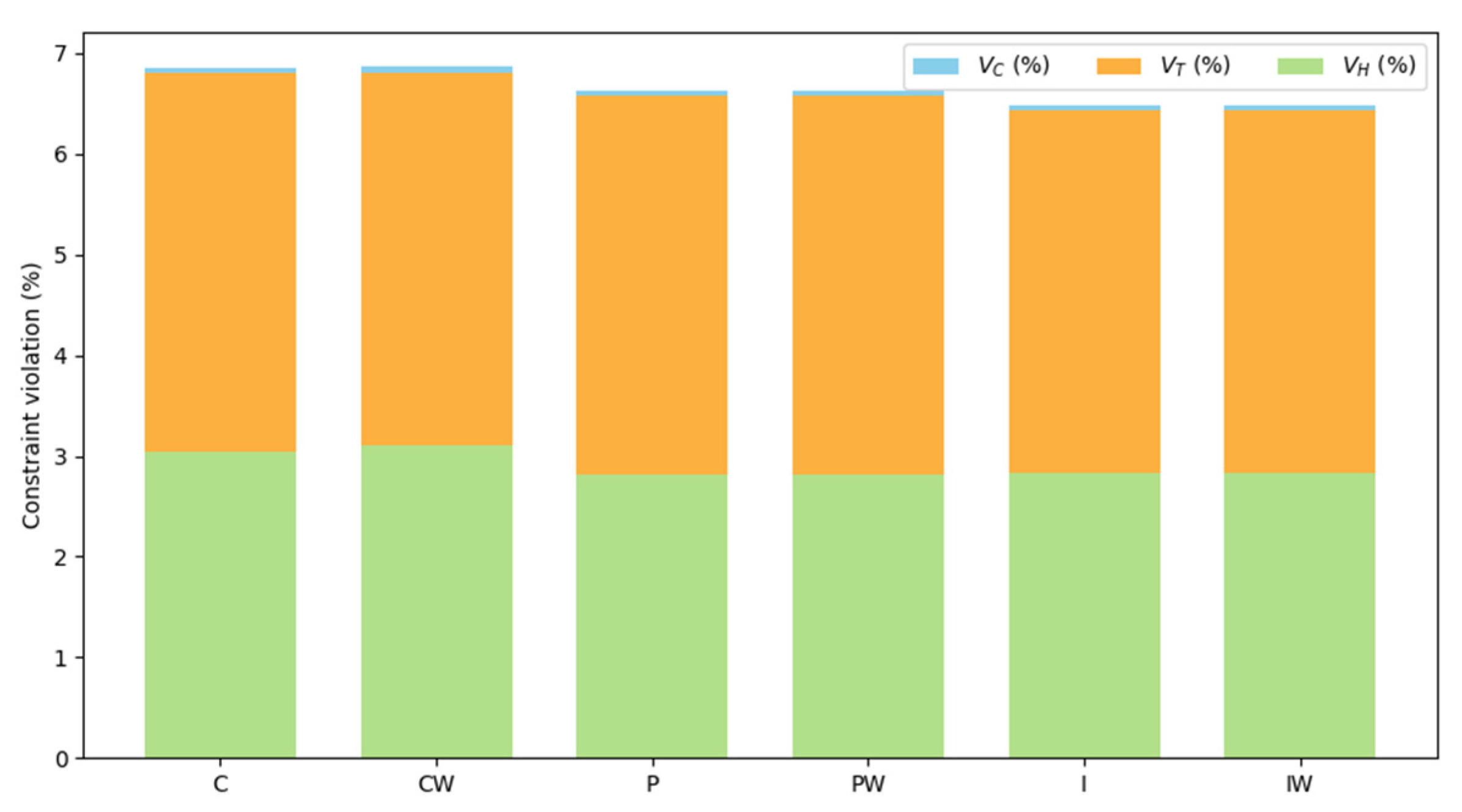
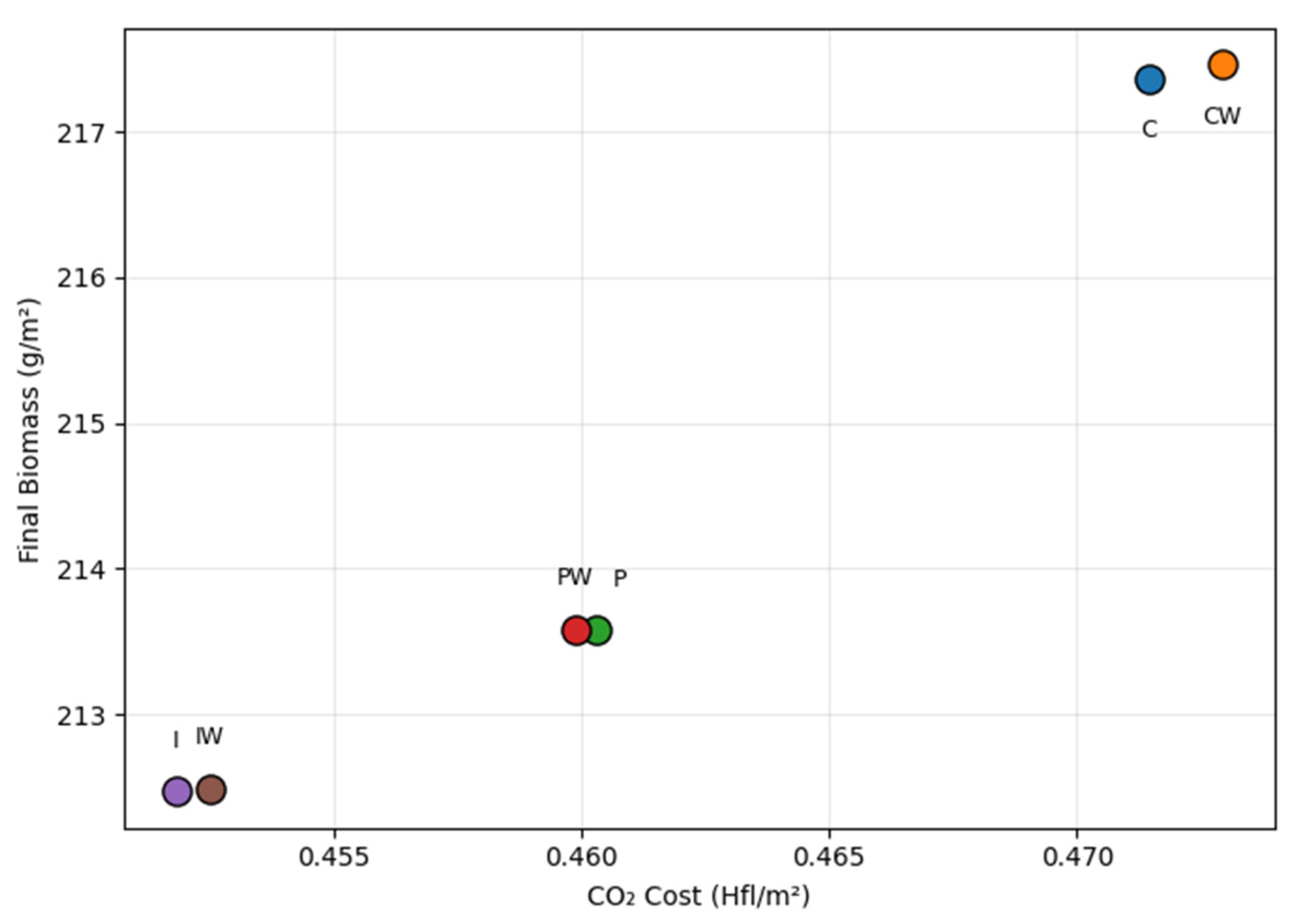
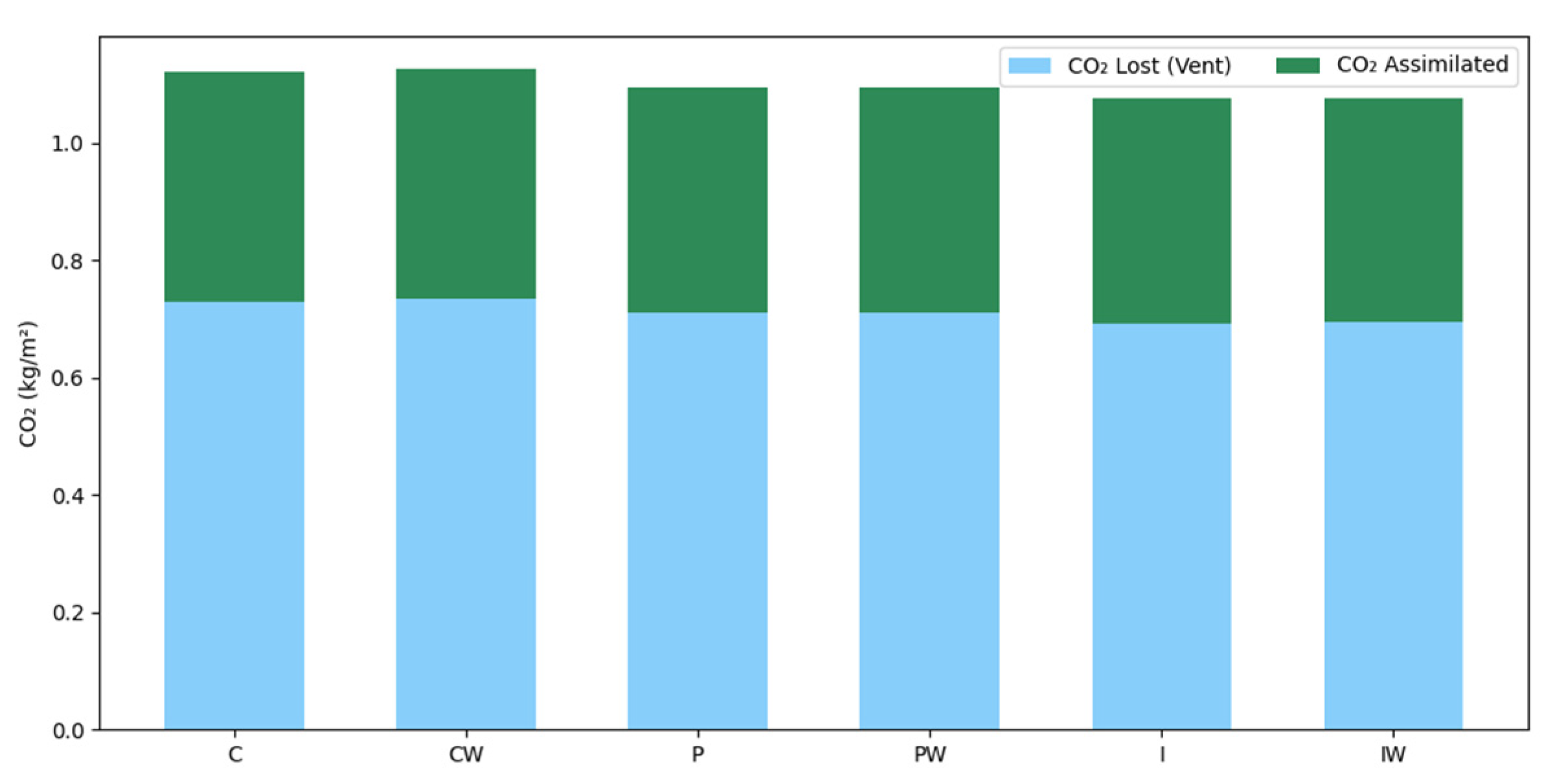
| Model | (g m−2) | (%) | (%) | (%) | (%) | (Hfl/kg) | (Hfl m−2) | (s) |
|---|---|---|---|---|---|---|---|---|
| NMPC-C | 217.362 | 6.861 | 0.054 | 3.758 | 3.049 | 3.833 | 2.658 | 0.457 |
| NMPC-CW | 217.459 | 6.866 | 0.054 | 3.700 | 3.112 | 3.815 | 2.663 | 0.320 |
| NMPC-P | 213.584 | 6.630 | 0.055 | 3.756 | 2.819 | 3.932 | 2.591 | 1.041 |
| NMPC-PW | 213.585 | 6.628 | 0.054 | 3.755 | 2.819 | 3.931 | 2.592 | 0.396 |
| NMPC-I | 212.472 | 6.479 | 0.046 | 3.594 | 2.839 | 3.894 | 2.586 | 0.908 |
| NMPC-IW | 212.492 | 6.480 | 0.046 | 3.598 | 2.836 | 3.899 | 2.585 | 0.308 |
| Controller | (Hfl/m2) | (Hfl/m2) | (Hfl/m2) |
|---|---|---|---|
| NMPC-C | 2.658 | 2.893 | 2.423 |
| NMPC-CW | 2.663 | 2.898 | 2.428 |
| NMPC-P | 2.591 | 2.821 | 2.361 |
| NMPC-PW | 2.592 | 2.822 | 2.362 |
| NMPC-I | 2.586 | 2.815 | 2.356 |
| NMPC-IW | 2.585 | 2.815 | 2.356 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, H.L.; Bui, V.-T. AI-Enhanced Nonlinear Predictive Control for Smart Greenhouses: A Performance Comparison of Forecast and Warm-Start Strategies. Appl. Sci. 2025, 15, 7988. https://doi.org/10.3390/app15147988
Le HL, Bui V-T. AI-Enhanced Nonlinear Predictive Control for Smart Greenhouses: A Performance Comparison of Forecast and Warm-Start Strategies. Applied Sciences. 2025; 15(14):7988. https://doi.org/10.3390/app15147988
Chicago/Turabian StyleLe, Hung Linh, and Van-Tung Bui. 2025. "AI-Enhanced Nonlinear Predictive Control for Smart Greenhouses: A Performance Comparison of Forecast and Warm-Start Strategies" Applied Sciences 15, no. 14: 7988. https://doi.org/10.3390/app15147988
APA StyleLe, H. L., & Bui, V.-T. (2025). AI-Enhanced Nonlinear Predictive Control for Smart Greenhouses: A Performance Comparison of Forecast and Warm-Start Strategies. Applied Sciences, 15(14), 7988. https://doi.org/10.3390/app15147988







