The Relationship between InSAR Coseismic Deformation and Earthquake-Induced Landslides Associated with the 2017 Mw 3.9 Ischia (Italy) Earthquake
Abstract
:1. Introduction
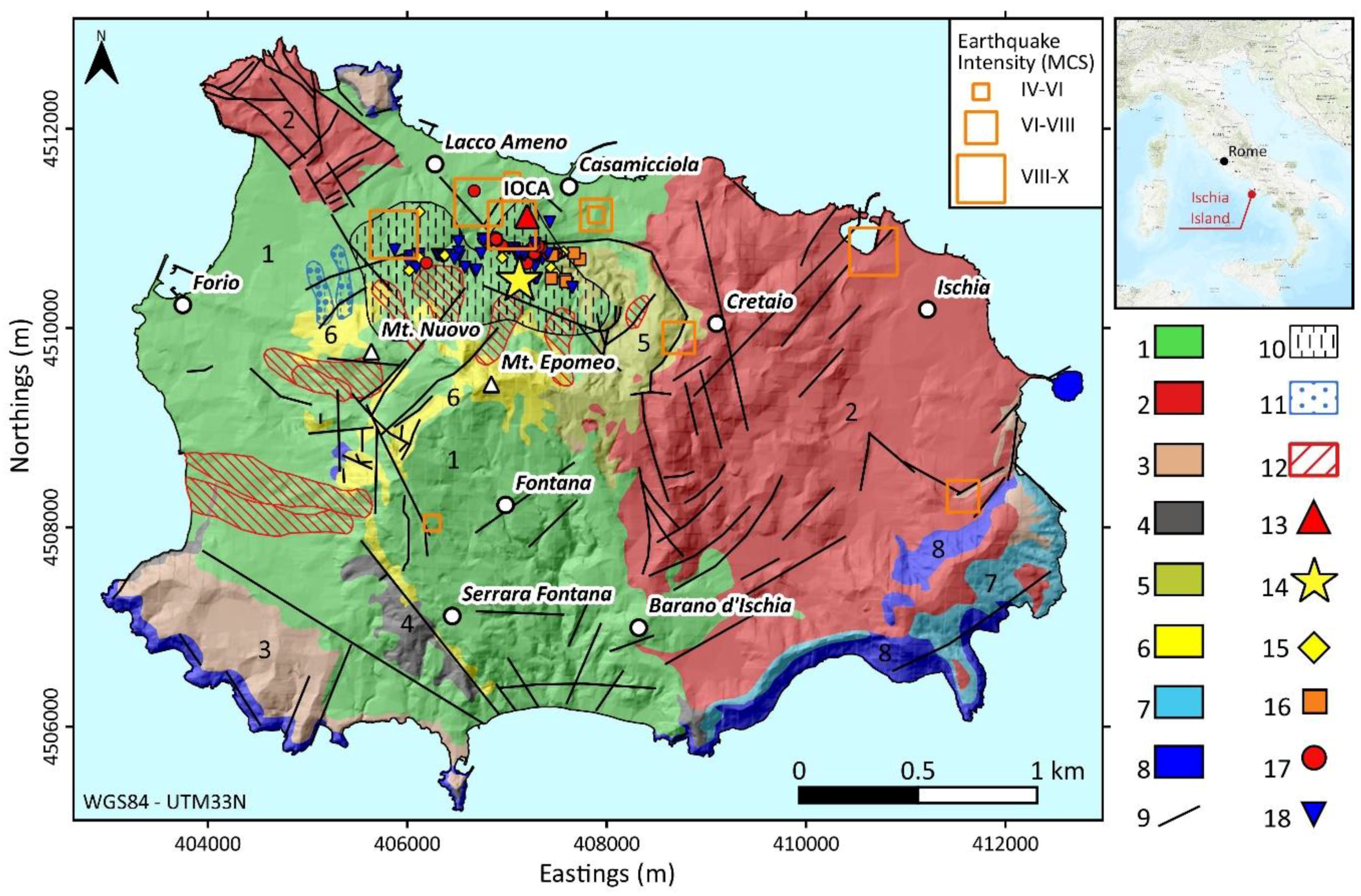
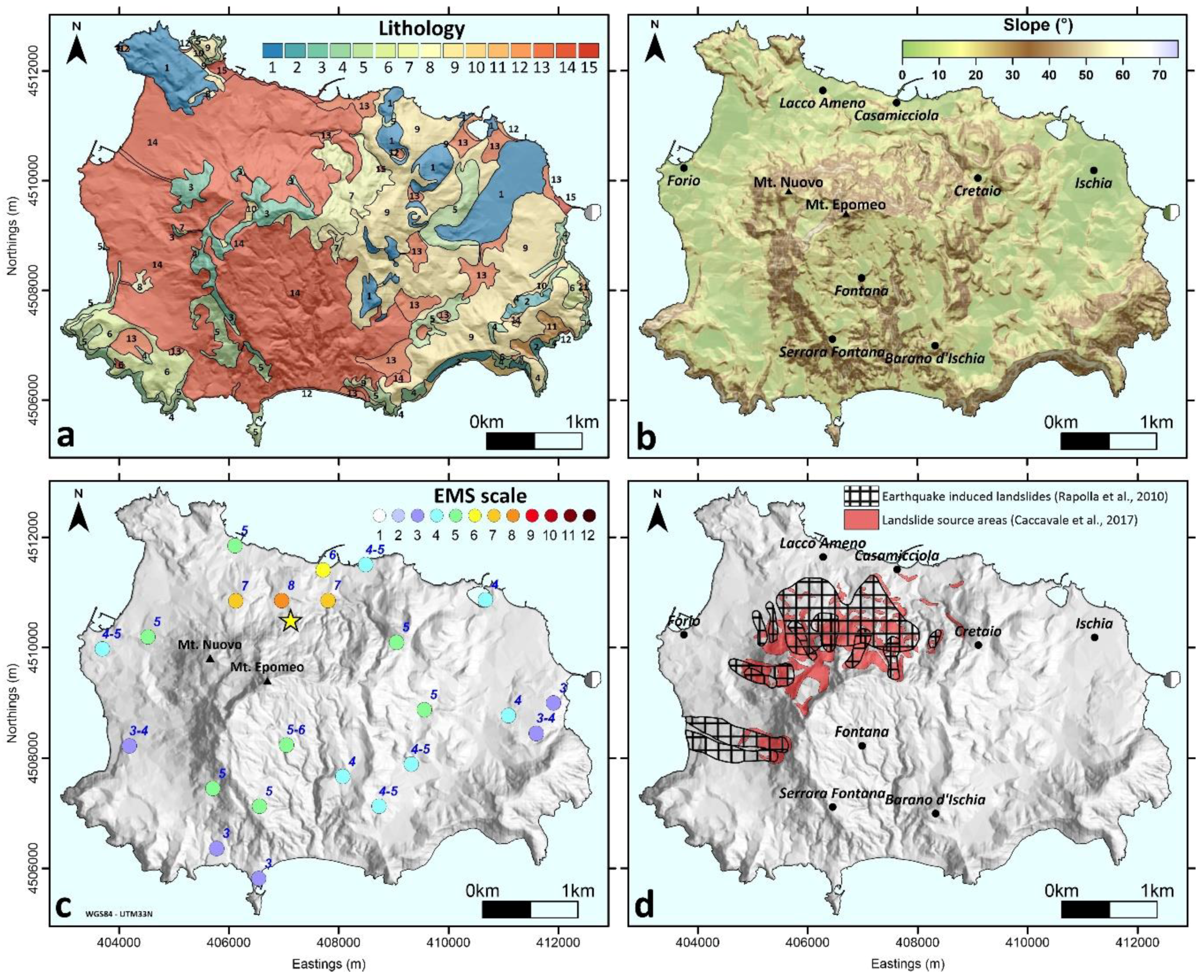
2. Geological Setting
3. Methods
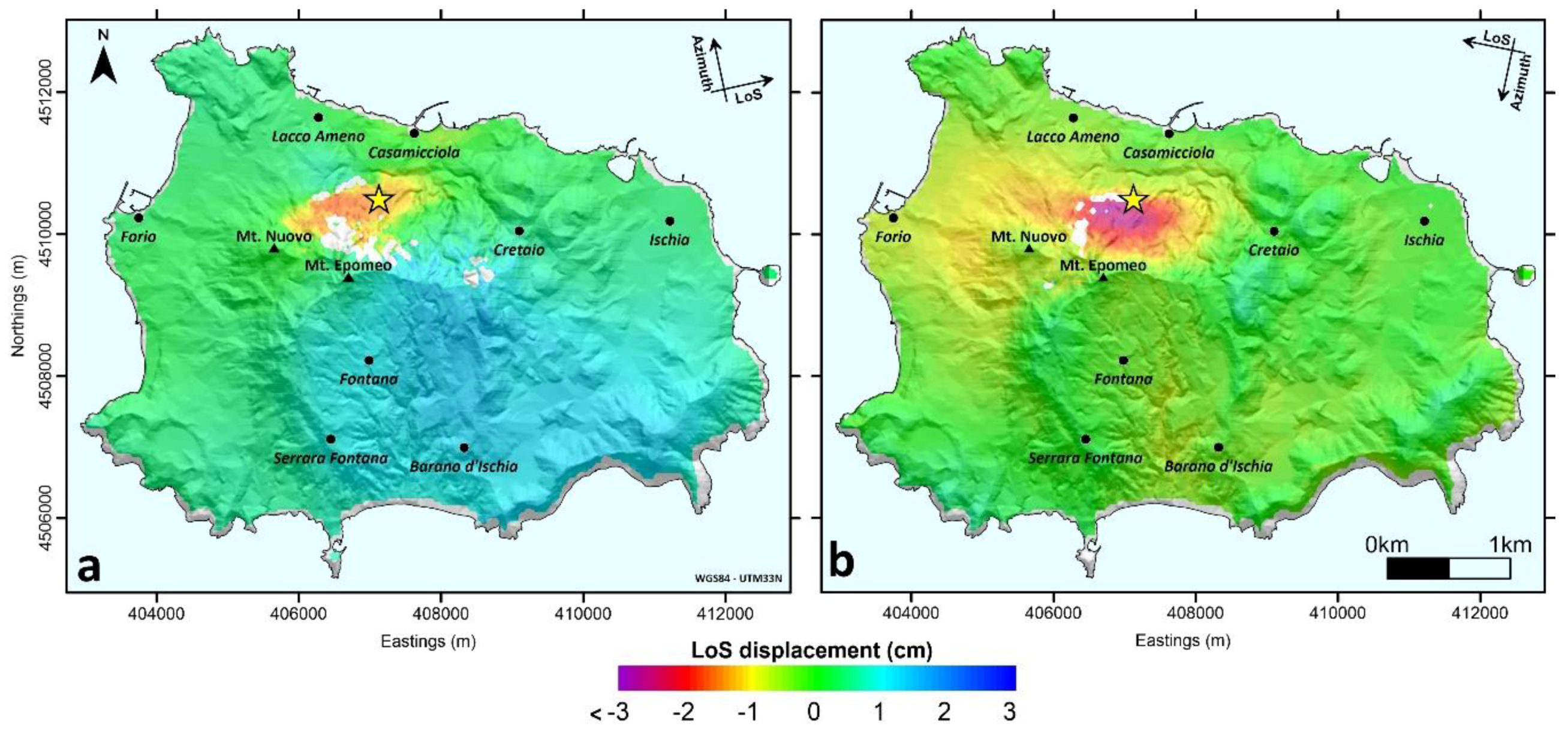
3.1. Interferometric Synthetic Aperture Radar (InSAR) Data and Analysis
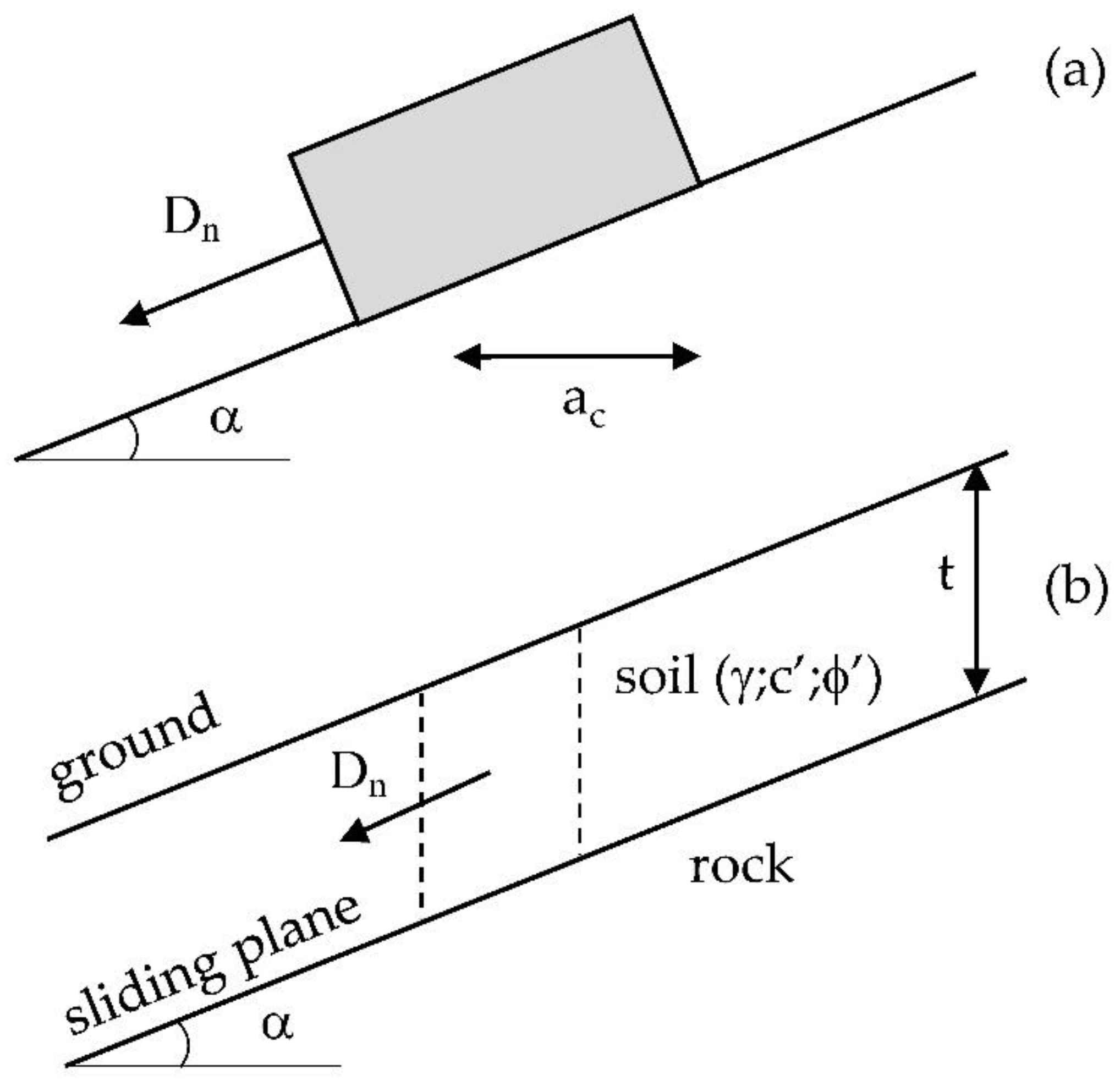
3.2. Landslide Modeling Approach
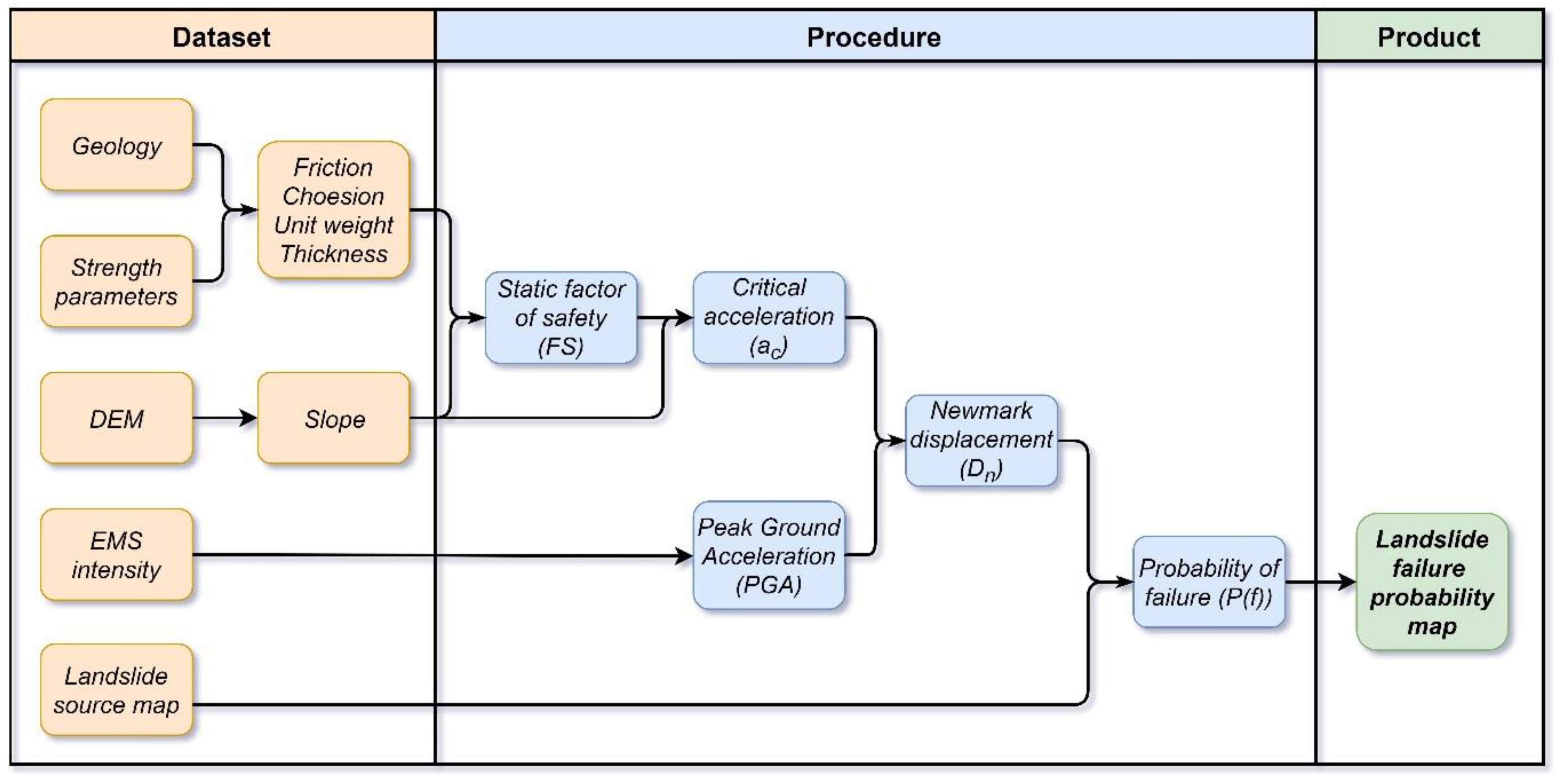
3.3. Modeling Procedure
- (a)
- normalize the Dn values at each grid cell by calculating the ratio between Dn and the computed maximum displacement (Dn_max) from Equation (3) for the Ischia earthquake, i.e., Dn/Dn_max;
- (b)
- group the Dn/Dn_max values into sequential intervals, e.g., the first interval contains Dn/Dn_max values ranging between 0 and 0.1, the second interval between 0.1 and 0.2, and so on;
- (c)
- compute for each interval the proportion of grid cells falling on areas affected by earthquake-induced landslides in the past. Such values correspond to the probability of landslide failure associated with each Dn/Dn_max interval, i.e., P(f);
- (d)
- plot the obtained P(f) values versus the mean Dn/Dn_max of each interval and fit with a Weibull distribution curve [20,46] (Equation (5)):where P(f) is the probability of failure associated to each mean Dn/Dn_max value and m, a and b are regression constants to be determined through a best-fit solution between the model and the data. Such an approach allows providing a continuous curve function that associates a probability of failure P(f) to each normalized Newmark displacement [20];
- (e)
- associate the likelihood of landslide failure P(f) to each grid cell using Equation (5).
4. Results
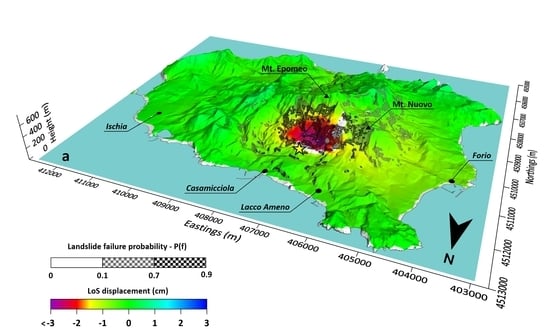
4.1. Coseismic Ground Displacements from InSAR
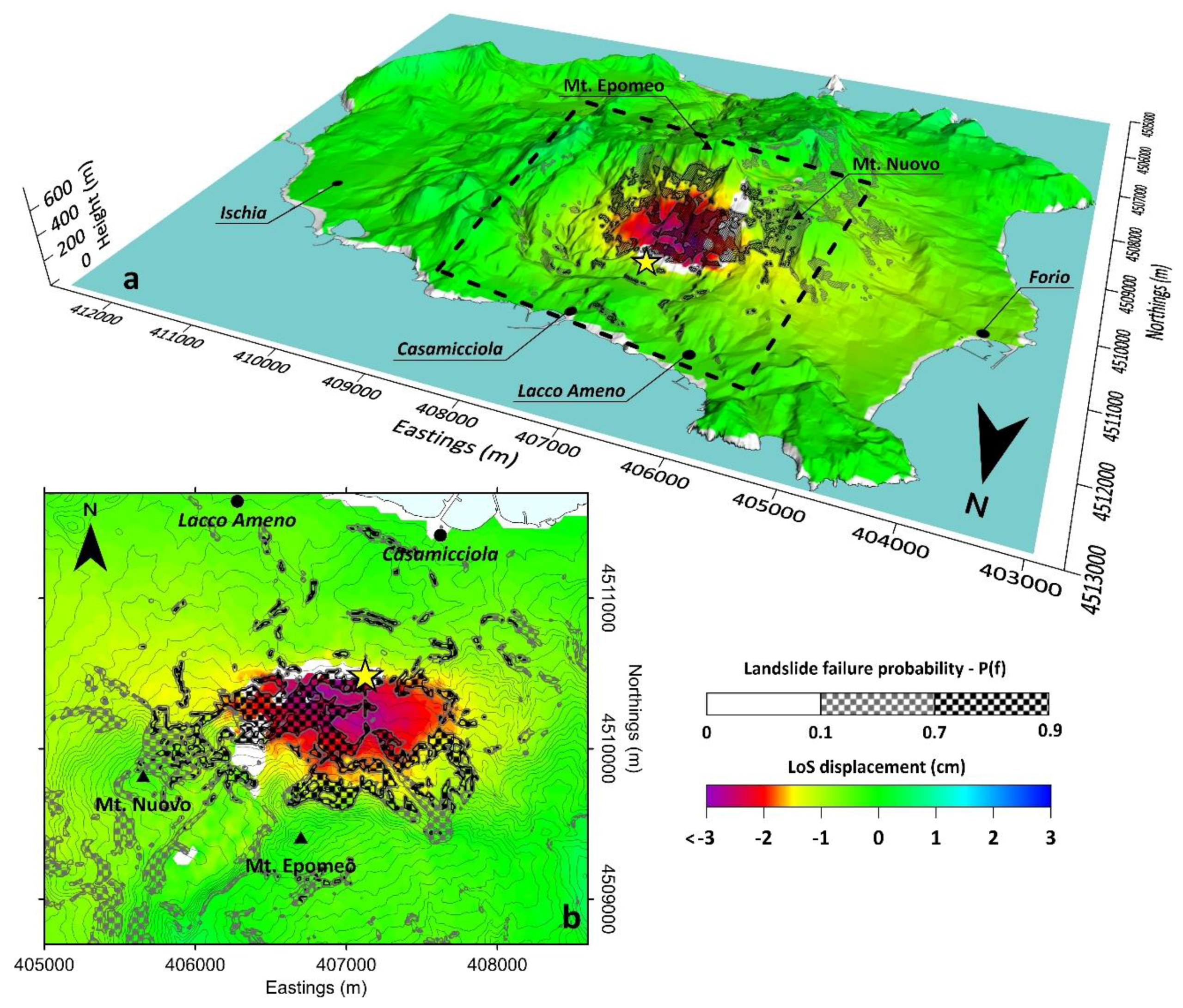
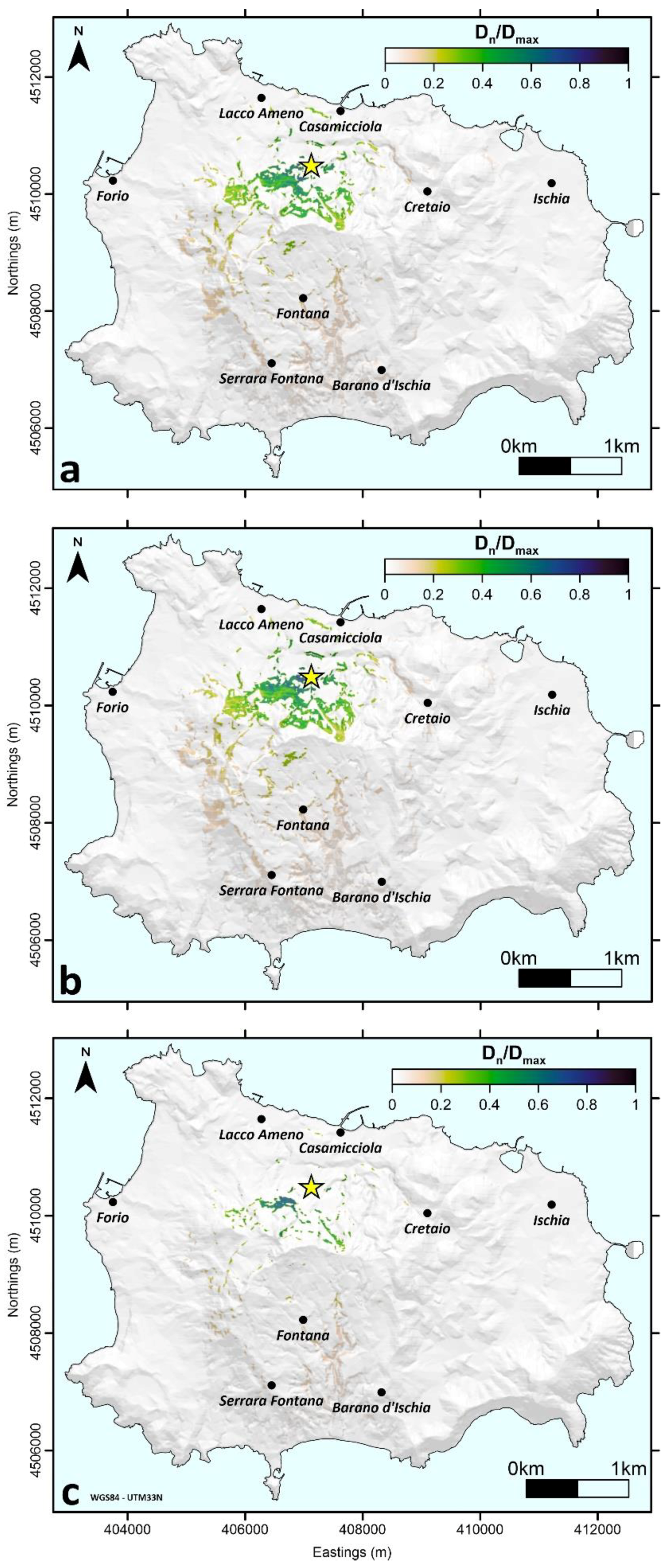
4.2. Landslide Failure Probability Estimation
4.2.1. Available Dataset
4.2.2. Results of the Procedure Applied to Ischia Island
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Azzaro, R.; Del Mese, S.; Martini, G.; Paolini, S.; Screpanti, A.; Verrubbi, V.; Tertulliani, A. QUEST—Rilievo Macrosismico per il Terremoto Dell’isola di Ischia del 21 Agosto 2017. National Institute of Geophysics and Volcanology: Rome, Italy, 2017. [Google Scholar]
- Alessio, G.; Esposito, E.; Ferranti, L.; Mastrolorenzo, G.; Porfido, S. Correlazione tra sismicità ed elementi strutturali nell’isola d’Ischia. Ital. J. Quat. Sci. 1996, 9, 303–308. [Google Scholar]
- Guadagno, F.M.; Mele, R. I movimenti franosi indotti da terremoti nell’isola d’Ischia. In Cinquant’anni Di Ricerca E Di Didattica Del Prof. Felice Ippolito, Naples; Vallario, A., Bonardi, G., De Vivo, B., Gasparini, P., Liguori, Eds.; Liguori Editore: Naples, Italy, 1995; pp. 127–137. [Google Scholar]
- Mele, R.; Del Prete, S. Fenomeni di instabilita dei versanti in Tufo Verde del Monte Epomeo (isola d’Ischia, Campania). Ital. J. Geosci. 1998, 117, 93–112. [Google Scholar]
- Nappi, R.; Alessio, G.; Gaudiosi, G.; Nave, R.; Marotta, E.; Siniscalchi, V.; Civico, R.; Pizzimenti, L.; Peluso, R.; Belviso, P.; et al. The 21 August 2017 Md 4.0 Casamicciola Earthquake: First Evidence of Coseismic Normal Surface Faulting at the Ischia Volcanic Island. Seismol. Res. Lett. 2018, 1–12. [Google Scholar] [CrossRef]
- Rapolla, A.; Paoletti, V.; Secomandi, M. Seismically-induced landslide susceptibility evaluation: Application of a new procedure to the island of Ischia, Campania Region, Southern Italy. Eng. Geol. 2010, 114, 10–25. [Google Scholar] [CrossRef]
- De Vita, S.; Sansivero, F.; Orsi, G.; Marotta, E.; Piochi, M. Volcanological and structural evolution of the Ischia resurgent caldera (Italy) over the past 10 ky. Spec. Pap. Geol. Soc. Am. 2010, 2464, 193–239. [Google Scholar]
- Rovida, A.; Locati, M.; Camassi, R.; Lolli, B.; Gasperini, P. (Eds.) CPTI15, the 2015 Version of the Parametric Catalogue of Italian Earthquakes; National Institute of Geophysics and Volcanology: Rome, Italy, 2016. [Google Scholar]
- De Novellis, V.; Carlino, S.; Castaldo, R.; Tramelli, A.; De Luca, C.; Pino, N.A.; Pepe, S.; Convertito, V.; Zinno, I.; De Martino, P.; et al. The 21 st August 2017 Ischia (Italy) earthquake source model inferred from seismological, GPS and DInSAR measurements. Geophys. Res. Lett. 2018. [Google Scholar] [CrossRef]
- Stramondo, S.; Trasatti, E.; Albano, M.; Moro, M.; Chini, M.; Bignami, C.; Polcari, M.; Saroli, M. Uncovering deformation processes from surface displacements. J. Geodyn. 2016, 15, 4373. [Google Scholar] [CrossRef]
- Chini, M.; Albano, M.; Saroli, M.; Pulvirenti, L.; Moro, M.; Bignami, C.; Falcucci, E.; Gori, S.; Modoni, G.; Pierdicca, N.; et al. Coseismic liquefaction phenomenon analysis by COSMO-SkyMed: 2012 Emilia (Italy) earthquake. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 65–78. [Google Scholar] [CrossRef]
- Atzori, S.; Tolomei, C.; Antonioli, A.; Merryman Boncori, J.P.; Bannister, S.; Trasatti, E.; Pasquali, P.; Salvi, S. The 2010–2011 Canterbury, New Zealand, seismic sequence: Multiple source analysis from InSAR data and modeling. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Moro, M.; Saroli, M.; Tolomei, C.; Salvi, S. Insights on the kinematics of deep-seated gravitational slope deformations along the 1915 Avezzano earthquake fault (Central Italy), from time-series DInSAR. Geomorphology 2009, 112, 261–276. [Google Scholar] [CrossRef]
- Albano, M.; Saroli, M.; Moro, M.; Falcucci, E.; Gori, S.; Stramondo, S.; Galadini, F.; Barba, S. Minor shallow gravitational component on the Mt. Vettore surface ruptures related to Mw 6, 2016 Amatrice earthquake. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
- Albano, M.; Barba, S.; Saroli, M.; Moro, M.; Malvarosa, F.; Costantini, M.; Bignami, C.; Stramondo, S. Gravity-driven postseismic deformation following the Mw 6.3 2009 L’Aquila (Italy) earthquake. Sci. Rep. 2015, 5, 16558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kargel, J.S.; Leonard, G.J.; Shugar, D.H.; Haritashya, U.K.; Bevington, A.; Fielding, E.J.; Fujita, K.; Geertsema, M.; Miles, E.S.; Steiner, J.; et al. Geomorphic and geologic controls of geohazards induced by Nepals 2015 Gorkha earthquake. Science 2016, 351. [Google Scholar] [CrossRef] [PubMed]
- Polcari, M.; Montuori, A.; Bignami, C.; Moro, M.; Stramondo, S.; Tolomei, C. Using multi-band InSAR data for detecting local deformation phenomena induced by the 2016–2017 Central Italy seismic sequence. Remote Sens. Environ. 2017, 201, 234–242. [Google Scholar] [CrossRef]
- Cheloni, D.; De Novellis, V.; Albano, M.; Antonioli, A.; Anzidei, M.; Atzori, S.; Avallone, A.; Bignami, C.; Bonano, M.; Calcaterra, S.; et al. Geodetic model of the 2016 Central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 2017, 44, 6778–6787. [Google Scholar] [CrossRef] [Green Version]
- Caccavale, M.; Matano, F.; Sacchi, M. An integrated approach to earthquake-induced landslide hazard zoning based on probabilistic seismic scenario for Phlegrean Islands (Ischia, Procida and Vivara), Italy. Geomorphology 2017, 295, 235–259. [Google Scholar] [CrossRef]
- Jibson, R.W.; Harp, E.L.; Michael, J.A. A method for producing digital probabilistic seismic landslide hazard maps. Eng. Geol. 2000, 58, 271–289. [Google Scholar] [CrossRef] [Green Version]
- Rittmann, A.-F. Geologie der Insel Ischia; D. Reimer: Berlin, Germany, 1930. [Google Scholar]
- Sepe, V.; Atzori, S.; Ventura, G. Subsidence due to crack closure and depressurization of hydrothermal systems: A case study from Mt Epomeo (Ischia Island, Italy). Terra Nova 2007, 19, 127–132. [Google Scholar] [CrossRef] [Green Version]
- Molin, P.; Acocella, V.; Funiciello, R. Structural, seismic and hydrothermal features at the border of an active intermittent resurgent block: Ischia Island (Italy). J. Volcanol. Geotherm. Res. 2003, 121, 65–81. [Google Scholar] [CrossRef]
- Orsi, G.; de Vita, S.; Di Vito, M.A.; Isaia, R.; Vane, R.; Heiken, G. Facing Volcanic and Related Hazards in the Neapolitan Area. In Earth Science in the City: A Reader, Volume 56; American Geophysical Union: Washington, DC, USA, 2013; pp. 121–170. [Google Scholar]
- De Vita, S.; Sansivero, F.; Orsi, G.; Marotta, E. Cyclical slope instability and volcanism related to volcano-tectonism in resurgent calderas: The Ischia island (Italy) case study. Eng. Geol. 2006, 86, 148–165. [Google Scholar] [CrossRef]
- Gillot, P.-Y.; Chiesa, S.; Pasquaré, G.; Vezzoli, L. <33,000-yr K–Ar dating of the volcano–tectonic horst of the Isle of Ischia, Gulf of Naples. Nature 1982, 299, 242–245. [Google Scholar] [CrossRef]
- Del Prete, S.; Mele, R. Il contributo delle informazioni storiche per la valutazione della propensione al dissesto nell’Isola d’Ischia (Campania). Rend. Sociatà Geol. Ital. 2006, 39–47. [Google Scholar]
- Della Seta, M.; Marotta, E.; Orsi, G.; de Vita, S.; Sansivero, F.; Fredi, P. Slope instability induced by volcano-tectonics as an additional source of hazard in active volcanic areas: The case of Ischia island (Italy). Bull. Volcanol. 2012, 74, 79–106. [Google Scholar] [CrossRef]
- Della Seta, M.; Esposito, C.; Marmdoni, G.M.; Martino, S.; Paciello, A.; Perinelli, C.; Sottili, G. Geological constraints for a conceptual evolutionary model of the slope deformations affecting Mt. Nuovo at Ischia (Italy). Ital. J. Eng. Geol. Environ. 2015, 15, 15–28. [Google Scholar] [CrossRef]
- Paparo, M.A.; Tinti, S. Analysis of Seismic-Driven Instability of Mt. Nuovo in the Ischia Island, Italy. Bull. Seismol. Soc. Am. 2017, 107, 750–759. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef] [Green Version]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes-A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Jibson, R.W. Regression models for estimating coseismic landslide displacement. Eng. Geol. 2007, 91, 209–218. [Google Scholar] [CrossRef]
- Wilson, R.C.; Keefer, D.K. Predicting Areal Limit of Earthquake-Induced Landsliding. In Evaluating Earthquake Hazards in the Los Angeles Region—An Earth-Science Perspective; US Geological Survey Professional Paper 1360; US Geological Survey: Reston, VA, USA, 1985; pp. 317–345. [Google Scholar]
- Gallen, S.F.; Clark, M.K.; Godt, J.W.; Roback, K.; Niemi, N.A. Application and evaluation of a rapid response earthquake-triggered landslide model to the 25 April 2015 Mw7.8 Gorkha earthquake, Nepal. Tectonophysics 2017, 714–715, 173–187. [Google Scholar] [CrossRef]
- Jibson, R.W. Predicting Earthquake-Induced Landslide Displacements Using Newmark’s Sliding Block Analysis; Transportation Research Board: Washington, DC, USA, 1993; pp. 9–17. [Google Scholar]
- Luzi, L.; Pacor, F.; Puglia, R. Italian Accelerometric Archive v 2.3. Istituto Nazionale di Geofisica e Vulcanologia, Dipartimento della Protezione Civile Nazionale; National Institute of Geophysics and Volcanology: Rome, Italy, 2017. [Google Scholar]
- Sieberg, A. Geologie der Erdbeben. In Handboch der Geophysic; Springer: Berlin, Germany, 1930; pp. 552–554. [Google Scholar]
- Sibson, R. A Brief Description of Natural Neighbor Interpolation. In Interpolating Multivariate Data; John Wiley & Sons, Ltd.: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Sambridge, M.; Braun, J.; McQueen, H. Geophysical parametrization and interpolation of irregular data using natural neighbours. Geophys. J. Int. 1995, 122, 837–857. [Google Scholar] [CrossRef] [Green Version]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do landslides follow landslides? Insights in path dependency from a multi-temporal landslide inventory. Landslides 2017, 14, 547–558. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W. Fundamentals of Rock Mechanics; Methuen & Co., Ltd.: London, UK, 1969; p. 513. [Google Scholar]
- Tarquini, S.; Isola, I.; Favalli, M.; Mazzarini, F.; Bisson, M.; Pareschi, M.T.; Boschi, E. TINITALY/01: A new Triangular Irregular Network of Italy. Ann. Geophys. 2007, 50, 407–425. [Google Scholar] [CrossRef]
- Tarquini, S.; Vinci, S.; Favalli, M.; Doumaz, F.; Fornaciai, A.; Nannipieri, L. Release of a 10-m-resolution DEM for the Italian territory: Comparison with global-coverage DEMs and anaglyph-mode exploration via the web. Comput. Geosci. 2012, 38, 168–170. [Google Scholar] [CrossRef] [Green Version]
- De Alteriis, G.; Violante, C. Catastrophic landslides off Ischia volcanic island (Italy) during prehistory. Geol. Soc. Lond. Spec. Publ. 2009, 322, 73–104. [Google Scholar] [CrossRef]
- Musson, R.M.; Cecić, I. Intensity and Intensity Scales. In New Manual of Seismological Observatory Practice 2 (NMSOP-2); Bormann, P., Ed.; Deutsches Geo Forschungs Zentrum: Potsdam, Germany, 2012; pp. 1–41. [Google Scholar]
- Manzo, M.; Ricciardi, G.P.; Casu, F.; Ventura, G.; Zeni, G.; Borgström, S.; Berardino, P.; Del Gaudio, C.; Lanari, R. Surface deformation analysis in the Ischia Island (Italy) based on spaceborne radar interferometry. J. Volcanol. Geotherm. Res. 2006, 151, 399–416. [Google Scholar] [CrossRef]
- Modoni, G.; Koseki, J.; Anh Dan, L.Q. Cyclic stress–strain response of compacted gravel. Géotechnique 2011, 61, 473–485. [Google Scholar] [CrossRef]
- Modoni, G.; Albano, M.; Salvatore, E.; Koseki, J. Effects of compaction on the seismic performance of embankments built with gravel. Soil Dyn. Earthq. Eng. 2018, 106, 231–242. [Google Scholar] [CrossRef]
- Bottari, C.; Albano, M.; Capizzi, P.; D’Alessandro, A.; Doumaz, F.; Martorana, R.; Moro, M.; Saroli, M. Recognition of Earthquake-Induced Damage in the Abakainon Necropolis (NE Sicily): Results From Geomorphological, Geophysical and Numerical Analyses. Pure Appl. Geophys. 2018, 175, 133–148. [Google Scholar] [CrossRef]
- Zhang, Y. Review of Studies on Earthquake-Induced Landslides; Springer: Singapore, 2018; pp. 11–39. [Google Scholar]
| N° | Lithology | Unit Weight—γ (kN/m3) | Cohesion—c′ (kPa) | Friction Angle—φ′ (Degree) |
|---|---|---|---|---|
| 1 | Lava | 27.25 | 1000 | 40 |
| 2 | Lithified yellow tuff | 17 | 325 | 25 |
| 3 | Welded tuff | 20 | 425 | 28 |
| 4 | Lava with welded scoriae | 25 | 800 | 40 |
| 5 | Lithified pyroclastic deposits | 19 | 600 | 34 |
| 6 | Tuff with pyroclastic deposits | 16 | 370 | 30 |
| 7 | Marine silty sandstones with tuffites | 18 | 30 | 35 |
| 8 | Brecciae | 20 | 100 | 35 |
| 9 | Loose pyroclastic deposits | 13.5 | 5 | 32 |
| 10 | Slope debris | 15.5 | 2 | 35 |
| 11 | Pumice and ash layers | 13.75 | 10 | 30 |
| 12 | Sandy and silty beach deposits | 14 | 0 | 32 |
| 13 | Eluvial-colluvial pyroclastic deposits | 15.75 | 2 | 25 |
| 14 | Landslide, debris and colluvial deposits | 13 | 2 | 25 |
| 15 | Dump materials and reworked soils | 13.5 | 0 | 25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albano, M.; Saroli, M.; Montuori, A.; Bignami, C.; Tolomei, C.; Polcari, M.; Pezzo, G.; Moro, M.; Atzori, S.; Stramondo, S.; et al. The Relationship between InSAR Coseismic Deformation and Earthquake-Induced Landslides Associated with the 2017 Mw 3.9 Ischia (Italy) Earthquake. Geosciences 2018, 8, 303. https://doi.org/10.3390/geosciences8080303
Albano M, Saroli M, Montuori A, Bignami C, Tolomei C, Polcari M, Pezzo G, Moro M, Atzori S, Stramondo S, et al. The Relationship between InSAR Coseismic Deformation and Earthquake-Induced Landslides Associated with the 2017 Mw 3.9 Ischia (Italy) Earthquake. Geosciences. 2018; 8(8):303. https://doi.org/10.3390/geosciences8080303
Chicago/Turabian StyleAlbano, Matteo, Michele Saroli, Antonio Montuori, Christian Bignami, Cristiano Tolomei, Marco Polcari, Giuseppe Pezzo, Marco Moro, Simone Atzori, Salvatore Stramondo, and et al. 2018. "The Relationship between InSAR Coseismic Deformation and Earthquake-Induced Landslides Associated with the 2017 Mw 3.9 Ischia (Italy) Earthquake" Geosciences 8, no. 8: 303. https://doi.org/10.3390/geosciences8080303