Ensemble Radar-Based Rainfall Forecasts for Urban Hydrological Applications
Abstract
:1. Introduction
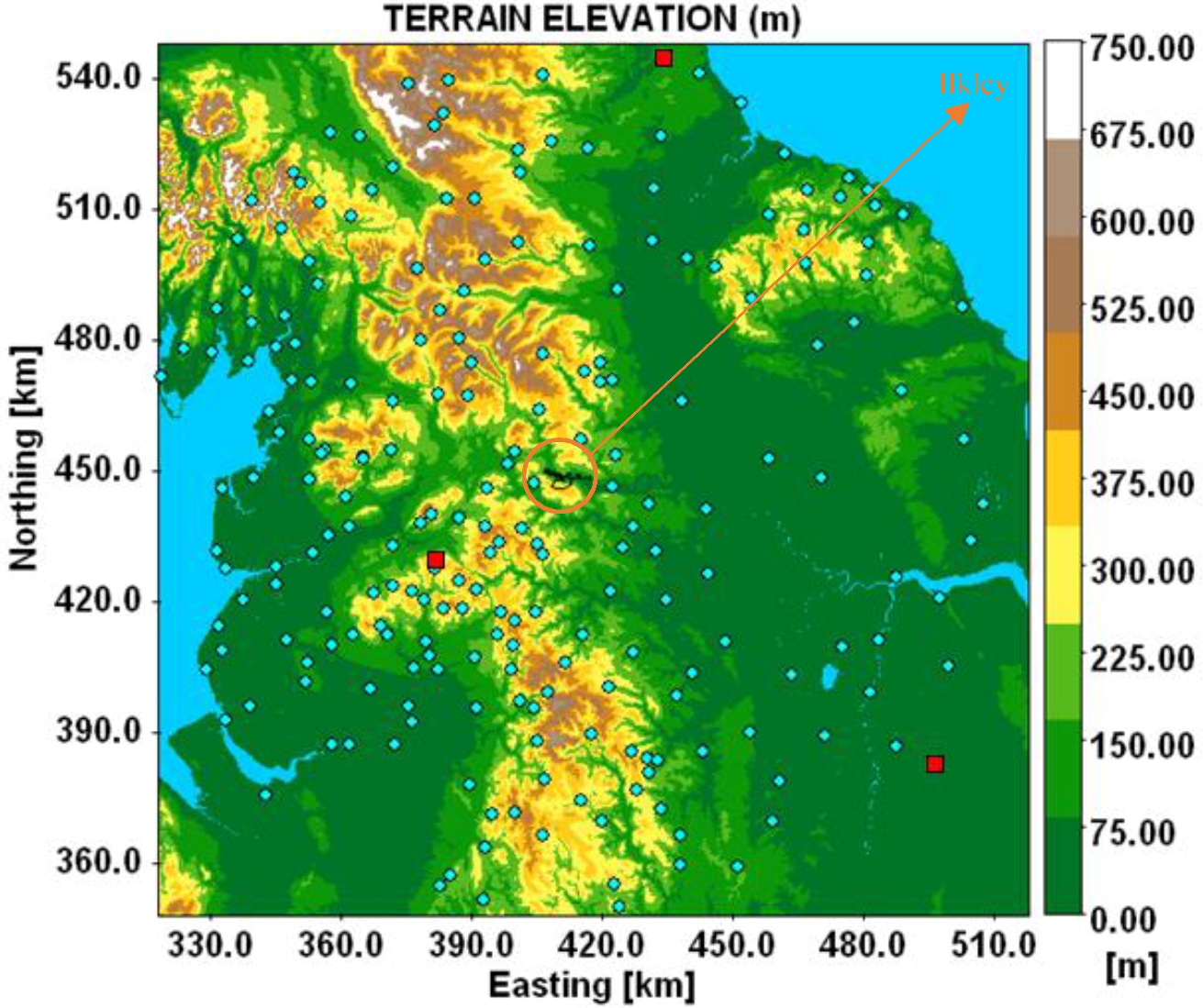
2. Materials and Methods
3. Results
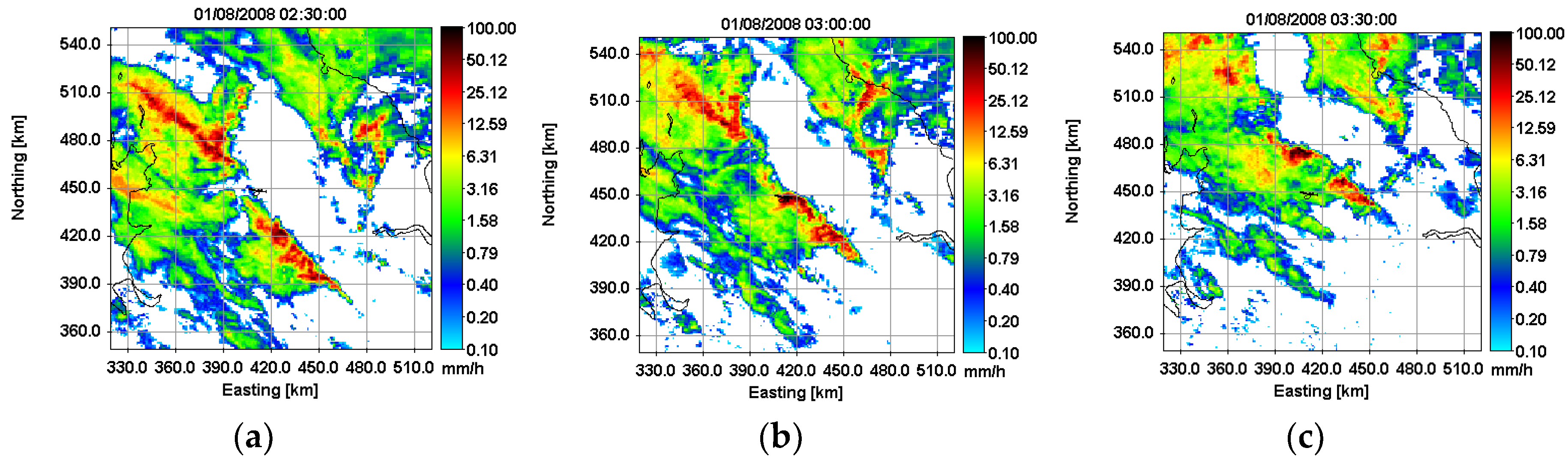
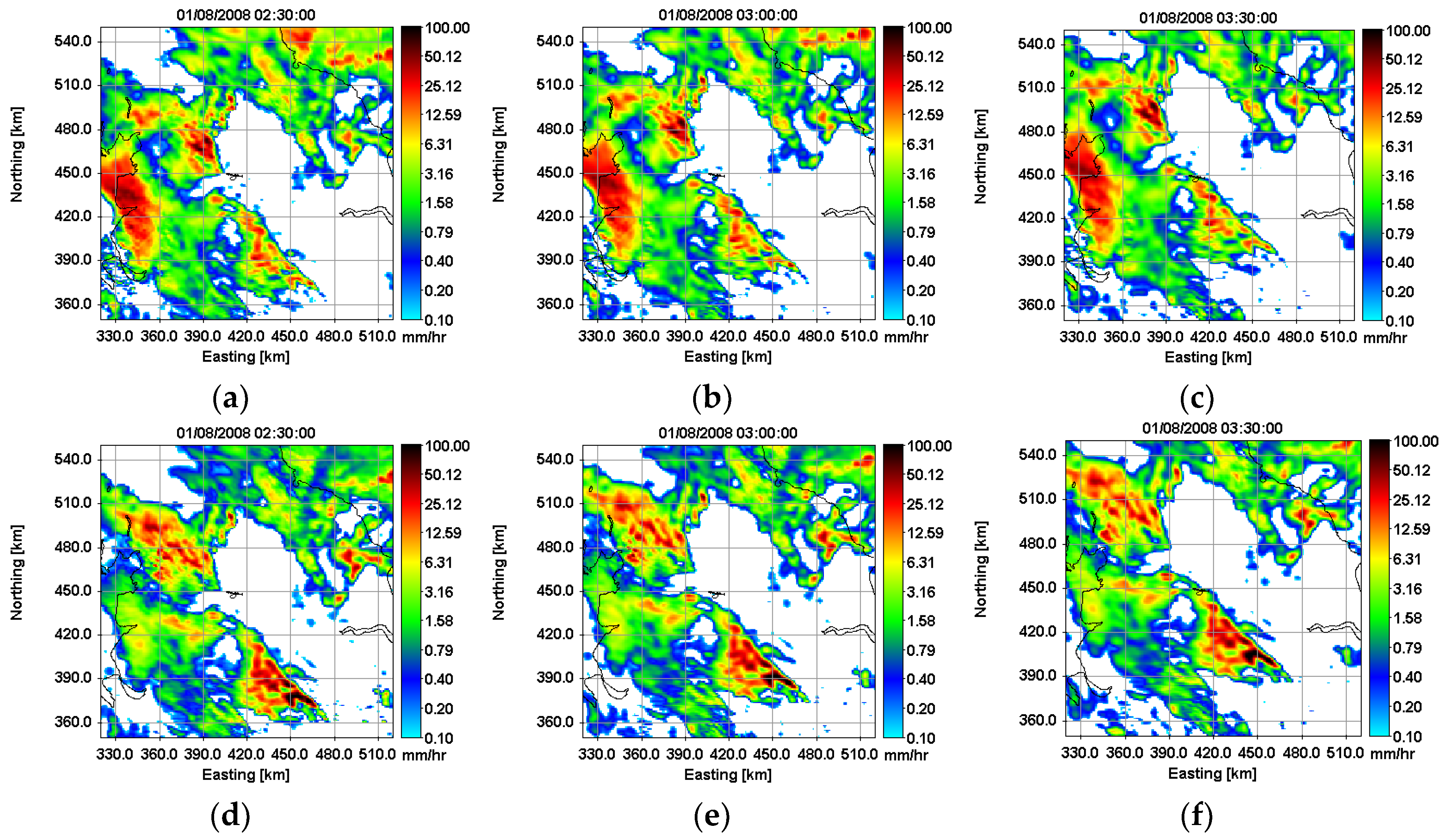
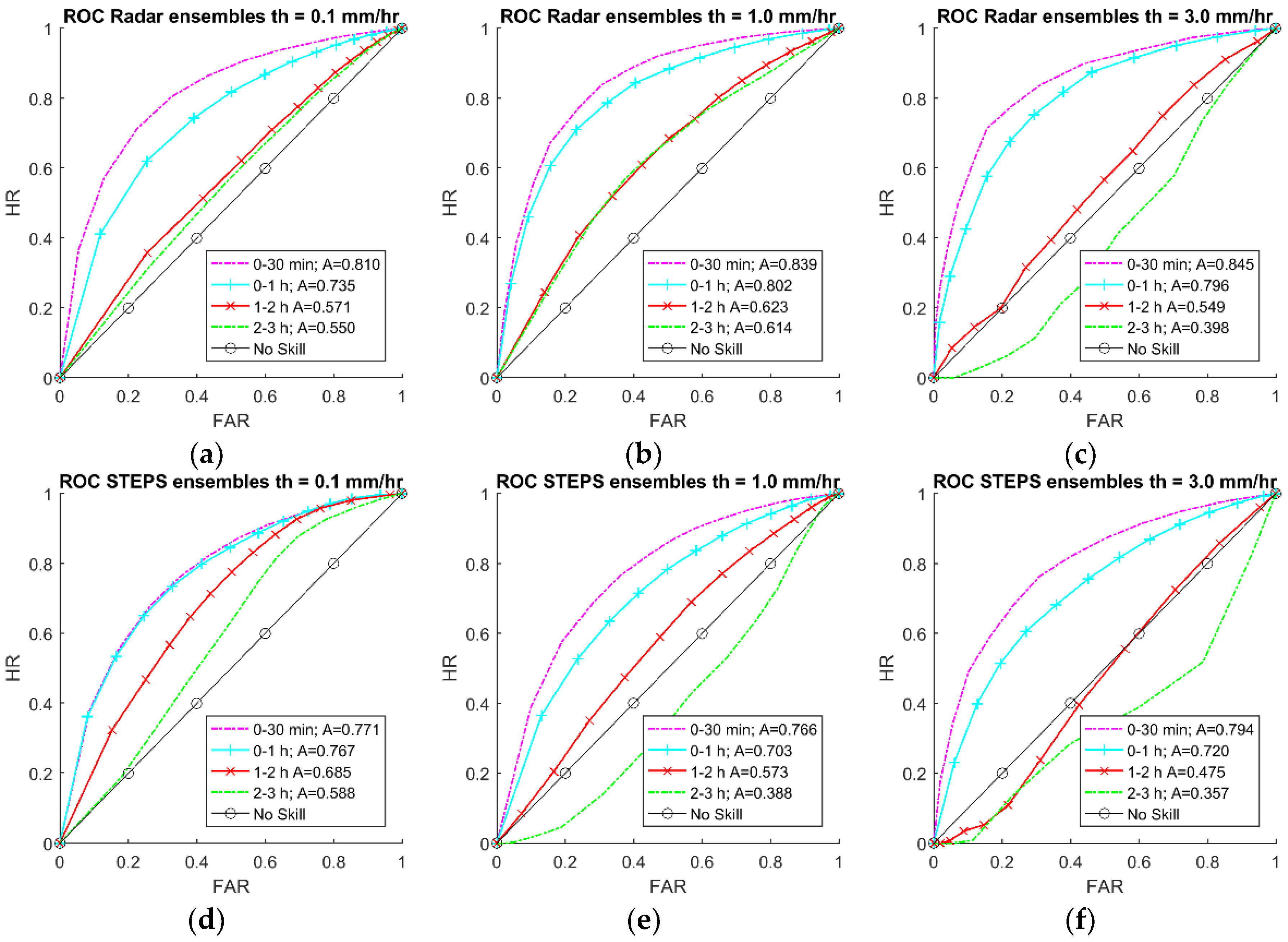
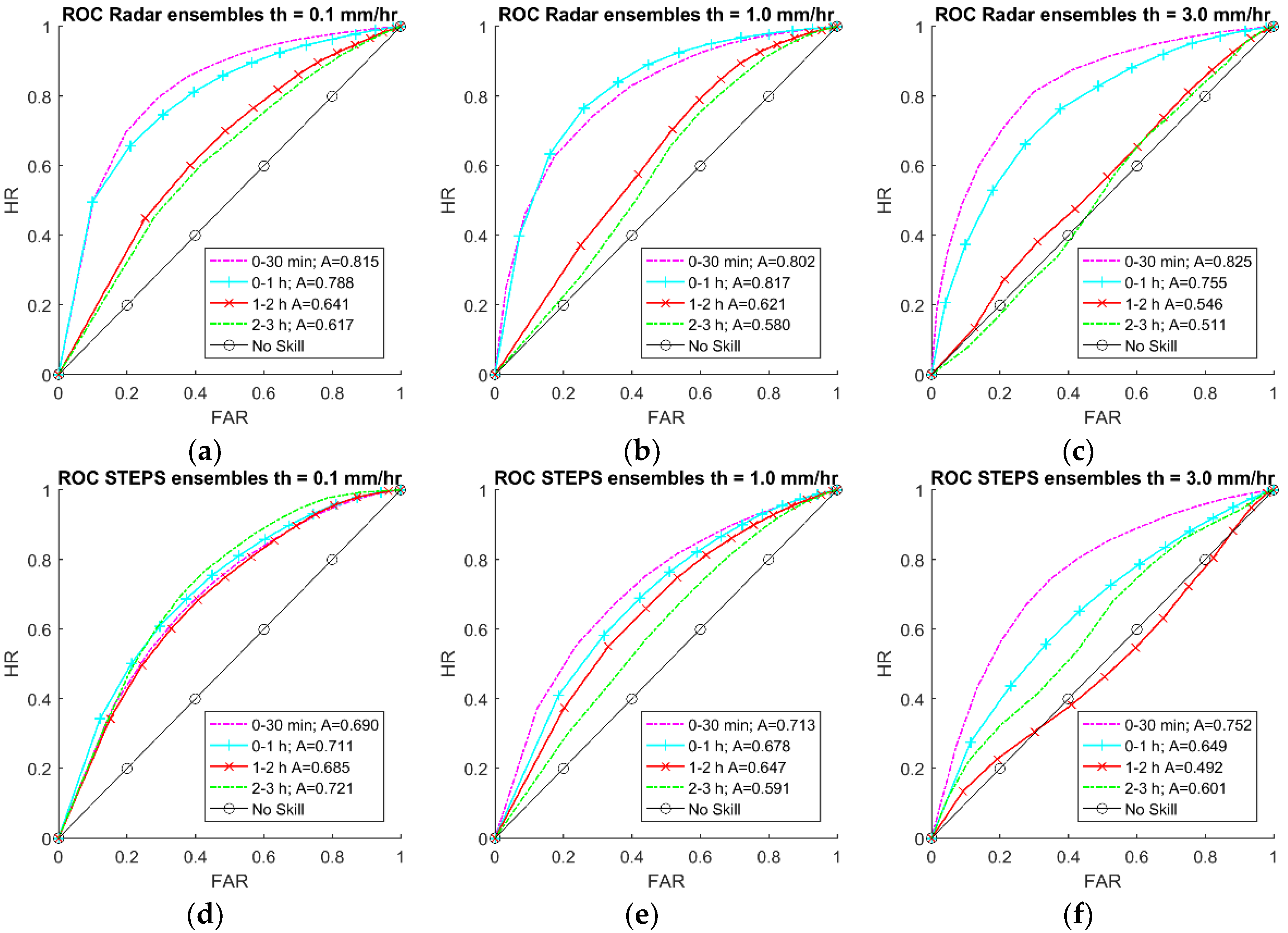
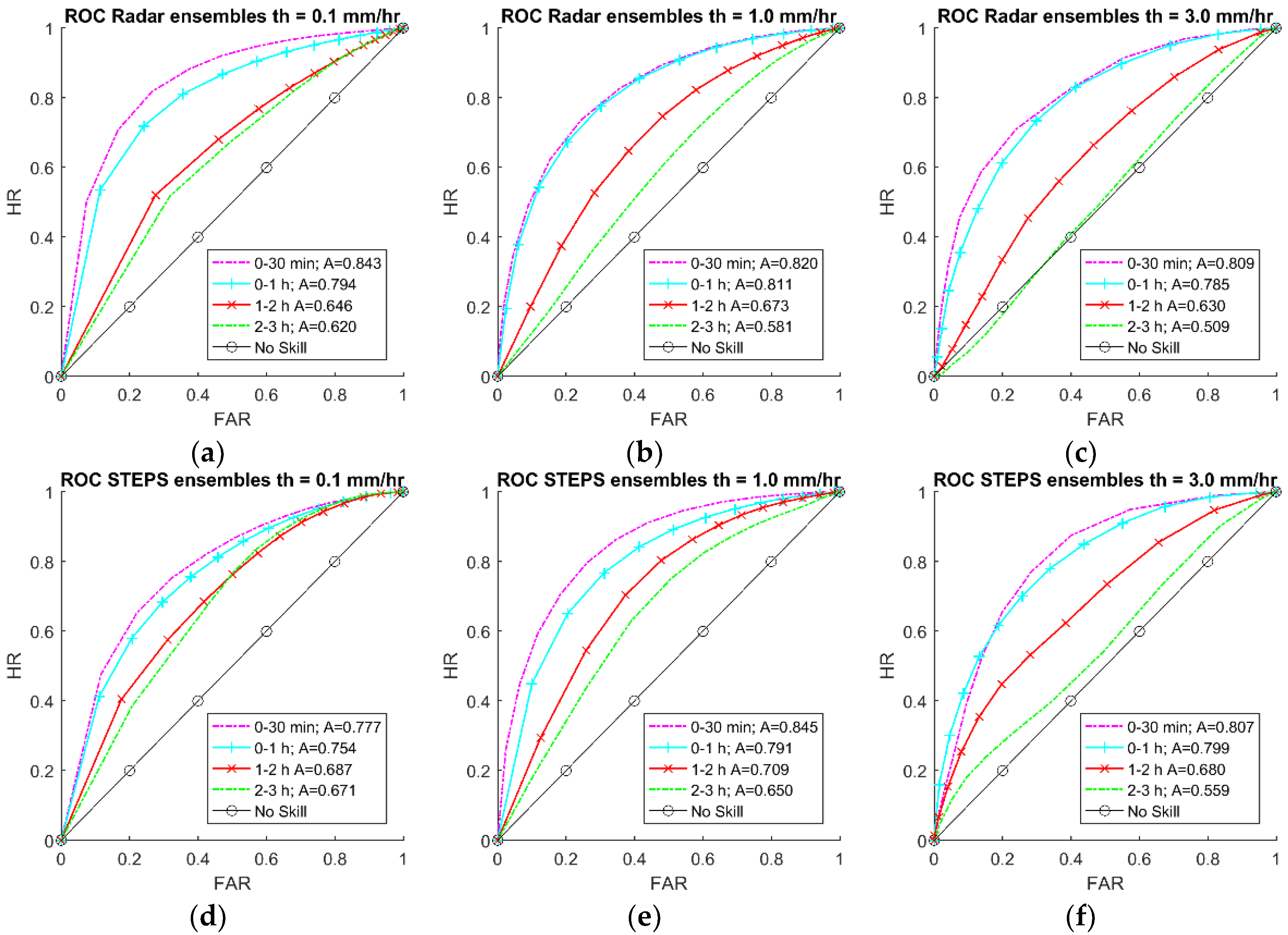
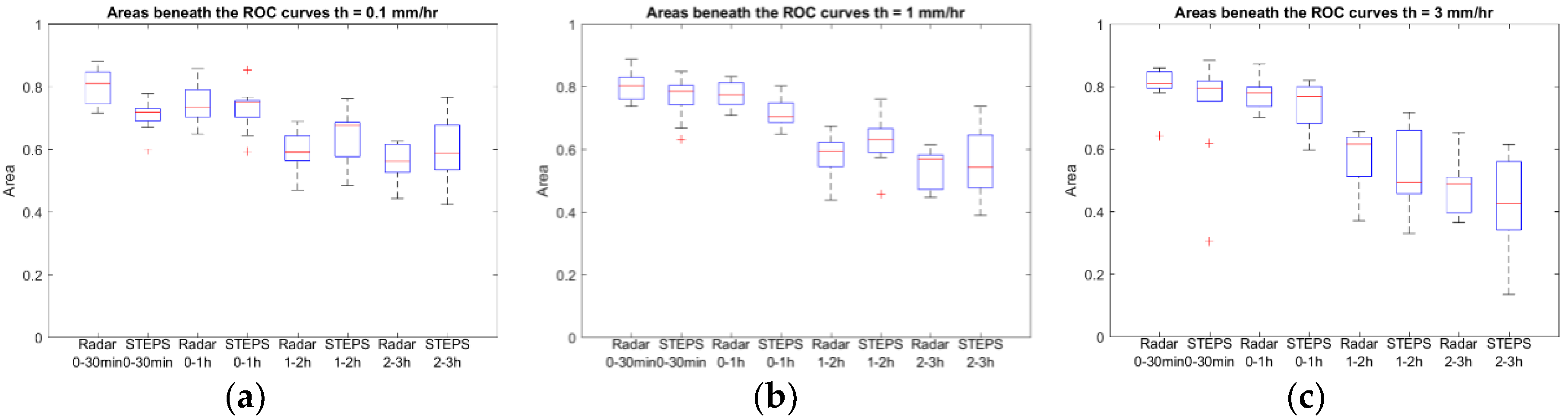
3.1. Rainfall Forecasting
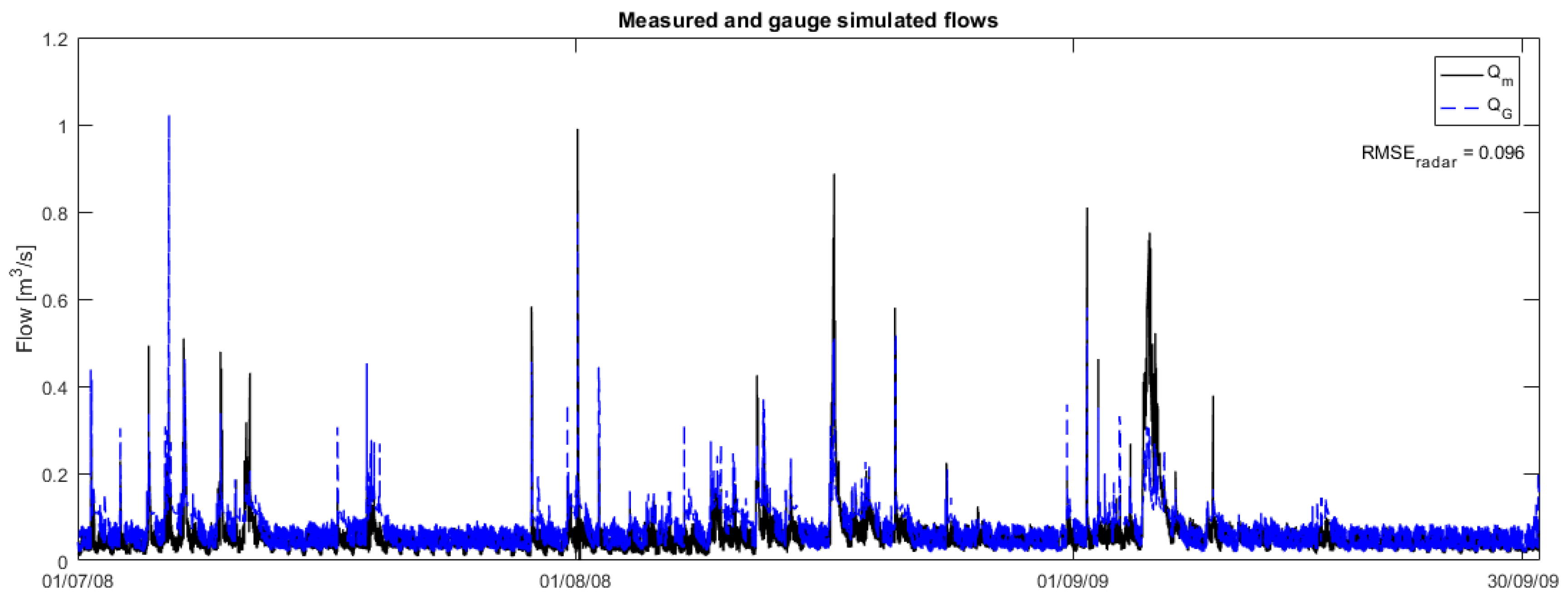
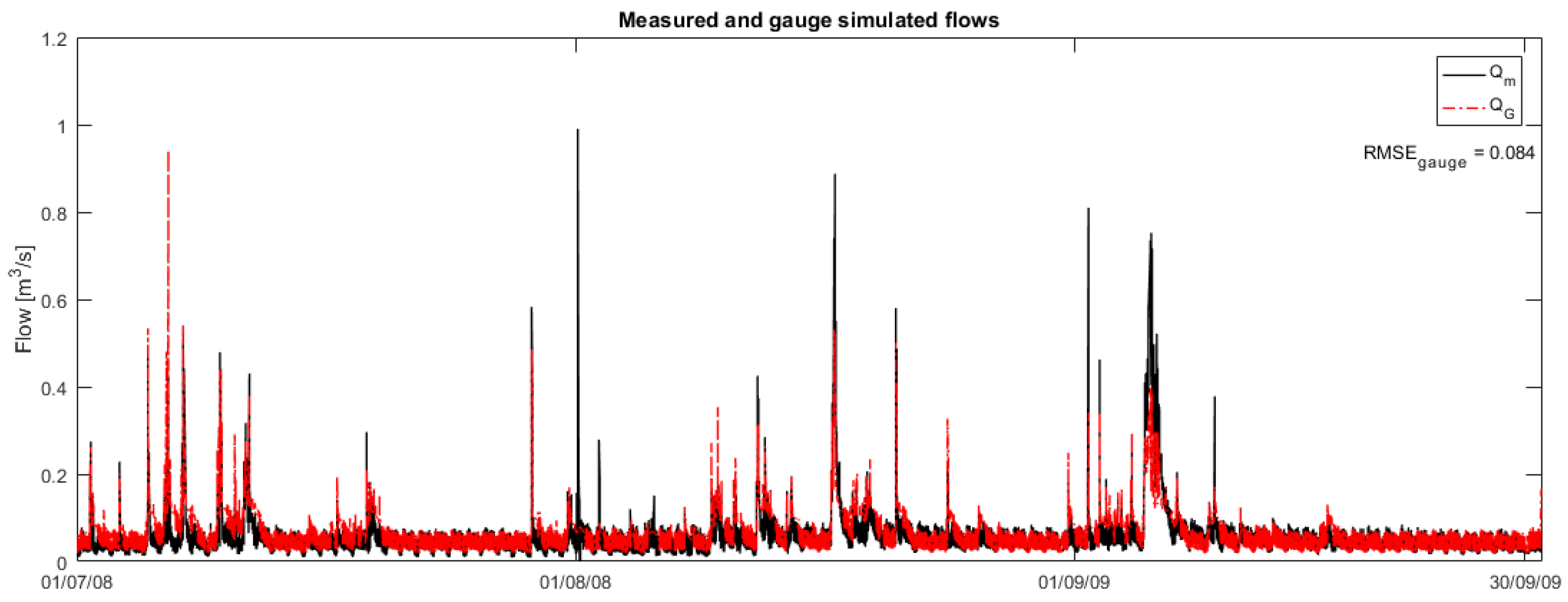
3.2. Sewer Flow Simulations
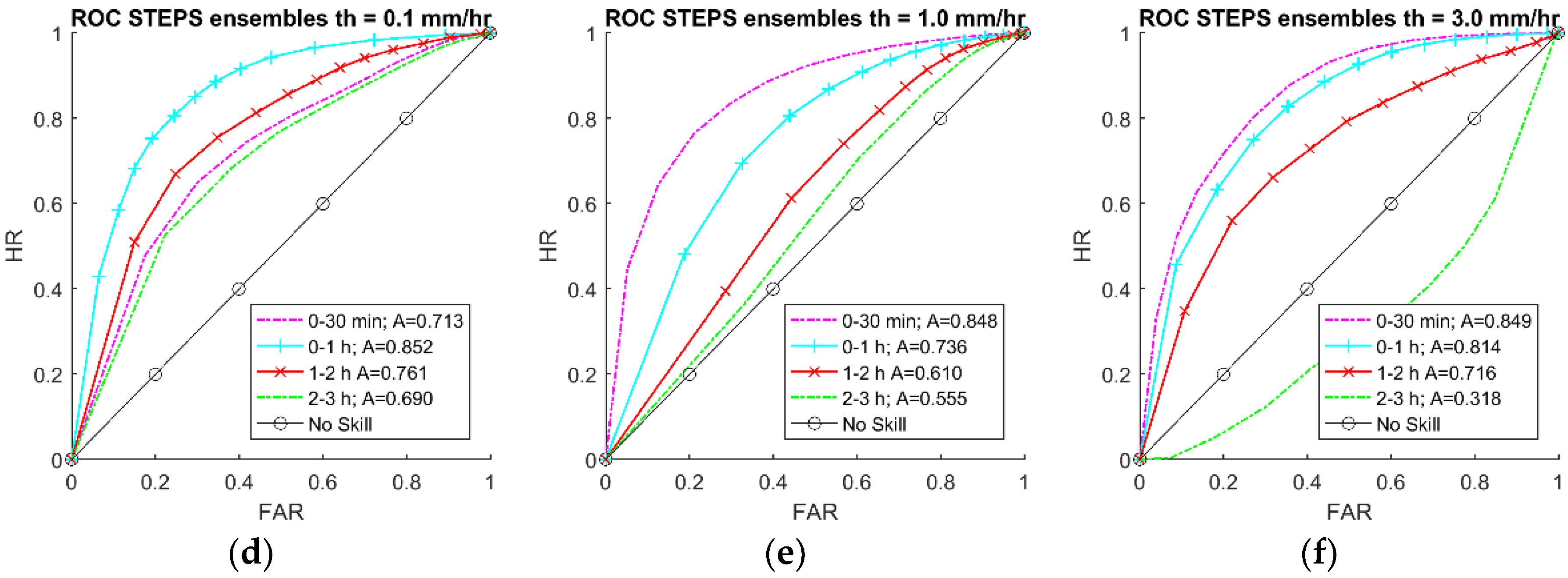
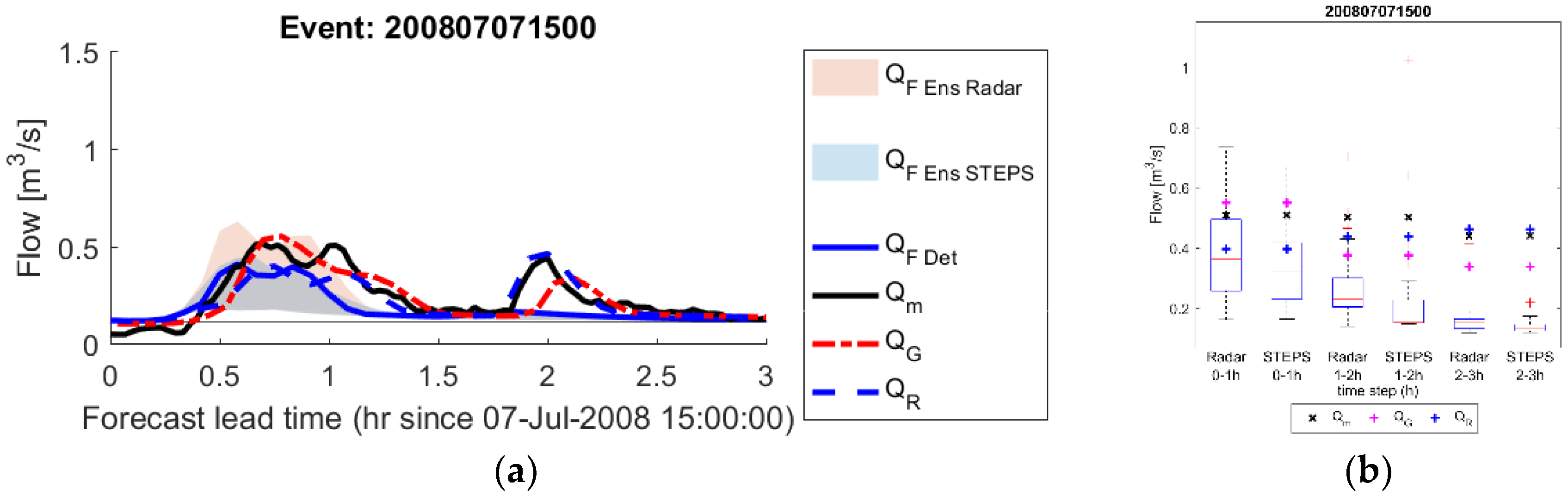
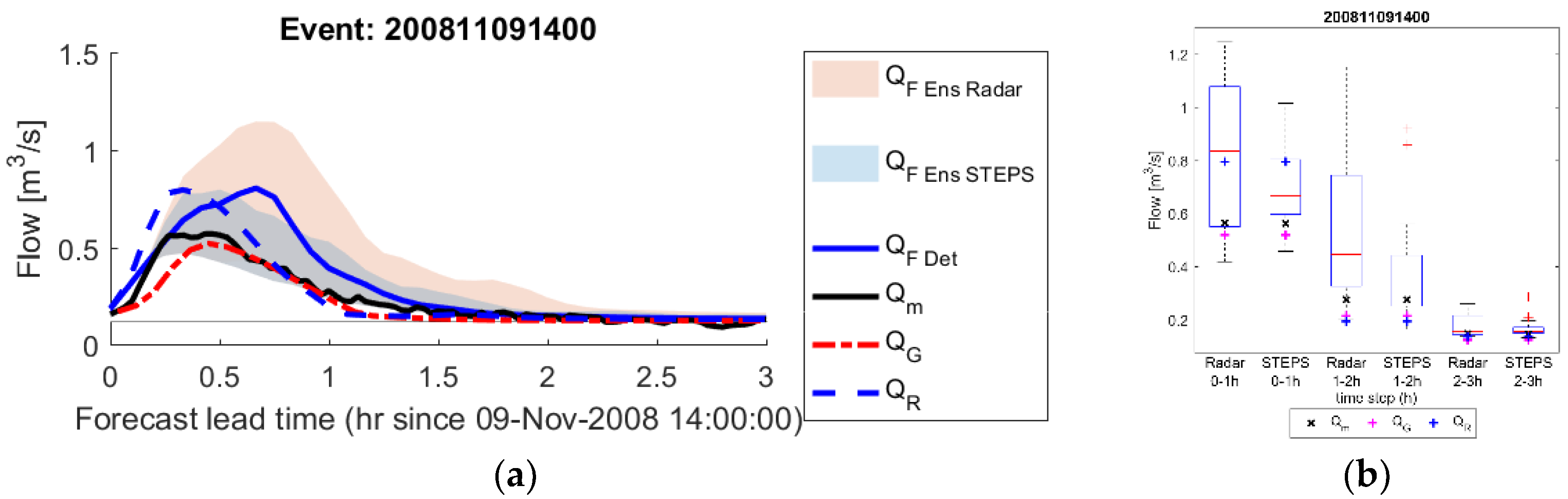
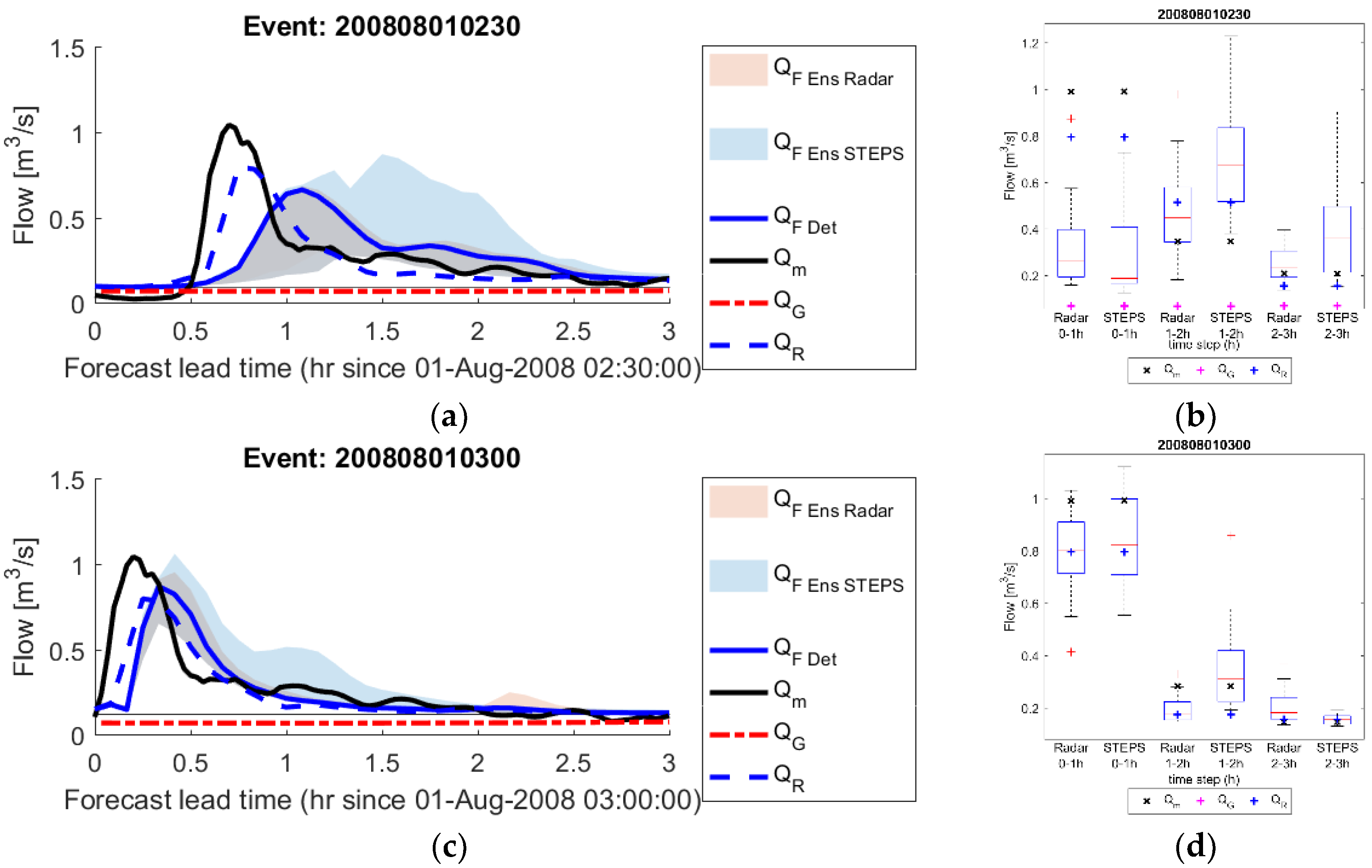
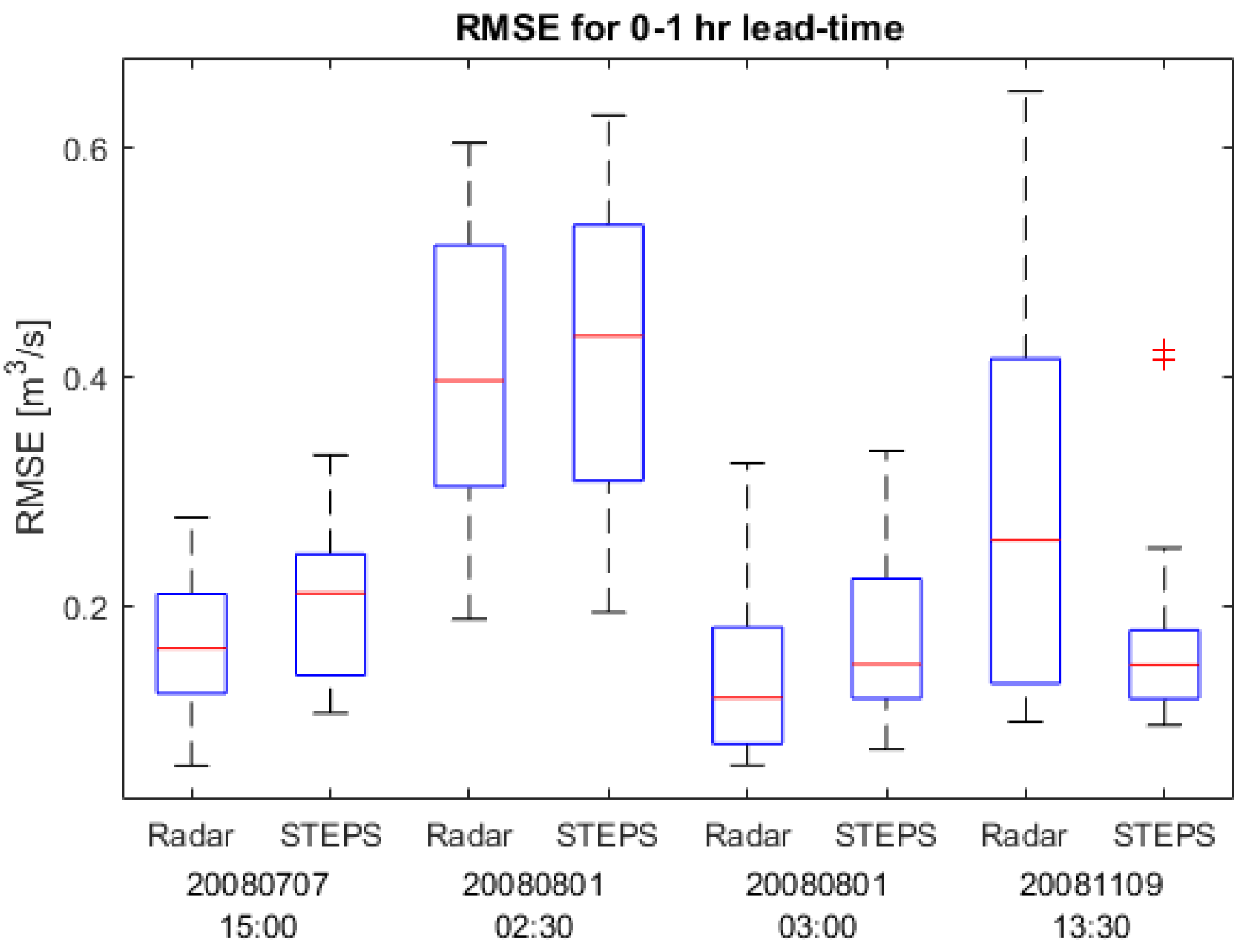
3.3. Forecasting Sewer Flows
4. Discussion
4.1. Rainfall Forecasting
4.2. Sewer Flow Simulations
4.3. Forecasting Sewer Flows
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lau, C.L.; Smythe, L.D.; Craig, S.B.; Weinstein, P. Climate change, flooding, urbanisation and leptospirosis: Fuelling the fire? Trans. R. Soc. Trop. Med. Hyg. 2010, 104, 631–638. [Google Scholar] [CrossRef] [PubMed]
- Brocca, L.; Melone, F.; Moramarco, T. Distributed rainfall-runoff modelling for flood frequency estimation and flood forecasting. Hydrol. Process. 2011, 25, 2801–2813. [Google Scholar] [CrossRef]
- Few, R. Flooding, vulnerability and coping strategies: Local responses to a global threat. Prog. Dev. Stud. 2003, 3, 43–58. [Google Scholar] [CrossRef]
- Golding, B.W. Long lead time flood warnings: Reality or fantasy? Meteorol. Appl. 2009, 16, 3–12. [Google Scholar] [CrossRef]
- Cloke, H.L.; Pappenberger, F. Ensemble flood forecasting: A review. J. Hydrol. 2009, 375, 613–626. [Google Scholar] [CrossRef]
- Pierce, C.E.; Hardaker, P.J.; Collier, C.G.; Haggett, C.M. GANDOLF: A system for generating automated nowcasts of convective precipitation. Meteorol. Appl. 2000, 7, 341–360. [Google Scholar] [CrossRef]
- Bowler, N.; Pierce, C.E.; Seed, A.W. STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP. Q. J. R. Meteorol. Soc. 2006, 132, 2127–2155. [Google Scholar] [CrossRef] [Green Version]
- Foresti, L.; Panziera, L.; Mandapaka, P.V.; Germann, U.; Seed, A.W. Retrieval of analogue radar images for ensemble nowcasting of orographic rainfall. Meteorol. Appl. 2015, 22, 141–155. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A.; Schellart, A.N.A.; Saul, A.J. Using probabilistic radar rainfall nowcasts and NWP forecasts for flow prediction in urban catchments. Atmos. Res. 2012, 103, 80–95. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–37. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Bowler, N.; Pierce, C.E.; Seed, A.W. Development of a precipitation nowcasting algorithm based upon optical flow techniques. J. Hydrol. 2004, 288, 74–91. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A. Using the radar rainfall error for probabilistic forecasting. In Proceedings of the Seventh European Conference on Radar in Meteorology and Hydrology, Toulouse, France, 25–29 June 2012. [Google Scholar]
- Germann, U.; Berenguer, M.; Sempere-Torres, D.; Zappa, M. REAL—Ensemble radar precipitation estimation for hydrology in a mountainous region. Q. J. R. Meteorol. Soc. 2009, 135, 445–456. [Google Scholar] [CrossRef] [Green Version]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. R. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef] [Green Version]
- Collier, C.G. Applications of Weather Radar Systems: A Guide to Uses of Radar Data in Meteorology and Hydrology, 2nd ed.; John Wiley: Chichester, UK, 1996; ISBN 0471960136. [Google Scholar]
- Harrison, D.L.; Driscoll, S.J.; Kitchen, M. Improving precipitation estimates from weather radar using quality control and correction techniques. Meteorol. Appl. 2000, 7, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.M.; Sharma, A.; Johnson, F.; Mariethoz, G.; Seed, A.W. Correcting bias in radar Z-R relationships due to uncertainty in point rain gauge networks. J. Hydrol. 2014, 519, 1668–1676. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V. Error structure of radar rainfall measurement at C-band frequencies with dual polarization algorithm for attenuation correction. J. Geophys. Res. 1996, 101, 26461–26471. [Google Scholar] [CrossRef]
- Cho, Y.H.; Lee, G.W.; Kim, K.E.; Zawadzki, I. Identification and removal of ground echoes and anomalous propagation using the characteristics of radar echoes. J. Atmos. Ocean. Technol. 2006, 23, 1206–1222. [Google Scholar] [CrossRef]
- Rico-Ramirez, M.A.; Cluckie, I.D. Classification of ground clutter and anomalous propagation using dual-polarization weather radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1892–1904. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Vignal, B.; Seo, B.C.; Villarini, G. Statistical model of the range-dependent error in radar-rainfall estimates due to the vertical profile of reflectivity. J. Hydrol. 2011, 402, 306–316. [Google Scholar] [CrossRef]
- Hall, W.; Rico-Ramirez, M.A.; Krämer, S. Classification and correction of the bright band using an operational C-band polarimetric radar. J. Hydrol. 2015, 531, 248–258. [Google Scholar] [CrossRef] [Green Version]
- Rico-Ramirez, M.A.; Cluckie, I.D. Bright-band detection from radar vertical reflectivity profiles. Int. J. Remote Sens. 2007, 28, 4013–4025. [Google Scholar] [CrossRef]
- Islam, T.; Rico-Ramirez, M.A.; Han, D.; Srivastava, P.K. Sensitivity associated with bright band/melting layer location on radar reflectivity correction for attenuation at C-band using differential propagation phase measurements. Atmos. Res. 2014, 135–136, 143–158. [Google Scholar] [CrossRef]
- Smyth, T.J.; Illingworth, A.J. Correction for attenuation of radar reflectivity using polarizatin data. Q. J. R. Meteorol. Soc. 1998, 124, 2393–2415. [Google Scholar] [CrossRef]
- Seo, D.-J.; Breidenbach, J.; Johnson, E. Real-time estimation of mean field bias in radar rainfall data. J. Hydrol. 1999, 223, 131–147. [Google Scholar] [CrossRef]
- Jewell, S.A.; Gaussiat, N. An assessment of kriging-based rain-gauge-radar merging techniques. Q. J. R. Meteorol. Soc. 2015, 141, 2300–2313. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.L.; Sorooshian, S.; Gourley, J.J.; Lakshmanan, V.; Hong, Y.; Bellerby, T. Quantitative Precipitation Nowcasting: A Lagrangian Pixel-Based Approach. Atmos. Res. 2012, 118, 418–434. [Google Scholar] [CrossRef] [Green Version]
- Liguori, S.; Rico-Ramirez, M.A. A review of current approaches to radar-based quantitative precipitation forecasts. Int. J. River Basin Manag. 2013, 12, 391–402. [Google Scholar] [CrossRef]
- Foresti, L.; Seed, A.W. The effect of flow and orography on the spatial distribution of the very short-term predictability of rainfall from composite radar images. Hydrol. Earth Syst. Sci. 2014, 18, 4671–4686. [Google Scholar] [CrossRef] [Green Version]
- Seed, A.W. A Dynamic and Spatial Scaling Approach to Advection Forecasting. J. Appl. Meteorol. 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Sokol, Z.; Kitzmiller, D.; Pesice, P.; Mejsnar, J. Comparison of precipitation nowcasting by extrapolation and statistical-advection methods. Atmos. Res. 2013, 123, 17–30. [Google Scholar] [CrossRef]
- Simonin, D.; Pierce, C.E.; Roberts, N.; Ballard, S.P.; Li, Z. Performance of Met Office hourly cycling NWP-based nowcasting for precipitation forecasts. Q. J. R. Meteorol. Soc. 2017, 143, 2862–2873. [Google Scholar] [CrossRef]
- Seed, A.W.; Pierce, C.E.; Norman, K. Formulation and evaluation of a scale decomposition-based stochastic precipitation nowcast scheme. Water Resour. Res. 2013, 49, 6624–6641. [Google Scholar] [CrossRef] [Green Version]
- Rico-Ramirez, M.A.; Liguori, S.; Schellart, A.N.A. Quantifying radar-rainfall uncertainties in urban drainage flow modelling. J. Hydrol. 2015, 528, 17–28. [Google Scholar] [CrossRef]
- Olsson, J.; Lindström, G. Evaluation and calibration of operational hydrological ensemble forecasts in Sweden. J. Hydrol. 2008, 350, 14–24. [Google Scholar] [CrossRef]
- Met Office 1 km Resolution UK Composite Rainfall Data from the Met Office Nimrod System [WWW Document]. NCAS British Atmospheric Data Centre. Available online: http://catalogue.ceda.ac.uk/uuid/27dd6ffba67f667a18c62de5c3456350 (accessed on 3 April 2017).
- Harrison, D.L.; Kitchen, M.; Scovell, R.W. High-resolution precipitation estimates for hydrological uses. Proc. ICE Water Manag. 2009, 162, 125–135. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Ciach, G.J. Towards Probabilistic Quantitative Precipitation WSR-88D Algorithms: Preliminary Studies and Problem Formulation; Final Report for the Office of Hydrologic Development; National Oceanic and Atmospheric Administration National Weather Service: Washington, DC, USA, 2003; Volume 59.
- Kitchen, M.; Blackall, R.M. Representativeness errors in comparisons between radar and gauge measurements of rainfall. J. Hydrol. 1992, 134, 13–33. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A. Quantitative assessment of short-term rainfall forecasts from radar nowcasts and MM5 forecasts. Hydrol. Process. 2012, 26, 3842–3857. [Google Scholar] [CrossRef]
- Liguori, S.; Rico-Ramirez, M.A. A practical approach to the assessment of probabilistic flow predictions. Hydrol. Process. 2013, 27, 18–32. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W. On the ROC score of probability forecasts. J. Clim. 2003, 16, 4145–4150. [Google Scholar] [CrossRef]
- Dai, Q.; Rico-Ramirez, M.A.; Han, D.; Islam, T.; Liguori, S. Probabilistic radar rainfall nowcasts using empirical and theoretical uncertainty models. Hydrol. Process. 2015, 29, 66–79. [Google Scholar] [CrossRef]
- Lewis, H.; Mittermaier, M.; Mylne, K.; Norman, K.; Scaife, A.; Neal, R.; Pierce, C.E.; Harrison, D.L.; Jewell, S.; Kendon, M.; et al. From months to minutes—Exploring the value of high-resolution rainfall observation and prediction during the UK winter storms of 2013/2014. Meteorol. Appl. 2015, 22, 90–104. [Google Scholar] [CrossRef]
- Panziera, L.; Germann, U.; Gabella, M.; Mandapaka, P.V. NORA-Nowcasting of Orographic Rainfall by means of analogues. Q. J. R. Meteorol. Soc. 2011, 137, 2106–2123. [Google Scholar] [CrossRef]
- Zappa, M.; Beven, K.; Bruen, M.; Cofino, A.S.; Kok, K.; Martin, E.; Nurmi, P.; Orfila, B.; Roulin, E.; Schroter, K.; et al. Propagation of uncertainty from observing systems and NWP into hydrological models: COST-731 Working Group 2. Atmos. Sci. Lett. 2010, 11, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Foresti, L.; Seed, A.W. On the spatial distribution of rainfall nowcasting errors due to orographic forcing. Meteorol. Appl. 2015, 22, 60–74. [Google Scholar] [CrossRef]
- Ordnance Survey. A Guide to Coordinate Systems in Great Britain V3.2. Available online: https://www.ordnancesurvey.co.uk/docs/support/guide-coordinate-systems-great-britain.pdf (accessed on 5 July 2018).
- Schellart, A.N.A.; Shepherd, W.J.; Saul, A.J. Influence of rainfall estimation error and spatial variability on sewer flow prediction at a small urban scale. Adv. Water Resour. 2012, 45, 65–75. [Google Scholar] [CrossRef]
- WaPUG Code of Practice for the Hydraulic Modelling of Sewer Systems; CIWEM: London, UK, 2002.
- Steiner, M.; Houze, R.A., Jr.; Yuter, S.E. Climatological characterization of three-dimensional storm structure from operational radar and rain gauge data. J. Appl. Meteorol. Climatol. 1995, 34, 1978–2007. [Google Scholar] [CrossRef]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. 2002, 128, 2145–2166. [Google Scholar] [CrossRef] [Green Version]
- Foresti, L.; Reyniers, M.; Seed, A.W.; Delobbe, L. Development and verification of a real-time stochastic precipitation nowcasting system for urban hydrology in Belgium. Hydrol. Earth Syst. Sci. 2016, 20, 505–527. [Google Scholar] [CrossRef] [Green Version]
- Foresti, L.; Nerini, D.; Sideris, I.; Besic, N.; Panziera, L.; Germann, U. Non-stationary radar precipitation ensembles: A stochastic nested generator and orographic precipitation growth and decay trends. Geophys. Res. Abstr. 2018, 20, 6739. [Google Scholar]

| Event Date | Starting Time | Duration (h) | Peak Flow (m3/s) | Max Average Rainfall (mm/h) | Storm Type |
|---|---|---|---|---|---|
| 29 April 2008 | 23:30 | 6.5 | 0.3974 | 5.344 | S |
| 30 April 2008 | 15:30 | 3.3 | 0.3477 | 8.511 | S |
| 12 May 2008 | 04:00 | 6 | 0.5582 | 4.117 | S |
| 26 June 2008 | 13:00 | 9 | 0.2869 | 11.426 | S |
| 7 July 2008 | 15:00 | 4 | 0.5024 | 7.144 | S |
| 29 July 2008 | 05:00 | 4 | 0.5826 | 6.444 | S |
| 1 August 2008 | 01:30 | 4.5 | 0.9904 | 8.073 | C |
| 20 August 2008 | 20:00 | 5 | 0.58 | 10.564 | S |
| 4 October 2008 | 15:00 | 13 | 0.3378 | 8.489 | S |
| 14 October 2008 | 15:00 | 5 | 0.2754 | 7.358 | C |
| 8 November 2008 | 20:00 | 5 | 0.2592 | 5.412 | S |
| 9 November 2008 | 13:30 | 7 | 0.563 | 18.41 | S |
| 13 December 2008 | 00:00 | 9 | 0.4551 | 1.813 | S |
| RMSE Mean (m3/s) | |||
|---|---|---|---|
| Event Date | Starting Time | Radar Ensembles | STEPS Ensembles |
| 7 July 2008 | 15:00 | 0.170 | 0.200 |
| 1 August 2008 | 02:30 | 0.405 | 0.430 |
| 1 August 2008 | 03:00 | 0.140 | 0.166 |
| 9 November 2008 | 14:00 | 0.287 | 0.169 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Codo, M.; Rico-Ramirez, M.A. Ensemble Radar-Based Rainfall Forecasts for Urban Hydrological Applications. Geosciences 2018, 8, 297. https://doi.org/10.3390/geosciences8080297
Codo M, Rico-Ramirez MA. Ensemble Radar-Based Rainfall Forecasts for Urban Hydrological Applications. Geosciences. 2018; 8(8):297. https://doi.org/10.3390/geosciences8080297
Chicago/Turabian StyleCodo, Mayra, and Miguel A. Rico-Ramirez. 2018. "Ensemble Radar-Based Rainfall Forecasts for Urban Hydrological Applications" Geosciences 8, no. 8: 297. https://doi.org/10.3390/geosciences8080297





