An Adaptive Command Scaling Method for Incremental Flight Control Allocation

Abstract

Modern aircraft usually employ control allocation to distribute virtual control commands among redundant effectors. Infeasible virtual command can occur frequently due to aggressive maneuvers and limited control authority. This paper proposes a lightweight command scaling law for incremental flight control allocation. The method scales the raw incremental virtual command by a direction-preserving gain $K\in$ [0,1]. It is updated via gradient descent on a Lyapunov function that balances allocation error against deviation from unity gain. The proposed adaptive update law ensures the convergence of K to a value that corresponds to the attainable portion of infeasible commands, independent of the specific allocator used. At the same time, feasible virtual commands will be preserved. Its performance was evaluated through open-loop ray sweeps of the attainable moment set and closed-loop INDI simulations for a yaw-limited eVTOL. The results demonstrate that the adaptive scaling gain closely approximates the linear programming ground truth while offering significantly higher computational efficiency. Furthermore, it effectively mitigates cross-axis coupling, reduces peak excursions, and alleviates rotor saturation. These findings highlight the method’s effectiveness, modularity, and suitability for real-time implementation in aerospace applications.

1. Introduction

Modern aircraft frequently employ over-actuation design, wherein the number of available control effectors exceeds the number of axes to be controlled. Particularly, novel configurations like electric vertical takeoff and landing (eVTOL) vehicles have many distributed electric propulsion units. This control redundancy offers benefits in flight performance and fault tolerance. It also necessitates a dedicated module, known as control allocation, to optimally distribute the desired motion commands to multiple effectors.

Control allocation serves as a modular component within the flight control architecture, receiving virtual commands (forces, moments, or accelerations) and translating them into physical commands for the redundant control effectors. This concept was developed in concert with feedback-linearization techniques like Nonlinear Dynamic Inversion (NDI) [1]. Within the past two decades, Incremental Nonlinear Dynamic Inversion (INDI) has gained tremendous popularity for its reduced sensitivity to model uncertainties and improved disturbance rejection [2]. It has been flight tested on different aircraft configurations [3,4,5]. One advantage of INDI is that it simplifies the allocation problem to a linear one through local linearization, enabling the use of efficient linear control allocators. A detailed review of control allocators can be found in many references such as Refs. [6,7]. Among these linear allocators, Moore–Penrose pseudo-inverse (PI)-based methods are widely used because they provide a closed-form solution and have a low and predictable computational footprint. These advantages make them highly suitable for real-time, safety-critical aerospace applications [8].

The physical capabilities of the effectors fundamentally limit the utility of any allocator. Actuators, rotors, and other control surfaces are subject to hard physical limitations on their positions and rates of movement, which define the Admissible Control Set (ACS). The mapping of this set through the control effectiveness matrix defines the Attainable Moment Set (AMS). Within an incremental control framework like INDI, these concepts correspond to an Admissible Set of Incremental Control and an Attainable Set of Incremental Moment. For clarity, this paper will use the terms ACS and AMS, while noting the distinction between absolute and incremental contexts. When a virtual command lies inside the AMS, it is feasible and can be realized to a large extent by pseudo-inverse methods such as redistributed pseudo-inverse. However, when a command lies beyond the AMS, it is infeasible, and no allocator can precisely achieve it. Such infeasible commands can arise from aggressive pilot inputs, strong external disturbances, system failures, or operation at the edges of the flight envelope [1]. It has been shown that when the (redistributed) pseudo-inverse allocators are used, these infeasible commands might cause significant allocation errors in magnitude and direction, leading to control saturation, degraded tracking performance, and compromised handling qualities [3,9].

Various methods have been proposed to address the issue of infeasible commands. Direct allocation techniques determine the intersection of the desired command vector with the boundary of the AMS, effectively scaling the command back to the boundary. While this approach preserves the intended command direction, it can be computationally intensive, as it requires either online geometric calculations or solving a linear programming problem [1,6,10]. Another strategy involves precomputing the AMS offline and storing it in lookup tables for onboard command limiting [11]. However, this method demands significant memory resources and lacks robustness against unexpected changes in the AMS. Approximation of AMS has also been suggested. For example, Ref. [12] approximated the AMS of a launch vehicle with elliptically constrained vectored nozzles using an internal ellipsoid. However, this approach is unsuitable for general flight control allocation scenarios with box control sets, and the internal ellipsoidal approximation might deviate significantly from the true AMS boundary. Finally, indirect methods have also been proposed, which focus on modifying the upstream reference model or controller state to address infeasible commands. A notable example is the pseudo control hedging (PCH) approach [13,14], which feeds back the allocation error into the reference model to effectively “slow down” the virtual command. While this method can mitigate allocation errors, it has certain limitations. Studies [14,15] have shown that PCH may not always protect against actuator dynamics and saturation. Moreover, it introduces complex coupling between the reference model and the error controller, which can distort the original command signal.

Therefore, there remains a need for gracefully handling infeasible commands without heavy online computation, a large database, or modifying upstream controller signals. In this work, we propose an adaptive command scaling approach that augments computationally efficient pseudo-inverse-based allocators. This method applies a scalar gain between 0 and 1 to the incremental virtual command, preserving the command’s original direction. The gain is governed by an adaptive law that ensures stability of both the allocation error and the gain itself. Intuitively, when a persistent allocation error is detected, the gain decreases, scaling down the infeasible command until it enters the feasible region. A recovery term is simultaneously included in the adaptive law to drive the gain back toward unity, preventing overly aggressive command suppression when the command is actually feasible.

The primary contribution of this paper is a novel command scaling algorithm applied to the incremental virtual command. This approach provides a stable allocation error mitigation strategy that operates within the control allocation module, preserving the integrity of upstream controller signals. The combination of the adaptive law and the recovery term provides a tradeoff between the instantaneous clipping of infeasible commands and the preservation of feasible ones. Most importantly, the algorithm is a pure algebraic process that involves no online optimization or iterative computation, making it ideal for real-time implementation.

The remainder of this paper is outlined as follows: In Section 2 we present the preliminaries of incremental control allocation and introduce the eVTOL aircraft model used as a case study. This is followed by the derivation of the adaptive scaling law and the algorithm in Section 3. A stability analysis of the INDI closed-loop under model uncertainties and allocation error appears in Section 4. Validation of the proposed method at both the control allocation level (Section 5) and within a closed-loop INDI system (Section 6) is carried out using the eVTOL example. Finally, Section 7 and Section 8 discuss the validation results, research limitations, and directions for future work.

2. Preliminaries

This section presents the foundational concepts of incremental nonlinear dynamic inversion control laws and incremental control allocation. Subsequently, an eVTOL platform is introduced as a testbed for analysis. In particular, its incremental ACS and AMS are investigated in detail.

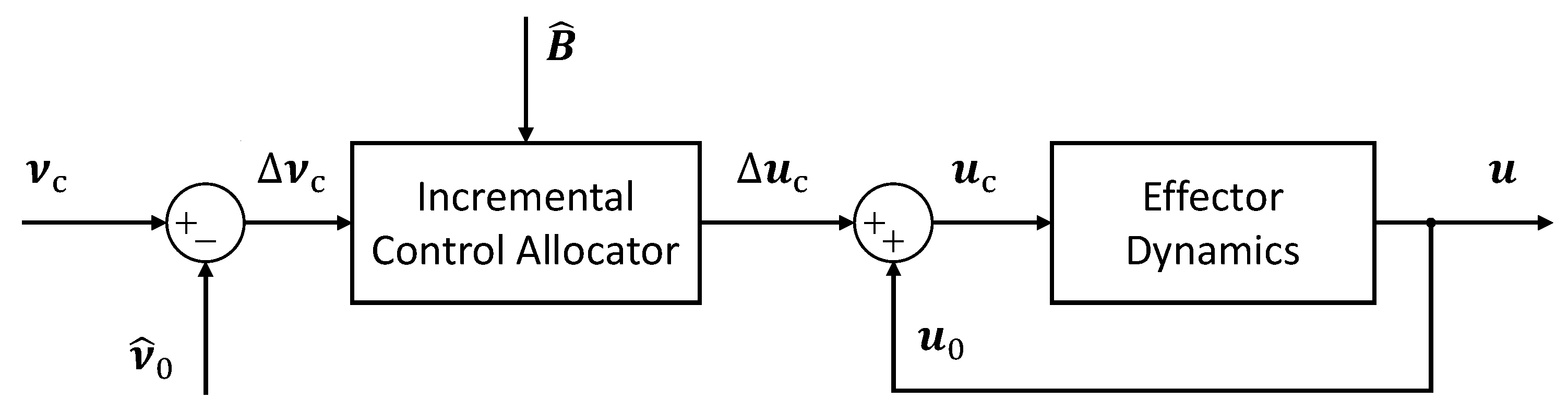
2.1. Incremental Nonlinear Dynamic Inversion Control

Consider the control-affine system with full relative degree and input–output linearization:

$${\mathit{y}}^{\left(\rho \right)}=\mathit{\alpha }\left(\mathit{x}\right)+\mathit{B}\left(\mathit{x}\right)\mathit{u},\mathit{y}\in {\mathbb{R}}^p,\mathit{u}\in {\mathbb{R}}^m,$$

(1)

where $\mathit{x}\in {\mathbb{R}}^n$ is the state vector, $\mathit{u}\in {\mathbb{R}}^m$ is the input vector, $\mathit{y}\in {\mathbb{R}}^p$ is the output vector, ${\mathit{y}}^{\left(\rho \right)}$ is the “virtual output” denoted by $\mathit{\nu }$, $\mathit{\alpha }\left(\mathit{x}\right)$ is the nonlinear term, and $\mathit{B}$ is the control effectiveness. In the INDI law, we linearize Equation (1) around $({\mathit{x}}_0,{\mathit{u}}_0)$ and obtain

$$\mathit{\nu }={\mathit{\nu }}_0+\mathit{B}\left({\mathit{x}}_0\right)\mathrm{\Delta }\mathit{u}+\delta (\mathit{x},\mathrm{\Delta }t),{\mathit{\nu }}_0:=\mathit{\alpha }\left({\mathit{x}}_0\right)+\mathit{B}\left({\mathit{x}}_0\right){\mathit{u}}_0,$$

(2)

where $\mathrm{\Delta }\mathit{u}=\mathit{u}-{\mathit{u}}_0$ is the incremental input, ${\mathit{\nu }}_0$ is the current “virtual control” (usually its estimation ${\widehat{\mathit{\nu }}}_0$ is used), and $\delta (\mathit{x},\mathrm{\Delta }t)$ captures truncation and unmodeled dynamics. With a desired virtual control command ${\mathit{\nu }}_c$ from the outer-loop, the desired incremental virtual control is

$$\mathrm{\Delta }{\mathit{\nu }}_c:={\mathit{\nu }}_c-{\widehat{\mathit{\nu }}}_0.$$

(3)

The control allocator receives the virtual command in Equation (3) and returns an admissible input increment. The relationship is governed by the linear equation

$$\mathrm{\Delta }{\mathit{\nu }}_c=\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c,$$

(4)

where $\widehat{\mathit{B}}$ is the estimated control effectiveness. As illustrated in Figure 1, this input increment $\mathrm{\Delta }{\mathit{u}}_c$ is then added to the measurement or estimation of current input value ${\mathit{u}}_0$ to form the final input command:

$${\mathit{u}}_c=\mathrm{\Delta }{\mathit{u}}_c+{\mathit{u}}_0.$$

(5)

The mathematical problem of determining this increment $\mathrm{\Delta }{\mathit{u}}_c$ is formulated as

$$minJ\left(\mathrm{\Delta }{\mathit{u}}_c\right)\mathrm{subject}\mathrm{to}\mathrm{\Delta }{\mathit{\nu }}_c=\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c\mathrm{and}\mathrm{\Delta }{\mathit{u}}_c\in S\left(\mathrm{\Delta }\mathit{u}\right),$$

(6)

where J is the secondary goal, $S\left(\mathrm{\Delta }\mathit{u}\right)$ is the set of admissible control increments. The most widely used solution is the Moore–Penrose pseudo-inverse (PI). It provides a closed-form solution that minimizes the 2-norm of $\mathrm{\Delta }{\mathit{u}}_c$:

$$\mathrm{\Delta }{\mathit{u}}_c={\widehat{\mathit{B}}}^{†}\mathrm{\Delta }{\mathit{\nu }}_c={\widehat{\mathit{B}}}^T{(\widehat{\mathit{B}}{\widehat{\mathit{B}}}^T)}^{-1}\mathrm{\Delta }{\mathit{\nu }}_c.$$

(7)

In this paper, the pseudo-inverse is computed using the MATLAB 2023b pinv function [16], which is based on a singular value decomposition. This implementation includes a protection mechanism for ill-conditioned matrices: singular values less than or equal to a specified tolerance are treated as zero when forming the pseudo-inverse.

Since control limits are not explicitly considered in the basic PI solution, iterative schemes such as the Redistributed Pseudo-Inverse (RPI) or Cascaded Generalized Inverse (CGI) have been developed. These methods handle saturation by iteratively calculating the allocation error resulting from saturated effectors and redistributing this error among the remaining unsaturated effectors. Details of these algorithms can be found in Refs. [1,6].

A distinct problem in incremental allocation is path dependency. Since the absolute effector position at any time is the sum of all previous increments, the control configuration can drift over time to suboptimal positions (e.g., positions that induce high drag). This issue can be managed by utilizing the null space of the control effectiveness matrix, $\aleph \left(\widehat{\mathit{B}}\right)$. An increment component from the null space, $\mathrm{\Delta }{\mathit{u}}_{null}$, can be added to the solution since $\widehat{\mathit{B}}(\mathrm{\Delta }{\mathit{u}}_c+\mathrm{\Delta }{\mathit{u}}_{null})=\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c$. This allows the allocator to restore the absolute effector positions toward preferred values without altering the achieved virtual command increment. This paper adopts the null space update strategy given in Ref. [17] to reduce the following secondary objective

$$J=\parallel \mathrm{\Delta }{\mathit{u}}_c-\mathrm{\Delta }{\mathit{u}}_{des}{\parallel }_2.$$

(8)

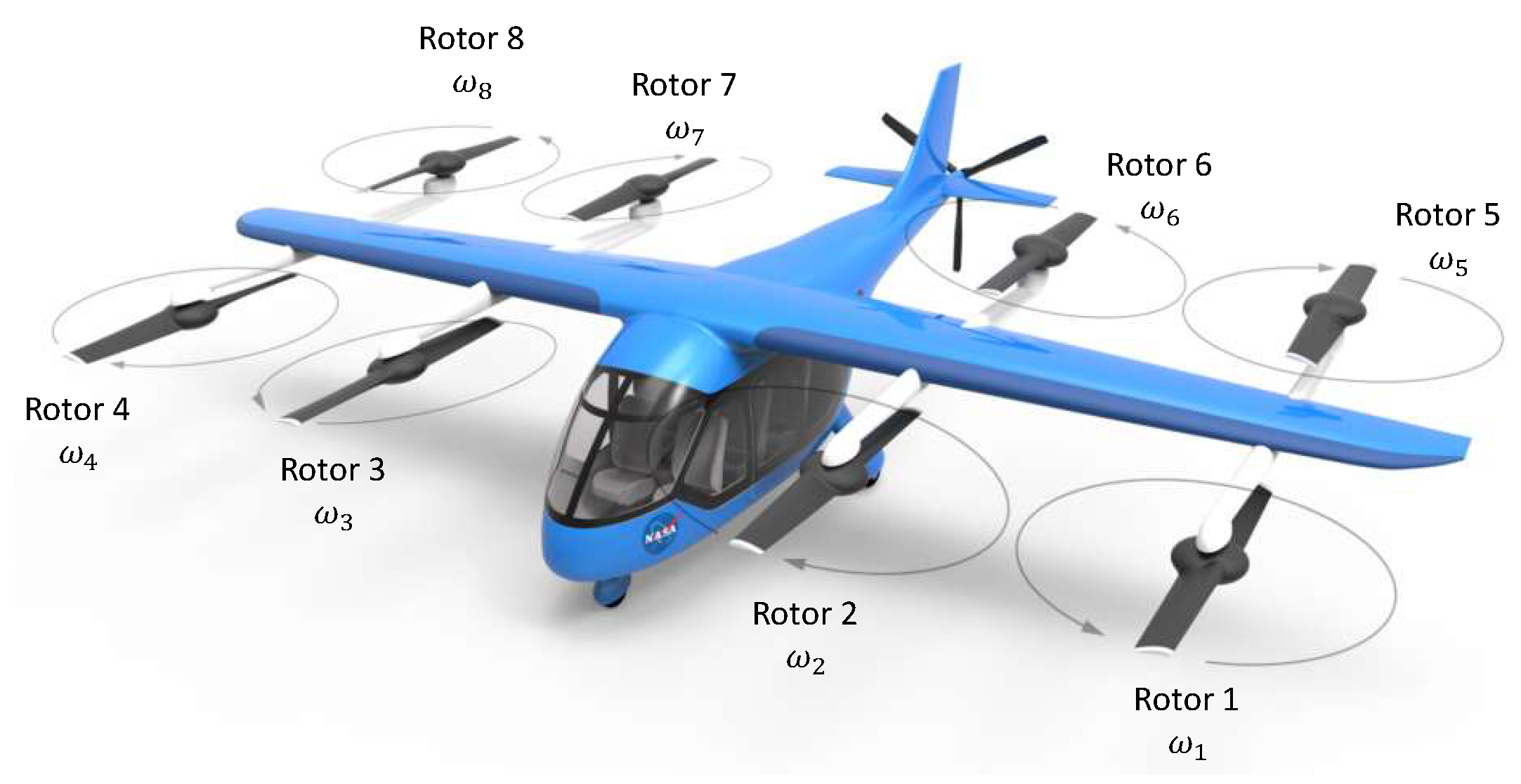
2.2. EVTOL Example

This paper focuses on an exemplary lift-plus-cruise eVTOL aircraft developed by NASA [18], as shown in Figure 2. Specifically, we consider the hover condition where the pusher propeller is idle and aerodynamic surfaces are ineffective. Attitude control is provided solely by eight lift rotors. Based on the standard thrust/torque-speed quadratic model, we define the control vector as the squared rotor speeds normalized by their maximum value:

$$\mathit{u}={\left[{\displaystyle \frac{{\omega }_1^2}{{\omega }_{\max }^2}},{\displaystyle \frac{{\omega }_2^2}{{\omega }_{\max }^2}},\dots ,{\displaystyle \frac{{\omega }_8^2}{{\omega }_{\max }^2}}\right]}^{\top },$$

(9)

where ${\omega }_i$ is the i-th rotor speed, and ${\omega }_{\max }$ is the maximum rotor speed. The properties of rotor dynamics are taken from the NASA eVTOL model [19] and listed in

Table 1. Aircraft and Rotor properties.

Property	Value	Unit
Total mass	2563	$\mathrm{kg}$
Wing area	17.28	${\mathrm{m}}^2$
Wing span	14.48	$\mathrm{m}$
Maximum speed ${\omega }_{max}$	167	$\mathrm{rad}/\mathrm{s}$
Minimum speed ${\omega }_{min}$	10	$\mathrm{rad}/\mathrm{s}$
Maximum acceleration ${\dot{\omega }}_{max}$	100	$\mathrm{rad}/{\mathrm{s}}^2$
Rotor time constant $T_{\omega }$	0.0796	$\mathrm{s}$

.

The control effectiveness from $\mathit{u}$ to body-frame angular acceleration is

$$\mathit{B}={\displaystyle \frac{\partial {\left[\dot{p},\dot{q},\dot{r}\right]}^{\top }}{\partial \mathit{u}}},$$

(10)

and this effectiveness is assumed constant in hover flight:

$$\mathit{B}=\left[\begin{array}{cccccccc}2.4941& 1.0651& -0.8678& -2.4782& 2.5473& 1.0729& -1.2410& -2.5795\\ 0.3967& 0.4043& 0.4088& 0.3992& -0.3924& -0.3505& -0.3335& -0.3979\\ 0.0715& -0.1271& 0.1291& -0.0735& -0.0444& 0.1456& -0.1395& 0.0561\end{array}\right].$$

(11)

The incremental virtual command is $\mathrm{\Delta }\mathit{\nu }={[\mathrm{\Delta }\dot{p},\mathrm{\Delta }\dot{q},\mathrm{\Delta }\dot{r}]}^{\top }$.

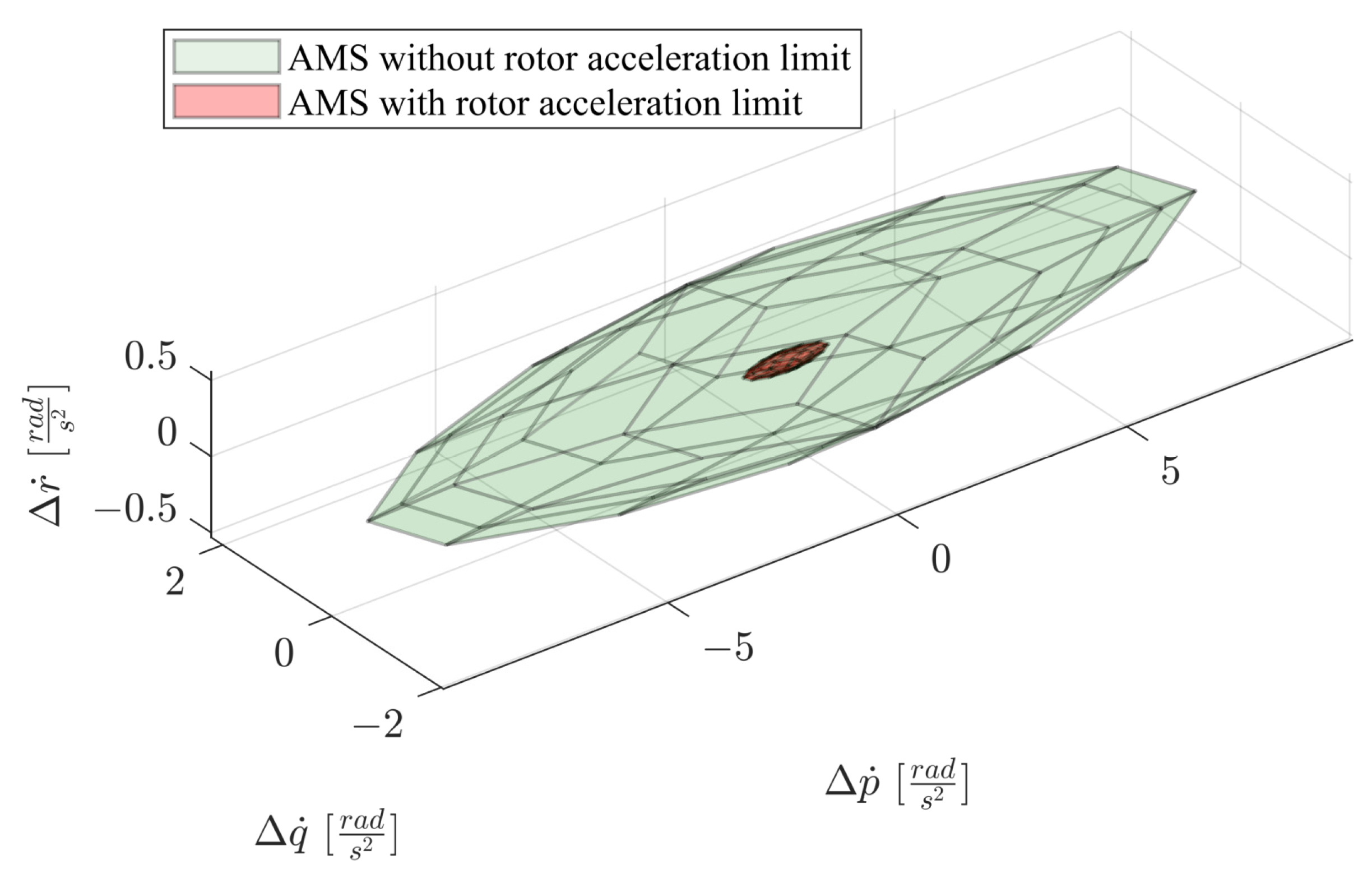
2.3. Incremental Control Set and Moment Set

In the incremental control framework, control allocation operates incrementally. This subsection discusses the admissible control set (ACS) and attainable moment set (AMS) of the eVTOL incremental control allocation.

Consider a first-order rotor dynamics model, which is a widely-used approximation in eVTOL rotor modeling [20,21]:

$$\dot{\omega }={\displaystyle \frac{1}{T_{\omega }}}\left({\omega }_c-\omega \right),$$

(12)

where $T_{\omega }$ is the time constant. The absolute and rate constraints on $\omega$ are

$${\omega }_{min}\le \omega \le {\omega }_{max},-{\dot{\omega }}_{max}\le \dot{\omega }\le {\dot{\omega }}_{max}.$$

(13)

For a step change in the rotor speed command ${\omega }_c=\omega +\mathrm{\Delta }{\omega }_c$, the peak physical rate occurs at $t=0^{+}$ and equals $\dot{\omega }={\displaystyle \frac{\mathrm{\Delta }{\omega }_c}{T_{\omega }}}$. Hence, the rate-safe command increment is

$$-{\dot{\omega }}_{max}{T}_{\omega }\le \mathrm{\Delta }{\omega }_c\le {\dot{\omega }}_{max}{T}_{\omega }.$$

(14)

Because the allocator works with squared rotor speed, $u={\omega }^2/{\omega }_{max}^2$, we need bounds on the incremental input command $\mathrm{\Delta }{u}_c\triangleq u_c-u$. Consider ${\omega }_c=\omega +\mathrm{\Delta }{\omega }_c$, and assume $\mathrm{\Delta }{\omega }_c$ is small, we can derive the following algebraic increment

$$\mathrm{\Delta }{u}_c={\displaystyle \frac{{(\omega +\mathrm{\Delta }{\omega }_c)}^2-{\omega }^2}{{\omega }_{max}^2}}={\displaystyle \frac{2\omega \mathrm{\Delta }{\omega }_c+{\left(\mathrm{\Delta }{\omega }_c\right)}^2}{{\omega }_{max}^2}}\approx {\displaystyle \frac{2\omega \mathrm{\Delta }{\omega }_c}{{\omega }_{max}^2}}.$$

(15)

This suggests that the allowable incremental input range depends on the current rotor speed:

$$-{\dot{\omega }}_{max}{T}_{\omega }{\displaystyle \frac{2\omega }{{\omega }_{max}^2}}\le \mathrm{\Delta }{u}_c\le {\dot{\omega }}_{max}{T}_{\omega }{\displaystyle \frac{2\omega }{{\omega }_{max}^2}}.$$

(16)

Intersected with the position limit, we obtain the admissible incremental move:

$$\mathrm{\Delta }{u}_c\in S\left(\mathrm{\Delta }u\right)=[max({\displaystyle \frac{{\omega }_{\min }^2}{{\omega }_{\max }^2}}-{\displaystyle \frac{{\omega }^2}{{\omega }_{\max }^2}},-{\dot{\omega }}_{max}{T}_{\omega }{\displaystyle \frac{2\omega }{{\omega }_{max}^2}}),min(1-{\displaystyle \frac{{\omega }^2}{{\omega }_{\max }^2}},{\dot{\omega }}_{max}{T}_{\omega }{\displaystyle \frac{2\omega }{{\omega }_{max}^2}})].$$

(17)

Let the nominal rotor speed be $\omega =90\mathrm{rad}/\mathrm{s}$ and consider rotor properties listed in Table 1. If the rotor acceleration constraint is neglected, the admissible incremental move for a single rotor at the operating point $\omega =90\mathrm{rad}/\mathrm{s}$ is

$$S\left(\mathrm{\Delta }u\right)=[{\displaystyle \frac{{\omega }_{\min }^2}{{\omega }_{\max }^2}}-{\displaystyle \frac{{\omega }^2}{{\omega }_{\max }^2}},1-{\displaystyle \frac{{\omega }^2}{{\omega }_{\max }^2}}]=\left[-0.2869,0.7096\right].$$

(18)

When the rotor acceleration bound is enforced via Equation (17), the admissible incremental move shrinks to

$$S\left(\mathrm{\Delta }u\right)=\left[-0.0514,0.0514\right],$$

(19)

which is about 5.1% of full-scale. For a given rotor state $({\omega }_1,\dots ,{\omega }_8)$, the corresponding incremental moment set is

$$\mathcal{M}=\{\mathrm{\Delta }\mathit{\nu }=\mathit{B}\mathrm{\Delta }\mathit{u}|\mathrm{\Delta }{u}_i\in S\left(\mathrm{\Delta }{u}_i\right)\forall i\}.$$

(20)

Figure 3 visualizes the images of (18) and (19) under the control effectiveness matrix $\mathit{B}$. The green polytope depicts the AMS without the acceleration constraint; the red polytope shows the AMS when the acceleration bound is active. The latter is drastically smaller, with a volume of only about $0.1\%$ of the former, which explains why incremental allocation saturates much more readily once rotor acceleration is constrained.

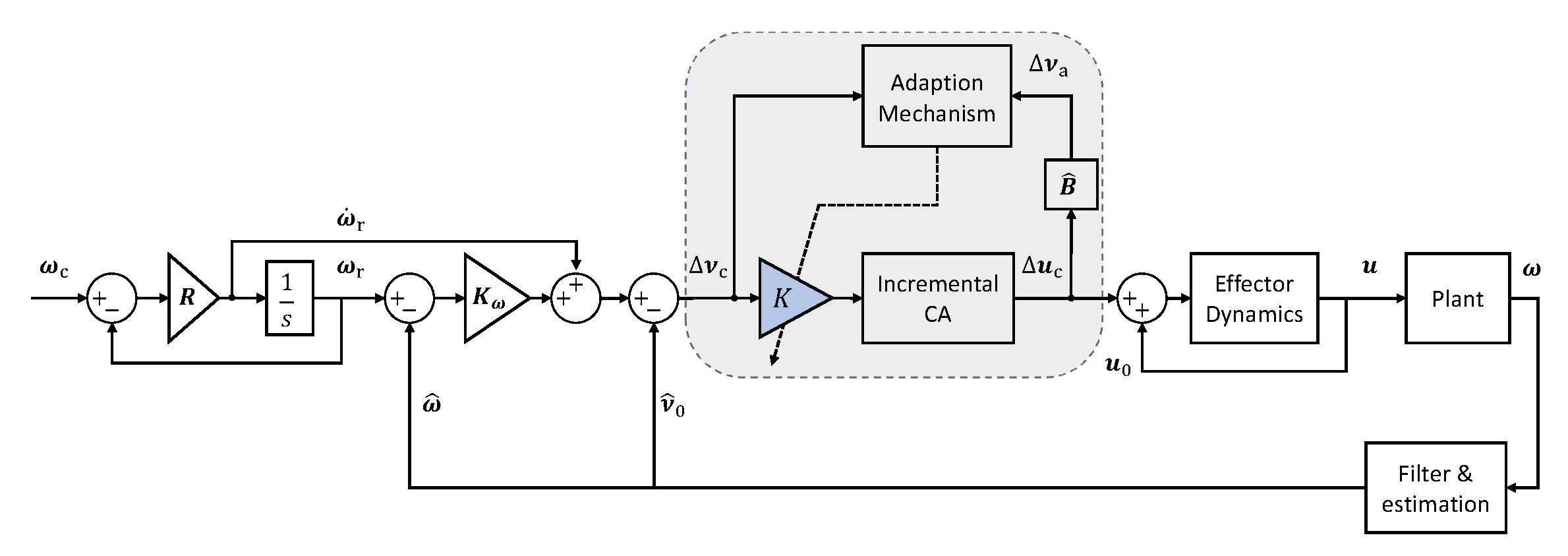
3. Adaptive Command Scaling Law

This section derives the adaptive command scaling law using the Lyapunov theory, and then presents a numerical algorithm design and implementation in simulation software.

3.1. Adaption Mechanism

Within the incremental allocation process, the achieved virtual control is $\mathrm{\Delta }{\mathit{\nu }}_a=\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c$, which might not match the command $\mathrm{\Delta }{\mathit{\nu }}_c$ due to incapability of the allocator or infeasible commands beyond the AMS. Our goal is to apply a scalar gain K to the incremental virtual command before it enters the allocator, as shown in Figure 4 and  Figure 5. This gain K is expected to achieve two goals:

• Scale down infeasible virtual commands to attainable level, as shown in the left subfigure of Figure 5;
• Preserve feasible virtual commands, as shown in the right subfigure of Figure 5.

Figure 4. Illustration of the incremental control allocation.

Figure 4. Illustration of the incremental control allocation.

Figure 5. Illustration of the scaling for infeasible (left) and feasible (right) commands. Red indicates the original command, and green indicates the scaled-down command.

Figure 5. Illustration of the scaling for infeasible (left) and feasible (right) commands. Red indicates the original command, and green indicates the scaled-down command.

An adaption mechanism for this scaling gain is derived in the following.

The raw allocation error between the raw virtual command and achieved amount is defined as

$${\mathit{e}}_{\nu 0}=\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a.$$

(21)

With a scaled command, the allocation error becomes

$${\mathit{e}}_{\nu }\left(K\right)=\mathrm{\Delta }{\mathit{\nu }}_s-\mathrm{\Delta }{\mathit{\nu }}_a=K\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a.$$

(22)

Choose the scalar Lyapunov candidate:

$$V\left(K\right)=\frac{1}{2}{\displaystyle \frac{\parallel {\mathit{e}}_{\nu }{\left(K\right)\parallel }^2}{\parallel \mathrm{\Delta }{\mathit{\nu }}_c{\parallel }^2}}+\frac{\lambda }{2}{(K-1)}^2,\lambda >0.$$

(23)

In this Lyapunov function, the first term is a dimensionless allocation error and the second term is a restoring term for $K=1$ (no scaling). Because ${\mathit{e}}_{\nu }\left(K\right)$ is affine in K, $V\left(K\right)$ is a strictly convex quadratic. Its gradient with respect to K is

$${\displaystyle \frac{dV}{dK}}={\displaystyle \frac{\mathrm{\Delta }{\mathit{\nu }}_c^{\top }{\mathit{e}}_{\nu }\left(K\right)}{\parallel \mathrm{\Delta }{\mathit{\nu }}_c{\parallel }^2}}+\lambda (K-1)=s\left(K\right)+\lambda (K-1),$$

(24)

with the “ray-aligned” scalar

$$s\left(K\right)={\displaystyle \frac{\mathrm{\Delta }{\mathit{\nu }}_c^{\top }{\mathit{e}}_{\nu }\left(K\right)}{\parallel \mathrm{\Delta }{\mathit{\nu }}_c{\parallel }^2}}=K-\rho ,\rho :={\displaystyle \frac{\mathrm{\Delta }{\mathit{\nu }}_c^{\top }\mathrm{\Delta }{\mathit{\nu }}_a}{\parallel \mathrm{\Delta }{\mathit{\nu }}_c{\parallel }^2}}.$$

(25)

The scalar $\rho$ intuitively denotes the fraction of $\mathrm{\Delta }{\mathit{\nu }}_c$ achieved along its own direction. We design the update law to move K in the direction that most rapidly decreases V. The updating law takes the form:

$$\dot{K}=-\gamma {\displaystyle \frac{dV}{dK}}=-\gamma \left[s\left(K\right)+\lambda (K-1)\right],\gamma >0.$$

(26)

This law enables a non-positive gradient of the Lyapunov function:

$$\dot{V}={\displaystyle \frac{dV}{dK}}\dot{K}=-\gamma {\left({\displaystyle \frac{dV}{dK}}\right)}^2\le 0.$$

(27)

Thus V is nonincreasing for any allocator, and the trajectories converge to the unique minimizer $K^{\ast }$ of V:

$${\displaystyle \frac{dV}{dK}}=0⟹(1+\lambda )K^{\ast }=\rho +\lambda ⟹K^{\ast }={\mathrm{\Pi }}_{[0,1]}\left({\displaystyle \frac{\rho +\lambda }{1+\lambda }}\right),$$

(28)

where ${\mathrm{\Pi }}_{[0,1]}$ means clipping to [0,1]. The dynamics of $K\left(t\right)$ in Equation (26) is rewritten as

$$\dot{K}=-\gamma (1+\lambda )K+\gamma (\rho +\lambda ).$$

(29)

Therefore, $K\left(t\right)$ converges to $K^{\ast }$ exponentially with rate $\gamma (1+\lambda )$. If the raw command is achievable along its ray $(\rho =1)$, then $K^{\ast }=1$ and $K\left(t\right)$ will rapidly snap back to 1. If the raw command is infeasible along that ray $(\rho <1)$, then $K^{\ast }$ is the weighted average between 1 and $\rho$ according to Equation (28). Larger $\lambda$ biases toward 1, smaller $\lambda$ adheres more to the allocator’s actual fraction $\rho$, therefore, $\lambda$ is a weighting between two contradictory goals of scaling down and restoring the command.

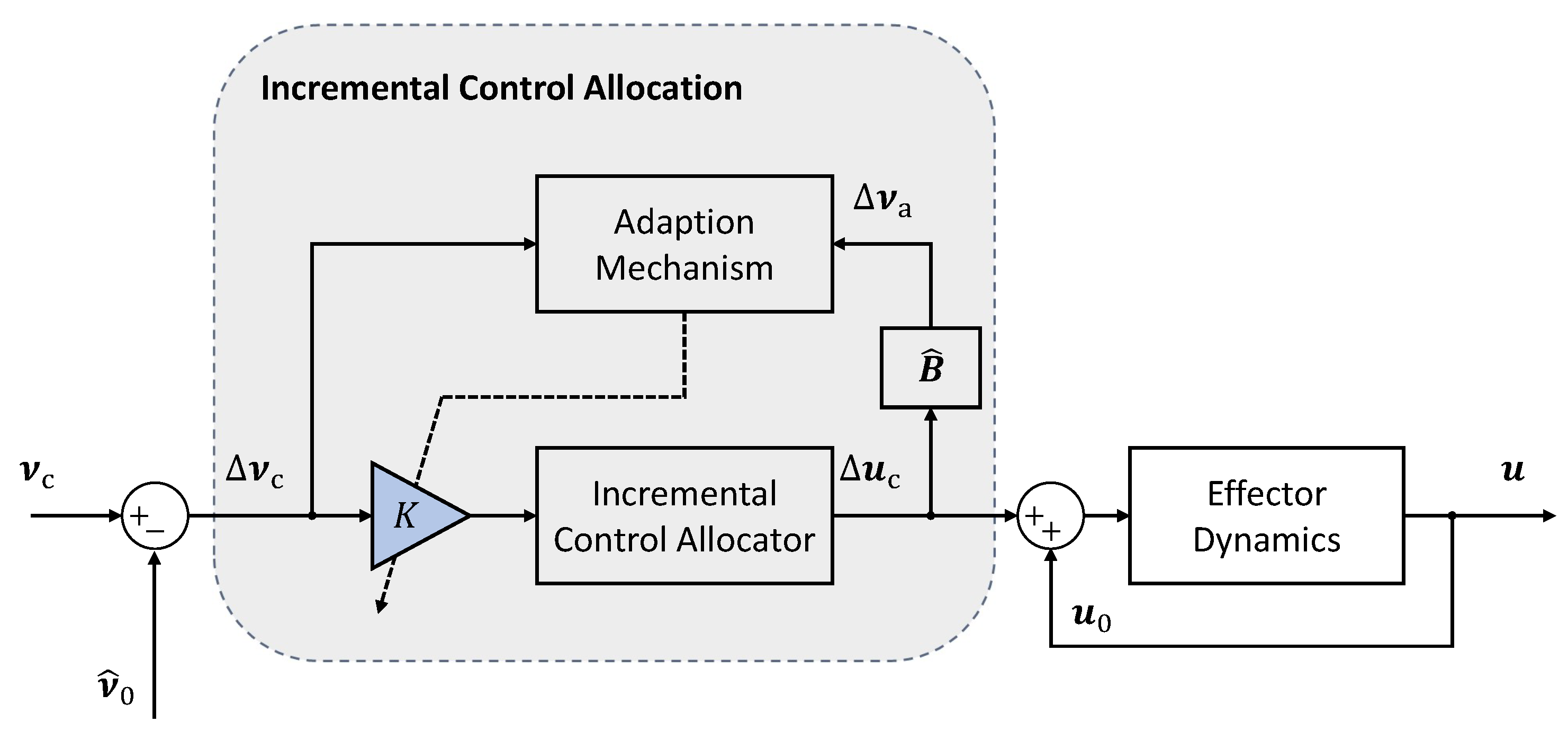
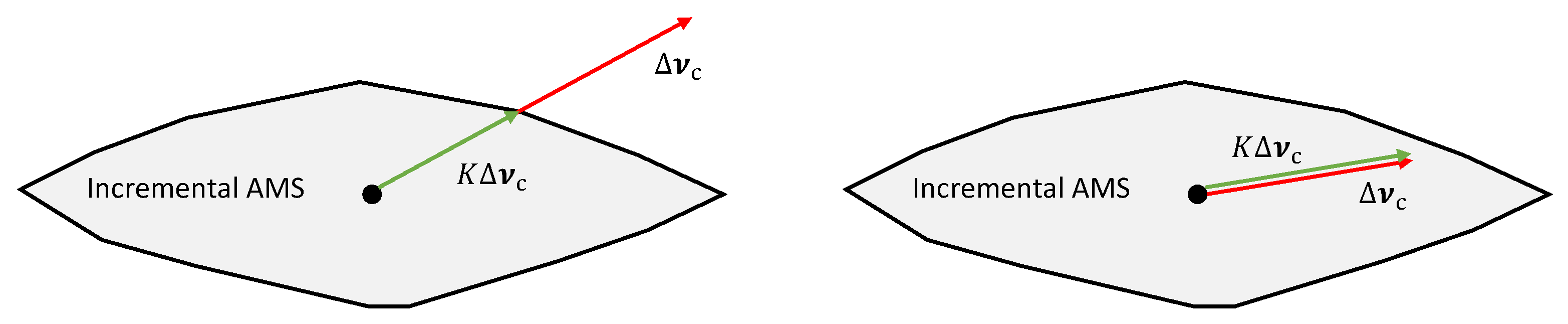
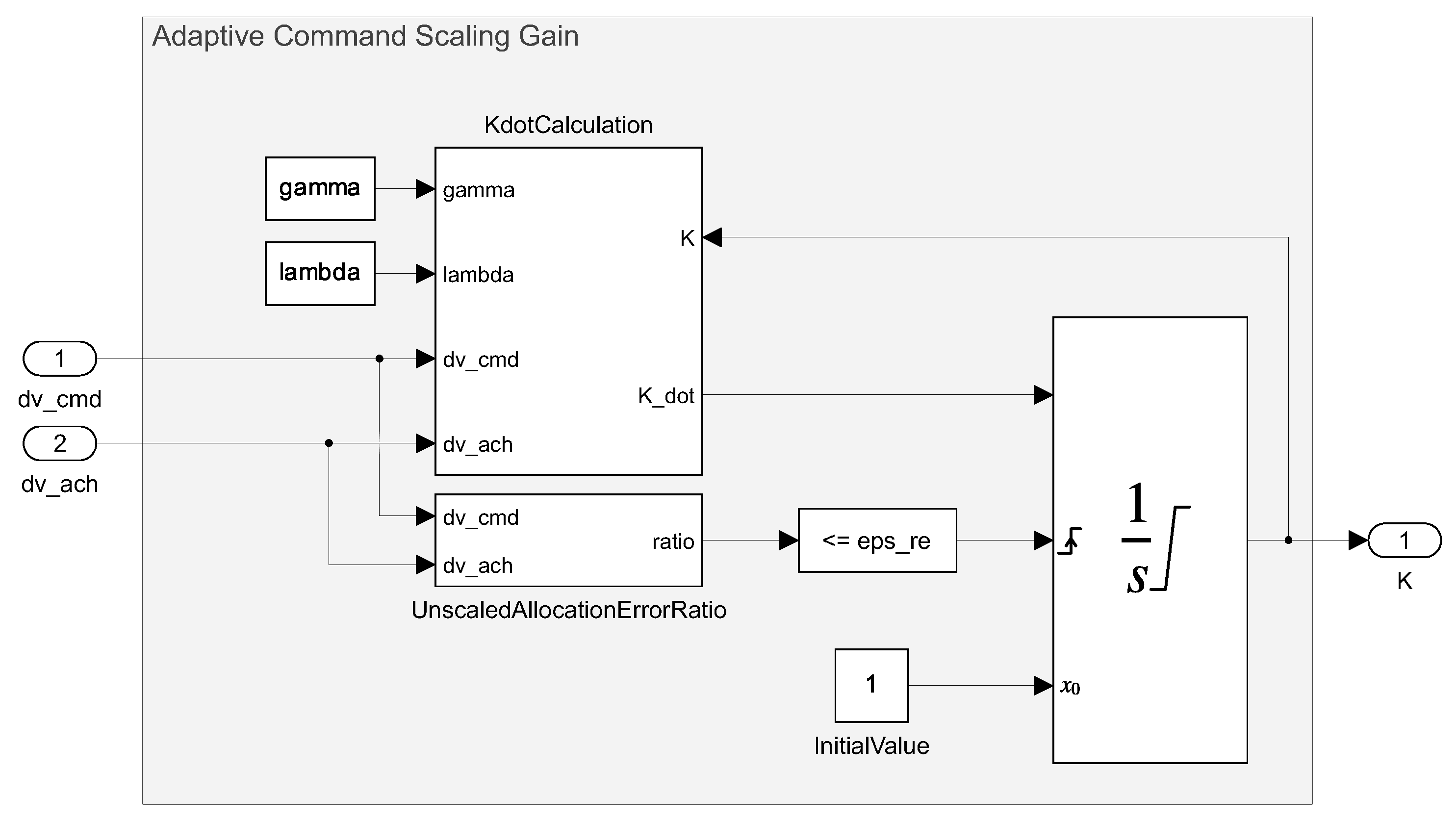
3.2. Algorithm Design

A pseudocode of the adaptive command scaling law is summarized in Algorithm 1.

In line five of Algorithm 1, the scalar gain K is updated using the forward-Euler integration scheme. This method can be substituted with other suitable numerical integration techniques if desired. Line six ensures that the gain is constrained within the range [0,1] through a simple clipping operation. The adaptation law includes a persistent “restoring force”, ensuring the gain value does not remain stuck at zero. To prevent nullifying commands entirely, the lower limit of K can be set to a small positive value. Lines 9–11 introduce an optional reset mechanism for the integrator. This mechanism activates when the actual allocation error becomes negligible. Figure 6 illustrates the integrator structure, which can guide implementation in simulation tools like Simulink [22].

Algorithm 1. Adaptive Scalar Command Scaling (single control tick)
Require: $\mathrm{\Delta }{\mathit{\nu }}_c\in {\mathbb{R}}^n$ (raw command), $\mathrm{\Delta }{\mathit{\nu }}_a\in {\mathbb{R}}^n$ (achieved by the allocator), $K\in$ [0,1]
(current gain), $\gamma >0$, $\lambda >0$, controller sample time $\mathrm{\Delta }t>0$, (optional) reset threshold
${\epsilon }_{re}\in$ (0,1), tiny positive tolerance ${\epsilon }_{tol}$ (e.g., 1 × 10−10)
Ensure: Updated $K\in$ [0,1]
1:	$\mathrm{den}\leftarrow max\left({\epsilon }_{tol},\mathrm{\Delta }{\mathit{\nu }}_c^{\top }\mathrm{\Delta }{\mathit{\nu }}_c\right)$
2:	${\mathit{e}}_{\nu }\leftarrow K\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a$	{scaled residual}
3:	$s\leftarrow {\displaystyle \frac{\mathrm{\Delta }{\mathit{\nu }}_c^{\top }{\mathit{e}}_{\nu }}{\mathrm{den}}}$
4:	$\dot{K}\leftarrow -\gamma s+\gamma \lambda (1-K)$
5:	$K\leftarrow K+\mathrm{\Delta }t\dot{K}$
6:	$K\leftarrow min\left(1,max(0,K)\right)$	{project to [0,1]}
7:	${\mathit{e}}_{\nu 0}\leftarrow \mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a$	{unscaled residual for reset}
8:	$\mathrm{ratio}\leftarrow {\displaystyle \frac{\parallel {\mathit{e}}_{\nu 0}\parallel }{\sqrt{\mathrm{den}}}}$
9:	if$\mathrm{ratio}\le {\epsilon }_{re}$   then
10:	$K\leftarrow 1$	{reset when raw command is feasible}
11:	end if
12:	return  K

4. Closed-Loop Stability

This section analyzes the closed-loop stability of the INDI control system in the presence of model uncertainties and the command scaling mechanism.

4.1. Virtual Output Under Uncertainty and Allocation Error

We explicitly consider two sources of uncertainty:

(1)

The estimated control effectiveness matrix $\widehat{\mathit{B}}$ may differ from the true effectiveness $\mathit{B}$.

(2)

The current virtual control is measured or estimated with error

$$\delta \left({\mathit{\nu }}_0\right):={\mathit{\nu }}_0-{\widehat{\mathit{\nu }}}_0,$$

(30)

where ${\mathit{\nu }}_0$ is the true virtual control at the linearization point and ${\widehat{\mathit{\nu }}}_0$ is its estimate.

According to the linearization Equation (2), the true virtual output under the allocated increment $\mathrm{\Delta }{\mathit{u}}_c$ is

$$\mathit{\nu }={\mathit{\nu }}_0+\mathit{B}\mathrm{\Delta }{\mathit{u}}_c+\delta (\mathit{x},\mathrm{\Delta }t).$$

(31)

Add and subtract $\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c$ and the estimated virtual control ${\widehat{\mathit{\nu }}}_0$:

$$\begin{array}{cc}\hfill \mathit{\nu }& ={\widehat{\mathit{\nu }}}_0+\left({\mathit{\nu }}_0-{\widehat{\mathit{\nu }}}_0\right)+\widehat{\mathit{B}}\mathrm{\Delta }{\mathit{u}}_c+\left(\mathit{B}-\widehat{\mathit{B}}\right)\mathrm{\Delta }{\mathit{u}}_c+\delta (\mathit{x},\mathrm{\Delta }t)\hfill \\ \hfill & ={\widehat{\mathit{\nu }}}_0+\delta \left({\mathit{\nu }}_0\right)+\mathrm{\Delta }{\mathit{\nu }}_a+(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c+\delta (\mathit{x},\mathrm{\Delta }t).\hfill \end{array}$$

(32)

The commanded incremental virtual control defined in Equation (3) is $\mathrm{\Delta }{\mathit{\nu }}_c:={\mathit{\nu }}_c-{\widehat{\mathit{\nu }}}_0$. Substituting ${\widehat{\mathit{\nu }}}_0={\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_c$ into the expression for $\mathit{\nu }$ gives

$$\begin{array}{cc}\hfill \mathit{\nu }& =({\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_c)+\delta \left({\mathit{\nu }}_0\right)+\mathrm{\Delta }{\mathit{\nu }}_a+(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c+\delta (\mathit{x},\mathrm{\Delta }t)\hfill \\ \hfill & ={\mathit{\nu }}_c+\delta \left({\mathit{\nu }}_0\right)+\delta (\mathit{x},\mathrm{\Delta }t)+(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c-(\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a)\hfill \\ \hfill & ={\mathit{\nu }}_c+\delta \left({\mathit{\nu }}_0\right)+\delta (\mathit{x},\mathrm{\Delta }t)+(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c-{\mathit{e}}_{\nu 0}.\hfill \end{array}$$

(33)

Thus, the actual virtual output can be written as

$$\mathit{\nu }={\mathit{\nu }}_c+{ϵ}_{\mathrm{tot}},$$

(34)

where the total residual is

$${ϵ}_{\mathrm{tot}}:=\underset{\mathrm{current}\mathrm{virtual}\mathrm{control}\mathrm{error}}{\underbrace{\delta \left({\mathit{\nu }}_0\right)}}+\underset{\mathrm{linearization}\mathrm{error}}{\underbrace{\delta (\mathit{x},\mathrm{\Delta }t)}}+\underset{\mathrm{effectiveness}\mathrm{error}}{\underbrace{(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c}}\underset{\mathrm{allocation}\mathrm{error}}{\underbrace{-{\mathit{e}}_{\nu 0}}}.$$

(35)

The adaptive command-scaling law modifies the command passed to the allocator from $\mathrm{\Delta }{\mathit{\nu }}_c$ to a scaled version $K\mathrm{\Delta }{\mathit{\nu }}_c$. This only affects the achieved increment $\mathrm{\Delta }{\mathit{\nu }}_a$ and thus the raw allocation error ${\mathit{e}}_{\nu 0}=\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a$. Importantly, the structure (35) remains valid irrespective of the presence of command scaling; the adaptive gain K appears only implicitly through ${\mathit{e}}_{\nu 0}$.

4.2. Stability of Tracking Error Dynamics

We now consider the input–output linearized system in canonical “chains of integrators” form [23]:

$$\dot{\mathit{\xi }}={\mathit{A}}_c\mathit{\xi }+{\mathit{B}}_c\mathit{\nu },\mathit{y}=\mathit{C}\mathit{\xi },$$

(36)

where $\mathit{\xi }$ is built from $y_i,{\dot{y}}_i,\dots ,y_i^{({\rho }_i-1)}$, $i=1,2,\dots ,p$, and ${\mathit{A}}_c,{\mathit{B}}_c,\mathit{C}$ are block-diagonal matrices representing integrator chains. For each output channel i,

$${\dot{\xi }}_{i,1}={\xi }_{i,2},{\dot{\xi }}_{i,2}={\xi }_{i,3},\dots ,{\dot{\xi }}_{i,{\rho }_i}=y_i^{\left({\rho }_i\right)}={\alpha }_i\left(\mathit{x}\right)+\sum _{j=1}^m{B}_{ij}\left(\mathit{x}\right)u_j.$$

(37)

We want the state $\mathit{\xi }$ to track a reference trajectory built from the desired output ${\mathit{y}}_r$. The reference vector $\mathcal{R}$ collects $y_{r,i},{\dot{y}}_{r,i},\dots ,y_{r,i}^{({\rho }_i-1)},i=1,\dots ,p.$ Define the tracking error

$$\mathit{e}:=\mathit{\xi }-\mathcal{R}.$$

(38)

Differentiating,

$$\begin{array}{cc}\hfill \dot{\mathit{e}}& =\dot{\mathit{\xi }}-\dot{\mathcal{R}}={\mathit{A}}_c\mathit{\xi }+{\mathit{B}}_c\mathit{\nu }-\dot{\mathcal{R}}.\hfill \end{array}$$

(39)

Writing $\mathit{\xi }=\mathit{e}+\mathcal{R}$ and choosing the reference dynamics as

$$\dot{\mathcal{R}}={\mathit{A}}_c\mathcal{R}+{\mathit{B}}_c{\mathit{y}}_r^{\left(\rho \right)},{\mathit{y}}_r^{\left(\rho \right)}:={[y_{r,1}^{({\rho }_1)},\dots ,y_{r,p}^{({\rho }_p)}]}^{\top },$$

(40)

we obtain

$$\begin{array}{cc}\hfill \dot{\mathit{e}}& ={\mathit{A}}_c(\mathit{e}+\mathcal{R})+{\mathit{B}}_c\mathit{\nu }-\left({\mathit{A}}_c\mathcal{R}+{\mathit{B}}_c{\mathit{y}}_r^{\left(\rho \right)}\right)\hfill \\ \hfill & ={\mathit{A}}_c\mathit{e}+{\mathit{B}}_c\left(\mathit{\nu }-{\mathit{y}}_r^{\left(\rho \right)}\right).\hfill \end{array}$$

(41)

We now close the loop by specifying the virtual control law. To avoid notational conflict with the command-scaling gain K, we denote the outer-loop feedback matrix by $\mathit{F}\in {\mathbb{R}}^{p\times p}$. The INDI virtual control is chosen as

$${\mathit{\nu }}_c={\mathit{y}}_r^{\left(\rho \right)}-\mathit{F}\mathit{e},$$

(42)

where $\mathit{F}$ is designed such that the nominal matrix ${\mathit{A}}_c-{\mathit{B}}_c\mathit{F}$ is Hurwitz. Substituting $\mathit{\nu }={\mathit{\nu }}_c+{ϵ}_{\mathrm{tot}}$ and (42) into (41) yields

$$\begin{array}{cc}\hfill \dot{\mathit{e}}& ={\mathit{A}}_c\mathit{e}+{\mathit{B}}_c\left({\mathit{\nu }}_c+{ϵ}_{\mathrm{tot}}-{\mathit{y}}_r^{\left(\rho \right)}\right)\hfill \\ \hfill & ={\mathit{A}}_c\mathit{e}+{\mathit{B}}_c\left({\mathit{y}}_r^{\left(\rho \right)}-\mathit{F}\mathit{e}+{ϵ}_{\mathrm{tot}}-{\mathit{y}}_r^{\left(\rho \right)}\right)\hfill \\ \hfill & =({\mathit{A}}_c-{\mathit{B}}_c\mathit{F})\mathit{e}+{\mathit{B}}_c{ϵ}_{\mathrm{tot}}.\hfill \end{array}$$

(43)

Thus, the adaptive command scaling and all modeling or estimation errors enter the tracking error dynamics only through the additive disturbance ${ϵ}_{\mathrm{tot}}$ defined in (35).

Since ${\mathit{A}}_c-{\mathit{B}}_c\mathit{F}$ is Hurwitz, there exist symmetric positive definite matrices $\mathit{P}$ and $\mathit{Q}$ satisfying the Lyapunov equation

$${({\mathit{A}}_c-{\mathit{B}}_c\mathit{F})}^{\top }\mathit{P}+\mathit{P}({\mathit{A}}_c-{\mathit{B}}_c\mathit{F})=-\mathit{Q}.$$

(44)

Consider the Lyapunov function

$$V\left(\mathit{e}\right)={\mathit{e}}^{\top }\mathit{P}\mathit{e}.$$

(45)

Along the trajectories of (43),

$$\begin{array}{cc}\hfill \dot{V}& ={\mathit{e}}^{\top }\left[{({\mathit{A}}_c-{\mathit{B}}_c\mathit{F})}^{\top }\mathit{P}+\mathit{P}({\mathit{A}}_c-{\mathit{B}}_c\mathit{F})\right]\mathit{e}+2{\mathit{e}}^{\top }\mathit{P}{\mathit{B}}_c{ϵ}_{\mathrm{tot}}\hfill \\ \hfill & =-{\mathit{e}}^{\top }\mathit{Q}\mathit{e}+2{\mathit{e}}^{\top }\mathit{P}{\mathit{B}}_c{ϵ}_{\mathrm{tot}}.\hfill \end{array}$$

(46)

Using Young’s inequality [24] (p. 49), for any $\eta >0$ we have

$$\begin{array}{cc}\hfill 2{\mathit{e}}^{\top }\mathit{P}{\mathit{B}}_c{ϵ}_{\mathrm{tot}}& \le 2\parallel \mathit{e}\parallel \parallel \mathit{P}{\mathit{B}}_c{ϵ}_{\mathrm{tot}}\parallel \le 2\parallel \mathit{e}\parallel \parallel \mathit{P}{\mathit{B}}_c\parallel \parallel {ϵ}_{\mathrm{tot}}\parallel \hfill \\ \hfill & \le {\eta \parallel \mathit{e}\parallel }^2+{\displaystyle \frac{\parallel \mathit{P}{\mathit{B}}_c{\parallel }^2}{\eta }}{\parallel {ϵ}_{\mathrm{tot}}\parallel }^2.\hfill \end{array}$$

(47)

Therefore, we have

$$\dot{V}\le -\left({\lambda }_{min}\left(\mathit{Q}\right)-\eta \right){\parallel \mathit{e}\parallel }^2+{\displaystyle \frac{\parallel \mathit{P}{\mathit{B}}_c{\parallel }^2}{\eta }}{\parallel {ϵ}_{\mathrm{tot}}\parallel }^2.$$

(48)

where ${\lambda }_{min}\left(\mathit{Q}\right)$ is the minimum eigenvalue of $\mathit{Q}$. Hence, according to Remark 2.4 in Ref. [25], the tracking error dynamics are input-to-state stable (ISS) with respect to the total residual ${ϵ}_{\mathrm{tot}}$. In the absence of uncertainties and allocation errors (${ϵ}_{\mathrm{tot}}\equiv 0$), the origin $\mathit{e}=\mathbf{0}$ is exponentially stable. For bounded ${ϵ}_{\mathrm{tot}}$, the tracking error remains bounded and ultimately enters a ball whose radius is proportional to ${sup}_t\parallel {ϵ}_{\mathrm{tot}}\left(t\right)\parallel$.

4.3. Effects of Uncertainty and Allocation Error

Equations (43) and (35) allow a clear interpretation of the individual contributions:

• Current virtual control error $\delta \left({\mathit{\nu }}_0\right)$: This term captures uncertainty or noise in the measurement or estimation of the current virtual control. In many INDI applications, ${\mathit{\nu }}_0$ is derived from high-pass or complementary filters, so this term is typically bounded.
• Linearization/model error $\delta (\mathit{x},\mathrm{\Delta }t)$: This term arises from the first-order Taylor expansion of the input–output map over one sampling interval. For sufficiently small sampling time and moderate state variations, $\delta (\mathit{x},\mathrm{\Delta }t)$ is small and bounded.
• Control-effectiveness error $(\mathit{B}-\widehat{\mathit{B}})\mathrm{\Delta }{\mathit{u}}_c$: This term represents a mismatch between the true control effectiveness and its estimate. Ref. [23] has proved that this term is bounded when the sampling frequency is sufficiently high and $\mathit{B}{\widehat{\mathit{B}}}^{-1}$ has a diagonally dominant structure.
• The focus of this paper is the allocation error term $-{\mathit{e}}_{\nu 0}$, which arises from input limits and the choice of control allocator. Unlike the other three residuals, ${\mathit{e}}_{\nu 0}$ can become large when the raw incremental command $\mathrm{\Delta }{\mathit{\nu }}_c$ lies near or outside the incremental admissible control set. The proposed adaptive command scaling law acts precisely on this term. When the raw command $\mathrm{\Delta }{\mathit{\nu }}_c$ is infeasible, K reduces the effective command magnitude so that the allocator operates in a valid region, thereby reducing the magnitude and direction errors between $\mathrm{\Delta }{\mathit{\nu }}_c$ and $\mathrm{\Delta }{\mathit{\nu }}_a$. This scaling tightens the ISS bound.

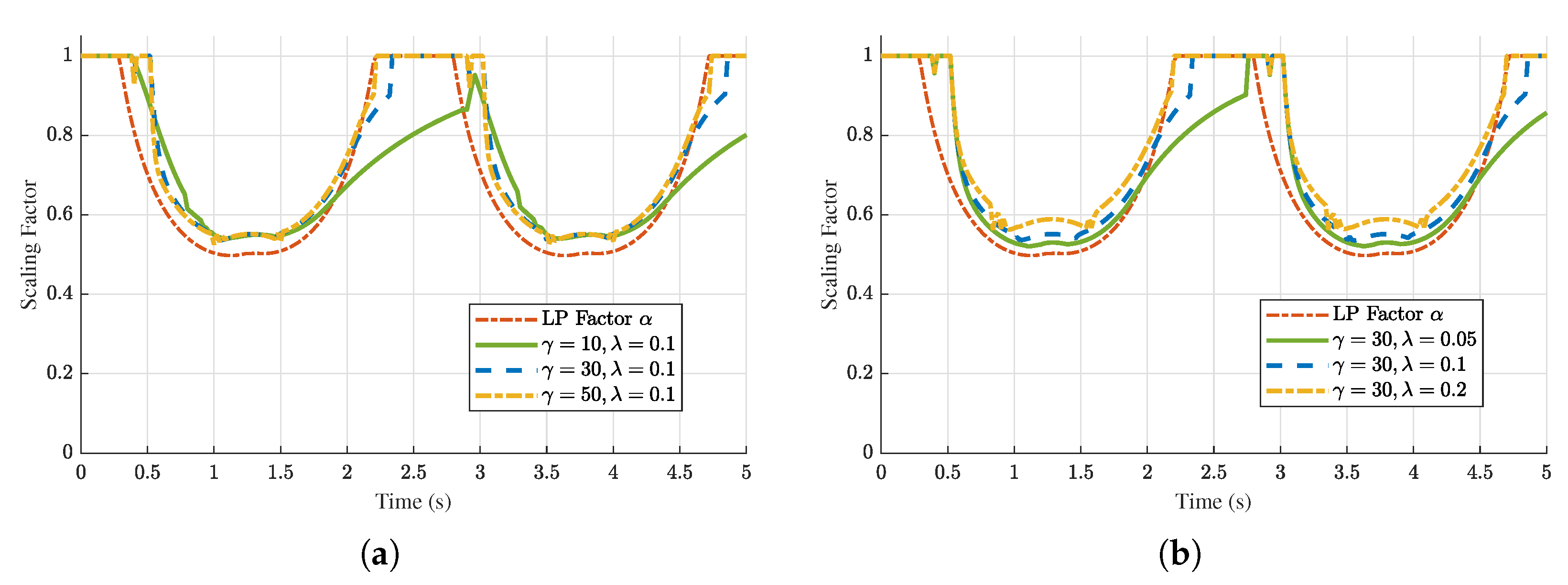
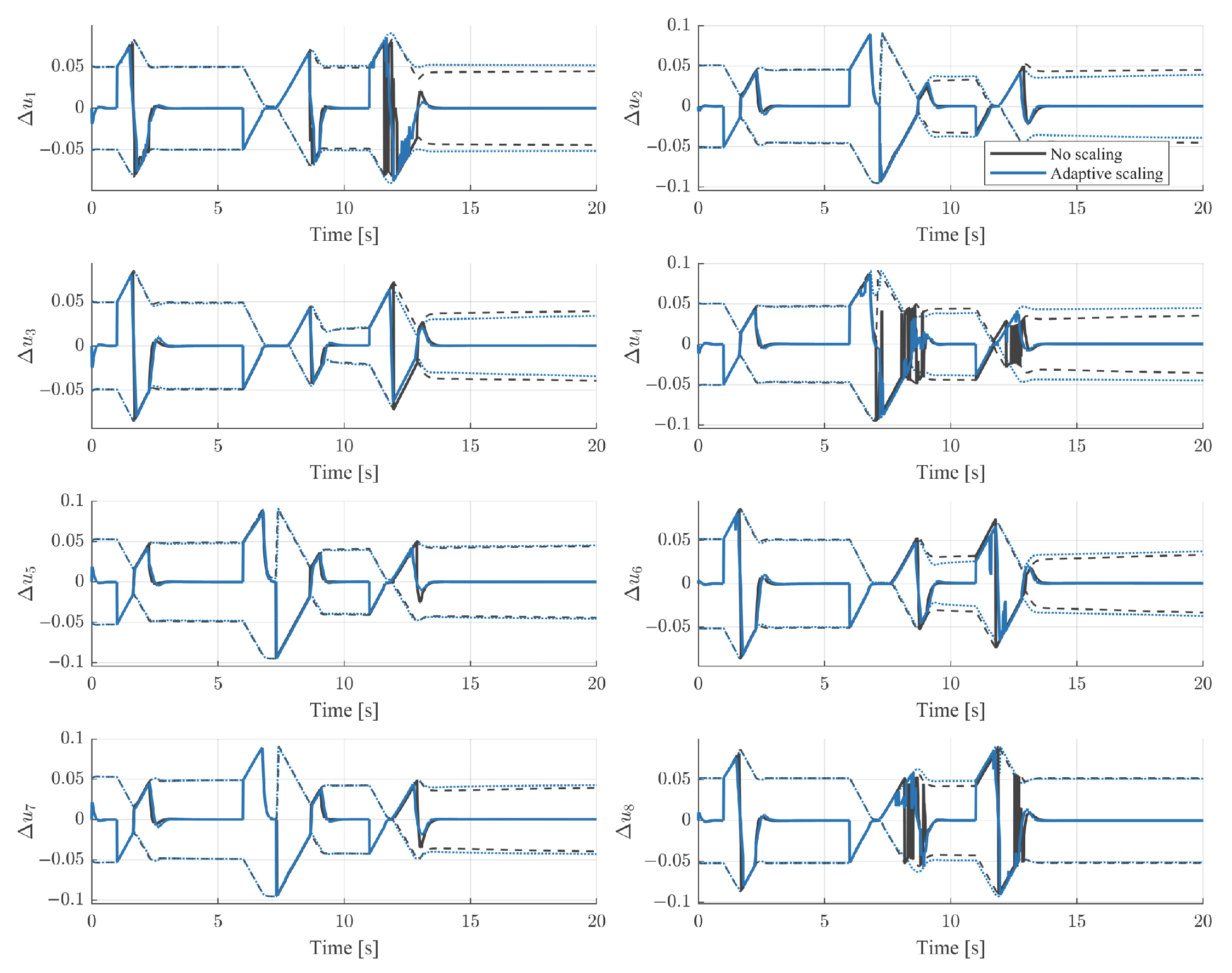
5. Command Scaling Performance

This section evaluates the performance of the proposed adaptive command scaling algorithm using a representative control allocation task. The RPI allocator is used as the benchmark incremental allocator. The goal is to assess the effectiveness of Algorithm 1 in maintaining command feasibility. Its performance is also compared against the theoretically optimal linear programming (LP) solution.

5.1. Allocation Task Setup

Consider the incremental moment set presented in Figure 3. In this test, we fix $\mathrm{\Delta }\dot{p}=0$ and sweep the command vector in the $(\mathrm{\Delta }\dot{q},\mathrm{\Delta }\dot{r})$-plane to simulate a continuous variation in the virtual control command along a circular trajectory. At time $t=0$, the ray starts from $(\mathrm{\Delta }\dot{q},\mathrm{\Delta }\dot{r})=(0.1\mathrm{rad}/{\mathrm{s}}^2,0)$, and then rotates counter-clockwise around the origin $(0,0)$ along a circle with radius $0.1\mathrm{rad}/{\mathrm{s}}^2$. The command completes one full revolution and returns to the initial position at $t=5\mathrm{s}$. During this sweeping, the virtual command alternates between feasible and infeasible regions of the AMS. Therefore, this task provides a comprehensive test of the adaptive scaling algorithm under both conditions.

To obtain the theoretical scaling ratio along each command ray, we compute the intersection of the ray with the AMS boundary by solving the following linear programming problem [1]:

$$\begin{array}{cc}\hfill \underset{\mathrm{\Delta }\mathit{u},\alpha }{min}& -\alpha \hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \alpha \mathrm{\Delta }{\mathit{\nu }}_c=B\mathrm{\Delta }\mathit{u},\hfill \\ \hfill & \mathrm{\Delta }{u}_i\in S\left(\mathrm{\Delta }{u}_i\right),\hfill \\ \hfill & \alpha \ge 0.\hfill \end{array}$$

(49)

The optimal $\alpha$ represents the maximum achievable scaling factor along the original command direction. If $\alpha \ge 1$, the command is feasible and can be executed directly, and we can clip $\alpha$ at 1 to preserve the feasible command; otherwise, $\alpha <1$ indicates that the command lies outside the AMS and should be scaled down proportionally.

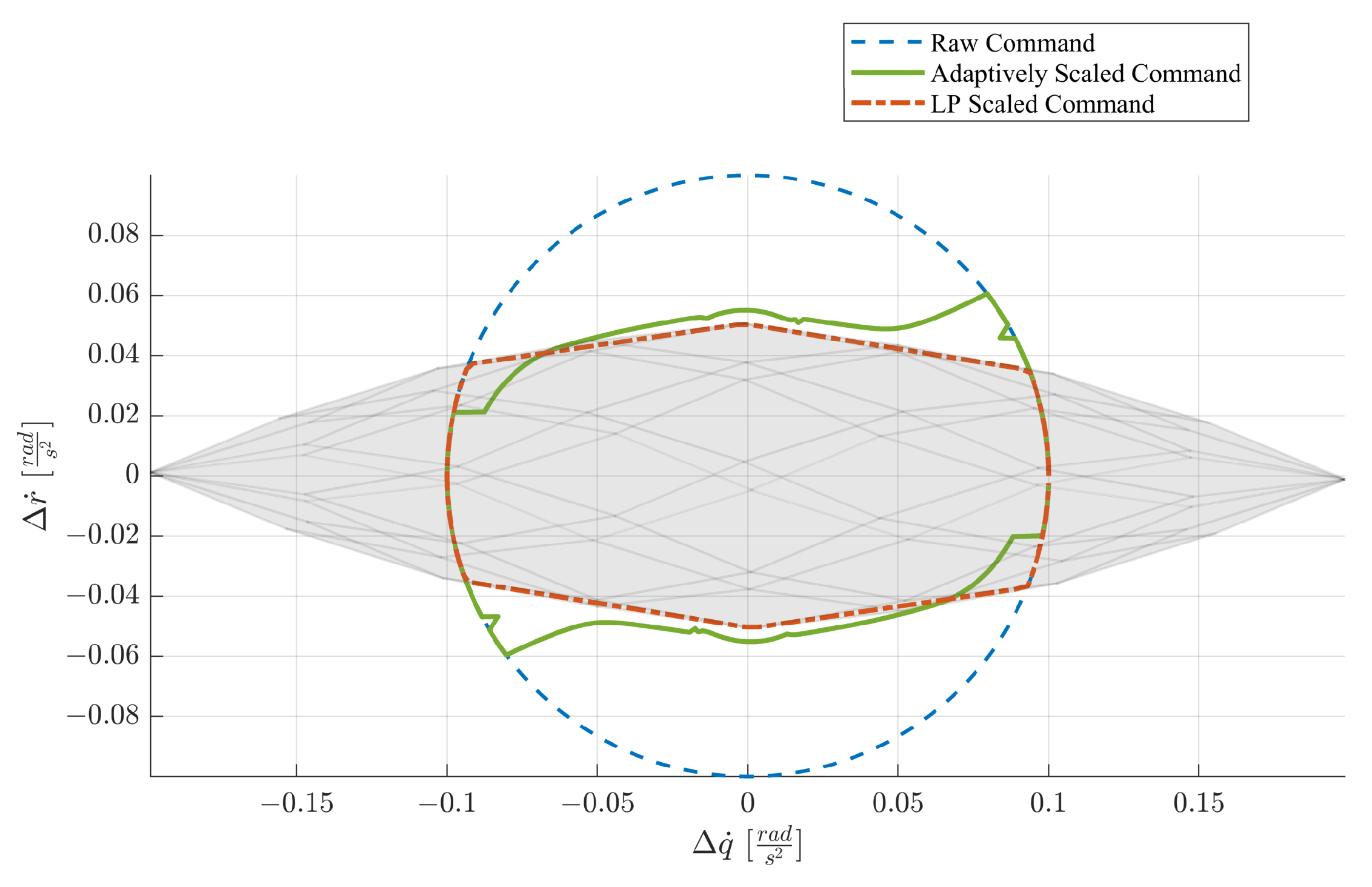
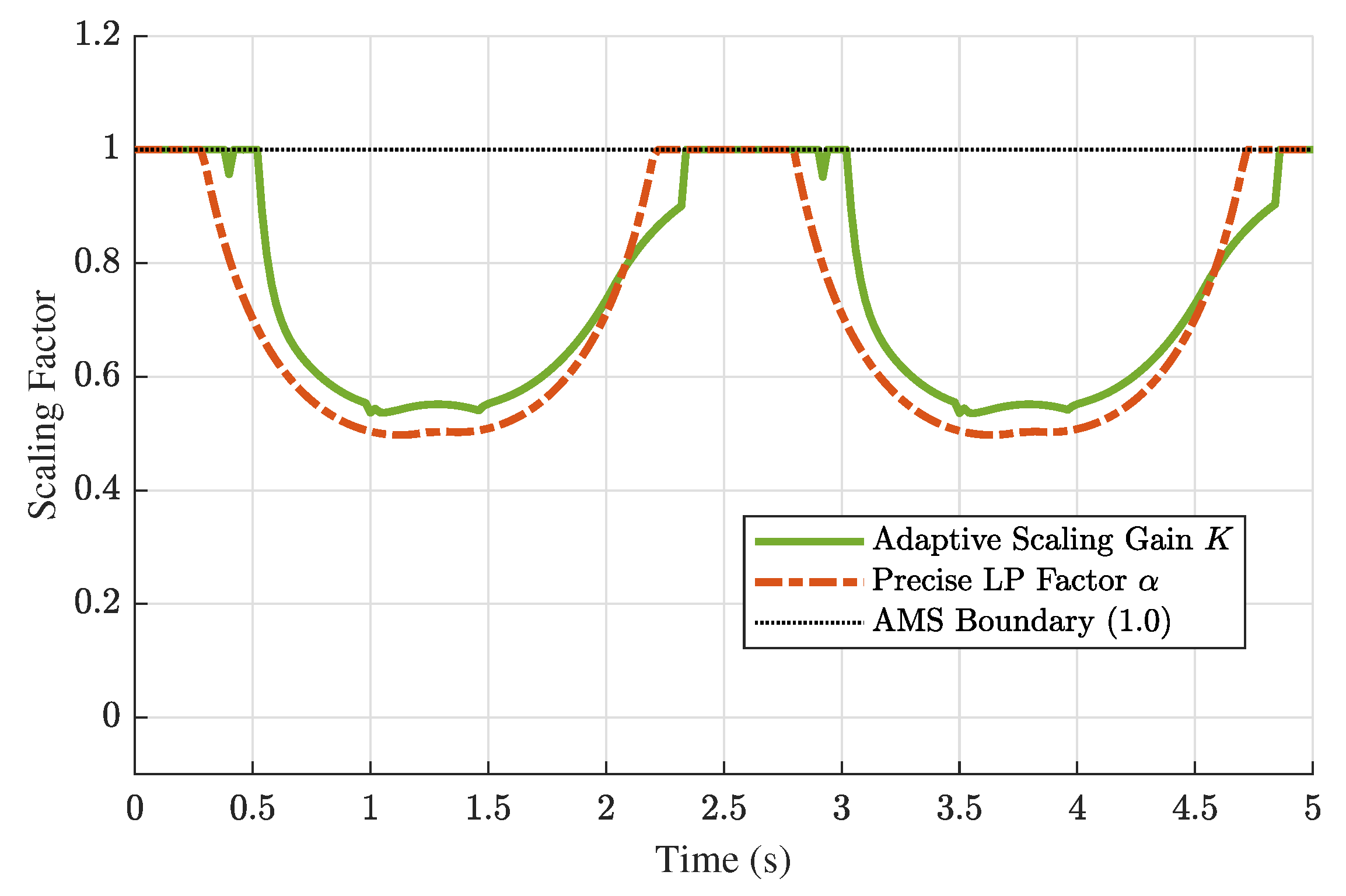
5.2. Performance Comparison

For the adaptive scaling algorithm, we select $\gamma =30$, $\lambda =0.1$, and ${\epsilon }_{re}=0.1$. These parameters correspond to a relatively strong “cutting-down” gain for infeasible commands, a weaker “restoring” gain that allows recovery toward $K=1$, and an allocation error threshold ${\epsilon }_{re}$ below which the gain is instantaneously reset to 1. Figure 7 and Figure 8 illustrates the command rays (trajectories) and the corresponding scaling behavior. The raw commands along the circular path are shown in blue, the LP-based scaled commands in red, and the adaptively scaled commands in green. Figure 9 compares the scaling factor returned by the LP solver and the adaptive scaling law.

From $t=0$ to $t\approx 0.28\mathrm{s}$, all commands remain within the AMS; thus, the LP solver yields $\alpha =1$, and the adaptive gain K remains constant at unity. Between $t=0.28\mathrm{s}$ and $t=2.22\mathrm{s}$, the commands gradually move outside the AMS boundary, resulting in $\alpha <1$. The adaptive gain begins to decrease only after $t\approx 0.52\mathrm{s}$, since initially the allocation error is small and the restoring term dominates the adaptation. When the command reenters the feasible region at $t\approx 2.22\mathrm{s}$, the LP factor $\alpha$ returns to one. The adaptive gain also recovers to unity but with a short delay of about $0.1\mathrm{s}$. This pattern repeats periodically as the command sweeps the circle. Overall, the adaptive scaling law successfully reduces infeasible commands to the vicinity of the AMS boundary and preserves feasible commands. Compared with LP solutions, the adaptive gain exhibits a small time lag due to the competing effects of the “cutting-down” and “restoring” components in the adaptation mechanism.

The average execution times of the LP solver and the adaptive scaling algorithm are compared in Figure 10. All tests were conducted on a Windows 11 laptop running MATLAB R2023b with an AMD Ryzen 7 CPU and 32 GB of RAM. The LP intersection calculation requires an average of $4.3\mathrm{ms}$ per command, while the proposed adaptive law requires only $0.97\mathsf{\mu }\mathrm{s}$, which is over four thousand times faster. The negligible computational cost makes the proposed adaptive scaling method appealing for real-time implementation.

To further investigate the influence of the adaptation gains, several values of $\gamma$ and $\lambda$ were tested (see Figure 11). The parameter $\gamma >0$ determines the overall adaptation speed of the scaling factor K. A larger $\gamma$ accelerates both the “cutting-down” phase and the “restoring” phase. As a result, increasing $\gamma$ reduces the time delay between the proposed scaling solution and the reference LP-based allocation. However, when $\gamma$ is chosen too large, the adaptation becomes overly aggressive, leading to small oscillations in K and chattering in the allocated incremental control. The parameter $\lambda >0$ weights the bias toward $K=1$ in the underlying cost function and therefore controls the restoring tendency of the scaling law. Larger $\lambda$ values put more emphasis on recovering K to unity, resulting in faster restoration of the full command authority. On the other hand, a large $\lambda$ reduces the relative weight of the allocation-error term in the adaptation, which can slow down the suppression of infeasible commands.

Based on these observations, a simple tuning procedure is as follows. First, select $\gamma$ such that the dynamics of K are faster than the dominant closed-loop dynamics, but slow enough to avoid noticeable oscillations in $K\left(t\right)$ in the considered operating conditions. Second, choose $\lambda$ to achieve a desired restoration time of K toward unity after constraints cease to be active. All simulation results in this paper were obtained using gains tuned according to this procedure. In additional numerical tests, we observed that moderate variations around the chosen $(\gamma ,\lambda )$ do not qualitatively alter the closed-loop behavior.

In summary, the adaptive command scaling law offers a computationally efficient and direction-preserving alternative to LP-based scaling. It dynamically reduces infeasible commands and restores full commands when feasible. It achieves real-time performance with negligible computational overhead. The tradeoff between response speed and smoothness can be tuned via the parameters $\gamma$ and $\lambda$, allowing flexible adjustment depending on the desired aggressiveness of adaptation.

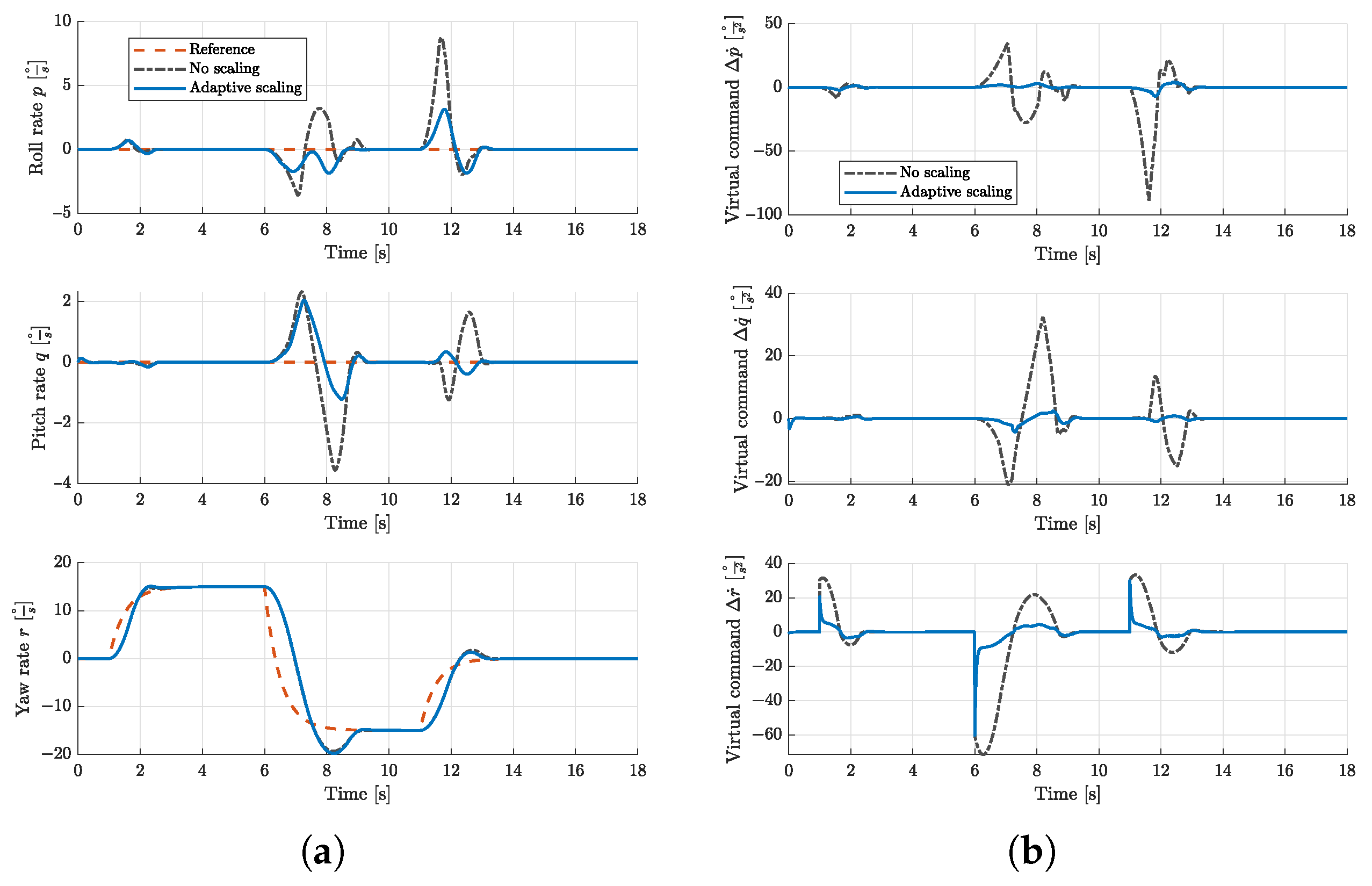
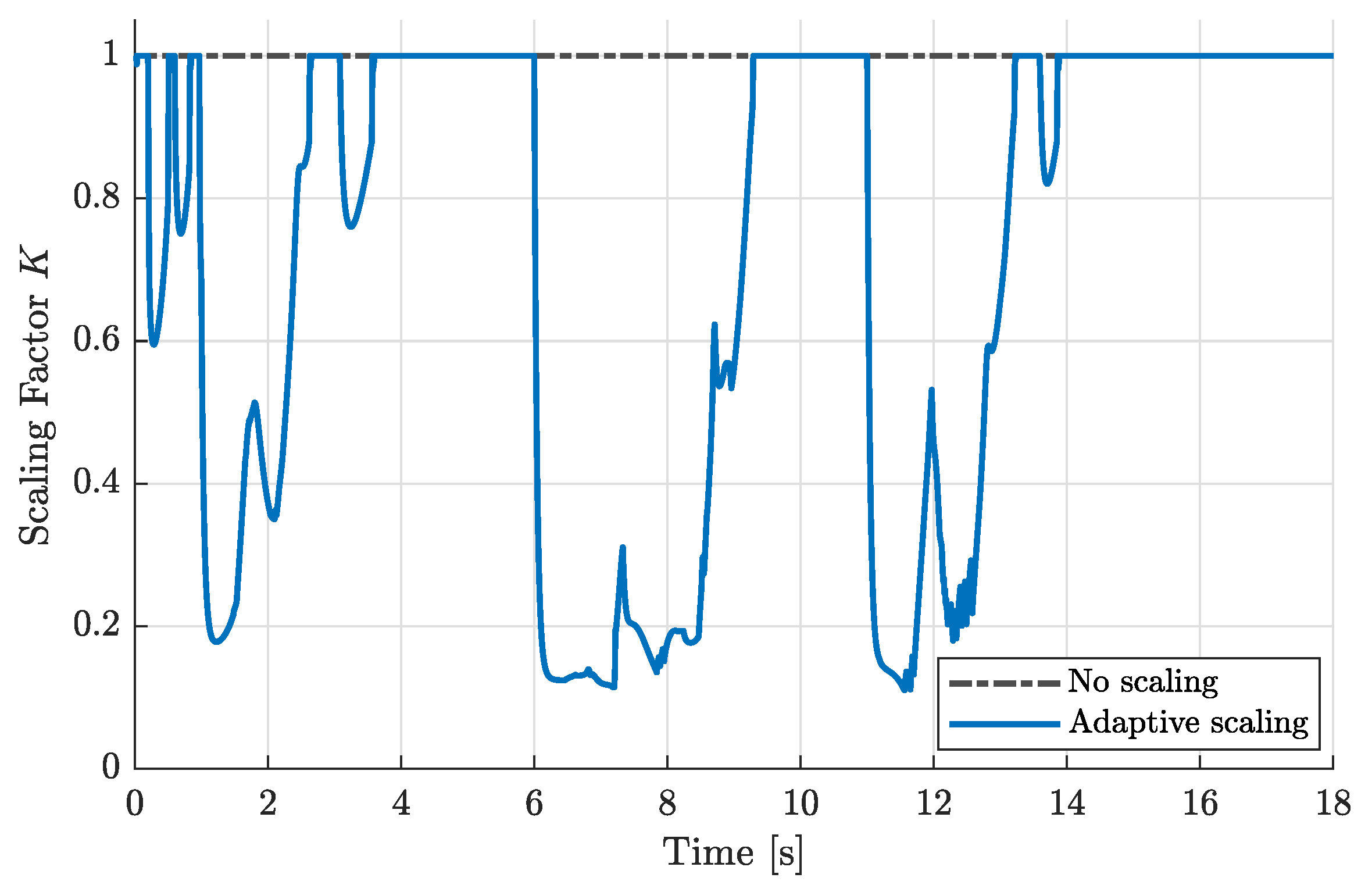
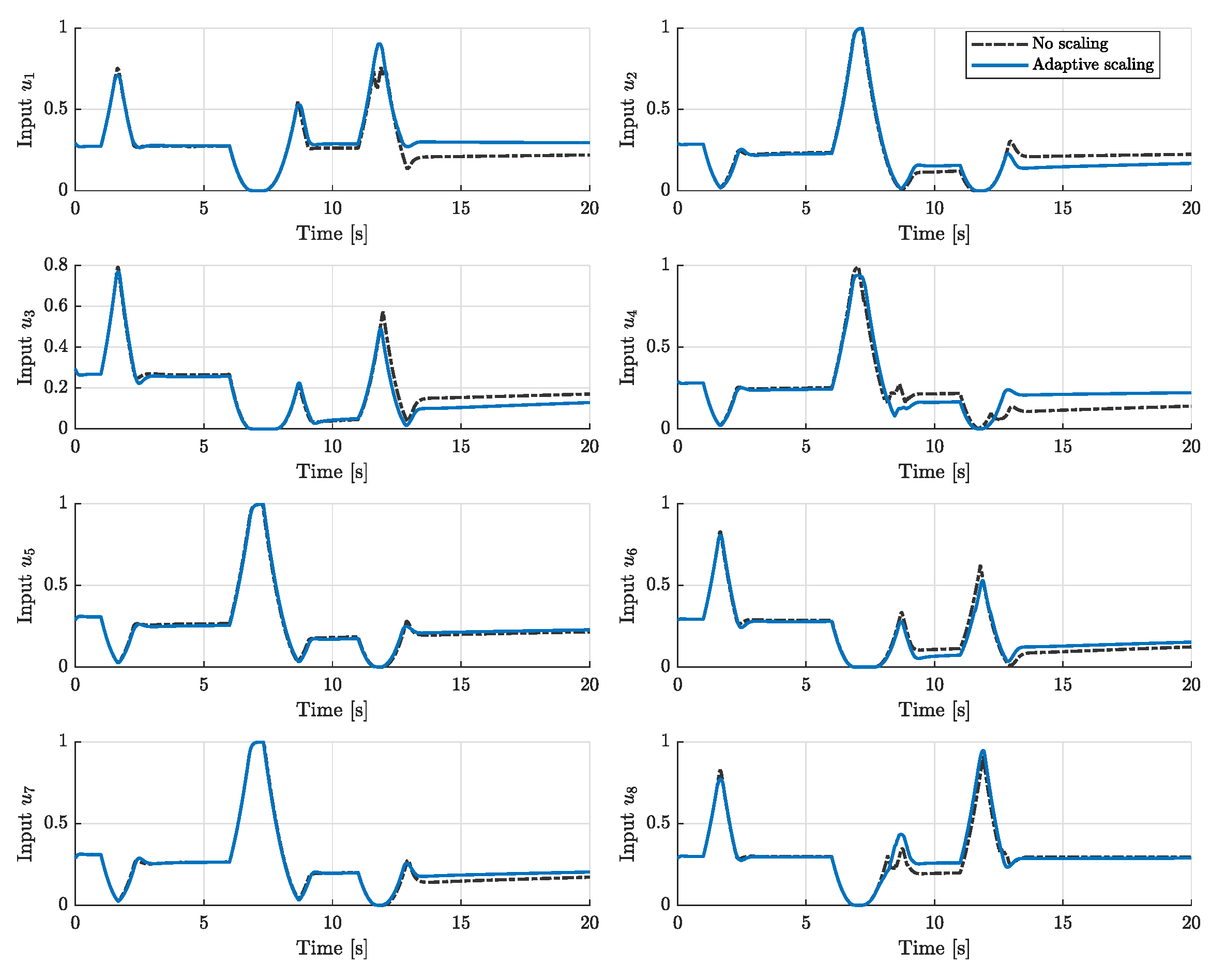
6. Closed-Loop INDI Flight Simulation

This section evaluates the proposed adaptive scalar command scaling within an INDI controller for the eVTOL’s rotational dynamics. Notably, we assume perfect virtual-control and control effectiveness estimates in order to isolate the effect of allocation and command scaling.

6.1. INDI Controller Setup

The controller structure is shown in Figure 12. A first-order reference model shapes the output-tracking dynamics for rotational rates $\mathit{\omega }={[p,q,r]}^{\top }$:

$${\dot{\mathit{\omega }}}_{\mathrm{r}}=\mathit{R}\left({\mathit{\omega }}_{\mathrm{c}}-{\mathit{\omega }}_{\mathrm{r}}\right).$$

(50)

The desired virtual control is the summary of the reference virtual control and error dynamics:

$${\mathit{\nu }}_{\mathrm{c}}={\dot{\mathit{\omega }}}_{\mathrm{r}}+{\mathit{K}}_{\omega }\left({\mathit{\omega }}_{\mathrm{r}}-\widehat{\mathit{\omega }}\right),$$

(51)

and the incremental virtual command is

$$\mathrm{\Delta }{\mathit{\nu }}_{\mathrm{c}}={\mathit{\nu }}_{\mathrm{c}}-{\widehat{\mathit{\nu }}}_0,$$

(52)

where $\widehat{\mathit{\omega }}$ and ${\widehat{\mathit{\nu }}}_0$ are obtained from filters or onboard model-based estimators. To isolate the impact of the scaling mechanism, we assume perfect state and virtual-control estimates ($\widehat{\mathit{\omega }}=\mathit{\omega }$, ${\widehat{\mathit{\nu }}}_0={\mathit{\nu }}_0$). In the following simulations, the reference model and error gain matrices are set to

$$\mathit{R}=\mathrm{diag}\left(3,3,2\right),{\mathit{K}}_{\omega }=\mathrm{diag}\left(8,8,4\right).$$

(53)

Control allocation uses the RPI allocator with null-space update (cf. Equation (8)). Steady-hover inputs correspond to rotor speeds of $90\mathrm{rad}/\mathrm{s}$, i.e., the dimensionless trim $u_i=0.29$ for each rotor. Input bounds are enforced as in Equation (17) to consider both rotor rotational rate limits and acceleration limits.

6.2. Tracking Scenario and Results

Given the low effectiveness in yaw, a yaw-rate doublet command in $[-15,15]\mathrm{deg}/\mathrm{s}$ is applied, while $p_{\mathrm{c}}\left(t\right)=q_{\mathrm{c}}\left(t\right)=0$. We compare two configurations: (i) Nominal INDI (no scaling), and (ii) INDI + adaptive scaling with $\gamma =20$, $\lambda =0.1$, and reset threshold ${\epsilon }_{\mathrm{re}}=0.1$.

Figure 13 shows the reference signals and rotational rates. In yaw, both configurations exhibit comparable tracking errors during the two saturation windows (around $t\approx 6–9\mathrm{s}$ and $t\approx 11–13\mathrm{s}$), consistent with the weak yaw effectiveness. In contrast, roll and pitch responses are different. Without scaling, the peak roll-rate deviation reaches $8.8\mathrm{deg}/\mathrm{s}$ at $t=11.7\mathrm{s}$, and peak pitch-rate deviation reaches $-3.5\mathrm{deg}/\mathrm{s}$ at $t=8.3\mathrm{s}$. These excursions arise from aggressive (infeasible) virtual commands and allocator cross-axis coupling when saturation occurs. With adaptive scaling, oscillations in roll/pitch are substantially suppressed: peak roll deviation drops to $3.13\mathrm{deg}/\mathrm{s}$ (around $t\approx 11\mathrm{s}$), and peak pitch rate deviation to $-1.22\mathrm{deg}/\mathrm{s}$ (around $t\approx 8.3\mathrm{s}$). Figure 13b plots the incremental virtual commands on all three axes. With scaling active, infeasible requests are drastically reduced toward the AMS boundary. The corresponding scalar gain K is shown in Figure 14. Infeasible commands are quickly cut down ($K<1$), while feasible commands are preserved as $K\to 1$ promptly whenever the allocation error becomes small. Beyond its control role, K serves as a proxy indicator of remaining control margin: $K\approx 1$ implies sufficient margin while $K\ll 1$ signals persistent saturation pressure and reduced margin. Figure 15 and Figure 16 show the incremental and absolute inputs of the eight rotors, respectively. Dark traces denote the nominal case; blue traces denote adaptive scaling. The scaling mechanism produces visibly smoother input variation during the aggressive maneuvers.

Table 2. Per-rotor saturation duration (seconds).

	${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$	${\mathit{u}}_6$	${\mathit{u}}_7$	${\mathit{u}}_8$
Nominal	2.11	3.05	4.21	2.38	2.52	3.98	3.00	2.92
Adaptive	1.76	2.82	3.83	2.03	2.25	3.61	2.85	2.25

reports the total time each rotor spends at the bound during the simulation. All eight rotors benefit from reduced saturation durations.

The closed-loop results align with the findings in Section 5: the adaptive scalar effectively trims infeasible virtual commands while preserving attainable commands. In the present maneuver, the primary benefit appears in the non-commanded axes (roll/pitch), where cross-axis couplings under saturation are moderated, yielding lower peaks and smoother responses.

7. Discussion

7.1. Simulation Results Discussion

In terms of the two goals stated in Section 3.1: “scale down infeasible commands” and “preserve feasible commands”, the open-loop ray sweeps in Section 5 and closed-loop INDI simulations in Section 6 demonstrate that our proposed adaptive scaling law can achieve these goals. Under saturation, the allocator might cause cross-axis coupling. By shrinking infeasible components along the command ray, the adaptive law reduces allocator stress, which explains the reduced roll/pitch peaks while preserving yaw performance. With protected virtual commands, input saturation is also alleviated. Moreover, the scalar trace $K\left(t\right)$ can also serve as a real-time indicator of remaining control margin.

Although the linear programming method provides theoretically exact scaling of infeasible commands, it incurs a high computational cost. On the contrary, the present method is a lightweight, allocator-agnostic gradient law that steers requests toward what the allocator can realize. It achieves behavior close to the LP benchmark but at orders-of-magnitude lower run-time.

7.2. Modular Design

Another key advantage of the proposed method is modularity: the adaptive scaling resides entirely within the control allocation block and reads only inputs/outputs local to it (e.g., the commanded $\mathrm{\Delta }{\mathit{\nu }}_c$ and the achieved $\mathrm{\Delta }{\mathit{\nu }}_a$). No outer-loop signals, additional sensors, or changes to the controller structure are required. This method is highly adaptable and can be seamlessly integrated into other flight control architectures that utilize a distinct allocation module (e.g., PID/LQR + allocator, backstepping/NDI + allocator, or Extended-INDI + allocator [26]). Without further details, we provide a diagram demonstrating the implementation of adaptive command scaling within the NDI control system, as shown in Figure 17. Readers are encouraged to explore the application of adaptive command scaling in even more diverse control architectures.

7.3. Time-Varying Control Effectiveness

The command scaling law presented in this paper assumes a constant control-effectiveness matrix $\mathit{B}$, while in many applications (e.g., aircraft with large flight envelopes) the true effectiveness is state- and time-dependent. We briefly discuss here how the proposed adaptive command scaling behaves when $\mathit{B}$ is time-varying and what additional challenges may arise.

From the closed-loop stability analysis in Section 4, the tracking error dynamics can be written as Equation (43). If we allow $\mathit{B}=\mathit{B}(x,t)$ and $\widehat{\mathit{B}}=\widehat{\mathit{B}}(x,t)$ to be time-varying (for example, through gain scheduling), the derivation remains valid with $\mathit{B}$ and $\widehat{\mathit{B}}$ interpreted pointwise in time. The term $\left(\mathit{B}-\widehat{\mathit{B}}\right)\mathrm{\Delta }{\mathit{u}}_c$ becomes a time-varying disturbance that still enters only through the additive residual ${ϵ}_{\mathrm{tot}}$. As long as ${ϵ}_{\mathrm{tot}}\left(t\right)$ in Equation (43) remains bounded, the input-to-state stability proof for the error dynamics is unchanged.

The adaptive command scaling module operates entirely in the virtual-control space and depends only on the instantaneous mapping between $\mathrm{\Delta }{\mathit{u}}_c$ and the achieved virtual control increment $\mathrm{\Delta }{\mathit{\nu }}_a=\widehat{\mathit{B}}(x,t)\mathrm{\Delta }{\mathit{u}}_c$. For each fixed time t, the geometry of the incremental admissible set and the relationship between the scaled command $K\mathrm{\Delta }{\mathit{\nu }}_c$ and the allocation error ${\mathit{e}}_{\nu 0}=\mathrm{\Delta }{\mathit{\nu }}_c-\mathrm{\Delta }{\mathit{\nu }}_a$ are determined by the current effectiveness estimate $\widehat{\mathit{B}}(x,t)$ and the current input limits. The proposed adaptive law then minimizes, at each instant, the allocation error along the commanded ray in this time-varying admissible set. Conceptually, this means that the command scaling algorithm generalizes to the case of time-varying $\widehat{\mathit{B}}(x,t)$. There are, however, some practical challenges when $\widehat{\mathit{B}}(x,t)$ varies rapidly. For example, the shape and orientation of the incremental admissible set become time-varying, so the “optimal” scaling factor $K^{\ast }\left(t\right)$ that minimizes the allocation error is also time-varying. The adaptive law for K then has to track a moving optimum. This is well-behaved if $\widehat{\mathit{B}}(x,t)$ varies slowly, but fast variations or large modeling errors may degrade the effectiveness of scaling. A detailed treatment of fast time-varying control effectiveness is beyond the scope of this paper and will be investigated in future work.

8. Conclusions

This paper introduced a lightweight command scaling law for incremental control allocation. This law is derived from minimizing a Lyapunov function that combines normalized allocation error and gain deviation from unity. From a theoretical standpoint, the adaptive law ensures the scaling gain will converge to a value close to the attainable portion of the raw command; thus, infeasible commands are reduced while feasible commands are preserved. The closed-loop stability analysis, incorporating various uncertainties, demonstrates that the INDI system with adaptive command scaling maintains input-to-state stability. Extensive simulations demonstrate the effectiveness of the command scaling. In open-loop ray sweeps, the scaled commands closely track the linear programming ground truth with negligible computation (about $0.97\mathsf{\mu }$s versus $4.3$ ms for LP). Within the INDI closed-loop system, the adaptive scaling effectively suppresses cross-axis coupling (e.g., with similar yaw tracking performance, peak roll rate and pitch rate are reduced by over 60%). The suppression of infeasible virtual commands also alleviates saturation durations for all rotors.

The resulting adaptive scaling algorithm is simple to tune and computationally efficient, and it provides favorable modularity. Beyond providing feasibility protection, the scalar trace $K\left(t\right)$ offers a practical indicator of remaining control margin. Future work will tighten guarantees under time-varying control effectiveness and validate the method in hardware experiments.