Strengthening Width on Local Damage to Circular Piers Caused by Rolling Boulder Impacts

Abstract

In response to the issue of local damage to mountainous bridges easily caused by rockfall impacts, carbon fiber cloth and steel plate strengthening methods were adopted to deeply study the impact of the width of carbon fiber cloth and steel plates on the strengthening effect. This study investigates the strengthening effectiveness of Carbon Fiber-Reinforced Polymer (CFRP) wraps and steel jackets on circular bridge piers, utilizing the ABAQUS finite element method. The analysis focuses on the effects of varying load conditions and confinement widths ranging from 100 to 200 cm, with a specific case study of a bridge pier in Nanchuan District, Chongqing. The research results show that the width of carbon fiber cloth and steel plates has a significant impact on the bridge pier’s impact resistance and damage resistance. There exists an optimal strengthening width that maximizes the strengthening effect. The stress distribution and displacement changes under different load conditions are affected by the width of the steel plate; the wider the steel plate, the better the strengthening effect, but the effect is not strictly linear. A comprehensive analysis method integrating multi-directional stress and displacement data was developed, incorporating weighting factors based on structural safety relevance. For both strengthening methods, a set of fitted formulas for widths between 100 cm and 200 cm was derived. This study provides systematic insights and practical guidance for the design of impact-resistant strengthening systems for bridge piers.

1. Introduction

With the continuous advancement of infrastructure construction in various countries, the economies of many mountainous areas have been rapidly developing. In order to strengthen the transportation network in mountainous areas, a large number of bridge projects have been completed. However, the unique complex terrain and frequent geological disasters in mountainous areas pose a serious challenge to the safe operation of bridges, especially the safety issues caused by rockfall impacts. Such impact events often cause local damage to bridge piers [1]; therefore, effective strengthening treatment for damage caused by rockfall impacts is of great significance to the integrity and durability of bridge structures.

The formulation of bridge pier strengthening schemes hinges on the rational selection of strengthening parameters. These parameters include the type, thickness, width, and number of layers of strengthening materials, which directly affect the strengthening effect and economy. Specifically, moderately increasing the width of strengthening materials can significantly enhance the bridge pier’s ability to resist rockfall impacts and improve its damage resistance, effectively reducing the damage caused by impacts. Therefore, when designing strengthening measures against rockfall impacts, it is necessary to fully consider the comprehensive effect of different strengthening parameters, aiming to optimize the strengthening effect while reasonably controlling cost-effectiveness.

Existing research on pier strengthening has been widely applied in practical engineering. Various strengthening methods have been developed to address different types of damage. For instance, some scholars have used steel reinforcement or GFRP (glass fiber-reinforced polymer) to enhance the seismic performance of piers [2,3]. Others [4] have applied carbon fiber materials to strengthen earthquake-damaged piers of continuous rigid-frame bridges. Additional studies [5,6,7] have adopted steel jacket strengthening to improve the safety and stability of bridge structures. Furthermore, research has been conducted on the effectiveness of external carbon fiber wrapping, concrete jacketing, and steel jacketing in mitigating damage caused by rolling boulder impacts [8]. Some researchers [9] have also employed ultra-high-performance fiber-reinforced concrete to strengthen piers, enhancing the self-centering capacity of RC piers. These studies provide valuable insights and methods for pier strengthening, contributing significantly to improving the seismic resistance and safety of bridges.

Currently, external carbon fiber wrapping and steel jacketing are commonly used strengthening techniques due to their efficiency and reliability [10,11,12,13]. This study aims to provide a theoretical foundation for steel jacket confinement mechanisms and their effectiveness in structural strengthening; establish validated methodologies for impact simulation using FEM, particularly for transient dynamic analysis; and support our approach to modeling composite behavior in strengthened piers under impact loading conditions. Most existing research focuses on strengthening against seismic damage and wear erosion, with limited analysis on damage caused by rolling boulder impacts. Although we have studied the reinforcement effects of external carbon fiber cloth reinforcement and external concrete reinforcement [14], the influence of strengthening width remains insufficiently explored. The research flowchart is shown in Figure 1.

This study aims to systematically investigate the effect of strengthening width in external carbon fiber wrapping and steel jacketing methods through theoretical analysis, numerical simulation, and statistical analysis, thereby providing more precise guidance for the design of bridge strengthening.

This study presents the first systematic analysis of the influence of strengthening width (from 100 cm to 200 cm) for both CFRP and steel jackets on the impact resistance of circular piers. We introduce and apply a sophisticated weighted analysis methodology that integrates multi-directional stress and displacement data based on their structural safety relevance. This research transforms the understanding of strengthening width from a qualitative concept into a quantitatively defined design variable, providing both novel insights and practical tools for enhancing the impact resistance of critical transportation infrastructure in mountainous regions. Of course, in the indoor experiments of this study, due to insufficient experimental conditions, there is still a gap compared with the actual conditions.

2. The Influence of Outsourced Carbon Fiber Cloth Width on Strengthening

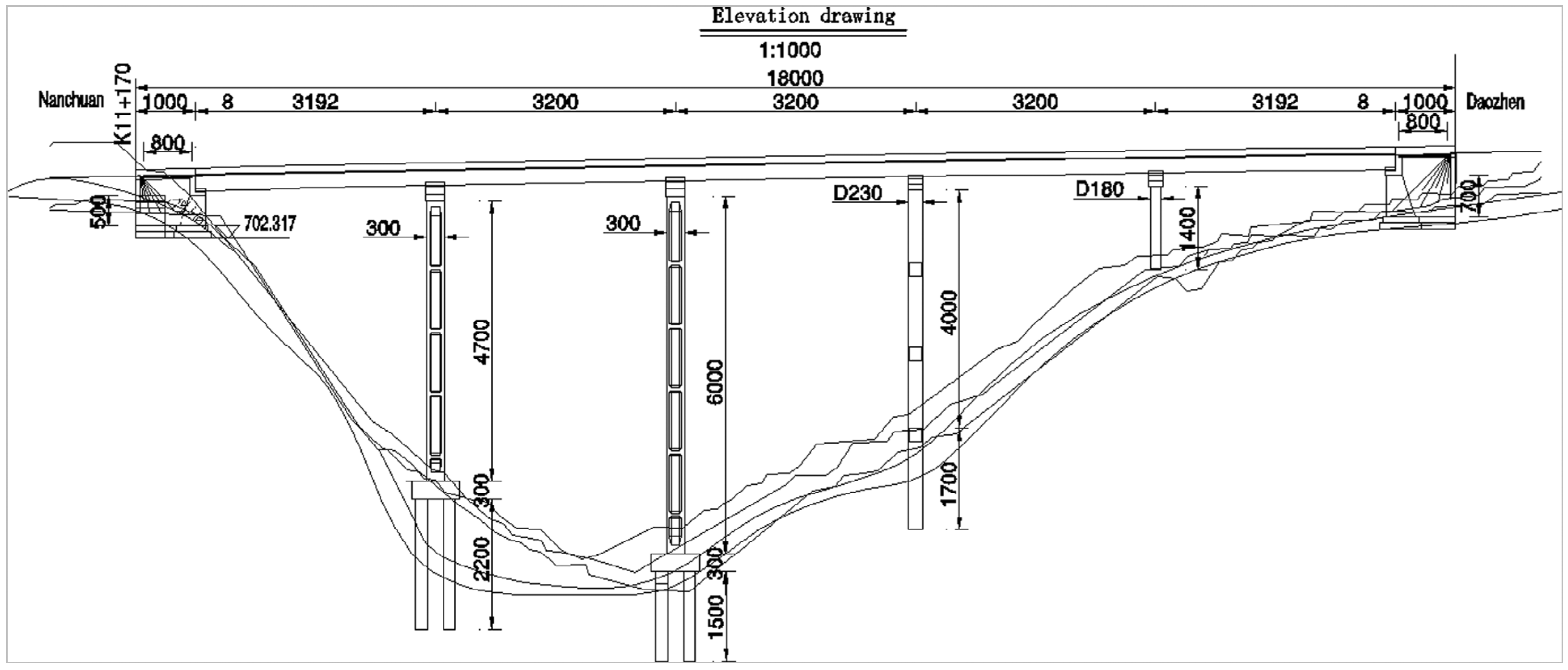
2.1. Engineering Background

The research object of this paper is a certain bridge located in Nanchuan District, Chongqing City, which adopts a round pier structure. The plan layout is shown in Figure 2, consisting of two sections on the left and right, each with 1 union: 5 × 32 m. The upper structure uses post-tensioned prestressed concrete T-beams; in the lower structure, pier 0 and pier 5 are U-type abutments, pier 1 and pier 2 are hollow piers, and the rest are column piers.

The overall elevation layout of the bridgeframe is shown in Figure 3. Pier ④ is a circular pier, 14 m high. Its cross-sectional view and real scene picture are shown in Figure 4 [12]. In the research, pier ④ was selected as the prototype to establish a scaled model for simulation research.

The pier is made of C30 concrete with a concrete cover thickness of 25 mm. The longitudinally arranged strengthening bars use HRB335 strength grade, with a total of 42 bars, each with a diameter of 28 mm. To further enhance the stability and seismic capacity of the pier, the pier is equipped with stirrups with a diameter of 10 mm and a spacing of 200 mm. A 2 m dense area is set at the bottom of the pile foundation and the top of the cap beam, with a spacing of 100 mm.

2.2. Experimental Model Analysis

This test is based on a single-degree-of-freedom damped system to simulate the process of boulder impact on bridge piers, comparing the dynamic responses and pier damage before and after external carbon fiber fabric strengthening. First, material preparation was carried out by selecting carbon fiber fabrics and other materials that met the requirements. Then, the model was designed, and a scaled-down model was established according to the scaling ratio. Subsequently, impact tests were performed on the cast scaled-down model before strengthening. Next, the damaged model [15] that had undergone boulder impact tests was strengthened using an external carbon fiber fabric strengthening scheme. After the model strengthening was completed, boulder impact tests were conducted again on the strengthened model. Finally, the strengthening was analyzed based on the dynamic response data of the bridge pier under different conditions, and the pier damage was recorded during the test. In the experimental design, the size of the test model was reduced by 1:10 of the original size according to the material of the prototype bridge. To simulate the prototype pier, the experimental model has a diameter of 180 mm and a height L of 1400 mm. An 8 g/cm³ density, 75 mm diameter metal sphere is used to simulate rolling stones. To provide stable support, the model is equipped with a rectangular base measuring 1200 mm × 500 mm × 200 mm at the bottom, and a trapezoidal abutment is set at the top. Reinforcement bar dense zones are established on both sides of the pier, with a spacing of 100 mm, while the spacing in the non-dense zones is 200 mm. The schematic diagram and test setup of this model are shown in Figure 5.

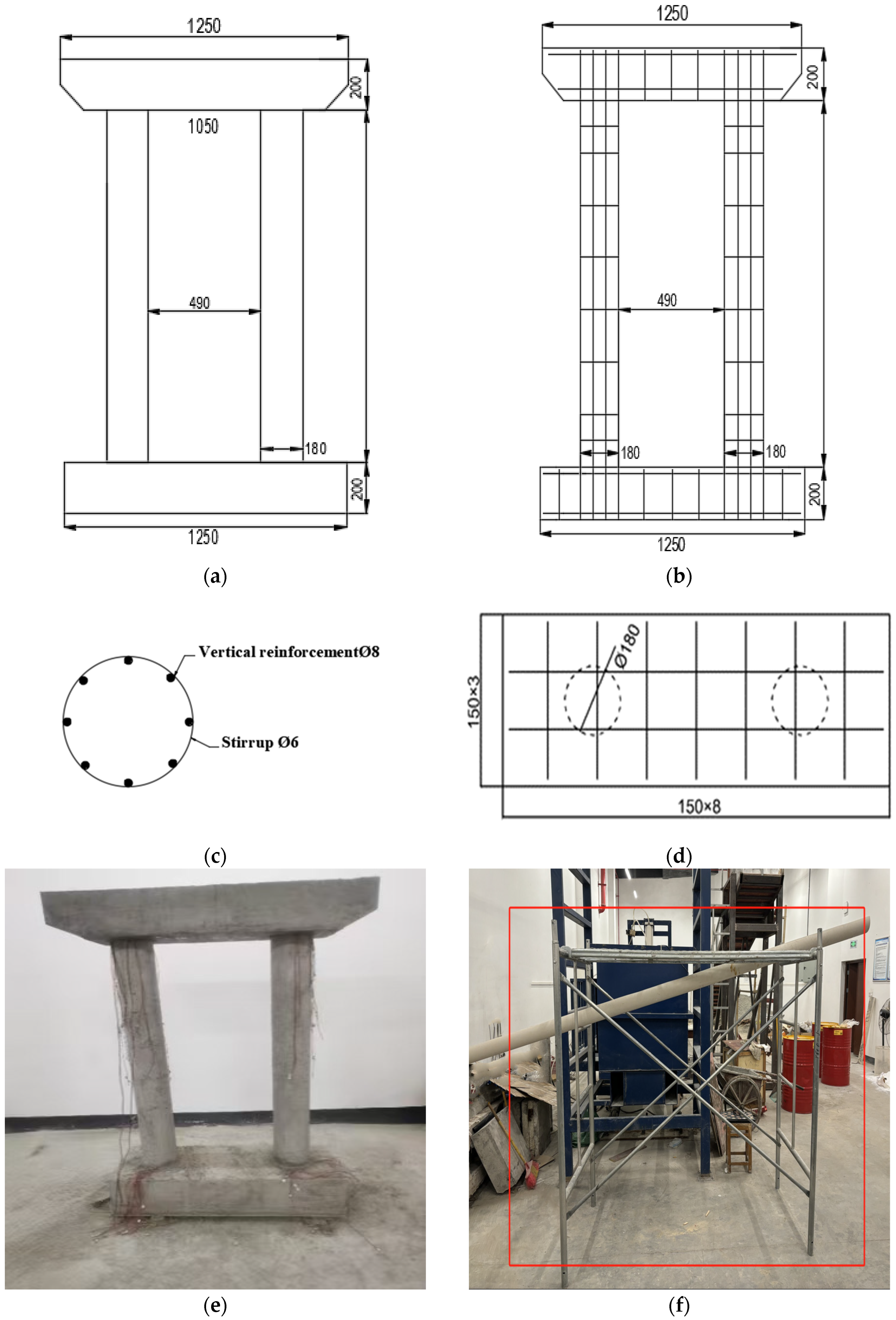
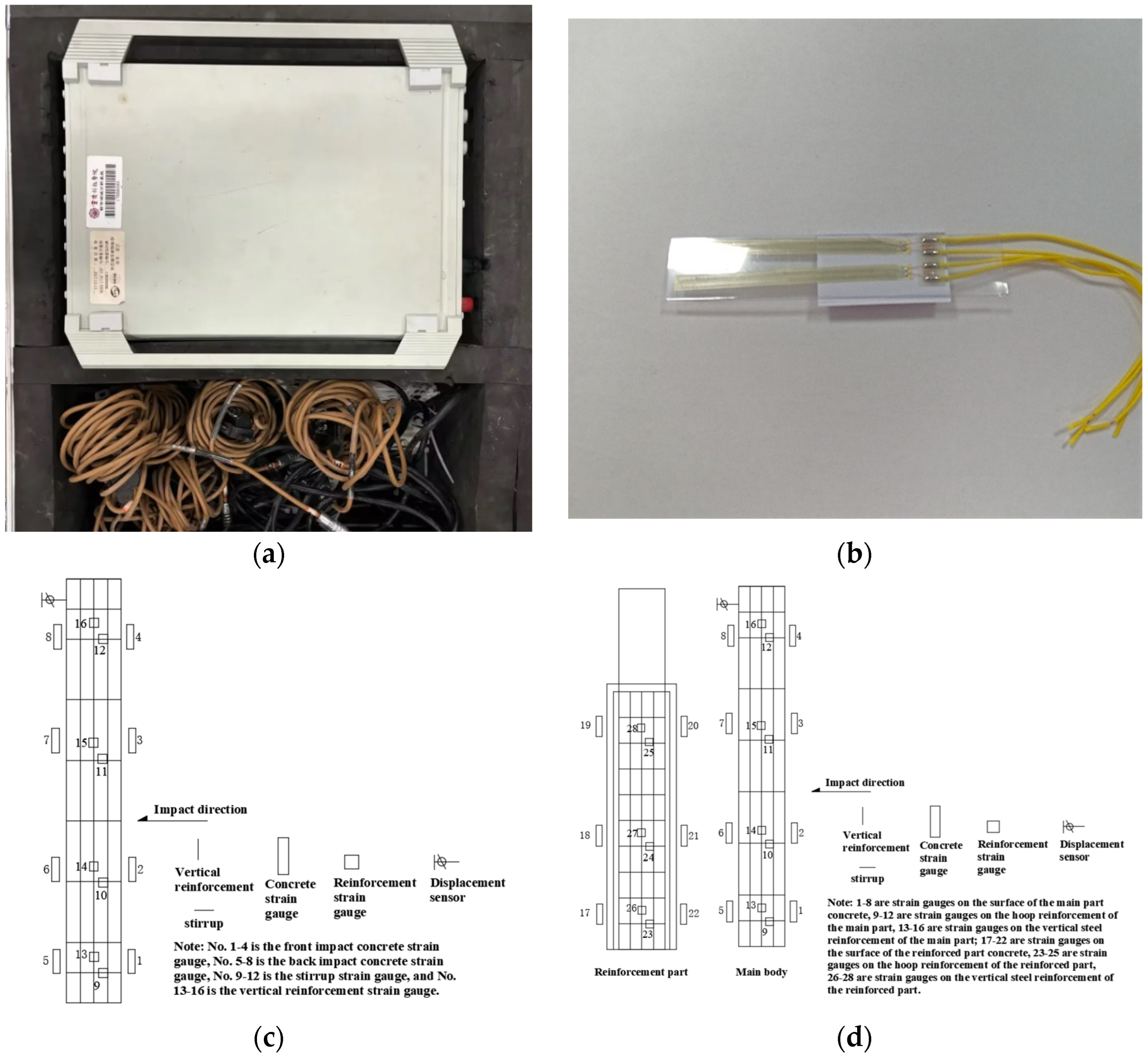
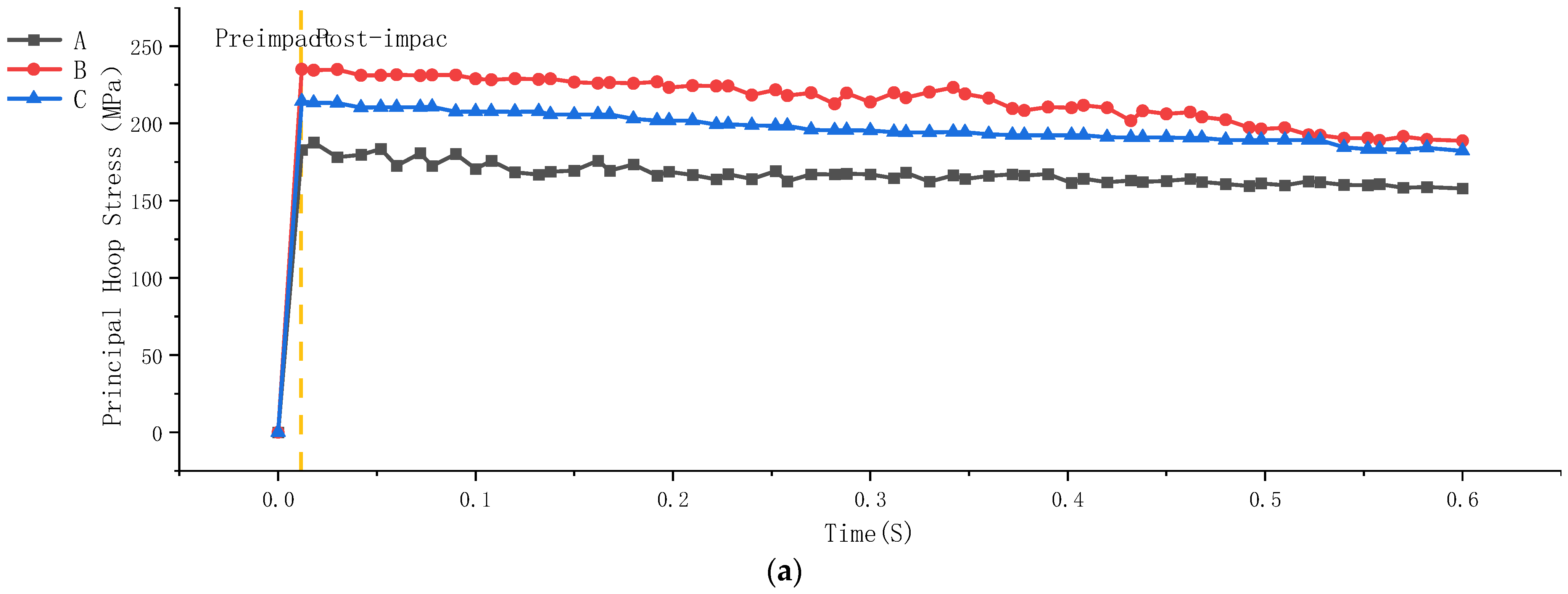
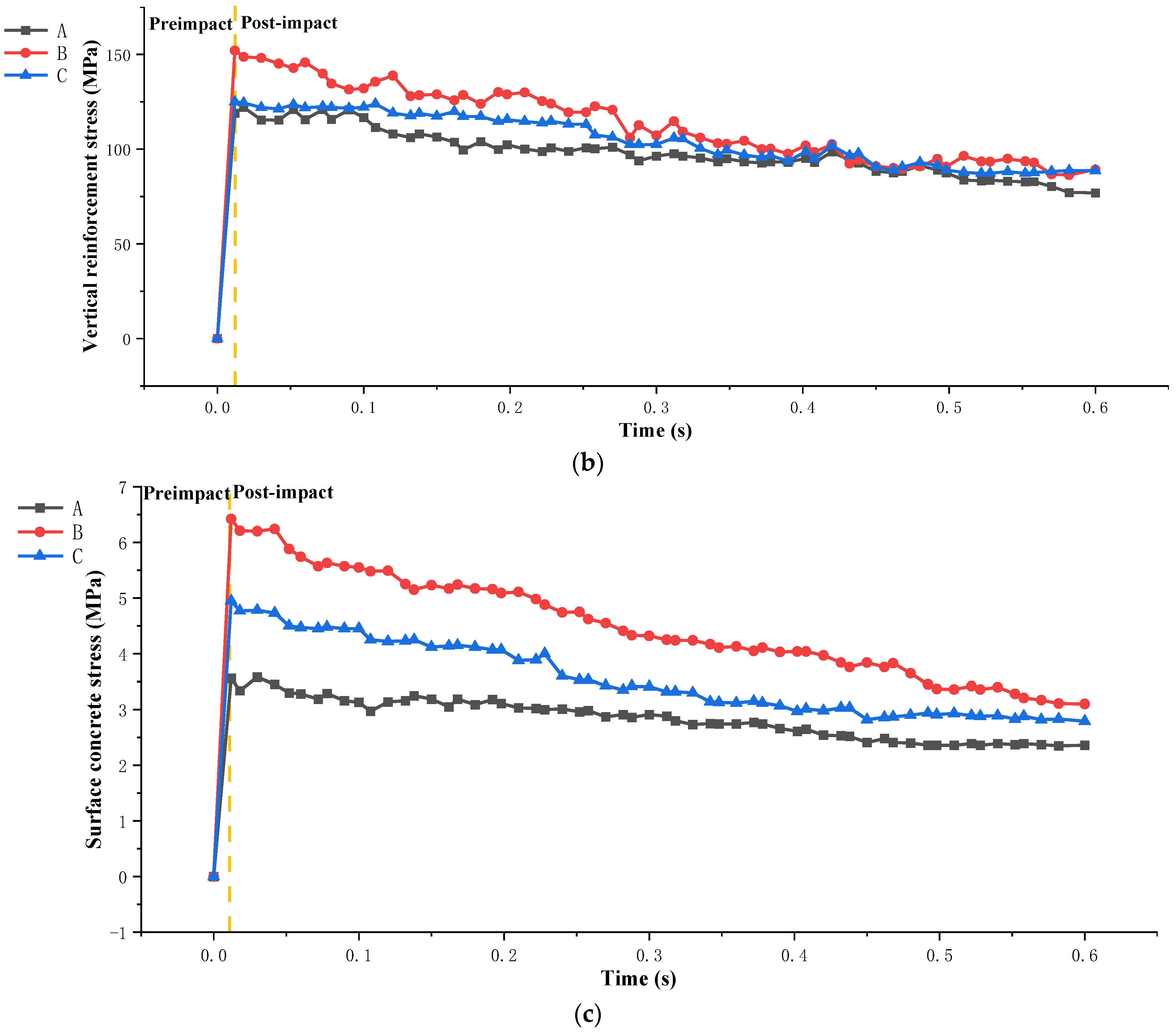
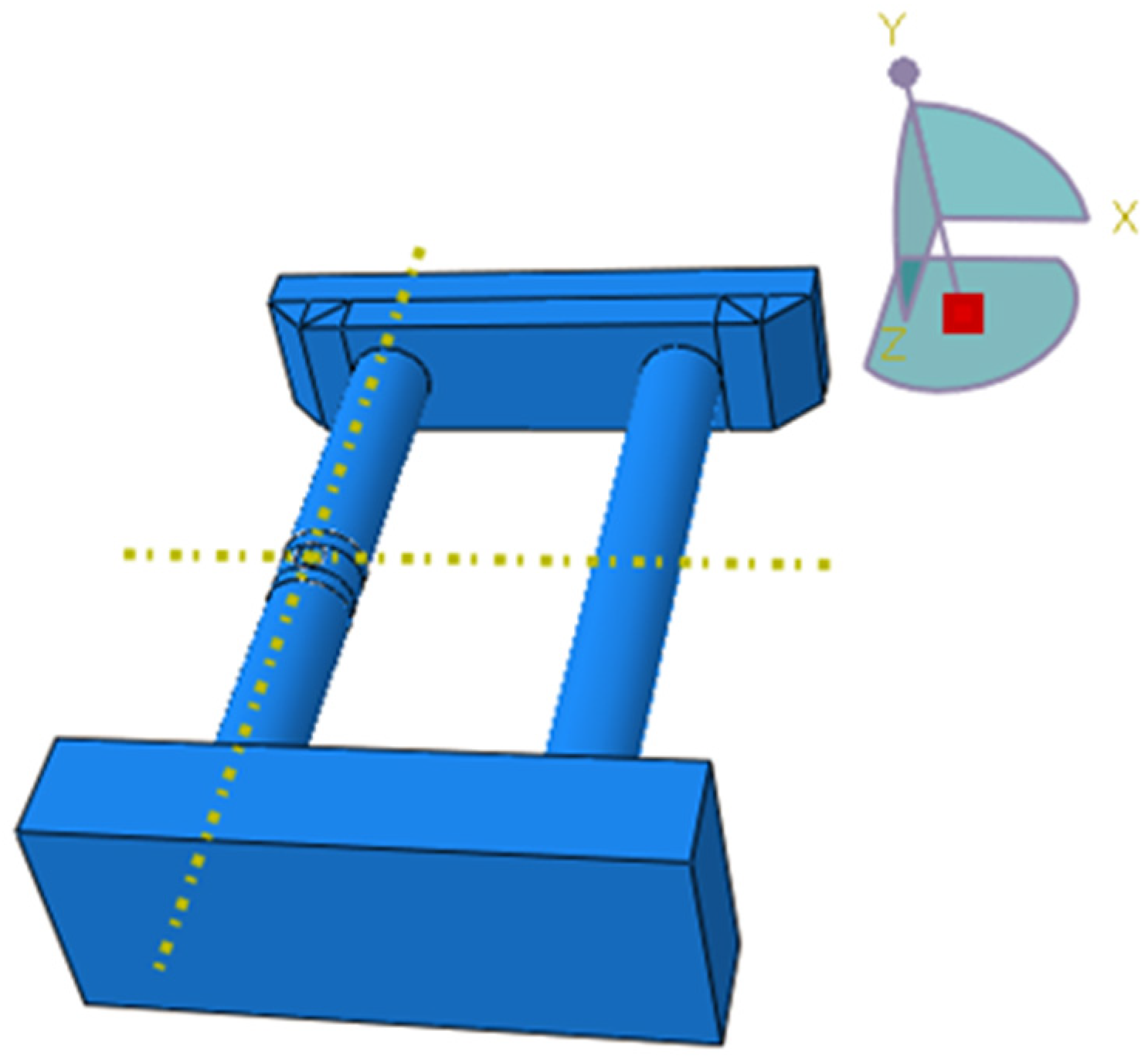
2.2.1. Bridge Pier Strengthening Impact Test

This test mainly simulates the impact of rolling stones on the bridge pier before strengthening. The test simulates a boulder impact at the mid-height of the pier (the L/2 position, where L represents the total height of the pier). The rail angle is controlled by the crossbar position of the wooden (45°), and the impact speed is controlled by the placement of the boulders (3.76 m/s). Two working conditions were set in this test: before and after damage to S. The test procedure is shown in Figure 6. The experiment utilizes the Donghua DHDAS dynamic signal acquisition and analysis system to collect data pertaining to structural performance. Strain measurements are obtained using both steel reinforcement strain gauges and concrete strain gauges, while the YHD-100 type dynamic displacement sensor is employed to measure the displacement at the top of the pier. The experimental detection equipment and the placement position of the strain gauge are shown in Figure 7.

As shown in Figure 8, the damaged model was strengthened with externally bonded carbon fiber fabric based on the local damage from the pre-strengthening impact test. The process included the following steps: surface treatment, sealant filling of damaged areas, fabric installation, smoothing, and curing. In this experiment, an external carbon fiber cloth was adopted. The carbon fiber cloth was of first-grade quality, with a specification of 300 g/m² and a width of 15 cm, and was sealed with Fosili carbon fiber cloth resin AB adhesive and AB epoxy resin sealing adhesive.

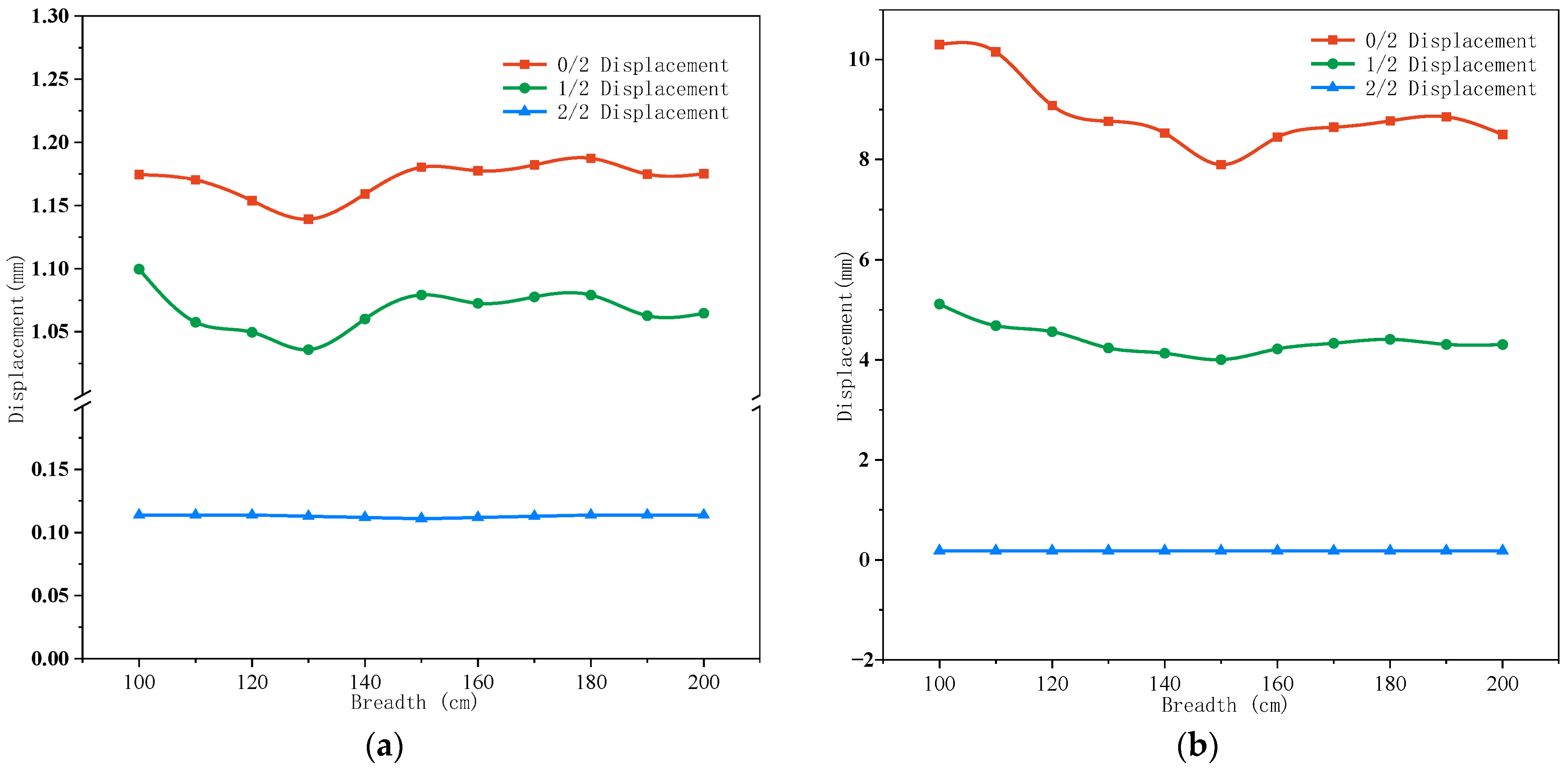
2.2.2. Analysis of Test Results

The impact damage to the bridge pier surface before and after damage, as well as after strengthening with carbon fiber fabric and the external concrete method, is recorded in

Table 1. Damage Status.

Case Number	Damage Status
SBefore Damage	Concrete surface is smooth and intact
SBefore Strengthening	Concrete surface spalling, obvious impact point indentation, damage range 7 × 8, 18 mm deep
SCFRP Strengthening	Slight impact point indentation, surface is smooth and intact

.

Although the current experimental setup does not directly measure energy dissipation during impact, the energy dissipation characteristics can be inferred through a comprehensive analysis of stress response and damage patterns:

Before damage, the pier’s concrete surface remained smooth after boulder impact. However, after initial damage, subsequent impacts caused concrete spalling and obvious indentation. This highlights the vulnerability of already damaged structures to further severe damage upon re-impact. After CFRP strengthening, only slight surface indentation occurred upon re-impact. This demonstrates the effectiveness of CFRP in repairing damage and its resilience in mitigating impact forces, thereby reducing surface damage.

After the boulder impact test on strengthened piers, stress and displacement measurements were taken at L/2: stirrup stress, longitudinal strengthening stress, surface concrete stress, impact point displacement, and pier top displacement. Figure 8 shows these results, where a~c correspond to stresses or displacements under three conditions: before damage, after damage, and after CFRP strengthening.

Figure 9 shows the real-time stress variation curves of strengthening and concrete at the L/2 bridge pier position under a boulder speed of 7.37 m/s. Stress variation peaks between 0.01 and 0.02 s, then decreases. After strengthening with externally bonded carbon fiber fabric, the stress on stirrups and longitudinal bars is significantly reduced.

Under identical rolling stone impact conditions, a comparative analysis of the stress variations in the stirrups and longitudinal reinforcement revealed that the unstrengthened pier exhibited the highest stress levels in both stirrups and longitudinal reinforcement among the three working conditions, while the pre-damaged condition showed the lowest stresses. The externally bonded CFRP strengthening demonstrated remarkable effectiveness, reducing the peak stress in stirrups by 6.22% and in longitudinal reinforcement by 15.30%. The CFRP strengthening method led to a 25.38% reduction in concrete stress. Overall, the externally bonded CFRP strengthening showed significant effectiveness in reducing concrete stress.

The damage patterns and dynamic response data also provide qualitative insights into the energy dissipation mechanisms. The unstrengthened pier dissipated the impact energy primarily through irreversible damage, namely concrete crushing and spalling, which is an inefficient and brittle form of energy absorption. In contrast, the piers strengthened with CFRP or steel jackets exhibited a significantly different response. The strengthening system, through its high tensile strength and effective confinement of the core concrete, allowed for a more distributed and ductile energy dissipation process. The reduction in peak stress and the control of damage to minor surface indentation suggest that a larger portion of the impact energy was converted into elastic strain energy within the strengthening material and distributed more uniformly throughout the pier, rather than being consumed in localized failure. This shift in failure mode underscores the role of the jacket in enhancing the pier’s overall energy absorption capacity.

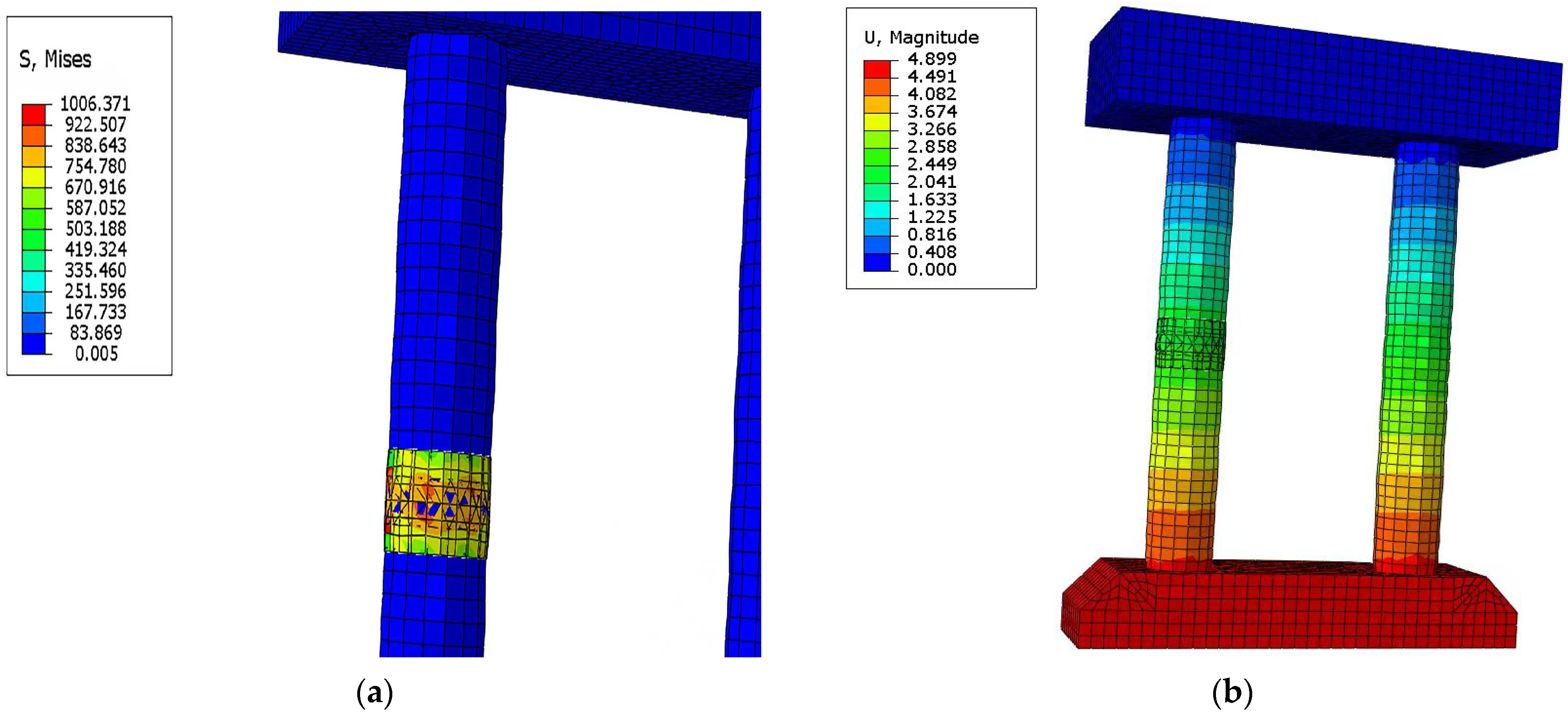
2.2.3. Comparative Analysis of Strengthening Test Results and Simulation Results

The scaled-down test, considering three distinct working conditions (pre-damage, post-damage, and CFRP strengthening), provided experimental results that were used to rigorously calibrate and validate the finite element model. As demonstrated in Figure 10 and Figure 11, the numerical simulations show good agreement with experimental measurements, accurately capturing stress variation trends in reinforcement and concrete as well as strain history and displacement responses at key locations. This validation confirms the model’s accuracy in representing global structural behavior under impact loading and establishes a reliable basis for subsequent parametric studies on strengthening width effects.

Following comparative analysis of stirrup stress, longitudinal reinforcement stress, and surface concrete stress under identical impact conditions through both experimental testing and numerical simulation, the numerical results demonstrate that in the CFRP-strengthened model, the maximum stress in stirrups decreased by 8.85%, longitudinal reinforcement stress reduced by 17.80%, and surface concrete stress declined by 22.90%. While the experimental data for steel reinforcement showed relatively lower values compared to the simulation results—attributable to numerous external disturbances during testing and certain optimizations/simplifications in the numerical model—the overall stress variation trends remained largely consistent between both approaches.

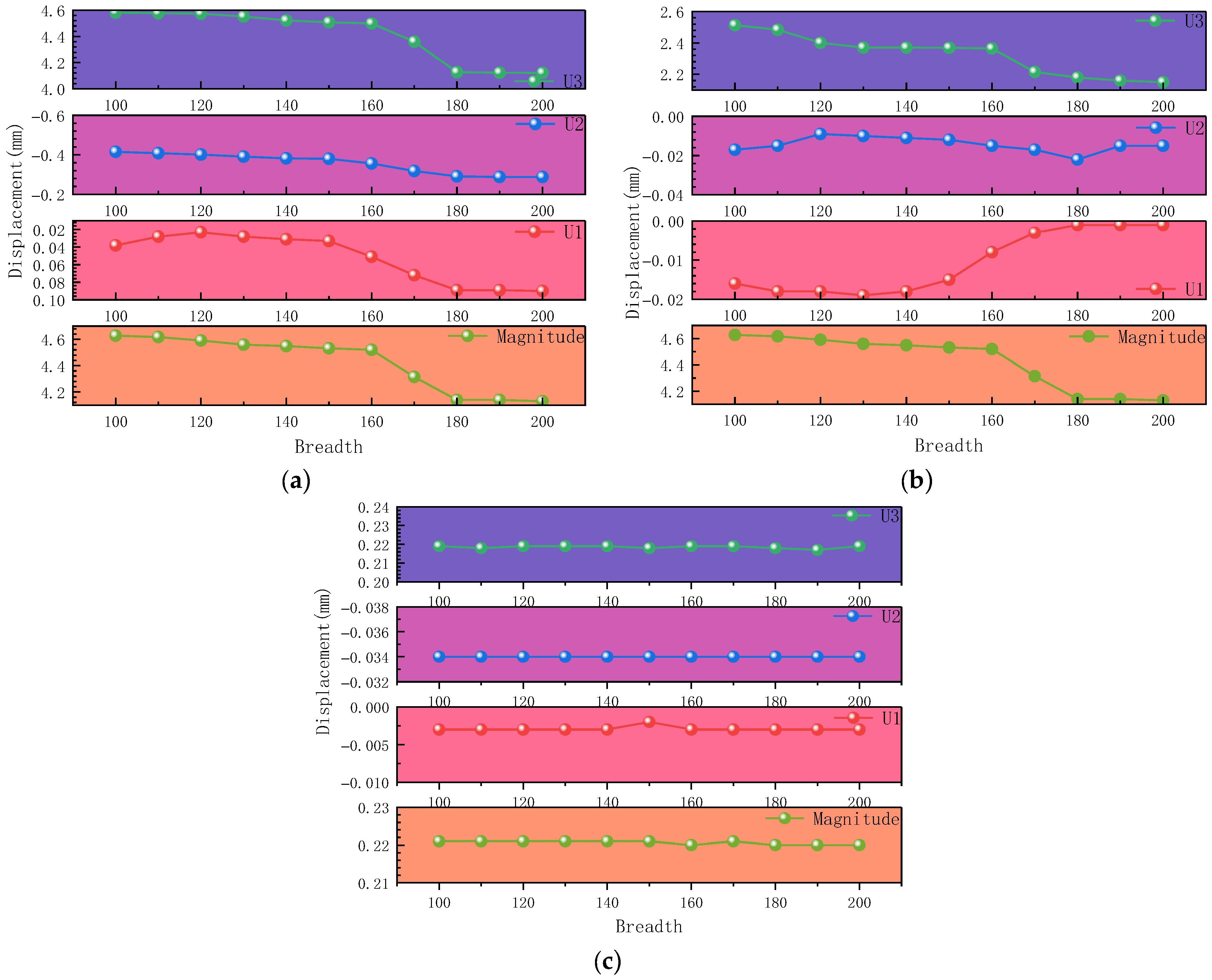
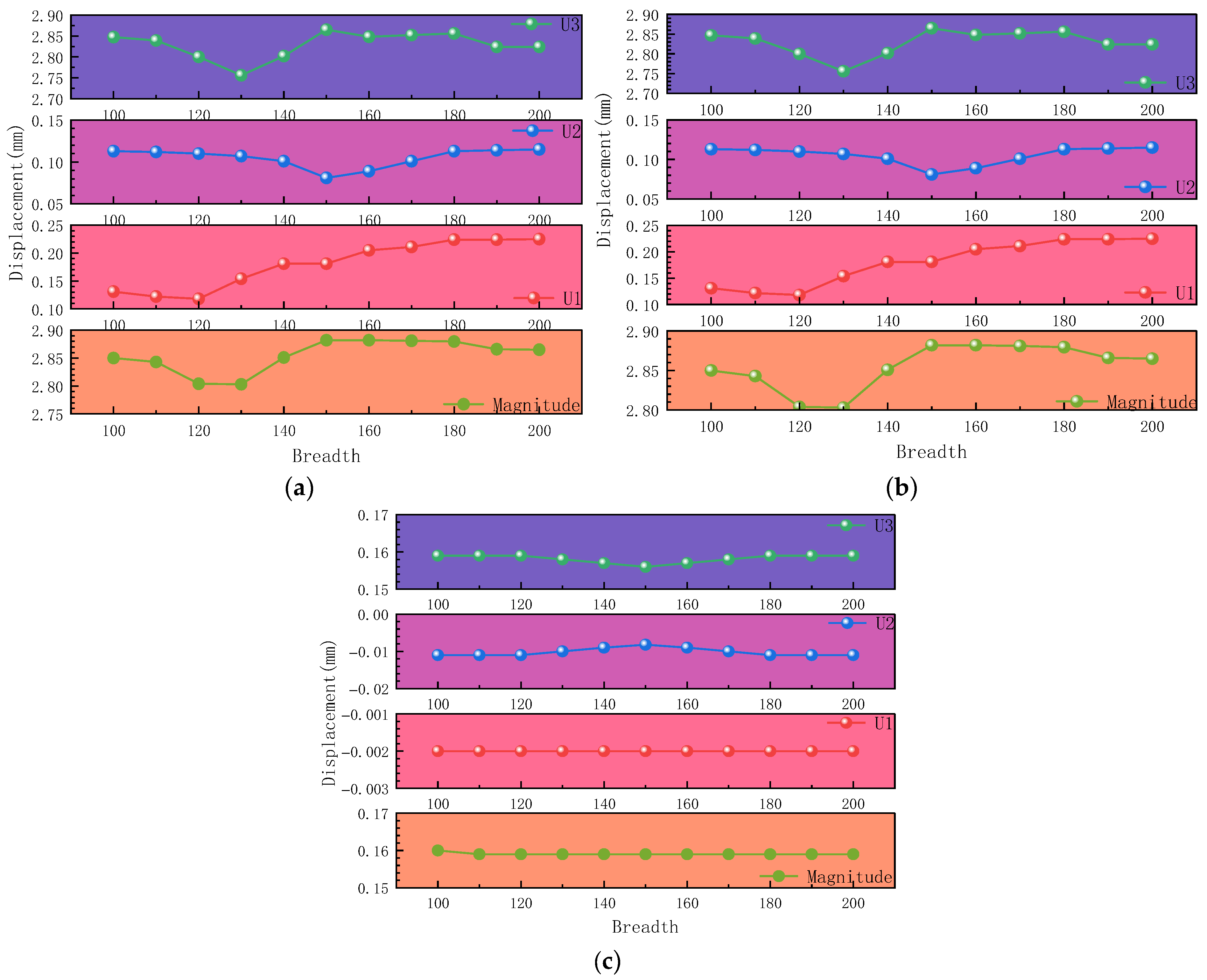
2.3. Finite Element Simulation of Outsourced Carbon Fiber Cloth

Although the method of reinforcing bridge piers with outsourced carbon fiber cloth has been proven to have a certain strengthening effect [16,17]. However, there is currently a lack of clear guidance on the specific specifications and size parameters for strengthening width, highlighting the necessity of studying the impact of strengthening width. Therefore, this study used ABAQUS 2020 finite element simulation technology to simulate the strengthening strategy of using the same thickness of carbon fiber cloth for horizontal winding. Two different dead load cases were considered in the study: Class A dead load, where the upper constant load of the entire bridge span is 3654.4 KN, and Class B dead load, which simulates the live load and gradually loads to reach 5154.5 KN. Through these simulations, the specific impact of different strengthening widths on the strengthening effect of the bridge pier was explored, providing strong technical support and a theoretical basis for future engineering practice. This systematic research method can provide more precise guidance for the application of carbon fiber cloth in bridge strengthening projects, optimize strengthening strategies, and improve the safety and durability of bridge structures.

2.3.1. Establishment of Finite Element Simulation for Outsourced Carbon Fiber Cloth Strengthening

To evaluate the effect of carbon fiber cloth strengthening on bridge piers, this study used ABAQUS finite element software for model establishment and analysis. The bridge pier model was solidly unit modeled at a 1:1 scale according to actual dimensions and material properties. The numerical model used the finite element simulation software ABAQUS for the simulation calculation. The rock was simplified as a rigid sphere for calculation, and according to the geological conditions near a certain bridge in Nanchuan District, Chongqing, the rock density was set to 3 g/cm³, the elastic modulus E = 20,000 MPa, and Poisson’s ratio to 0.3. The strengthening structure was simulated using truss units. The carbon fiber cloth was also modeled using solid units. In the model, the interaction between the carbon fiber cloth and the bridge pier was constrained by defining appropriate adhesive behavior to ensure effective connection between the two. The boundary conditions considered the complete consolidation of the three faces of the base, and in addition, a force point was set at the center of the cap beam surface for load application and coupling analysis, simulating the various loads that the actual bridge may bear during operation.

The establishment of this model strictly followed the coordinate axis position shown in Figure 10, ensuring that the direction of the model was consistent with the direction of the actual bridge structure. During post-processing analysis, all directions were based on the coordinate axis in Figure 12, which was done to ensure that the simulation results could accurately reflect the physical behavior of the actual system. By maintaining this consistency, the accuracy of the simulation results can be improved, and the analysis process can be more reliable and comparable.

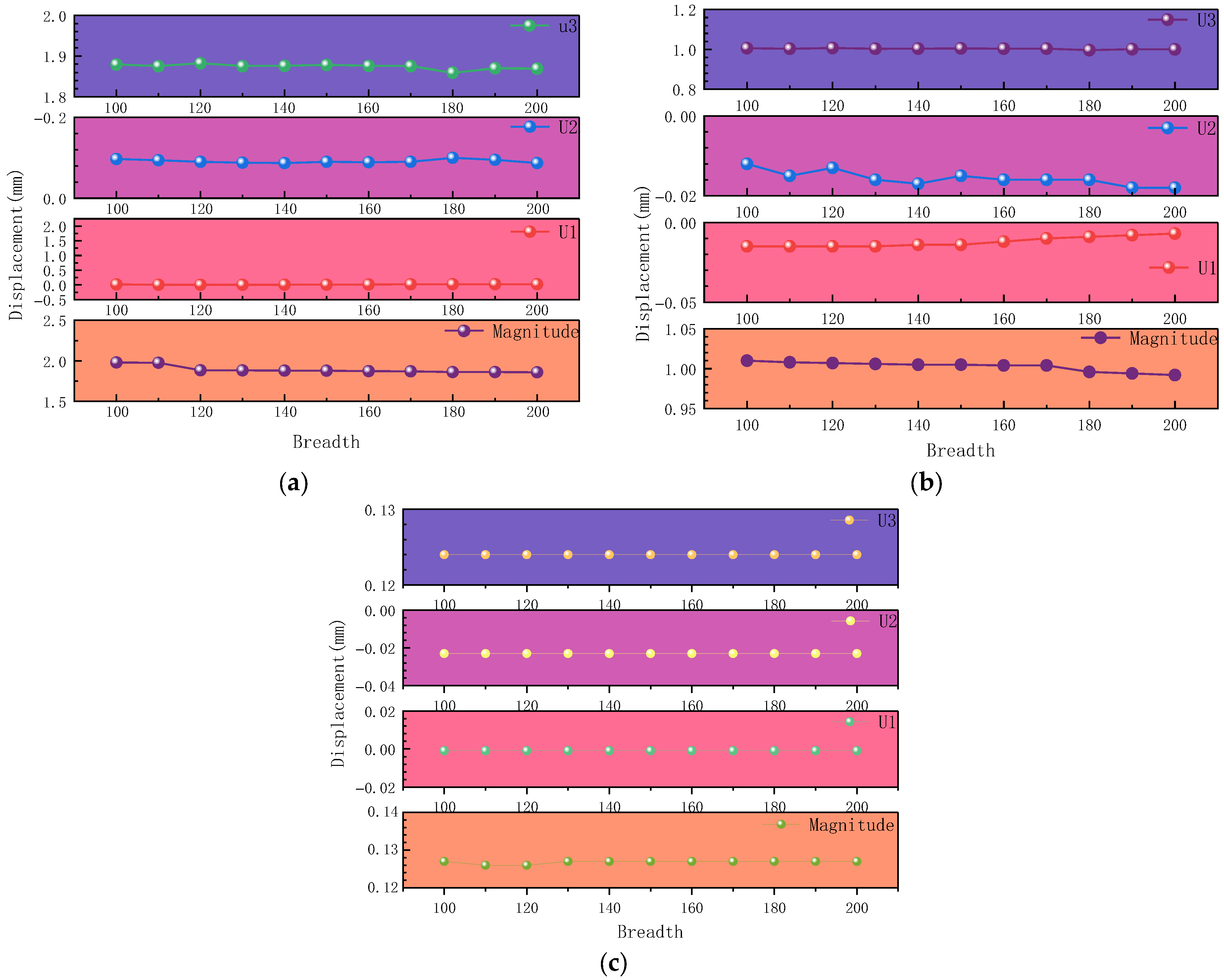
2.3.2. Simulation Under the Action of Class A Dead Load

For the strengthening of local damage to such bridge piers, carbon fiber cloth with a width of 100 cm to 200 cm was used for outsourced carbon fiber cloth strengthening, and Class A dead load was applied to compare the changes in surface stress and bridge pier displacement values at the impact point and along the pier shaft (0/2, 1/2, and 2/2) of the bridge pier, analyzing the strengthening effect of carbon fiber cloth.

After the ABAQUS finite element simulation, the stress variation charts obtained for each face are shown in Figure 13, where S11, S22, and S33 represent the stresses in the X, Y, and Z directions, respectively. S12 represents the stress in the YZ plane along the Y direction, S13 represents the stress in the YZ plane along the Z direction, and S23 represents the stress in the XZ plane along the Z direction. U1, U2, and U3 correspond to the translational degrees of freedom in the X, Y, and Z axes, respectively, and Magnitude is the scalar part of the total displacement.

Figure 13 clearly illustrates the stress distribution of the bridge structure at the 0/2, 1/2, and 2/2 positions under the action of Class A constant loads. The observations indicate that the strain responses at the 0/2 and 2/2 positions are relatively smooth. In contrast, the stress variation is more stable at a width of 120 cm, while the strain variation at the 1/2 position is more pronounced. Further analysis reveals that the strengthening effect at the 1/2 position significantly improves with the increase in the width of the carbon fiber fabric, suggesting a certain correlation between stress variation and the width of the carbon fiber fabric. The strengthening of carbon fiber fabric has a significant impact on the stress variation at specific locations, such as the 1/2 position. The stress variation at the 1/2 position changes significantly with the increase in the width of the carbon fiber fabric, indicating that the strengthening effect of the carbon fiber fabric is effective at this location. This may be because the 1/2 position is a critical area of force on the bridge pier, where the application of carbon fiber fabric can more effectively constrain the concrete, enhancing its compressive and tensile strength.

By simulating under Class A constant loads and extracting the displacement values at various positions, the displacement variation plot is shown in Figure 14.

Upon detailed examination, it is observed that in the U1 direction, the displacement variation at the 0/2 position exhibits a distinct “U”-shaped distribution characteristic. Additionally, in the U2 direction, the displacement variation at this position shows a certain degree of fluctuation. Despite these fluctuations, overall, the strengthening effect significantly improves with the increase in the width of the carbon fiber fabric. This indicates that the carbon fiber fabric strengthening can effectively limit the displacement of the bridge pier, enhancing the stability and safety of the structure. The high modulus characteristic of the carbon fiber fabric makes it highly effective in constraining concrete and controlling crack propagation. The strengthening of carbon fiber fabric has a positive impact on the overall displacement trend of the bridge pier. Apart from the 0/2 position, the displacement in other directions decreases with the increase in the width of the carbon fiber fabric. This suggests that the strengthening of carbon fiber fabric is not only effective at specific locations but also plays a positive role in controlling the overall displacement of the bridge pier. The application of carbon fiber fabric increases the overall stiffness of the bridge pier, reducing deformation under load. The strengthening of carbon fiber fabric optimizes the local stress distribution of the bridge pier. At the 0/2 and 2/2 positions, the stress variation is not significant, which may imply that the stress distribution in these areas is already relatively reasonable, or the strengthening effect of the carbon fiber fabric in these areas is not as pronounced as at the 1/2 position. This suggests that when designing strengthening schemes, we should choose strengthening locations and materials based on the specific loading conditions and damage status of the bridge pier.

Further analysis indicates that for other monitoring positions, the overall trend of displacement variation in both the U1 and U2 directions decreases with the increase in the width of the carbon fiber fabric. This phenomenon demonstrates that the strengthening of carbon fiber fabric plays a positive role in suppressing the increase in displacement, thereby enhancing the stability and load-bearing capacity of the structure.

2.3.3. Simulation Under Class B Permanent Loads

Based on Section 2.2.2, models of bridge piers reinforced with carbon fiber fabric of varying widths were subjected to Class B permanent loads. This simulation aimed to investigate the stress and displacement changes under larger permanent loads in order to determine the influence of carbon fiber fabric width on the strengthening effectiveness under different magnitudes of permanent loads. The stress variations at various locations are depicted in Figure 15.

Observations from Figure 10 clearly indicate that under Class B permanent loads, the stress distribution on the surface of the bridge pier changes significantly with the increase in the width of the carbon fiber fabric, particularly at the 1/2 position of the bridge pier. This suggests that the width of the carbon fiber fabric is a crucial factor affecting the strengthening effectiveness. Wider carbon fiber fabric can more effectively distribute and withstand stress, thereby enhancing the overall load-bearing capacity and durability of the structure. The strengthening effects of carbon fiber fabric vary in different directions. In the S12 direction, the strengthening effect of carbon fiber fabric is significantly enhanced. Although fluctuations in stress variation are observed in the S33 direction, the overall trend is consistent with other directions and positions; that is, the strengthening effect increases with the increase in the width of the carbon fiber fabric. This phenomenon indicates that the strengthening effect of carbon fiber fabric in different directions may be influenced by the loading characteristics and structural geometry. These factors should be considered when designing strengthening schemes to achieve optimal strengthening effects.

Further analysis was conducted to extract the displacement values at various positions under Class B permanent loads, and the variation is shown in Figure 16.

Under the action of Class B loads, observations from Figure 11 clearly demonstrate that the trend of displacement variation in the magnitude of combined displacements decreases with the increase in the width of the carbon fiber fabric. This indicates that the strengthening provided by the carbon fiber fabric plays a positive role in suppressing the increase in displacement. Additionally, similar to the stress variations in other directions, larger loads also result in fluctuating displacement changes. This suggests that when designing strengthening schemes, it is essential to fully consider the magnitude and characteristics of the loads to ensure the stability and safety of the structure under various loading conditions. The effectiveness of carbon fiber fabric strengthening does not increase linearly. Although increasing the width of the carbon fiber fabric generally enhances the strengthening effect, fluctuations in strengthening effectiveness occur in certain positions and directions due to non-uniform loading. This highlights the importance of selecting strengthening locations and materials based on the specific loading conditions and damage status of the bridge pier when designing strengthening schemes. Larger permanent loads can lead to fluctuating displacement changes.

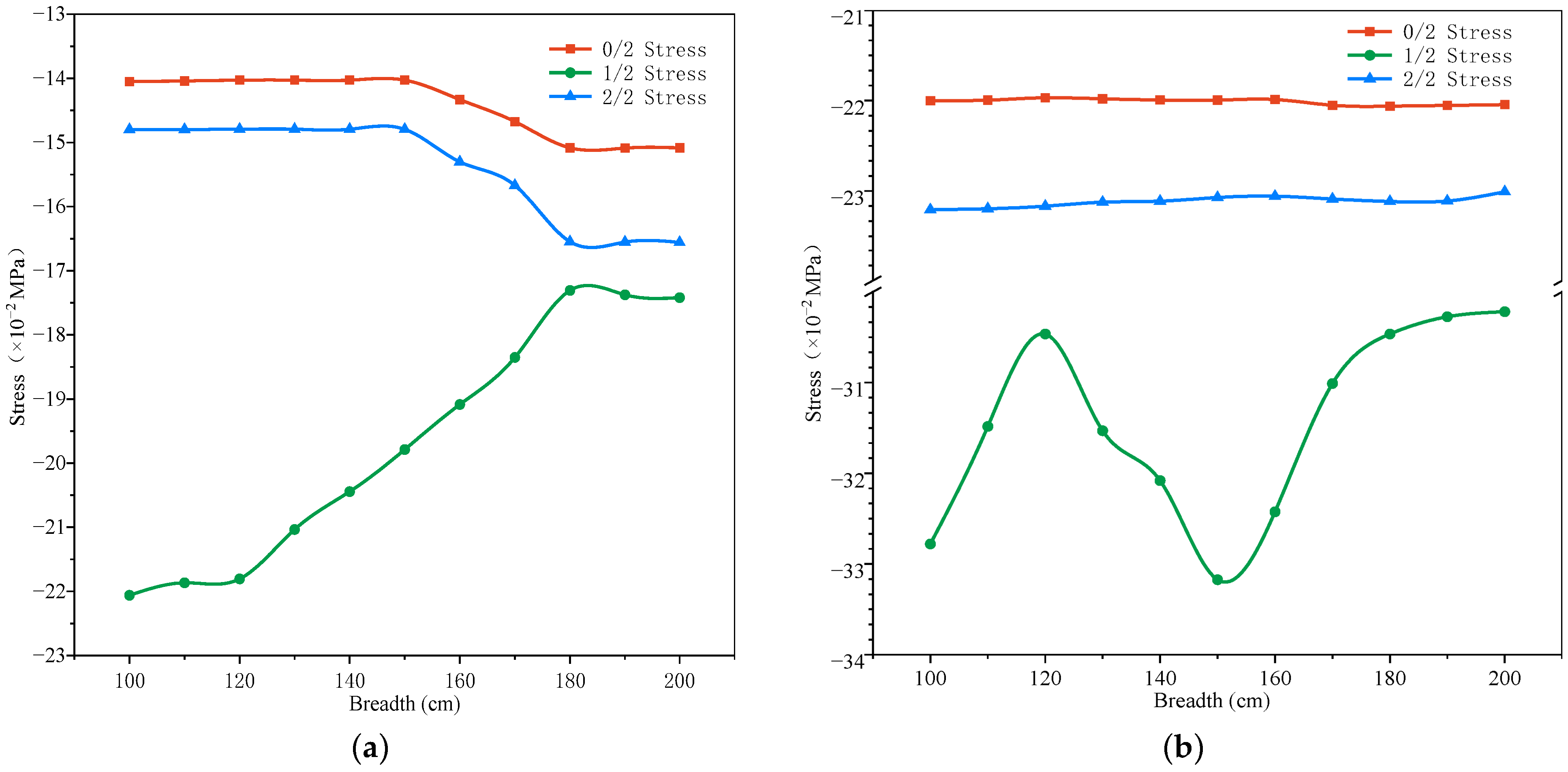
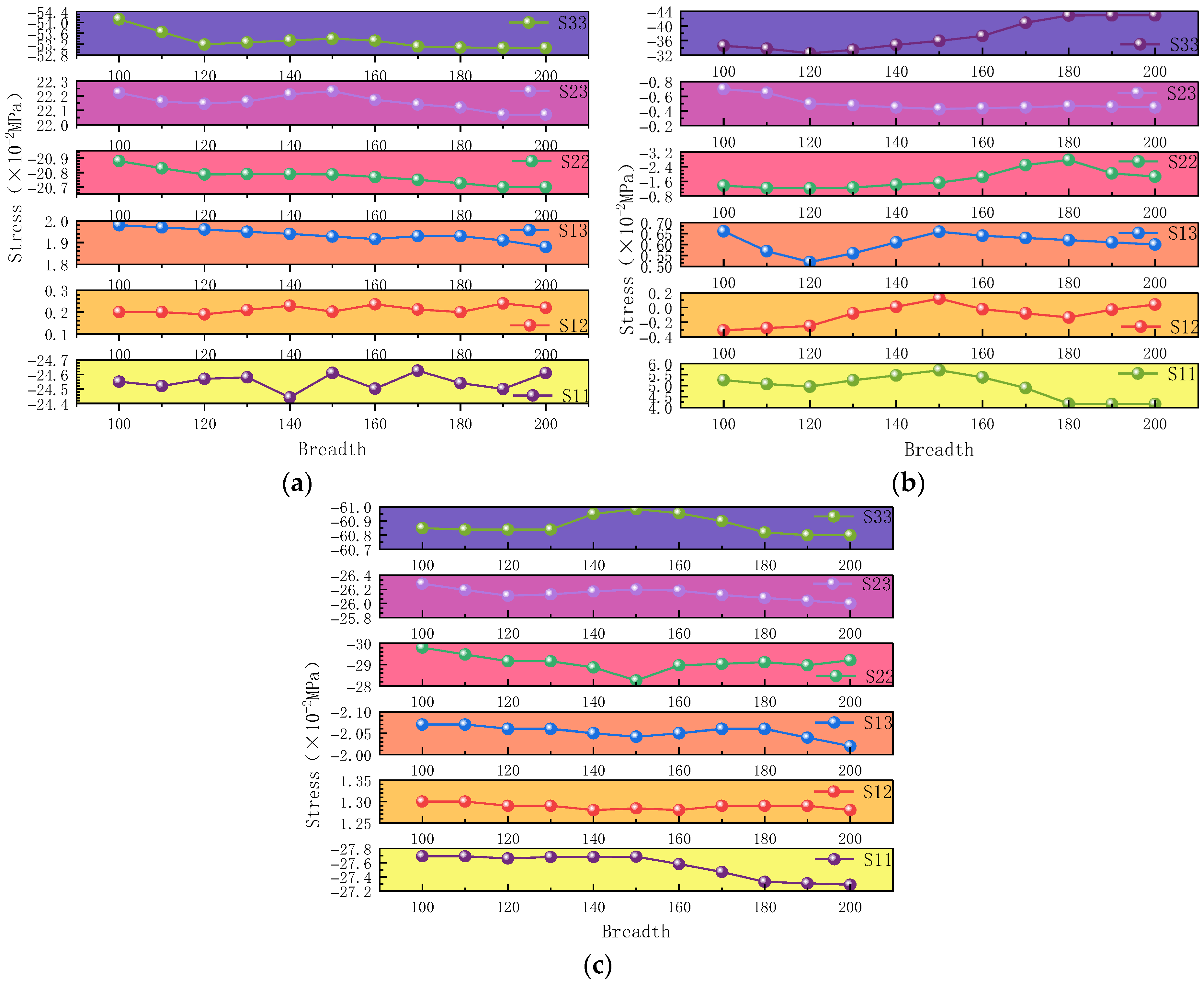
2.4. Influence Function of Carbon Fiber Fabric Width

In the finite element simulation using ABAQUS, there are multifaceted variations in stress and displacement data across different directions. To comprehensively consider the impacts from all directions, this paper adopts an integrated analysis method. Initially, the method extracts stress and displacement data from each direction from the simulation results. Subsequently, the data from each direction are averaged to obtain the mean stress and displacement values. To ensure comparability of the data, these mean values are normalized, bringing the data from different directions to the same scale. In structural analysis, the stress and displacement in different directions have varying effects on the safety and stability of the structure. When the structure is subjected to forces, it often experiences influences from multiple directions simultaneously. Through weighted averaging, the impacts from all directions can be comprehensively considered, yielding a comprehensive analysis result that reflects the changes in all directions. In accordance with the “Code for Strengthening Design of Highway Bridges” [18] (JTG/T 3310-2018), when applying the weighted averaging method, different weights are assigned to different directions based on actual needs, considering that the stress in the vertical and horizontal directions may have different impacts on the safety and stability of the structure. The weights are shown in

Table 2. Weighting Table.

Stress Direction	Weight	Stress Direction	Weight
S11	0.15	U1	0.10
S22	0.10	U2	0.20
S33	0.40	U3	0.70
S12	0.10
S13	0.10
S23	0.15

. Finally, the results of the weighted averaging are synthesized to derive a comprehensive analysis result that fully reflects the changes in all directions. This method not only effectively integrates data from all directions but also provides a comprehensive change analysis for research and offers a feasible numerical analysis method for engineering practice.

Based on the weighting values shown in Table 2, the stress values for Type A and Type B dead loads were calculated, and the resulting stress variations are illustrated in Figure 17.

Due to the limited number of data points, attempts were made to fit the data using quadratic or cubic polynomials. The fitting was performed using the NumPy library in Python 3.7, and the resulting fitting formulas for the width range of 100 cm to 200 cm are as follows:

(1)

Type A Dead Load:

f(x) = −1.247 × 10−5x2 + 0.0336x − 14.285	(0/2 Stress)
f(x) = 2.15 × 10−5x2 − 0.1105x − 22.328	(1/2 Stress)
f(x) = −6.71 × 10−5x2 − 0.0652x − 15.278	(2/2 Stress)

(2)

Type B Dead Load:

f(x) = 3.64 × 10−6x2 − 0.0034x − 21.451	(0/2 Stress)
f(x) = −1.04 × 10−5x2 + 0.0057x − 32.689	(1/2 Stress)
f(x) = 1.55 × 10−5x2 − 0.0108x − 22.726	(2/2 Stress)

Based on the weighting values shown in Table 2, the displacement values for Type A and Type B dead loads were calculated, and the resulting displacement variations are illustrated in Figure 18.

Similarly, the fitting was performed using the NumPy library in Python, and the resulting fitting formulas for the width range of 100 cm to 200 cm are as follows:

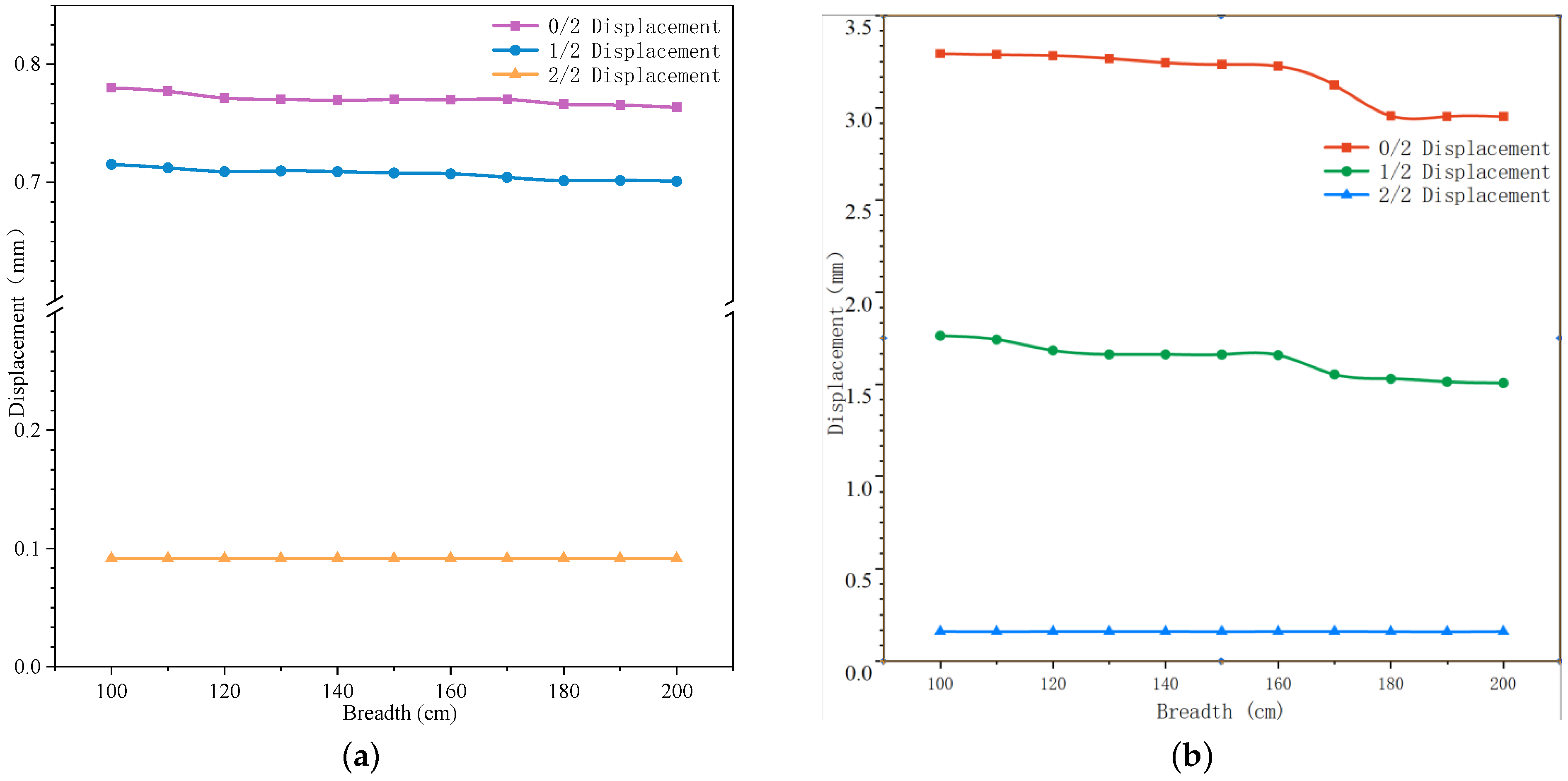
(1)

Type A Dead Load:

f(x) = 1.1543 × 10−6x2 − 0.0021x − 0.9143	(0/2 Stress)
f(x) = −3.5714 × 10−6x2 + 0.0076x − 0.02	(1/2 Stress)
f(x) = 0.0092	(2/2 Stress)

(2)

Type B Dead Load:

f(x) = −6.9 × 10−4x2 + 0.1425x − 0.64	(0/2 Stress)
f(x) = −2.82 × 10−5x2 + 0.0105x − 0.382	(1/2 Stress)
f(x) = −1.81 × 10−5x2 + 0.0039x + 1.73	(2/2 Stress)

3. Study on the Influence of Outer Steel Plate Width

This study utilized ABAQUS finite element simulation to investigate piers reinforced with the same outer steel plate method. Simulation experiments for Type A and Type B dead loads were conducted on outer steel plate schemes with varying widths (each plate thickness being 4 cm). The research aims to systematically analyze the influence of different outer steel plate widths on strengthening effectiveness.

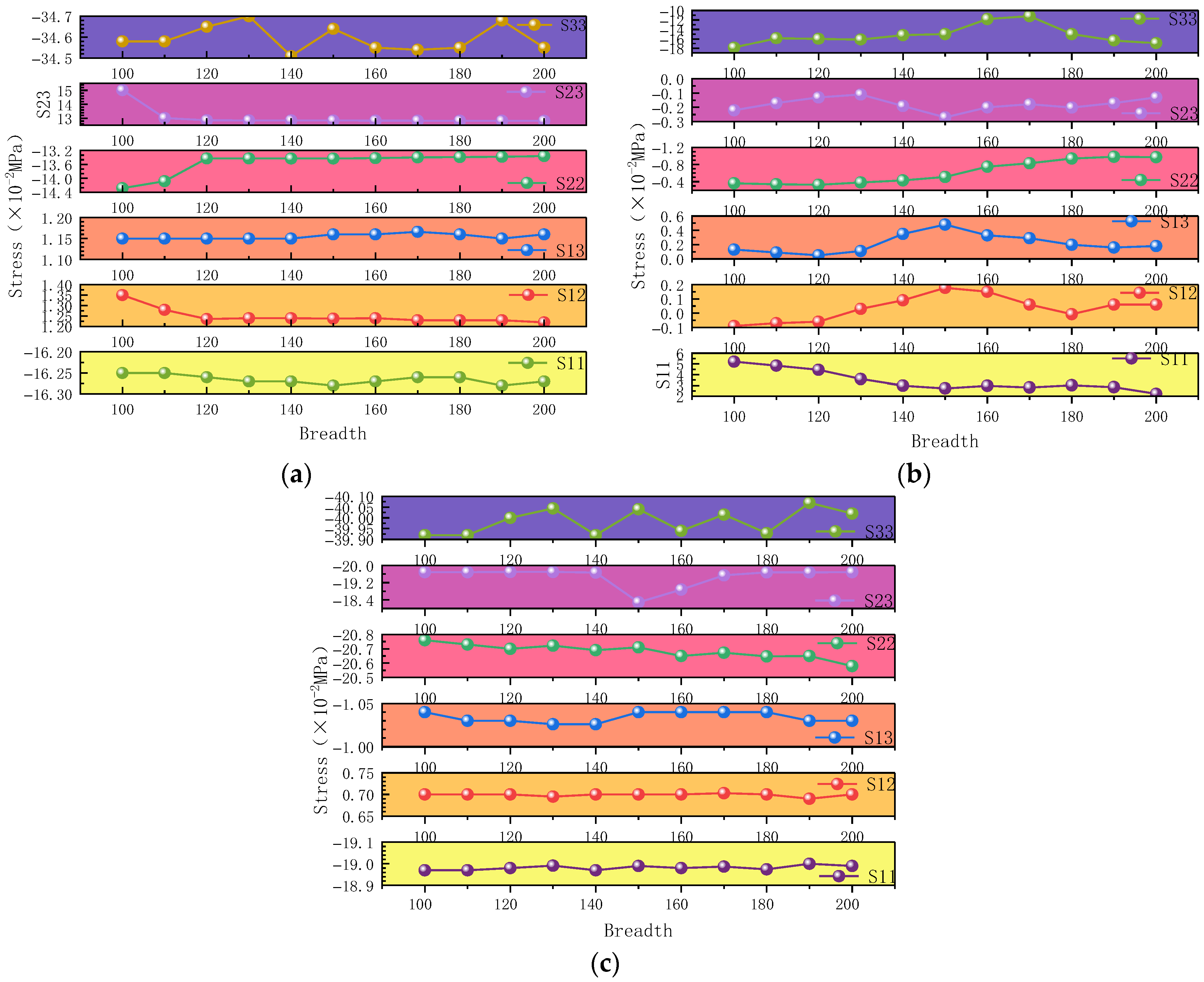
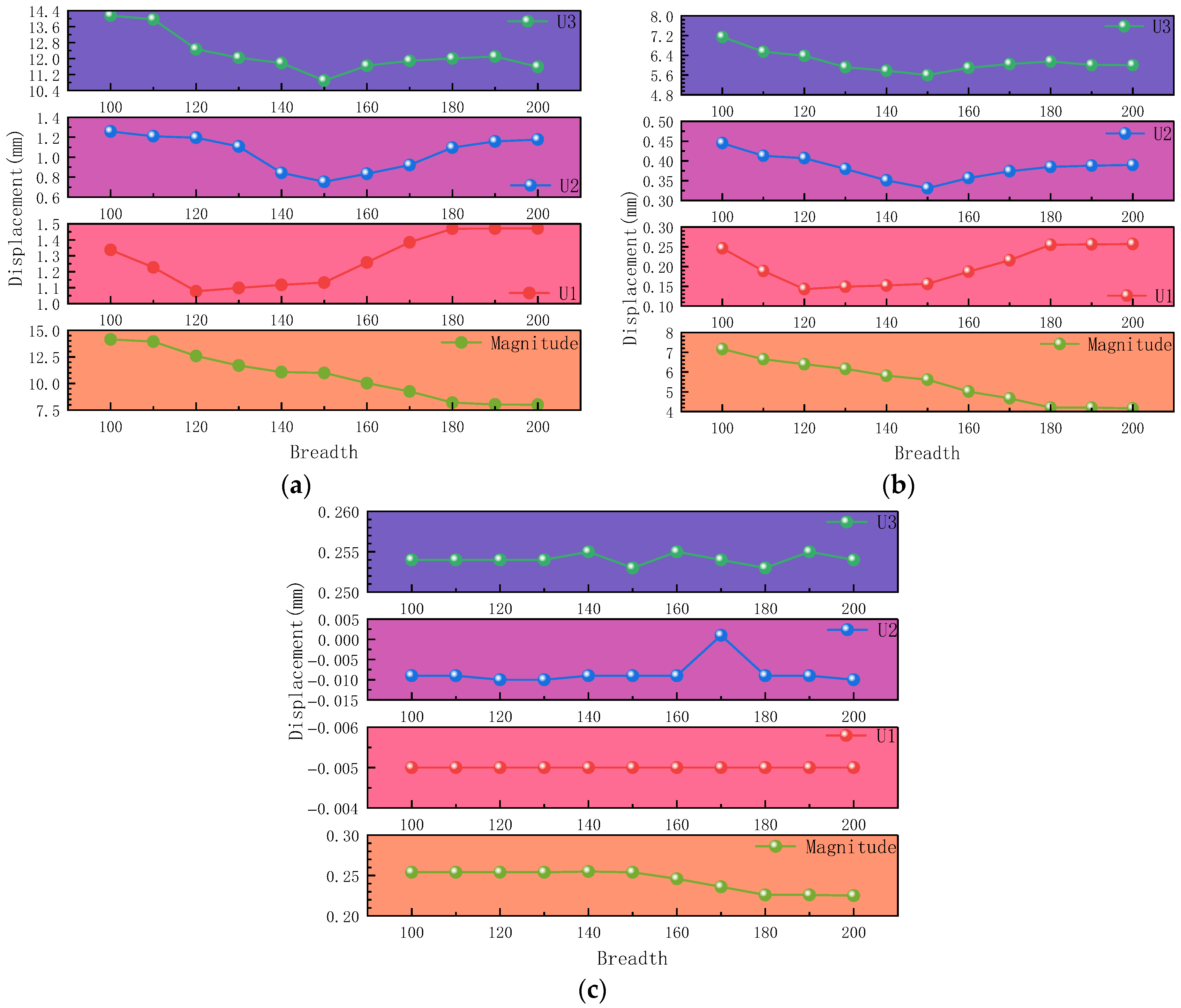
3.1. Establishment of Finite Element Simulation for Outer Steel Plate Strengthening

This study employed the ABAQUS finite element software for model establishment and analysis. The pier was modeled using 1:1 solid elements based on its actual dimensions, with strengthening represented by truss elements and the outer steel plates modeled as solid elements. The model establishment in this chapter is consistent with the conditions described in Section 2.3.1, and a schematic diagram of the model is shown in Figure 19.

3.2. Simulation of Outer Steel Plate Strengthening

3.2.1. Simulation Under Type A Dead Load

To reinforce the local damage of such piers, outer steel plates with widths ranging from 100 cm to 200 cm were applied. Under Type A dead load, the surface stresses and displacement values at the impact points and connection points (0/2 Stress, 1/2 Stress, and 2/2 Stress) of the piers were compared to analyze the strengthening effectiveness of the outer steel plates.

The Stress Variation Plots obtained from the ABAQUS finite element simulation for each surface are shown in Figure 9, where S11, S22, and S33 represent the stresses in the X, Y, and Z directions, respectively. S12 denotes the stress along the Y direction on the YZ plane, S13 represents the stress along the Z direction on the YZ plane, and S23 indicates the stress along the Z direction on the XZ plane.

As shown in Figure 20, the stress variations at 0/2 Stress, 1/2 Stress, and 2/2 Stress of the pier under Type A dead load exhibit distinct characteristics. While the strain changes at 0/2 Stress and 2/2 Stress are not significant, the stress variation at 1/2 Stress shows a pronounced inverted “U” shape, except in the S22 and S23 directions. This trend is primarily attributed to the self-weight of the outer steel plates and the interactions during the component repair process. This observation indicates that the stress variation at 1/2 Stress is influenced by the width of the steel plates, but this influence does not increase linearly with the width.

Further finite element simulation under Type A dead load was conducted to extract displacement variations at various locations, and the Displacement Variation Plot is shown in Figure 21.

As shown in Figure 17, except for 2/2 Stress, the U1 direction exhibits a continuous upward trend, indicating a reduction in strengthening effectiveness in the U1 direction. This trend may be due to the influence of the steel plate’s self-weight, but the small magnitude of change has a limited impact on the overall deformation. It is particularly noteworthy that the stress variation at the 0/2 position in the U1 direction shows a “U”-shaped distribution, with the optimal strengthening effect achieved at a plate width of 150 cm. This suggests that there may be an optimal steel plate width at this location that most effectively distributes stress.

Furthermore, for stress variations in other directions, the overall trend is that the strengthening effect improves with increasing outer steel plate width, while the displacement trend generally decreases. This indicates that increasing the plate width can enhance the pier’s load-bearing capacity in these directions.

3.2.2. Simulation Under Type B Dead Load

Based on Section 3.2.1, Type B dead load was applied to the pier models reinforced with steel plates of varying widths to simulate stress and displacement variations under larger dead loads, aiming to determine the influence of carbon fiber sheet width on strengthening effectiveness under different dead load magnitudes. The stress variations at various locations are shown in Figure 22.

As shown in Figure 22, specific trends in stress variation emerge with increasing steel plate width, particularly at the 1/2 Stress of the pier. The stress variation in the S12 direction exhibits a fluctuating upward pattern, likely due to the structural nonlinear response or local stress concentration, causing the stress to fluctuate and rise with increasing width. Notably, in the S33 direction, the stress increases with the width due to factors such as self-weight, stabilizing at a width of 180 cm. In other directions, the strengthening effect improves with increasing plate width, with the regions showing the largest variations exhibiting fluctuations. This phenomenon indicates that initially increasing the plate width can significantly enhance the strengthening effect, but as the width continues to increase, the improvement in strengthening effectiveness may fluctuate.

The displacement values under Type B dead load were extracted for various locations, and the variations are shown in Figure 23.

As shown in Figure 23, under Type B load, the overall trend of displacement in the magnitude resultant displacement decreases with increasing plate width, indicating that increasing the steel plate width can effectively reduce the total displacement of the pier under Type B load, which is a direct reflection of the strengthening effect. In other directions, particularly at the 0/2 position in U2, the displacement exhibits fluctuating changes due to the larger load. This may be related to the local structural characteristics at this position, such as material inhomogeneity or local structural damage, leading to unstable displacement responses under larger loads.

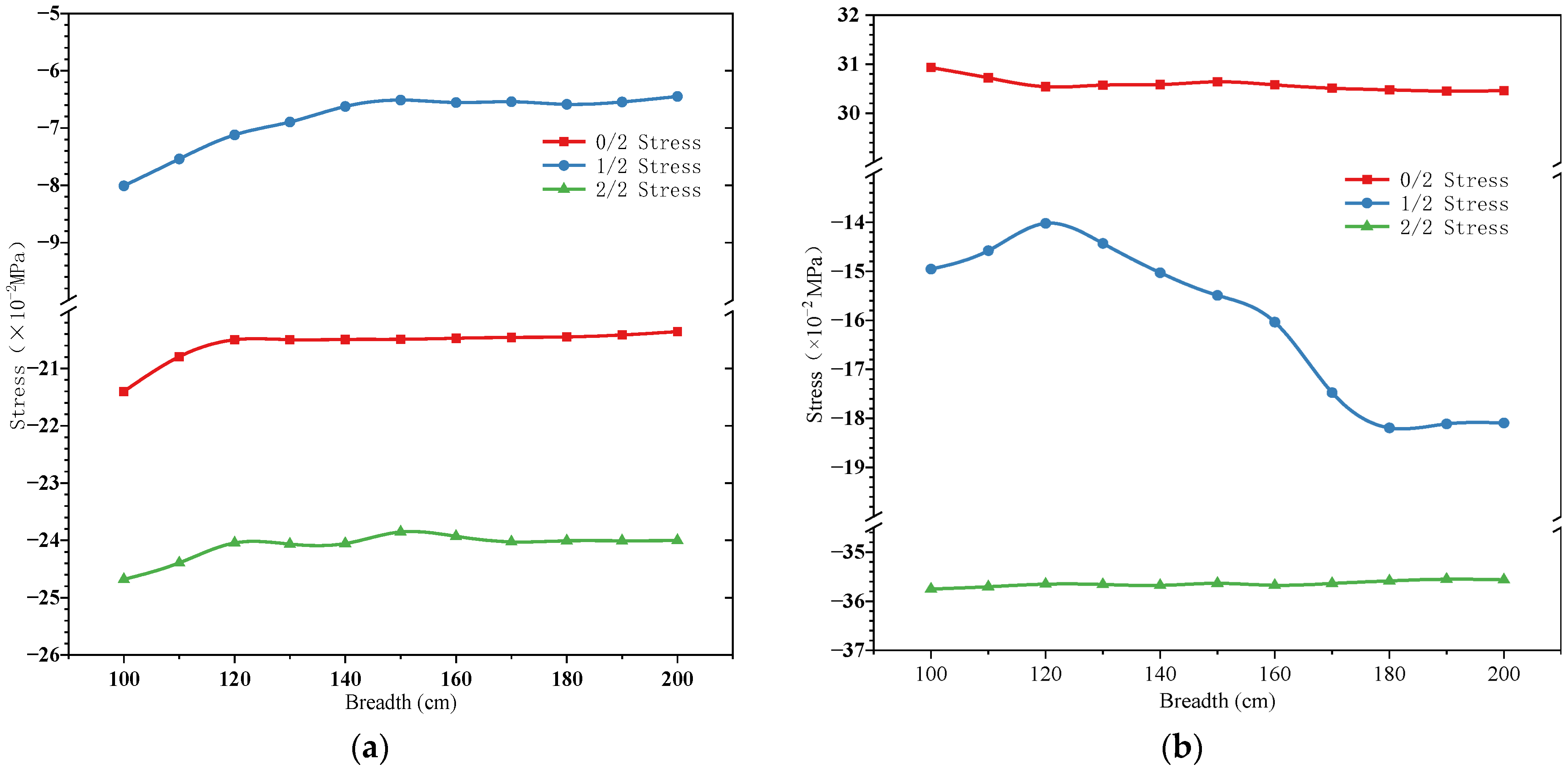
3.3. Influence Function of Steel Plate Width

In the ABAQUS finite element simulation, the stress and displacement data in various directions may exhibit multifaceted variations. This chapter follows the weighted average calculation method described in Chapter 1, with the weights as shown in Table 2. The stress values for Type A and Type B dead loads were calculated based on the weighting values shown in Table 2, and the resulting stress variations are illustrated in Figure 24.

Based on the weighted stress variations obtained from Figure 21, the data were fitted using quadratic or cubic polynomials. The fitting was performed using the NumPy library in Python, and the resulting fitting formulas for the width range of 100 cm to 200 cm are as follows:

(1)

Type A Dead Load:

f(x) = −4.86 × 10−4x2 + 0.0942x − 22.1	(0/2 Stress)
f(x) = 0.0004x2 − 0.1405x − 14.84	(1/2 Stress)
f(x) = −7.196 × 10−5x2 − 0.0032x − 24.75	(2/2 Stress)

(2)

Type B Dead Load:

f(x) = −5.663 × 10−6x2 + 5.359 × 10 − 3x + 29.39	(0/2 Stress)
f(x) = −1.346 × 10−2x2 + 2.076x − 57.52	(1/2 Stress)
f(x) = −1.68 × 10−3x2 + 0.248x − 35.35	(2/2 Stress)

Based on the weighting values shown in Table 2, the displacement values for Type A and Type B dead loads were calculated, and the resulting displacement variations are illustrated in Figure 25.

Similarly, the fitting was performed using the NumPy library in Python, and the resulting fitting formulas for the width range of 100 cm to 200 cm are as follows:

(1)

Type A Dead Load:

f(x) = −1.761 × 10−5x2 + 0.0034x + 1.045	(0/2 Stress)
f(x) = −6.648 × 10−6x2 + 2.488 × 10 − 4x + 1.078	(1/2 Stress)
f(x) = −3.551 × 10−7x2 + 7.28 × 10 − 5x + 0.11	(2/2 Stress)

(2)

Type B Dead Load:

f(x) = 3.079 × 10−4x2 + 0.1781x − 232.5	(0/2 Stress)
f(x) = −1.581 × 10−4x2 + 0.06149x − 610.4	(1/2 Stress)
f(x) = −3.611 × 10−7x2 + 6.372 × 10 − 5x + 0.1482	(2/2 Stress)

4. Conclusions

This study systematically investigated the influence of strengthening width on the impact resistance of circular bridge piers strengthened with CFRP wraps and steel jackets. Through combined experimental and numerical analysis, the following main conclusions are drawn:

(1)

Strengthening width significantly affects the structural response, with the most pronounced effect observed at the pier’s mid-height (L/2) section. Both stress distribution and displacement variations show substantial sensitivity to width changes under different loading conditions.

(2)

The width–effectiveness relationship demonstrates a positive but nonlinear characteristic. While wider strengthening generally enhances performance, an optimal width exists beyond which marginal benefits diminish due to factors such as material self-weight and stress redistribution.

(3)

The developed weighted analysis methodology, integrating multi-directional stress and displacement data based on structural safety relevance, provides a more comprehensive assessment framework than conventional single-parameter evaluations.

(4)

Practical design tools have been established through fitted formulas for both CFRP and steel jacket strengthening methods within the 100–200 cm width range, offering direct guidance for engineering applications against rockfall impacts.

Based on the findings and limitations of this study, future research should aim to develop instrumented impact tests for quantifying energy dissipation mechanisms; investigate localized failure mechanisms through refined modeling techniques for stress distribution around impact indentations; and explore the coupled effects of strengthening width, number of CFRP layers, and material thickness to develop more comprehensive design methodologies.