An Isotropic Model for Cyclic Plasticity Calibrated on the Whole Shape of Hardening/Softening Evolution Curve
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Testing
2.2. Kinematic and Isotropic Plasticity Models: Theoretical Background
2.2.1. Kinematic Material Model
2.2.2. Isotropic Material Model
2.2.3. Material Model Calibration
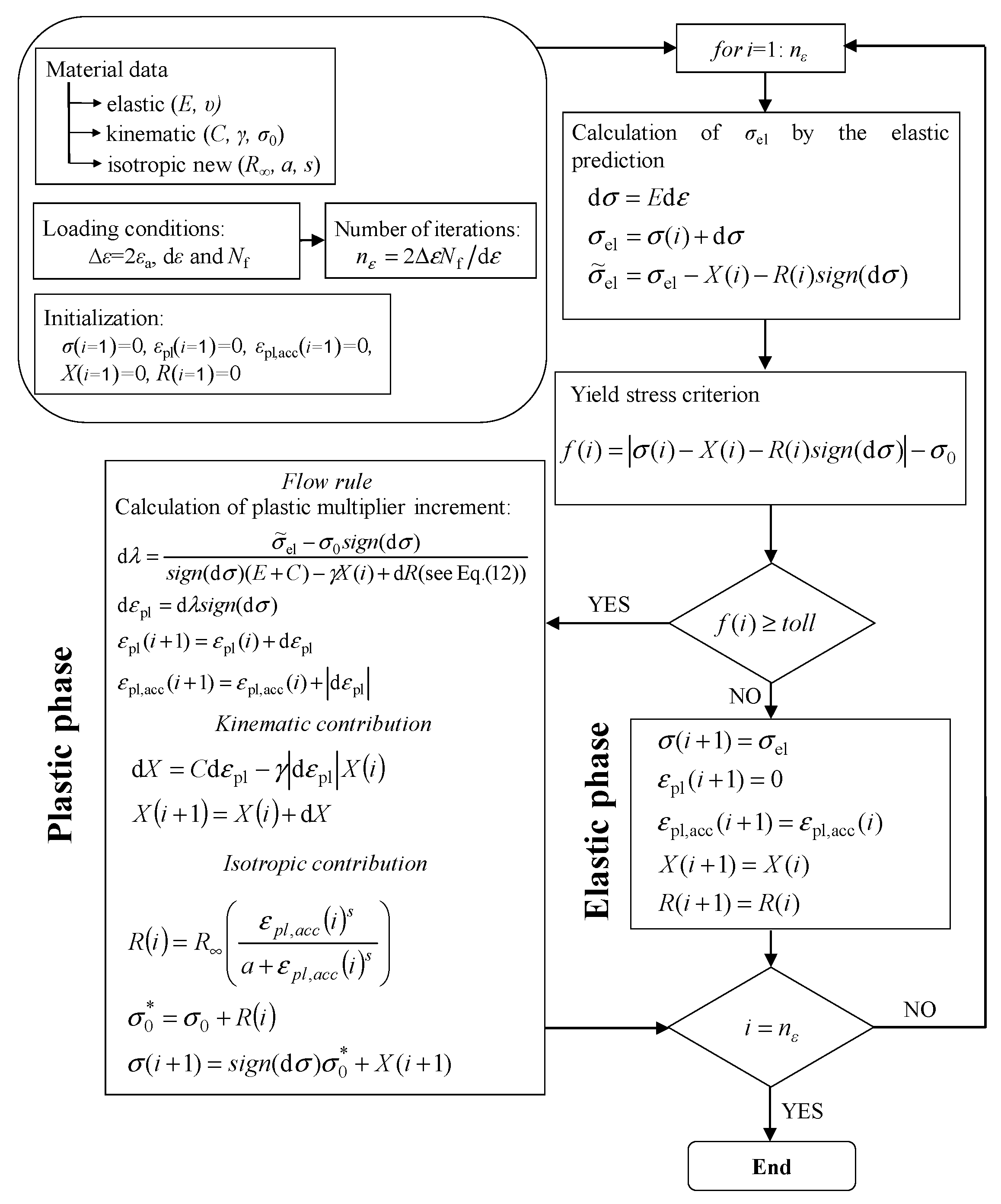
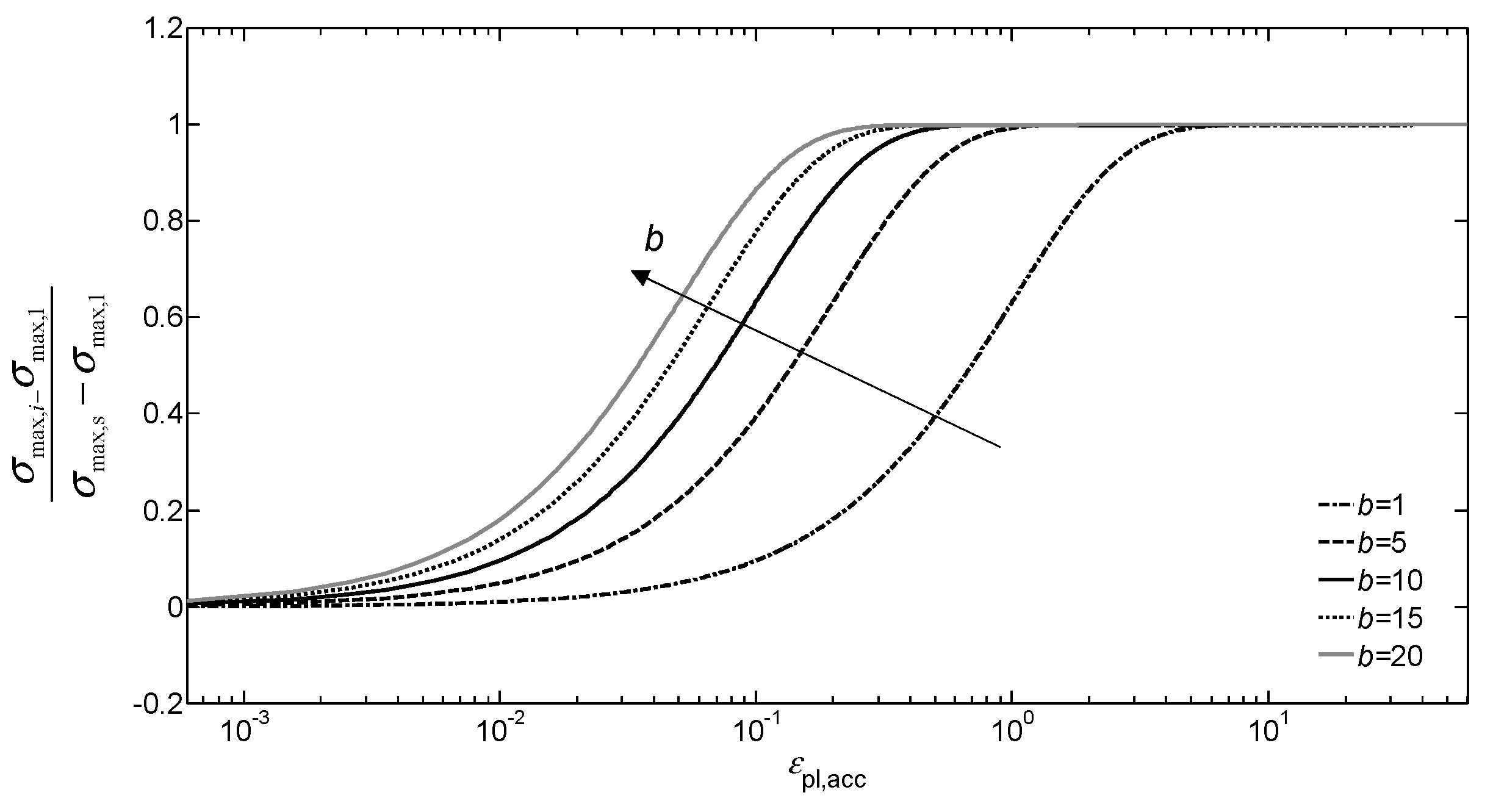
3. Proposed Isotropic Model
4. Results and Discussion
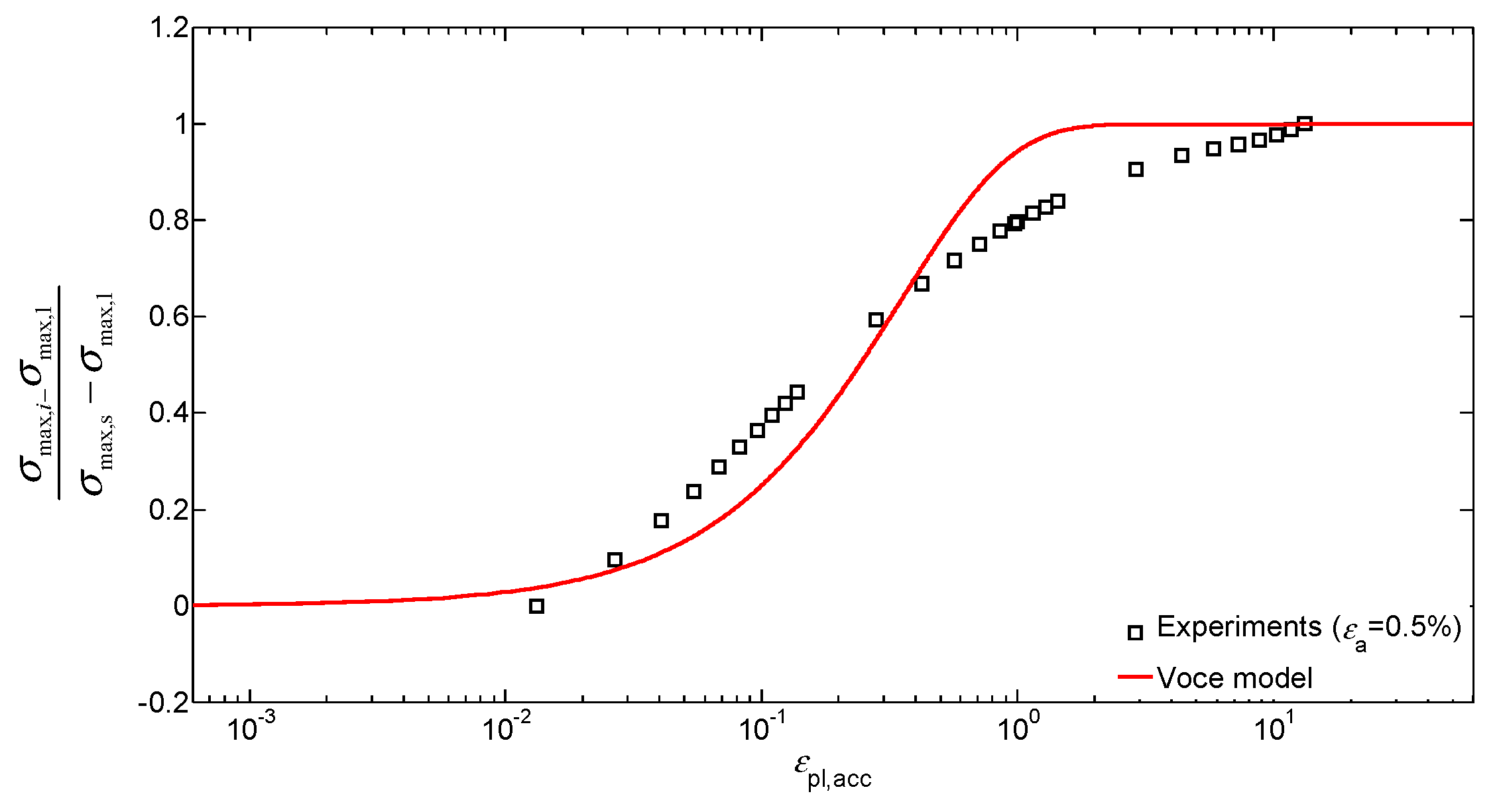
4.1. Stress-Strain Behavior: Isotropic Model (Voce)
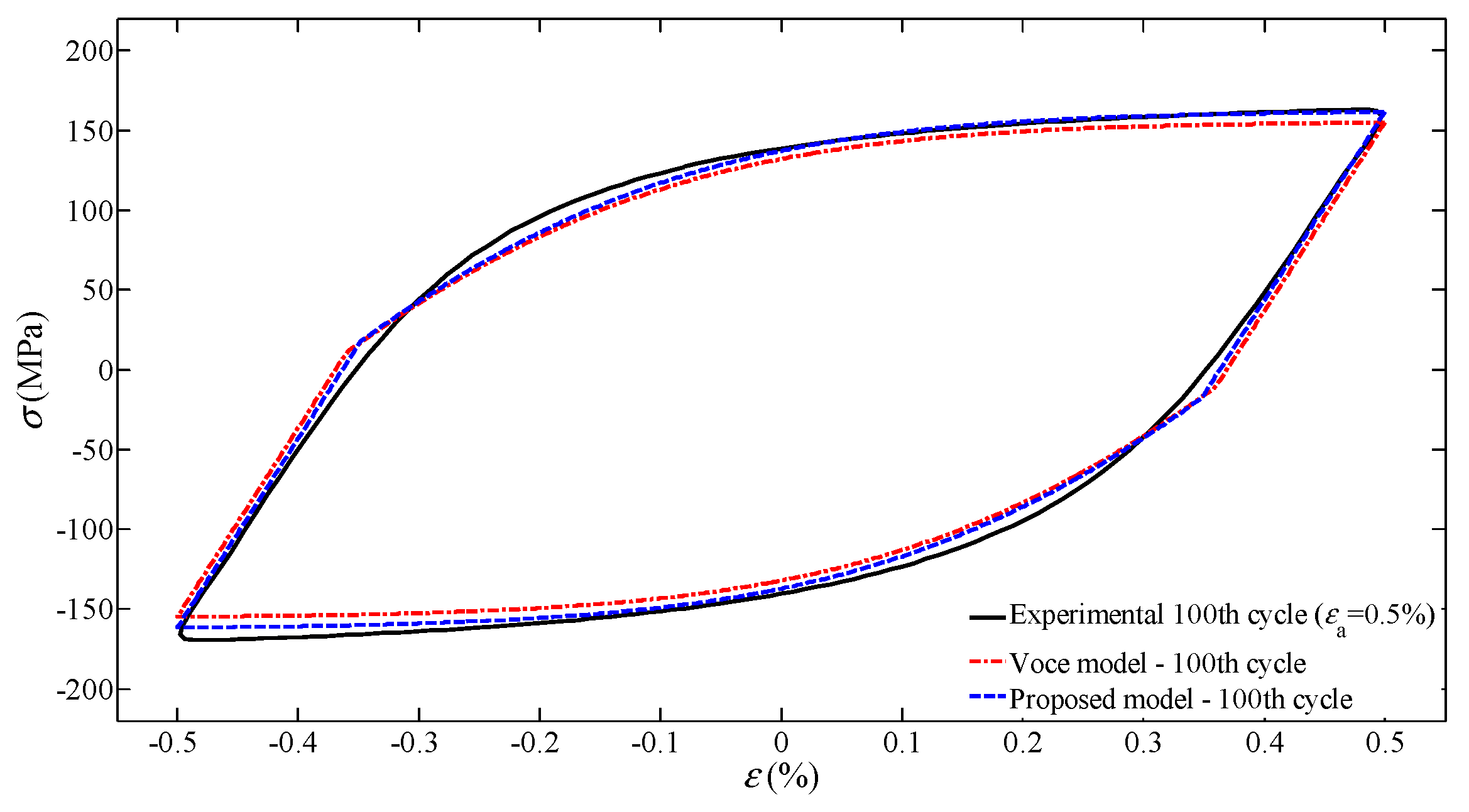
4.2. Stress-Strain Behavior: Proposed Isotropic Model
4.3. Error Analysis
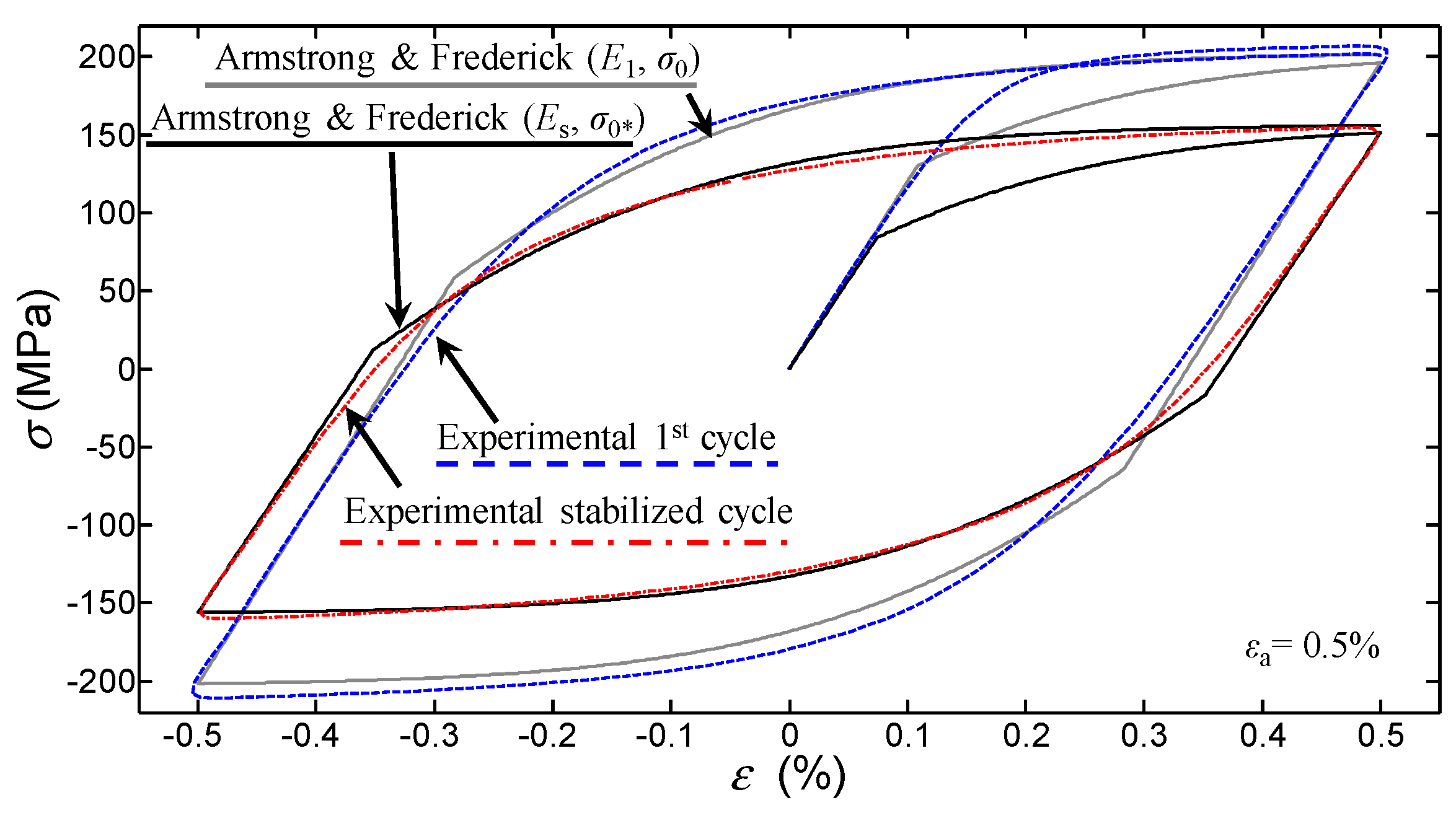
4.4. Combined Armstrong-Frederick with Proposed Isotropic Model: Stress-Strain Evolution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Moro, L.; Benasciutti, D.; De Bona, F. Simplified numerical approach for the thermo-mechanical analysis of steelmaking components under cyclic loading: An anode for electric arc furnace. Ironmaking Steelmaking 2019, 46, 56–65. [Google Scholar] [CrossRef]
- Moro, L.; Srnec Novak, J.; Benasciutti, D.; De Bona, F. Thermal distortion in copper moulds for continuous casting of steel: Numerical study on creep and plasticity effect. Ironmaking Steelmaking 2019, 46, 97–103. [Google Scholar] [CrossRef]
- You, J.H.; Miskiewicz, M. Material parameters of copper and CuCrZr alloy for cyclic plasticity at elevated temperatures. J. Nucl. Mater 2008, 373, 269–274. [Google Scholar] [CrossRef] [Green Version]
- Hatanaka, K.; Yamada, T.; Hirose, Y. An effective plastic strain component for low cycle fatigue in metals. JSME 1980, 23, 791–797. [Google Scholar] [CrossRef]
- Benasciutti, D.; Srnec Novak, J.; Moro, L.; De Bona, F.; Stanojevic, A. Experimental characterization of a CuAg alloy for thermo-mechanical applications. Part 1: Identifying parameters of non-linear plasticity models. Fatigue Fract. Eng. Mater Struct. 2018, 41, 1364–1377. [Google Scholar] [CrossRef]
- Goodall, I.W.; Hales, R.; Walters, D.J. On constitutive relations and failure criteria of an austenitic steel under cyclic loading at elevated temperature. In IUTAM Symp. Creep in Structures; Ponter, A.R.S., Hayhurst, D.R., Eds.; Springer: Leicester, UK, 1980; pp. 103–127. [Google Scholar]
- Basan, R.; Franulovic, M.; Prebil, I.; Kunc, R. Study on Ramberg-Osgood and Chaboche models for 42CrMo4 steel and some approximations. J. Constr. Steel Res. 2017, 136, 65–74. [Google Scholar] [CrossRef]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Kang, G.; Ohno, N.; Nebu, A. Constitutive modeling of strain range dependent cyclic hardening. Int. J. Plast. 2003, 19, 1801–1819. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Dang Van, K.; Cordier, G. Modelization of the strain memory effect on cyclic hardening of 316 stainless steel. In Proceedings of the Conference on Structural Mechanics in Reactor Technology, SMiRT 5, Berlin, Germany; 1979. [Google Scholar]
- ASTM B 124-B 124M. Standard Specification for Copper and Copper Alloy Forging Rod, Bar, and Shapes; ASTM International: West Conshohocken, PA, USA, 2008. [Google Scholar]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Chaboche, J.L. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Chaboche, J.L. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Dunne, F.; Petrinic, N. Introduction to Computational Plasticity; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Chen, W.F.; Zhang, H. Plasticity for Structural Engineers; Springer: New York, NY, USA, 1988. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: New York, NY, USA, 1998. [Google Scholar]
- Voce, E. A practical strain hardening function. Metallurgia 1955, 51, 219–226. [Google Scholar]
- Chaboche, J.L.; Cailletaud, G. On the calculation of structures in cyclic plasticity or viscoplasticity. Comput. Struct. 1986, 23, 23–31. [Google Scholar] [CrossRef]
- Novak, S.J.; Stanojevic, A.; Benasciutti, D.; De Bona, F.; Huter, P. Thermo-mechanical finite element simulation and fatigue life assessment of a copper mould for continuous casting of steel. Procedia Eng. 2015, 133, 688–697. [Google Scholar] [CrossRef]
- Novak, S.J.; Benasciutti, D.; De Bona, F.; Stanojevic, A.; De Luca, A.; Raffaglio, Y. Estimation of material parameters in nonlinear hardening plasticity models and strain life curves for CuAg alloy. Mater. Sci. Eng. 2016, 119, 1–9. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 6th ed.; John Wiley Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Zhao, L.G.; Tong, B.; Vermeulen, B.; Byrne, J. On the uniaxial mechanical behaviour of an advanced nickel base superalloy at high temperature. Mech. Mater. 2001, 33, 593–600. [Google Scholar] [CrossRef]



| Strain Amplitude | Material Parameters | Error Index (SSE) | ||||
|---|---|---|---|---|---|---|
| εa | R∞ (MPa) | Voce | Proposed | Voce | Proposed | |
| b | a | s | ||||
| 0.15% | −56 | 1.307 | 0.514 | 0.923 | 1.914 | 1.601 |
| 0.175% | −71 | 1.197 | 0.491 | 0.978 | 0.654 | 0.455 |
| 0.2% | −80 | 3.145 | 0.316 | 0.778 | 0.464 | 0.063 |
| 0.3% | −84 | 3.620 | 0.223 | 0.802 | 0.338 | 0.022 |
| 0.4% | −83 | 4.488 | 0.179 | 0.855 | 0.292 | 0.016 |
| 0.5% | −52 | 2.871 | 0.234 | 0.893 | 0.269 | 0.014 |
| 0.6% | −52 | 2.581 | 0.290 | 0.853 | 0.298 | 0.019 |
| 0.7% | −69 | 4.208 | 0.101 | 1.203 | 0.069 | 0.017 |
| Single values | R∞,ave1 | ball1 | aall1 | sall1 | 3.401 | 1.766 |
| −68 | 2.352 | 0.199 | 0.965 | |||
| Strain Amplitude | Error Index (SSE) | |
|---|---|---|
| εa | Voce | Proposed |
| 0.3% | 0.493 | 0.080 |
| 0.5% | 0.289 | 0.021 |
| 0.7% | 0.340 | 0.094 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srnec Novak, J.; De Bona, F.; Benasciutti, D. An Isotropic Model for Cyclic Plasticity Calibrated on the Whole Shape of Hardening/Softening Evolution Curve. Metals 2019, 9, 950. https://doi.org/10.3390/met9090950
Srnec Novak J, De Bona F, Benasciutti D. An Isotropic Model for Cyclic Plasticity Calibrated on the Whole Shape of Hardening/Softening Evolution Curve. Metals. 2019; 9(9):950. https://doi.org/10.3390/met9090950
Chicago/Turabian StyleSrnec Novak, Jelena, Francesco De Bona, and Denis Benasciutti. 2019. "An Isotropic Model for Cyclic Plasticity Calibrated on the Whole Shape of Hardening/Softening Evolution Curve" Metals 9, no. 9: 950. https://doi.org/10.3390/met9090950





