Next Article in Journal
Microstructural Evolution and Fatigue Behavior of Laser-Welded Joints in Air-Cooled Steel
Previous Article in Journal
Impact of Diamond Indenter Sliding Velocity on Shear Deformation and Hardening of AISI 304 Steel Surface Layer in Nanostructuring Burnishing: Simulation and Experiment
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 16
Issue 1
10.3390/met16010064
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Universal Empirical Criterion for Martensitic Transformation Temperature in Ni-Mn-Based Heusler Alloys

by
Michal Rameš
and
Oleg Heczko
*
FZU—Institute of Physics of the Czech Academy of Sciences, Na Slovance 1999/2, 182 00 Prague, Czech Republic
*
Author to whom correspondence should be addressed.
Metals 2026, 16(1), 64; https://doi.org/10.3390/met16010064 (registering DOI)
Submission received: 7 November 2025 / Revised: 19 December 2025 / Accepted: 24 December 2025 / Published: 4 January 2026
(This article belongs to the Section Metallic Functional Materials)
Browse Figures
Versions Notes

Abstract

We studied the changes of martensite average temperature TM in a wide range of Heusler alloys derived from a Ni-Mn-Ga multifunctional compound prepared by arc melting. Based on prepared alloys and supplemented by the literature data, we demonstrated that criteria based on valence electron or non-bonding electron concentration per atom often failed in many different cases, in particular for isoelectronic compounds and Heusler alloys with Sb and Sn. Thus, we suggest an empirical criterion for estimating the temperature of martensitic transformation TM in Ni-Mn-based Heusler alloys. It is built on valence electron concentration per atomic volume. Suggested criterion well-describes the experiment and data available in literature. Although it can be used for predicting TM in complexly alloyed Ni-Mn-based Heusler alloys.

1. Introduction

Multiferroic behavior of Heusler alloys are conditioned by the existence of martensitic transformation (MT). This first order, diffusionless displacive transformation from the parent high symmetry phase called austenite to low symmetry phase called martensite, establishes the ferroelastic order in the martensite. Together with the existence of ferromagnetic ordering, it results in multiferroic elasto-magnetic coupling [1], allowing structure manipulation by magnetic field [2] or mechanical manipulation of the magnetic state [3,4]. Moreover, the martensitic transformation is behind the large magnetocaloric effect [5], potentially more efficient than traditional vapor technology used today.
Heusler alloys, in general, are ternary compounds of X2YZ formula where X and Y are transition metals and Z is usually semimetal. The existence of MT is not a general property of Heusler alloys, and Heusler alloys exhibiting MT are often Ni-based. While the existence of MT can be tailored by changing the ratio of basic elements (i.e., in off-stoichiometric alloys) usually for obtaining MT in suitable temperature range, the basic compounds are further alloyed by other, sometimes even several, transition elements forming complex Heusler compounds.
Considering this complex problem with a large variable space of multiple alloying, the advancement in compound development is hindered by the apparent lack of suitable criteria for the estimation of martensite transformation temperature, i.e., ability to predict the MT temperature of the given Ni-Mn-based Heusler alloys just from their chemical composition. To get closer to that a quantity depending just on alloy chemical composition has to be introduced such that martensitic transformation temperature as a function of the quantity follows a simple trend. The existence of MT can be determined from the ab-initio calculation but the prediction is still not very reliable. One can assume that a predicted low symmetry structure at 0 K predicts the existence of MT in some finite temperature, but it is not guaranteed [6]. Moreover, the temperature at which MT occurs is the most important parameter, but is even more difficult to predict.
There are several empirical criteria for predicting MT at finite temperature in complex compounds. The most established is the e/a criterion considering the average valence electron density per atom. This originates from the classical rule of Hume–Rothery, and for many compounds, it works fairly well. However, it fails for isoelectronic compounds. Several improvements have been suggested. One is the usage of not-bonding electrons originating from the Miedema consideration [7]. The criterion considering Ne/a for the prediction may bring about some improvement in predicting power but often fails. Thus, here we suggest a new empirical criterion based on valence electrons per atomic volume approximated by atomic radii of constituent atoms. The concept is not entirely new; Ramudu et al. [8] suggested a similar criterion to deal with single isoelectronic compounds, but it is not entirely clear how the authors calculated the variable.
We applied the newly suggested criterion on our newly prepared alloys and also on our published data [9,10,11]. This was supplemented by a large collection of experimental data from the literature [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. We used the same production steps to prepare the alloys and for analysis to secure consistency in the results. However, this is not valid for the literature data that may differ in preparation methods, structural, and in particular, chemical analyses. This may bring additional inaccuracies which can distort suggested criterion. The inconsistencies are well visible in some of the data from the literature, as later shown.
Here, we focus on Ni-(Mn)-based as the potentially most promising compounds and suggest a new empirical criterion for these compounds. It may not be fully universal, but we believe that it is simple and has a predictive power. Theoretical calculations and machine learning (ML) approach are very powerful, e.g., [35,36,37,38] but these still often assume different (and often oversimplified) crystal structure of low temperature phase i.e., martensite, than the actual one.

2. Materials and Methods

All prepared alloys were based on stoichiometric Ni2MnGa with the addition of 5 atom% of two transitional elements X and Y, which ranged from Cr to Cu including alloys with X = Y (i.e., only one element was added, resulting in a 10 atom% amount). The alloys were prepared by arc-melting from elements with a purity of at least 99.9%, under an overpressure of an argon atmosphere using a MAM–1 furnace (Edmund Bühler GmbH, Bodelshausen, Germany). To maintain consistency with previous results, we used the same procedures as before. Thus, the details of the preparation can be found in [9,11]. The nominal compositions were checked using an energy dispersion X-ray fluorescence (XRF) Orbis Micro-XRF Analyzer. With the typical error of the method, about 0.5 at.% [39], the compositions were within the nominal ones and are listed in the table.
The phase analysis was performed by X-ray diffraction at room temperature using a PANalytical X’Pert PRO diffractometer (PANalytical, Almeo, The Netherlands) equipped with a Co tube, in divergent and parallel beam geometry. Several scans of each sample were measured for different sample orientations to collect a sufficient number of reflections for confident phase analysis. We used divergent beam geometry with wide slits for the initial phase analysis measurements to count given the complicated nature of the samples, in which some samples were oligocrystals or, in contrast, had a highly textured polycrystalline nature with a possible mixture of the small and very large grains. Also, some samples seemed to exhibit several phases. From all the samples prepared, we selected only samples in which XRD indicated a single phase, i.e., all XRD peaks could be assigned to single crystal structure. Details about the structure of alloys will be published elsewhere.
The magnetic and transformation properties were measured by the Physical Property Measurement System (PPMS) with a 9 T superconducting coil (Quantum Design, Inc., San Diego, CA, USA). We used a vibrating sample magnetometer option of PPMS to measure magnetization curves up to 9 T and temperature dependence of magnetization at temperatures between 10 and 1000 K at low field 0.01 T and at 2 T close to saturation to determine martensitic transformation temperature TM. The PPMS measurements above 400 K were done using VSM Oven option, where the sample is warmed up by Joule heated sample holder. The sample is fixed to the holder by its full covering by Zircar cement and wrapped by a copper foil to prevent radiation losses. The sample chamber is evacuated at high vacuum prior to measurement. As the sample is fully wrapped the manganese loss during relatively short measurements is expected to be small. Since the martensitic and austenitic phases strongly differ in their magnetic properties, the phases can be easily distinguished [11]. The change of magnetic behavior indicating MT can be used even above TC, i.e., in paramagnetic state as demonstrated by Kopecky et el. [9]. Due to limited range, though, the precision of determining TM at high temperatures close to 1000 K is limited.
To relate our measurements to other published experiments [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], we used the traditional e/a parameter, which represents the average number of valence electrons per atom in formula unit [27,28]. To compare isoelectronic compounds, a criterion based on parameter Ne/a was suggested [8]. The Ne/a stands for an average number of non-bonding electrons per atom in one formula unit or so-called effective valence electrons [7,9]. The expression is given by the formula Ne/a = e/a − (NWS1/3)3 = e/a − NWS, where NWS originates from the empirical model of Miedema et al. [7] and is defined as the electron density at the boundary of the Wigner–Seitz cell. In addition, considering the newly suggested criterion, we also listed the covalent and metallic radii of used elements. All relevant parameters are listed in Table 1.
For example, the alloy Ni45Mn25Ga20Fe5Cu5 has an e/a ratio calculated from the formula e/a = (45 × 10 + 25 × 7 + 20 × 3 + 5 × 8 + 5 × 11)/100 = 7.80, based just on knowledge of the chemical composition of the alloy and of the valence electron number in each constituting chemical element (see Table 1). The quantity Ne/a of the alloy is calculated as Ne/a = [45 × (10 − 1.753) + 25 × (7 − 1.613) + 20 × (3 − 1.313) + 5 × (8 − 1.773) + 5 × (11 − 1.473)]/100 = 3.46, again according to the chemical composition of the alloy and to the quantity NWS for the given constituting element (Table 1).
To take differences in atomic radii of the elements into account, we introduce the volume valence electron concentration e/V as a ratio of the quantities e/a and V/a. Here, V/a is the effective atomic volume calculated again just from known chemical composition of the alloy and from the assumption that the atoms in the alloy form rigid spheres. We assumed that the radii in Ni-Mn-based Heusler alloys correspond to purely covalent chemical bonds. This is justified by the fact that the alloys cannot be considered as metals, but rather belong to the intermetallics group, often exhibiting modulated structures that do not occur in metals. Considering purely covalent bonds for the subsequent discussion, the respective atomic radii are listed in Table 2. The calculation for the discussed alloy Ni45Mn25Ga20Fe5Cu5 gives V/a = {[45 × (4π/3) × 1103 + 25 × (4π/3) × 1193 + 20 × (4π/3) × 1243 + 5 × (4π/3) × 1163 + 5 × (4π/3) × 1123]/100} pm3 = 6.49 Å3, and henceforth e/Vcovalent ≡ e/V = 1.20 Å−3.
If we assume atoms as rigid spheres with purely metallic bonds, we can calculate e/V in a full analogy with the case of purely covalent bonds. However, for the above-mentioned reasons, this was not carried out. The metallic radii are listed only for illustration in Table 2. Moreover, for Sn and Sb, the metallic radii do not exist at all, which precludes the analysis of transformation temperatures TM as a function of e/V in Ni-Mn-Sn and Ni-Mn-Sb.
In order to estimate how big part of the crystal volume is occupied by atoms in Ni-Mn-based alloys we calculated occupancy factor in stoichiometric Ni50Mn25Ga25 alloy in cubic austenite phase. If we assume purely covalent bonds and Ni, Mn, and Ga atoms as rigid spheres, according to austenite lattice parameter a = 5.825 Å, we obtain about a 53% occupancy factor (i.e., more than one half of the Ni50Mn25Ga25 austenite alloy unit cell volume is occupied by atoms. The occupancy factor can vary between different Ni-Mn-based alloys, but anyway the atoms occupy significant part of the alloys. Since martensitic transformation is diffusionless process, we do not expect big difference of the occupancy factor between austenite and martensite phases of the particular alloy. Moreover, we assume that all strucures considered are cubic L21 ordered structures and thus the volume is related to the atomic sizes. These facts support the introduction of the new criterion e/V for martensitic transformation.

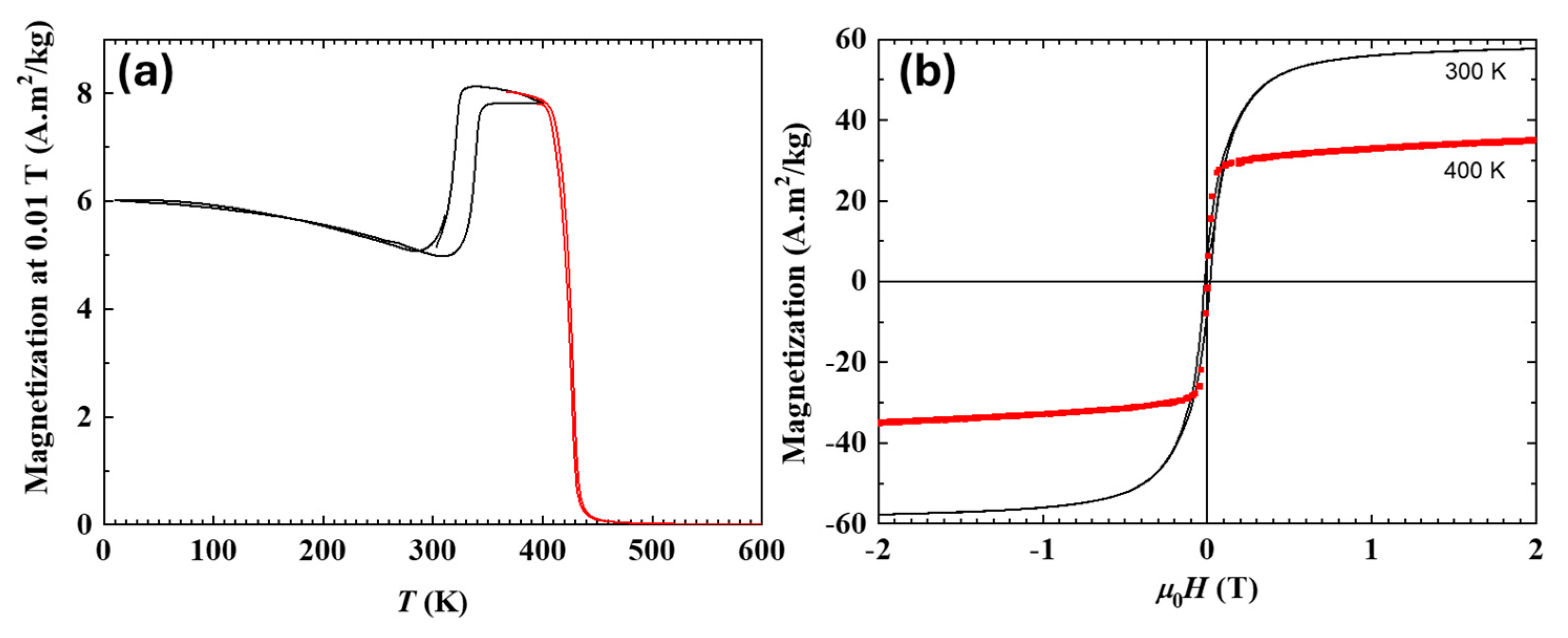
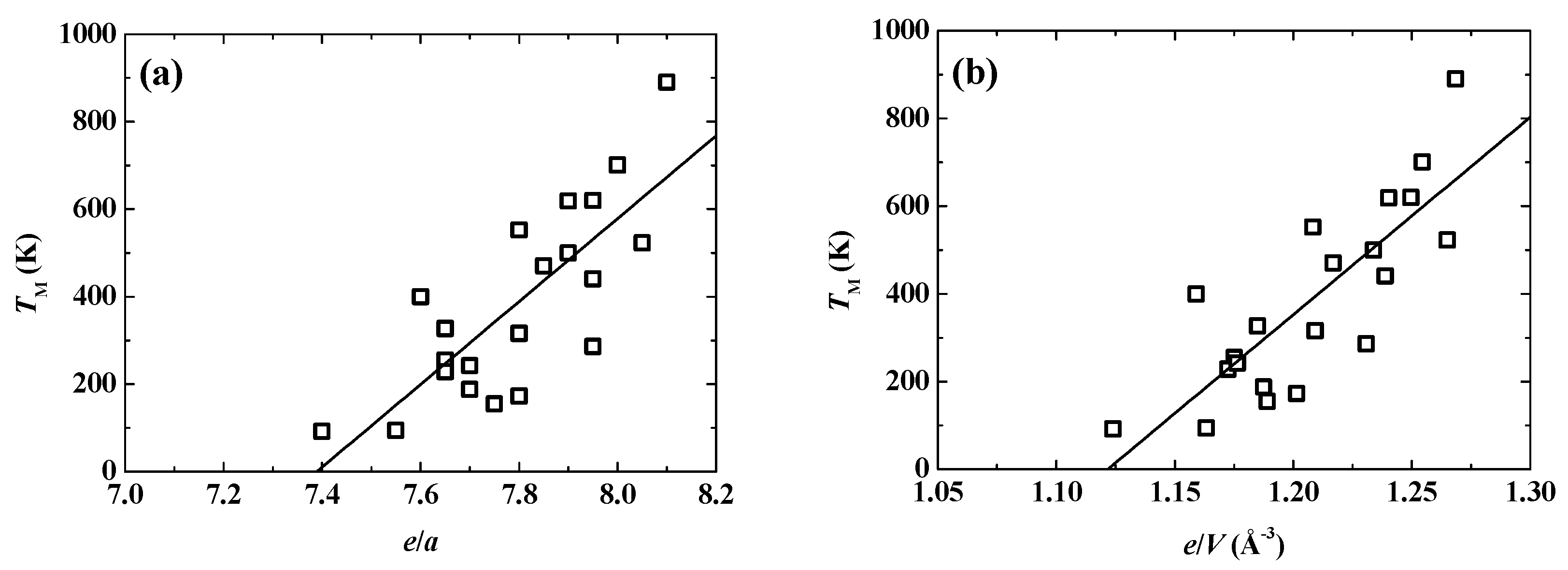
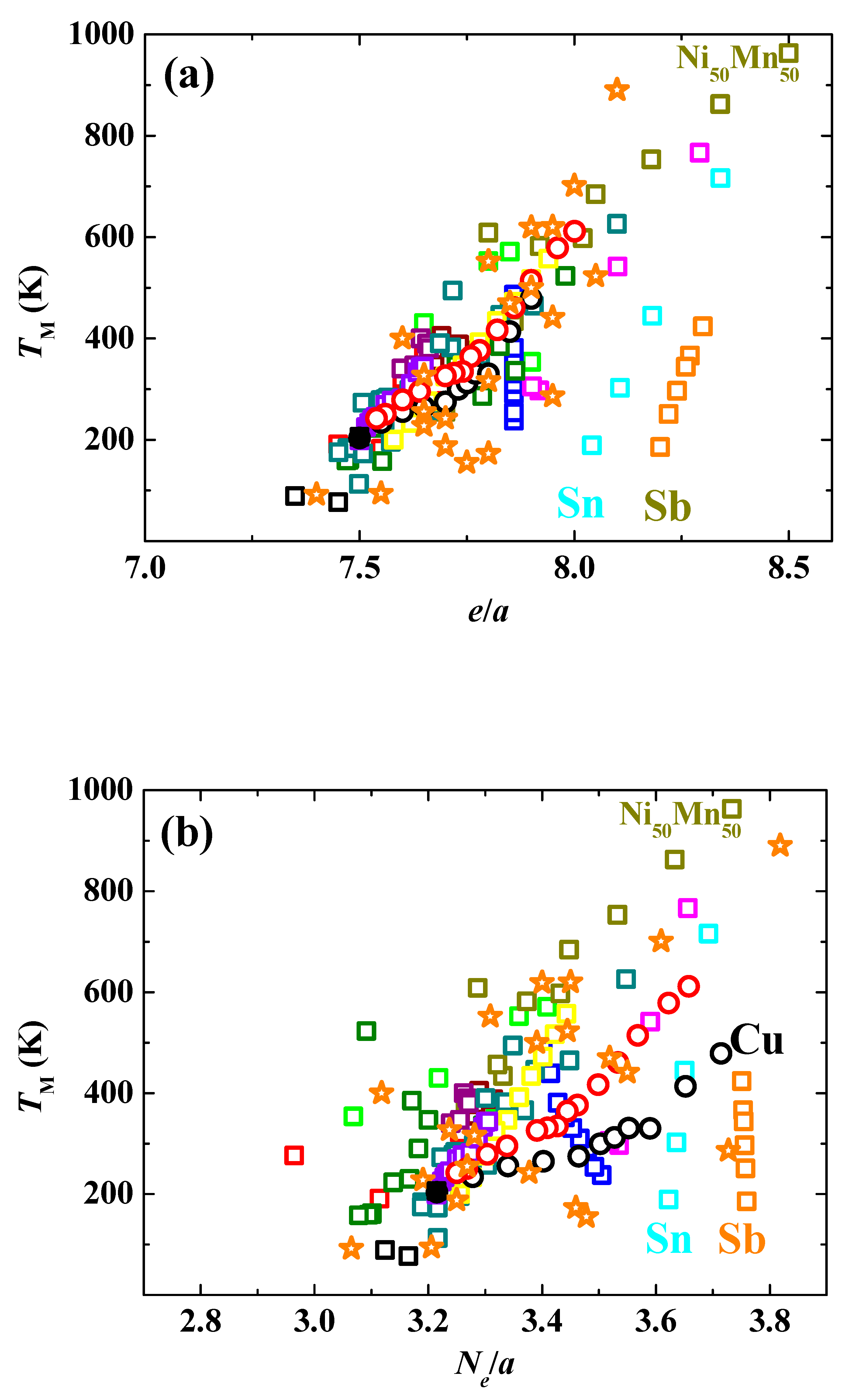
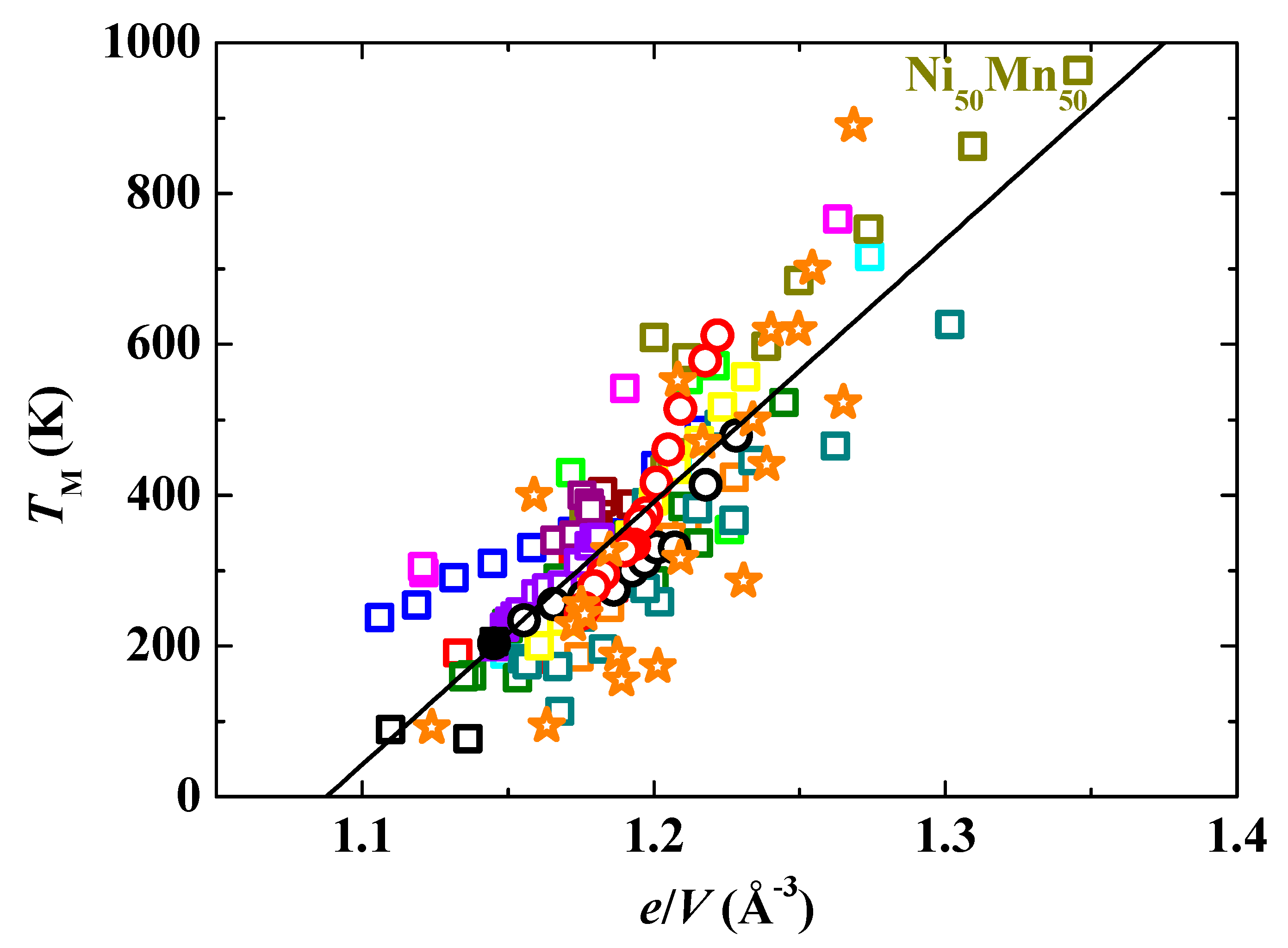
3. Results

We selected the stoichiometric Ni2MnGa as a well-defined baseline. Each element (Ni, Mn, Ga) in the stoichiometric composition was substituted by X and Y transitional metals, resulting in several groups shown (e.g., substitution of Ni with X and Mn with Y can be written as (Ni45×5)(Mn20Y5)Ga25). Prepared samples are listed in Table 2, but these do not exhaust all possible variations. Here, we strictly considered only the chemical composition replacement and did not consider the possible element displacement and disorder.
The example of the magnetic measurement in the selected sample Ni50(Mn15Fe5Cr5)Ga25 is shown in Figure 1. The transformation martensite temperature was determined from the thermomagnetic curve as a sharp decrease in low field magnetization in low temperature. The decrease is due to increasing magnetocrystalline anisotropy in the low symmetry phase (i.e., martensite) [29]. As the transformation exhibited thermal hysteresis, the martensitic transformation temperature TM was calculated as an arithmetic mean of austenite start temperature As, austenite finish temperature Af, martensite start temperature Ms and martensite finish temperature Mf, i.e., TM = (As + Af + Ms + Mf)/4. The temperatures As, Af, Ms, and Mf were determined from measured thermomagnetic curves using tangent method [9]. The existence of an anisotropic martensite phase was confirmed by a change of magnetization loops upon transition, as shown in Figure 1b. The decrease in magnetization to zero without hysteresis signifies the Curie ferromagnetic point. The determined martensite temperatures TM are listed in Table 2. The Curie temperatures TC varied much less and did not follow any trend in agreement with previous experiments [9,11]. Invariantly, the highest TC was observed in the alloys with no MT. A further discussion about magnetic properties and connection with martensitic transformation will be published elsewhere.
The martensitic transformation temperature TM as a function of electron concentration per atom (e/a) and newly defined criterion electron concentration per volume (e/V) is drawn in Figure 2. It demonstrates the increase in TM with increasing e/a resp. e/V. Some spread can be caused by errors in chemical composition [9], but the spread also demonstrates that the criteria can only be a rough guide, and other effects should be considered, in particular, different occupancy and increasing disorder [30]. The difference between using traditional e/a and newly defined e/V criterion is small, as all substitution elements do not differ in their covalent diameter significantly. The data shown in Figure 2 suggest a linear dependence for both criteria with marginal improvement for e/V. However, our dataset, although broad, it is still limited and for testing the criteria and the larger dataset is needed. Additional data were obtained from literature [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

4. Discussion

Newly obtained experimental data are put into the context of published results [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. First, we demonstrated a breakdown of traditional criteria e/a and Ne/a for isoelectronic compound and some other alloys (Figure 3). It is apparent that this criterion for TM is valid only very approximately in contrast to the statement in [27]. The limited validity of e/a and it was noted previously in the substitution of Ga by In (Figure 3a). These are isoelectronic compounds, (i.e., having the same e/a, but the moderate substitution of Ga by In suppresses the martensitic transformation entirely) [23,24]. We also demonstrated a certain failure in our experiment with 5 atom% substitutional alloying [11]. The valence electron per atom e/a criterion is usually used for evaluating the effect of alloying or substitution on magnetic and transformation properties and there is good correlation in TM for several compounds especially for Ni-Mn-Sb [15] and Ni-Mn-Sn [13] as demonstrated by Entel et al. [33]. However, the slope is different for each alloying element as it can be also inferred from Figure 3.
For isoelectronic compounds, the valence electron (e/a) criterion will fail. In this case (e.g., isoelectronic Ni-Mn-Ga-In system), a criterion based on non–bonding electrons per atom (Ne/a) was suggested. A decreasing trend of TM with increasing Ne/a has been reported, which is somehow opposite to that of other compounds [8]. We demonstrated that this criterion may be suitable for transition metals Ni, Fe, Co [9]; in contrast to e/a, it predicted a disappearance of martensitic transformation in Ni45Fe5Mn25Ga25 alloy and premartensite transformation temperature [9], but for early and late transitional metal substitution such as Cr and Cu [11], there was no good correlation.
Moreover, the spread of data using the Ne/a variable was even larger than for e/a. The collected literature data also demonstrated that the criterion is not suitable for Sn and Sb alloys, as in previous case, and also alloys Ni-Mn-Cu-Ga [22] significantly deviated from the trend (Figure 3b).
Since atomic radii of Ga and In atoms differ significantly, Ramudu et al. [8], based on previous works [31,32,33], suggest that the atomic volume is significant. They reported increasing TM with increasing non-bonding electron concentration per unit volume Ne/V in the Ni-Mn-Ga-In system, but without a detailed description of the calculation performed, moreover, only for this system. However, the volume dependence was noticed but not further evaluated for other systems. We followed their suggestion and formulated the e/V criterion as defined above. The calculated volume based on atomic radii serves as reasonable proxy since we assume that parent phase of all studied alloys is cubic with L21 order. This is quite strong assumption which may contribute to further uncertainty for the criterion. Data for all prepared alloys together with literature data are collected in Figure 4. In principle, the new criterion does not take into account the thermal hysteresis of the martensitic transition, here we report average thermodynamical value TM as described above. All data reasonably followed the trend with increasing TM with increasing concentration e/V.
The dependence of martensitic transformation temperature TM on (e/V) with respect on (e/a) were fitted by functions TM(e/V) = −3862 + 3554 × (e/V), and TM(e/a) = −3565 + 505 × (e/a). The respective linear regression coefficient (Pearson correlation coefficient) was much closer to 1 for TM (e/V) compared to the simple e/a criterion [33]. This indicates that the effect of atomic volume on TM should be included [8,31,32]. Namely, the correlation coefficients were 0.84 and 0.71 for the TM(e/V) and TM(e/a) dependences, respectively. The spread can be partially ascribed to the error in the determination of the chemical composition of the alloys, usually determined by XRF.
The closer inspection of the experimental data suggests that the deviation from the dependence increases for multiple elements alloying. Here we can speculate about the role of chemical disorder and other factors similar to high entropy alloys [40]. Broader set of experimental alloys with higher alloying ratio is needed for further evaluation.

5. Conclusions

Based on our extensive investigation of many complex Ni-Mn based Heusler alloys and the literature data, we suggested an empirical criterion for martensitic transformation based on the average electron density per volume approximated by atomic radii of constituent atoms.
The suggested criterion well-described the experimentally observed dependences of the martensitic transformation temperature TM of diverse Heusler alloys, in particular, it is suitable for isoelectronic compounds in contrast to the failure of the traditional e/a criterion. The good fit indicates the importance of atomic volume for martensitic transformation.
The criterion is clearly only a rough guide as other effects which may affect TM are not included. Theoretical justification of the observed universal dependence is needed, but on the other hand the new criterion can serve as a guide for future calculation.

Author Contributions

Conceptualization, O.H.; methodology, O.H. and M.R.; investigation, O.H. and M.R.; resources, O.H. and M.R.; writing—original draft preparation, O.H. and M.R.; writing—review and editing, O.H. and M.R.; supervision, O.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Czech Science Foundation (project No. 23-04806S) and by the Ferroic Multifunctionalities project (FerrMion) [Project No. CZ.02.01.01/00/22008/0004591] by the Ministry of Education (MEY S), co-funded by the European Union. Magnetic measurements were performed at MGML (mgml.eu), which is supported within the program of Czech Research Infrastructures (project no. LM2023065).

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).

Acknowledgments

The authors thank Martin Dušák for the consistent and careful preparation of the studied alloys.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
  2. Heczko, O.; Sozinov, A.; Ullakko, K. Giant field-induced reversible strain in magnetic shape memory NiMnGa alloy. IEEE Trans. Magn. 2000, 36, 3266–3268. [Google Scholar] [CrossRef]
  3. Straka, L.; Heczko, O. Superelastic response of Ni-Mn-Ga martensite in magnetic fields and a simple model. IEEE Trans. Magn. 2003, 39, 3402–3404. [Google Scholar] [CrossRef]
  4. Han, D.K.; Chiu, W.T.; Tahara, M.; Nohira, N.; Chernenko, V.; Lanceros-Mendez, S.; Hosoda, H. An unusual approach significantly improving the magnetostrain performance of Ni-Mn-Ga composite materials. Scr. Mater. 2025, 261, 116624. [Google Scholar] [CrossRef]
  5. Scheibel, F.; Gottschall, T.; Taubel, A.; Fries, M.; Skokov, K.P.; Terwey, A.; Keune, W.; Ollefs, K.; Wende, H.; Farle, M.; et al. Hysteresis design of magnetocaloric materials—From basic mechanisms to applications. Energy Technol. 2018, 6, 1397–1428. [Google Scholar] [CrossRef]
  6. Kratochvílová, M.; Klicpera, M.; Malý, F.; Valenta, J.; Veis, M.; Colman, R.H.; Heczko, O. Systematic experimental search for Fe2YZ Heusler compounds predicted by ab-initio calculation. Intermetallics 2021, 131, 107073. [Google Scholar] [CrossRef]
  7. Miedema, A.; de Châtel, P.; de Boer, F. Cohesion in alloys—Fundamentals of a semi-empirical model. Phys. B + C 1980, 100, 1–28. [Google Scholar] [CrossRef]
  8. Ramudu, M.; Kumar, A.S.; Seshubai, V.; Rajasekharan, T. Correlation of martensitic transformation temperatures of Ni- Mn-Ga/Al-X alloys to non-bonding electron concentration. IOP Conf. Ser. Mater. Sci. Eng. 2015, 73, 012074. [Google Scholar] [CrossRef]
  9. Kopecký, V.; Rameš, M.; Veřtát, P.; Colman, R.H.; Heczko, O. Full Variation of Site Substitution in Ni-Mn-Ga by Ferromagnetic Transition Metals. Metals 2021, 11, 850. [Google Scholar] [CrossRef]
  10. Armstrong, A.; Nilsén, F.; Rameš, M.; Colman, R.H.; Veřtát, P.; Kmječ, T.; Straka, L.; Müllner, P.; Heczko, O. Systematic Trends of Transformation Temperatures and Crystal Structure of Ni–Mn–Ga–Fe–Cu Alloys. Shape Mem. Superelasticity 2020, 6, 97–106. [Google Scholar] [CrossRef]
  11. Heczko, O.; Rameš, M.; Kopecký, V.; Veřtát, P.; Varga, M.; Straka, L. Magnetic and transformation properties of Ni2MnGa combinatorically substituted with 5 at.% of transition elements from Cr to Cu–Experimental insight. J. Magn. Magn. Mater. 2024, 589, 171510. [Google Scholar] [CrossRef]
  12. Liu, Z.H.; Li, G.T.; Wu, Z.G.; Ma, X.Q.; Liu, Y.; Wu, G.H. Tailoring martensitic transformation and martensite structure of NiMnIn alloy by Ga doping In. J. Alloys. Compd. 2012, 535, 120–123. [Google Scholar] [CrossRef]
  13. Krenke, T.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Martensitic transitions and the nature of ferromagnetism in the austenitic and martensitic states of Ni-Mn-Sn alloys. Phys. Rev. B 2005, 72, 014412. [Google Scholar] [CrossRef]
  14. Krenke, T.; Acet, M.; Wassermann, E.F.; Moya, X.; Mañosa, L.; Planes, A. Ferromagnetism in the austenitic and martensitic states of Ni-Mn-In alloys. Phys. Rev. B 2006, 73, 174413. [Google Scholar] [CrossRef]
  15. Sutou, Y.; Imano, Y.; Koeda, N.; Omori, T.; Kainuma, R.; Ishida, K.; Oikawa, K. Magnetic and martensitic transformations of NiMnX (X = In, Sn, Sb) ferromagnetic shape memory alloys. Appl. Phys. Lett. 2004, 85, 4358–4360. [Google Scholar] [CrossRef]
  16. Kainuma, R.; Nakano, H.; Ishida, K. Martensitic Transformations in NiMnAl Phase Alloys. Metal. Mater. Trans. A 1996, 27, 4153–4162. [Google Scholar] [CrossRef]
  17. Rolfs, K.; Wimpory, R.C.; Petry, W.; Schneider, R. Effect of alloying Ni-Mn-Ga with Cobalt on thermal and structural properties. J. Phys. Conf. Ser. 2010, 251, 012046. [Google Scholar] [CrossRef]
  18. Xu, X.; Kanomata, T.; Kainuma, R. Specific heat and entropy change during martensitic transformation in Ni50Mn50-xGax ferromagnetic shape memory alloys. Acta Mater. 2014, 79, 159–167. [Google Scholar] [CrossRef]
  19. Khovailo, V.V.; Oikawa, K.; Abe, T.; Takagi, T. Entropy change at the martensitic transformation in ferromagnetic shape memory alloys Ni2+xMn1−xGa. J. Appl. Phys. 2003, 93, 8483–8485. [Google Scholar] [CrossRef]
  20. Chernenko, V.A.; Cesari, E.; Kokorin, V.V.; Vitenko, I.N. The development of new ferromagnetic shape memory alloys in Ni-Mn-Ga system. Scr. Metall. Mater. 1995, 33, 1239–1244. [Google Scholar] [CrossRef]
  21. Kataoka, M.; Endo, K.; Kudo, N.; Kanomata, T.; Nishihara, H.; Shishido, T.; Umetsu, R.Y.; Nagasako, M.; Kainuma, R. Martensitic transition, ferromagnetic transition, and their interplay in the shape memory alloys Ni2Mn1−xCuxGa. Phys. Rev. B 2010, 82, 214423. [Google Scholar] [CrossRef]
  22. Endo, K.; Kanomata, T.; Kimura, A.; Kataoka, M.; Nishihara, H.; Umetsu, R.Y.; Obara, K.; Shishido, T.; Nagasako, M.; Kainuma, R.; et al. Magnetic phase diagram of the ferromagnetic shape memory alloys Ni2MnGa1−xCux. Mater. Sci. Forum 2011, 684, 165–176. [Google Scholar] [CrossRef]
  23. Xu, X.; Yoshida, Y.; Omori, T.; Kanomata, T.; Kainuma, R. Magnetic properties and phase diagram of Ni50Mn50-xGax/2Inx/2 magnetic shape memory alloys. Shape Mem. Superelasticity 2016, 2, 371–379. [Google Scholar] [CrossRef]
  24. Cejpek, P.; Proschek, P.; Straka, L.; Heczko, O. Dependence of martensite transformation temperature on magnetic field in Ni2MnGa and Ni2MnGa0.95In0.05 single crystals. J. Alloy. Compd. 2022, 908, 164514. [Google Scholar] [CrossRef]
  25. Chen, X.Q.; Lu, X.; Wang, D.Y.; Qin, Z.X. The effect of Co–doping on martensitic transformation temperatures in Ni–Mn–Ga Heusler alloys. Smart Mater. Struct. 2008, 17, 065030. [Google Scholar] [CrossRef]
  26. Belosludtseva, E.S.; Kuranova, N.N.; Marchenkova, E.B.; Popov, A.G.; Pushin, V.G. Effect of gallium alloying on the structure, the phase composition, and the thermoelastic martensitic transformations in ternary Ni–Mn–Ga alloys. Tech. Phys. 2016, 61, 547–553. [Google Scholar] [CrossRef]
  27. Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
  28. Jin, X.; Marioni, M.; Bono, D.; Allen, S.M.; O’Handley, R.C.; Hsu, T.Y. Empirical mapping of Ni–Mn–Ga properties with composition and valence electron concentration. J. Appl. Phys. 2002, 91, 8222–8224. [Google Scholar] [CrossRef]
  29. Heczko, O.; Straka, L. Compositional dependence of structure, magnetization and magnetic anisotropy in Ni–Mn–Ga magnetic shape memory alloys. J. Magn. Magn. Mat. 2004, 272, 2045–2046. [Google Scholar] [CrossRef]
  30. Soto-Parra, D.E.; Alvarado-Hernandez, F.; Ayala, O.; Ochoa-Gamboa, R.A.; Flores-Zuniga, H.; Rios-Jara, D. The effect of Fe addition on the transformation temperatures, lattice parameter and magnetization saturation of Ni52.5−XMn23Ga24.5FeX ferromagnetic shape memory alloy. J. Alloys Compd. 2008, 464, 288–291. [Google Scholar] [CrossRef]
  31. Chen, F.; Wang, H.B.; Zheng, Y.F.; Cai, W.; Zhao, L.C. Effect of Fe addition on transformation temperatures and hardness of NiMnGa magnetic shape memory alloys. J. Mater. Sci. 2005, 40, 219–221. [Google Scholar] [CrossRef]
  32. Soto, D.; Hernández, F.A.; Flores-Zúñiga, H.; Moya, X.; Mañosa, L.; Planes, A.; Aksoy, S.; Acet, M.; Krenke, T. Phase diagram of Fe-doped Ni-Mn-Ga ferromagnetic shape-memory alloys. Phys. Rev. B 2008, 77, 184103. [Google Scholar] [CrossRef]
  33. Entel, P.; Siewert, M.; Gruner, M.E.; Herper, H.C.; Comtesse, D.; Arróyave, R.; Singh, N.; Talapatra, A.; Sokolovskiy, V.V.; Buchelnikov, V.D.; et al. Complex magnetic ordering as a driving mechanism of multifunctional properties of Heusler alloys from first principles. Eur. Phys. J. B 2013, 86, 65. [Google Scholar] [CrossRef]
  34. Kowalska, M.; Ríos, M.; Lázpita, P.; Chernenko, V.; Salazar, D.; Szczerba, M.J. Transformation behavior and magnetic properties of Ni-Mn-Ga melt-spun ribbons tuned by tandem of Co and Cu dopants. J. Alloy. Compd. 2025, 1046, 184784. [Google Scholar] [CrossRef]
  35. Zelený, M.; Straka, L.; Sozinov, A.; Heczko, O. Transformation Paths from Cubic to Low-Symmetry Structures in Heusler Ni2MnGa Compound. Sci. Rep. 2018, 8, 7275. [Google Scholar] [CrossRef]
  36. Zhang, Y.; Bai, J.; Guo, K.; Liu, D.; Gu, J.; Morley, N.; Ma, Q.; Gao, Q.; Zhang, Y.; Esling, C.; et al. An alloying strategy for tuning magnetism, thermal hysteresis, and mechanical properties in Ni-Mn-Sn-based Heusler alloys. J. Alloy. Compd. 2024, 979, 173593. [Google Scholar] [CrossRef]
  37. Tian, X.; Shi, D.; Zhang, K.; Li, H.; Zhou, L.; Ma, T.; Wang, C.; Wen, Q.; Tan, C. Machine-learning model for prediction of martensitic transformation temperature in NiMnSn-based ferromagnetic shape memory alloys. Comput. Mater. Sci. 2022, 215, 111811. [Google Scholar] [CrossRef]
  38. Tang, Y.C.; Cao, K.Y.; Ma, R.N.; Wang, J.B.; Zhang, Y.; Zhang, D.Y.; Zhou, C.; Tian, F.H.; Fang, M.X.; Yang, S. Accurate prediction of magnetocaloric effect in NiMn-based Heusler alloys by prioritizing phase transitions through explainable machine learning. Rare Metals. 2025, 44, 639. [Google Scholar] [CrossRef]
  39. Haschke, M.; Haschke, M. (Eds.) Laboratory Micro-X-Ray Fluorescence Spectroscopy. In Instrumentation and Applications; Springer: Cham, Switzerland, 2014; pp. 157–199. [Google Scholar] [CrossRef]
  40. Chang, S.H.; Lin, P.T.; Tsai, C.W. High-temperature martensitic transformation of CuNiHfTiZr high-entropy alloys. Sci Rep. 2019, 9, 19598. [Google Scholar] [CrossRef] [PubMed]
Metals 16 00064 g001
Figure 1. An example of (a) magnetization vs. temperature (black—low temperature, red high temperature measurements) and (b) magnetization curves in austenite (400 K, red squares) and martensite (300 K, black line) for the Ni50(Mn15Fe5Cr5)Ga25 Heusler alloy.
Figure 1. An example of (a) magnetization vs. temperature (black—low temperature, red high temperature measurements) and (b) magnetization curves in austenite (400 K, red squares) and martensite (300 K, black line) for the Ni50(Mn15Fe5Cr5)Ga25 Heusler alloy.
Metals 16 00064 g001
Metals 16 00064 g002
Figure 2. Martensitic transformation temperature TM as a function of (a) valence electron concentration (e/a) and (b) electron concentration per volume e/V. The line is linear fit of experimental data from Table 2 neglecting alloys with no transformation. Linear fit: (a) TM = -7047 + 953(e/a) with R = 0.79 and (b) TM = -5079 + 4526(e/V) with R = 0.82.
Figure 2. Martensitic transformation temperature TM as a function of (a) valence electron concentration (e/a) and (b) electron concentration per volume e/V. The line is linear fit of experimental data from Table 2 neglecting alloys with no transformation. Linear fit: (a) TM = -7047 + 953(e/a) with R = 0.79 and (b) TM = -5079 + 4526(e/V) with R = 0.82.
Metals 16 00064 g002
Metals 16 00064 g003
Figure 3. Martensitic temperature for all alloys as a function of (a) average electron concentration per atom e/a, and (b) for average non-bonding electrons concentration Ne/a. Several alloyed series and compound Ni50Mn50 are marked in the figure. Black full square marked the stoichiometric composition Ni2MnGa. The experimental data (Table 2) are marked by orange stars. As the data are collected from different sources the errors are difficult to specify. For our experiment the error in chemical composition is about double size of the points.
Figure 3. Martensitic temperature for all alloys as a function of (a) average electron concentration per atom e/a, and (b) for average non-bonding electrons concentration Ne/a. Several alloyed series and compound Ni50Mn50 are marked in the figure. Black full square marked the stoichiometric composition Ni2MnGa. The experimental data (Table 2) are marked by orange stars. As the data are collected from different sources the errors are difficult to specify. For our experiment the error in chemical composition is about double size of the points.
Metals 16 00064 g003
Metals 16 00064 g004
Figure 4. Martensitic temperature for all alloys with multiple alloying as a function of average electron concentration per volume based on the literature data [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] and our previous data [9,10,11] and experiments marked by orange stars. Full black square denotes stoichiometric (i.e., Ni2MnGa alloy). The line is linear fit as excluding alloys having no transformation: TM = −3791 + 3485 × (e/V) with R = 0.84.
Figure 4. Martensitic temperature for all alloys with multiple alloying as a function of average electron concentration per volume based on the literature data [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34] and our previous data [9,10,11] and experiments marked by orange stars. Full black square denotes stoichiometric (i.e., Ni2MnGa alloy). The line is linear fit as excluding alloys having no transformation: TM = −3791 + 3485 × (e/V) with R = 0.84.
Metals 16 00064 g004
Table 1. Valence electron number, non-bonding electron density and covalent and metallic radii for elements used in complex Heusler alloys.
Table 1. Valence electron number, non-bonding electron density and covalent and metallic radii for elements used in complex Heusler alloys.
ElementValence Electron Number e/aNWS1/3Covalent Atomic Radius (pm)Metallic Radius (pm)
Cr61.73122128
Mn71.61119127
Fe81.77116126
Co91.75112128
Ni101.75110124
Cu111.47112128
Ga31.31124135
In31.17142167
Al31.39126143
Sn41.24140-
Sb51.26140-
Table 2. The list of prepared alloys, corresponding calculated e/a, Ne/a, and e/V parameters and martensitic transformation temperature TM for each alloy. If no martensitic transformation was detected, it is marked by n/a.
Table 2. The list of prepared alloys, corresponding calculated e/a, Ne/a, and e/V parameters and martensitic transformation temperature TM for each alloy. If no martensitic transformation was detected, it is marked by n/a.
Alloye/aNe/ae/Vcovalent (Å−3)TM (K)
Ni45Mn25Ga20Fe5Cu57.803.461.20173
Ni45Mn30Ga20Co57.653.271.18255
Ni55Mn20Ga20Cr57.803.311.21552
Ni45Mn20Ga30Cr57.102.921.06n/a
Ni50Mn20Ga20Cr107.603.121.16400
Ni45Mn20Ga25Cr5Co57.403.061.1292
Ni50Mn20Ga20Fe5Cu57.953.551.24441
Ni50Mn20Ga20Cu108.103.821.27902
Ni50Mn20Ga20Co5Cu58.003.611.25701
Ni40Mn25Ga25Fe5Co57.353.061.11n/a
Ni50Mn15Ga25Fe5Co57.653.241.18327
Ni50Mn25Ga15Fe5Co58.053.441.26523
Ni50Mn20Ga20Fe107.803.281.21316
Ni45Mn25Ga20Fe5Co57.703.251.19188
Ni45Mn25Ga20Fe107.653.191.17228
Ni45Mn20Ga25Co107.553.211.1694
Ni45Mn20Ga25Fe5Co57.503.151.15n/a
Ni45Mn20Ga25Fe107.453.091.13n/a
Ni50Mn20Ga20Co107.903.401.24619
Ni55Mn20Ga20Co57.953.451.25620
Ni55Mn20Ga20Fe57.903.391.23500
Ni45Mn25Ga20Cr5Cu57.703.381.18242
Ni45Mn30Ga20Cu57.753.481.19155
Ni45Mn20Ga25Cr5Fe57.353.011.11n/a
Ni45Mn25Ga20Co5Cu57.853.521.22470
Ni45Mn25Ga20Cu107.953.731.23286
Ni50Mn25Ga257.503.211.15206
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rameš, M.; Heczko, O. Universal Empirical Criterion for Martensitic Transformation Temperature in Ni-Mn-Based Heusler Alloys. Metals 2026, 16, 64. https://doi.org/10.3390/met16010064

AMA Style

Rameš M, Heczko O. Universal Empirical Criterion for Martensitic Transformation Temperature in Ni-Mn-Based Heusler Alloys. Metals. 2026; 16(1):64. https://doi.org/10.3390/met16010064

Chicago/Turabian Style

Rameš, Michal, and Oleg Heczko. 2026. "Universal Empirical Criterion for Martensitic Transformation Temperature in Ni-Mn-Based Heusler Alloys" Metals 16, no. 1: 64. https://doi.org/10.3390/met16010064

APA Style

Rameš, M., & Heczko, O. (2026). Universal Empirical Criterion for Martensitic Transformation Temperature in Ni-Mn-Based Heusler Alloys. Metals, 16(1), 64. https://doi.org/10.3390/met16010064

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop