Sensitivity of Texture Evolution and Performance to Eccentricity, Misalignment, and Oil Supply in Journal Bearings with the Circumferential Oil Groove: An Adjoint-Based Optimization Study
Abstract
1. Introduction
2. Theoretical Formulation
2.1. Overview
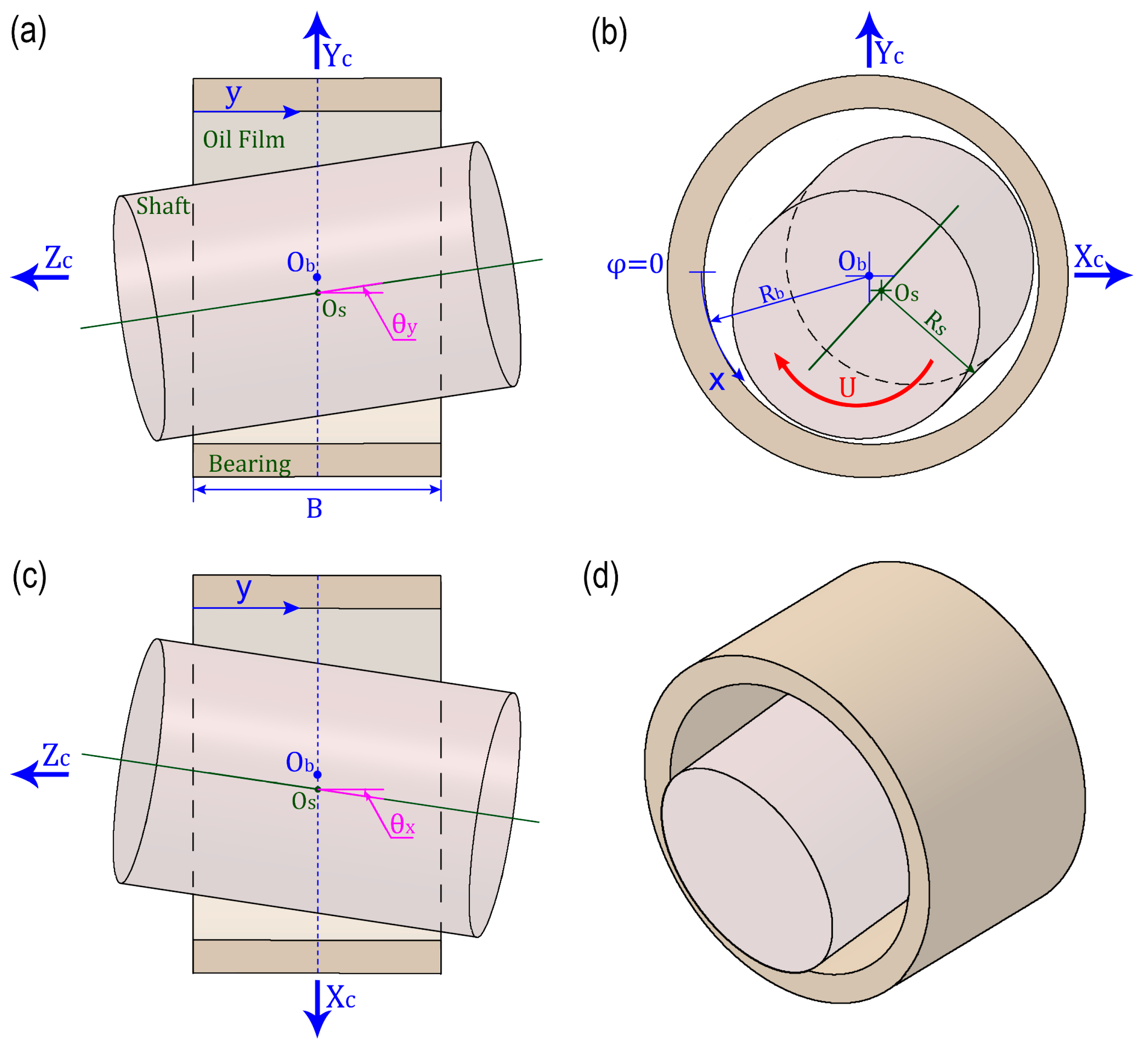
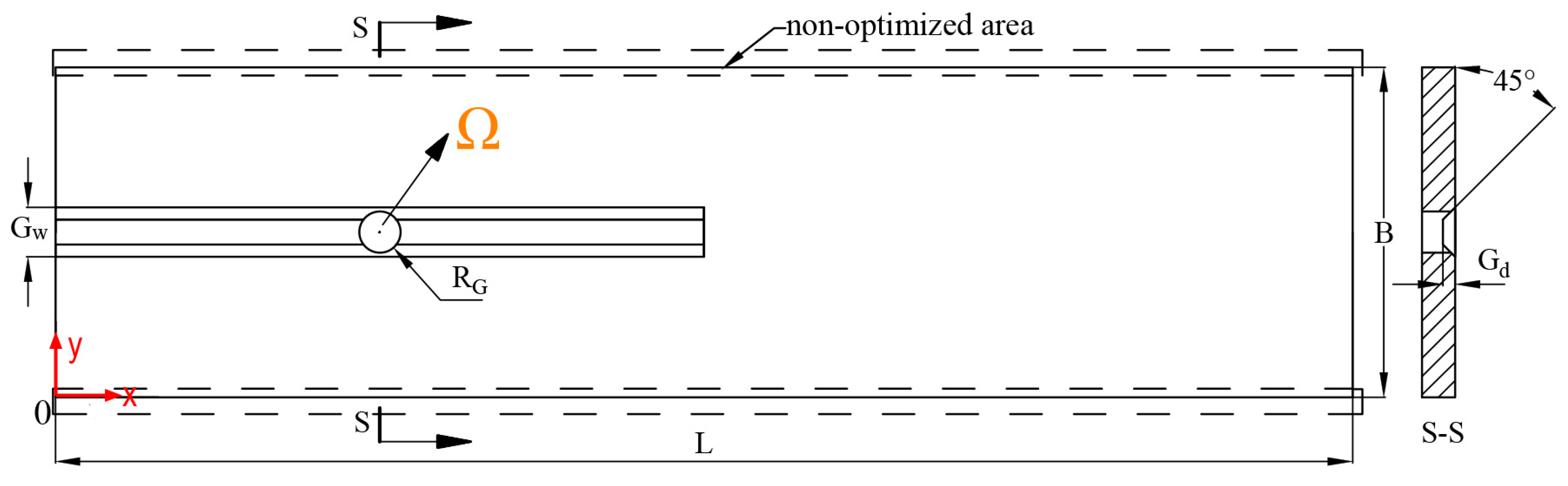
2.2. Geometric Model
2.3. The Mixed Lubrication Model
2.4. Oil Film Thickness
2.5. Performance Metrics
2.6. Optimization Through the Adjoint Method
3. Model Validation
4. Results and Discussion
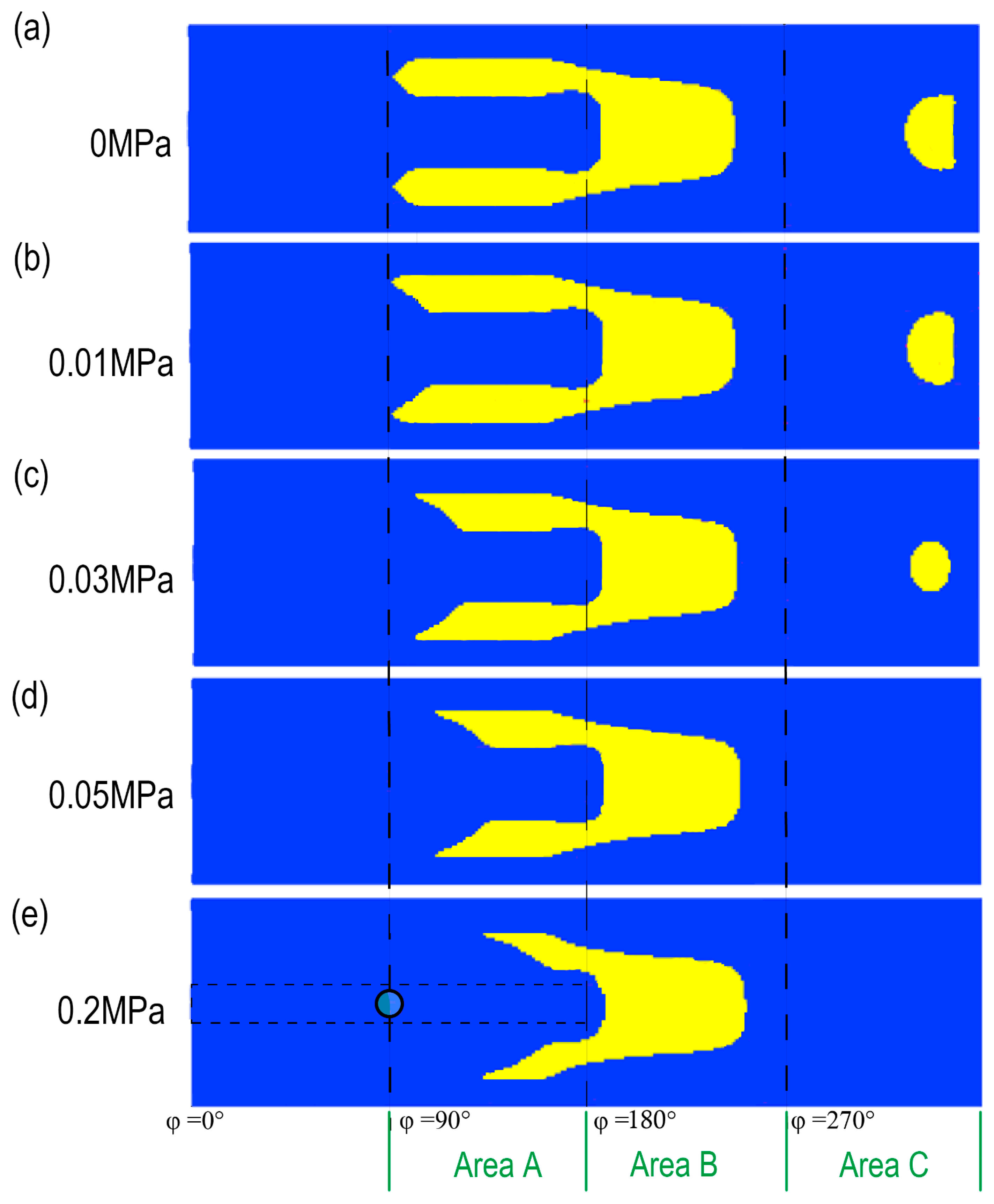
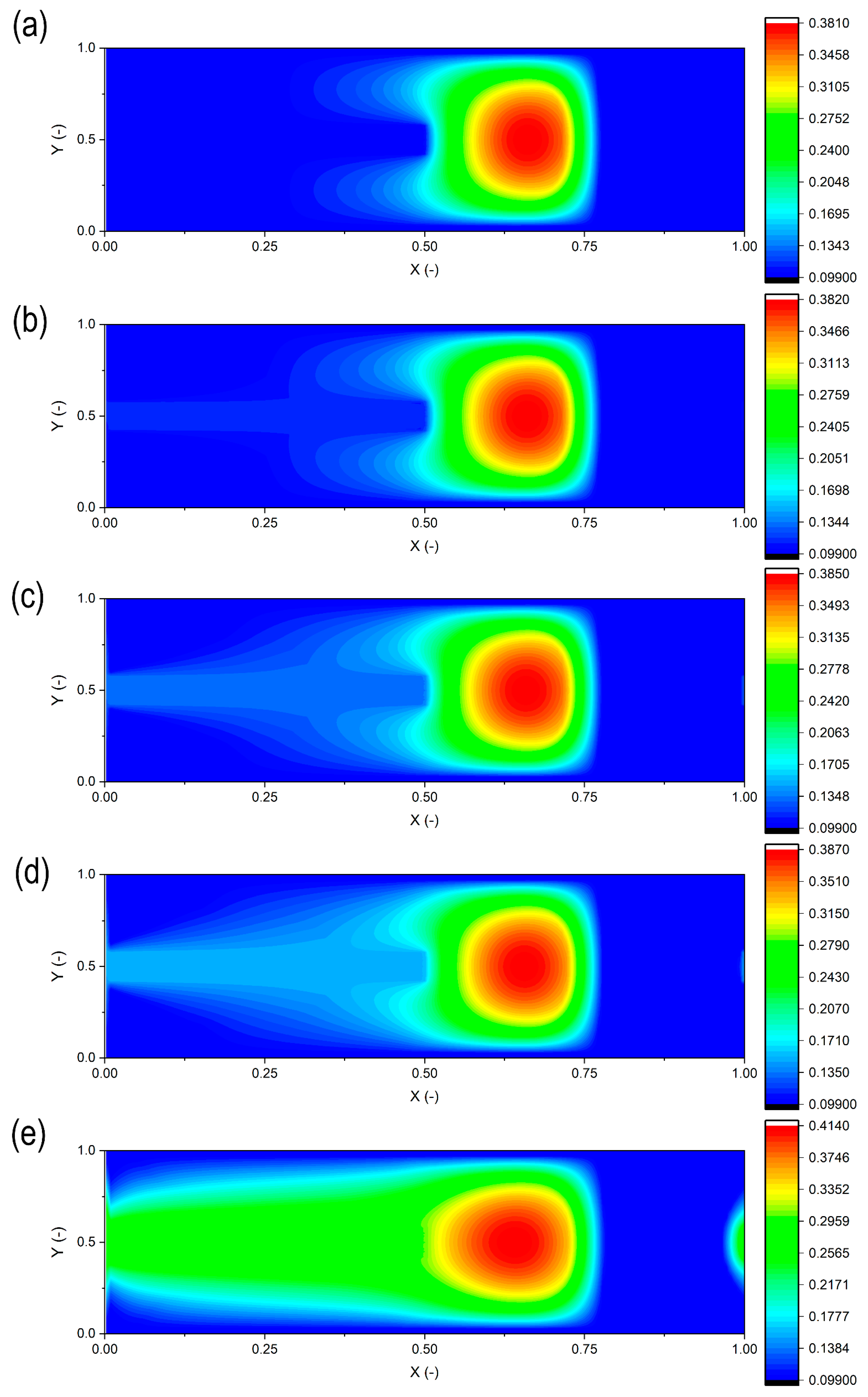
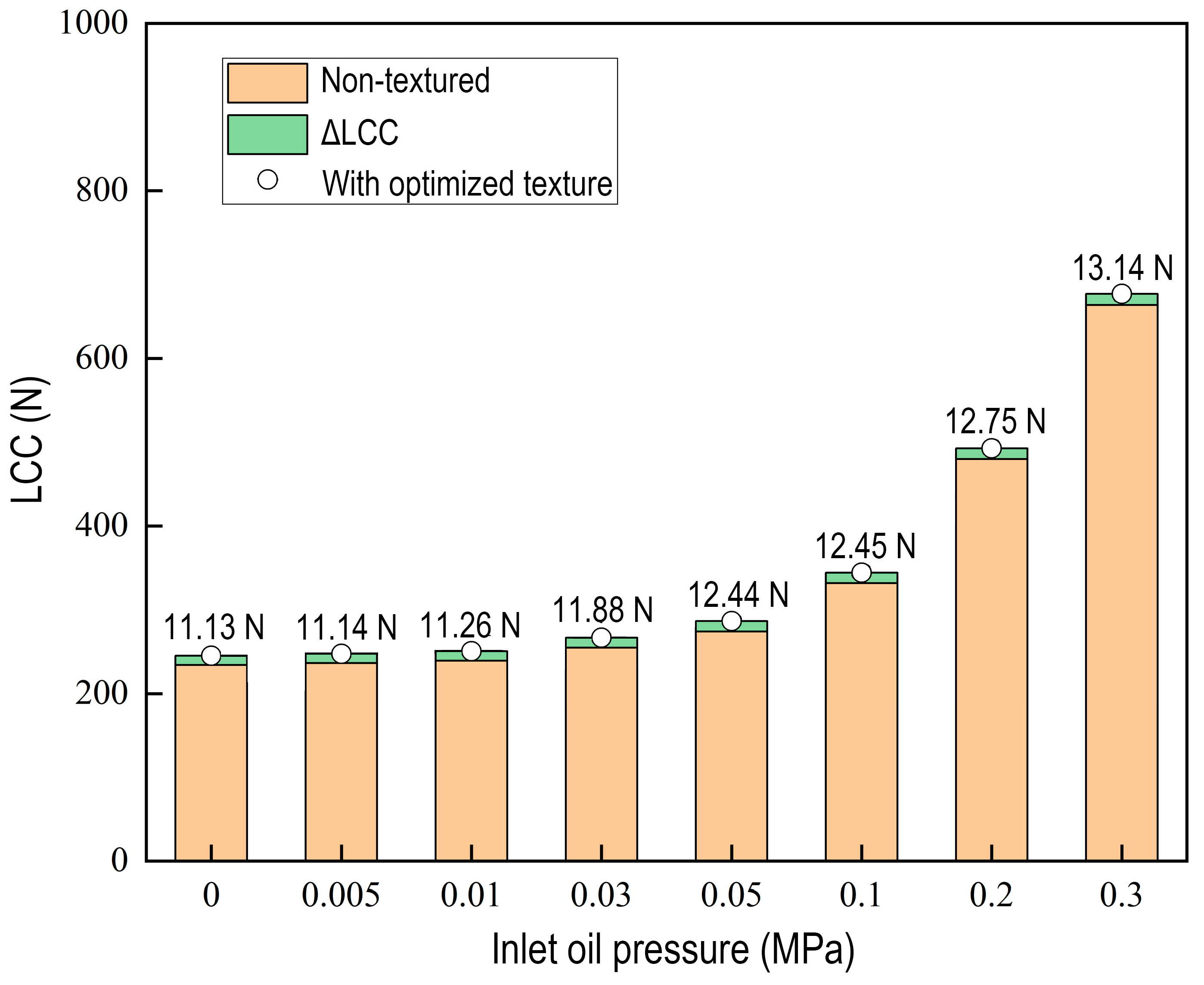
4.1. The Influence of Inlet Oil Pressure
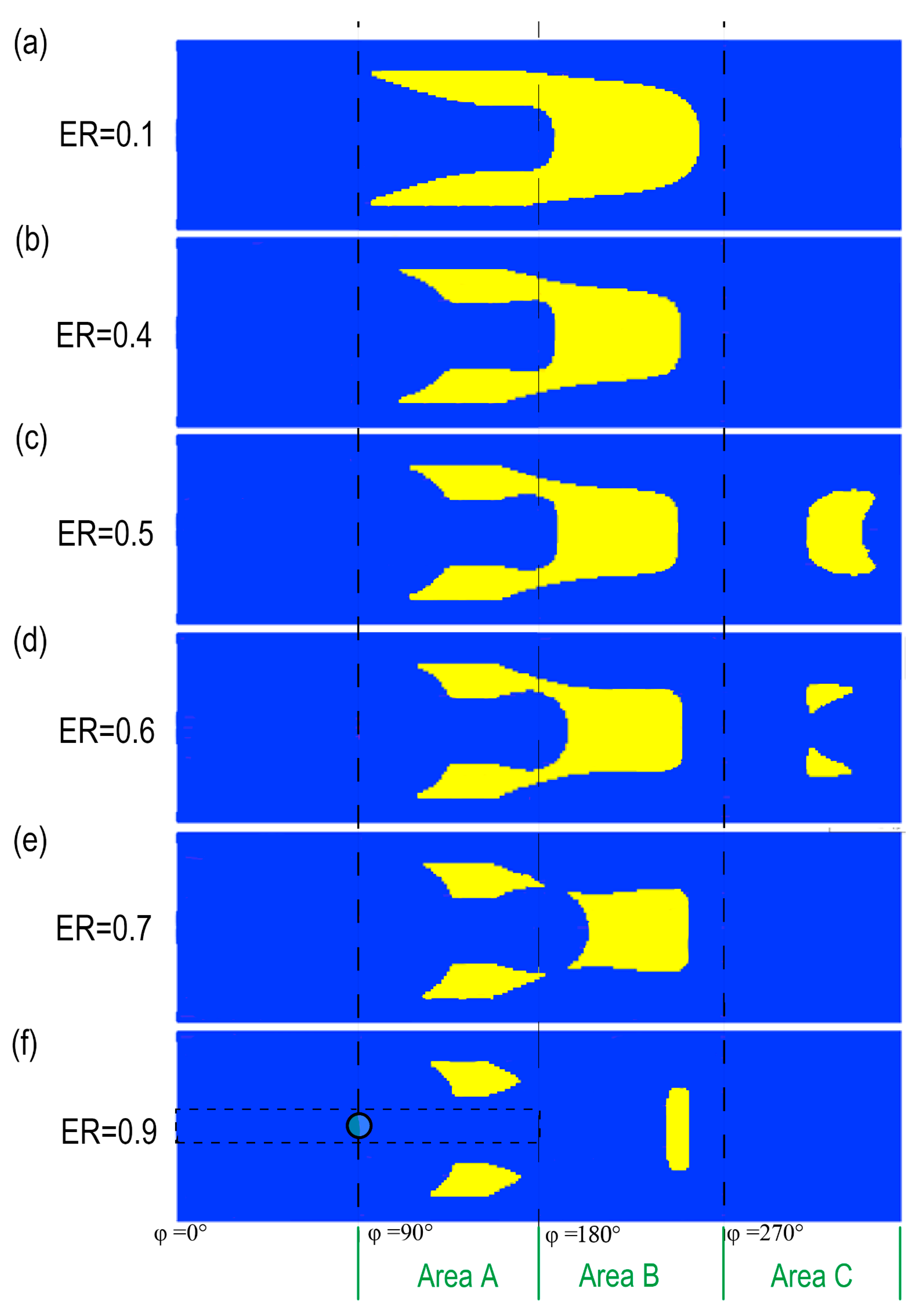
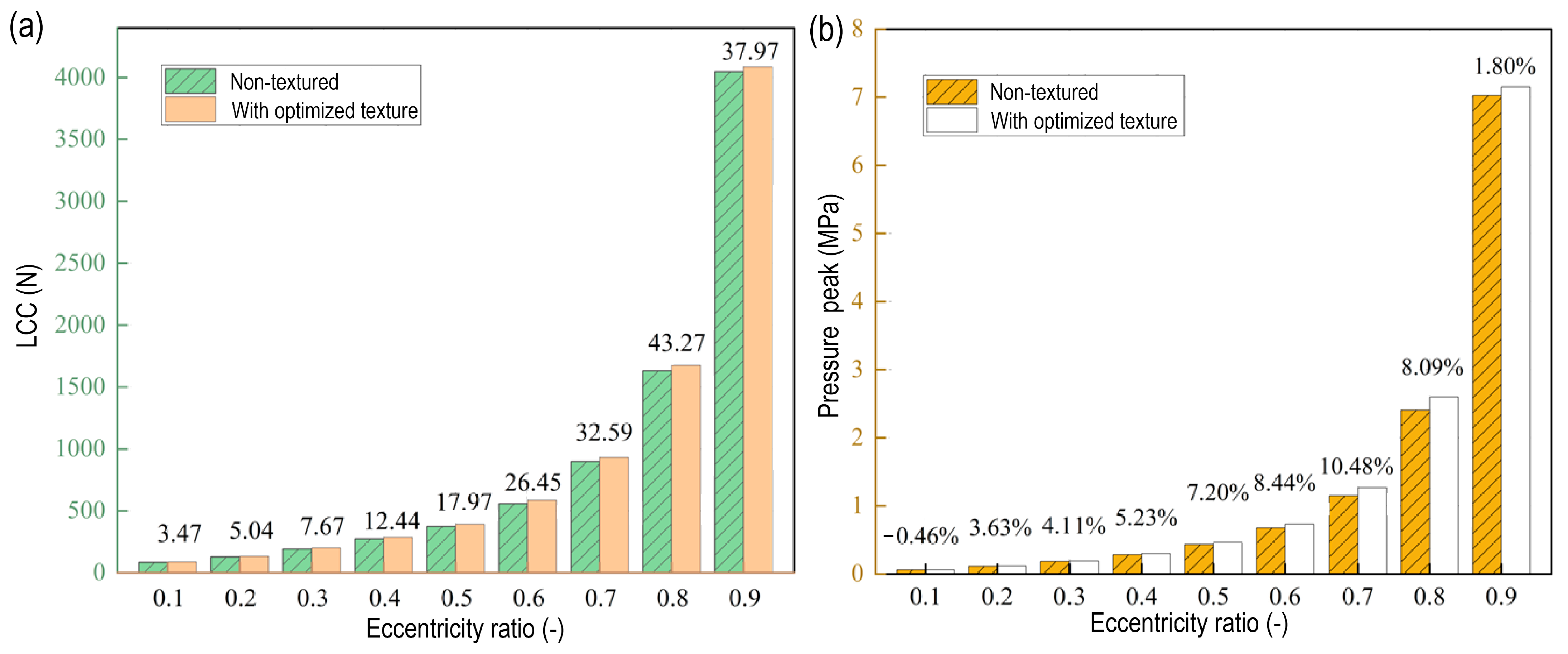
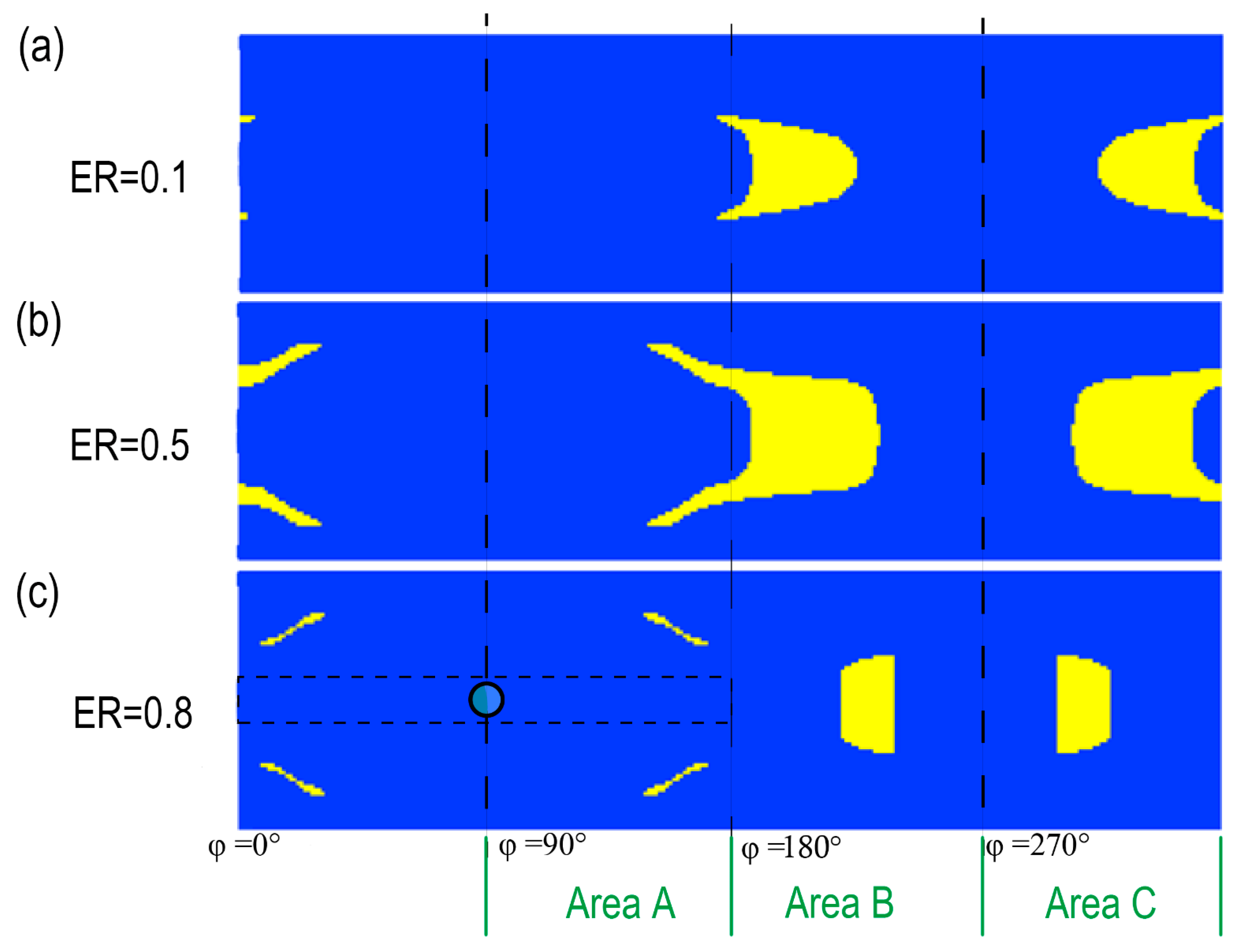
4.2. The Influence of Eccentricity Ratio
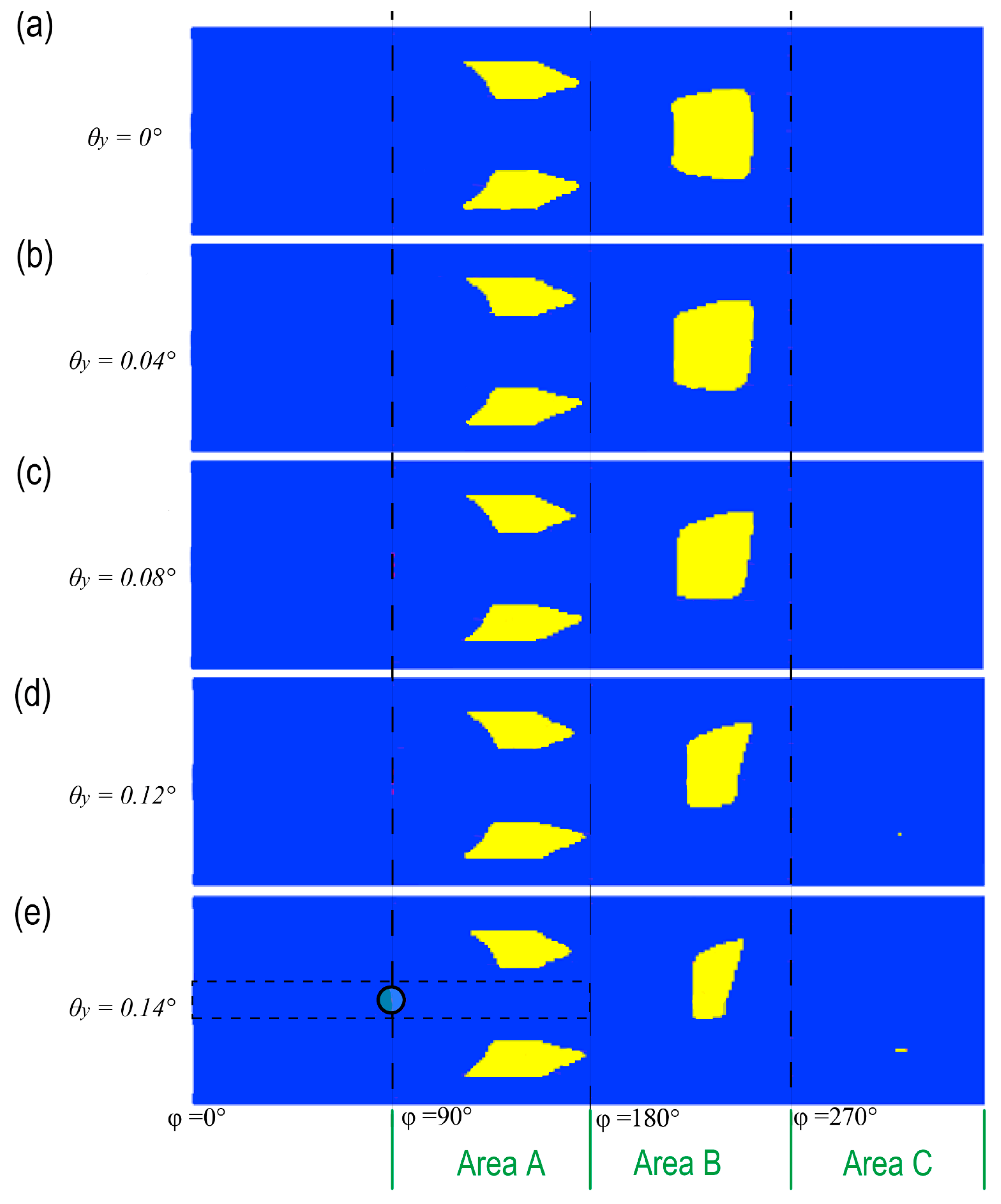
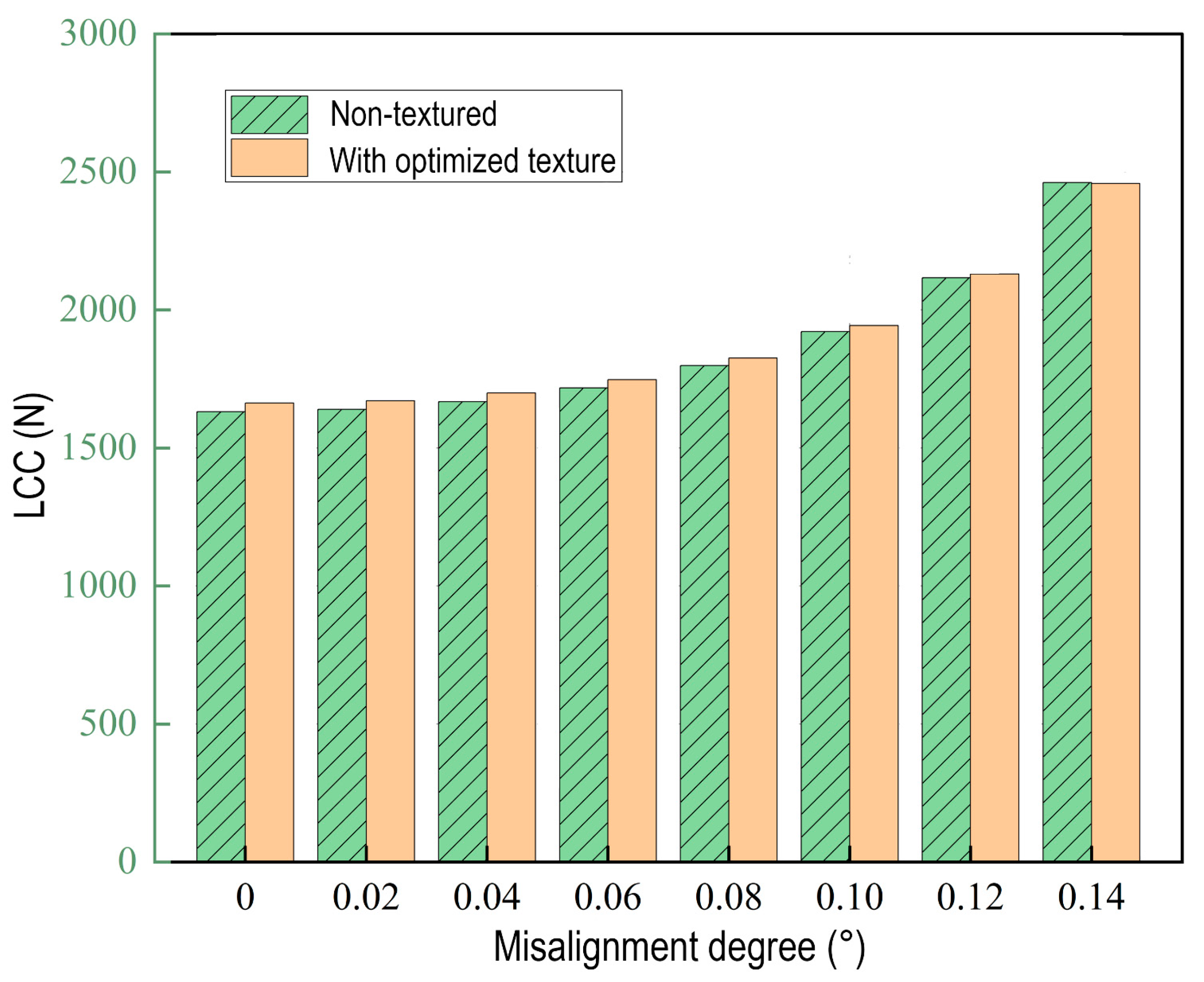
4.3. The Influence of Misalignment
4.4. The Influence of Rotation Direction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Asperity radius (m) | |
| Bearing radial clearance (m) | |
| The adjoint pressure (-) | |
| The adjoint cavitation factor (-) | |
| The cavity fraction (-) | |
| The elastic modulus of shaft (MPa) | |
| The elastic modulus of bearing (MPa) | |
| The asperity density (1/m2) | |
| The component of the LCC (N) | |
| The component of the LCC (N) | |
| Groove depth (m) | |
| Groove width (m) | |
| h | Oil film thickness (m) |
| The film thickness change caused by the oil groove (m) | |
| The oil film thickness without taking the texture into consideration (m) | |
| The optimized texture distribution (m) | |
| , the film thickness ratios (-) | |
| LCC | Load-carrying capacity (N) |
| MMV | Moving morphable void (-) |
| Lubricant viscosity (Pa·s) | |
| Poisson ratio of shaft (-) | |
| Poisson ratio of bearing (-) | |
| Oil inlet hole area (m2) | |
| The computational domain (m2) | |
| Hydrodynamic pressure (Pa) | |
| Asperity contact pressure (Pa) | |
| The contact factor (-) | |
| Shear flow factor (-) | |
| Pressure flow factors (-) | |
| Density of lubricant (kg/m3) | |
| Equivalent surface roughness (m) | |
| SQP | Sequential Quadratic Programming (-) |
| The misalignment parameter () | |
| Shaft velocity (m/s) | |
| The position of the shaft (-) | |
| The position of the shaft center (-) |
References
- Chaudhary, S.; Verma, R. A Comprehensive Review of Journal Bearing Models: Comparative Analysis of Thermal, Elastic, and Hydrodynamic Approaches Considering Misalignment, Surface Texture, Turbulence, and Cavitation. J. Tribol. 2025, 147, 110802. [Google Scholar] [CrossRef]
- Jeon, W.-J.; Hong, S.-H. A New Type of Misaligned Journal Bearing with Flexible Structure. Lubricants 2023, 11, 256. [Google Scholar] [CrossRef]
- Cupillard, S.; Glavatskih, S.; Cervantes, M.J. Computational fluid dynamics analysis of a journal bearing with surface texturing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2008, 222, 97–107. [Google Scholar] [CrossRef]
- Yu, R.; Chen, W.; Li, P. The analysis of elastohydrodynamic lubrication in the textured journal bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1197–1208. [Google Scholar] [CrossRef]
- Wang, L.; Han, Z.; Chen, G.; Su, H. Thermo-hydrodynamic analysis of large-eccentricity hydrodynamic bearings with texture on journal surface. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 232, 3564–3569. [Google Scholar] [CrossRef]
- Morris, N.J.; Shahmohamadi, H.; Rahmani, R.; Rahnejat, H.; Garner, C.P. Combined experimental and multiphase computational fluid dynamics analysis of surface textured journal bearings in mixed regime of lubrication. Lubr. Sci. 2018, 30, 161–173. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Wang, S.; Ding, X. Modeling a Hydrodynamic Bearing With Provision for Misalignments and Textures. J. Tribol. 2020, 142, 41801–41812. [Google Scholar] [CrossRef]
- Jin, J.; Chen, X.; Fu, Y.; Chang, Y. Optimal design of the slip–texture on a journal-bearing surface. Ind. Lubr. Tribol. 2020, 73, 230–237. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Kumar, R.; Mishra, P.C. Material modeling and optimization of rough elliptic bore journal bearing. Mater. Today Proc. 2021, 44, 1021–1027. [Google Scholar] [CrossRef]
- Gu, C.; Cui, Y.; Zhang, D. Research on the Optimal Design Approach of the Surface Texture for Journal Bearings. Lubricants 2024, 12, 111. [Google Scholar] [CrossRef]
- Khatri, C.B.; Yadav, S.K.; Thakre, G.D.; Rajput, A.K. Design optimization of vein-bionic textured hydrodynamic journal bearing using genetic algorithm. Acta Mech. 2023, 235, 167–190. [Google Scholar] [CrossRef]
- Codrignani, A.; Savio, D.; Pastewka, L.; Frohnapfel, B.; van Ostayen, R. Optimization of surface textures in hydrodynamic lubrication through the adjoint method. Tribol. Int. 2020, 148, 106352. [Google Scholar] [CrossRef]
- Ramos, D.J.; Daniel, G.B. Microgroove optimization to improve hydrodynamic bearing performance. Tribol. Int. 2022, 174, 107667. [Google Scholar] [CrossRef]
- Pattnayak, M.R.; Pandey, R.K.; Dutt, J.k. Performance improvement of an oil-lubricated journal bearing using bionic-textures fused micro-pockets. J. Tribol. 2021, 144, 41804. [Google Scholar] [CrossRef]
- Zhang, W.; Tian, H.; Zhu, B.; Guo, X.; Youn, S.K. Multi-Set MMV Topology Optimization Approach for Sliding Surface Texture Design. Int. J. Numer. Methods Eng. 2024, 126, e7612. [Google Scholar] [CrossRef]
- Tucker, P.G.; Keogh, P.S. A Generalized Computational Fluid Dynamics Approach for Journal Bearing Performance Prediction. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1995, 209, 99–108. [Google Scholar] [CrossRef]
- Lijesh, K.P.; Muzakkir, S.M.; Hirani, H.; Thakre, G.D. Control on wear of journal bearing operating in mixed lubrication regime using grooving arrangements. Ind. Lubr. Tribol. 2016, 68, 458–465. [Google Scholar] [CrossRef]
- Nichols, B.R.; Fittro, R.L.; Goyne, C.P. Steady-State Tilting-Pad Bearing Performance Under Reduced Oil Supply Flow Rates. J. Tribol. 2018, 140, 51701. [Google Scholar] [CrossRef]
- Brito, F.P.; Miranda, A.S.; Claro, J.C.P.; Teixeira, J.C.; Costa, L.; Fillon, M. Thermohydrodynamic modelling of journal bearings under varying load angle and negative groove flow rate. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 955–973. [Google Scholar] [CrossRef]
- Profito, F.J.; Vladescu, S.C.; Reddyhoff, T.; Dini, D. Numerical and experimental investigation of textured journal bearings for friction reduction. Tribol. Int. 2024, 195, 109643. [Google Scholar] [CrossRef]
- Mehrjardi, M.Z.; Shooroki, A.R.; Rabani, M.; Rabani, M. Effect of Surface Texture Depth with Various Geometric Shapes on the Steady-State Performance and Dynamic Stability of Noncircular Lobed Journal Bearings. Appl. Sci. 2025, 15, 4412. [Google Scholar] [CrossRef]
- Kong, H.; Gu, C.; Zhang, D.; Wu, L. Topology Optimization of Textured Journal Bearings. Lubricants 2025, 13, 251. [Google Scholar] [CrossRef]
- Li, Y.; Ning, Y.; Zhang, D.; Zhi, Y. A Model of Hydrodynamic Bearings With Circumferential Parallel Arranged Grooves. J. Tribol. 2023, 145, 104102. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, S.; Wang, K. Influence of Structural Parameters of Water-Lubricated Bearings on Vibration Characteristics of Marine Magnetic Pumps. Water 2023, 15, 4060. [Google Scholar] [CrossRef]
- Zhu, J.; Li, H.; Fu, J.; Liu, X. Hydrodynamic Lubrication Performance Analysis of the Self-Cooled Bearing Structure in Aero-Gear Pump Considering the Cavitation Effect. In Proceedings of the 2018 9th International Conference on Mechanical and Aerospace Engineering (ICMAE), Budapest, Hungary, 10–13 July 2018; pp. 472–477. [Google Scholar]
- Zhang, X.; Liu, C.; Zhao, B. An optimization research on groove textures of a journal bearing using particle swarm optimization algorithm. Mech. Ind. 2021, 22, 1. [Google Scholar] [CrossRef]
- Han, Y.; Fu, Y. Influence of micro-grooves on the lubrication performance of a misaligned bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 887–899. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and experimental investigation on the influences of misalignment on the lubrication performances and lubrication regimes transition of water lubricated bearing. Mech. Syst. Signal Process. 2021, 149, 107211. [Google Scholar] [CrossRef]
- Sahu, K.; Sharma, S.C.; Ram, N. Misalignment and Surface Irregularities Effect in MR Fluid Journal Bearing. Int. J. Mech. Sci. 2022, 221, 107196. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Kumar, R.; Mishra, P.C. Grey-Fuzzy Hybrid Optimization for Thermohydrodynamic Performance Prediction of Misaligned Rough Elliptic Bore Journal Bearing. Lubricants 2022, 10, 274. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, X.; Gryllias, K.; Zhu, H.; Liu, X. Optimization of Stern Bearing Lubrication Performance Under Misaligned Journal Conditions Based on Length-to-Diameter Ratio. J. Tribol. 2026, 148, 14102. [Google Scholar] [CrossRef]
- Sun, X.; Chocholaty, B.; Liu, Y.; Marburg, S. Nonlinear dynamic behavior of a rotor-bearing system considering time-varying misalignment. Int. J. Mech. Sci. 2024, 284, 109772. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Li, X.; Shi, Z.; Gu, F. Tribo-dynamic performance analysis of engine main bearings with provision for wear progression and dynamic misalignment. Eng. Fail. Anal. 2025, 169, 109196. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Greenwood, J.; Williamson, J. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Ausas, R.F.; Jai, M.; Buscaglia, G.C. A Mass-Conserving Algorithm for Dynamical Lubrication Problems With Cavitation. J. Tribol. 2009, 131, 31702. [Google Scholar] [CrossRef]
- Tala-Ighil, N.; Maspeyrot, P.; Fillon, M.; Bounif, A. Effects of surface texture on journal-bearing characteristics under steady-state operating conditions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 623–633. [Google Scholar] [CrossRef]
- Rohde, S.M.; McAllister, G.T. On the optimization of fluid film bearings. Proc. R. Soc. Lond. A Math. Phys. Sci. 1997, 351, 481–497. [Google Scholar] [CrossRef]
- Shen, C.; Khonsari, M.M. Numerical optimization of texture shape for parallel surfaces under unidirectional and bidirectional sliding. Tribol. Int. 2015, 82, 1–11. [Google Scholar] [CrossRef]


| Parameters | Results from Tala-Ighil et al. [38] | Present Work |
|---|---|---|
| Applied load (N) | 12,600 | 12,600 |
| Eccentricity ratio | 0.601 | 0.601 |
| Maximum pressure (MPa) | 7.70 | 7.72 |
| ) | 1.217 | 1.220 |
| Attitude angle (degree) | 50.5 | 50.7 |
| Parameter | Value | Unit |
|---|---|---|
| Bearing diameter | 50 | |
| 0.25 | ||
| 38 | ||
| 6 | ||
| 1.5 | ||
| 2.5 | ||
| Journal mass | 3.2 | |
| 10 | ||
| ) | 66 (210) | |
| ) | 0.33 (0.269) | - |
| 0.124 | ||
| 844.560 | ||
| 0.55383 | ||
| 0.064589 | - | |
| 0.045045 | - |
| Eccentricity Ratio | Unidirectional Optimized Results | Bidirectional Optimized Results | |
|---|---|---|---|
| 0.1 | 3.47 | 3.85 | 4.84 |
| 0.5 | 17.97 | 1.98 | 12.01 |
| 0.8 | 43.27 | −19.53 | 12.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wei, H.; Gu, C. Sensitivity of Texture Evolution and Performance to Eccentricity, Misalignment, and Oil Supply in Journal Bearings with the Circumferential Oil Groove: An Adjoint-Based Optimization Study. Lubricants 2025, 13, 479. https://doi.org/10.3390/lubricants13110479
Zhang D, Wei H, Gu C. Sensitivity of Texture Evolution and Performance to Eccentricity, Misalignment, and Oil Supply in Journal Bearings with the Circumferential Oil Groove: An Adjoint-Based Optimization Study. Lubricants. 2025; 13(11):479. https://doi.org/10.3390/lubricants13110479
Chicago/Turabian StyleZhang, Di, Haijun Wei, and Chunxing Gu. 2025. "Sensitivity of Texture Evolution and Performance to Eccentricity, Misalignment, and Oil Supply in Journal Bearings with the Circumferential Oil Groove: An Adjoint-Based Optimization Study" Lubricants 13, no. 11: 479. https://doi.org/10.3390/lubricants13110479
APA StyleZhang, D., Wei, H., & Gu, C. (2025). Sensitivity of Texture Evolution and Performance to Eccentricity, Misalignment, and Oil Supply in Journal Bearings with the Circumferential Oil Groove: An Adjoint-Based Optimization Study. Lubricants, 13(11), 479. https://doi.org/10.3390/lubricants13110479






