Polarization Vector Rotations: Real, Spurious, Hidden and Imaginary
Abstract
:1. Introduction
2. Search for Rotations
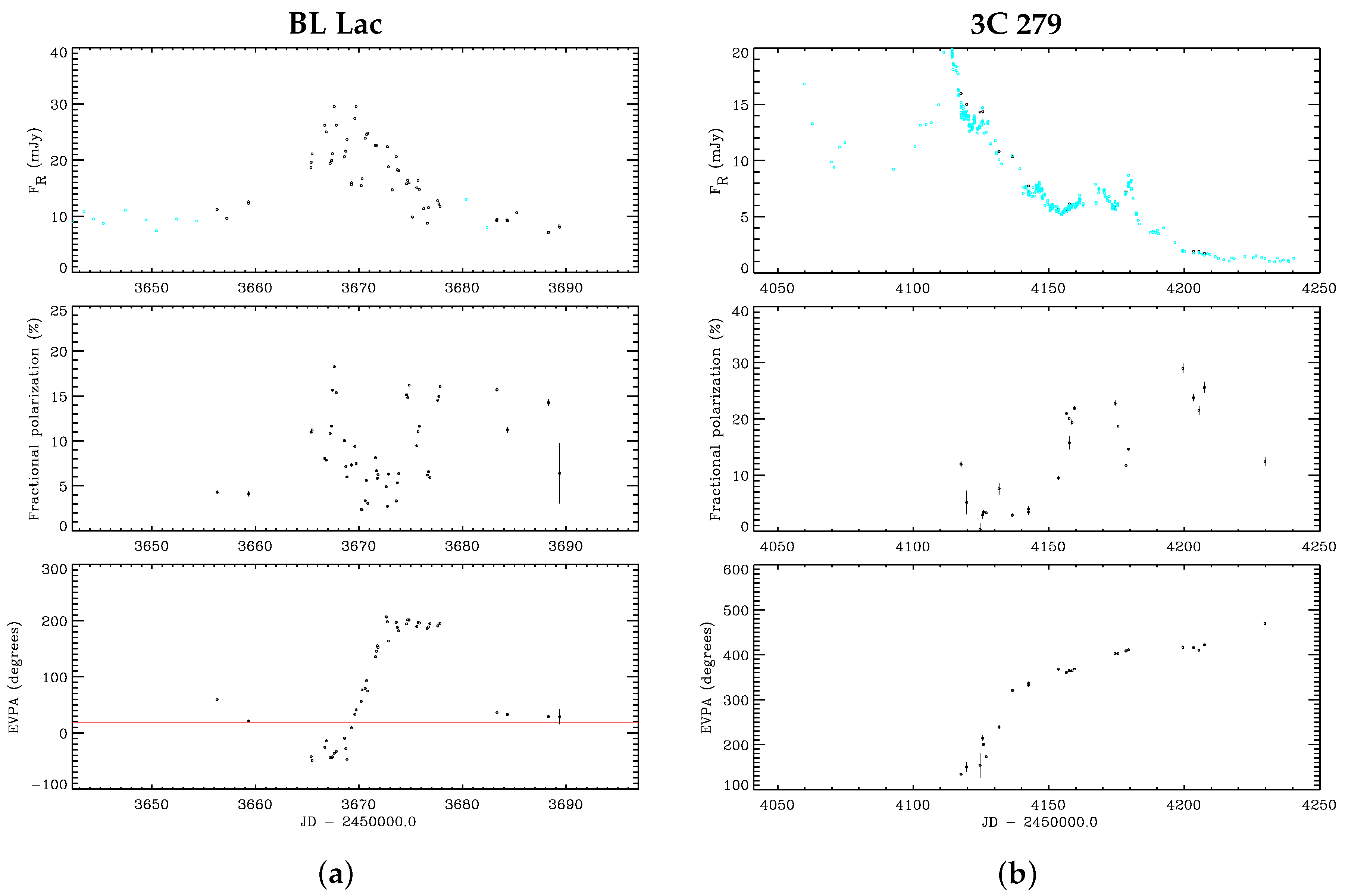
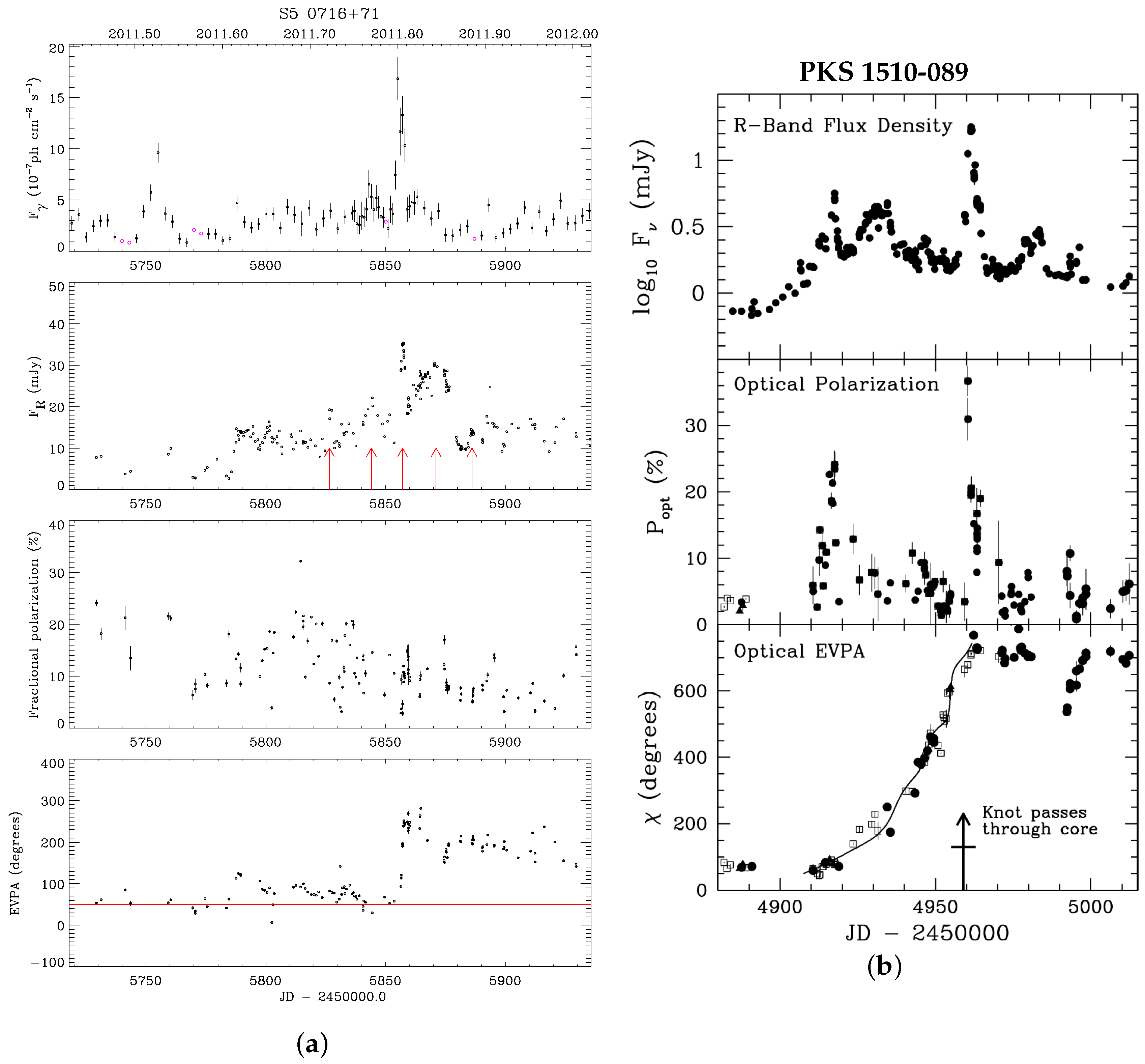
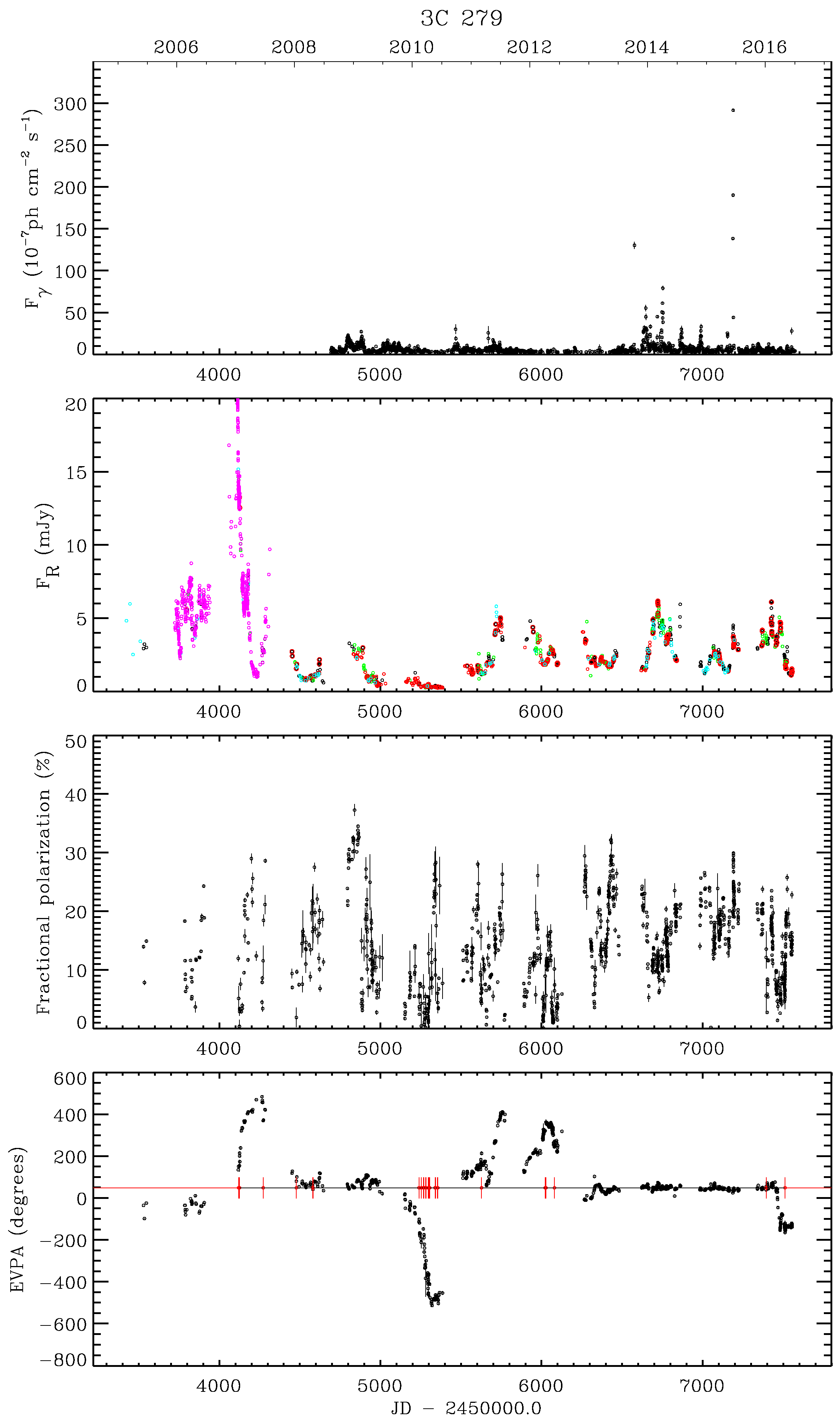
2.1. Rotations: Real
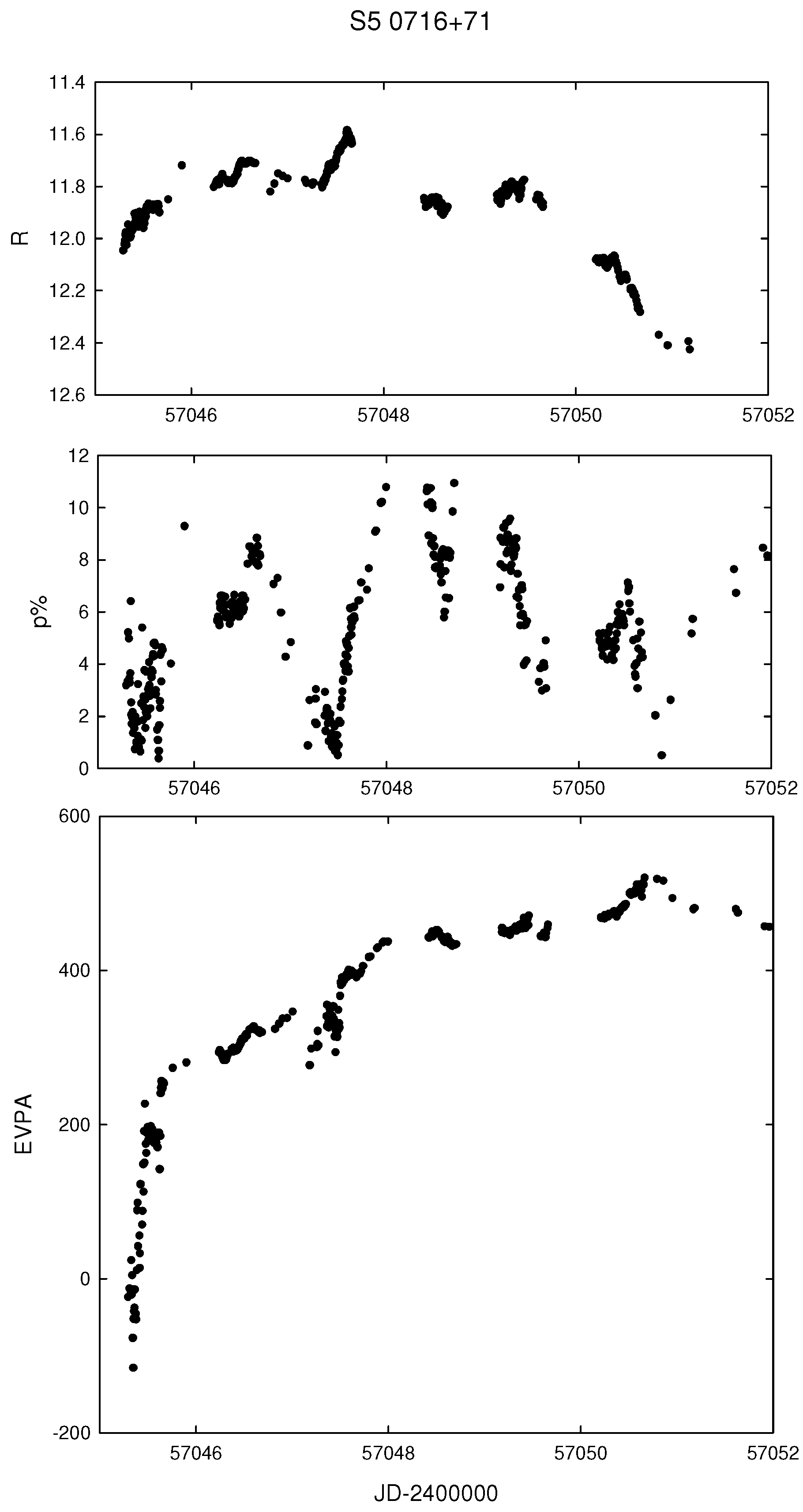
2.2. Rotations: Spurious and False
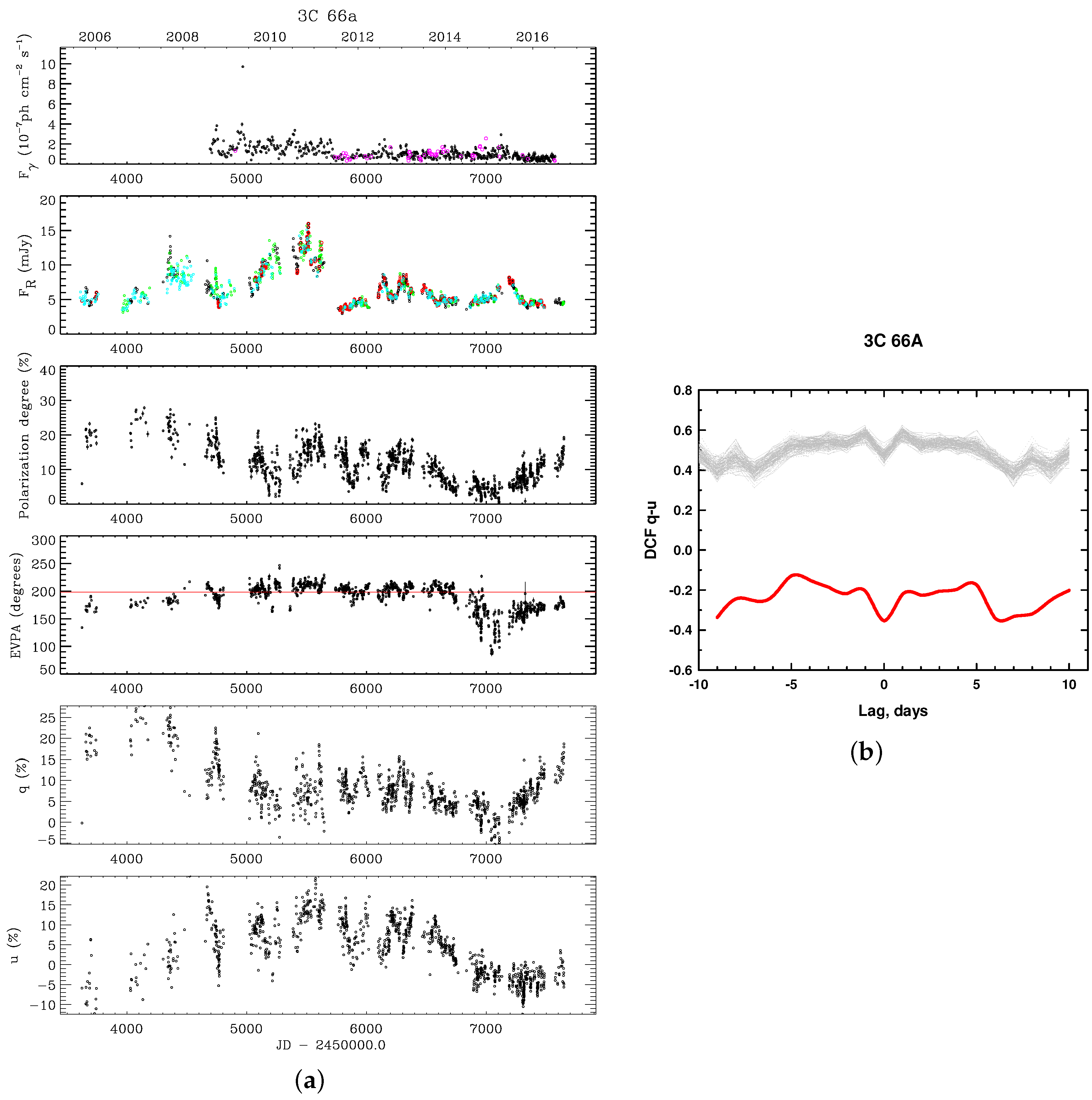
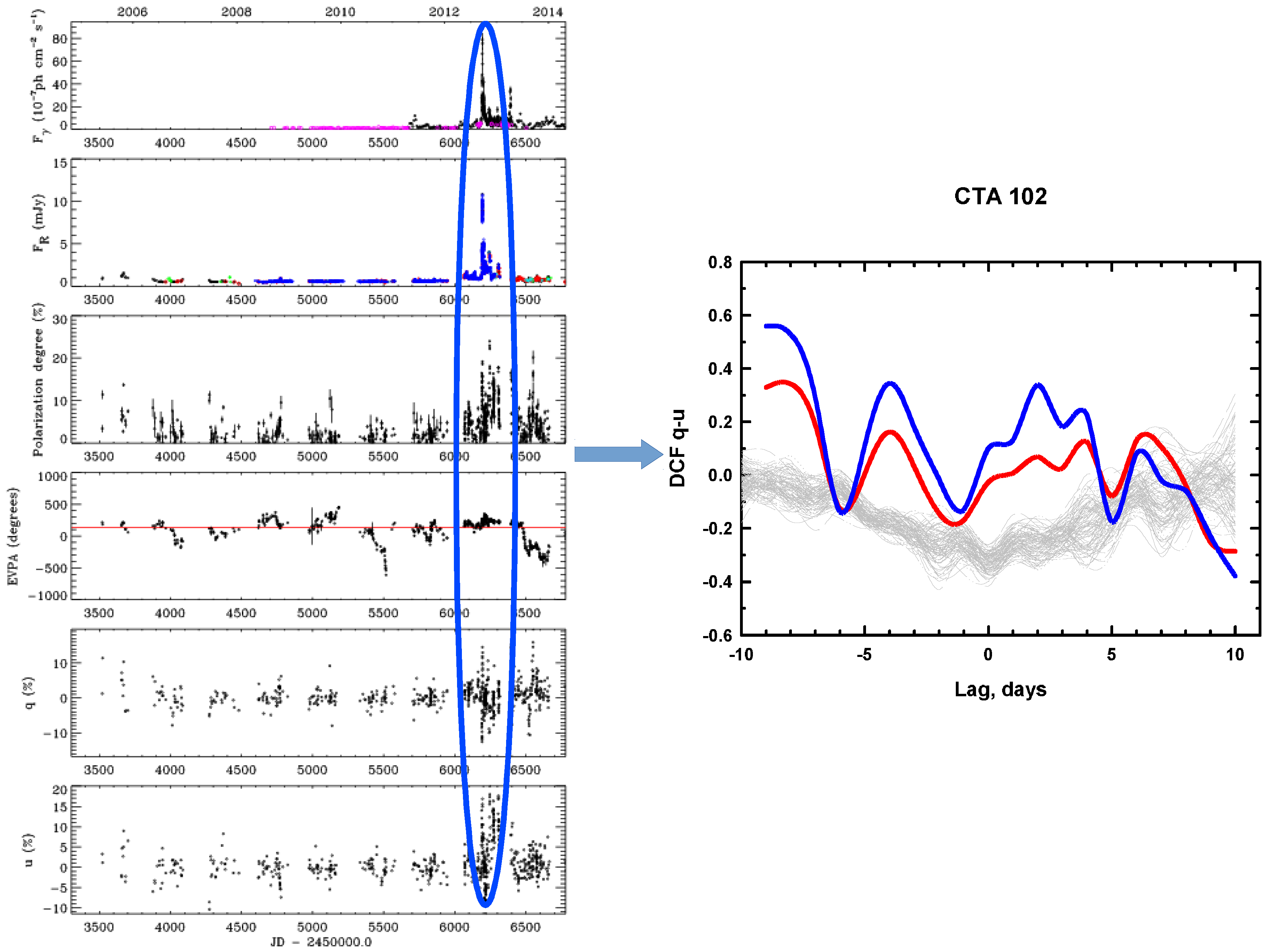
2.3. Rotations: Hidden
3. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marscher, A.P.; Jorstad, S.G.; D’Arcangelo, F.D.; Smith, P.S.; Williams, G.G.; Larionov, V.M.; Oh, H.; Olmstead, A.R.; Aller, M.F.; Aller, H.D.; et al. The inner jet of an active galactic nucleus as revealed by a radio-to-γ-ray outburst. Nature 2008, 452, 966–969. [Google Scholar] [CrossRef] [PubMed]
- Larionov, V.M.; Jorstad, S.G.; Marscher, A.P.; Raiteri, C.M.; Villata, M.; Agudo, I.; Aller, M.F.; Arkharov, A.A.; Asfandiyarov, I.M.; Bach, U.; et al. Results of WEBT, VLBA and RXTE monitoring of 3C 279 during 2006–2007. Astron. Astrophys. 2008, 492, 389–400. [Google Scholar] [CrossRef]
- Marscher, A.P.; Jorstad, S.G.; Larionov, V.M.; Aller, M.F.; Aller, H.D.; Lähteenmäki, A.; Agudo, I.; Smith, P.S.; Gurwell, M.; Hagen-Thorn, V.A.; et al. Probing the Inner Jet of the Quasar PKS 1510-089 with Multi-Waveband Monitoring During Strong Gamma-Ray Activity. Astrophys. J. 2010, 710, L126–L131. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Baughman, B.M.; Bechtol, K.; et al. A change in the optical polarization associated with a γ-ray flare in the blazar 3C 279. Nature 2010, 463, 919–923. [Google Scholar] [CrossRef] [PubMed]
- Larionov, V.M.; Jorstad, S.G.; Marscher, A.P.; Morozova, D.A.; Blinov, D.A.; Hagen-Thorn, V.A.; Konstantinova, T.S.; Kopatskaya, E.N.; Larionova, L.V.; Larionova, E.G.; et al. The Outburst of the Blazar S5 0716+71 in 2011 October: Shock in a Helical Jet. Astrophys. J. 2013, 768, 40. [Google Scholar] [CrossRef]
- Larionov, V.M.; Villata, M.; Raiteri, C.M.; Jorstad, S.G.; Marscher, A.P.; Agudo, I.; Smith, P.S.; Acosta-Pulido, J.A.; Arévalo, M.J.; Arkharov, A.A.; et al. Exceptional outburst of the blazar CTA 102 in 2012: The GASP-WEBT campaign and its extension. Mon. Not. R. Astron. Soc. 2016, 461, 3047–3056. [Google Scholar] [CrossRef]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87–96. [Google Scholar] [CrossRef]
- Kiehlmann, S.; Savolainen, T.; Jorstad, S.G.; Sokolovsky, K.V.; Schinzel, F.K.; Marscher, A.P.; Larionov, V.M.; Agudo, I.; Akitaya, H.; Benítez, E.; et al. Polarization angle swings in blazars: The case of 3C 279. Astron. Astrophys. 2016, 590, A10. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.; Kiehlmann, S.; Panopoulou, G.; Liodakis, I.; King, O.G.; Angelakis, E.; Baloković, M.; Das, H.; et al. RoboPol: First season rotations of optical polarization plane in blazars. Mon. Not. R. Astron. Soc. 2015, 453, 1669–1683. [Google Scholar] [CrossRef]
- Blinov, D.; Pavlidou, V.; Papadakis, I.E.; Hovatta, T.; Pearson, T.J.; Liodakis, I.; Panopoulou, G.V.; Angelakis, E.; Baloković, M.; Das, H.; et al. RoboPol: Optical polarization-plane rotations and flaring activity in blazars. Mon. Not. R. Astron. Soc. 2016, 457, 2252–2262. [Google Scholar] [CrossRef]
- Kikuchi, S.; Mikami, Y.; Inoue, M.; Tabara, H.; Kato, T. A synchronous variation of polarization angle in OJ 287 in the optical and radio regions. Astron. Astrophys. 1988, 190, L8–L10. [Google Scholar]
- Sillanpää, A.; Takalo, L.O.; Nilsson, K.; Kikuchi, S. Photopolarimetry of Bl-Lacertae. Astrophys. Space Sci. 1993, 206, 55–70. [Google Scholar] [CrossRef]
- Edelson, R.A.; Krolik, J.H. The discrete correlation function—A new method for analyzing unevenly sampled variability data. Astrophys. J. 1988, 333, 646–659. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larionov, V.M.; Jorstad, S.G.; Marscher, A.P.; Smith, P.S. Polarization Vector Rotations: Real, Spurious, Hidden and Imaginary. Galaxies 2016, 4, 43. https://doi.org/10.3390/galaxies4040043
Larionov VM, Jorstad SG, Marscher AP, Smith PS. Polarization Vector Rotations: Real, Spurious, Hidden and Imaginary. Galaxies. 2016; 4(4):43. https://doi.org/10.3390/galaxies4040043
Chicago/Turabian StyleLarionov, Valeri M., Svetlana G. Jorstad, Alan P. Marscher, and Paul S. Smith. 2016. "Polarization Vector Rotations: Real, Spurious, Hidden and Imaginary" Galaxies 4, no. 4: 43. https://doi.org/10.3390/galaxies4040043





