Quantum Numbers and the Eigenfunction Approach to Obtain Symmetry Adapted Functions for Discrete Symmetries

Abstract

The eigenfunction approach used for discrete symmetries is deduced from the concept of quantum numbers. We show that the irreducible representations (irreps) associated with the eigenfunctions are indeed a shorthand notation for the set of eigenvalues of the class operators (character table). The need of a canonical chain of groups to establish a complete set of commuting operators is emphasized. This analysis allows us to establish in natural form the connection between the quantum numbers and the eigenfunction method proposed by J.Q. Chen to obtain symmetry adapted functions. We then proceed to present a friendly version of the eigenfunction method to project functions.

Keywords

quantum numbers; discrete systems; symmetry projection; eigenfunction method; ${\text{H}}_3^{+}$; CH₄

1. Introduction

The importance of symmetry at the level of fundamental laws of nature (e.g., in high energy physics, subnuclear physics, nuclear and atomic physics) is widely recognized [1,2,3,4,5]. Symmetry presents a high level of impact in solid state physics and also in chemistry, as testified by the diversity of textbooks concerned with the application of symmetry to problems in various field of chemistry such as molecular orbitals, crystal field theory, molecular vibrations, hybrid orbitals and band theory [6,7,8,9,10,11,12,13,14]. We may consider that the importance of symmetry has two aspects. On one hand it allows a labeling scheme for the energy levels, a fundamental feature in spectroscopy since it permits to establish the selection rules of the system. On the other hand, when the symmetry is taken into account, a remarkable simplification in the calculations becomes manifest.

Quantum numbers appears in natural form when dealing with continuum transformations, as stated by the Noether’s theorem, which establish the existence of conserved quantities when the Euler–Lagrange equations are invariant under a coordinate transformation [5]. Hence once the transformations that commute with the Hamiltonian are identified, a complete set of commuting operators (CSCO) is set up using the invariant operators of the symmetry group of the system. In this form, the simultaneous diagonalization of those operators provides eigenvalues that are identified with quantum numbers of the system. For example, in the nonrelativistic approximation, the symmetry group of the hydrogen atom is $O\left(4\right)$ and the Casimir operators associated with the chain $O\left(4\right)\supset O\left(3\right)\supset O\left(2\right)$ establish a CSCO, whose diagonalization provides the eigenstates $|nlm\rangle$ carrying the well-known quantum numbers [15]. This approach can be generalized in a more elegant context using the concept of dynamical group, which is defined as the group whose generators are used to expand any dynamical variable of the system including the Hamiltonian [16]. Hence, although the identification of the quantum numbers is clear when dealing with continuum transformations, the quantum numbers associated with discrete symmetries is not obvious, since the concept of a Casimir operators cannot be translated in a straightforward way.

For discrete systems like molecules and crystals, the general labeling scheme consists in assigning to the states an irrep of the symmetry group together with the Hamiltonian eigenvalue, since several eigenstates may carry the same irreducible representation. It is not stressed enough, however, the fact that the irreps correspond in reality to a set of quantum numbers associated with eigenvalues of the class operators of the group. This fact can be verified in the textbooks by the way of introducing the character tables through the representations theory, without establishing the direct connection with the Wigner’s theorem. On the other hand, during the seventies and eighties, J.Q. Chen developed a theory, known as the eigenfunction approach, which allowed in a particularly efficient way to carry out the projection of a basis set of functions to the space of functions spanning irreps. This approach is presented in detail in his book from a mathematical point of view, establishing the connection with the traditional theory of representations of groups [17]. One of his incentives to develop his theory was to establish a theory of discrete groups in complete analogy to the theory of continuum groups. In the latter case, Casimir operators play the fundamental role to establish a complete set of commuting operators (CSCO), a necessary tool to provide a complete set of labels. On the other hand, in the former case the fundamental ingredient is given by the classes, which allows a CSCO to be constructed. Chen’s theory is at first sight quite complicated, which may explain the fact that the eigenfunction approach is practically unknown by the community of chemists and spectroscopists, and little known in other fields where discrete symmetries are relevant. But a remarkable fact concerning the eigenfunction approach is that the method itself is indeed suggested when a CSCO is established to identify the quantum numbers in systems of discrete symmetry. We believe that this fact makes quite clear the goal of the theory. Hence the aim of this work is to provide the connection between the eigenfunction approach and the search for the identification of the quantum numbers associated with the symmetry of the system. This point of view makes quite natural the introduction of the eigenfunction approach. In addition we present the eigenfunction approach in a friendly fashion in order to make the approach accessible to the community of chemists and spectroscopists, without the need of an expertise background in group theory.

The paper is organized as follows. In Section 2 the quantum numbers associated with a system of discrete symmetry are identified with the eigenvalues of the class operators of a chain of groups. Section 3 is devoted to make the connection with the eigenfunction approach, as well as the main steps to take advantage of this approach. The projection of the stretching coordinates of methane is presented in Section 4 as a complete example of the projection method. Finally in Section 5 a summary and the conclusions are presented.

2. Irreducible Representations and Quantum Numbers

One of the fundamental concepts in quantum mechanics is the complete set of commuting operators (CSCO). The essence of this concept lies on the necessity of labeling without ambiguity the eigenstates of the Schrödinger equation for stationary states

$$\widehat{\mathcal{H}}|\Psi \rangle =E|\Psi \rangle$$

(1)

It should be clear that the Hamiltonian itself can be considered as part of the set of the CSCO, since the energy E provides a label for the eigenstate $|\Psi \rangle$ through (1). If α stands for an index introduced to distinguish different energies, a more precise form of expressing the Equation (1) is

$$\widehat{\mathcal{H}}|{\Psi }_i^{\alpha }\rangle =E_{\alpha }|{\Psi }_i^{\alpha }\rangle ;i=1,\dots ,g_{\alpha }$$

(2)

where the subindex i accounts for the possibility of appearing several functions (in this case $g_{\alpha }$ functions) associated with the same energy. In practice, since the exact solutions $|{\Psi }_i^{\alpha }\rangle$ cannot be found, they are expanded in terms of a set of n known orthonormal kets $|{\varphi }_j\rangle$

$$|{\Psi }_i^{\alpha }\rangle =\sum _{j=1}^n{s}_{j;\alpha ,i}|{\varphi }_j\rangle$$

(3)

The substitution of this equation into (2) leads to the system of eigenvalues [21]

$$\sum _{j=1}^n(h_{kj}-E_{\alpha }{\delta }_{kj})s_{j;\alpha ,i}=0$$

(4)

where

$$h_{kj}=\langle {\varphi }_k|\widehat{\mathcal{H}}|{\varphi }_j\rangle$$

(5)

are the matrix elements of the Hamiltonian in the basis ${\mathcal{L}}_n=\left\{\right|{\varphi }_i\rangle ,i=1,\dots ,n\}$. The homogeneous linear set of Equation (4) is equivalent to the diagonalization of the matrix $\mathbf{H}\equiv \left|\right|h_{kj}\left|\right|$, e.g.,

$${\mathbf{S}}^{-\mathbf{1}}\mathbf{H}\mathbf{S}=\Lambda$$

(6)

where Λ is a diagonal matrix with elements given by the eigenvalues $E_{\alpha }$, and $\mathbf{S}\equiv \left|\right|s_{j;\alpha ,i}\left|\right|$. The CSCO is concerned with the procedure to distinguish (adding labels corresponding to eigenvalues of additional operators) the set of kets $\left\{\right|{\Psi }_i^{\alpha }\rangle ,i=1,\dots ,g_{\alpha }\}$. The criterion to establish the CSCO is based on symmetry concepts, where the machinery of group representation theory emerges as a fundamental tool.

By definition, the maximum set of transformations that leaves the Hamiltonian invariant corresponds to the symmetry group G. Technically, if $R_i\in G$, then the associated operator ${\mathcal{O}}_{R_i}$ acting on the physical space commute with the Hamiltonian

$$[{\mathcal{O}}_{R_i},\widehat{\mathcal{H}}]=0;i=1,2,\dots ,|G|$$

(7)

where $\left|G\right|$ stands for the number of elements of the group. We may thus think that the set of operators $\{\widehat{\mathcal{H}},{\mathcal{O}}_{R_i};i=1,\dots ,|G|\}$ is useful to define a CSCO, but in general $[{\mathcal{O}}_{R_i},{\mathcal{O}}_{R_j}]\ne 0$, unless the group is Abelian. This problem is solved by selecting subsets of G, which turn out to be the conjugate classes of the group. A conjugate class $K_i$ with number of elements $|K_i|$ is defined by the set of elements $\{g_j^{\left(i\right)};j=1,\dots |K_i|\}$, which are connected by at least one element $u\in G$ through

$$g_j^{\left(i\right)}=u{g}_k^{\left(i\right)}{u}^{-1}$$

(8)

The class operator for the i-th class is defined by

$${\widehat{K}}_i=\sum _{\beta =1}^{|K_i|}\widehat{\mathcal{O}}{g}_{\beta }^{\left(i\right)}$$

(9)

From (7), it is clear that

$$[\widehat{H},{\widehat{K}}_i]=0,\forall {\widehat{K}}_i$$

(10)

and since every class $K_i$ commutes with any element $u\in G$, we have that $[K_i,u]=0$, a property followed from (8). As a consequence we also have the remarkable property

$$[K_j,K_i]=0,\forall i,j$$

(11)

Hence the Hamiltonian together with the classes of the group constitutes a set of commuting operators and they can be diagonalized simultaneously in any space of independent functions. Let ${\mathcal{L}}_n=\left\{\right|{\varphi }_i\rangle ,i=1,\dots ,n\}$ the space to be chosen, which may be constituted by atomic orbitals or internal coordinates, for instance. The set $\left\{\right|{\Psi }_i^{\alpha }\rangle ,i=1,\dots ,g_{\alpha }\}$ given by (3) are eigenvectors of $\widehat{H}$. We may now construct the representation matrix of the class $K_p$ in this basis

$$\left|\right|\langle {\Psi }_j^{\alpha }|{\widehat{K}}_p|{\Psi }_i^{\alpha }\rangle \left|\right|;i,j=1,\dots g_{\alpha }$$

(12)

The diagonalization of this matrix provides eigenvectors of type $\{|{\Psi }_k^{\alpha ,{\lambda }_p}\rangle ,k=1,\dots ,g_{\alpha ,{\lambda }_p}\}$, with the property

$$\widehat{\mathcal{H}}|{\Psi }_l^{\alpha ,{\lambda }_p}\rangle =E_{\alpha }|{\Psi }_l^{\alpha ,{\lambda }_p}\rangle ,{\widehat{K}}_p|{\Psi }_l^{\alpha ,{\lambda }_p}\rangle ={\lambda }_p|{\Psi }_l^{\alpha ,{\lambda }_p}\rangle$$

(13)

where ${\lambda }_p$ is the label that distinguish the different eigenvalues of the class operator ${\widehat{K}}_p$, and l accounts for the degeneracy. We may now proceed to obtain the matrix representation of the next class ${\widehat{K}}_q$ in the new basis $|{\Psi }_l^{\alpha ,{\lambda }_p}\rangle$, to obtain eigenvectors with the additional label ${\lambda }_q$

$${\widehat{K}}_p|{\Psi }_l^{\alpha ,{\lambda }_p,{\lambda }_q}\rangle ={\lambda }_q|{\Psi }_l^{\alpha ,{\lambda }_p,{\lambda }_q}\rangle$$

(14)

where the subindex l considers again the possibility of a degeneracy. We may follow this procedure with the rest of the classes to obtain a set of states $\{|{\Psi }_l^{\alpha ,{\lambda }_1,\dots ,{\lambda }_{\left|K\right|}}\}$ characterized by the eigenvalues

$$\{\alpha ,{\lambda }_1,\dots ,{\lambda }_{\left|K\right|}\}$$

(15)

This set of labels is not complete, and a degeneracy still remains. To see why this is the case, we should note that the classes $\{K_i;i=1,\dots ,|K\left|\right\}$ are linearly independent and consequently there are as many different sets $\{{\lambda }_1,\dots ,{\lambda }_{\left|K\right|}\}$ as number of classes. But we know that the number of irreps is equal to the number of classes and consequently the set of labels $\{{\lambda }_1,\dots ,{\lambda }_{\left|K\right|}\}$ is expected to specify an irrep. Introducing the label ν for the possible solutions (irreps), a more precise labeling should be

$$\{{\lambda }_1^{\nu },{\lambda }_2^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }\}$$

(16)

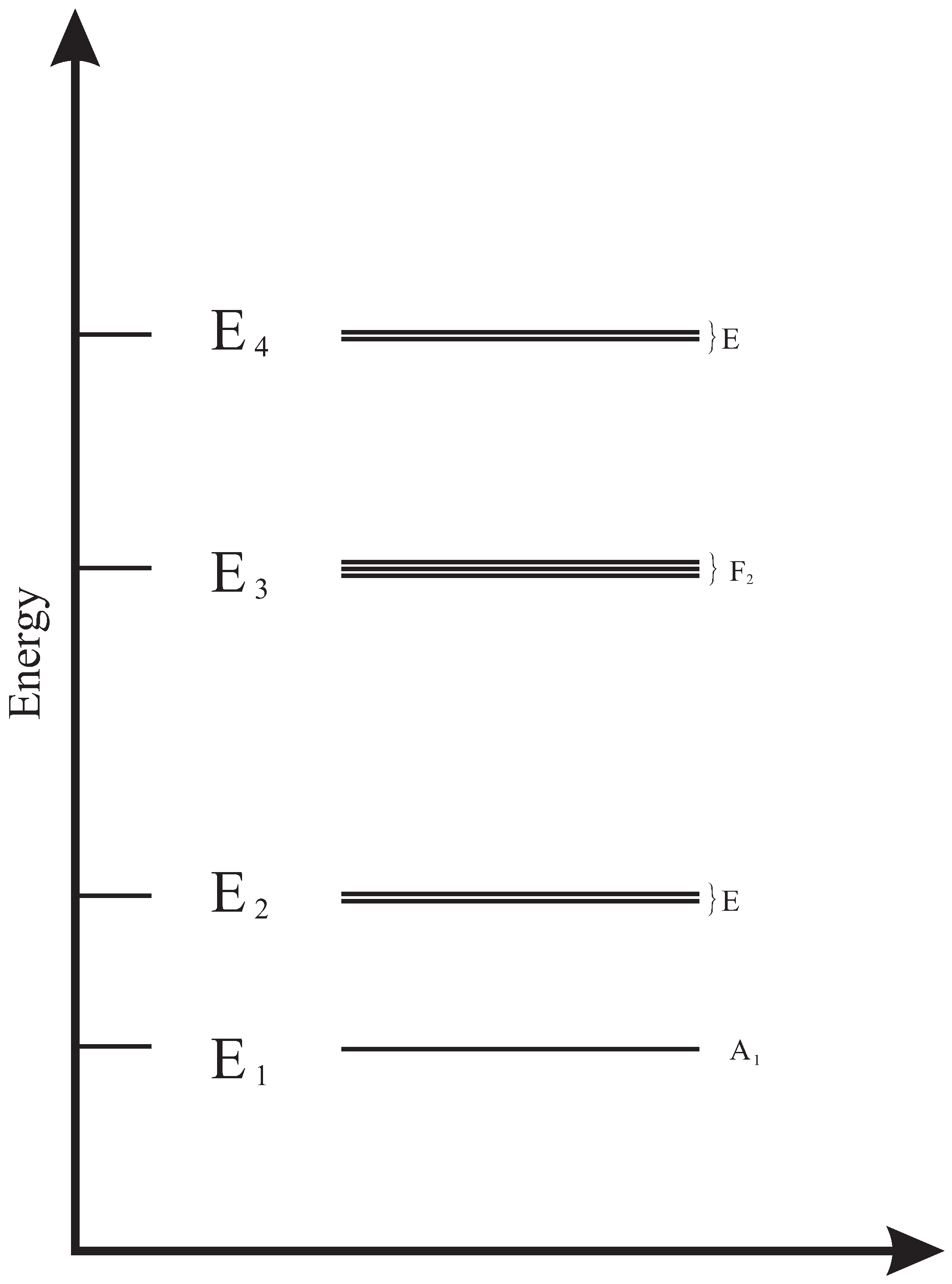
This is a formal way to name an irrep. For two and three dimensional irreps (E and F), for instance, a degeneracy still remains, which by the way is not broken by the Hamiltonian since the energy $E_{\alpha }$ only distinguish different sets with the same irrep. This situation is illustrated in Figure 1.

Figure 1. Eigenstates labeled with the energy and the irreps. A degeneracy still remains due to the degeneracy of the irreps.

Figure 1. Eigenstates labeled with the energy and the irreps. A degeneracy still remains due to the degeneracy of the irreps.

The question that arises is concerned with the identification of the new set of operators capable to distinguish the states associated with the degeneracy of the irreps. The answer is given by the classes of a subgroup.

Let H be a subgroup of G:$H\subset G$. Suppose that H has $\left|k\right|$ classes $\{k_1,\dots ,k_{\left|k\right|}\}$ which clearly satisfy

$$[k_p,k_q]=0$$

(17)

But the classes $\{K_i,i=1,\dots ,|K\left|\right\}$ of the group G commute with any element of the group, and consequently commute also with the classes of the subgroup

$$[K_i,k_p]=0,\forall i,p$$

(18)

This fact suggests to diagonalize the operators ${\widehat{k}}_p$ in the basis $\{|{\Psi }_l^{\alpha ,{\lambda }_1,\dots ,{\lambda }_{\left|K\right|}}\rangle \}$ to obtain a complete labeling for the components of the irreps. Indeed, it can be proved that this is the case as long as a suitable subgroup forming a canonical chain is chosen. This will be discussed in the next section. For the moment we just affirm that after this procedure of diagonalization the matrix representation of the classes of the subgroup H, we arrive to the complete labeling scheme

$$|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_1^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }}\rangle$$

(19)

where the subindices ${\lambda }_p^{\mu }$ are defined by

$${\widehat{k}}_p|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_1^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }}\rangle ={\lambda }_p^{\mu }|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_1^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }}\rangle$$

(20)

considering that μ labels the irreps of the subgroup H. In the next section we shall see that the process of labeling is very simple and that it is not necessary to use all the classes to establish an unambiguous labeling scheme. In fact, the relevant involved classes are intended to contain the generators of the group and subgroup, a resulting set with cardinality less than the total number of classes $\left|K\right|$.

Let us now turn our attention to the identification of the labels involved in (19) as quantum numbers. The time evolution of the expected value of an operator $\widehat{A}$ is given by [19,21]

$$\frac{d}{dt}\langle \Psi |\widehat{A}|\Psi \rangle =\langle \Psi |[\widehat{H},\widehat{A}]|\Psi \rangle +\langle \Psi |\frac{\partial \widehat{A}}{\partial t}|\Psi \rangle$$

(21)

where $[\widehat{H},\widehat{A}]$ is the commutator of the Hamiltonian with the operator $\widehat{A}$. Hence, a remarkable consequence is that if the operator $\widehat{A}$ does not depend explicitly on time and commute with the Hamiltonian, then the expected value is constant in time:

$$\frac{d}{dt}\langle \Psi |\widehat{A}|\Psi \rangle =0;[\widehat{H},\widehat{A}]=0,\frac{\partial \widehat{A}}{\partial t}=0$$

(22)

Suppose now that the states are chosen to be eigenstates of the Hamiltonian together with the classes of the group G and subgroup H. Then

$$|\Psi \rangle \to |{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_1^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }}\rangle$$

(23)

and the set of Equation (22) translates into

$$\frac{d}{dt}{E}_{\alpha }=0;\frac{d}{dt}{\lambda }_i^{\nu }=0;\frac{d}{dt}{\lambda }_p^{\mu }=0;i=1,\dots ,\left|K\right|;p=1,\dots ,\left|k\right|$$

(24)

when $\widehat{A}$ is substituted by $\widehat{\mathcal{H}}$, ${\widehat{K}}_i$ and ${\widehat{k}}_p$. Hence the eigenvalues of the set of operators $\{\widehat{\mathcal{H}};{\widehat{K}}_1,\dots ,K_{\left|K\right|};{\widehat{k}}_1,\dots ,k_{\left|k\right|}\}$ are independent of time and consequently are quantum numbers. In the next section we shall see that this fact derives into the eigenfunction approach to obtain symmetry adapted functions, a powerful method that allow us to deal with the technical point of view of symmetry in an efficient form.

3. The Eigenfunction Approach

For a given energy eigenvalue α there is a set of ${\lambda }_i^{\nu }$ values characterizing the ν-th irrep in accordance with (16). As mentioned before this fact suggests a connection between the ${\lambda }_i^{\nu }$ values and the characters ${\chi }_i^{\left(\nu \right)}$ of the group as we next show.

For a given irrep ν the representation of a class $K_i$ is given by

$${\mathbf{D}}^{\left(\nu \right)}\left(K_i\right)=\sum _{\beta =1}^{|K_i|}{\mathbf{D}}^{\left(\nu \right)}(g_{\beta }^{\left(i\right)})$$

(25)

But since

$$[{\mathbf{D}}^{\left(\nu \right)}\left(K_i\right),{\mathbf{D}}^{\left(\nu \right)}\left(R\right)]=0;\forall R\in G$$

(26)

it follows by Schur’s Lema II [20] that ${\mathbf{D}}^{\left(\nu \right)}\left(K_i\right)$ must be proportional to the unit matrix. In fact, we have [20]

$${\mathbf{D}}^{\left(\nu \right)}\left(K_i\right)=\frac{|K_i|{\chi }_i^{\left(\nu \right)}}{n_{\nu }}\mathbf{1}$$

(27)

But the eigenvalues of the classes are given by

$${\mathbf{D}}^{\left(\mu \right)}\left(K_i\right)={\lambda }_i^{\nu }\mathbf{1}$$

(28)

and consequently

$${\lambda }_i^{\nu }=\frac{|K_i|}{n_{\nu }}{\chi }_i^{\left(\nu \right)};i=1,\dots ,\left|K\right|$$

(29)

where $n_{\nu }$ refers to the dimension of the ν-th irrep. A similar relation holds for ${\lambda }_p^{\mu }$ and the characters of the subgroup H. Note that the expression (29) basically tell us that the character tables constitute the set of quantum numbers, a remarkable feature not mentioned explicitly in textbooks. Indeed, the Equation (29) is so important that leads to the most efficient projection technique, as we next explain.

The relation (29) itself suggests a projection method based on the diagonalization of class operators. This assertion may be appreciated because of the following: any set of symmetry adapted functions $\{|{\psi }_i^{\left(\nu \right)}\rangle ,i=1,n_{\nu }\}$ spanning the ν-th irrep of dimension $n_{\nu }$ satisfies

$${\widehat{K}}_i|{\psi }_i^{\left(\nu \right)}\rangle ={\lambda }_i^{\nu }|{\psi }_i^{\left(\nu \right)}\rangle ;i=1,\dots ,n_{\nu }$$

(30)

which is a consequence of (28) and it means that the functions $|{\psi }_i^{\left(\nu \right)}\rangle$ are eigenvectors of the class operators with eigenvalue ${\lambda }_i^{\nu }$. This remarkable result suggests to proceed in the other way around to obtain (19): We start diagonalizing the class operators and at the end the Hamiltonian is diagonalized taking advantage that its representation in such basis is block diagonal. This approach leads to the eigenfunction method of projecting functions [17].

Here it is convenient to point out the difference between the approach presented here and the Chen’s approach to the eigenfunction method. As the reader noticed, our approach is based on the Wigner’s theorem and the concept of CSCO to label the eigenstates. In this way the concept of quantum numbers is intrinsically connected with the eigenvalues of the class operators, which in turn are related to irreps of the symmetry group.

In contrast, in the Chen’s theory, the main ingredient is that the eigenvectors in the class space are identified as projector operators, while the Wigner’s theorem is discussed separately. The whole representation theory is developed in detail but it seems disconnected with the fundamental Wigner’s theorem [17].

We now introduce the series of steps to apply the eigenfunction approach. In practice we proceed in the following form to project an arbitrary set of orthonormal functions $\left\{\right|{\varphi }_i\rangle ,i=1,\dots ,n\}$ with $\langle {\varphi }_i|{\varphi }_j\rangle ={\delta }_{ij}$. First we chose a subset of classes of G as well as of H that allows their corresponding irreps to be distinguished. A linear combination of the selected classes provides eigenvectors carrying the ν-th irrep. Let us consider an example to illustrate this idea. Suppose we want to obtain the symmetry projected functions from the space ${\mathcal{L}}_3=\left\{\right|s_1\rangle ,|s_2\rangle ,|s_3\rangle \}$ corresponding to the atomic s-orbitals of the H${}_3^{+}$ molecule. The symmetry group of this molecule is ${\mathcal{D}}_{3h}$. However, since the s-orbitals are invariant under the reflection through the plane of the molecule, we can simplify our analysis by considering the subgroup ${\mathcal{D}}_3$, whose character table is given in Table 1, with symmetry elements displayed in Figure 2.

Figure 2. Molecule H${}_3^{+}$ and the symmetry elements of the group ${\mathit{D}}_3$.

Figure 2. Molecule H${}_3^{+}$ and the symmetry elements of the group ${\mathit{D}}_3$.

Table 1. Character table of the group ${\mathcal{D}}_3$. The notation for the classes is the following: $K_1=\left\{E\right\},K_2=\{C_3,C_3^2\}$ and $K_3=\{C_2^a,C_2^b,C_2^c\}$.

${\mathcal{D}}_3$	$K_1$	$K_2$	$K_3$
$A_1$	1	1	1
$A_2$	1	1	$-1$
E	2	$-1$	0

Table 1. Character table of the group ${\mathcal{D}}_3$. The notation for the classes is the following: $K_1=\left\{E\right\},K_2=\{C_3,C_3^2\}$ and $K_3=\{C_2^a,C_2^b,C_2^c\}$.

${\mathcal{D}}_3$	$K_1$	$K_2$	$K_3$
$A_1$	1	1	1
$A_2$	1	1	$-1$
E	2	$-1$	0

Let us now construct a table of eigenvalues of the classes, which we call it the ${\lambda }^{\prime }s$ table, by using the expression (29). The result is given in Table 2, from which we note that the class $K_3$ by itself distinguishes the irreps (it contains the generators of the group) and consequently the eigenvectors in (23) may be simplified to

$$|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_1^{\nu },\dots ,{\lambda }_{\left|K\right|}^{\nu }}\rangle \to |{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{\nu }}\rangle$$

(31)

where

$$\begin{array}{ccc}\hfill {\widehat{K}}_3|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_1}}\rangle & =& {\lambda }_3^{A_1}|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_1}}\rangle =+3|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_1}}\rangle \hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill {\widehat{K}}_3|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_2}}\rangle & =& {\lambda }_3^{A_2}|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_2}}\rangle =-3|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^{A_2}}\rangle \hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\widehat{K}}_3|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^E}\rangle & =& {\lambda }_3^E|{\Psi }_{{\lambda }_1^{\mu },\dots ,{\lambda }_{\left|k\right|}^{\mu }}^{\alpha ,{\lambda }_3^E}\rangle =0\hfill \end{array}$$

(34)

in accordance with Table 2.

Table 2. λ’s table for the group ${\mathcal{D}}_3$ obtained from the character table and the relation (29).

${\mathcal{D}}_3$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$
$A_1$	1	2	3
$A_2$	1	2	$-3$
E	1	$-1$	0

Table 2. λ’s table for the group ${\mathcal{D}}_3$ obtained from the character table and the relation (29).

${\mathcal{D}}_3$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$
$A_1$	1	2	3
$A_2$	1	2	$-3$
E	1	$-1$	0

This analysis suggests to deal with the representation of the class $K_3$ in the space ${\mathcal{L}}_3$ as a first step to obtain the projection. Consider now the element $C_2^a\in {\mathcal{D}}_3$. From Figure 2 we obtain the transformation of the s-orbitals under the rotation $C_2^a$: $C_2^a|s_1\rangle \to |s_1\rangle ,C_2^a|s_2\rangle \to |s_3\rangle ,C_2^a|s_3\rangle \to |s_2\rangle$. In matrix form

$$\begin{array}{c}\hfill {\widehat{C}}_2^a\left(\right|s_1\rangle ,|s_2\rangle ,|s_3\rangle )=\left(\right|s_1\rangle ,|s_2\rangle ,|s_3\rangle )\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\equiv \left(\right|s_1\rangle ,|s_2\rangle ,|s_3\rangle )\Delta \left(C_2^a\right)\end{array}$$

(35)

where we have introduced the definition for the representation $\Delta \left(C_2^a\right)$ associated with the operator $C_2^a$ in the space ${\mathcal{L}}_3$. Following the same approach for the rotations $C_2^b$ and $C_2^c$ we obtain their corresponding matrix representations

$$\Delta \left(C_2^b\right)=\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right),\Delta \left(C_2^c\right)=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right)$$

(36)

These results allows the matrix representation of the class $K_3$ to be constructed in a straightforward way. In fact, the representation is given by

$$\Delta \left(K_3\right)=\Delta \left(C_2^a\right)+\Delta \left(C_2^b\right)+\Delta \left(C_2^c\right)=\left(\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right)$$

(37)

The diagonalization of this matrix provides the eigensystem given in Table 3.

Table 3. Eigensystem associated with the matrix representation of the class operator $K_3$.

Irrep	Eigenvalue	Eigenvector
$A_1$	3	$(1,1,1)$
E	0	$(1,0,-1)$
E	0	$(1,-1,0)$

Table 3. Eigensystem associated with the matrix representation of the class operator $K_3$.

Irrep	Eigenvalue	Eigenvector
$A_1$	3	$(1,1,1)$
E	0	$(1,0,-1)$
E	0	$(1,-1,0)$

We should note that the eigenvalues correspond to the values 3 and 0 of the λ’s Table 2. The eigenvectors of Table 3 give rise to the following symmetry adapted functions

$$\begin{array}{ccc}\hfill |{\Psi }^{+3}\rangle & =& \frac{1}{\sqrt{3}}\left(\right|s_1\rangle +|s_2\rangle +|s_3\rangle )\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {|}_1{\Psi }^0\rangle & =& \frac{1}{\sqrt{3}}\left(\right|s_1\rangle -|s_3\rangle )\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill {|}_2{\Psi }^0\rangle & =& \frac{1}{\sqrt{3}}\left(\right|s_1\rangle -|s_2\rangle )\hfill \end{array}$$

(40)

where we have temporarily introduced an arbitrary left subindex in order to distinguish the degenerate eigenvectors associated with the irrep E (eigenvalue 0 in accordance to Table 2). We now proceed to introduce a suitable subgroup H in order to establish the labels ${\lambda }_p^{\mu }$ associated with the classes $k_p$ in (31). Let us propose the subgroup ${\mathcal{C}}_2^a=\{E,C_2^a\}$, a selection that is usually expressed in the form of the chain of subgroups

$${\mathcal{D}}_3\supset {\mathcal{C}}_2^a$$

(41)

To know whether this is a suitable chain to label the states we should obtain the irreps of the subgroup ${\mathcal{C}}_2^a$ contained in the irrep E. To this end it is convenient to present the character table of the subgroup ${\mathcal{C}}_2^a$, including the characters of the irreps of the group ${\mathcal{D}}_3$ (correlation table). This analysis is displayed in Table 4, where the last three rows corresponds to the irreps of ${\mathcal{D}}_3$ and are obtained by taking the characters of Table 1 corresponding to each irrep, selecting the columns $K_1$ and $K_3$ where the elements of the subgroup ${\mathcal{C}}_2^a$ are located.

Table 4. Irreps of ${\mathcal{C}}_2^a$ contained in the irreps of the group ${\mathcal{D}}_3$.

${\mathcal{C}}_2^a$	E	$C_2^a$
A	1	1
B	1	$-1$
$A_1$	1	1	A
$A_2$	1	$-1$	B
E	2	0	$A\oplus B$

Table 4. Irreps of ${\mathcal{C}}_2^a$ contained in the irreps of the group ${\mathcal{D}}_3$.

${\mathcal{C}}_2^a$	E	$C_2^a$
A	1	1
B	1	$-1$
$A_1$	1	1	A
$A_2$	1	$-1$	B
E	2	0	$A\oplus B$

The last column corresponds to the reduction of the irreps of ${\mathcal{D}}_3$ into irreps of ${\mathcal{C}}_2^a$, and may be obtained by choosing the linear combinations of irreps of ${\mathcal{C}}_2^a$ that provide the characters of the irreps of ${\mathcal{D}}_3$. A formal approach to obtain the number of times $a_{\mu }^{\nu }$ that the μ-th irrep of ${\mathcal{C}}_2^a$ is contained in the ν-th irrep of ${\mathcal{D}}_3$ is through the formula [6,7]

$$a_{\mu }^{\nu }=\frac{1}{|{\mathcal{C}}_2^a|}\sum _{p=1}^{\left|k\right|}\left|k_p\right|{\chi }_p^{\mu *}{\chi }_p^{\nu }$$

(42)

where $|{\mathcal{C}}_2^a|$ is the number of elements of the subgroup ${\mathcal{C}}_2^a$, $|k_p|$ stands for the number of elements in the class $k_p$ of the subgroup, while ${\chi }_p^{\mu *}$ and ${\chi }_p^{\nu }$ are the characters of the subgroup and the group, respectively. We note that no repetition of irreps of ${\mathcal{C}}_2^a$ appears in the reduction of E. When this is the case it is said that the chain (41) is canonical, a property that must be satisfied by the selected chain.

We may now identify the class that determines the irreps of the subgroup following the same approach that was used in the group. Since in the subgroup ${\mathcal{C}}_2^a$ all the irreps are one dimensional the λ’s table coincide with the character table and consequently we can identify in a straightforward way the class $k_2=C_2^a$ to distinguish the irreps. This means that if we diagonalize the matrix representation of the operator ${\widehat{C}}_2^a$ in the basis (3), the corresponding eigenvalues will be $+1,-1$, for irreps A and B respectively, in accordance with Table 4. Indeed, the representation of the operator $C_2^a$ in the basis (3) turns out to be

$$\begin{array}{ccc}\hfill {\widehat{C}}_2^a\left(\right|{\Psi }^{+3}\rangle {,|}_1{\Psi }^0{\rangle ,|}_2{\Psi }^0\rangle )& =& \left(\right|{\Psi }^{+3}\rangle {,|}_1{\Psi }^0{\rangle ,|}_2{\Psi }^0\rangle )\left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right)\hfill \end{array}$$

$$\begin{array}{ccc}& \equiv & \left(\right|{\Psi }^{+3}\rangle {,|}_1{\Psi }^0{\rangle ,|}_2{\Psi }^0\rangle )\Delta \left(C_2^a\right)\hfill \end{array}$$

(43)

where we have used (35) and (36). The representation $\Delta \left(C_2^a\right)$ is a block diagonal matrix, an expected result since the operators ${\widehat{C}}_2^a$ cannot mix functions of different irreps of the group ${\mathcal{D}}_3$. The diagonalization of the matrix $\Delta \left(C_2^a\right)$ provides the eigenvectors

$$\begin{array}{ccc}\hfill |{\Psi }_1^0\rangle & =& {|}_1{\Psi }^0{\rangle +|}_2{\Psi }^0\rangle =\frac{1}{\sqrt{6}}\left(2\right|s_1\rangle -|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill |{\Psi }_{-1}^0\rangle & =& {|}_1{\Psi }^0\rangle -{}_2|{\Psi }^0\rangle =\frac{1}{\sqrt{2}}\left(\right|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(45)

where the subindex appearing in the new functions corresponds to the eigenvalues of the operator ${\widehat{C}}_2^a$. But from Table 2 and Table 4 we now the correspondence of the eigenvalues with the traditional labeling of the irreps. For the group ${\mathcal{D}}_3$

$$+3\leftrightarrow A_1;0\leftrightarrow E$$

(46)

while for the subgroup

$$+1\leftrightarrow A;-1\leftrightarrow B$$

(47)

We may now identify the functions in the usual notation

$$\begin{array}{ccc}\hfill |{\Psi }^{+3}\rangle & \equiv & |{\Psi }^{A_1}\rangle =\frac{1}{\sqrt{3}}\left(\right|s_1\rangle +|s_2\rangle +|s_3\rangle )\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill |{\Psi }_1^0\rangle & \equiv & |{\Psi }_A^E\rangle =\frac{1}{\sqrt{6}}\left(2\right|s_1\rangle -|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill |{\Psi }_{-1}^0\rangle & \equiv & |{\Psi }_B^E\rangle =\frac{1}{\sqrt{2}}\left(\right|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(50)

To obtain the functions (3) we have carried out two diagonalizations, corresponding to the operators ${\widehat{K}}_3$ and ${\widehat{k}}_2={\widehat{C}}_2^a$. We may simplify this procedure by diagonalizing a unique operator obtained as a linear combination of the operators $K_3$ and ${\widehat{k}}_2$. To obtain the appropriate combination we construct a table containing the possible eigenvalues according to the λ’s table for ${\mathcal{D}}_3$ and ${\mathcal{C}}_2^a$, together with the reduction given in Table 4. The results are given the Table 5.

Table 5. Eigenvalues associated with the operators ${\widehat{K}}_3$ and ${\widehat{k}}_2={\widehat{C}}_2^a$ corresponding to the chain of groups ${\mathcal{D}}_3\supset {\mathcal{C}}_2^a$.

${\mathcal{D}}_3$	${\lambda }_3^{\nu }$	${\mathcal{C}}_2^a$	${\lambda }_2^{\mu }$	${\lambda }_3^{\nu }+{\lambda }_2^{\mu }$
$A_1$	$+3$	A	$+1$	$+4$
$A_2$	$-3$	B	$-1$	$-4$
E	0	A	$+1$	$+1$
E	0	B	$-1$	$-1$

Table 5. Eigenvalues associated with the operators ${\widehat{K}}_3$ and ${\widehat{k}}_2={\widehat{C}}_2^a$ corresponding to the chain of groups ${\mathcal{D}}_3\supset {\mathcal{C}}_2^a$.

${\mathcal{D}}_3$	${\lambda }_3^{\nu }$	${\mathcal{C}}_2^a$	${\lambda }_2^{\mu }$	${\lambda }_3^{\nu }+{\lambda }_2^{\mu }$
$A_1$	$+3$	A	$+1$	$+4$
$A_2$	$-3$	B	$-1$	$-4$
E	0	A	$+1$	$+1$
E	0	B	$-1$	$-1$

In the last column we have included the sum of the eigenvalues. As noted all the numbers are different, a fact that implies that we can define the operator $C_{II}$ as

$$C_{II}\equiv {\widehat{K}}_3+{\widehat{k}}_2=2{\widehat{C}}_2^a+{\widehat{C}}_2^b+{\widehat{C}}_2^c$$

(51)

whose diagonalization provides the symmetry adapted functions in a straightforward way in one step. Proceeding in this manner we obtain the representation matrix

$$\Delta \left(C_{II}\right)=\left(\begin{array}{ccc}2& 1& 1\\ 1& 1& 2\\ 1& 2& 1\end{array}\right)$$

(52)

The diagonalization of this matrix provides the eigensystem presented in Table 6, from which we identify immediately the symmetry adapted functions (3) in the form

$$\begin{array}{ccc}\hfill |{\Psi }^{+4}\rangle & \equiv & |{\Psi }^{A_1}\rangle =\frac{1}{\sqrt{3}}\left(\right|s_1\rangle +|s_2\rangle +|s_3\rangle )\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill |{\Psi }^1\rangle & \equiv & |{\Psi }_A^E\rangle =\frac{1}{\sqrt{6}}\left(2\right|s_1\rangle -|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill |{\Psi }^{-1}\rangle & \equiv & |{\Psi }_B^E\rangle =\frac{1}{\sqrt{2}}\left(\right|s_2\rangle -|s_3\rangle )\hfill \end{array}$$

(55)

Table 6. Eigensystem associated with the matrix representation of the class operator ${\widehat{C}}_{II}$.

Irreps	Eigenvalue	Eigenvector
$A_1$	$+4$	$(1,1,1)$
$(E,A)$	$+1$	$(2,-1,-1)$
$(E,B)$	$-1$	$(0,1,-1)$

Table 6. Eigensystem associated with the matrix representation of the class operator ${\widehat{C}}_{II}$.

Irreps	Eigenvalue	Eigenvector
$A_1$	$+4$	$(1,1,1)$
$(E,A)$	$+1$	$(2,-1,-1)$
$(E,B)$	$-1$	$(0,1,-1)$

This example allows us to establish the series of steps to obtain symmetry adapted functions for any molecular system:

Step 1. From the character table of the symmetry group G, the λ’s table is generated using (29).

Step 2. We proceed to identify the column that distinguish the irreps of the group G. In general more than one column is needed to achieve this goal. In such case a linear combinations of columns are selected in such a way that the eigenvalues are all different. This process defines the linear combination of classes, which we shall identify with the operator $\widehat{C}$.

Step 3. A subgroup H is proposed in such a way that the irreps of G are not contained more than once in H.

Step 4. From the character table of H, we construct the λ’s table and identify the columns that distinguish the irreps. The columns involved define a linear combination of classes of the subgroup that define the operator $\widehat{C}\left(s\right)$. This operators is the equivalent of $\widehat{C}$ in the group G.

Step 5. A table of eigenvalues associated with G and H is constructed (Table 5 in our example). A linear combination of λ’s is identified to define a new operator ${\widehat{C}}_{II}$.

Step 6. The representation of the operator ${\widehat{C}}_{II}$ is generated using the space to be projected. The diagonalization of the matrix representation $\Delta \left(C_{II}\right)$ provides the symmetry adapted functions.

We should stress that up to Step 5, no dependence of the space appears. Given a molecular system, the first 4 steps are general and are useful to project any representation space; electronic functions, rotational functions, vibrational function or spin functions. Only the last step is a function of the space. In the next section we shall present a more elaborate example of projection in order to exemplify the approach.

4. An Example: Stretching Degrees of Freedom of Methane

In this section we shall obtain the projection of the stretching internal coordinates in the molecule of methane, whose symmetry group is ${\mathcal{T}}_d$. The symmetry elements are displayed in Figure 3. We shall follow the steps presented in the previous section.

Figure 3. Molecule of methane and the symmetry elements of the group ${\mathcal{T}}_d$.

Figure 3. Molecule of methane and the symmetry elements of the group ${\mathcal{T}}_d$.

Step 1. From the character table of the group ${\mathcal{T}}_d$ given in Table 7, we obtain the λ’s table using the relation (29), which is displayed in Table 8.

Table 7. Character table of the group ${\mathcal{T}}_d$.

${\mathcal{T}}_d$	$K_1$	$K_2$	$K_3$	$K_4$	$K_5$
	E	$4C_3,4C_3^2$	$3C_2$	$3S_4,3S_2^3$	$6{\sigma }_d$
$A_1$	1	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$A_2$	1	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$
E	2	$-1$	$\phantom{-}2$	$\phantom{-}0$	$\phantom{-}0$
$F_1$	3	$\phantom{-}0$	$-1$	$\phantom{-}1$	$-1$
$F_2$	3	$\phantom{-}0$	$-1$	$-1$	$\phantom{-}1$

Table 7. Character table of the group ${\mathcal{T}}_d$.

${\mathcal{T}}_d$	$K_1$	$K_2$	$K_3$	$K_4$	$K_5$
	E	$4C_3,4C_3^2$	$3C_2$	$3S_4,3S_2^3$	$6{\sigma }_d$
$A_1$	1	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$	$\phantom{-}1$
$A_2$	1	$\phantom{-}1$	$\phantom{-}1$	$-1$	$-1$
E	2	$-1$	$\phantom{-}2$	$\phantom{-}0$	$\phantom{-}0$
$F_1$	3	$\phantom{-}0$	$-1$	$\phantom{-}1$	$-1$
$F_2$	3	$\phantom{-}0$	$-1$	$-1$	$\phantom{-}1$

Table 8. λ’s table of the group ${\mathcal{T}}_d$.

${\mathcal{T}}_d$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$	${\lambda }_4^{\nu }$	${\lambda }_5^{\nu }$
$A_1$	1	8	3	6	6
$A_2$	1	8	3	$-6$	$-6$
E	1	$-4$	3	0	0
$F_1$	1	0	$-1$	2	$-2$
$F_2$	1	0	$-1$	$-2$	2

Table 8. λ’s table of the group ${\mathcal{T}}_d$.

${\mathcal{T}}_d$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$	${\lambda }_4^{\nu }$	${\lambda }_5^{\nu }$
$A_1$	1	8	3	6	6
$A_2$	1	8	3	$-6$	$-6$
E	1	$-4$	3	0	0
$F_1$	1	0	$-1$	2	$-2$
$F_2$	1	0	$-1$	$-2$	2

Step 2. From the λ’s table we note that the either the class $K_4$ or $K_5$ are suitable to be chosen as $\widehat{C}$ since in both cases all the eigenvalues are different (both contain generators of the group). We propose

$$\widehat{C}={\widehat{K}}_5$$

(56)

because in practice the reflections are more suitable to be used in the calculation of matrix elements. In general the selected classes must contain the generators of the group.

Step 3. We propose the subgroup ${\mathcal{C}}_{2v}$ to distinguish the different components of the irreps E, $F_1$ and $F_2$. To check if the group ${\mathcal{C}}_{2v}$ is appropriate we proceed to find the irreps of this subgroup contained in the irreps of the group using (42). To this end we write down the character table of the subgroup ${\mathcal{C}}_{2v}$ including the irreps of the group ${\mathcal{T}}_d$, together with the reductions obtained through (42), as indicated in Table 9. Since there is no repetition of the irreps of ${\mathcal{C}}_{2v}$ contained in the irreps of ${\mathcal{T}}_d$, the proposed subgroup ${\mathcal{C}}_{2v}$ is suitable to label the states.

Step 4. From the character table of ${\mathcal{C}}_{2v}$ we construct the corresponding λ’s table as given in Table 10. It is clear that there is no column that is able to distinguish the irreps by itself, as expected. So we have to propose a linear combination of them. In fact we propose ${\lambda }_2^{\nu }+3{\lambda }_3^{\nu }$, whose values are included in the table. This means that the operator $C\left(s\right)$ is defined as

$$\widehat{C}\left(s\right)={\widehat{C}}_2^z+3{\widehat{\sigma }}_d^I$$

(57)

In general the coefficients of the classes should be prime numbers to avoid ambiguities.

Table 9. Subduction ${}_{\mu }{\mathcal{T}}_d\downarrow {\mathcal{C}}_{2v}$.

${\mathcal{C}}_{2v}$	E	$C_2^z$	${\sigma }_d^I$	${\sigma }_d^{II}$
$A_1$	1	1	1	1
$A_2$	1	1	$-1$	$-1$
$B_1$	1	$-1$	1	$-1$
$B_2$	1	$-1$	$-1$	1
$A_1$	1	1	1	1	$A_1$
$A_2$	1	1	$-1$	$-1$	$A_2$
E	2	2	0	0	$A_1\oplus A_2$
$F_1$	3	$-1$	$-1$	$-1$	$A_2\oplus B_1\oplus B_2$
$F_2$	3	$-1$	1	1	$A_1\oplus B_1\oplus B_2$

Table 9. Subduction ${}_{\mu }{\mathcal{T}}_d\downarrow {\mathcal{C}}_{2v}$.

${\mathcal{C}}_{2v}$	E	$C_2^z$	${\sigma }_d^I$	${\sigma }_d^{II}$
$A_1$	1	1	1	1
$A_2$	1	1	$-1$	$-1$
$B_1$	1	$-1$	1	$-1$
$B_2$	1	$-1$	$-1$	1
$A_1$	1	1	1	1	$A_1$
$A_2$	1	1	$-1$	$-1$	$A_2$
E	2	2	0	0	$A_1\oplus A_2$
$F_1$	3	$-1$	$-1$	$-1$	$A_2\oplus B_1\oplus B_2$
$F_2$	3	$-1$	1	1	$A_1\oplus B_1\oplus B_2$

Table 10. λ’s table of the group ${\mathcal{C}}_{2v}$.

${\mathcal{C}}_{2v}$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$	${\lambda }_4^{\nu }$	${\lambda }_2^{\nu }+3{\lambda }_3^{\nu }$
$A_1$	1	1	1	1	$+4$
$A_2$	1	1	$-1$	$-1$	$-2$
$B_1$	1	$-1$	1	$-1$	$+2$
$B_2$	1	$-1$	$-1$	1	$-4$

Table 10. λ’s table of the group ${\mathcal{C}}_{2v}$.

${\mathcal{C}}_{2v}$	${\lambda }_1^{\nu }$	${\lambda }_2^{\nu }$	${\lambda }_3^{\nu }$	${\lambda }_4^{\nu }$	${\lambda }_2^{\nu }+3{\lambda }_3^{\nu }$
$A_1$	1	1	1	1	$+4$
$A_2$	1	1	$-1$	$-1$	$-2$
$B_1$	1	$-1$	1	$-1$	$+2$
$B_2$	1	$-1$	$-1$	1	$-4$

Step 5. We now proceed to display the Table 11 of eigenvalues associated with ${\mathcal{T}}_d$ and ${\mathcal{C}}_{2v}$.

Table 11. λ’s table of the groups ${\mathcal{T}}_d$ and ${\mathcal{C}}_{2v}$ to determine the CSCO-II.

${\mathcal{T}}_d$	ν	${\mathcal{C}}_{2v}$	m	$\nu +3m$
$A_1$	6	$A_1$	4	18
$A_2$	$-6$	$A_2$	$-2$	$-12$
E	0	$A_1$	4	12
E	0	$A_2$	$-2$	$-6$
$F_1$	$-2$	$A_2$	$-2$	$-4$
$F_1$	$-2$	$B_1$	2	4
$F_1$	$-2$	$B_2$	$-4$	$-14$
$F_2$	2	$A_1$	4	14
$F_2$	2	$B_1$	2	8
$F_2$	2	$B_2$	$-4$	$-10$

Table 11. λ’s table of the groups ${\mathcal{T}}_d$ and ${\mathcal{C}}_{2v}$ to determine the CSCO-II.

${\mathcal{T}}_d$	ν	${\mathcal{C}}_{2v}$	m	$\nu +3m$
$A_1$	6	$A_1$	4	18
$A_2$	$-6$	$A_2$	$-2$	$-12$
E	0	$A_1$	4	12
E	0	$A_2$	$-2$	$-6$
$F_1$	$-2$	$A_2$	$-2$	$-4$
$F_1$	$-2$	$B_1$	2	4
$F_1$	$-2$	$B_2$	$-4$	$-14$
$F_2$	2	$A_1$	4	14
$F_2$	2	$B_1$	2	8
$F_2$	2	$B_2$	$-4$	$-10$

In this table the eigenvalues of $\widehat{C}$ are called ν, while the eigenvalues of $\widehat{C}\left(s\right)$ are called m. The linear combination $\nu +3m$ provides with different eigenvalues, which means that the operator

$${\widehat{C}}_{II}=\widehat{C}+3\widehat{C}\left(s\right)={\widehat{K}}_5+3({\widehat{C}}_2^z+3{\widehat{\sigma }}_d^I)$$

(58)

is able to provide a complete set of labels to the symmetry adapted functions.

Step 6. We now consider the space of stretching coordinates of methane with the labeling displayed in Figure 3. The matrix representation of the of the operator $C_{II}$ in this basis is given by

$$\Delta \left(C_{II}\right)=\left(\begin{array}{cccc}12& 4& 1& 1\\ 4& 12& 1& 1\\ 1& 1& 3& 13\\ 1& 1& 13& 3\end{array}\right)$$

(59)

The diagonalization of this matrix provides the following set of eigenvalues and eigenvectors displayed in Table 12.

Table 12. Eiganvalues and eigenvectors of the matrix representation (59).

Irreps	Eigenvalue	Eigenvector
$A_1$	$+18$	$(1,1,1,1)$
$(F_2,A_1)$	$+14$	$(1,1,-1,-1)$
$(F_2,B_1)$	8	$(-1,1,0,0)$
$(F_2,B_2)$	$-10$	$(0,0,-1,1)$

Table 12. Eiganvalues and eigenvectors of the matrix representation (59).

Irreps	Eigenvalue	Eigenvector
$A_1$	$+18$	$(1,1,1,1)$
$(F_2,A_1)$	$+14$	$(1,1,-1,-1)$
$(F_2,B_1)$	8	$(-1,1,0,0)$
$(F_2,B_2)$	$-10$	$(0,0,-1,1)$

Identifying the eigenvalues with the irreps in Table 11, we finally obtain the symmetry adapted functions

$$\begin{array}{ccc}\hfill {\Psi }^{A_1}& =& \frac{1}{2}(r_1+r_2+r_3+r_4)\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill {\Psi }_{A_1}^{F_2}& =& \frac{1}{2}(r_1+r_2-r_3-r_4)\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill {\Psi }_{B_1}^{F_2}& =& \frac{1}{\sqrt{2}}(r_1-r_2)\hfill \end{array}$$

(62)

$$\begin{array}{ccc}\hfill {\Psi }_{B_2}^{F_2}& =& \frac{1}{\sqrt{2}}(r_3-r_4)\hfill \end{array}$$

(63)

We have thus obtained the symmetry adapted functions through the diagonalization of the representation of only one operator, which is defined in a simple way by considering the appropriate linear combinations in the λ’s tables. This is a systematic and very powerful method useful when dealing with spaces of high dimension [18,22].

In the examples analyzed above, the reduction of the reducible space does not involve the case when the irreps appear more than once. In such case it is necessary to introduce additional operators to distinguish the irreps. This situation has been extensively discussed in [17,18,22]. Here we constrained ourselves to establish the connection between the eigenfunction approach and the concept of quantum numbers in discrete systems. The extended case may be consulted in the above references.

5. Summary and Conclusions

In this work we have presented a deep insight into the importance and meaning of the irreducible representations used to label the states of molecular systems. We suggest an alternative way to show that the irreps are indeed quantum numbers in the context of finite symmetry groups. The basic idea behind this approach is the concept of a complete set of commuting operators. In the case of finite groups, a subset of classes together with the Hamiltonian constitutes a complete set of operators that provide an unambiguous labeling scheme. The classes must be selected from the group and a suitable subgroup associated with a canonical chain.

The relation of the eigenvalues of the classes with the characters of the group has been used to establish in natural form the connection with the eigenfunction approach proposed by Chen [17]. It has been shown that the projection technique basically consists in identifying a linear combination of classes that provides a complete set of labels. To obtain the suitable combinations is enough to know the character tables of the group as well as the subgroup. It is important to stress that the subgroup must be associated with a canonical chain in order to assure the unambiguous labeling of the states. On the other hand, to achieve the projection, only the effect of the elements involved in the classes are needed, a fact that is in contrast to the traditional approach based on the projection operator where all the elements of the group should be taken into account, even when the projection vanishes [6,7].

The approach we have presented is a simplified version of the original eigenfunction approach, which has several advantages. Given a space to be projected, it is not necessary to know the irreps contained in the space to proceed with the projection; the irreps are identified with the eigenvalues. In addition, it is not necessary to know explicitly the coupling coefficients, because they are calculated always they are needed, avoiding the problem of phases.

To determine the combinations of classes that define the operator ${\widehat{C}}_{II}$ only the character table is basically needed. It is also necessary to obtain the irreps of the proposed subgroup contained in the irreps of the group, but there is a very well-known procedure to achieve this task that involves only a sum of products of characters. Following this method, the diagonalization of the Hamiltonian is just an additional step in the process of successive diagonalizations. This approach has been proved to be very powerful in establishing general codes to construct symmetry adapted functions [18,22].

Since the goal of a projection method consists in diagonalizing the representation of the Hamiltonian at the end, the partial diagonalization of the representation of the CSCO-II may present multiplicity of states carrying the same irrep of the symmetry group. The appearance of this multiplicity leads to the introduction of the CSCO of type III, which turns out to depend on the space. In this case, it is necessary to provide a chain of new groups, called intrinsic groups, which may be basically the same groups but with some constraints and multiplication rules associated with an anti-isomorphism. This situation is present in the description of rotations, where we have a $SO\left(3\right)$ group associated with rotations referred to a system parallel to laboratory, and on intrinsic $\overline{SO}\left(3\right)$ rotational group referred to the rotated system fixed in the molecule. Both are used to label the rigid rotor function [22]. Indeed this situation suggested the introduction of the intrinsic groups for discrete symmetries. The theory however is more elaborated than the approach presented here, although the machinery to establish the chain and the eigenvalues is similar [17,18,22].

Finally, it is worth mentioning that the importance of symmetry goes beyond the contest of linear systems. Even in the presence of nonlinearity, the use of irreducible representations to perform the classifications of solutions has proven to be very useful for their classification [23].