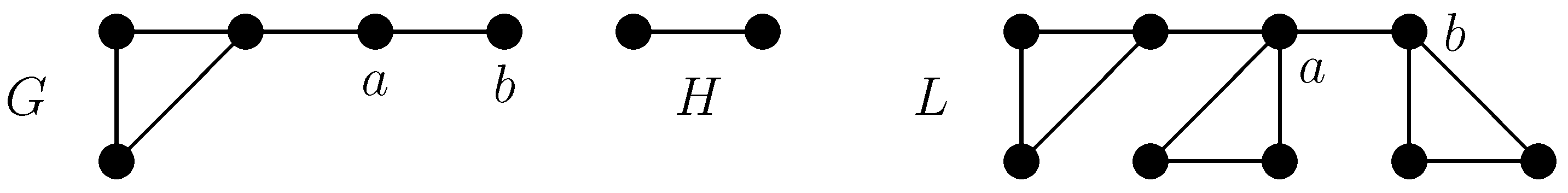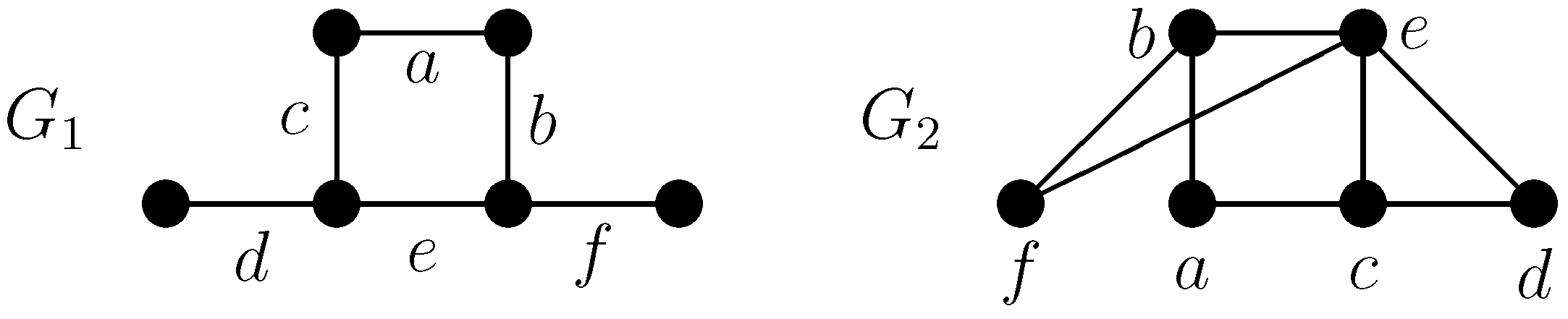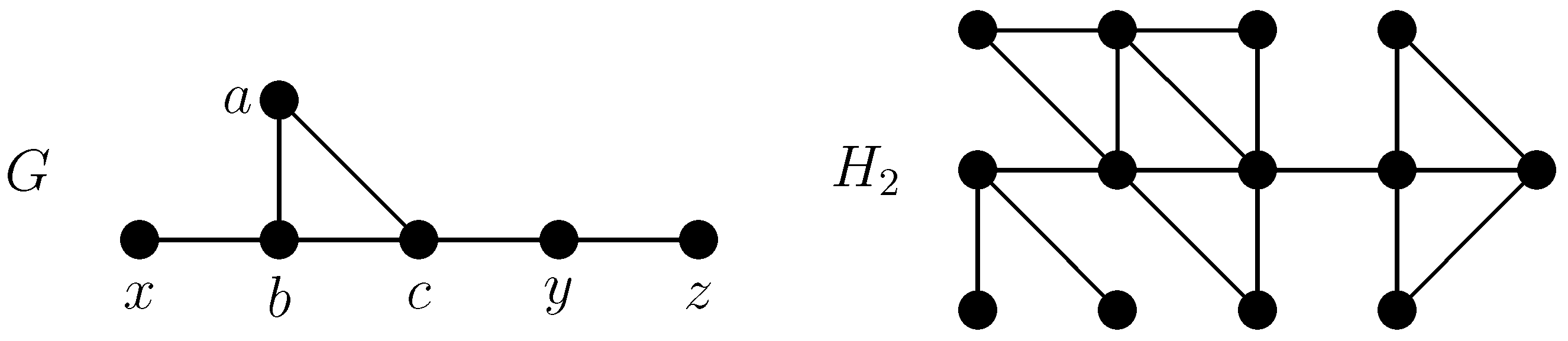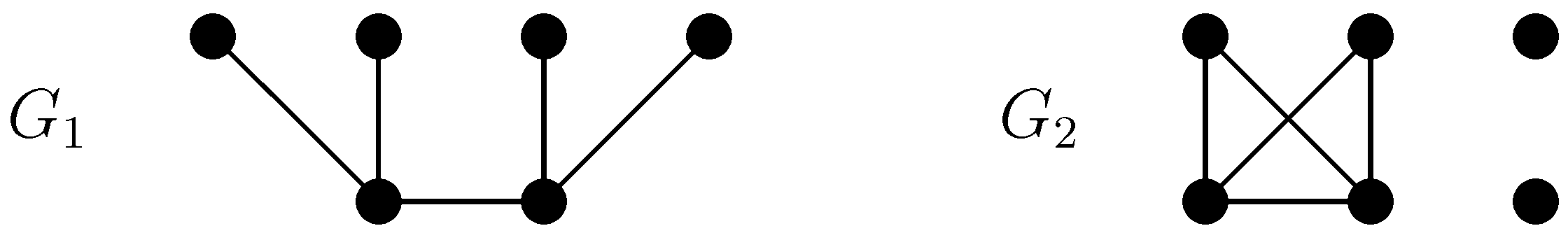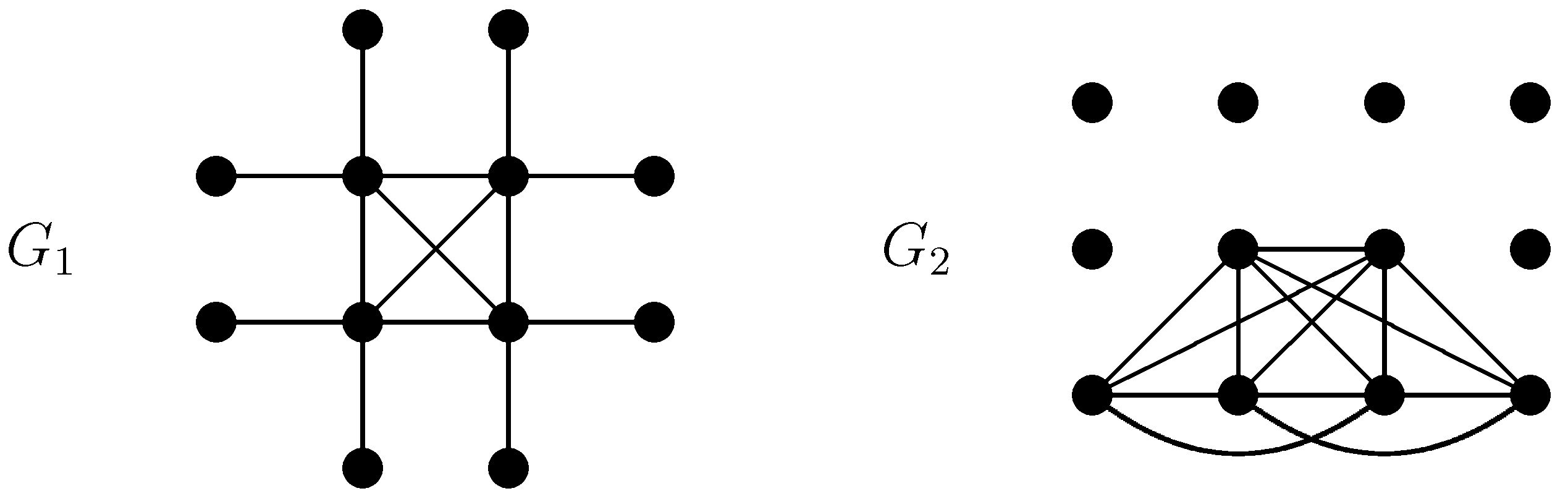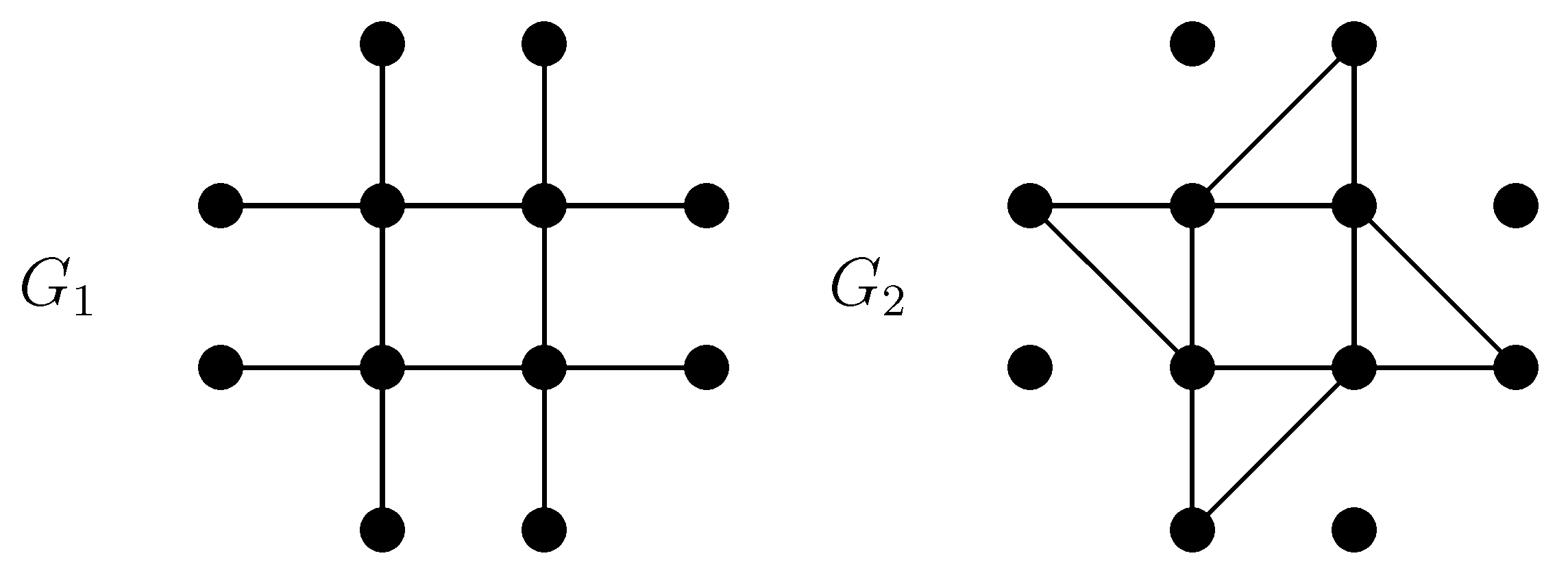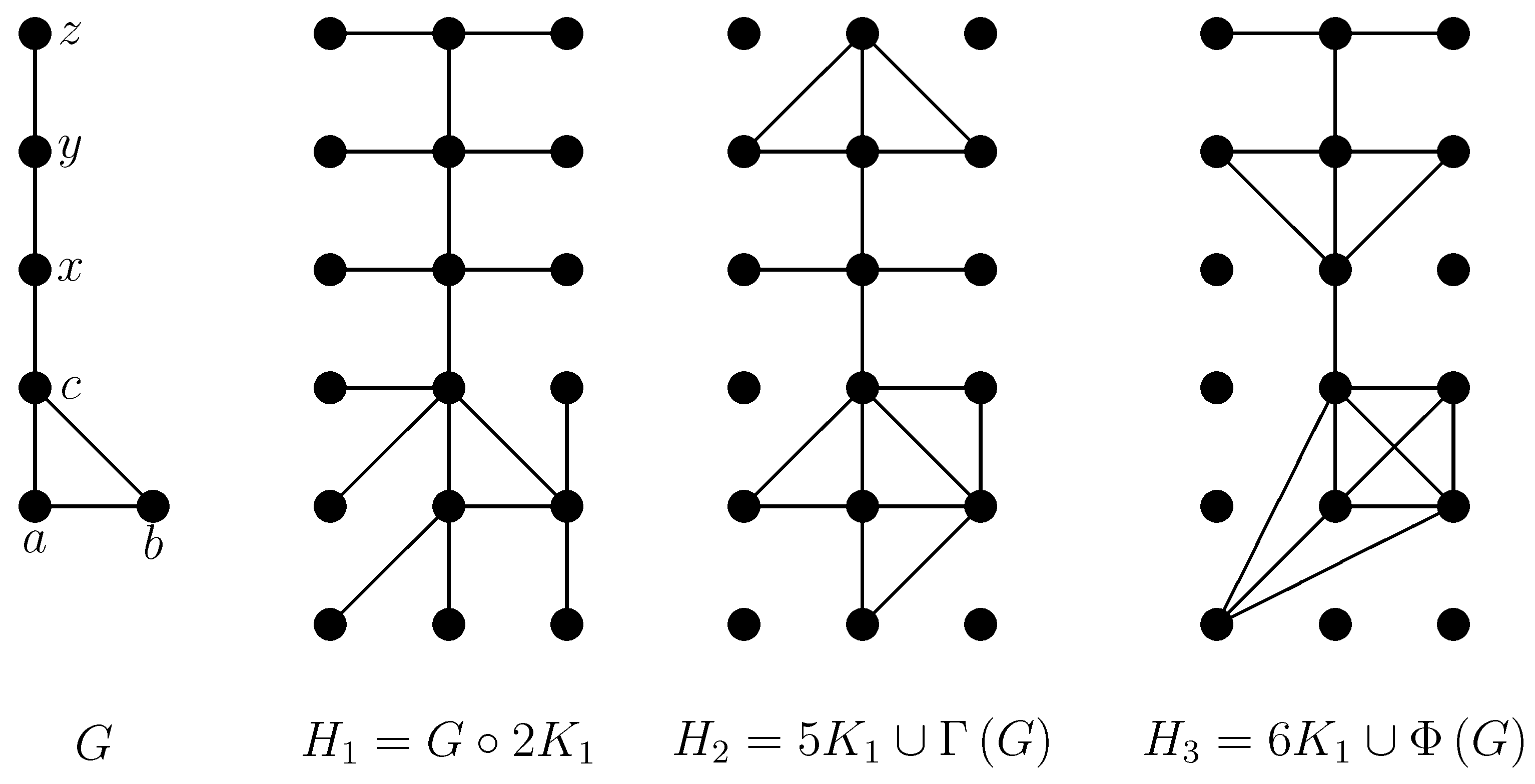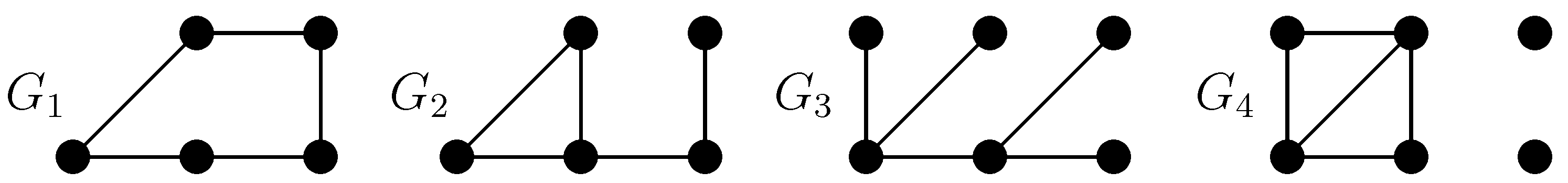1. Introduction
Throughout this paper is a simple (i.e., a finite, undirected, loopless and without multiple edges) graph with vertex set and edge set If , then is the subgraph of G spanned by X. By we mean the subgraph , if . We also denote by the partial subgraph of G obtained by deleting the edges of F, for , and we write shortly , whenever F .
The neighborhood of a vertex is the set and , while ; if there is no ambiguity on G, we write and .
denote, respectively, the complete graph on vertices, the chordless path on vertices, and the chordless cycle on vertices.
The disjoint union of the graphs is the graph having as vertex set the disjoint union of , and as edge set the disjoint union of . In particular, denotes the disjoint union of copies of the graph G.
If
are disjoint graphs,
, then the
Zykov sum of
with respect to
, is the graph
with
as vertex set and
as edge set [
1]. If
and
, we simply write
.
The
corona of the graphs
G and
H with respect to
is the graph
obtained from
G and
copies of
H, such that every vertex belonging to
A is joined to all vertices of a copy of
H [
2]. If
we use
instead of
(see
Figure 1 for an example).
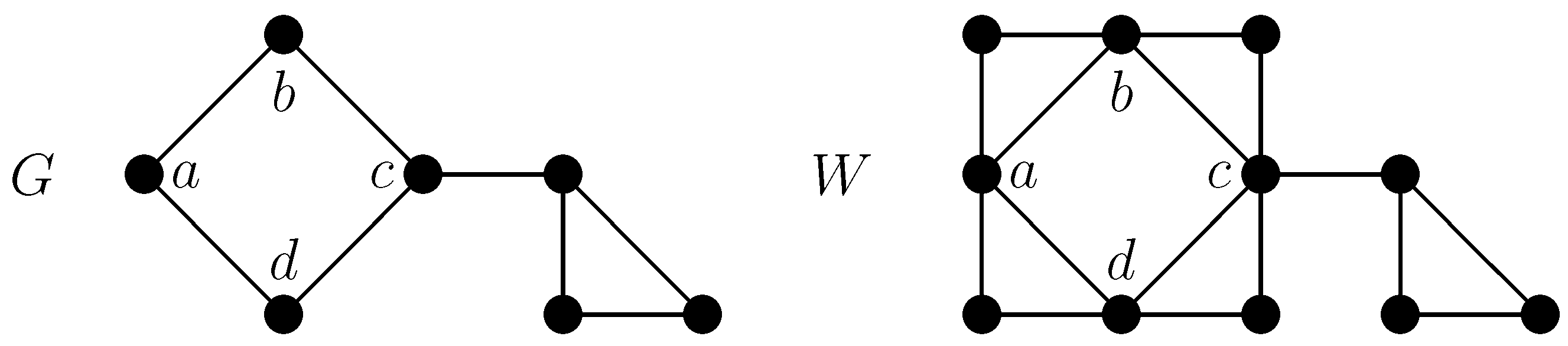
Let
be two graphs and
C be a cycle on
q vertices of
G. By
we mean the graph obtained from
G and
q copies of
H, such that each two consecutive vertices on
C are joined to all vertices of a copy of
H (see
Figure 2 for an example).
An independent (or a stable) set in G is a set of pairwise non-adjacent vertices. By we mean the family of all independent sets of G. An independent set of maximum size will be referred to as a maximum independent set of G, and the independence number of G, denoted by , is the cardinality of a maximum independent set in G.
Let
be the number of independent sets of size
k in a graph
G. The polynomial
is called the
independence polynomial of
G [
3,
4], the
independent set polynomial of
G [
5]. In [
6], the
dependence polynomial of a graph
G is defined as
.
A matching is a set of non-incident edges of a graph G, while is the cardinality of a maximum matching. Let be the number of matchings of size k in G.
The polynomial
is called the
matching polynomial of
G [
7].
The independence polynomial has been defined as a generalization of the matching polynomial, because the matching polynomial of a graph
G and the independence polynomial of its line graph are identical. Recall that given a graph
G, its
line graph is the graph whose vertex set is the edge set of
G, and two vertices are adjacent if they share an end in
G. For instance, the graphs
and
depicted in
Figure 3 satisfy
and, hence,
.
In [
3] a number of general properties of the independence polynomial of a graph are presented. As examples, we mention that:
The following equalities are very useful in calculating of the independence polynomial for various families of graphs.
Theorem 1.1. Let be a graph of order n. Then the following identities are true:
(i)
holds for each [3].(ii)
for every graph H [8]. A finite sequence of real numbers is said to be:
unimodal if there is some , such that ;
log-concave if ;
symmetric (or palindromic) if .
It is known that every log-concave sequence of positive numbers is also unimodal.
A polynomial is called unimodal (log-concave, symmetric) if the sequence of its coefficients is unimodal (log-concave, symmetric, respectively).
For instance, the independence polynomial:
is log-concave;
is unimodal, but it is not log-concave, because ;
is non-unimodal;
is symmetric and log-concave;
is symmetric and non-unimodal.
It is easy to see that if and is symmetric, then it is also log-concave.
For other examples, see [
9,
10,
11,
12,
13,
14]. Alavi
et al. proved that for every permutation
of
there is a graph
G with
such that
[
9].
The following conjecture is still open.
Conjecture 1.2. The independence polynomial of every tree is unimodal [9]. Hence to prove the unimodality of independence polynomials is sometimes a difficult task. Moreover, even if the independence polynomials of all the connected components of a graph
G are unimodal, then
is not for sure unimodal [
15]. The following result shows that symmetry gives a hand to unimodality.
Theorem 1.3. If P and Q are both unimodal and symmetric, then is unimodal and symmetric [16]. A
clique cover of a graph
G is a spanning graph of
G, each connected component of which is a clique. A
cycle cover of a graph
G is a spanning graph of
G, each connected component of which is a vertex, an edge, or a proper cycle. In this paper we give an alternative proof for the fact that the polynomials
,
, and
are symmetric for every clique cover
, and every cycle cover
of a graph
G, where
and
are graphs built by Stevanović’s rules [
17]. Our main finding claims that the polynomial
is divisible both by
and
.
The paper is organized as follows.
Section 2 looks at previous results on symmetric independence polynomials,
Section 3 presents our results connecting symmetric independence polynomials derived by Stevanović’s rules [
17], while
Section 4 is devoted to conclusions, future directions of research, and some open problems.
2. Related Work
The symmetry of the matching polynomial and the characteristic polynomial of a graph were examined in [
18], while for the independence polynomial we quote [
17,
19,
20]. Recall from [
18] that
G is called an
equible graph if
for some graph
H. Both matching polynomials and characteristic polynomials of equible graphs are symmetric [
18]. Nevertheless, there are non-equible graphs whose matching polynomials and characteristic polynomials are symmetric.
It is worth mentioning that one can produce graphs with symmetric independence polynomials in different ways. For instance, the independence polynomial of the disjoint union of two graphs having symmetric independence polynomial is symmetric as well. Another basic graph operation preserving symmetry of the independence polynomial is the Zykov sum of two graphs with the same independence number. We summarize other constructions respecting symmetry of the independence polynomial in what follows.
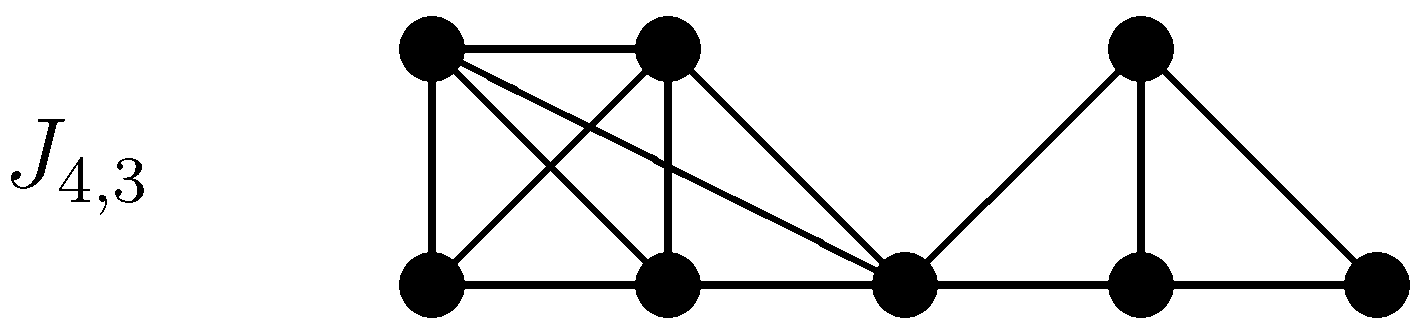
2.1. Gutman’s Construction [21]
For integers
,
, let
be the graph built in the following manner [
21]. Start with three complete graphs
,
and
whose vertex sets are disjoint. Connect the vertex of
with
vertices of
and with
vertices of
(see
Figure 4 as an example).
The graph thus obtained has a unique maximum independent set of size three, and its independence polynomial is equal to
Hence the independence polynomial of
is
which is clearly symmetric and log-concave.
2.2. Bahls and Salazar’s Construction [20]
The -path of length is the graph with and . Such a graph consists of k copies of , each glued to the previous one by identifying certain prescribed subgraphs isomorphic to . Let be an integer. The d-augmented path is defined by introducing new vertices and edges . Let and be a subset of its vertices. Let and define the cone of G on U with vertex v, denoted , where . Given G and U and a graph H, we write instead of .
Theorem 2.1. Let , and be integers, and let be a graph with a distinguished subset of vertices. Suppose that each of the graphs G, , and has a symmetric and unimodal independence polynomial, and . Then the independence polynomial of the graph is symmetric and unimodal [20]. 2.3. Stevanović’s Constructions [17]
Taking into account that and , it follows that if is symmetric, then and , i.e., G has only one maximum independent set, say S, and independent sets, of size , that are not subsets of S.
Theorem 2.2. If there is an independent set S in G such that holds for every independent set , then is symmetric [17]. The following result is a consequence of Theorem 2.2.
Corollary 2.3. (i)
If , and for the unique stability system S of G it is true that for each , then is symmetric [17]; (ii)
If G is a claw-free graph with , then is symmetric. Corollary 2.3 gives three different ways to construct graphs having symmetric independence polynomials [
17].
For an example, see the graphs in
Figure 5:
, while
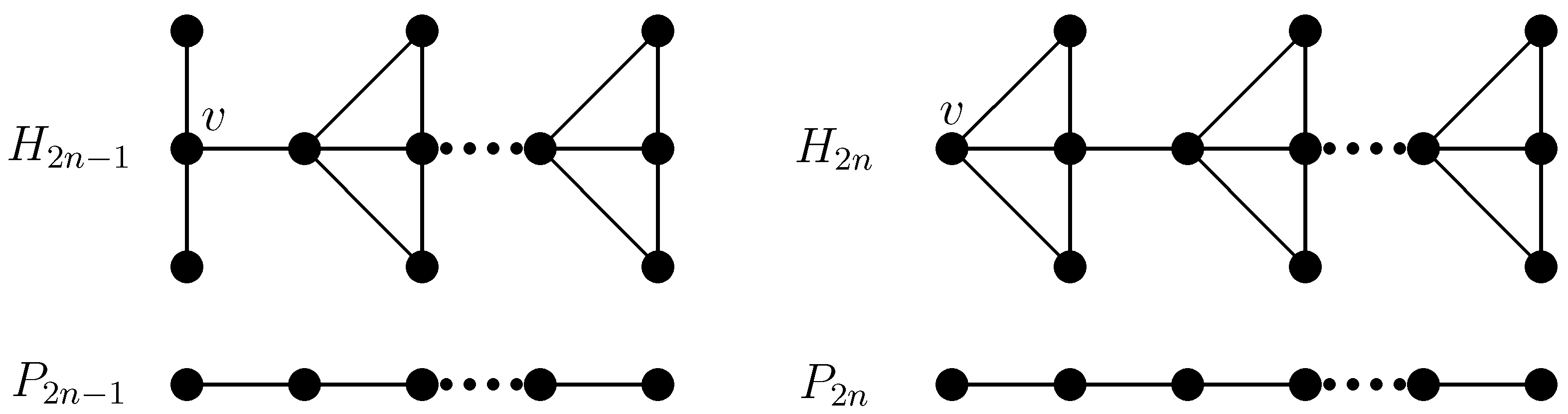
A cycle cover of a graph G is a spanning graph of G, each connected component of which is a vertex (which we call a vertex-cycle), an edge (which we call an edge-cycle), or a proper cycle. Let be a cycle cover of G.
Rule 2. Construct a new graph H from G, denoted by , as follows: if is
(i) a vertex-cycle, say v, then add two vertices and join them to v;
(ii) an edge-cycle, say , then add two vertices and join them to both u and v;
(iii) a proper cycle, with
then add
s vertices, say
and each of them is joined to two consecutive vertices on
C, as follows:
is joined to
, then
is joined to
, further
is joined to
,
etc.
Figure 6 contains an example, namely,
, while
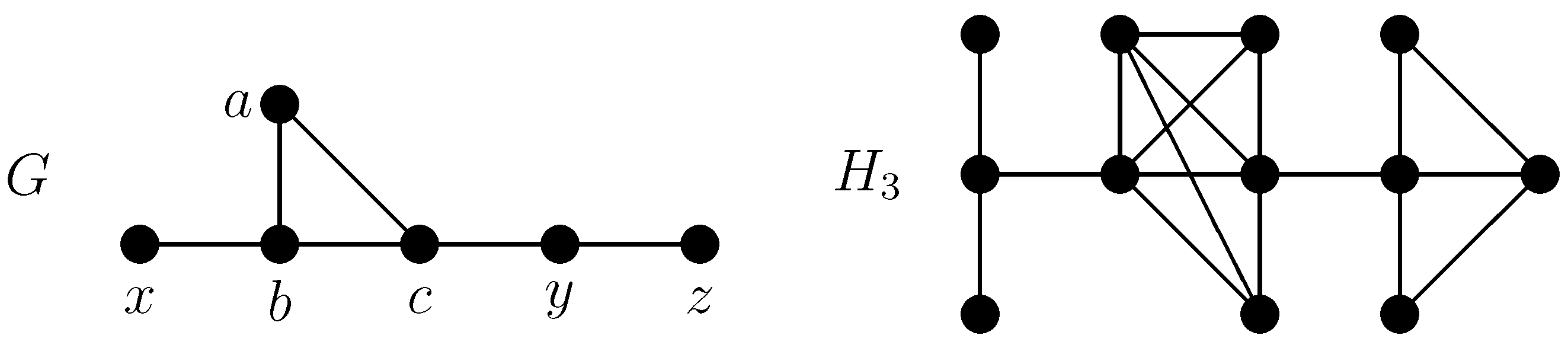
Rule 3. Construct a new graph H from G, denoted by , as follows: for each , add two non-adjacent vertices and join them to all the vertices of Q.
Figure 7 contains an example, namely,
, while
Theorem 2.4. Let H be the graph obtained from a graph G according to one of the Rules 1, 2 or 3. Then H has a symmetric independence polynomial [17]. Let us remark that
and
, where
and
are depicted in
Figure 5,
Figure 6, and
Figure 7, respectively.
2.4. Inequalities and Equalities Following from Theorem 2.4
When inequalities connecting coefficients of the independence polynomial is under consideration, the symmetry mirrors the area, where they are already established. The following results illustrate this idea.
Proposition 2.5. Let be with , and be the coefficients of . Then is symmetric, and [22] Theorem 2.6. Let H be a graph of order , Γ be a cycle cover of H that contains no vertex-cycles, G be obtained by Rule 2, and . Then is symmetric and its coefficients satisfy the subsequent inequalities [22] Let
, be the graphs obtained according to
Rule 3 from
, as one can see in
Figure 8.
Theorem 2.7. If , then [23] (i)
and , satisfies the following recursive relations:(ii) is both symmetric and unimodal.
It was conjectured in [
23] that
is log-concave and has only real roots. This conjecture has been resolved as follows.
Theorem 2.8. (i)
the independence polynomial of is(ii) has only real zeros, and, therefore, it is log-concave and unimodal.
4. Conclusions
In this paper we have given algebraic proofs for the assertions in Theorem 2.4, due to Stevanović [
17]. In addition, we have shown that for every clique cover
, and every cycle cover
of a graph
G, the polynomial
is divisible both by
and
.
For instance, the graphs from
Figure 12 have:
, while
The characterization of graphs whose independence polynomials are symmetric is still an open problem [
17].
Let us mention that there are non-isomorphic graphs with the same independence polynomial, symmetric or not. For instance, the graphs
,
,
,
presented in
Figure 13 are non-isomorphic, while
Recall that a graph having at most two vertices with the same degree is called
antiregular [
25]. It is known that for every positive integer
there is a unique connected antiregular graph of order
n, denoted by
, and a unique non-connected antiregular graph of order
n, namely
[
26]. In [
27] we showed that the independence polynomial of the antiregular graph
is:
Let us mention that
and
, where
denotes the complete bipartite graph on
vertices. Notice that the coefficients of the polynomial
satisfy
for
, while
, i.e.,
is “
almost symmetric”.
Problem 4.1. Characterize graphs whose independence polynomials are almost symmetric.
It is known that the product of a polynomial and its reciprocal is a symmetric polynomial. Consequently, if and are reciprocal polynomials, then the independence polynomial of is symmetric, because .
Problem 4.2. Describe families of graphs whose independence polynomials are reciprocal.