Dynamic Behaviors Analysis of Asymmetric Stochastic Delay Differential Equations with Noise and Application to Weak Signal Detection
Abstract
:1. Introduction
2. Theoretical Analysis
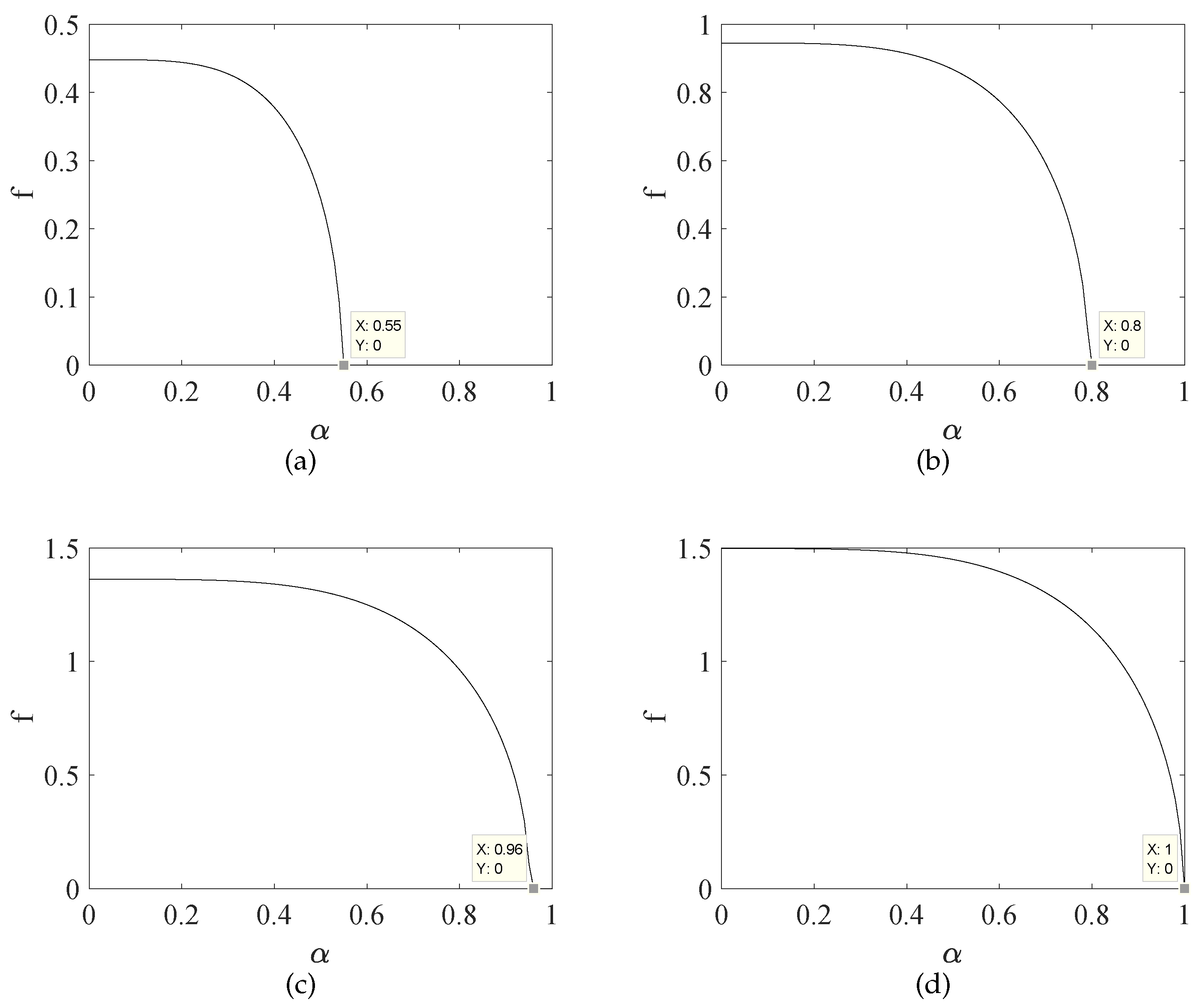
2.1. Stability Analysis
2.2. Stochastic Equation
3. Weak Signal Detection
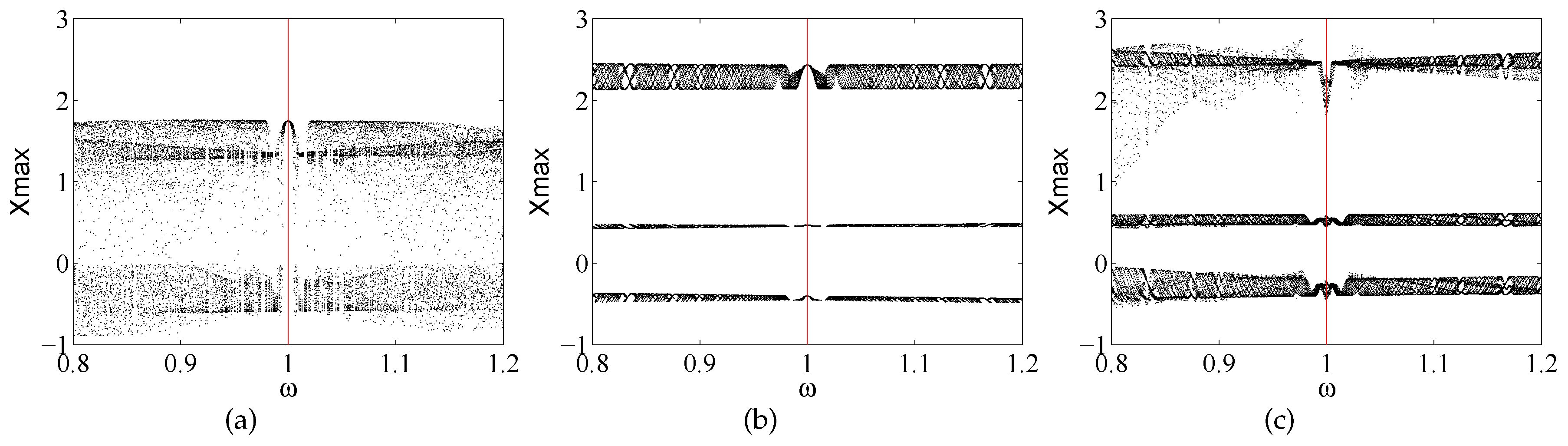
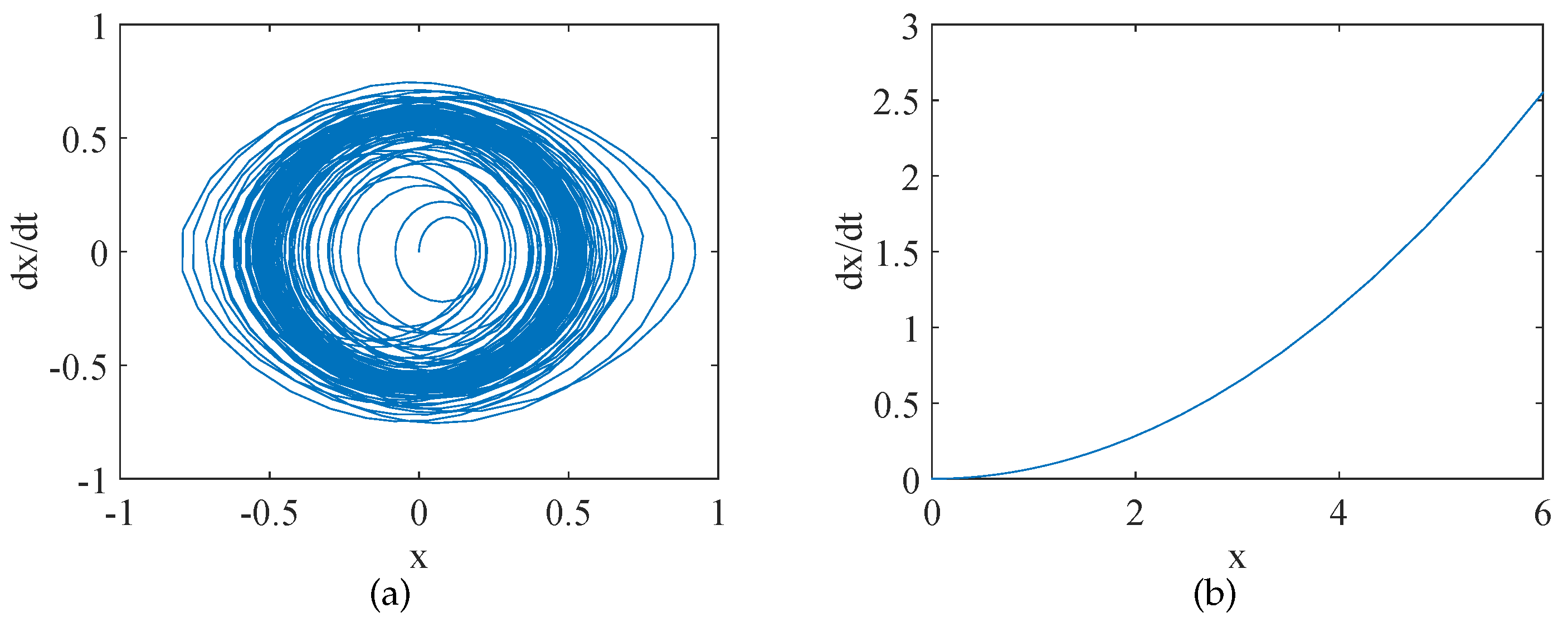
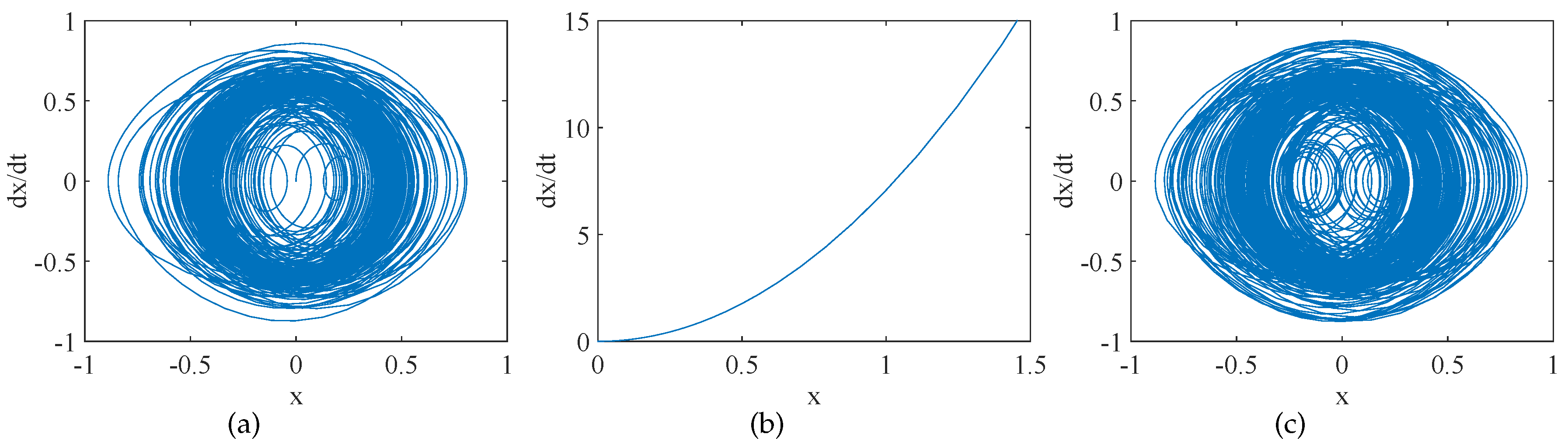
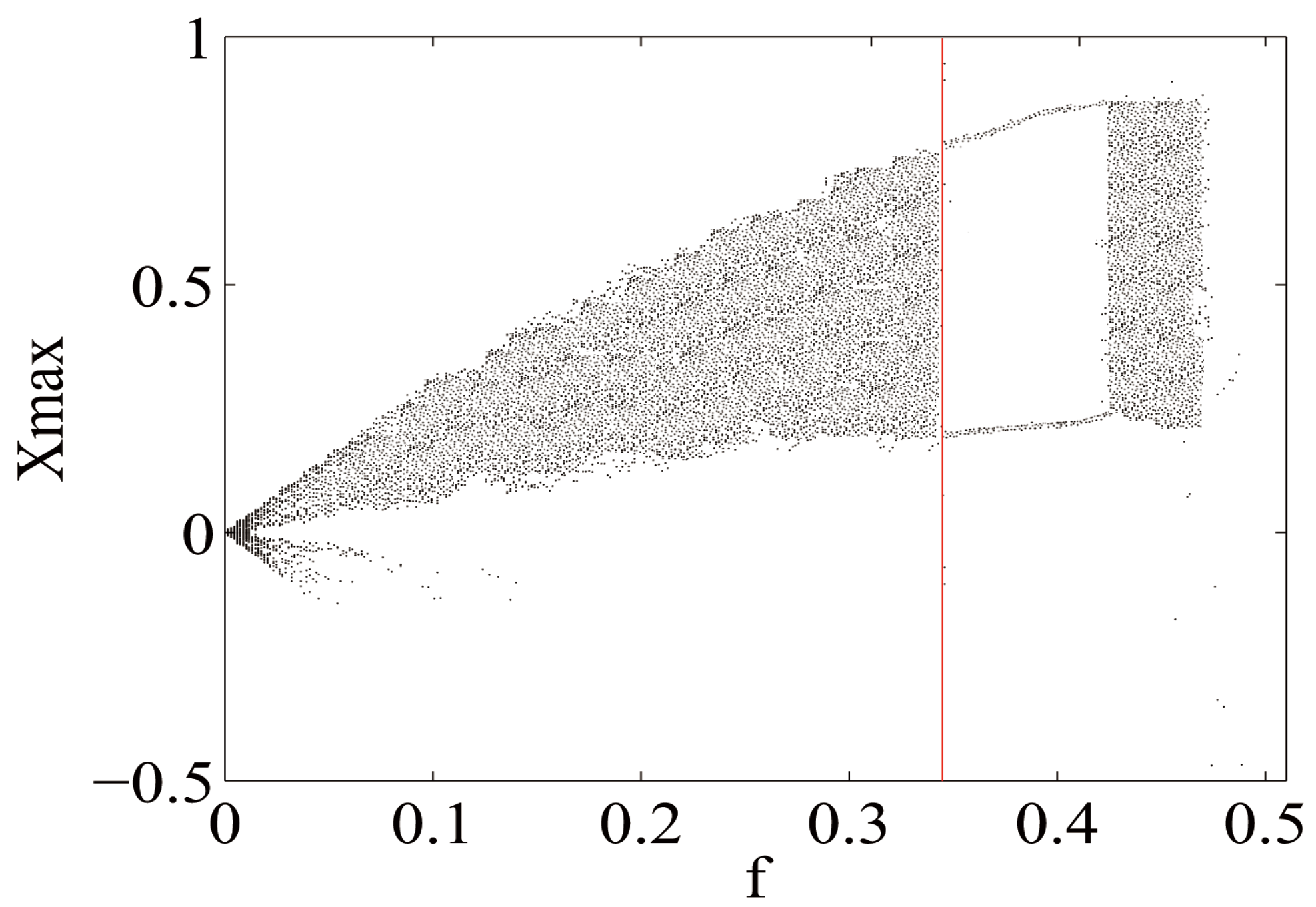
3.1. Chaos in the Asymmetric Stochastic Delay Differential Equation
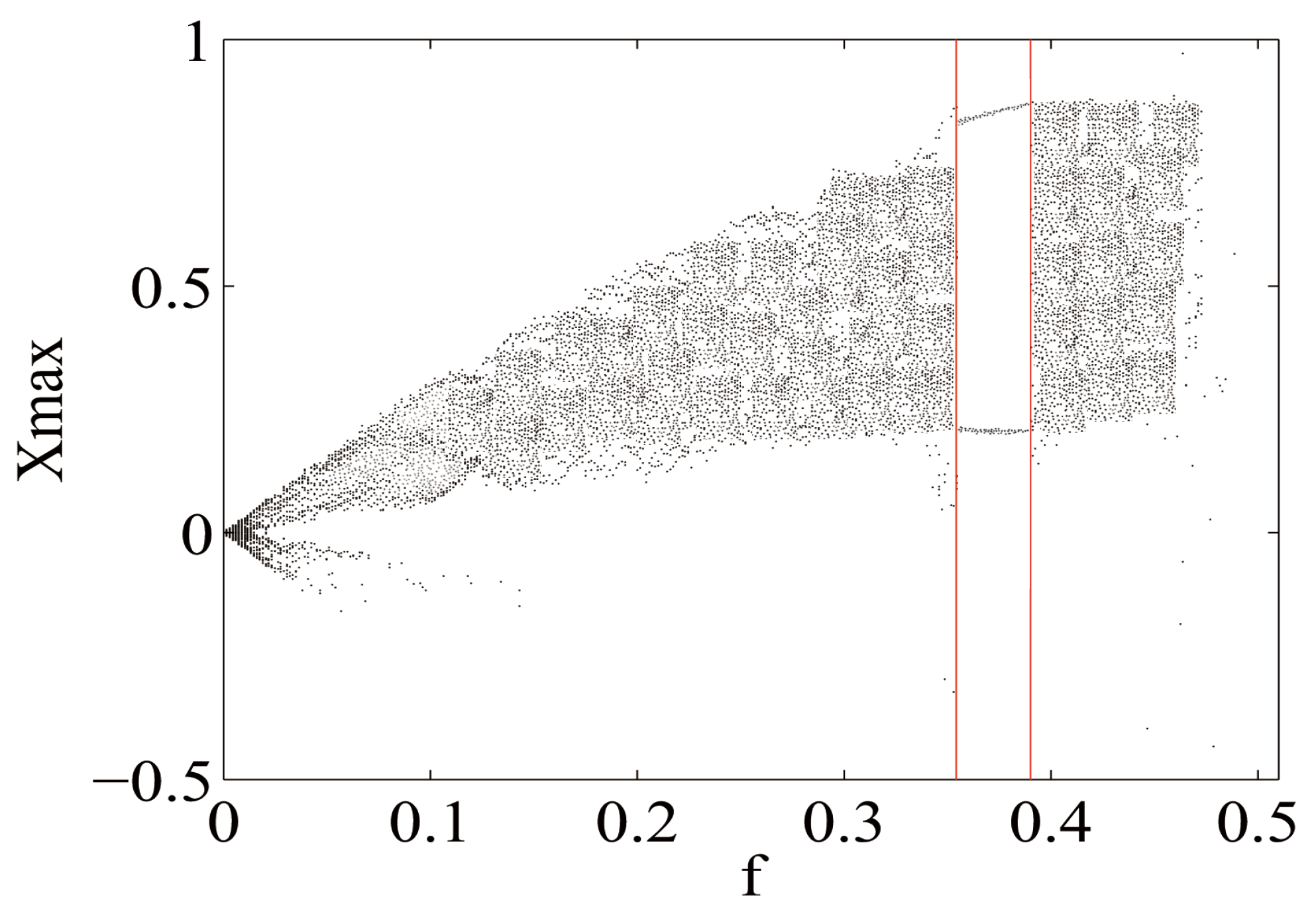
3.2. Time-Delayed Feedback and System Detection Capability
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Martínez-García, M.; Zhang, Y.; Wan, J.; McGinty, J. Visually Interpretable Profile Extraction with an Autoencoder for Health Monitoring of Industrial Systems. In Proceedings of the International Conference on Advanced Robotics and Mechatronics, Toyonaka, Japan, 3–5 July 2019; pp. 649–654. [Google Scholar]
- Zhao, Z.H.; Yang, S.P. Application of van der Pol–Duffing oscillator in weak signal detection. Comput. Electr. Eng. 2015, 41, 1–8. [Google Scholar]
- Zheng, S.Y.; Guo, H.X.; Li, Y.A.; Wang, B.; Zhang, P. A new method for detecting line spectrum of ship-radiated noise using Duffing oscillator. Chin. Sci. Bull. 2007, 52, 1906–1912. [Google Scholar] [CrossRef]
- Shi, H.C.; Li, W.L. Research on Weak Resonance Signal Detection Method Based on Duffing Oscillator. Procedia Comput. Sci. 2017, 107, 460–465. [Google Scholar] [CrossRef]
- Wang, L.Z.; Gao, Y.F. Detection of weak signal in strong noise based on nbs chaos system. Procedia Eng. 2011, 23, 754–759. [Google Scholar] [CrossRef]
- He, B.; Huang, Y.; Wang, D.; Yan, B.; Dong, D. A parameter-adaptive stochastic resonance based on whale optimization algorithm for weak signal detection for rotating machinery. Measurement 2019, 136, 658–667. [Google Scholar] [CrossRef]
- Lu, S.; Zheng, P.; Liu, Y.; Cao, Z.; Yang, H.; Wang, Q. Sound-aided vibration weak signal enhancement for bearing fault detection by using adaptive stochastic resonance. J. Sound Vib. 2019, 449, 18–29. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, S.; Zhang, Q.; Lei, S.; Qiao, X. A weak signal detection method based on adaptive parameter-induced tri-stable stochastic resonance. Chin. J. Phys. 2018, 56, 1187–1198. [Google Scholar] [CrossRef]
- Li, Z.X.; Shi, B.Q. A piecewise nonlinear stochastic resonance method and its application to incipient fault diagnosis of machinery. Chin. J. Phys. 2019, 59, 126–137. [Google Scholar] [CrossRef]
- Wu, X.; Guo, W.; Cai, W.; Shao, X.; Pan, Z. A method based on stochastic resonance for the detection of weak analytical signal. Talanta 2003, 61, 863–869. [Google Scholar] [CrossRef]
- Kosko, B.; Mitaim, S. Stochastic resonance in noisy threshold neurons. Neural Netw. 2003, 16, 755–761. [Google Scholar] [CrossRef]
- Mitaim, S.; Kosko, B. Adaptive stochastic resonance. Proc. IEEE 1998, 86, 2152–2183. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B. The chaotic detection of periodic short-impulse signals under strong noise background. J. Electron. 2002, 19, 431–433. [Google Scholar] [CrossRef]
- Wang, G.; Zheng, W.; He, S. Estimation of amplitude and phase of a weak signal by using the property of sensitive dependence on initial conditions of a nonlinear oscillator. Signal Process. 2002, 82, 103–115. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, D.; Zhang, T. The analysis of stochastic resonance and bearing fault detection based on linear coupled bistable system under lévy noise. Chin. J. Phys. 2018, 56, 2718–2730. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, G.; Tian, R. Periodic Solution of a Non-Smooth Double Pendulum with Unilateral Rigid Constrain. Symmetry 2019, 11, 886. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, R.; Xu, C.; Huang, R.; Hao, X. Stability analysis of integrated power system with pulse load. Int. J. Electr. Power Energy Syst. 2020, 115, 105462. [Google Scholar] [CrossRef]
- Schwaller, B.; Ensminger, D.; Dresp-Langley, B.; Ragot, J. State estimation for a class of nonlinear systems. Int. J. Appl. Math. Comput. Sci. 2013, 23, 383–394. [Google Scholar] [CrossRef]
- Wang, Q. Bifurcation analysis in a predator–prey model for the effect of delay in prey. Int. J. Biomath. 2016, 9, 1650061. [Google Scholar] [CrossRef]
- Liu, M.Z.; Wang, Q. Numerical Hopf bifurcation of linear multistep methods for a class of delay differential equations. Appl. Math. Comput. 2009, 208, 462–474. [Google Scholar] [CrossRef]
- Wang, Q.; Li, D.; Liu, M.Z. Numerical Hopf bifurcation of Runge–Kutta methods for a class of delay differential equations. Chaos Solitons Fractals 2009, 42, 3087–3099. [Google Scholar] [CrossRef]
- Martínez-García, M.; Zhang, Y.; Gordon, T. Memory Pattern Identification for Feedback Tracking Control in Human–Machine Systems. Hum. Factors 2019. [Google Scholar] [CrossRef] [PubMed]
- Grigoriu, M. Control of time delay linear systems with Gaussian white noise. Probabilistic Eng. Mech. 1997, 12, 89–96. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A. Time delay induced effects on control of linear systems under random excitation. Probabilistic Eng. Mech. 2001, 16, 43–51. [Google Scholar] [CrossRef]
- Guo, Q.; Sun, Z.K.; Xu, W. Bifurcations in a fractional birhythmic biological system with time delay. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 318–328. [Google Scholar] [CrossRef]
- Lepine, F.; Vinals, J. Pitchfork and Hopf bifurcation threshold in stochastic equations with delayed feedback. arXiv 2008, arXiv:0810.4348. [Google Scholar]
- Fofana, M.S. Asymptotic stability of a stochastic delay equation. Probabilistic Eng. Mech. 2002, 17, 385–392. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Cai, G.Q. Introduction to Stochastic Dynamics; Science Press: Beijing, China, 2017; p. 72. [Google Scholar]
- Martinez-Garcia, M.; Zhang, Y.; Gordon, T. Modeling lane keeping by a hybrid open-closed-loop pulse control scheme. IEEE Trans. Ind. Inform. 2016, 12, 2256–2265. [Google Scholar] [CrossRef]
- Wang, S.; Wang, F.; Wang, S.; Li, G. Detection of multi-frequency weak signals with adaptive stochastic resonance system. Chin. J. Phys. 2018, 56, 994–1000. [Google Scholar] [CrossRef]
- Guo, W.; Zhou, Z.; Chen, C.; Li, X. Multi-frequency weak signal detection based on multi-segment cascaded stochastic resonance for rolling bearings. Microelectron. Reliab. 2017, 75, 239–252. [Google Scholar] [CrossRef]
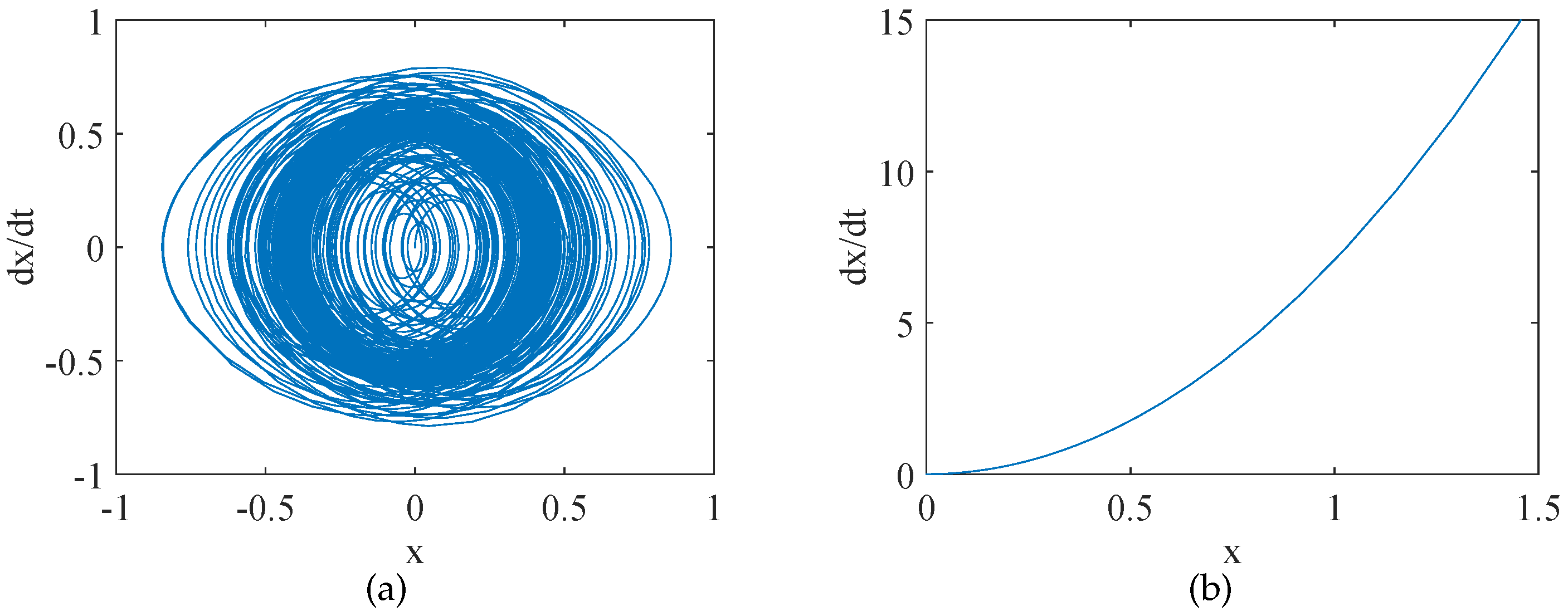
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zhang, X.; Yang, Y. Dynamic Behaviors Analysis of Asymmetric Stochastic Delay Differential Equations with Noise and Application to Weak Signal Detection. Symmetry 2019, 11, 1428. https://doi.org/10.3390/sym11111428
Wang Q, Zhang X, Yang Y. Dynamic Behaviors Analysis of Asymmetric Stochastic Delay Differential Equations with Noise and Application to Weak Signal Detection. Symmetry. 2019; 11(11):1428. https://doi.org/10.3390/sym11111428
Chicago/Turabian StyleWang, Qiubao, Xing Zhang, and Yuejuan Yang. 2019. "Dynamic Behaviors Analysis of Asymmetric Stochastic Delay Differential Equations with Noise and Application to Weak Signal Detection" Symmetry 11, no. 11: 1428. https://doi.org/10.3390/sym11111428



