1. Introductory Remarks and Example
Impact loads applied to physical systems are often modeled with Dirac’s generalized functions (distributions) by ignoring the short-term load profiles and using their integral effects instead. However, the presence of distributions in a differential equation of motion requires the entire equation to be considered within the theory of distributions that leads to theoretical complications especially in nonlinear cases [
1,
2]. In the present work, we illustrate non-smooth temporal substitutions incorporating the pulse effects into a periodic time folding argument. Substituting such an argument into the differential equation of motion generates singularities of derivatives that can be effectively used to balance the loading Dirac’s delta impulses or discontinuities from the differential equations. In this introductory section, we outline necessary analytical manipulations based on general time symmetries of periodic processes regardless their temporal mode shapes. Namely, any periodic process admits time shifts with reflections. Such properties can be easily incorporated into the corresponding differential equations at the preliminary stage of study by means of the following standard pair of non-smooth periodic functions
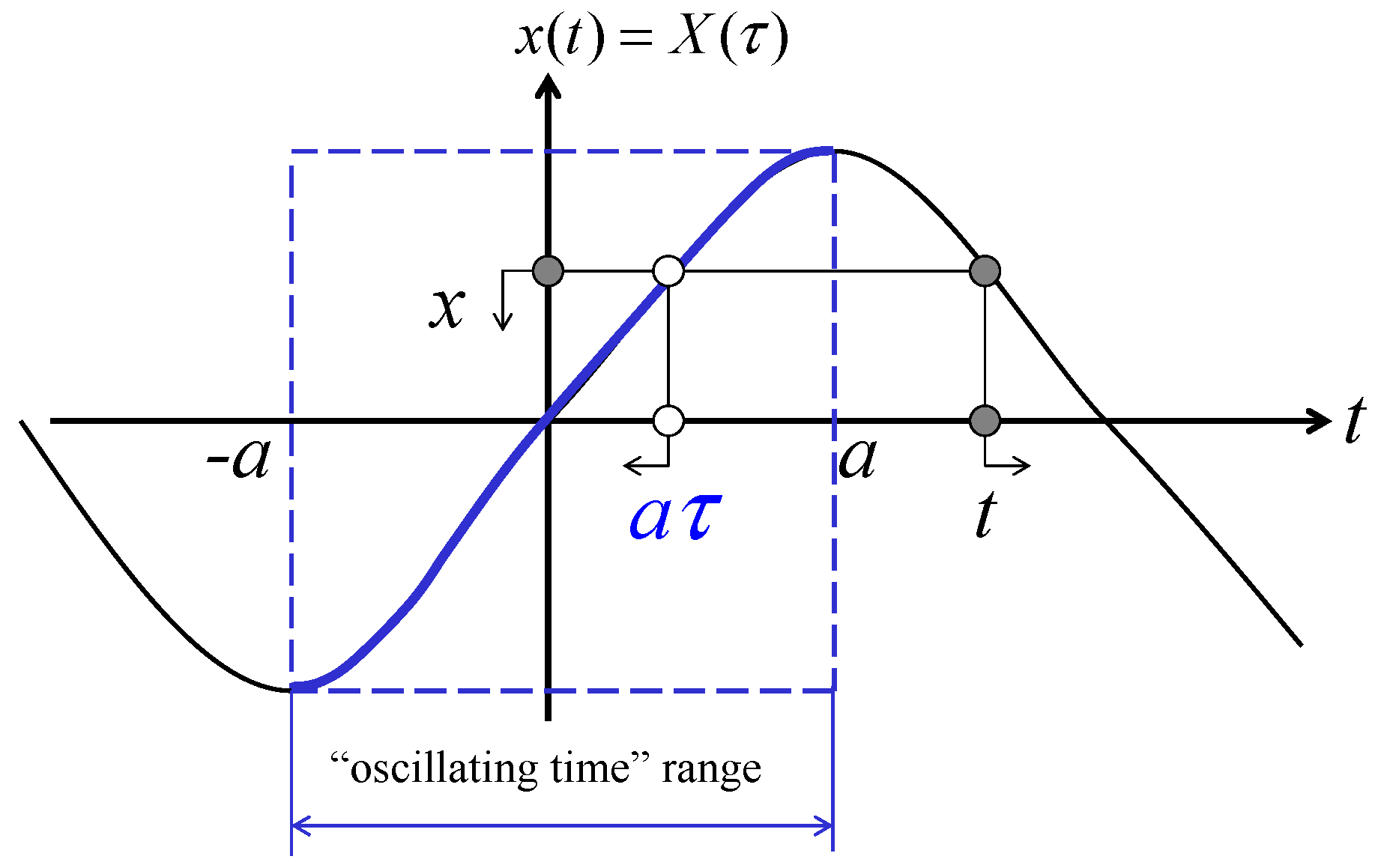
As follows from the graphical illustration in
Figure 1, the couple of functions
and
can be interpreted as a coordinate and velocity of a small particle oscillating between two perfectly stiff barriers without energy loss.
Note that the derivative
remains undefined at discontinuity points
. Also, since
is a rectangular cosine-wave with step-wise discontinuities, its first
generalized derivative is given by the periodic sequence of Dirac’s
- functions as
Distribution (2) associates with the impulsive force applied from the barriers to the particle whenever the particle strikes the barriers. In addition, the following differential and algebraic properties hold
Although functions (1) are quite specific, they create a general basis for considering a broader class of oscillating processes. This is based on the statement that any periodic process
of the period
admits representation in the form of ‘hyperbolic number’ [
3,
4]
where
,
, and
Here, the terms
and
depict the sin- and cos-type symmetries, and can be viewed as “real” and “imaginary” parts of the hyperbolic number due to the relationship
(3). Note that the term ‘hyperbolic number’ represents one of the multiple versions typically applied to the abstract algebraic combination [
5],
(
). In our case, the
unipotent is represented by the periodic step-wise discontinuous function
describing the velocity of impact oscillator. Identity (4) can be easily proved by substituting (5) in (4) and considering the result on one period
; see
Appendix A. The following example reveals temporal symmetries of the both components in (4)
In particular, if a periodic function
is even with respect to the quarter of period
, then
and identity (4) has only the “real component”
. The corresponding geometrical interpretation is shown in
Figure 2.
Let us outline some algebraic and differential properties of representation (4).
Therefore, due to condition (8), derivative (7) still preserves the structure of hyperbolic number. If then the procedure (7)–(8) can be reiterated n times by sequentially imposing boundary conditions on the functions , and their derivatives at .
Further, we use the identity (4) as a representation for solutions of differential equations by considering
and
as a couple of new unknown functions of the temporal argument
. In order to illustrate the corresponding manipulations, let us consider the equation
where the input function is periodic step-wise discontinuous rectangle cosine of the period
T = 4. Let us seek continuous periodic solutions of Equation (9) of the same period in the form of representation (4). Setting
, substituting (4) in (9), and taking into account condition (8) gives
It is seen that the left-hand side of Equation (10) is an element of ‘hyperbolic algebra’. Setting its both components separately to zero and including conditions (8) gives the autonomous boundary value problem with no discontinuities, which can be treated in a classical way,
Namely, eliminating
from the second equation gives the second-order linear differential equation
with the general solution
. Then satisfying the boundary conditions, determining
, and substituting both
and
in (4) gives periodic solution of Equation (9) in the final form
Although Equation (9) is linear and can be solved by other means, such as Laplace transforms, Fourier expansions, or matching different solutions between the impulses at pulse times, solution (12) has the closed form and represents an element of the hyperbolic algebra. These properties can essentially facilitate further algebraic, differential, and integral manipulations whenever such types of solutions serve as a basis of different asymptotic procedures [
4].
2. Nonlinear Oscillators under Periodic Impulses
Now let us consider an oscillator with a general form of the restoring force characteristic under the periodic impulsive excitation
where the upper dot indicates time derivative, the impulses are assumed to be two-directional, and the restoring force function,
, to be continuous with respect to all the arguments.
We seek a steady state continuous periodic solution of Equation (13) in the form of representation (4). Assuming that condition (8) holds and taking first derivative of (4) gives
Then, substituting (4) and (14) in (13) and using the algebraic rules, as outlined in the previous section, one obtains
Equation (15) gives two differential equations for the components
and
with the boundary condition for
. Then the resulting boundary value problem takes the form
Equations (17) do not include any singularities but appear to be coupled. However, under certain symmetry conditions, the number of equations can be reduced by one. For instance, one can consider the boundary value problem only for
provided that
as
. The latter condition always holds, for instance in the conservative case, when the restoring force characteristic depends only upon the coordinate,
, and thus (17) is reduced to
Let us assume now that the restoring force characteristic has the form
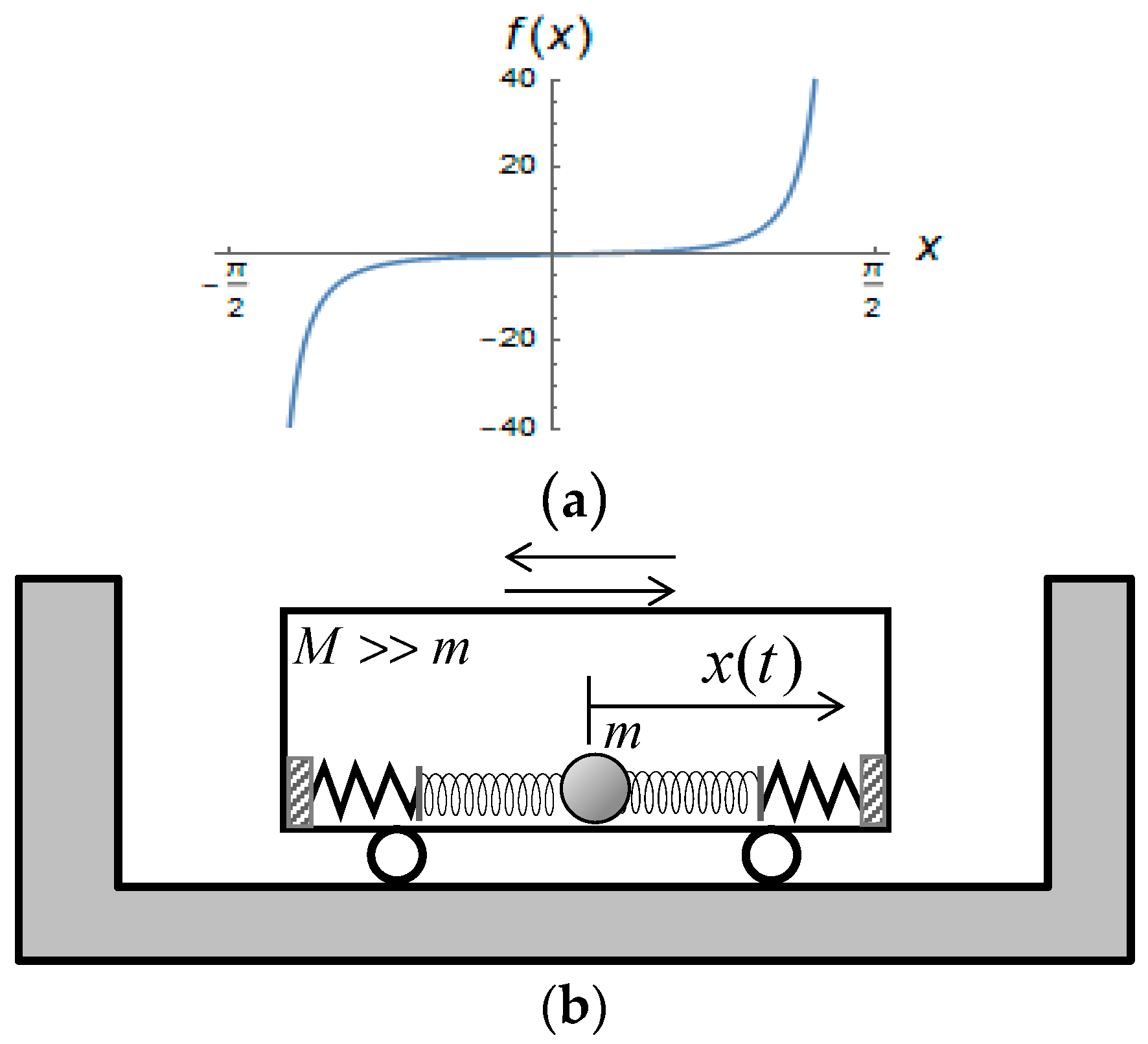
Figure 3a shows dependence (20) whereas
Figure 3b gives its possible physical interpretation, where the effect of combined springs and amplitude limiters is approximated with the smooth function (20) within the interval
. The reason for using function (20) as a fit is that the free conservative oscillator
is known to have the exact analytical solution in terms of elementary functions [
6,
7]
. Note that, despite of the formal similarity of this function with the triangle wave
(1), transition to the non-smooth limit
is impossible due to the singularity caused by the term
. Typically, the presence of external loads invalidates solutions obtained for the corresponding free oscillators. However, in the present case of the impulsive load, the form of solution obviously holds in between any two consecutive pulses. From the physical standpoint, the impulsive load can practically occur in the situation illustrated by
Figure 3b. The moving platform periodically strikes the perfectly stiff walls creating the impulsive inertia load on the oscillator inside the moving noninertial frame. A one parameter family of solutions can be represented as
where
is an arbitrary constant, which is sufficient for satisfying both equations in (19) due to the oddness of solution (21),
.
As follows from expression (21), and as . Therefore can be viewed as a parameter characterizing the amplitude of and thus restricted to be positive.
Substituting (21) in (19) and conducting analytical manipulations with trigonometric functions gives four sets of solutions for the quarter of period. Such solutions can be combined as
and
where
is the period of response, and
.
Note that solution (21) represents a one parameter set of particular solutions imposing the initial conditions on the original variables as
and
. In (22) and (23), such type of the initial conditions associates with even
, whereas the odd numbers
reveal another subset of the periodic solutions with the negative initial velocities. Both of the subsets are covered by the following modification of (21)
It can be shown that solutions (22) and (23) exist in the interval
Figure 4 illustrates the sequence of branches of solutions (22) and (23) at different numbers
under the fixed parameter of the strength of pulses,
. The diagram reveals such combinations of the period and amplitude at which the oscillator has a periodic response with the loading period,
. The upper and lower branches of each loop correspond to positive and negative signs in expression (22), respectively. In particular, relationship (23) corresponds to the number
and has only the upper branch. For the selected value of
, the minimal amplitude is
, corresponding to the left boundary of the amplitude-period loops in
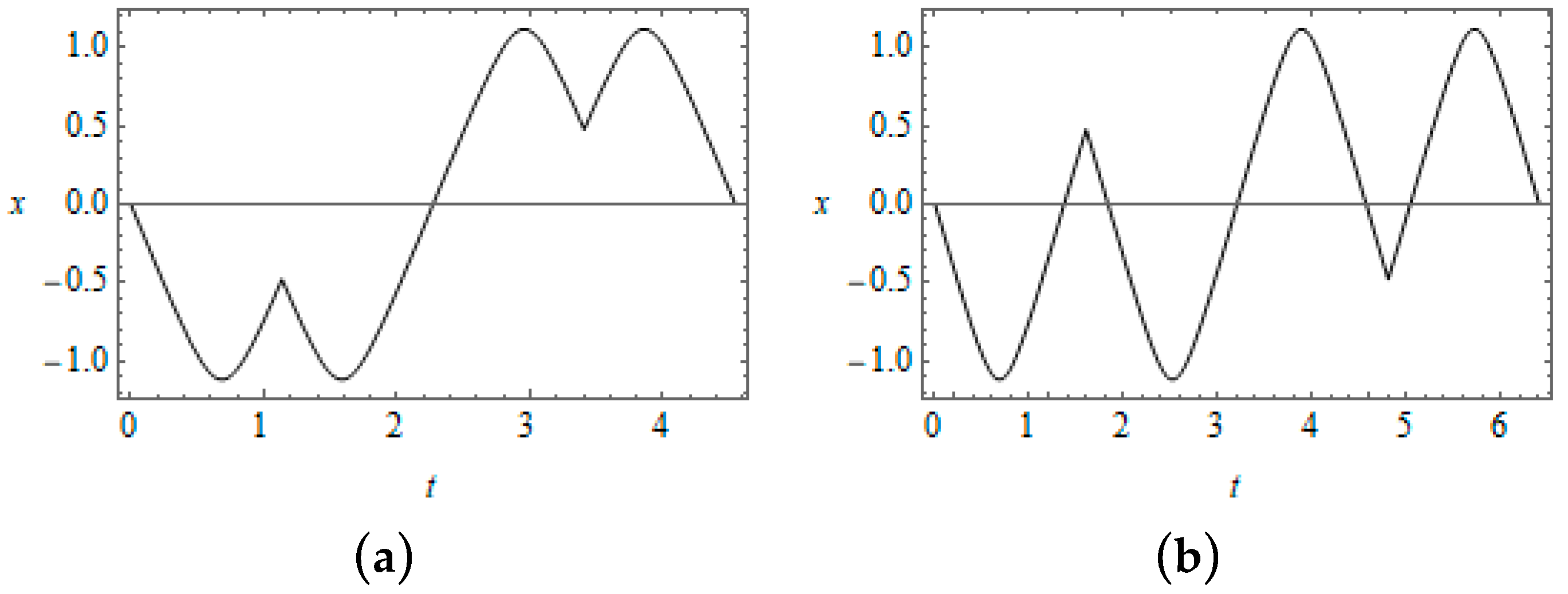
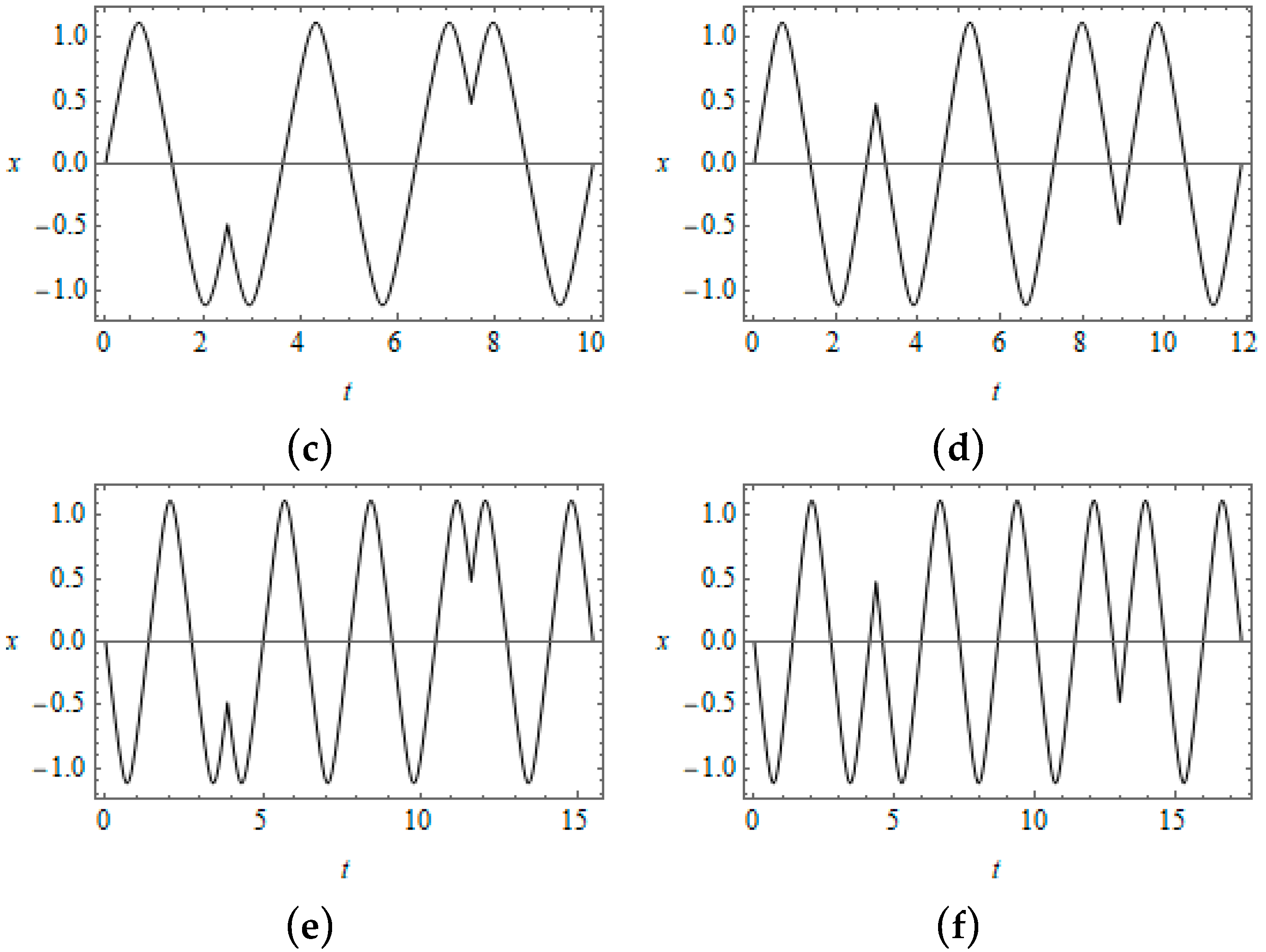
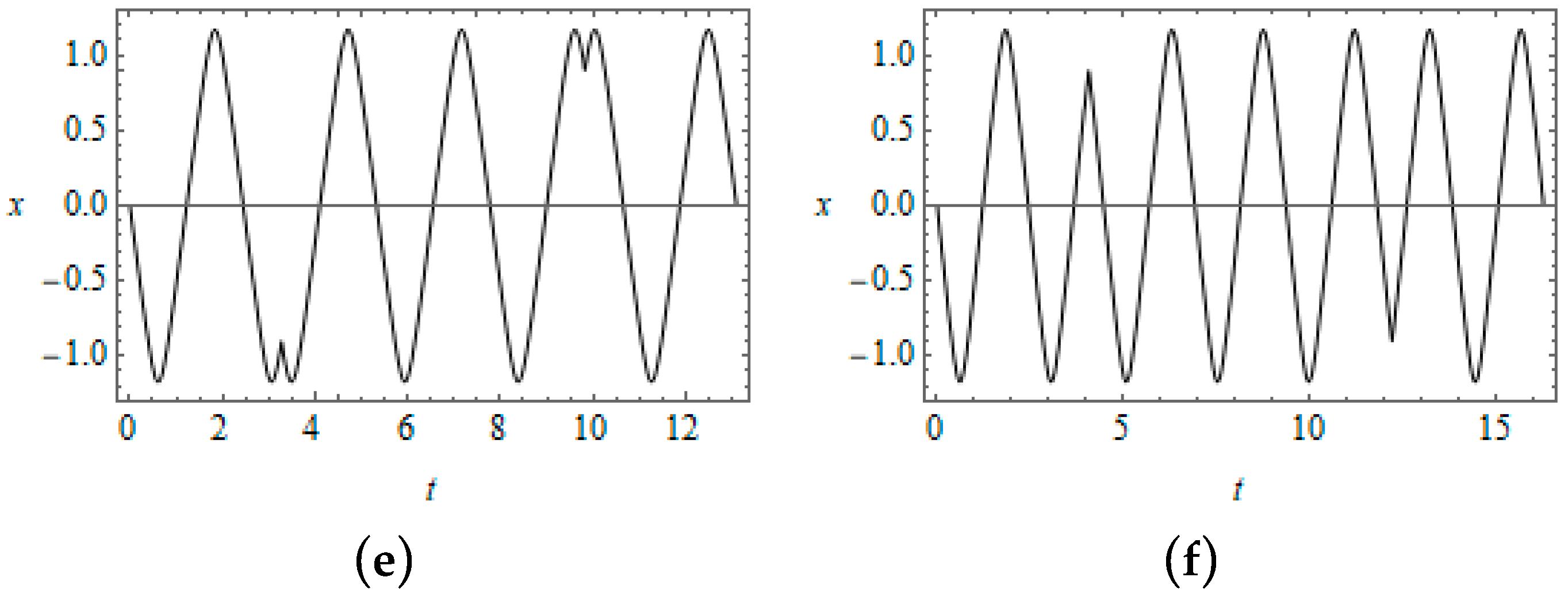
Figure 4. A slight shift to the right from this boundary leads to bifurcations of solutions as seen from the time histories in
Figure 5. The series of graphs illustrates only the first three couples of new solutions from the infinite set of solutions. Further evolution of the temporal shapes due to the amplitude increase is shown in
Figure 6. One can observe quite a significant difference in both periods and temporal shapes of vibrations comparing the left and right fragments of
Figure 6. This is explained by the high sensitivity of solutions near the left boundary with respect to the amplitude variation as follows from
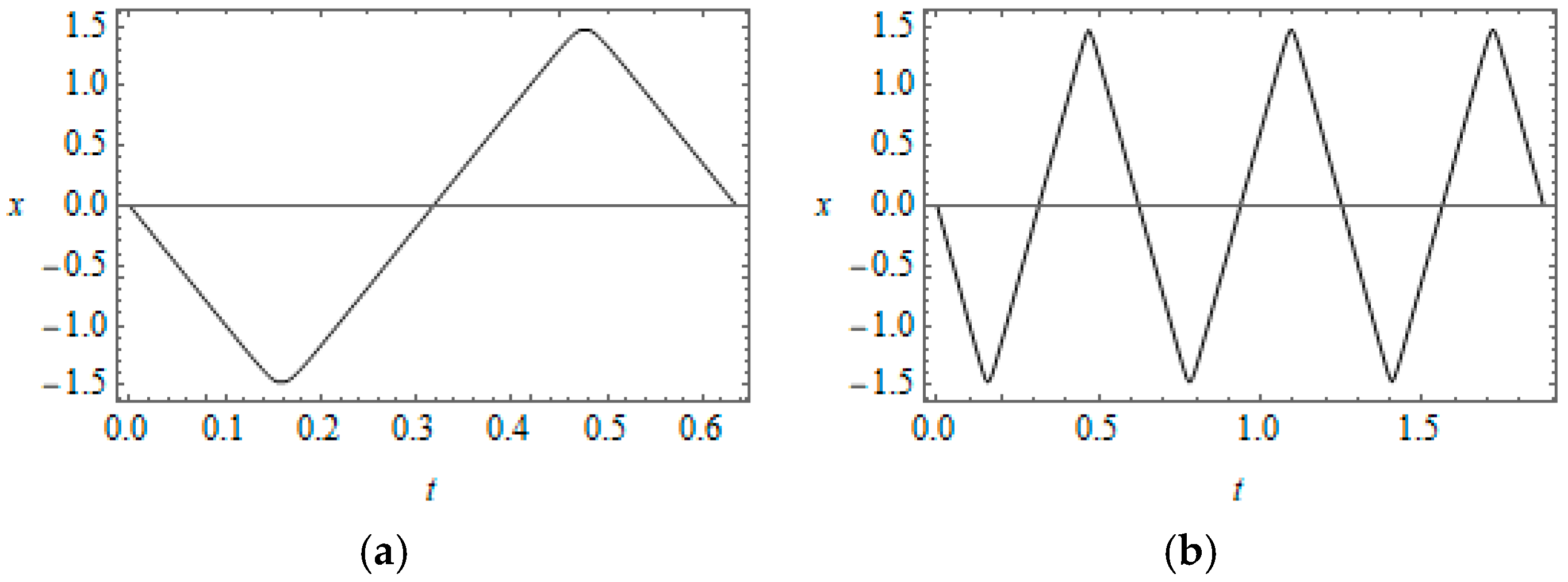
Figure 4. Finally, when the amplitude becomes close to its maximum
, the restoring force of the oscillator itself generates quite strong pulses compared to the external loading as seen from the temporal mode shapes in
Figure 7. As a result, the effect of external pulses is effectively vanishing. The oscillator’ response can be viewed rather as a free vibration whose amplitude and period are dictated by the loading period.
Analyzing the link between
Figure 4 and
Figure 5 shows that solutions corresponding to different loops of the period-amplitude dependence differ by the number of half cycles between any two consecutive pulses applied to the oscillator. These graphs were reproduced by solving the original equation numerically with the
Mathematica® NDSolve package using the
WhenEvent option for conditioning the velocity steps
when passing the impulses under the initial conditions imposed by solution (24); see
Appendix B for the code.
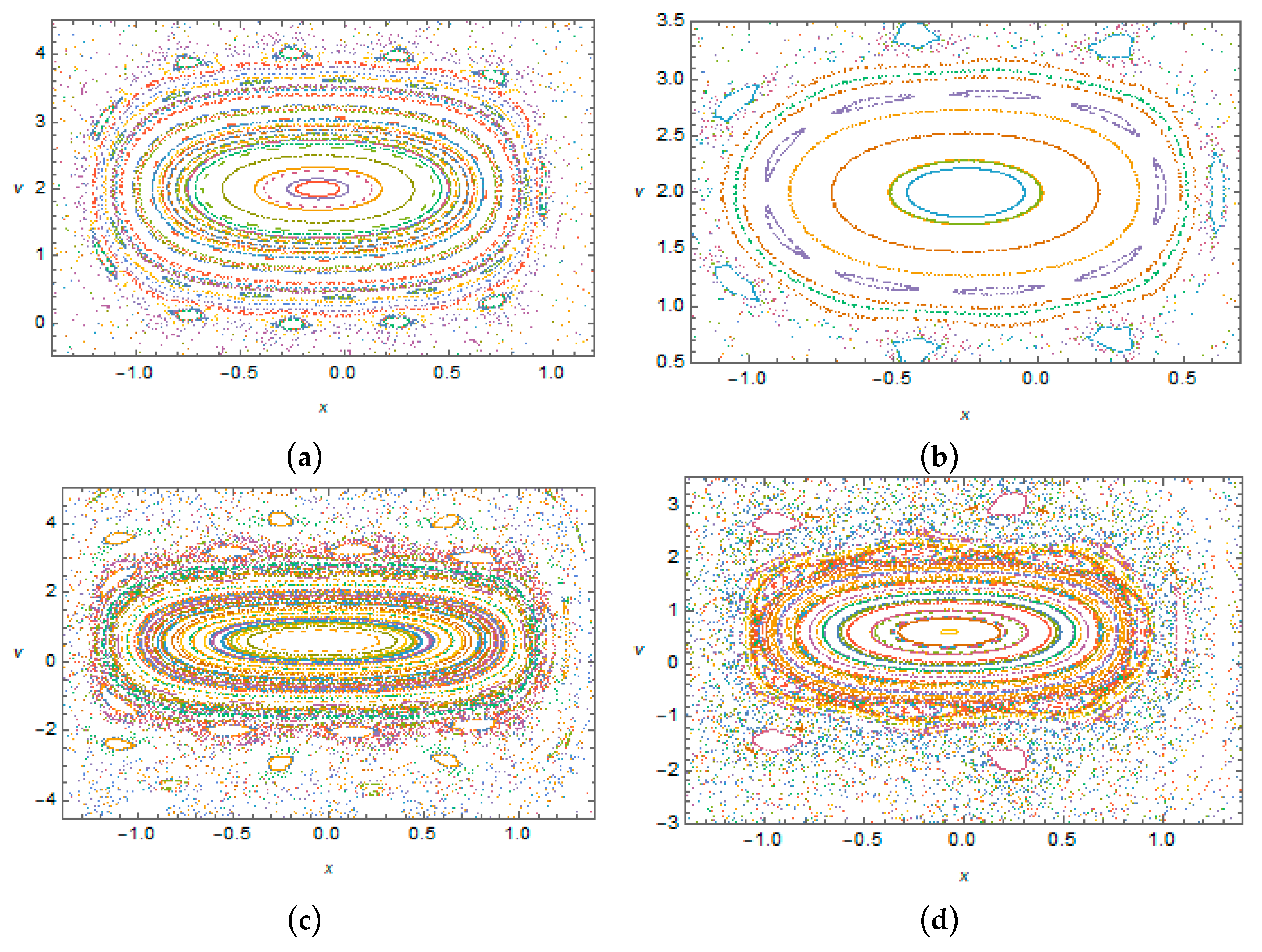
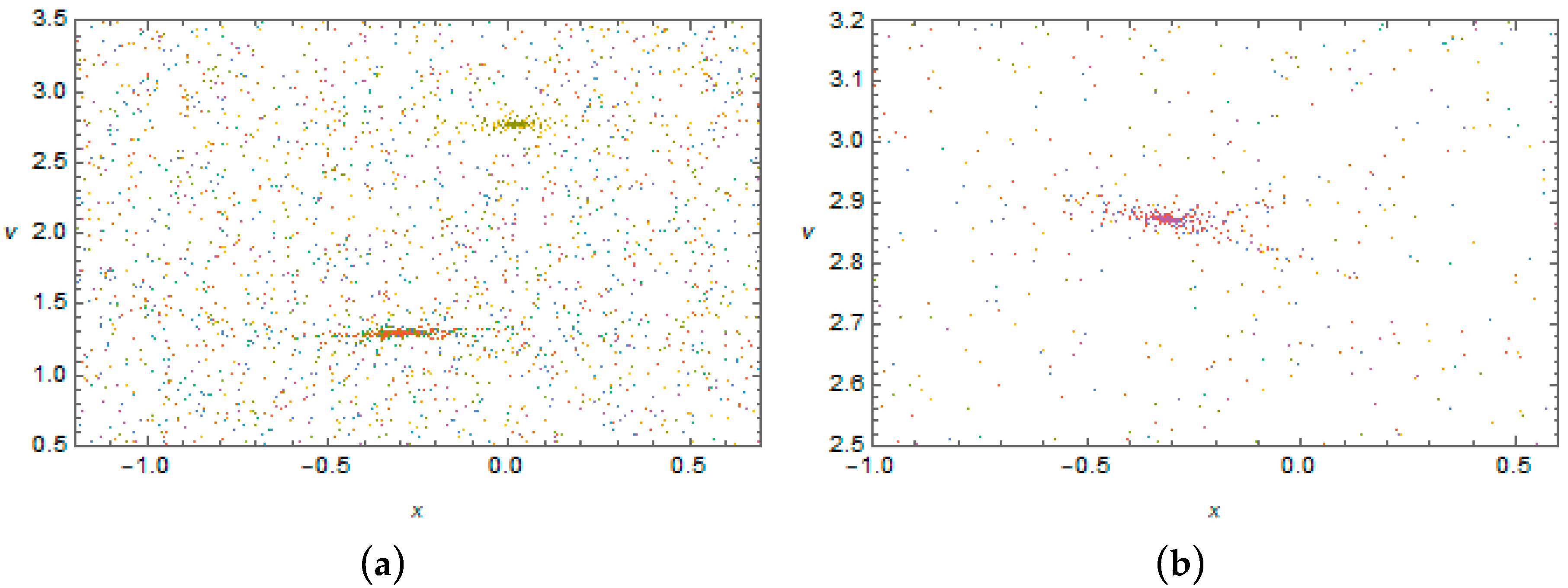
Note that, away from the curves of
Figure 4, the response may appear to be quite complicated. This is confirmed by the Poincaré sections in
Figure 8 and
Figure 9 below. In particular,
Figure 8 shows the Poincaré sections obtained for the case of short loading periods under a set of randomly chosen initial conditions. Then
Figure 8a–d represents a weakly damped case, in which the energy inflow is sufficient for keeping the oscillator amplitudes large enough for a “resonance” interaction between the oscillator and the impulsive load. With the increase of dissipation, the initial energies of the oscillator dissipate leading to the decrease of its own frequencies. As a result, the high frequency impulsive loading becomes effectively quasi dynamic as reflected by the drastic change in Poincaré sections; see
Figure 8e,f.
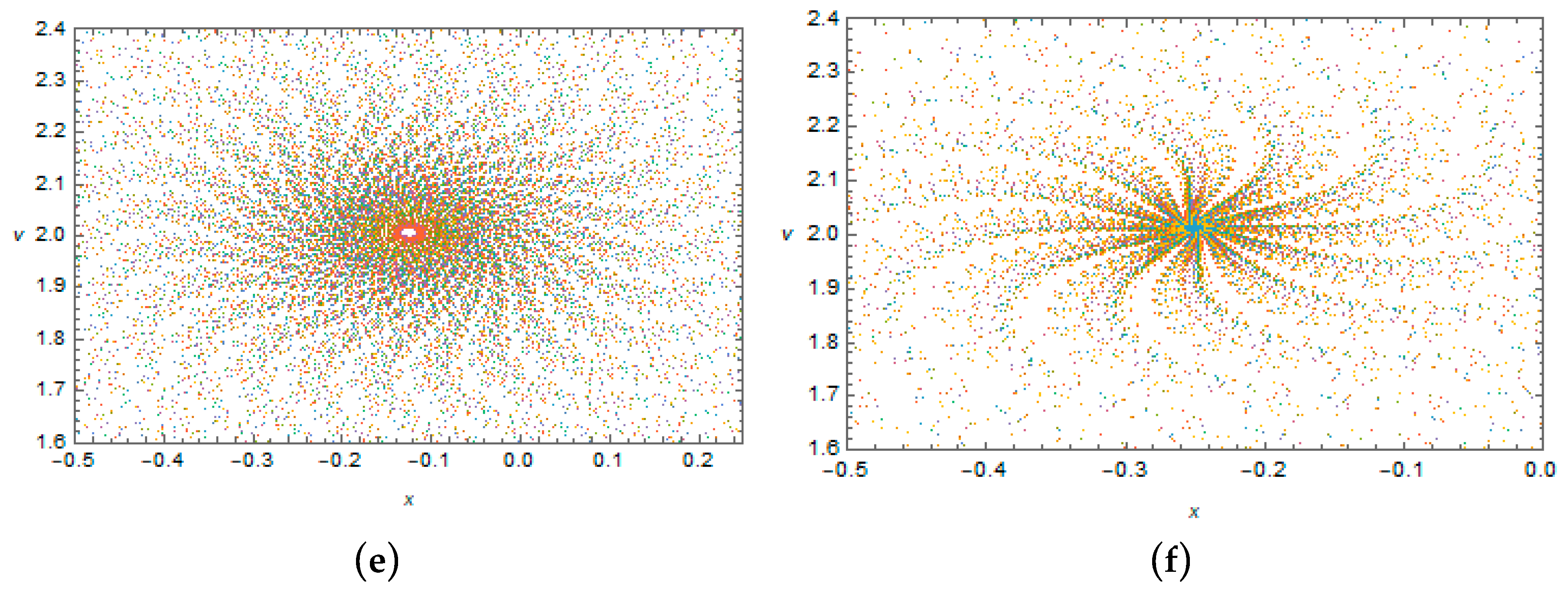
Finally,
Figure 9 illustrates the case of a long-period impulsive loading under a relatively large damping, compared to the cases of
Figure 8a–d. The difference between this case and the case represented by
Figure 8e,f is that the distance between pulses is now long enough compared to the period of linearized oscillator whose period is the longest possible. As a result, the quasi dynamic branching in the Poincaré maps disappears.