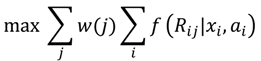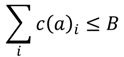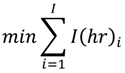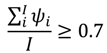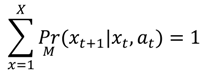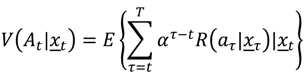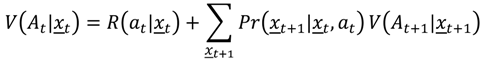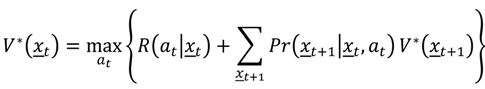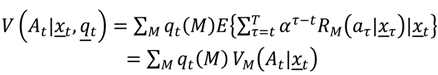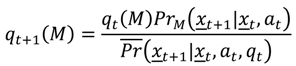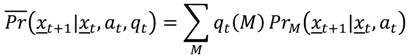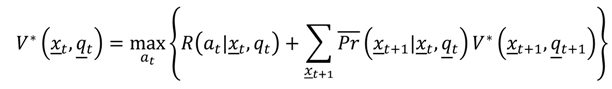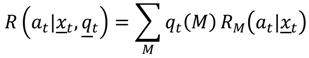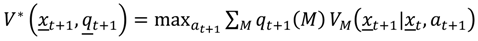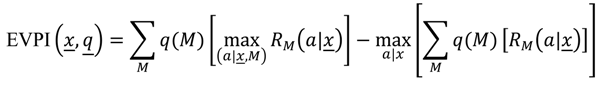1. Introduction
Land cover modeling is becoming increasingly important for informing natural resource management [
1,
2]. In the rare cases in which system responses to environmental change and management actions are precisely known, land cover maps and models are used to make state-dependent decisions. In the more common case in which system responses are not well known, science is used to reduce this uncertainty (learn) and enable better decisions. A common approach is for scientists either to develop land cover maps corresponding to snapshots in time or to actually develop models of land cover dynamics in a manner that permits projection of future land cover patterns. In either case, scientists conduct these studies that have potential to inform land management and then provide these results and findings to decision makers, who choose whether and how to use the information. This two-step process is inefficient, at best, providing little opportunity for real interaction between scientists and decision makers and frequently leading to the dissatisfaction of both groups. Decision makers often complain of scientific results that, although somewhat relevant, do not fill the critical information needs of the decision process. Scientists frequently complain that decision makers do not pay adequate attention to the scientific information that they provide. Adaptive resource management (ARM) [
3,
4] provides an alternative approach to management that better integrates science into the decision-making process [
5]. Adaptive management was developed as an approach to making recurrent decisions that are characterized by potentially resolvable uncertainty. Adaptive management essentially embeds science within a broader management process, providing an opportunity to learn about system responses to management actions and a clear path to use what is learned to make better decisions. Hypotheses are compared and tested under ARM, but the hypotheses are precisely those most relevant to management, and test results are directly used in subsequent decisions.
We believe that there are many cases where the science of land cover modeling is not integrated as well as it could be with decision processes, leading to reduced utility of the science. For example, it is common to observe mismatches between the focal scales of science and decisions. Another common limitation of science utility is the focus of scientists on static depictions of land cover (e.g., maps), whereas the needs of decision makers are frequently on dynamics and predictions (e.g., transition probabilities). In addition, even when scientists do focus on change, it is not on the specific kind of change most relevant to land managers; those changes associated with specific management actions.
We have been involved with one ARM project in which land cover modeling plays an important role, but believe that there are many more opportunities for the integration of land cover modeling and ARM. Virtually all land management programs that take actions to modify habitat and land cover require model-based projections of land cover changes expected to accompany such actions [
6]. Even for management actions that are not directed at modifying habitat, land cover dynamics are frequently relevant to system responses to management and, hence, to management programs [
7]. This relevance is especially true as rapid global change associated with increasing human populations, climate change,
etc., results in substantial alterations in land cover patterns and dynamics. For these reasons, we expect land cover modeling to become increasingly important for ARM programs directed at a variety of different conservation problems.
The current program in which land cover modeling supports ARM is based on managing habitat to assist in the recovery of the Florida scrub-jay (FSJ),
Aphelocoma coerulescens, an endangered bird that resides in scrub ecosystems adapted to frequent fire, but that has been subjected to substantial habitat loss, fragmentation and degradation. In our approach, land cover is characterized by discrete successional stages that represent habitat quality, as defined on a geographic scale (10 ha), representing average territory size and, therefore, relevant to FSJ recruitment and survival (
Table 1, [
8,
9,
10]).
Table 1.
Habitat states used to quantify landscape units as potential territories (10 ha) of Florida scrub-jays (FSJs) directly related to long-term demographic performance (yearling production rates; breeder mortality rates) and fire history successional patterns (adapted from [
8,
9,
10]). Populations are expected to increase in landscapes dominated by source territories (positive demographic performance) or to decrease in landscapes dominated by sink territories (negative demographic performance). We also include predictions about the fuels hazards associated with these states.
Table 1.
Habitat states used to quantify landscape units as potential territories (10 ha) of Florida scrub-jays (FSJs) directly related to long-term demographic performance (yearling production rates; breeder mortality rates) and fire history successional patterns (adapted from [8,9,10]). Populations are expected to increase in landscapes dominated by source territories (positive demographic performance) or to decrease in landscapes dominated by sink territories (negative demographic performance). We also include predictions about the fuels hazards associated with these states.
| State | Characteristics | Demographic Performance | Fuels Hazard |
|---|
| Short | Oak < 1.2 m-tall and recent fires (<4 years ago) that completely burned territories | −0.32 | Low |
| Open-medium | Medium-height (1.2–1.7 m) oak > 0.4 ha, often as a mosaic amongst short, but not tall, scrub (>1.7 m) > 0.4 ha; many open sandy areas | 0.49 | Low |
| Closed-medium | Medium-height (1.2–1.7 m) oak > 0.4 ha, often as a mosaic amongst short scrub, but no openings or tall scrub (>1.7 m) > 0.4 ha, | 0.15 | Moderate |
| Tall mix | Mosaic of short or medium scrub amongst tall scrub > 0.4 ha | −0.24 | High |
| Tall | All scrub > 1.7 m-tall and unburned > 20 years | −0.31 | High |
The highest quality habitat (open-medium) for FSJ is a transitional state, and therefore, recovering the species requires imposing a disturbance regime using prescribed fires, which are necessary, because habitat fragmentation restricts the spread of natural fires across landscapes, and society generally requires that wildfires be suppressed [
10,
11]. Because optimal habitat conditions for FSJ are generally those needed by other scrub-adapted species, the species is considered a management indicator species [
12].
There is a need to balance species conservation and fuel management to protect human interests on many continents [
13,
14,
15,
16,
17]. Funding for conducting prescribed fires is often specified for fuel management and not necessarily for species habitat management; administrators from agencies often measure the performance of prescribed fire programs using the acreage burned each year, which provides little information on scrub habitat quality trajectories, because fire intensity and outcomes are heterogeneous [
10]. Our studies have shown that an emphasis on fuel management will not achieve species conservation goals on many conservation lands [
9,
18]. Wildland fire managers and ecologists agree that prescribed fires can be beneficial, and we believe that differences in management approaches are reconcilable, but require stakeholders to acknowledge multiple values and agree: (1) on the legitimacy of objectives arising from these values; (2) on how to measure whether management is attaining those objectives; and (3) on how decisions should be made.
There is a large number of studies associated with fuel management that focus on risk assessment and associated uncertainties in decision-making [
19,
20,
21]. Our approach differs from these other, two-step efforts in that we explicitly integrate management objectives, available actions, predictive modeling and learning in a transparent way to develop conditionally optimal decisions. Our objectives here are to describe a scientific management approach that can be used to integrate both fuels and habitat management, specific to the Florida scrub system. We provide examples of approaches to perform this integration of science and management, because we believe that such approaches are broadly applicable to other fire risk and endangered species applications worldwide. Land cover modeling and land cover monitoring, endeavors that are sometimes viewed as stand-alone activities, are given important and explicit roles in this integrated process.
2. Management of Florida Scrub: Fuel Management vs. Ecological Benefit
Land cover studies have shown that Florida ecosystems have been severely degraded by a reduction in fire frequency due to wildfire suppression and because human landscape features (cities, highways,
etc.) minimize the spread of natural lightning fires across landscapes [
11,
22,
23]. This degradation has resulted in catastrophic impacts to biological diversity; fire managers and ecologists agree that introducing fire back into the system is a priority [
24,
25]. Prescribed fires differ from wildfires, because of their size, spatial pattern, season and differences in weather when these events occur [
26]. One reason that prescribed fires often have limited ecological benefit is that fire managers often burn out the flammable parts of a landscape so that patches are less likely to reignite or produce smoke and other hazards. The success of prescribed fire programs is often measured as the annual burn acreage rather than by remaining fuel levels or the ecological value of the fires. Extensive fires that produce a large proportion of the short vegetation state within FSJ territories (
Table 1) result in poor FSJ fitness, and repeated extensive fires can result in catastrophic population declines [
8]. Scrub management guidelines, focused on biological diversity, specify mosaic fires that produce mostly open-medium territories [
12].
The second reason prescribed fires alone have limited success is that tall scrub often does not burn during prescribed fires without mechanical cutting, an expensive management option [
27]. Although tall scrub does not ignite easily, it represents a hazard once it ignites. Because scrub regrowth is often a function of underground biomass, many ecologists have observed that tall scrub recovers much faster than scrub that has been subjected to frequent fires [
9]. Fire managers usually rely on a return interval to determine when a managed area needs to burn, which differs from the typical ARM approach, which recommends using current values of time-specific state variables (e.g., habitat states from
Table 1) to determine the optimal management action [
18].
Many ecologists agree that burning more frequently might hasten returning degraded scrub to a more desired ecological state [
10], but this would require significant management effort and willingness to value mosaic fires for ecological benefit. Fire managers recognize that mosaic fires are difficult to achieve and observe that burning early in the vegetation recovery cycle often achieves less reduction in fuels than waiting until fuels become mature and more continuous. Although mosaic fires may increase the risk of flare-ups and smoke, burning early might reduce the threat of wild fires between prescribed fires. Many fire managers hold the view that the habitat states used to describe FSJ habitat are largely reflective of fuel loads and continuities, although this topic represents an area needing more research.
Landscapes dominated by short and open-medium territories have relatively low fuel and high fuel discontinuities, whereas landscapes dominated by a closed-medium and tall mix have hazardous fuel loading and possibly high fuel continuities. Burning earlier requires fire managers to recognize that actions to further ecological objectives may also be of value to fuel management, e.g., fires that only burn small areas create open sandy areas interspersed with oak scrub, which promote both valuable ecological objectives and may minimize the risk of more extensive wildfires in the future [
10,
28]. We argue that the objectives and measurement of the efficacy of scrub and fuel management should be based on ecological benefits and the risk of fuels present on landscapes, rather than the total acreage burned. Because fire risks to humans are often highly context-specific, fuels are generally used as surrogates for risk measures, and we chose to focus our efforts here on habitat and fuel hazards.
Decision makers, to a large extent, are biologists and fire bosses associated with conservation areas, but decisions and funding are greatly influenced by administrators, often far away, where the focus is on hazardous fuel reduction. Our experience has generally been with the local decision makers and stakeholders interested in biodiversity management. The local decision makers are generally instructed to use adaptive management, and they have largely requested that we focus our efforts on advancing the best approach to manage for FSJ, recognizing that many factors influence decisions and that some of these factors are too idiosyncratic to easily be supported by ARM. Advancing ARM does not require that managers implement all recommended decisions, but we recommend that managers record the actions implemented at each decision point and that the system response be monitored to enable us to confront model predictions with observations.
Adaptive resource management was developed for management in the face of uncertainty [
3]. In particular, managers frequently face “structural uncertainty;”
i.e., different hypotheses and corresponding models about how potential management actions translate into system responses. As an example that builds on the above discussion of scrub management, we identify two competing models that differ in their views of the efficacy of implementing different kinds of prescribed fire. The key source of uncertainty is whether it is possible to implement different types of fires to have different effects on habitat or whether different fire types are likely to result in similar habitat responses. In particular, we define two kinds of fires, “fuel reduction fires”, which correspond to most historic prescribed fires (status quo) and “habitat fires” that attempt to produce mosaic fires, as recommended and described above. We describe two competing models, where the first model predicts that the two types of prescribed fires can be implemented successfully to produce different consequences (probabilistically), while the second model predicts that the consequences of these two types of prescribed fires cannot be differentiated (
i.e., that it is not really possible to implement habitat fires; thus both kinds of fires produce the same system responses). In our example, we rely on estimates already made for fuel reduction fires [
9,
18] and estimates solicited from managers and biologists that can be updated by monitoring.
The objectives differ between the two competing fire management treatments and are reflected in the probabilities in
Box 1. Conceptually, the main difference is that in fuel reduction prescriptions, fuels are ignited with little focus on habitat state, while habitat fires specifically target habitat states. For a habitat fire, scrub that passed through the open-medium state is burned and returned to short or, preferably, open-medium. This achieves two objectives; first, it keeps the habitat rotating into open-medium, while, secondly, it minimizes the need to mechanically treat tall scrub. The differing objectives of these two types of prescribed fire are reflected in differences in their associated transition matrices. For example, the habitat fire matrix shows increased probabilities of tall-mix and tall scrub being returned to an earlier successional state relative to the fuel reduction fire matrix. Under the habitat fire, there is an increased probability (relative to the fuel reduction fire) of open-medium staying open-medium, as tall fuels are strategically removed. The basic rationale underlying the proposed habitat fires is to provide a sequence of decisions that can maximize the time territories spend in the open-medium state and minimize time spent in tall mix and tall states, returning territories to open-medium or short, rejuvenating the cycle when necessary.
Box 1. An example of competing models that represent structural uncertainty. The habitat states of potential territories, Sh (short), Om (open-medium), Cm (closed-medium), Tm (Tall mix) and Ta (tall), are described in
Table 1.
Hypothesis/Model 1:
This hypothesis assumes that the transition probabilities (the probability that a patch in one habitat state at time t is in a specific habitat state at time t + 1, given that a particular fire type was implemented between times t and t + 1) for “fuel reduction” and “habitat” fires are different. We assume the “fuel reduction fire” matrix is similar to previously measured prescribed fire transition probabilities. Using expert opinion, we predicted transition probabilities for a “habitat fire” matrix, where ignition techniques target small, mosaic fires in parts of management units dominated by short, open-medium and closed medium potential territories and hotter and more extensive fires in areas with tall-mix and tall territories.
| Fuel Reduction Fire Matrix | Habitat Fire Matrix |
|---|
| Sht | Omt | Cmt | Tmt | Tat | | Sht | Omt | Cmt | Tmt | Tat |
|---|
| Sht + 1 | 0.78 | 0.21 | 0.20 | 0.05 | 0.00 | Sht + 1 | 0.85 | 0.19 | 0.23 | 0.27 | 0.35 |
| Omt + 1 | 0.11 | 0.56 | 0.27 | 0.00 | 0.00 | Omt + 1 | 0.11 | 0.74 | 0.34 | 0.22 | 0.01 |
| Cmt + 1 | 0.11 | 0.14 | 0.38 | 0.01 | 0.00 | Cmt + 1 | 0.04 | 0.07 | 0.36 | 0.01 | 0.01 |
| Tmt + 1 | 0.00 | 0.09 | 0.15 | 0.01 | 0.11 | Tmt + 1 | 0.00 | 0.00 | 0.07 | 0.50 | 0.40 |
| Tat + 1 | 0.00 | 0.00 | 0.00 | 0.93 | 0.89 | Tat + 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.23 |
Hypothesis/Model 2:
This hypothesis asserts that it is virtually impossible to implement a habitat or mosaic fire, and that any fire is likely to produce the same overall responses as current fuel reduction fires. Under this hypothesis, transition probabilities for “fuel reduction fire” and “habitat fire” are the same as previous fuel reduction-prescribed fire transition probabilities.
| Fuel Reduction Fire Matrix | Habitat Fire Matrix |
|---|
| Sht | Omt | Cmt | Tmt | Tat | | Omt | Cmt | Tmt | Tat | Omt |
|---|
| Sht + 1 | 0.78 | 0.21 | 0.20 | 0.05 | 0.00 | Sht + 1 | 0.78 | 0.21 | 0.20 | 0.05 | 0.00 |
| Omt + 1 | 0.11 | 0.56 | 0.27 | 0.00 | 0.00 | Omt + 1 | 0.11 | 0.56 | 0.27 | 0.00 | 0.00 |
| Cmt + 1 | 0.11 | 0.14 | 0.38 | 0.01 | 0.00 | Cmt + 1 | 0.11 | 0.14 | 0.38 | 0.01 | 0.00 |
| Tmt + 1 | 0.00 | 0.09 | 0.15 | 0.01 | 0.11 | Tmt + 1 | 0.00 | 0.09 | 0.15 | 0.01 | 0.11 |
| Tat + 1 | 0.00 | 0.00 | 0.00 | 0.93 | 0.89 | Tat + 1 | 0.00 | 0.00 | 0.00 | 0.93 | 0.89 |
3. Adaptive Resource Management
ARM has come to be defined and viewed in many different ways, so we begin with a brief description of our specific view of this process. As noted above, we view ARM as a process for making informed decisions for recurrent management problems characterized by potentially resolvable uncertainty. ARM requires the following components essential to any informed decision process [
29,
30,
31]: clearly specified objectives, a set of potential management actions, models for projecting system response to actions, monitoring for estimating the state of the system and other relevant parameters and a decision algorithm that uses these components to select the appropriate decision. The establishment of an ARM program begins with a deliberative or setup phase during which the listed components are developed and assembled. Objectives drive the entire process and must be developed in a manner that engages and obtains input from all relevant stakeholders. The development of the set of potential actions is based on the specified objectives and, again, typically requires input from relevant stakeholders. Based on specified objectives and actions, models are developed to predict the consequences of potential actions to the managed system.
Because substantial uncertainty frequently characterizes predictive modeling, it is often necessary to develop multiple models in order to include the most important sources of uncertainty about system response to actions (
i.e., those uncertainties that impede decision-making). Relative degrees of confidence in the different models are reflected by model “weights”, numbers that sum to one for all of the members of the model set. A monitoring program is then established for the specific purpose of informing the decision process, and a decision algorithm is selected in order to translate information from all of these process components into a recommended decision. The decision algorithm can be very formal, as with a dynamic optimization algorithm [
32,
33,
34].
This deliberative phase is then followed by the actual implementation of ARM in an iterative phase. At each decision point, the decision algorithm is used to select the appropriate action based on the objectives, available actions, models and current estimates of system state (from the monitoring program). The selected action is implemented and drives the system to a new state, which is identified by the monitoring program. In the typical case of multiple models, the estimated system state is compared with the predictions made by each of the system models. Model weights are increased for models that predicted well and decreased for models that predicted poorly, using Bayes’ theorem (e.g., [
33]). At the next decision point, armed with these new model weights and the new estimate of system state, the decision algorithm is again used with the existing objectives, actions and models to select the next action. The iterative process proceeds in this manner with model weights and estimates of the system state changing from one decision point to the next. Learning is accomplished by the comparison of model predictions with the estimated system state at each time step and is reflected in the updating of model weights. Because the model weights determine the relative influence of the different models in the decision algorithms, the learning is incorporated directly into each decision. Note that this step of evolving degrees of confidence in different models based on a comparison of predictions against observations (
i.e., estimates of the true system response) effectively incorporates science within the larger management process.
The iterative phase proceeds in this manner, simultaneously promoting both wise management and learning for better management in the future. However, at any time during the iterative phase, it is possible to revisit any of the ARM components, effectively returning to the deliberative phase. Stakeholder objectives may change; the ineffectiveness of management actions may motivate a search for new actions; the system response may not be predicted well by any members of the model set; or monitoring may be ineffective at estimating relevant quantities. Returns to the deliberative phase after obtaining experience with the ARM process are referred to as double-loop learning [
35,
36]. Any changes made to process components during this double-loop deliberative phase are then incorporated into ARM for the next round of iterative phase decisions. Finally, we reiterate that adaptive management is viewed in different ways by many managers and scientists. Our purpose in laying out our view of this process is not to suggest to readers that this view is in any sense the only “correct” perspective, but rather to ensure that the reader has a clear idea of what we mean by ARM.
4. Defining Objective Functions
For any informed decision, the decision maker and stakeholders are required to formulate the problem with clearly-defined and quantifiable management objectives. In decision theory, objectives are representative statements about how we value the outcomes of alternative management actions. An objective function is the formalized, mathematical expression of such statements, translated into measurable management goals, and can be written to capture multiple (possibly competing) benefits, as well as conditional on constraints and management costs. By quantifying the costs and benefits (the “return”) expected to result from implementing a management policy, the objective function serves as the basis for an optimization or tradeoff analysis [
33,
37]. A common formulation of conservation objectives is the maximal coverage problem, where the goal is to find the solution that achieves the greatest return given budget (or personnel) constraints [
38,
39]. If the management problem has multiple-objectives, we would define the system state (e.g., of a habitat patch) based on variables that represent each objective. We could then assign a management return to that state variable, reflecting its benefit to each objective. For example, a habitat patch may be observed as being in a closed-medium state, which is medium quality for FSJ, but also of moderate risk for wildfire (
Table 1). These characteristics define the system state for the patch, and we would assign a value to each component and then sum these to produce the management return for that patch. There are many ways to assign management values to system states, including utility functions that describe the relationship between state variables and benefits. Alternatively, values can be assigned directly to each level of the state variable (e.g., medium (FSJ) = 0.75, moderate (fuel) = 0.5). A generalized objective function for a multiple objective problem is:
given that
where
f(
Rij|
xi,
ai) is a function that identifies the management return for objective
j at site
i, conditional on being in system state
x and implementing action
a, and w(
j) is the weight assigned to objective
j. The cost of implementing action
a at site
i is
c(
a)
i and
B is the total resources (dollars, staff hours) available for allocation. The utility function
f can take on a number of functional forms (e.g., linear, convex/concave, step,
etc.) to describe state-dependent management values or can simply be used to assign a return to each possible state of the system. The selection of weights reflects the relative values of the decision maker with respect to each objective and can be elicited using formalized methods (e.g., analytic hierarchy process, swing weighting) or negotiated in the case of multiple decision makers. A sensitivity analysis is recommended to determine the effect of weight distribution on the recommended decision.
The objectives of the National Fire Plan, followed by the U.S. Fish and Wildlife Service and many land managers responsible for scrub habitat, are to reduce the risk of catastrophic wildfire by reducing hazardous fuel loads (especially near communities), restore fire-adapted ecosystems and reduce suppression costs. The Fire Plan bases the objectives on minimizing fuel hazard by maximizing the probability of an area transitioning from high to low risk, while minimizing the probability of the system transitioning from low to high risk.
The objectives of habitat management for FSJ recovery can be specified in multiple ways, and we present two examples. Johnson
et al. [
18] describe an adaptive management program in which the FSJ population growth rate is modeled as a function of scrub-height classes (
Table 1). The management objective is to maximize population growth rates by implementing habitat treatments at the management unit level, and the utility function increases linearly with the growth rate. Thus, the management return (
R) in Equation (1) is equivalent to the expected FSJ population growth rate in each habitat category and
w(
pop. growth) = 1. A related scrub habitat management program in mainland Florida has chosen territory occupancy of FSJ as an appropriate state variable (
ψ is the probability that a local site is occupied). The probabilities of a site transitioning between occupancy states are functions of scrub-height class, soil substrate, management action and the presence of FSJ in neighboring territories. The management objective under this program is to maximize the number of occupied territories within each management unit, with a sigmoidal utility function to represent a species recovery goal of 0.70 occupancy in a given conservation reserve. In both cases, the goal of the analysis was to produce unconstrained optimal decisions, so neither cost nor other objectives, such as fuel load, were included in the objective function. However, cost constraints were recognized as an important consideration for future iterations of the decision model.
Neither of the existing approaches explicitly considers fuel management, focusing instead on objectives that concern FSJ status. To account for the distinctions in objectives between fuel hazard and habitat-species management, we believe there would be considerable benefit to the development of an objective function that integrates the goals of both resource management programs. One approach to developing an objective function that incorporates two components is similar to the maximal coverage problem, where we would optimize the return for one component of the system state (i.e., one of the variables used to classify patches to state), conditional on achieving a minimum level (a constraint) for a second system state variable. For example, we could produce a policy to minimize the number of territories in a management unit that contain fuels biomass in a high-risk state, conditional on achieving a minimum occupancy level of 0.70.
given that
where
I is the total number of territories and
I(
hr)
i = 1 for territories in the high-risk state and 0 for territories not in the high-risk state. The objective function could also be written to maximize FSJ occupancy subject to the constraint of maintaining fuel load below some threshold level. Alternatively, we could address the problem by maximizing the total return for two objectives (fuel reduction and FSJ, each with its respective weight w(
j)), subject to a budget constraint (as in Equations (1) and (2)).
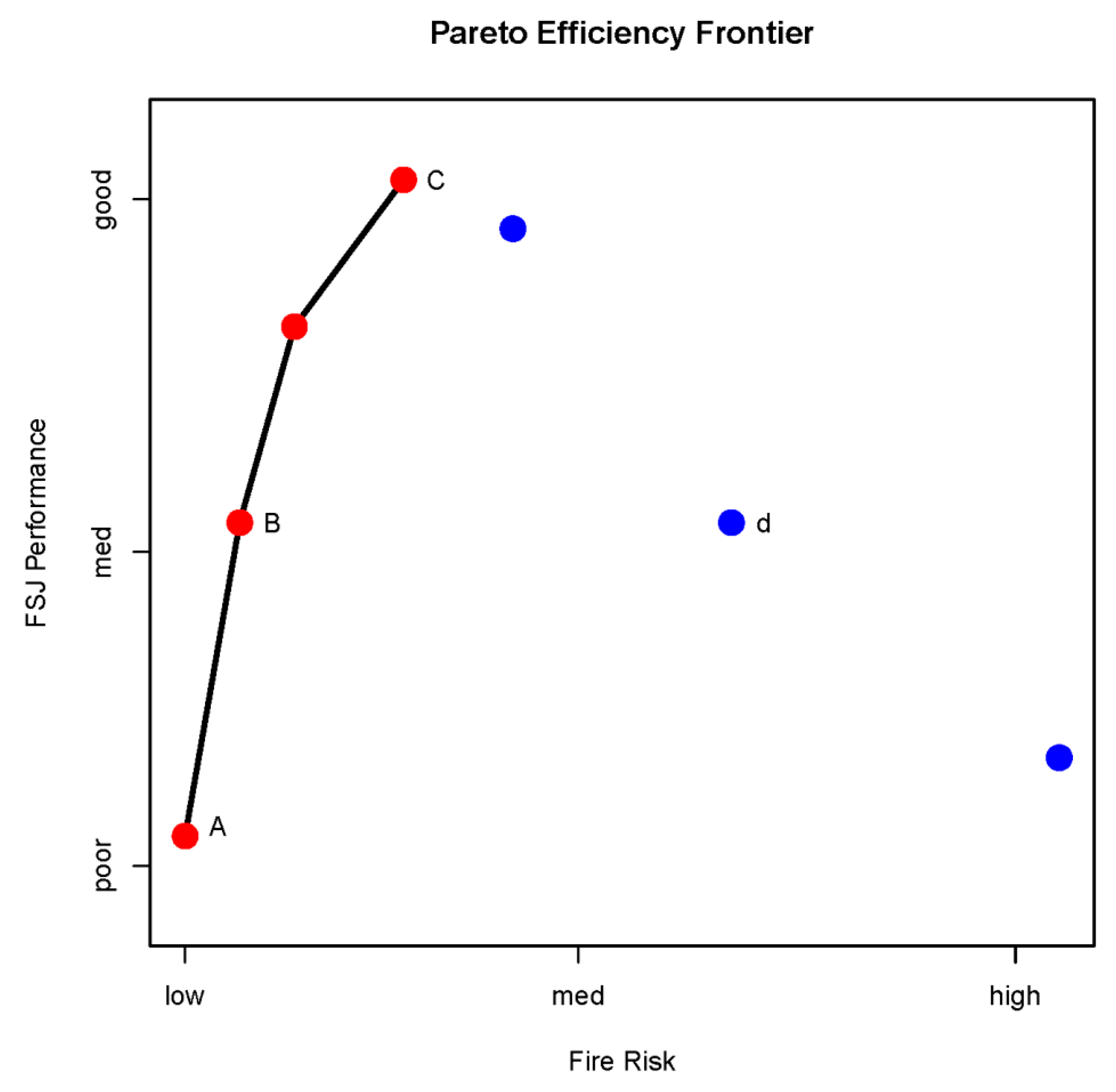
A third option is to evaluate the return on management actions for each objective separately and to seek a Pareto-efficient solution [
40,
41]. Pareto optimality identifies a multi-dimensional efficient frontier of possible solutions in which improvement in one component of objectives cannot occur without a loss to another, providing maximum benefit for one objective at any given value of another objective (
Figure 1). This efficiency frontier would represent an optimal range of trade-offs between FSJ and fuel management objectives for which a negotiated solution based on managers’ values could then be reached.
Figure 1 is a hypothetical depiction of this multi-objective efficiency and trade-off. Each point represents the return for any management strategy (
i.e., the set of actions applied to the
I territories within a management unit), and the line depicts the efficient frontier, with points in red being Pareto optimal. Moving along this line from A to C, Pareto-optimal policies resulting in higher FSJ performance can only be achieved by incurring a higher fire risk, although it is clear from the figure that rapid benefits to FSJ are gained with relatively small increases to fire risks. Points to the right and below the frontier (in blue) represent non-optimal or dominated strategies: significant fire risk reductions can be achieved over Strategy d with no loss incurred to FSJ performance (Strategy B).
Figure 1.
A plot of management strategy returns (benefits), parsed by two objectives: fire risk and response by Florida scrub-jays (FSJs). The line passes through those strategies that are Pareto optimal (red dots), which depict the most efficient solution for one objective at a given benefit for the other objective. The efficiency frontier suggests that no greater benefit can be achieved for one objective without a loss to the other and represents the subset of solutions for which it makes sense to negotiate a final strategy. The blue points are sub-optimal or dominated solutions, which can be improved upon for one or both objectives (up to the efficient frontier) without loss to the other.
Figure 1.
A plot of management strategy returns (benefits), parsed by two objectives: fire risk and response by Florida scrub-jays (FSJs). The line passes through those strategies that are Pareto optimal (red dots), which depict the most efficient solution for one objective at a given benefit for the other objective. The efficiency frontier suggests that no greater benefit can be achieved for one objective without a loss to the other and represents the subset of solutions for which it makes sense to negotiate a final strategy. The blue points are sub-optimal or dominated solutions, which can be improved upon for one or both objectives (up to the efficient frontier) without loss to the other.
6. Models
When land cover states can be classified in terms that represent progress towards or away from something we hope to achieve, estimates of land cover transition probabilities under differing management regimes can be used to guide optimal decision-making for realizing positive impacts on resources, processes and ecosystem services [
18]. Most habitats are subject to natural succession dynamics, and the application of a management action is intended, by definition, to transition land cover states in a desired direction, although often with considerable uncertainty. This uncertainty can be represented by alternative hypotheses of how the system functions, with corresponding models to express these beliefs (
Section 2;
Box 1). Therefore, land cover change can be effectively described using discrete-time, first-order Markov models, characterized as random processes in which the system state at any point in time depends only on the state in the previous time step and the management action applied. A vector of probabilities describes the transition from a single known state in time
t to any of a finite number of other states in time
t + 1. Because the state space (
X = 5 total habitat states in our case) for a Markov model is discrete and comprehensive, we constrain these probabilities, such that:
where the transition probabilities at time
t are conditional not only on the state at time
t, but also on the management action
a selected at that time and our belief about how the system operates (
i.e., model
M is used to describe the likely outcome of implementing action
a;
Box 1). Although some management actions can produce deterministic outcomes (
i.e., the vector of transition probabilities comprises all zeroes except for one state with a value of one), it is more common that management actions result in probabilistic outcomes due to the partial controllability of the action achieving its intended result, variation in environmental conditions under which the action is implemented or averaging across unmodeled variation in the conditions of the managed sites.
Essential considerations when modeling land cover change in this way include: (1) defining the possible states of the system in terms that are appropriate for the management context; (2) matching the time step of the state transition probabilities to the management cycle and; (3) specifying a transition matrix for each combination of hypothesis and action available to managers. With regard to the first consideration, habitat state selection, for example, should encompass characteristics or quantities that represent different values that we might assign to management outcomes. Choice of habitat states must also take into account the spatial scale at which actions are applied and the practicalities of identifying the system state at any point in time with minimal error (
i.e., via monitoring), both of which permit state-dependent decision-making. In the case of scrub management for ecological benefits, we can define the system as a combination of discrete states with values corresponding to the demographic performance of the FSJ (
Table 1). The spatial scale at which we describe habitat state is that at which fire decisions are implemented, the fire management unit (FMU), and the time step of the state transition estimates is the annual decision cycle used by land managers. With the additional objective of managing habitat for fire risk, we anticipate the need to modify how habitat state is defined (see above: Defining Objective Functions). We instead characterize the state space as a combination of vegetation structure and discrete categories of fuel biomass, biomass connectivity (
i.e., ability to carry a fire), adjacency to another site with high fuel biomass (
i.e., as a measure of risk) or direct estimates of risk itself.
Finally, individual transition probabilities must be specified for all system states, for all possible management actions from which the decision maker is able to select and for all hypotheses representing the range of beliefs that exists regarding the response of the system to management. When novel management actions are being considered, these probabilities must be elicited as best estimates from experts [
42,
43]. When land cover history data exist, state-action transition probabilities can be estimated empirically using a variety of techniques, including binomial or multinomial logit models implemented using Bayesian MCMC methods (e.g., using Dirichlet priors; [
44]) or maximum-likelihood approaches ([
9,
45]). If the history of a system state and management action is known for each managed site over time, modeling individual site histories (e.g., land cover state at each time step) using maximum-likelihood methods is an efficient way to estimate transition parameters as a function of management actions and site conditions. When few or no data are available for empirical estimates, managers’ knowledge can be elicited as the best estimates. Those transition probabilities in which managers have the least confidence (
i.e., parameters with the greatest uncertainty) can form the basis of alternative models to be used in the decision optimization (see below). Transition probabilities are required for every state
x action
x model combination; thus, a large number of estimates must often be produced for even highly simplified decision problems. Note that when land cover state histories are observed imperfectly (e.g., using remote sensing), methods to account for state misclassification have been developed [
44,
46,
47,
48].
In
Box 1, we described two possible models reflecting structural uncertainty in the ability to implement two types of fire (fuel reduction and habitat). Under Model 1, the implementation of these two different fire types is believed to be possible, yielding a model with two different transition matrices corresponding to the two fire types. However, Model 2 represents the belief that the implementation of these two fire types is not really possible, yielding identical transition matrices for the two types of fire. This uncertainty means that there are different predictions for the expected consequences of applying the habitat fire type,
a′t,
i.e.,
PrM1(
xt+1|
xt,
a′t) ≠
PrM2(
xt+1|
xt,
a′t). Because optimization determines the actions for which predicted consequences yield the highest returns, we need to be able to specify the relative degrees of belief in these two models in order to compute an optimal solution. We can express our relative degrees of belief in the two models as model weights, q
m, numbers between zero and one that sum to one for the members of the model set (in our case, of
M1 and
M2,
q1 +
q2 = 1). For example, model weights of 0.5 for each model reflect complete uncertainty, with no basis for believing one model to be a better predictor than another. On the other hand, if
q1 = 0.75,
q2 = 0.25, then we have three-times greater belief in the predictive ability of Model 1 than Model 2. Initial model weights at the beginning of an ARM program may be based on analyses of historical data, or perhaps on stakeholder beliefs. However, after the first decision, these weights are updated formally by comparing predicted habitat state changes under the different models with what is observed via monitoring. This evidence-based updating is continued throughout the ARM process, leading to the evolution of our relative beliefs in the two models. These weights not only quantify our current belief in the models, but they are also used in the optimization (see below), effectively giving more influence to the models with the higher weights.
7. Monitoring
Monitoring programs provide data that play at least four important roles in management programs. (1) Estimates of system state variables (e.g., the number of sites in the management unit in each habitat or habitat + fuel load state) are used to make state-dependent management decisions. (2) Estimates of state variables and other quantities related to objectives are used to assess progress towards management objectives. (3) Estimates of state variables and other parameters (e.g., model vital rates) can be compared against model-based predictions in order to discriminate among competing models. This comparison of empirical data against model-based predictions for the purpose of discriminating among competing hypotheses constitutes the key step in science. Thus, this role of monitoring entails the embedding of a scientific step in the larger management program. (4) Monitoring data are also used to obtain updated estimates of key model parameters used to predict system responses to management. As with other elements of the ARM program, the nature of the monitoring program is driven by the management context. If management focus is on sites characterized by habitat state and fuel load state, then a monitoring program would ideally provide estimates of habitat-fuel load state each year for all, or a subset, of sites that are in the management program.
As noted above, the comparisons of model-based predictions with actual monitoring results (monitoring Role 3) lead to changes in model weights, with weight increasing for models that predict relatively well and decreasing for models that predict relatively poorly. For the example of model uncertainty in
Box 1, assume that the optimal decision was to apply a habitat fire to 20 territories in the tall-mix state at time
t. Assume that monitoring in year
t + 1 indicated that six of these 20 territories were now in the short state, another four in open-medium, nine in tall-mix and one in tall. This observed distribution of states in time
t + 1 is much closer to the predictions of Model 1 than Model 2 (see
Box 1), and the weight for Model 1 would thus increase and that for Model 2 decrease as a result of these comparisons.
Land cover monitoring can be conducted either remotely (e.g., satellite imagery, aerial photography) or with actual visits to each monitored site. One of the greatest challenges in land cover monitoring to support ARM is obtaining imagery to classify habitat states in a timely manner, for example where high resolution is necessary to detect small, but important habitat features. The states used herein are simple enough that they can be practically classified in the field each year in all but the largest conservation areas, which may need to rely on new technologies, such as unmanned aerial systems [
18]. Such monitoring serves the four roles noted above for the ARM process.
Although not a part of the iterative ARM process, we note that we can also use time series of satellite imagery to maintain a fire history database and to map fire boundaries [
26,
49]. Such data are used during the deliberative or set-up phase of ARM in order to obtain estimates that populate the transition probability matrices described above. For example, we used this sort of approach to estimate the probability that a fire was successful in moving a site from one habitat state to another as a function of the initial habitat state and environmental conditions [
9].
8. Decision Algorithm
The final component of an informed decision process is a decision algorithm that uses the other process components described above, objectives, actions, models and monitoring, to decide which action is most likely to produce returns that are “best” with respect to the specified objectives. Dynamic optimization methods are often used for solving sequential decision problems in natural resource management [
50,
51,
52]. Sequential decision problems are ubiquitous in conservation; examples include the harvesting or stocking of animals, the control of invasive plants and animals and habitat management for imperiled species [
53,
54].
Dynamic optimization methods combine objective functions that value present and future consequences of alternative management actions with models of ecological system change (see the Objectives and Modeling sections, above). The general resource management problem involves a temporal sequence of decisions, where the optimal action at each decision point depends on time and/or system state [
52]. The goal of the manager is to develop a decision rule (or management policy) that prescribes management actions for each time and system state that are optimal with respect to the objective function. A key advantage of dynamic optimization is its ability to produce a feedback policy specifying optimal decisions for possible realized future system states rather than expected future states [
50]. In practice, this makes stochastic dynamic optimization appropriate for systems that behave stochastically, absent any assumptions about the system remaining in an equilibrium state or about the production of a constant stream of resource returns.
Similar to our organization of the preceding discussion, a framework for dynamic optimization requires specification of: (1) an objective function for evaluating alternative management policies; (2) predictive models of system dynamics that are formulated using quantities relevant to the stated management objectives; (3) a finite set of alternative management actions, including any constraints on their use; and (4) a monitoring program to follow the system’s evolution and responses to management. More formally, let:
characterize system dynamics, where
xt = {
x1,
x2, …
xI} for
I sites and
at and
zt represent management actions and environmental variation, respectively, at time
t. Environmental and other sources of variation induce Markovian transition probabilities
Pr(
xt+1|
xt,
at). Let policy
At specify an action for every system state
xt at every time in the time frame {
t,
t+1, …
T}. Benefits and costs attend management actions, which are included in returns
R(
at|
xt) that, in turn, are accumulated in an objective or value function:
where the expectation is with respect to stochastic influences on the process and
α discounts future returns. This function can be decomposed into current and future returns by:
which makes clear that future returns are conditioned on the effect of current actions on future states. A value
V(
At|
xt) can be obtained for every possible policy
At over the time frame, and the optimal policy satisfies [
55,
56]:
A key consideration in dynamic optimization is the uncertainty attendant to management outcomes. This uncertainty may stem from environmental variation, errors in measurement and sampling of ecological systems (partial system observability), incomplete control of management actions (partial controllability) and incomplete knowledge of system behavior (structural or model uncertainty) [
57]. Model uncertainty, an issue of particular importance in adaptive management, can be characterized by continuous or discrete probability distributions of model parameters or by discrete distributions of alternative model forms that are hypothesized or estimated from historic data. Important advances have followed from the recognition that these probability distributions are not static, but evolve over time as new observations of system behaviors are accumulated from the management process. Indeed, the defining characteristic of adaptive management is the attempt to account for the temporal dynamics of this uncertainty in making management decisions [
3,
58,
59,
60,
61]. Here, we express uncertainty with alternative system models that are characterized by model index
M (e.g., in our case,
M1 or
M2, to denote the fire models):
with random demographic and environmental variation inducing model-specific Markovian transition probabilities
PrM(
xt+1|
xt,
at). The alternatives described by
M might include the alternative hypotheses in
Box 1, with initial probabilities that are based on prior experience or expert opinion. Policy value is again given in terms of accumulated returns, except, in this case, the returns are averaged over alternative models:
The distribution
qt is referred to as a model state, representing the relative probability that each model is an appropriate representation of the system dynamics. Model state can evolve through time according to Bayes’ theorem:
with:
Note that this evolution is based on the likelihoods of the observed state changes under each model,
PrM(
xt+1|
xt,
at). The optimal policy satisfies [
62]:
with:
and:
Note that current returns in Equation (14) are averaged using the prior probabilities of the alternative models Equation (15), whereas future returns are weighted by the posterior probabilities Equation (16). A management action is chosen at each point in time, depending on the resource state and model state
qt, and the action, in turn, influences future resource states, as well as changes in the model state. Optimal management consists of actions that maximize objective returns, not learning,
per se, with model discrimination (
i.e., learning) pursued only to the extent that it increases long-term returns. This approach can be described as active adaptive management, in that it explicitly accounts for the effect of management actions on learning and the effect of that learning on future returns. We characterize this form of adaptive management as “learning while doing,” as opposed to an experimental approach to adaptive management [
58,
63] that might be characterized as “learn, then do”.
10. Landscape Resilience and Restoration
It is noteworthy that not everyone concerned with the conservation of natural resources agrees about the utility of decision analysis and optimization [
71,
72,
73]. Proponents of “resilience thinking” have been particularly critical [
74]. Resilience is defined as the magnitude of disturbance a system can absorb while still retaining essentially the same function, structure, identity and feedbacks [
75] or as the disturbance that can be absorbed without shifting the system to an alternative stability regime (or “domain of attraction”) [
76]. Important concerns for ecosystem management are: (1) the loss of resilience as the system state approaches a (perhaps unknown) threshold and the attendant increase in the probability that some disturbance will shift the system to a less desirable stability regime; and (2) changes in the parameters governing the size and shape of the domains of attraction that make system shifts more or less likely [
77]. Systems with alternative stable states can also exhibit hysteresis, in which a loss of resilience is followed by a system change and, thereafter, with an increase in resilience, so that reversing the change is difficult [
78,
79].
In our example, scrub that has been subject to long periods of fire suppression may exhibit hysteresis. During periods of fire suppression, closure of the oak canopy and the buildup of the root system displaces flammable plants (grasses) from the landscape. Eventually, the system shifts to an alternative stability regime that is fire resistant, with rapid re-growth and loss of open areas after disturbance. In such cases, it may take a long period of frequent burning to return the system to a more desirable stability regime. The presence of hysteresis implies that knowledge of the system’s history is required to make reliable predictions about the future; thus, system transitions are not strictly Markovian. Approaches to the conduct of dynamic optimization for systems whose dynamics are influenced by history and characterized by substantive time lags have been developed conceptually [
30], but implementation can be challenging. One possible approach for incorporating history into dynamic optimization is to include a state variable that describes fire history (e.g., the number of fires over some time frame), thus changing models of system dynamics back to first-order Markovian. Although a number of researchers have begun to formulate models that can be used to explore properties of resilience [
78,
79,
80], more needs to be done to develop models that can be used to provide practical advice for those concerned with ecosystem management. We believe that a useful approach will be to use the described methods of decision analysis, but to modify objectives (stressing outcomes that are robust) and models in a manner consistent with resilience ideas [
81].