A Moving-Window Based Method for Floor Water Inrush Risk Assessment in Coal Mines

Abstract

In recent years, with the continuous increase in coal mining depth and intensity, hydrogeological conditions in coal mines have become increasingly complex, and the risk of floor water inrush has risen significantly. To address the limitations of the global weighting pattern in traditional floor water inrush risk evaluation systems, this study, taking a coal mine in Shaanxi Province as a case, develops a local water inrush risk evaluation method based on the Monte Carlo Analytic Hierarchy Process (MAHP) combined with a circular moving window, and compares it with the water inrush coefficient method and the global evaluation method. The results demonstrate that the proposed local evaluation model achieves higher accuracy, provides a more refined delineation of high-risk zones, and shows stronger consistency with actual mining conditions. Further comparison of window radii of 100 m, 500 m, and 900 m indicates that the 500 m radius performs best in terms of spatial morphology, area proportion, and water inrush point identification rate (89.3%). Moreover, its application in Yangcheng Coal Mine further confirms that this method can accurately identify high-risk zones, thereby offering reliable scientific support for the prevention and control of coal seam floor water inrush.

1. Introduction

For decades, coal has served as a fundamental pillar of China’s national energy consumption and industrial production. However, with the progressive depletion of coal resources in eastern China, the focus of coal mining has gradually shifted westward, accompanied by a continuous increase in mining depth and intensity [1]. In recent years, the deepening of mining activities has led to increasingly complex hydrogeological conditions, resulting in a significantly elevated risk of coal seam floor water inrush [2], which has caused severe casualties and substantial economic losses. For instance, on 25 May 2017, a catastrophic water inrush accident occurred on the floor of the working face at the Pan’er Coal Mine in Huainan City, Anhui Province, with a maximum inflow of 14,520 m³/h, flooding the mine and resulting in a direct economic loss of CNY 23.42 million. On 10 June 2021, another major water inrush accident occurred at Dahongcai Mining Co., Ltd. in Dai County, Xinzhou City, Shanxi Province, which claimed 13 lives and caused a direct economic loss of CNY 39.36 million. These incidents highlight the urgency of developing accurate assessment methods and effective prevention strategies for coal seam floor water hazards. Therefore, conducting reliable hazard evaluations and implementing targeted control measures prior to mining operations are of vital importance to reducing disaster risks and ensuring the safety of both human lives and property [3].

For the evaluation of coal seam floor water inrush risk, the most traditional method is the water inrush coefficient method. The water inrush coefficient (T) refers to the water pressure that can be borne by an aquifer per unit thickness, and is expressed by the formula T = P/M, where P is the water pressure of the aquifer and M is the thickness of the floor aquiclude [4,5]. Owing to its intuitive physical concept and the simplicity of calculation and application, this method has been widely applied for several decades. However, floor water inrush is the result of multiple interacting factors [6], whereas the water inrush coefficient method only considers two parameters—aquifer water pressure and aquiclude thickness—while neglecting other critical influences such as geological structures (e.g., faults and folds) and coal seam burial depth. Consequently, this method is inadequate for risk assessment of floor water inrush under complex hydrogeological conditions.

Therefore, in order to reasonably evaluate the risk of coal seam floor water inrush, many scholars have established multi-indicator evaluation systems and proposed various evaluation models, such as the vulnerability index method, fuzzy comprehensive evaluation method [7,8,9,10], and grey system theory method [11]. Wu Qiang [12,13,14,15] and others, after summarizing the main controlling factors of floor water inrush, employed ArcGIS (10.8) in combination with the Analytic Hierarchy Process (AHP), CRITIC, and entropy weight methods, and conducted a comprehensive evaluation of floor water inrush risk using the vulnerability index method. Hu et al. [16] constructed an AHP-EWM risk index model to evaluate the water inrush risk of the Qiuji coal mine working face. Niu et al. [17] (2020) applied a linear weighting method to develop an improved water inrush coefficient model to predict the floor water inrush risk of coal seams overlying a limestone aquifer. Wang et al. [9] proposed a computational model based on nonlinear fuzzy mathematics and the Analytic Hierarchy Process (AHP), and obtained the final evaluation level using the method of relative superiority analysis.

However, the existing evaluation methods still have certain limitations. In terms of weight assignment of evaluation indicators, most studies adopt a globally fixed weighting scheme. In practice, however, the same indicator should have differentiated weights in different locations of the study area [18]. For instance, in regions where the aquiclude is relatively thick and the water pressure is low, the thickness of the aquiclude plays a dominant role in controlling water inrush risk; thus, it should be assigned a higher weight, while the weight of water pressure should be correspondingly reduced. This indicates that weight assignment should fully reflect the actual controlling effect of different indicators across regions to achieve spatial adaptability. In addition, the adoption of a global weighting scheme often leads to large-area clustering of water inrush risk zones, resulting in blurred boundaries and insufficiently precise delineation, thereby reducing the reliability of evaluation results [19,20,21].

In recent years, with the advancement of artificial intelligence (AI) technologies, an increasing number of studies have explored AI-based approaches for evaluating the risk of coal seam floor water inrush [22]. Li et al. [23] integrated Principal Component Analysis (PCA) with Fisher Discriminant Analysis to develop a water source identification model for floor water inrush, which effectively reduced redundancy among indicators and enhanced recognition accuracy. Zhang et al. [24] proposed a predictive framework combining PCA with a Deep Belief Network (DBN) and Back Propagation Neural Network (BPNN) to assess water inrush risks in actual working faces. In another study, Zhang et al. [25] selected ten key controlling factors from fourteen potential indicators and comparatively analyzed the predictive performance of GRU, SVM, and BPNN models. Moreover, Convolutional Neural Networks (CNNs) [26,27] and other AI techniques have also been applied to floor water inrush risk prediction. Recent studies on cave mines (e.g., the Deep Ore Zone mine) have applied machine learning techniques such as random forest models to analyze inrush events, achieving about 85% accuracy and identifying key influencing factors including draw rate, fragment size, and prior inrush history [28]. Nevertheless, such models typically demand extensive field datasets for training, rendering the computational process complex and the overall application efficiency relatively low [29,30].

To address the above issues, this study develops a local water inrush risk evaluation method that integrates the Monte Carlo Analytic Hierarchy Process (MAHP) with a circular moving window. A case study was conducted in a coal mine in Shaanxi Province, where the evaluation results were validated using historical water inrush events and compared with those obtained from the traditional water inrush coefficient method and the global evaluation approach. In addition, based on previous studies [31], several key indicators were reselected to evaluate floor water inrush risk, and the effects of different moving window radii on assessment accuracy were systematically analyzed. The method was further applied to a coal mine in Shandong Province to verify its applicability and reliability.

Compared with conventional approaches that rely on globally fixed weights, the proposed MAHP–moving window method introduces dynamic spatial weight adjustment and uncertainty quantification mechanisms, which significantly enhance the model’s local adaptability and robustness, effectively overcoming the limitation of traditional AHP in neglecting the spatial heterogeneity of aquiclude conditions.

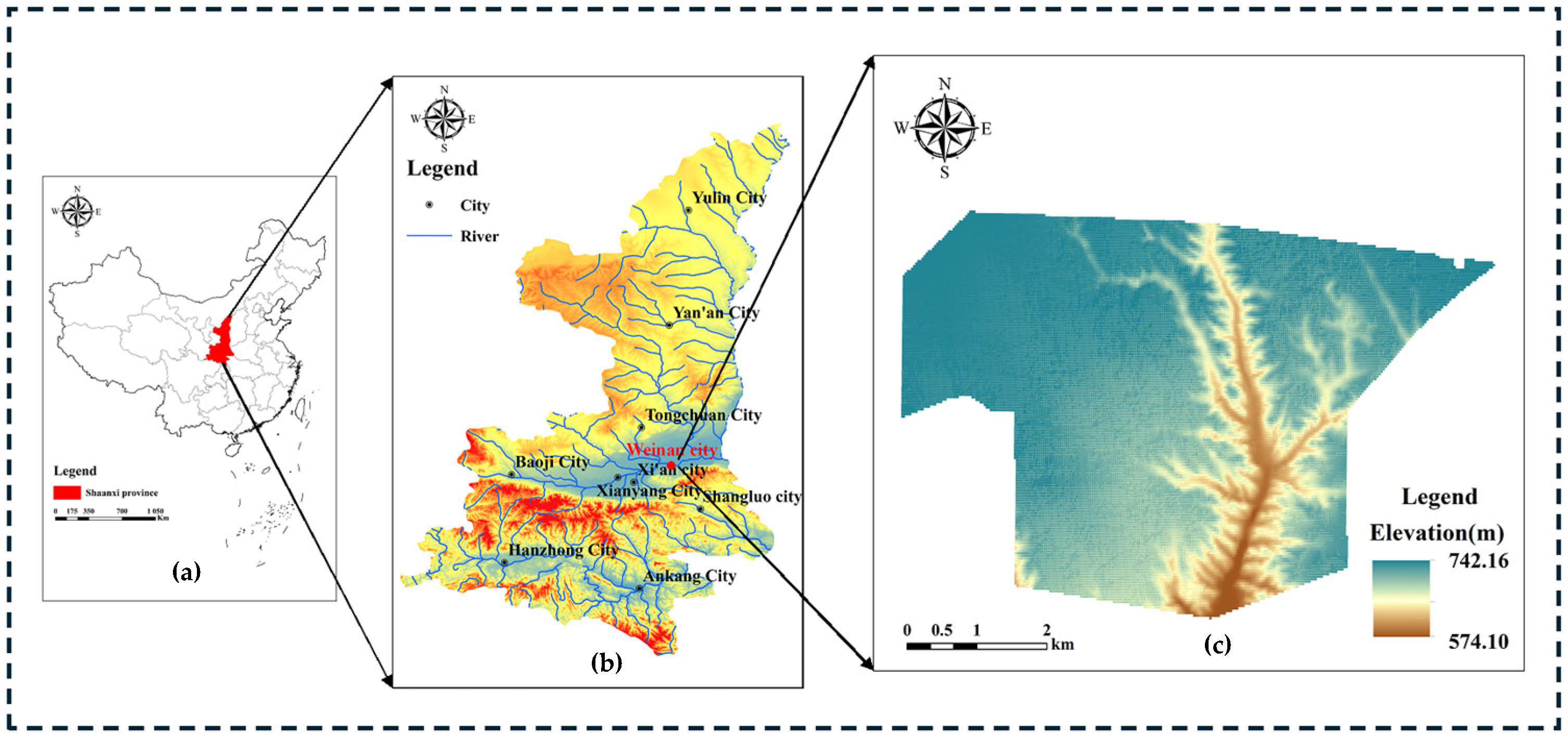
2. Overview of the Study Area

2.1. Geographical Condition

The Dongjiahe Coal Mine is situated in Dongjiahe Village, Chengguan Town, southwest Chengcheng County, Weinan City, Shaanxi Province (Figure 1). It belongs to the Chenghe mining district of the Weibei Carboniferous–Permian coalfield. The minefield extends 4.7–8.4 km from east to west and 2.8–5.8 km from north to south, with its boundary delineated by 23 turning points, covering a total area of 31.8722 km².

The western part of the Chenghe mining district is characterized by loess tablelands interspersed with gully landforms. The tableland surface is relatively wide and flat, and except for river valley areas, it is generally covered by loess deposits with a thickness of 150–180 m. The terrain of the study area is higher in the north and lower in the south, with a relative elevation difference of 150–200 m. Ground elevation ranges from +500 m to +726 m, while the surface elevation within the minefield varies between +540 m and +726 m.

Climatically, the study area belongs to the warm temperate semi-arid continental monsoon zone. The region experiences warm and dry springs, hot and rainy summers and autumns, and cold and dry winters. Its main climatic features are low annual precipitation and high evaporation, which exert significant influence on hydrogeological conditions.

The designed production capacity of the Dongjiahe Mine is 1.2 Mt/a. The mineable seams in the study area include No. 3, No. 5, and No. 11, among which the No. 5 seam is the principal mining seam. The mine is developed by inclined shafts with multiple mining levels, employing the strike longwall mining method and total caving for roof management. The No. 5 seam is mined at elevations ranging from +420 m to +150 m, occurring at the base of the Shanxi Formation. It exhibits good overall stability and is mineable across most parts of the study area.

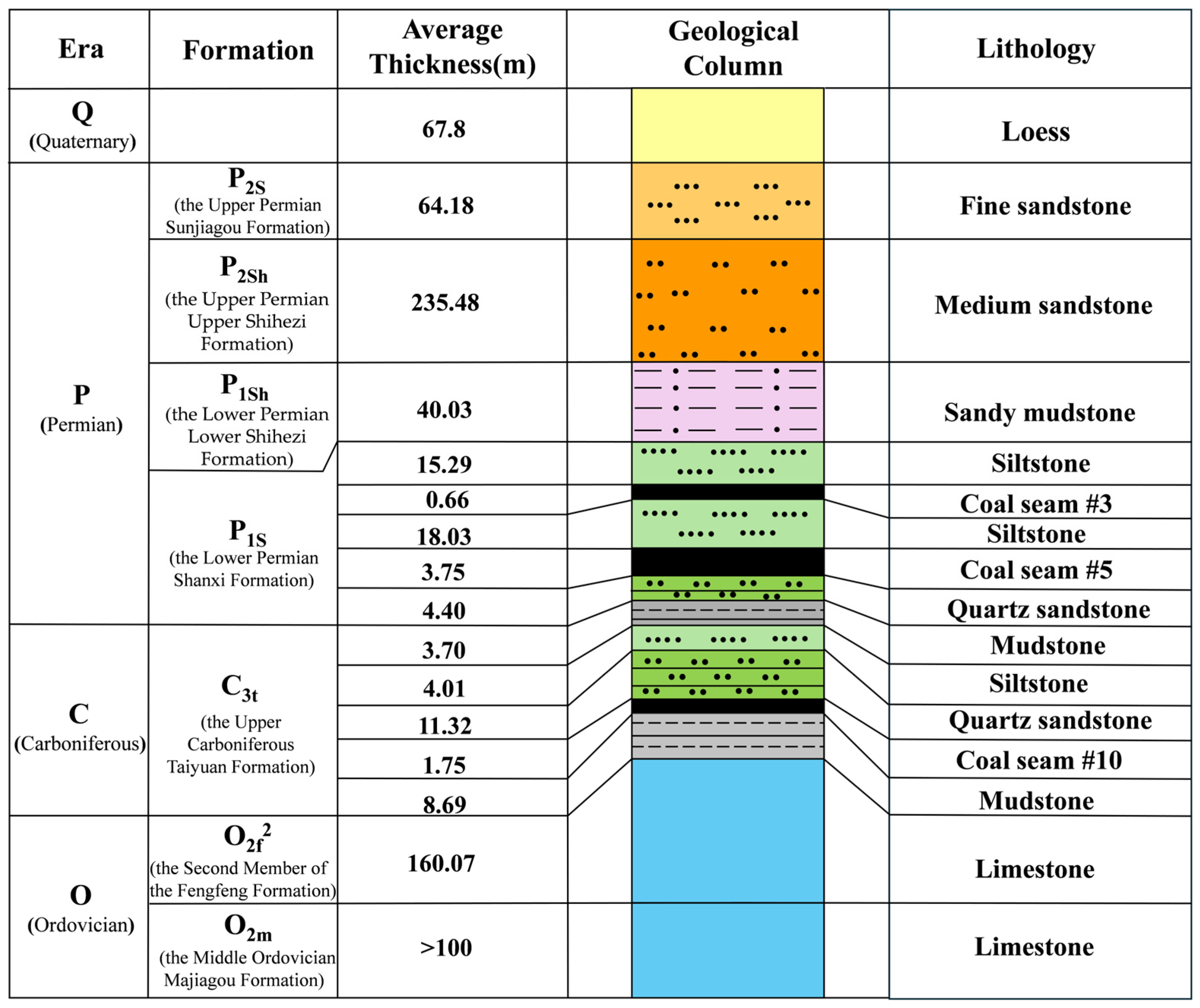
2.2. Geological Setting

Based on surface outcrops and borehole data, the stratigraphic sequence within the minefield, from oldest to youngest, is as follows: the Middle Ordovician Majiagou Formation (O₂m); the Second Member of the Fengfeng Formation (O₂f₂); the Upper Carboniferous Taiyuan Formation (C₃t); the Lower Permian Shanxi Formation (P₁s); the Lower Permian Lower Shihezi Formation (P₁sh); the Upper Permian Upper Shihezi Formation (P₂sh); the Upper Permian Sunjiagou Formation (P₂s); and the Quaternary (Q). The stratigraphic column is shown in Figure 2.

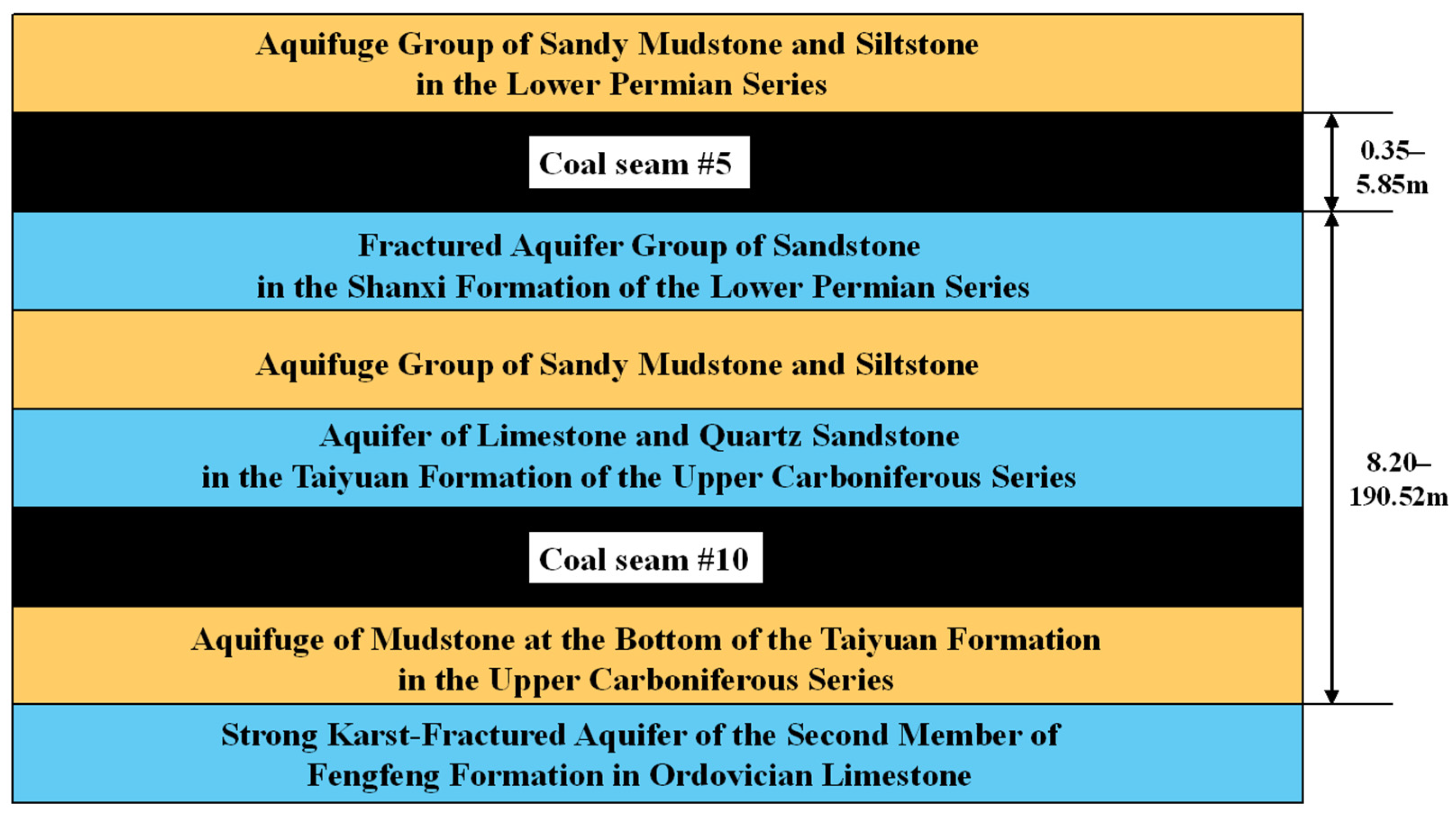
2.3. Hydrological and Geological Conditions

The floor aquifers underlying the No. 5 coal seam consist of the K₃ and K₂ aquifers of the Taiyuan Formation, as well as the Ordovician limestone aquifer. The K₂ and K₃ aquifers are mainly characterized by static reserves, and in the absence of recharge from the Ordovician limestone aquifer, they pose only a minor threat to the mining of the No. 5 coal seam. The distance between the Ordovician limestone aquifer and the No. 5 coal seam ranges from 8.20 to 190.52 m.

Within the planned mining area, the mining elevation of the No. 5 seam is primarily between +240 m and +270 m, while the water level of the Ordovician limestone aquifer currently remains stable at approximately +371 m. This indicates that roadway excavation and working face mining are threatened by potential water inrush from the Ordovician limestone aquifer. During mining, if water-conducting channels connect the coal seam with the Ordovician limestone aquifer, water inrush is likely to occur in the working face. Furthermore, in zones of intensive fracturing and vertically developed water-conducting structures, the Ordovician limestone aquifer can recharge the overlying aquifers, thereby increasing their threat to the safe extraction of the No. 5 seam.

The spatial relationship and separation distance between the No. 5 coal seam and the aquifers are shown in Figure 3.

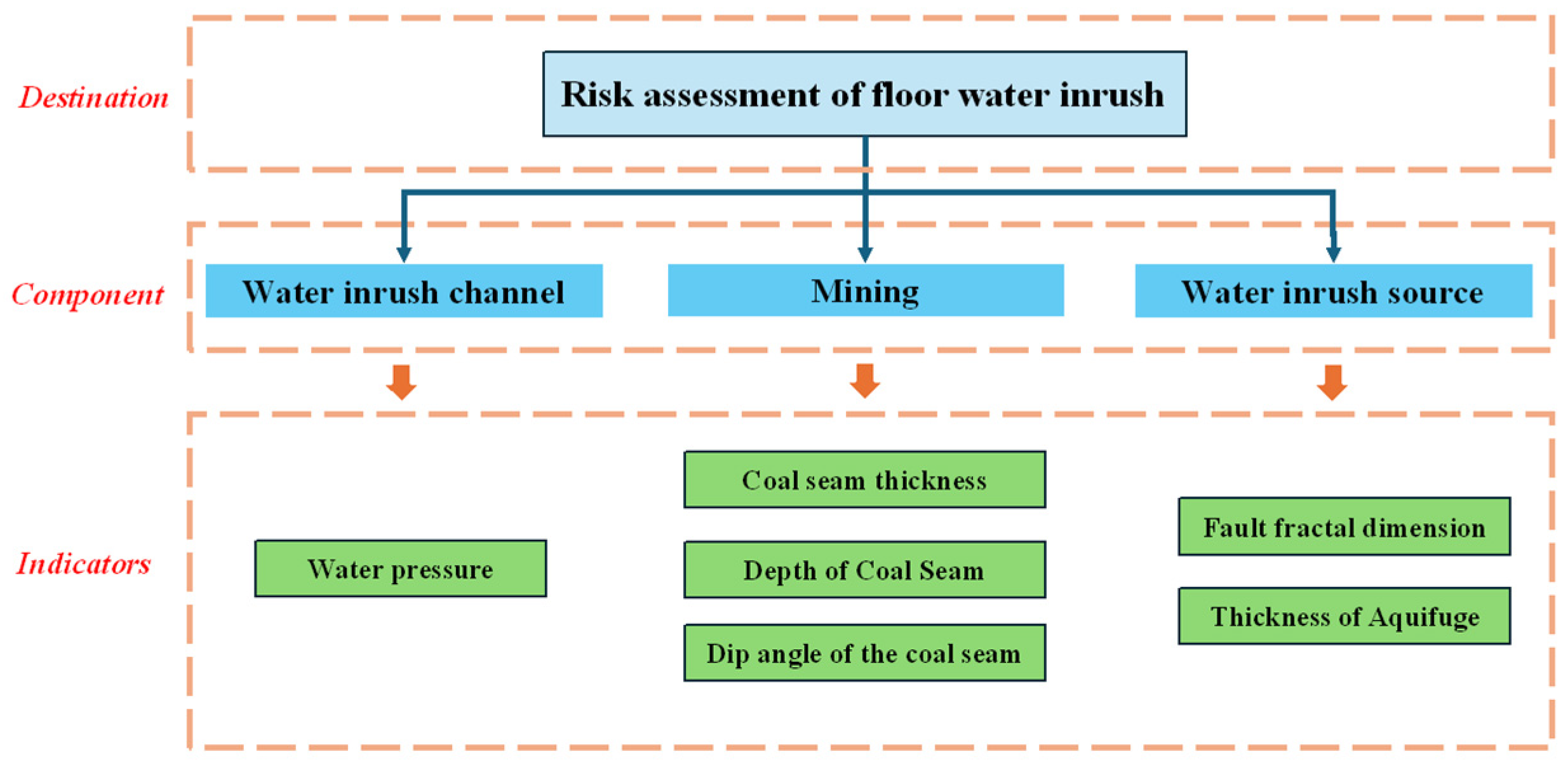
3. Main Evaluation Indicators for the Risk of Floor Water Gushing

Coal seam floor water inrush is a complex geological process driven by multiple interacting factors, and the construction of a scientific and rational evaluation index system is essential for accurate risk assessment. Considering the geological structures, hydrogeological conditions, and mining characteristics of the study area, and based on hydrogeological data and borehole records, six core evaluation indicators were selected in this study. The mechanisms by which each indicator influences water inrush risk are as follows:

(1)

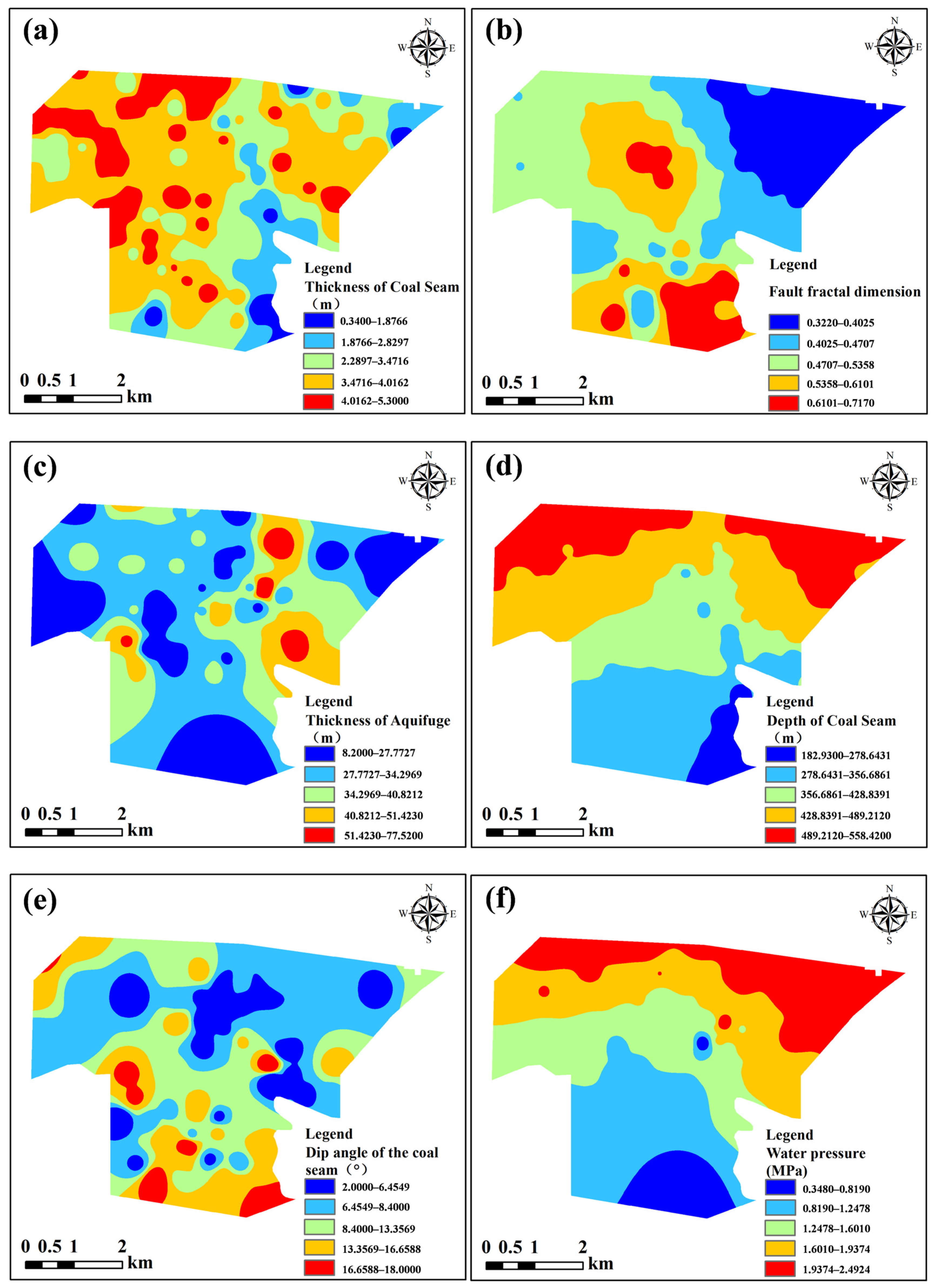
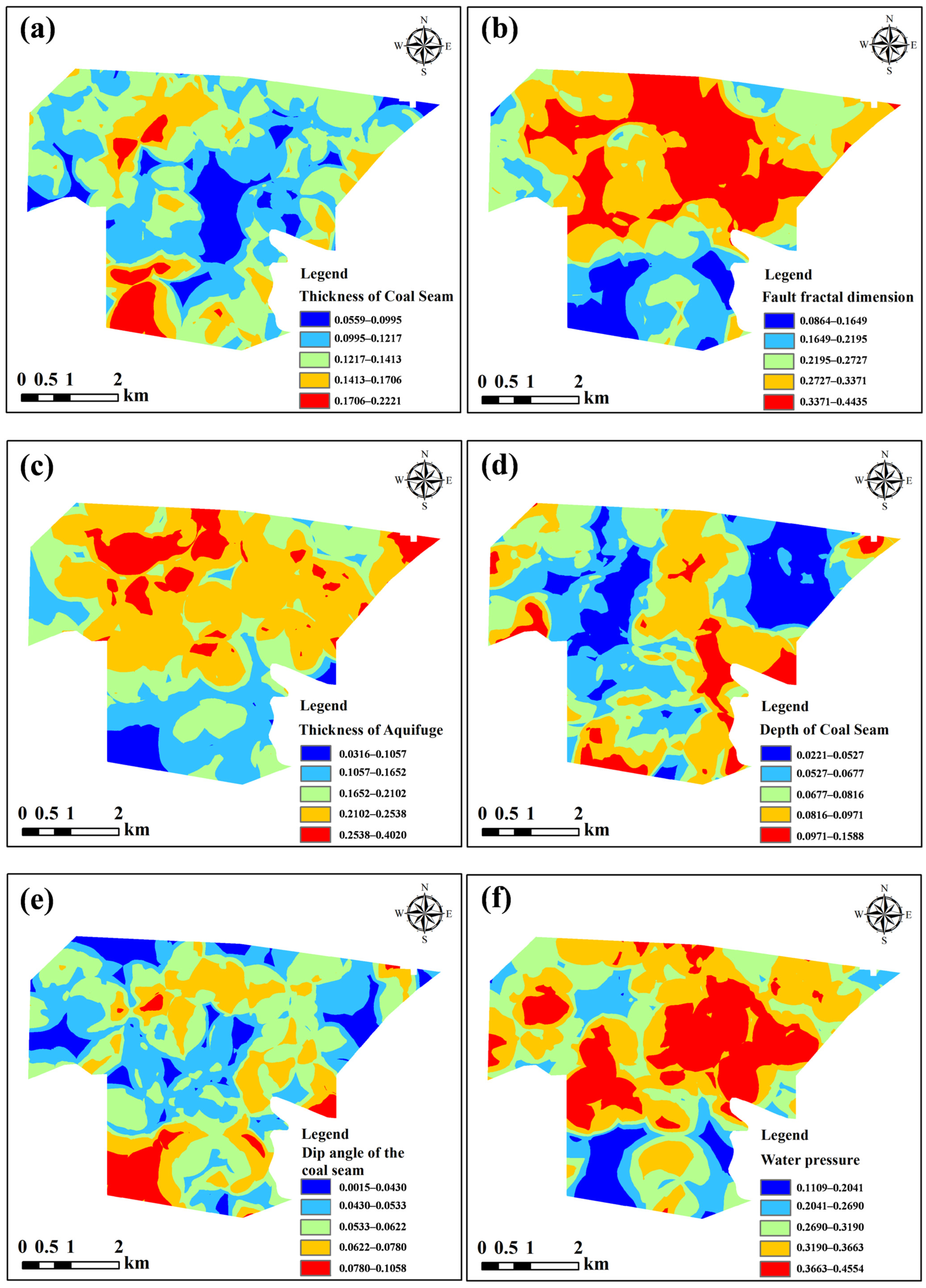
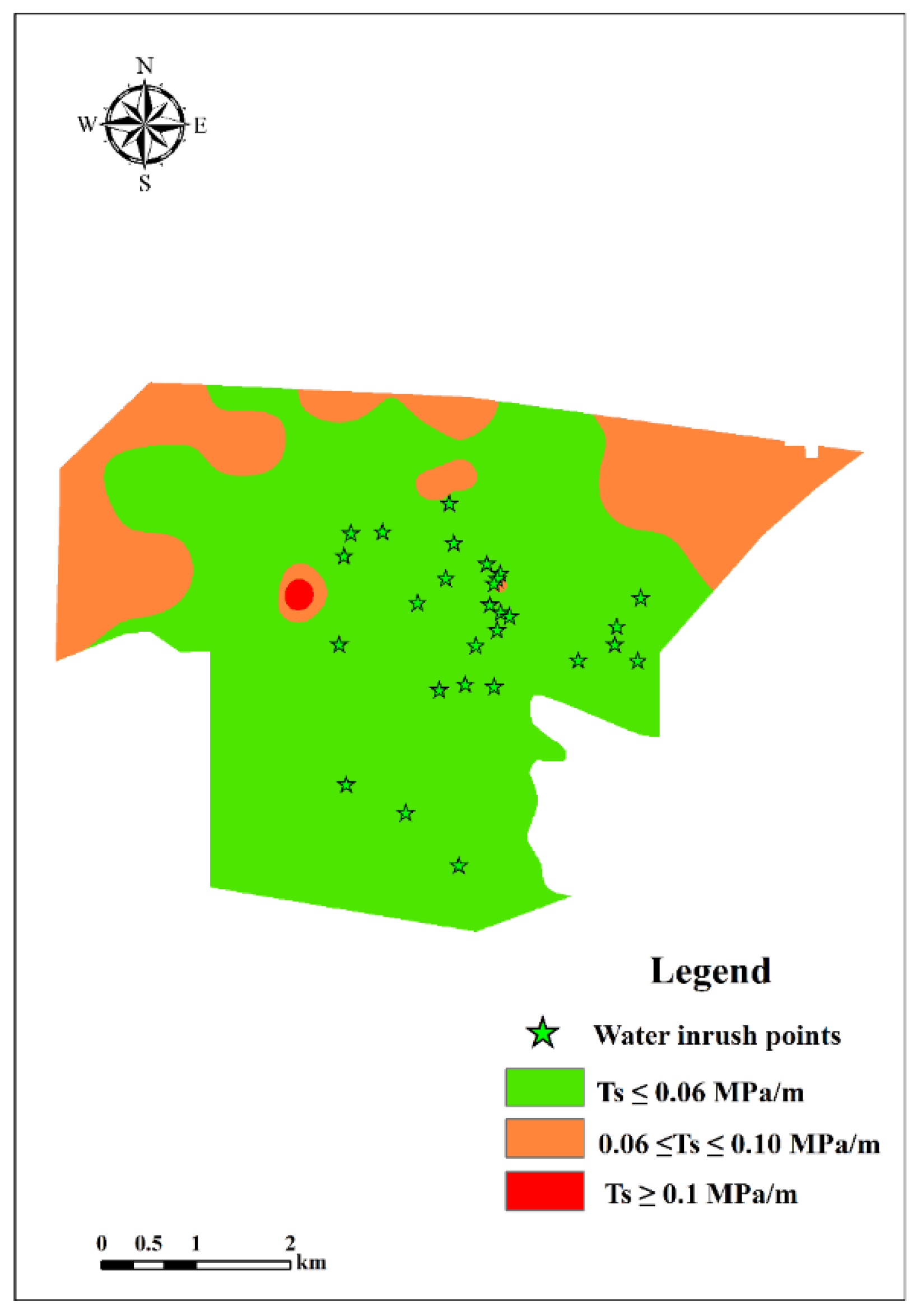
Water pressure: The water pressure acting on the coal seam floor is strongly positively correlated with the risk of water inrush. Higher water pressure not only increases the likelihood of floor water inrush but also enhances the softening effect on the aquiclude, thereby reducing its strength. According to hydrogeological and borehole data, the water level of the Ordovician limestone aquifer in the study area has remained stable at approximately +371 m, and the calculated water pressure at the coal seam floor ranges from 0.348 to 2.947 MPa.

(2)

Coal seam thickness: Greater coal seam thickness leads to more extensive and intense overburden failure induced by mining, which facilitates the formation of water-conducting channels that connect aquifers. In addition, during the extraction of thick seams, the stress distribution borne by the floor becomes more complex, and the manifestation of mining pressure is more pronounced, thereby promoting the further development of fractures in the floor strata and increasing the risk of water inrush. According to borehole data analysis, the thickness of the No. 5 coal seam in the study area ranges from 0.34 to 5.30 m.

(3)

Coal seam burial depth: The risk of floor water inrush increases with greater burial depth. Increased depth directly influences the stress distribution and the height of overburden failure after mining. As burial depth increases, the original rock stress acting on the coal seam floor intensifies, making the floor strata more prone to fracturing and thus creating pathways for water inrush. Borehole data analysis indicates that the burial depth of the No. 5 coal seam in the study area ranges from 182.93 to 584.87 m.

(4)

Coal seam dip angle: The dip angle of the coal seam directly affects the movement pattern and stress distribution of the overburden after mining. Larger dip angles result in more significant gravitational components during mining, leading to asymmetric rock deformation and sliding, as well as an enlarged failure range, thereby increasing the probability of water inrush. Moreover, the dip angle determines the stress difference in mining and water pressure on both sides of the panel, thereby influencing the location of potential water inrush. Borehole data analysis shows that the dip angle of the No. 5 coal seam in the study area ranges from 2.0° to 18.0°.

(5)

Fault fractal dimension: Faults, as geological structures formed by rock rupture under stress and relative displacement, influence floor water inrush primarily in two aspects. First, faults can serve as water-conducting channels, directly connecting aquifers with mining spaces and triggering water inrush. Even when the fault itself has low permeability, secondary fractures generated in its surrounding zones due to stress concentration may form additional water-conducting pathways, thereby indirectly enhancing groundwater migration capacity. Second, the cutting effect of faults can disrupt the continuity of aquicludes, weakening their capacity to withstand aquifer pressure and thus inducing water inrush.

However, prediction models for floor water inrush are often constrained by fault distribution, fault intersections, and fault terminations, making quantitative assessment difficult and reducing prediction accuracy. To address this limitation, this study introduces a Fault Control Index to comprehensively represent multiple fault-related factors. By collecting and analyzing fault data from the Dongjiahe Coal Mine, and applying grey relational analysis, the Fault Control Index is integrated with fault influence factors to derive a comprehensive measure of fault control.

The Fault Control Index (D_s) directly reflects fault density, and its calculation is expressed in Equation (1) [32].

$$Ds=\dim F(r)\underset{i\to 0}{\lim }{\displaystyle \frac{\lg N(r)}{-\lg r}}$$

(1)

where r is the grid division ratio, and N(r) represents the number of grids containing faults.

The calculation formula for the fault influence factor E is given in Equation (2) [32]:

$$E={\displaystyle \frac{1}{S}}{\displaystyle \sum _{i=1}^t{l}_i{h}_i+M (t=\mathrm{1,2,3},\dots , t)}$$

(2)

where E is the fault influence factor; S is the partition area (m²); l_i is the length of fault strike within a unit (m); h_i is the fault throw (m); n is the number of faults within the unit; and M is the normalized value of structural intersections and terminations.

The grey relational analysis method was employed to calculate the correlation among the Fault Control Index (FCI), the fault influence factor, and the water inflow in the Dongjiahe Coal Mine [32]. The calculation formula of the FCI is given in Equation (3):

$$FCI=0.411Ds+0.598E$$

(3)

(6)

Aquiclude thickness: The aquiclude is generally composed of one or more water-resisting strata, which serve to block the hydraulic connection between the aquifer and the coal seam and inhibit fracture development. A greater thickness of the aquiclude prevents mining-induced fractures from penetrating the aquifer, thereby stopping pressurized water from entering the working face and ensuring safe coal extraction. Thus, the thicker the aquiclude, the lower the risk of floor water inrush during coal mining. According to borehole data analysis in the study area, the thickness of the aquiclude underlying the No. 5 coal seam ranges from 8.20 to 77.52 m.

The borehole data were obtained from detailed hydrogeological surveys and mine exploration drilling conducted in the study area. Water pressure was measured using piezometers, while aquiclude thickness, coal seam thickness, and coal seam dip angle were determined through core sampling. The burial depth of the coal seam was calculated based on borehole depth records obtained during drilling. To minimize measurement errors and data uncertainty, the average value of multiple measurements at different depths within each borehole was used for all parameters as shown in

Table 1. Statistical summary of borehole data in the study area.

ID	Borehole	Fault Fractal Dimension	Coal Seam Dip Angle (°)	Water Pressure (MPa)	Aquiclude Thickness (m)	Coal Seam Thickness (m)	Coal Seam Burial Depth (m)
1	36	0.417	6.1	0.30	30.00	3.15	319.47
2	39	0.458	3.2	1.41	47.00	2.59	338.07
3	117	0.412	8.7	0.16	16.00	3.73	298.41
4	118	0.568	10.3	0.34	34.00	4.09	318.34
5	123	0.717	15.4	0.24	24.00	4.03	301.61
6	129	0.717	16.3	0.26	26.00	2.09	250.95
7	131	0.525	4.5	0.93	31.00	3.36	375.18
9	201	0.591	7.3	0.34	34.00	3.84	322.07
10	203	0.462	11.4	0.62	31.00	3.62	363.23
11	204	0.652	14.8	0.20	20.00	1.51	299.24
…	…	…	…	…	…	…	…
…	…	…	…	…	…	…	…
…	…	…	…	…	…	…	…
117	XB52	0.349	5.9	1.91	27.29	3.55	487.15
118	XB53	0.339	13.0	2.07	23.00	2.35	525.15
119	XB54	0.340	10.6	2.28	32.57	2.60	536.45
120	XB55	0.341	15.3	2.28	28.50	3.80	531.95
121	XB56	0.346	14.8	2.19	31.29	3.45	513.75
122	XB57	0.373	13.1	1.99	33.17	3.50	495.15
123	XB58	0.322	7.9	2.41	30.13	3.25	552.05
124	XB59	0.332	9.4	2.33	25.89	2.95	558.00
125	XB60	0.339	10.4	2.10	23.33	2.50	534.05
126	XB61	0.361	11.6	1.64	27.33	0.60	477.85
127	XB62	0.348	6.7	1.92	19.20	2.35	524.90

. In addition, six thematic maps of the main evaluation indicators for floor water inrush risk were generated using the Kriging interpolation method in ArcGIS (10.8) (Figure 4), providing fundamental data support for the subsequent evaluation.

4. Methods

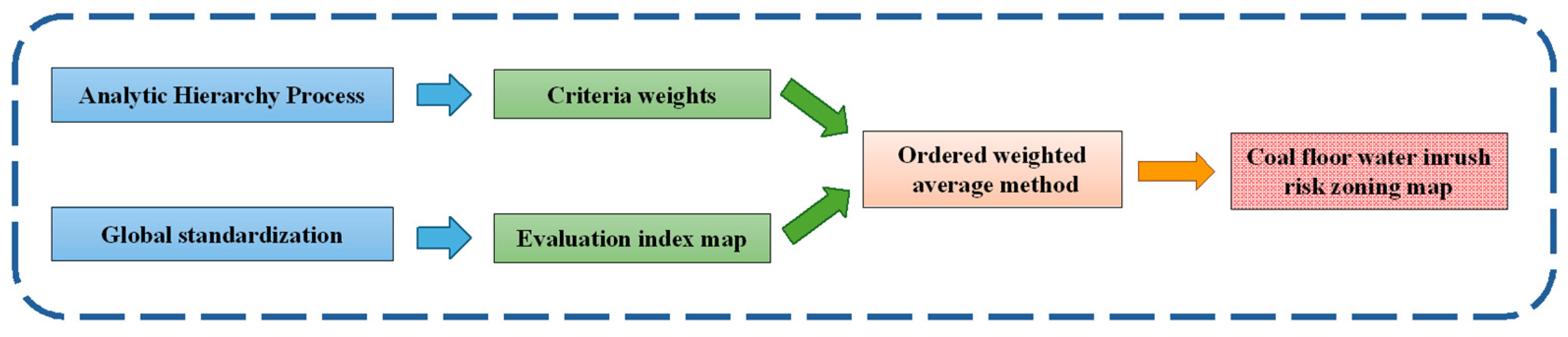
4.1. Global Evaluation Method

The global evaluation method employs the Analytic Hierarchy Process (AHP) to construct a decision-making framework for assessing the floor water inrush risk [12,13,14,15,16,17,18] (Figure 5). In this framework, AHP is used to determine the weights of the evaluation criteria, while the Ordered Weighted Averaging (OWA) method serves as the decision rule, integrating the criterion attribute values with their weights to produce a comprehensive evaluation result.

4.1.1. Analytic Hierarchy Process

The Analytical Hierarchy Process (AHP) is a multi-criteria decision-making method that combines qualitative and quantitative analysis [31]. The principle of AHP is to rank indicators hierarchically, establishing a structure divided into the goal layer, the criteria layer, and the indicator layer. It is a subjective judgment decision-making method that integrates qualitative and quantitative approaches. AHP provides a simple mathematical tool for solving complex, multi-objective, multi-criteria, or unstructured decision problems, particularly in situations where decision outcomes are difficult to measure directly or accurately [32].

Step 1: Select evaluation indicators and construct the hierarchical structure model (Figure 6).

Step 2: Construct the judgment matrix A and perform the consistency test

Using the expert scoring method, the indicators at the same level are compared and evaluated to determine their relative importance. Based on this, the judgment matrix A is constructed (Equation (4)).

$$A={(a_{ij})}_{n\times n}=\left(\begin{array}{ccc}{a}_{11}& \dots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \dots & a_{nn}\end{array}\right)$$

(4)

Step 3: Calculate the maximum eigenvalue (λmax) and the eigenvector of the judgment matrix, then compute the Consistency Index (CI) and the Random Index (RI) for the consistency test (Equation (5)).

$$CR=CI/RI$$

(5)

Only after the consistency test is passed can the weight calculation be performed.

In the equation, CR represents the Consistency Ratio; CI represents the Consistency Index; and RI represents the average Random Consistency Index.

If CR ≥ 0.1, the consistency test of the matrix fails; if CR < 0.1, the matrix passes the consistency test.

Step 4: After the matrix passes the consistency test, normalize the eigenvector to obtain the weights Wai.

4.1.2. Establishment of the Global Evaluation Model

Most existing water inrush risk evaluation methods adopt a global evaluation approach, with the specific calculation steps as follows (Figure 7):

(1)

Global standardization of evaluation indicators

Given the irregularity of water inrush indicators, a global standardization method is applied to eliminate dimensional inconsistencies. Meanwhile, considering that different evaluation indicators have varying degrees of influence on floor water inrush risk, appropriate formulas are selected for processing. When an indicator is positively correlated with the risk of floor water inrush, Formula (6) is applied for standardization; conversely, Formula (7) is used.

$$Y_{ij}={\displaystyle \frac{X_{ij}-\min (X_i)}{\max (X_i)-\min (X_i)}}$$

(6)

$$Y_{ij}={\displaystyle \frac{\max (X_i)-X_{ij}}{\max (X_i)-\min (X_i)}}$$

(7)

where Y_ij is the normalized data, X_ij is the original data, and min (x_ij) and max (x_ij) represent the minimum and maximum quantified values of each primary evaluation indicator, respectively.

(2)

Establishment of the global evaluation model

On the basis of the globally standardized thematic maps of evaluation indicators, and combined with the criterion weights calculated through AHP, a global evaluation model for water inrush risk is established using Formula (8).

$$RI(GA)={\displaystyle \sum _{i=1}^n{w}_i\cdot f(x,y)}$$

(8)

where RI(GA) represents the global water inrush risk coefficient; w_i denotes the weight of each evaluation criterion, which is calculated using the AHP method; n is the number of evaluation criteria; and f(x,y) refers to the dimensionless attribute map of the evaluation criteria.

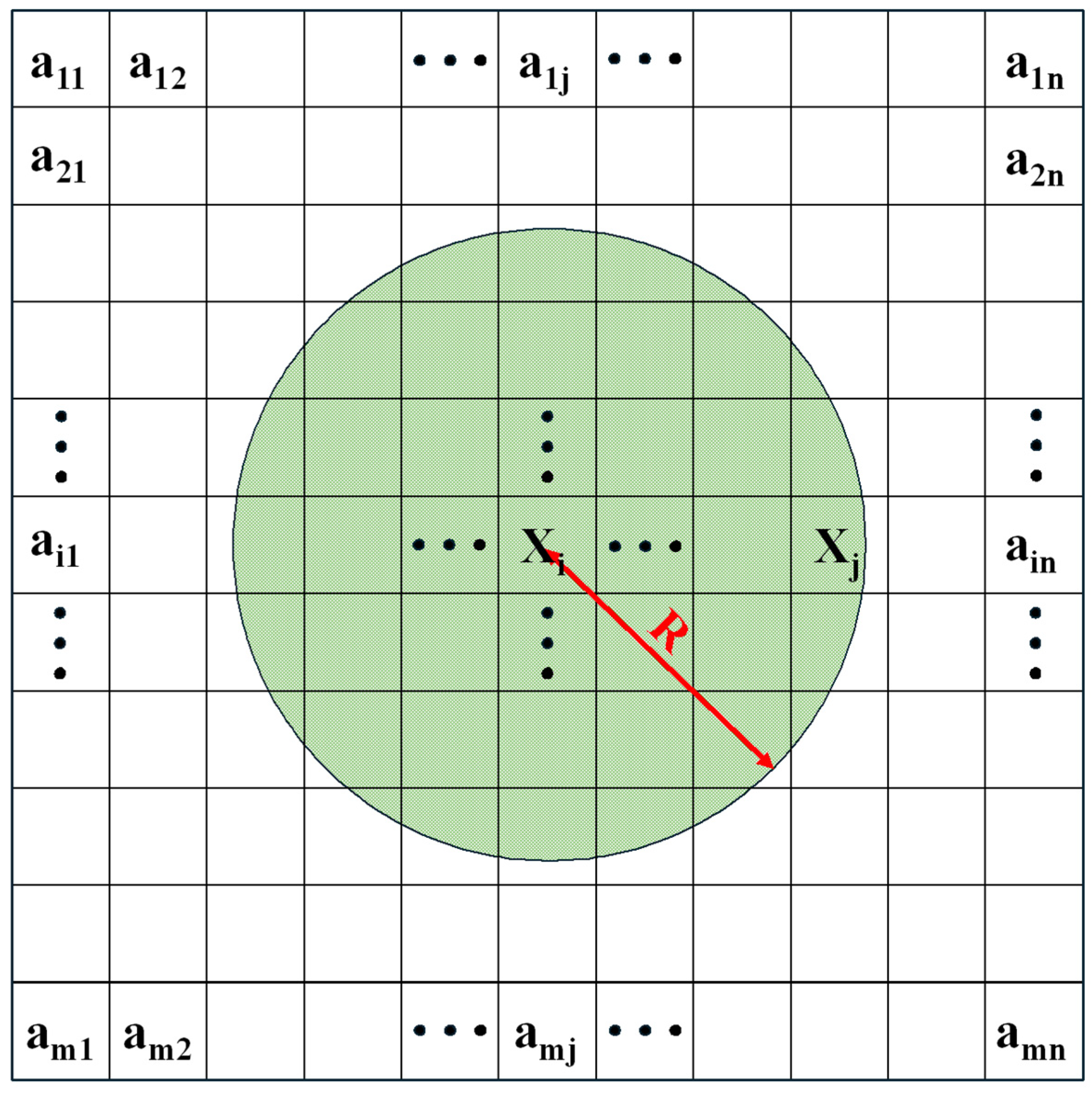
Figure 7 presents the complete flowchart of the global evaluation method.

4.2. Local Evaluation Method

The local evaluation method establishes a decision-making framework for assessing floor water inrush risk by integrating the Monte Carlo Analytic Hierarchy Process (MC-AHP) with local standardization based on a moving window, as shown in Figure 8. In this framework, the Monte Carlo Analytic Hierarchy Process is applied to determine the weights of evaluation criteria, while the moving-window local standardization is used to process the attribute values of evaluation indicators.

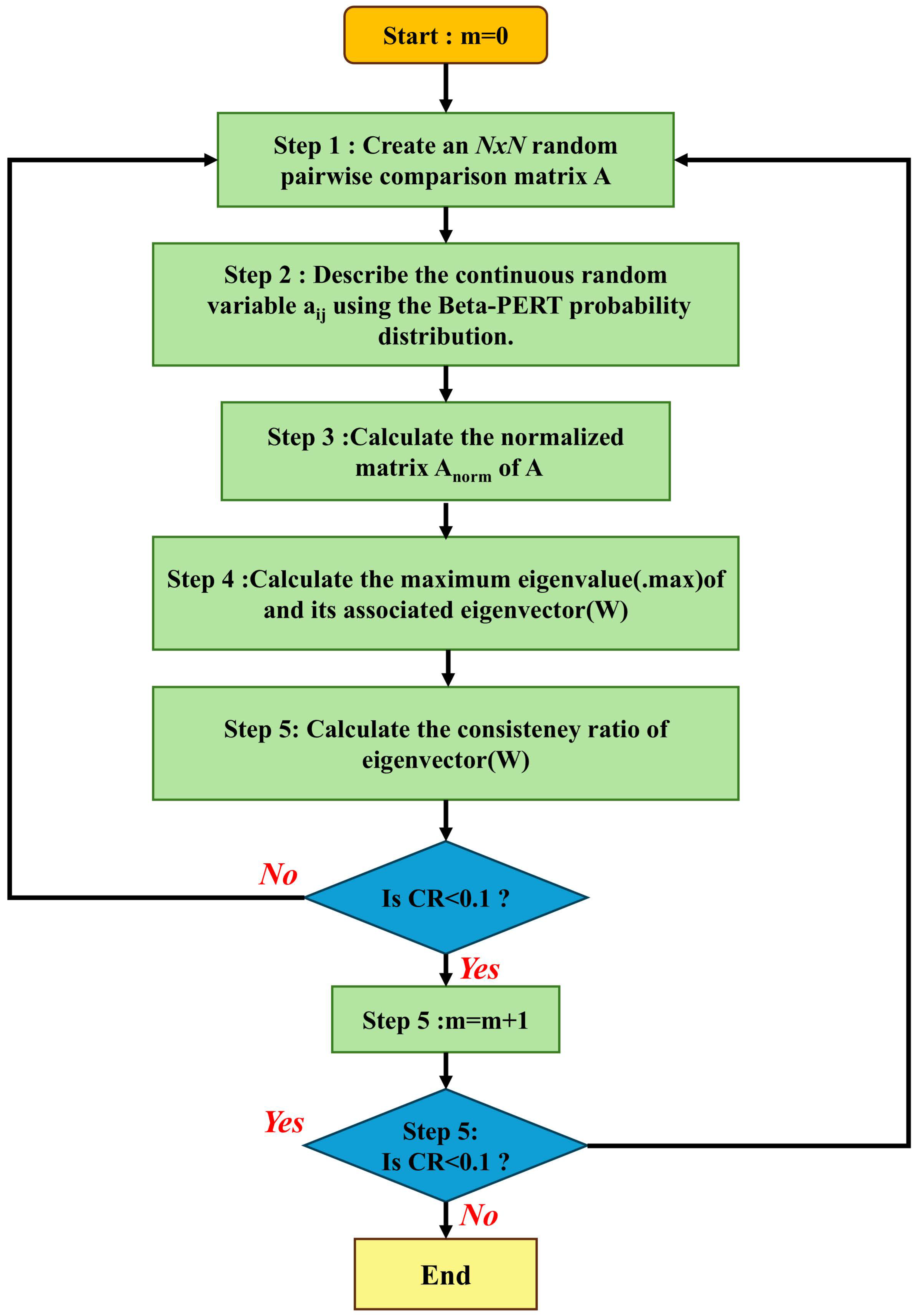
4.2.1. Monte Carlo Analytic Hierarchy Process (MAHP)

The Analytic Hierarchy Process (AHP) is a widely used multi-criteria decision-making method that structures complex problems into an orderly hierarchical framework and evaluates indicator weights by combining qualitative judgments with quantitative analysis. Nevertheless, its practical application is subject to several inherent limitations:

(1)

Strong subjectivity: The outcomes are highly dependent on the knowledge, experience, and preferences of decision-makers. Consequently, different experts may construct substantially different judgment matrices, which reduces the stability and objectivity of the results.

(2)

Strict independence assumption: AHP presumes that all factors are mutually independent. However, in complex real-world problems, interdependence and interactions among factors are common, making this assumption difficult to satisfy.

(3)

Limited capacity to address uncertainty: AHP demonstrates insufficient capability when applied to problems involving fuzzy information or high levels of uncertainty.

To address these shortcomings, this study adopts the Monte Carlo Analytic Hierarchy Process (MAHP) for calculating indicator weights. By integrating Monte Carlo simulation with AHP, this method employs probability distributions to characterize the variability of elements in the pairwise comparison matrix and leverages simulation techniques to further examine the uncertainty associated with criterion weights. In doing so, it enhances both the robustness and the reliability of the evaluation results.

The specific calculation steps for determining the weights of evaluation criteria using the Monte Carlo Analytic Hierarchy Process (MC-AHP) are as follows (Figure 9):

Step 1 (Generation of random judgment matrix):

Random sampling is used to generate an N × N judgment matrix A, where each element a_ij represents a pairwise comparison between decision criteria and is treated as a continuous random variable.

$$A=[a_{ij}] i,j=1,2,\dots ,n$$

(9)

Step 2 (Probabilistic description of expert judgment):

In general, the Beta-PERT probability distribution is used to characterize the continuous random variable a_ij. As a special form of the Beta distribution, it requires only the minimum value, the most likely value, and the maximum value of the variable to determine the distribution. This feature reduces data requirements while allowing the distribution to approximate uniform, normal, and other common forms, making it highly suitable for describing expert opinions in decision-making.

The probability density function of the Beta-PERT distribution is:

$$f(x)=\{\begin{array}{c}{\displaystyle \frac{x^{a-1}{(1-x)}^{b-1}}{B(v,w)}} 0\le x\le 1; v,w>0\\ 0 \mathrm{else}\end{array}$$

(10)

where B(a,b) is the standard Beta function, expressed as follows:

$$B(a,b)={\displaystyle \frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}}$$

(11)

where Γ(a) is the Gamma function, which is expressed as follows:

$$\Gamma (a)={\displaystyle {\int }_0^{\propto }{t}^{q-1}{e}^{-t}dt}$$

(12)

By substituting Equation (12) into Equation (11), the following Beta function is obtained:

$$B(a,b)={\displaystyle \underset{0}{\overset{1}{\int }}{t}^{a-1}(1-t)b^{-1}dt}$$

(13)

The calculation formulas for the parameters a and b in Equation (13) are as follows:

$$\mathrm{a}=\left[{\displaystyle \frac{x_{\mathrm{mean}}-x_{\min }}{x_{\max }-x_{\min }}}\right]\left[{\displaystyle \frac{2x_{\mathrm{mode}}-x_{\min }-x_{\max }}{x_{\mathrm{mode}}-x_{\mathrm{mean}}}}\right]$$

(14)

$$b=a\left[{\displaystyle \frac{x_{\max }-x_{\mathrm{mean}}}{x_{\max }-x_{\min }}}\right]$$

(15)

$$x_{\mathrm{mean}}={\displaystyle \frac{x_{\min }+4x_{\mathrm{mode}}+x_{\max }}{6}}$$

(16)

where x_min, x_max, x_mode, x_mean represent the minimum value, maximum value, most likely value, and mean value, respectively.

Step 3 (Matrix normalization):

Normalize the judgment matrix A to obtain the normalized matrix A_norm.

The elements $\overline{a_{ij}}$ of the normalized matrix A_norm are calculated as follows:

$$\overline{a_{ij}}=a_{ij}/{\displaystyle \sum _{i=1}^n{a}_{ij}} i,j=1,2,\dots ,n$$

(17)

Step 4 (Preliminary weight calculation):

Solve for the maximum eigenvalue λ_max of the normalized matrix A_norm and its corresponding eigenvector W. The eigenvector W serves as the preliminary estimate of the indicator weights.

$$A_{\mathrm{norm}}W={\lambda }_{\max }W$$

(18)

$$\overline{a_{ij}}=a_{ij}/{\displaystyle \sum _{i=1}^n{a}_{ij}} i,j=1,2,\dots ,n$$

(19)

$$w_i={\displaystyle \frac{{\displaystyle \sum _{j=1}^n\stackrel{-}{a_{ij}}}}{{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n\stackrel{-}{a_{ij}}}}} i,j=1,2,\dots ,n$$

(20)

Step 5 (Consistency check):

Verify the rationality of the matrix using the Consistency Ratio (CR).

The calculation formula of the Consistency Ratio (CR) is as follows:

$$CR={\displaystyle \frac{CI}{RI}}$$

(21)

where RI (random index) represents the average random consistency index, and CI (consistency index) denotes the consistency index, which is calculated as follows:

$$CI={\displaystyle \frac{{\lambda }_{\max }-n}{n-1}}$$

(22)

If CR ≥ 0.1, the current matrix is discarded and regenerated; if CR < 0.1, the weight vector corresponding to the matrix is retained.

Step 6 (Simulation iteration and weight determination):

Repeat Steps 1–4 to collect all valid weight vectors. By applying statistical analysis (e.g., mean and standard deviation), the final weights of each indicator are determined. This process transforms the weights from a single deterministic value into a probability distribution, thereby enhancing the robustness of the results.

4.2.2. Establishment of Local Evaluation Model

The global evaluation method takes the entire assessment area, such as a mining field or coal district, as the object of study. It conducts comprehensive assessments based on a unified indicator system and fixed weights. However, it has several notable limitations:

(1)

Neglect of local heterogeneity, leading to imprecise risk localization. In actual mines, local geological features—such as minor faults, fracture zones, abrupt changes in aquiclude thickness, and abnormal water pressure areas—are often the key triggers of floor water inrush. Within a global evaluation framework, these local factors are likely to be downplayed or overlooked, resulting in misidentification of water inrush points.

(2)

Fixed indicator weights with poor adaptability. The global evaluation method generally adopts uniform indicator weights, which may reflect regional-scale patterns but fail to capture the dominant factors specific to different sub-areas, thereby reducing adaptability.

(3)

Insufficient use of small-scale data, limiting evaluation accuracy. Global evaluation relies heavily on macro-scale regional data (e.g., average aquiclude thickness or overall water pressure distribution) but has weak integration of micro-scale data such as borehole-revealed local aquiclude discontinuities. Yet, such micro-scale information is often the direct controlling factor of localized water inrush. Ignoring it diminishes the model’s sensitivity to micro-level risks and constrains the precision of the evaluation.

Step 1: Local standardization of evaluation indicators

This study applies the circular moving-window method to perform local standardization of the evaluation indicator maps, with the calculation principle illustrated in Figure 10. The window serves as the core mechanism for defining the spatial extent of local analysis. Specifically, a circular region is constructed with the target pixel as its center, and all pixels falling within this window are included as the objects of analysis. Subsequent calculations are then conducted on these pixels.

In spatial multi-criteria decision analysis, the most commonly used attribute standardization technique is the range transformation method. When an evaluation indicator is positively correlated with the risk of floor water inrush, Formula (23) is applied for standardization; conversely, when negatively correlated, Formula (24) is applied [33,34].

$$f(x_{ij})={\displaystyle \frac{x_{ij}-\underset{Q}{\min \left\{x_{ij}\right\}}}{r_j}}$$

(23)

$$f(x_{ij})={\displaystyle \frac{\underset{Q}{\max \left\{x_{ij}\right\}}-x_{ij}}{r_j}}$$

(24)

$$r_j=\underset{Q}{\max (x_{ij})}-\underset{Q}{\min (x_{ij})}$$

(25)

In Formulas (23) and (24), x_ij represents the attribute value at the focal pixel; $\underset{Q}{\min \left\{x_{ij}\right\}}$ and $\underset{Q}{\max \left\{x_{ij}\right\}}$ denote the local minimum and maximum values within the window Q, respectively; and r_j refers to the attribute value range within the circular window.

Step 2: Local weighting of evaluation factors

The relative importance of evaluation indicators varies across different parts of the study area. Once the size of the local region is defined, the local weights of the evaluation criteria are calculated using Formula (26).

$$w_j^q={\displaystyle \frac{\frac{w_j{r}_j^q}{r_j}}{{\displaystyle \sum _{i=1}^n\frac{w_j{r}_j^q}{r_j}}}}, 0\le w_j^q\le 1, {\displaystyle \sum _{j=1}^n{w}_j^q=1, }{\displaystyle \sum _{i=1}^n{w}_j^q=1, }$$

(26)

In Equation (26), w_j^q represents the local weight of the evaluation indicator; w_j denotes the global weight of the evaluation criterion obtained from the MAHP calculation; r_j is the global attribute value range of the criterion; and r_j^q is the local attribute value range.

Step 3: Establishment of the local evaluation model for water inrush risk

Based on the locally standardized thematic maps of evaluation indicators and the thematic maps of local indicator weights, a local evaluation model for water inrush risk is constructed, as expressed in Formula (27).

$$RI(LC)={\displaystyle \sum _{i=1}^{n}w(x,y)\cdot f(x,y)}$$

(27)

In Equation (27), w(x,y) denotes the thematic layer of local weights of the evaluation factors, and f(x,y) represents the dimensionless attribute map of the evaluation criteria after local standardization.

Figure 11 presents the flowchart of the local evaluation method.

5. Evaluation Results of Water Inrush Hazard

5.1. Global Evaluation Result

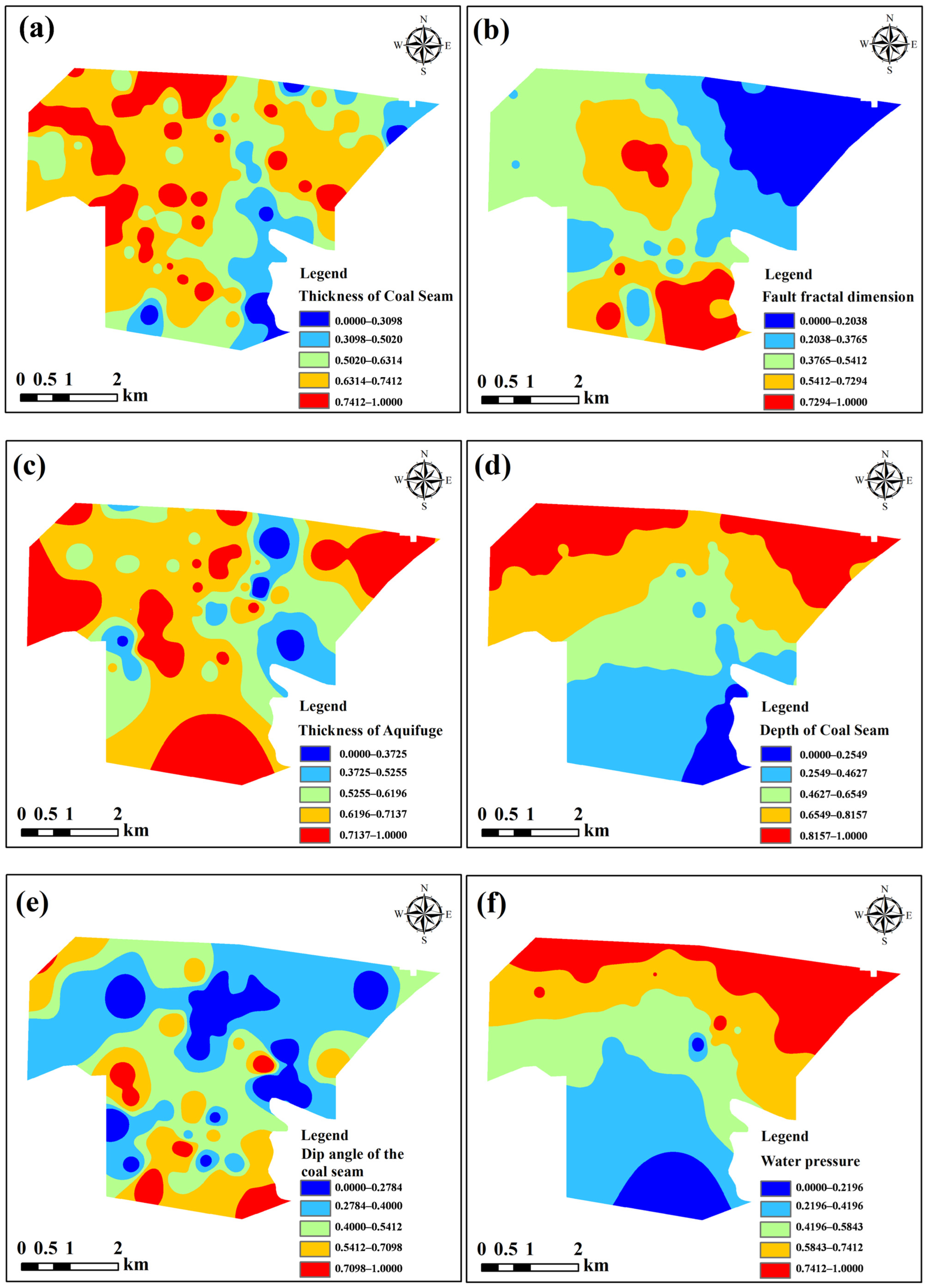
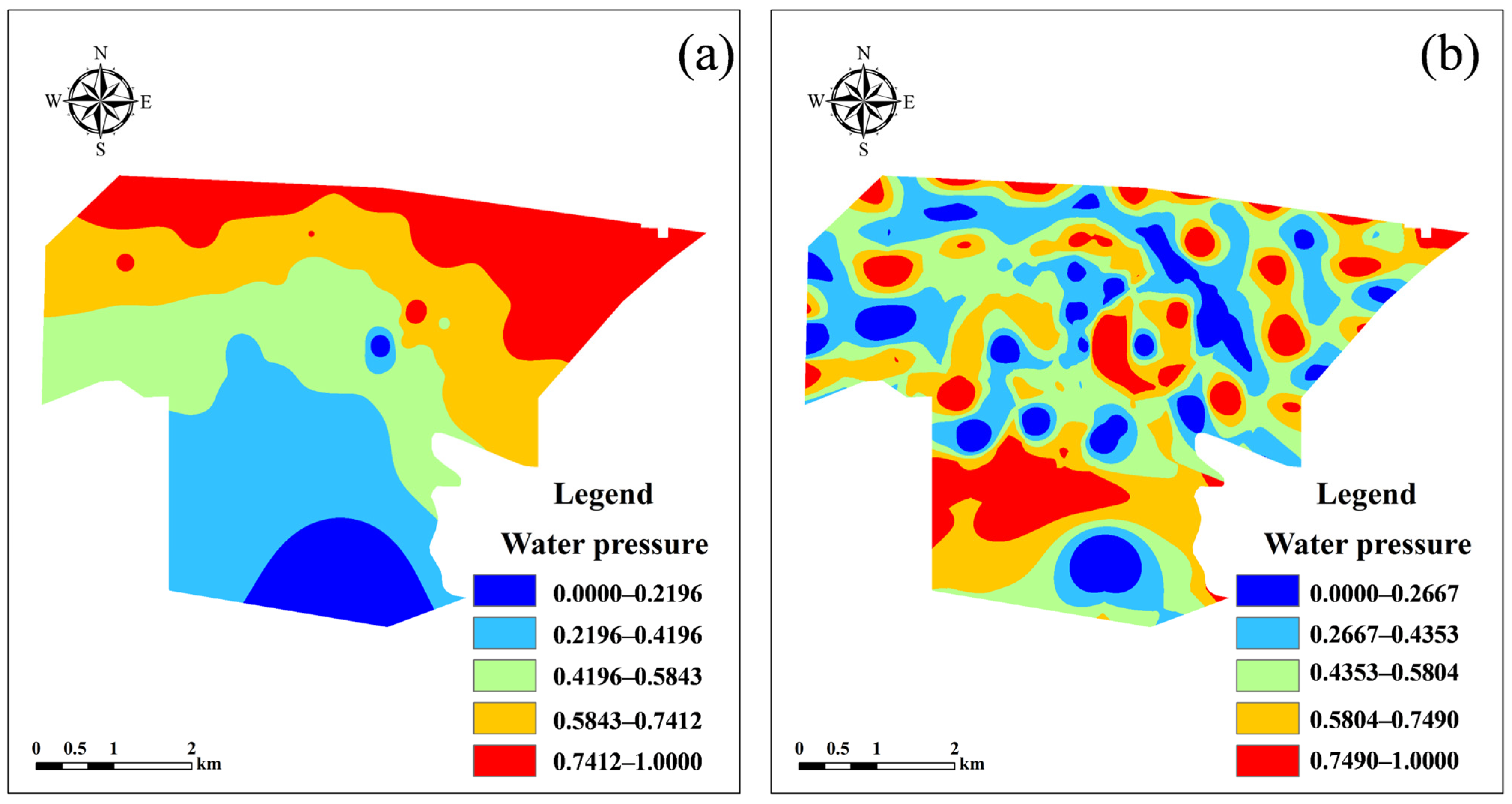
5.1.1. The Overall Standardized Result of the Evaluation Indicators

The evaluation indicators were analyzed as follows: coal seam thickness, coal seam dip angle, coal seam burial depth, fault control dimension, and water pressure are positively correlated with the risk of floor water inrush, and thus were standardized using Formula (6). In contrast, aquiclude thickness is negatively correlated with the risk of floor water inrush and was therefore standardized using Formula (7). The dimensionless maps of locally standardized evaluation indicators were generated in ArcGIS (10.8), as shown in Figure 12.

5.1.2. Global Weight of Evaluation Indicators

According to the above steps of the Analytic Hierarchy Process (AHP), a hierarchical analysis model for water inrush risk assessment of the Dongjiahe Coal Mine was established, and the following matrix was generated.

$$TA=\left[\begin{array}{llllll}0.0000\hfill & 1.6949\hfill & 1.7501\hfill & 0.1212\hfill & 1.5186\hfill & 1.7131\hfill \\ 0.5900\hfill & 1.0000\hfill & 1.0553\hfill & 0.1118\hfill & 0.8502\hfill & 1.0182\hfill \\ 0.5714\hfill & 0.9476\hfill & 1.0000\hfill & 0.1111\hfill & 0.8120\hfill & 0.9643\hfill \\ 8.2499\hfill & 8.9447\hfill & 9.0000\hfill & 1.0000\hfill & 8.7685\hfill & 8.9630\hfill \\ 0.6585\hfill & 1.1762\hfill & 1.2315\hfill & 0.1140\hfill & 1.0000\hfill & 1.1945\hfill \\ 0.5837\hfill & 0.9821\hfill & 1.0370\hfill & 0.1116\hfill & 0.8372\hfill & 1.0000\hfill \end{array}\right]$$

(28)

All matrices passed the consistency test, with the maximum eigenvalue of matrix TA being λmax = 6.0238, and CR = 0.0038.

The weights corresponding to the indicators at each hierarchical level were then calculated, and the weight ranking of these indicators was obtained. Finally, the overall weights of each indicator with respect to the total objective were derived (

Table 2. Results of weight calculation using AHP.

Indicators	Aquiclude Thickness	Coal Seam Thickness	Fault Control Index	Burial Depth	Dip Angle	Water Pressure
Wai	0.10237	0.064401	0.061851	0.63466	0.073174	0.063541

).

5.1.3. Global Evaluation Model

(1)

Establishment of the evaluation model

Based on the evaluation factor weights calculated using AHP, a global model for roof water inrush risk assessment was established, as shown in Equation (29).

$$\begin{array}{ll}RI(GA)=& 0.064401f_1(x,y)+0.061851f_2(x,y)+0.10237f_3(x,y)+0.63466f_4(x,y)+\\ & 0.073174f_5(x,y)+0.063541f_6(x,y)\end{array}$$

(29)

In Equation (29), RI denotes the water inrush risk index, and f(x,y) represents the dimensionless maps of the evaluation factors.

(2)

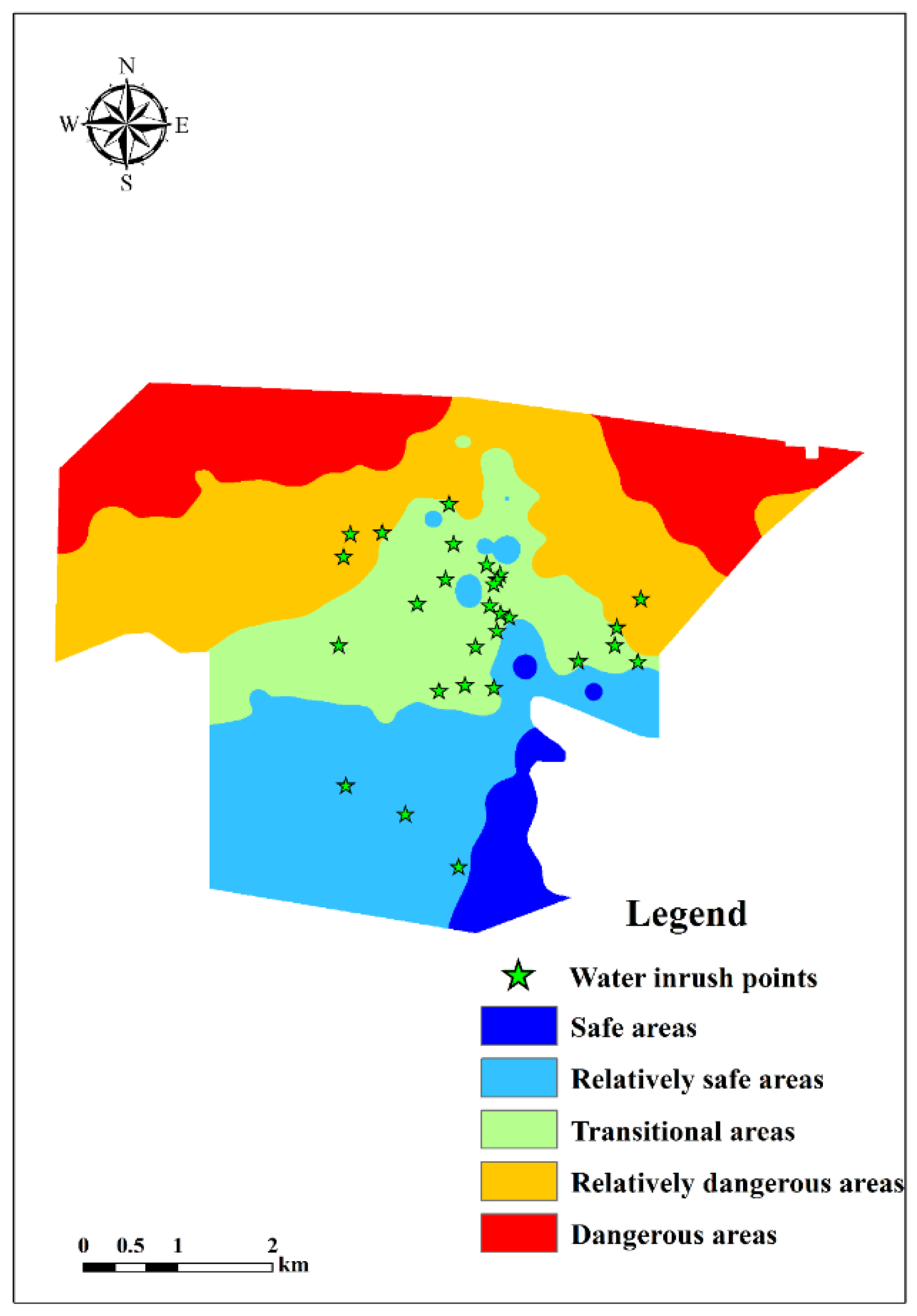
Evaluation results of floor water inrush risk

Based on the dimensionless indicator maps obtained in Section 5.1.1 and the global evaluation mathematical model established in Section 5.1.3, the six thematic maps of evaluation indicators were integrated in ArcGIS (10.8) to generate a zoning map of water inrush risk under the global evaluation model, as shown in Figure 13. Using the natural breaks method in ArcGIS (10.8), the risk zoning map was classified into five categories: Safe areas, Relatively safe areas, Transitional areas, Relatively dangerous areas, and Dangerous areas.

5.1.4. Model Validation

The evaluation results indicate that the southern part of the study area is predominantly characterized by safe and relatively safe zones, whereas the northern part is mainly composed of dangerous and relatively dangerous zones. Within the transitional belt, several relatively safe zones are scattered. As presented in

Table 3. Statistics of water inrush point identification under the global evaluation model.

	Risk Zones	Safe Areas	Relatively Safe Areas	Transitional Areas	Relatively Dangerous Areas
Water Inrush Points
Number of Water Inrush Points (n)		0	3	19	6
Proportion (%)		0	10.7	67.9	21.4

, among the 28 documented water inrush points in the Dongjiahe Coal Mine, only six are located within relatively dangerous zones, and none occur in the dangerous zones. The proportion of inrush points falling within the relatively dangerous and dangerous zones accounts for merely 21.4%. These findings suggest that the global evaluation method provides an inaccurate delineation of water inrush risk zones and fails to align well with the actual spatial distribution of water inrush events.

5.2. Local Evaluation Results

5.2.1. Local Standardization of Evaluation Indicators

In this study, three local standardization radii—100 m, 500 m, and 900 m—were selected to perform indicator standardization and weight calculation, and a reasonable radius was determined based on the final results. Among the factors, coal seam thickness, coal seam dip angle, coal seam burial depth, fault control dimension, and water pressure are positively correlated with the risk of floor water inrush and were therefore standardized using Formula (23). In contrast, aquiclude thickness is negatively correlated with the risk of floor water inrush and was standardized using Formula (24). The dimensionless maps of locally standardized evaluation indicators were generated in ArcGIS (10.8) (taking the evaluation model with a circular radius of 500 m as an example), as shown in Figure 14.

5.2.2. Local Weight of Evaluation Indicators

The traditional Analytic Hierarchy Process (AHP) has notable limitations in determining the relative importance of evaluation criteria. Since it relies on experts’ subjective judgments, discrepancies often arise due to differences in knowledge background, practical experience, and understanding of geological conditions among experts. Such divergences in ranking the same set of criteria essentially reflect the fuzziness of subjective judgment, resulting in significant randomness in the final weight values and limiting their ability to objectively capture the true influence of evaluation criteria in water inrush risk assessment.

To overcome these shortcomings, this study introduces the Monte Carlo Analytic Hierarchy Process (MC-AHP) for probabilistic treatment. By constructing probability density functions to describe the relative importance of criteria, the method extends a single judgment matrix into random matrices that follow specified probability distributions. During computation, Monte Carlo simulation is used to perform large-scale random sampling of these distributions, generating multiple judgment matrices consistent with the distribution characteristics. The weights corresponding to each matrix are then calculated, and statistical analysis is applied to obtain the probability distribution characteristics of each criterion’s weight.

This approach not only addresses the randomness and uncertainty inherent in weight determination but, more importantly, provides the relative importance ranking of water inrush evaluation criteria in a probabilistic sense. Unlike traditional AHP results that depend heavily on the subjective judgment of individual experts, the ranking derived from MC-AHP is grounded in statistical regularities, offering a more robust and reliable basis for weight determination in floor water inrush risk evaluation.

Using the local weights of each evaluation indicator obtained through MAHP in ArcGIS (10.8), weight distribution maps were generated. Taking the evaluation model with a circular radius of 500 m as an example, the results are shown in Figure 15.

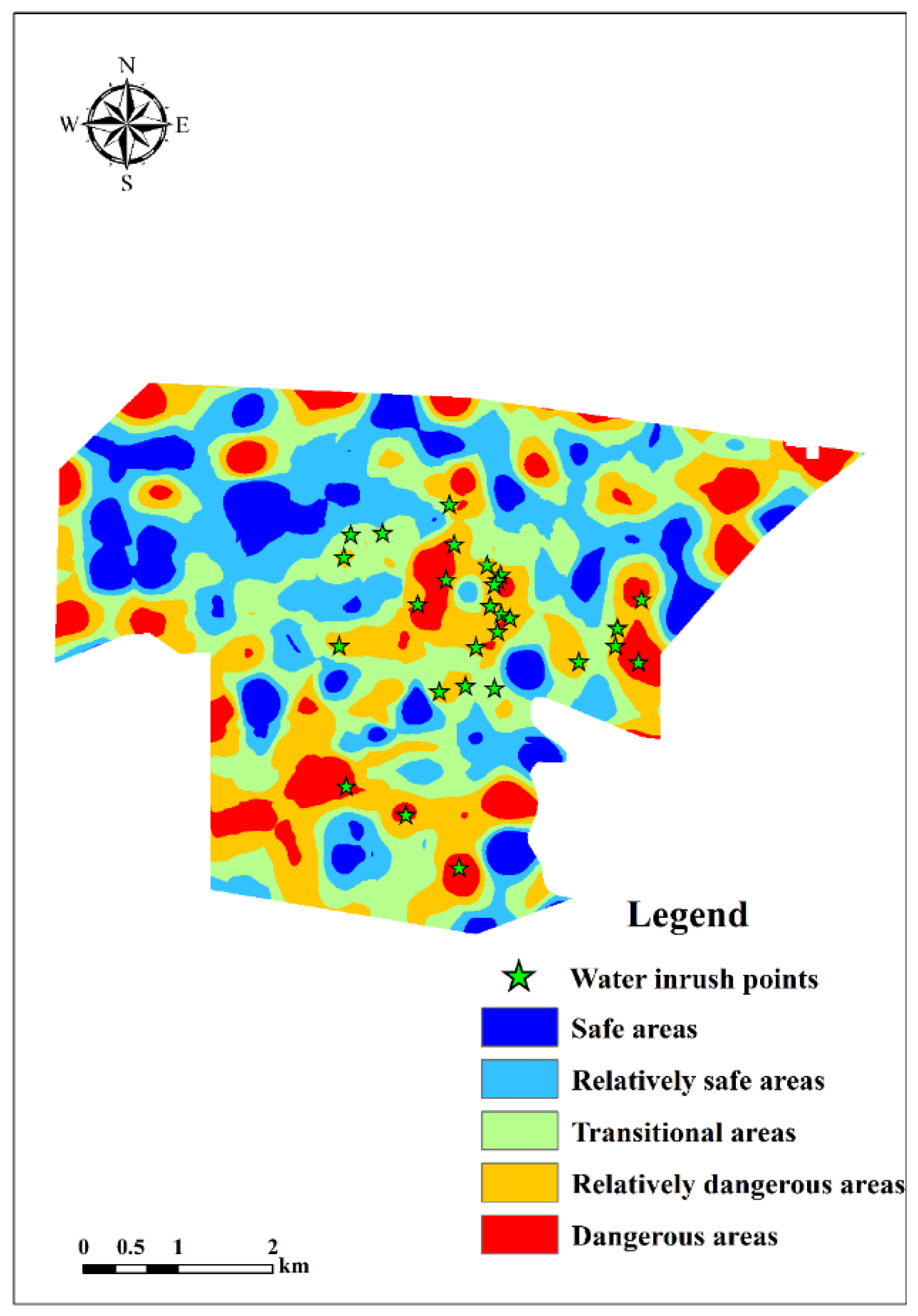
5.2.3. Local Evaluation Model

According to the local risk evaluation mathematical method described in Section 4.2.2, the dimensionless maps of locally standardized evaluation indicators obtained in Section 5.2.1 were integrated with their corresponding weight distribution layers in ArcGIS (10.8). This process generated zoning maps of floor water inrush risk with local standardization radii of 100 m, 500 m, and 900 m, as shown in Figure 16. Similarly, the natural breaks method in ArcGIS (10.8) was applied to classify the risk zoning maps into five categories: Safe areas, Relatively safe areas, Transitional areas, Relatively dangerous areas, and Dangerous areas.

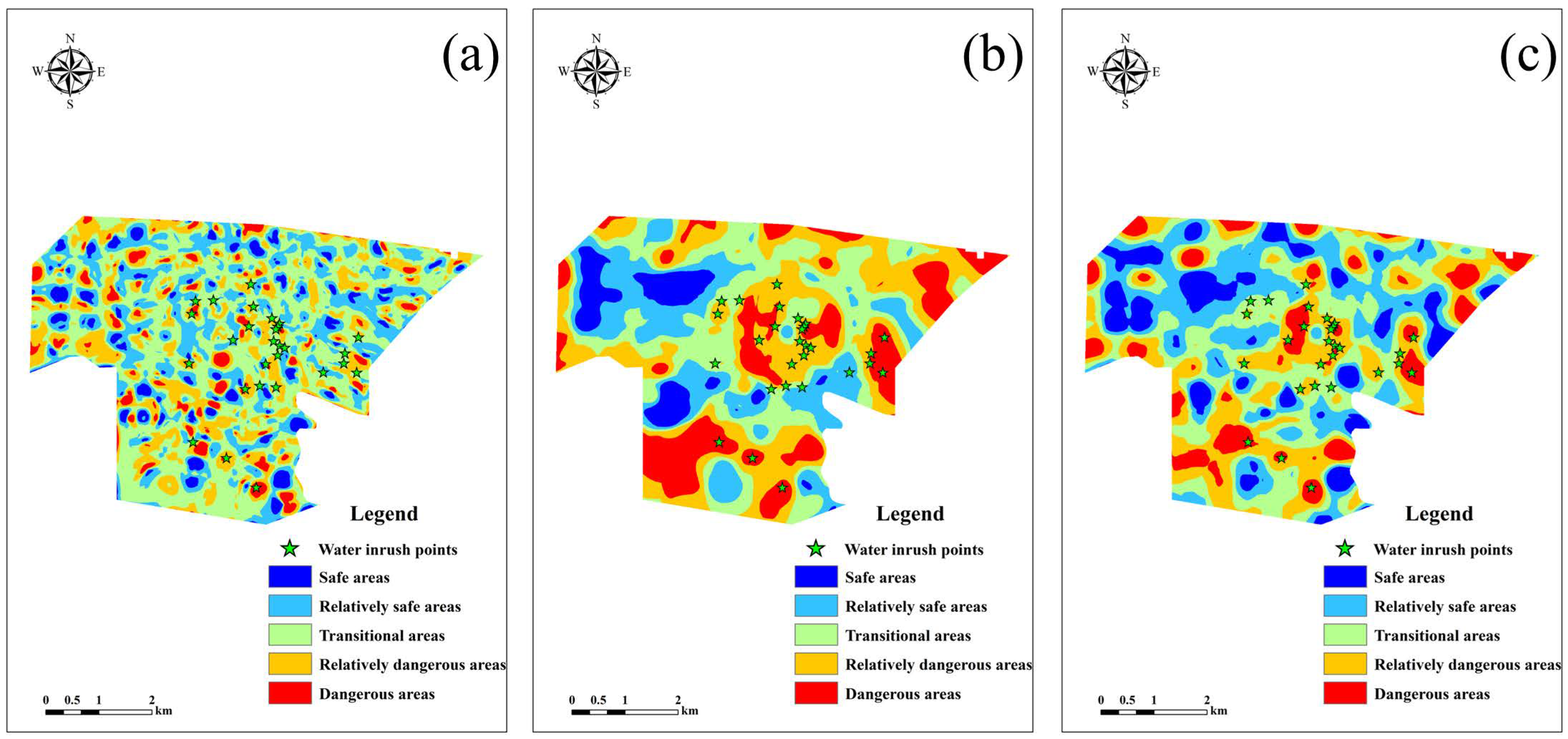
5.2.4. Model Verification

The combined MAHP (Monte Carlo Analytic Hierarchy Process) and moving-window approach proposed in this study demonstrates a higher level of refinement in the delineation of hazardous zones. Taking the 500 m local standardization radius as an example, validation using 28 known water inrush points shows that 25 points are accurately located within the delineated dangerous zones, while only three fall within the transitional zones. The proportion of inrush points falling within the dangerous and relatively dangerous zones reaches 89.3%.(

Table 4. Statistics of water inrush point identification under the local evaluation model (radius = 500 m).

	Risk Zones	Safe Areas	Relatively Safe Areas	Transitional Areas	Relatively Dangerous Areas
Water Inrush Points
Number of Water Inrush Points (n)		0	0	3	18
Proportion (%)		0	0	10.7	54.3

) This indicates that the proposed method not only significantly improves the accuracy of water inrush point identification but also, through localized analysis with the moving window, greatly refines the boundaries and extent of hazardous zones—effectively avoiding the excessive enlargement of dangerous areas common in traditional global evaluations and ensuring that the spatial distribution of high-risk zones is more consistent with actual geological conditions.

6. Discussion

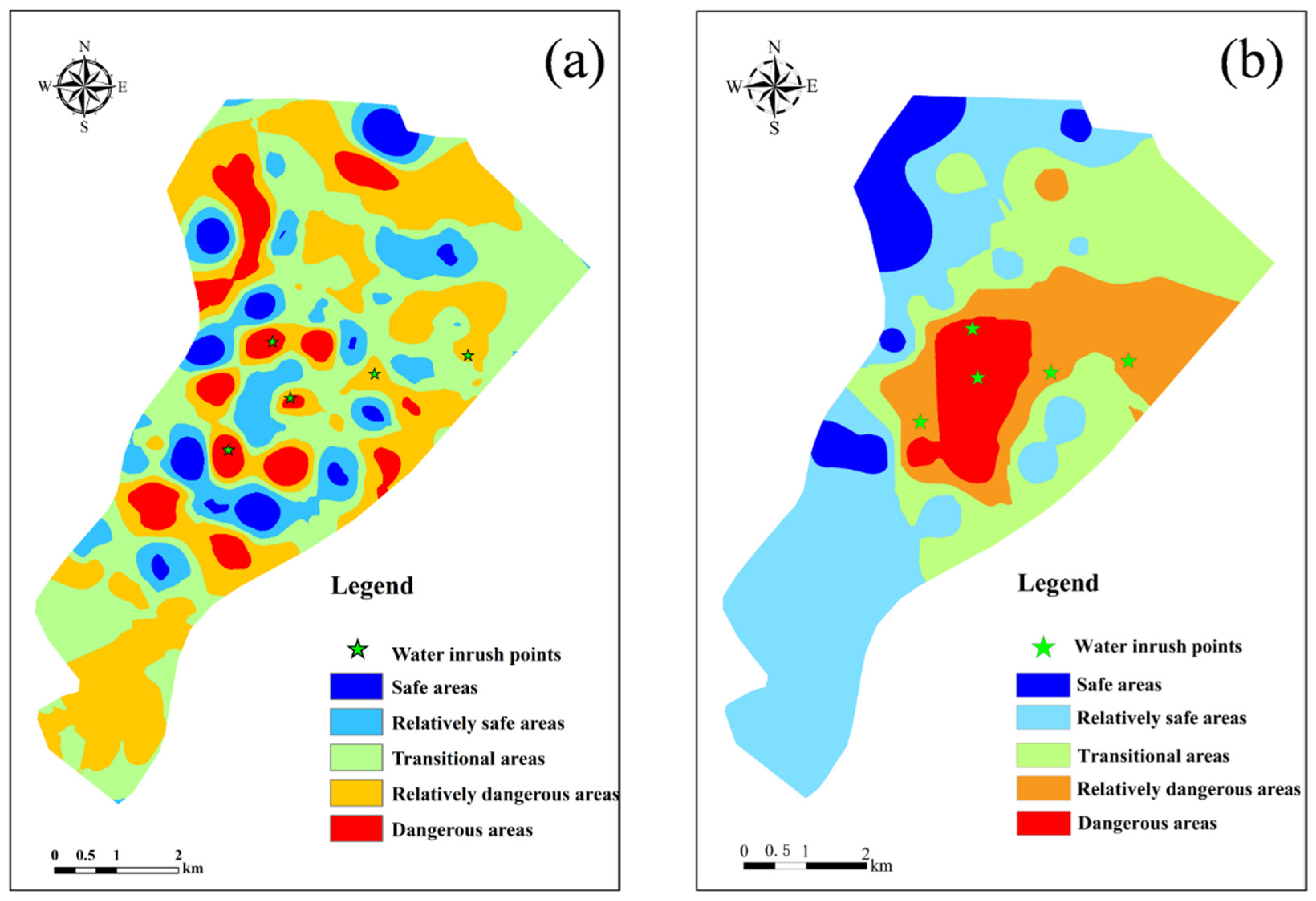
6.1. Comparison of the Spatial Distribution Characteristics of Standardized Attribute Values at the Local and Global Levels

To better illustrate the differences between local and global standardization, aquifer water pressure was selected as an example to demonstrate the spatial pattern variations in attribute values under global standardization and local standardization (using a 500 m radius as an example), as shown in Figure 17.

The spatial distribution patterns of water pressure under global and local standardization exhibit distinct differences.

Under the global standardization scheme, water pressure shows a relatively simple and ordered gradient: high values (red zones) are mainly concentrated in the northern part of the study area, whereas low values (blue zones) are distributed in the central and southern regions. The water pressure increases gradually from south to north, forming a continuous gradient. This reflects the integrative nature of global standardization, which applies a unified reference across the entire study area. By simplifying relative differences, it highlights the macroscopic spatial trend, with high and low values forming large, cohesive clusters. While this emphasizes overall distribution patterns, it diminishes the representation of local details.

In contrast, the spatial pattern under local standardization is more complex and fragmented. High- and low-pressure zones appear in an interwoven manner, discarding the clear macroscopic gradient and instead scattering across the study area in a more irregular and random fashion. Essentially, local statistics break the global spatial dependence by using micro-scale spatial units as the basis of analysis, thereby capturing local variations with greater precision. Local standardization accentuates subtle differences at small scales, fully revealing intra-regional variations and providing a more accurate reflection of spatial heterogeneity in potential water inrush risks.

6.2. Comparison of the Spatial Distribution Characteristics of the Weights of Local and Global Evaluation Criteria

In terms of weight assignment, the traditional global evaluation model exhibits pronounced spatial uniformity. Each evaluation criterion is assigned a fixed, constant weight that does not vary with spatial location. For example, aquifer water pressure is assigned a weight of 0.322, which is applied indiscriminately across all spatial units of the study area. Regardless of whether water pressure exerts a strong or weak influence on local water inrush risk, its contribution remains unchanged. This approach emphasizes the average importance of the criterion at the regional scale but fails to capture the specific relationships between criterion attributes and water inrush risk in different sub-areas. As a result, local risks may be either exaggerated or underestimated, leading to evaluation outcomes that deviate from actual conditions.

In contrast, the local evaluation model produces weight distributions with distinct spatial dynamics. Taking aquifer water pressure as an example, its weight ranges from 0.111 to 0.455. In areas of high water pressure, the destructive effect of pressurized water on the aquiclude becomes more pronounced, resulting in a higher weight that highlights its dominant contribution to local water inrush risk. Conversely, in areas of lower water pressure, its weight decreases, and other factors—such as aquiclude thickness and coal seam burial depth—play a more significant role in controlling water inrush risk.

This dynamic adjustment stems from the local model’s mechanism of redistributing weights based on the relative strength of criterion attributes within each spatial unit: when the influence of an attribute on risk intensifies, its weight increases accordingly, and when its influence weakens, the weight decreases. By assigning differentiated weights to different locations, the local evaluation model captures the spatial variability of criterion importance and aligns more closely with the actual mechanisms of water inrush formation. Consequently, it substantially enhances both the scientific validity and spatial relevance of regional risk assessments.

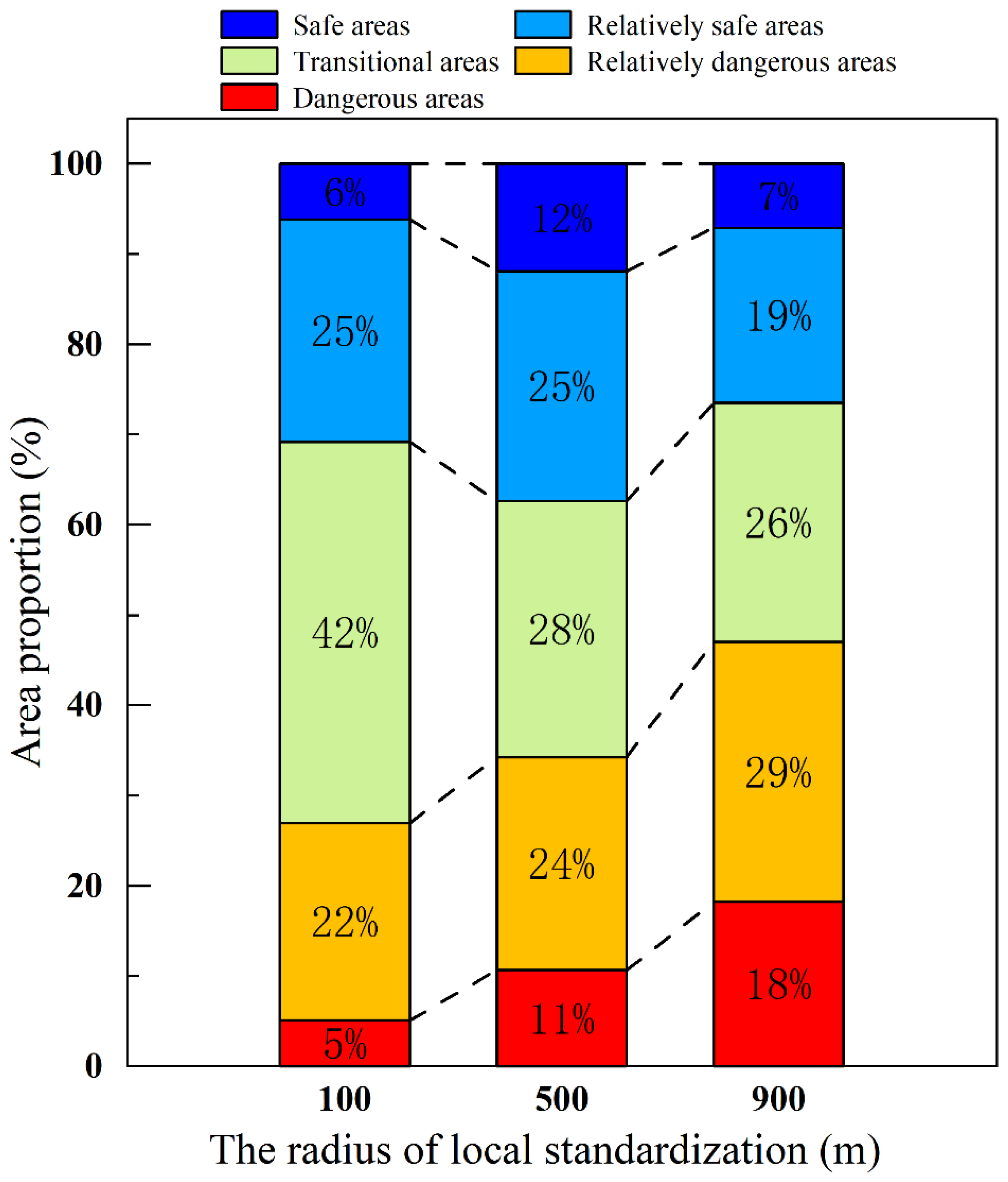
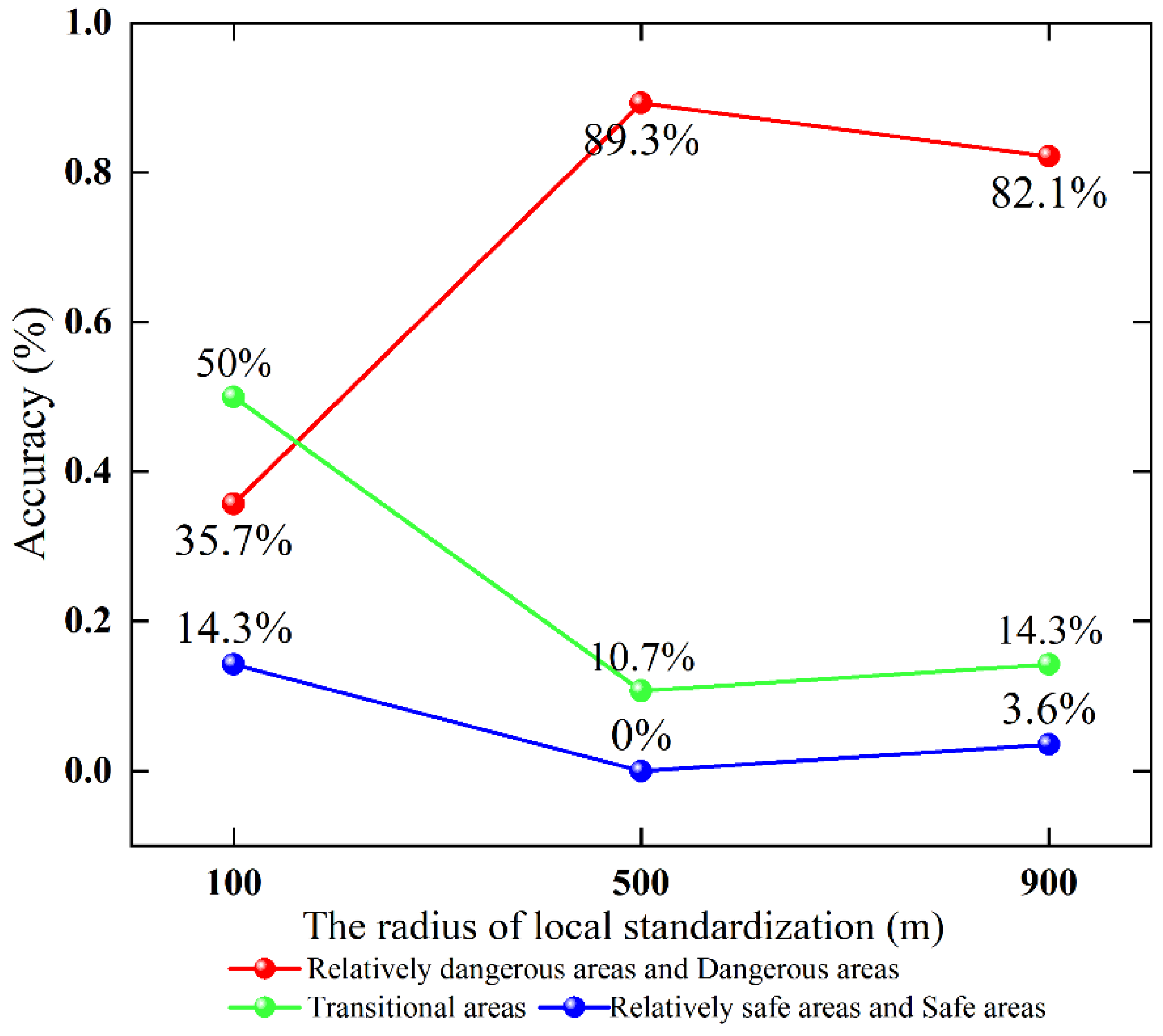
6.3. Selection of Different Radii for Local Standardization

In the previous section, different radii were selected for local standardization, and corresponding water inrush risk evaluation maps of the study area were obtained. To determine the most appropriate radius, a comparative analysis is conducted in this study from the following three aspects (Figure 18).

(1)

Spatial morphological characteristics

With a local standardization radius of 100 m, the spatial distribution of dangerous and relatively dangerous zones (red and yellow) and safe zones (blue and dark blue) appears highly fragmented. Dangerous zones mostly occur as scattered patches embedded within transitional areas (green), lacking any clear macroscopic orientation. This pattern arises because the 100 m radius excessively amplifies local variations, magnifying micro-scale attribute differences into independent risk units. As a result, spatial continuity is disrupted, making it difficult to identify overall risk patterns and increasing the uncertainty of risk delineation.

With a 500 m radius, the spatial continuity of risk zoning is significantly improved, and the boundaries between dangerous and safe zones become more regular. Dangerous zones are distributed as discontinuous blocks in the northern and southwestern parts of the study area, while appearing as continuous zones in the central region. Safe zones are mainly concentrated in the northwest, forming large and coherent contiguous areas. Overall, the regional risk pattern is presented more clearly.

When the radius is increased to 900 m, dangerous zones expand into large continuous areas, while safe zones shrink into isolated patches, and the boundaries of risk zones become smoother. This configuration reflects the dominance of overall regional trends in risk determination under a larger radius. Although it captures the macroscopic orientation of risk distribution, it weakens local heterogeneity and obscures small-scale risk anomalies, resulting in an overgeneralization of hazardous areas.

(2)

Area statistics comparison

In the process of local standardization, the radius serves as a critical parameter of the moving window and has a significant impact on the reconstruction of risk zoning areas. To further compare the results obtained under different radii, the areas of each risk zone corresponding to different radii were calculated and plotted as statistical charts (

Table 5. Area statistics of risk zoning under different local standardization radii.

	Radius of Local Standardization (m)	100	500	900
Area of Risk Zones (km2)
Safe areas		1.822	3.517	2.094
Relatively safe areas		7.305	7.552	5.751
Transitional areas		12.497	8.407	7.846
Relatively dangerous areas		6.490	6.988	8.527
Dangerous areas		1.507	3.157	5.402

and Figure 19).

From the area proportion changes shown in Figure 19, it is evident that the proportions of different risk zones vary significantly with the increase in the local standardization radius. The proportion of safe zones follows a “rise–fall” pattern: 6% at a 100 m radius, increasing to 12% at 500 m, and then decreasing to 7% at 900 m. The proportion of relatively safe zones remains relatively stable, maintaining 25% at 500 m; the 100 m radius shows no notable change in the overall pattern, while at 900 m the proportion drops to 19% due to compression by expanding high-risk areas. The proportion of transitional zones decreases continuously with increasing radius, from 42% at 100 m to 28% at 500 m, and further down to 26% at 900 m. In contrast, the proportions of relatively dangerous zones and dangerous zones increase steadily: the relatively dangerous zones account for 22%, 24%, and 29% at 100 m, 500 m, and 900 m, respectively, while the dangerous zones rise from 5% to 11% and 18%.

These variations are primarily driven by the interplay between “local heterogeneity” and “macroscopic trends” under different radii. At 100 m, local differences are excessively magnified, leading to fragmented risk zoning. The safe zones shrink, the transitional zones dominate in area proportion, and the expansion of relatively dangerous and dangerous zones is constrained. At 900 m, local heterogeneity is weakened, and macroscopic trends dominate. The safe, relatively safe, and transitional zones are compressed, while high-pressure aquifer regions and fault zones are integrated into the risk evaluation, causing a significant expansion of relatively dangerous and dangerous zones, particularly with a sharp increase in the proportion of dangerous zones. At 500 m, a balance is achieved between local and regional characteristics. This radius preserves the ability to identify local anomalies while capturing overall spatial trends, leading to more reasonable expansions of safe and dangerous zones, a reduction in transitional zones, and a more stable distribution of proportions. Consequently, the spatial delineation of water inrush risk zones aligns more closely with actual geological conditions.

(3)

Comparison of identification accuracy of water inrush points

To further determine the most suitable standardization radius, it is necessary to incorporate the spatial distribution characteristics of water inrush points. In this study, the identification accuracy of water inrush points under different radii was statistically analyzed to evaluate the impact of radius variation on risk identification results (

Table 6. Statistics of water inrush point identification under local evaluation models with different radii.

	Radius of Local Standardization (m)	100	500	900
Number of Water Inrush Points
Safe and relatively safe zones		4	0	1
Transitional zone		14	3	4
Dangerous and relatively dangerous zones		10	25	23
Total		28

).

From the trend shown in Figure 20, at a 100 m radius, the identification accuracy of water inrush points located in dangerous and relatively dangerous zones is only 35.7%. Half of the water inrush points (50%) fall within transitional zones, while 14.3% are located in safe and relatively safe zones, indicating a relatively low overall accuracy. This occurs because, under the 100 m local standardization radius, local differences are excessively amplified, resulting in highly fragmented risk zoning. High-risk areas exist as discrete patches rather than continuous belts, which weakens their ability to capture water inrush points. Consequently, transitional zones, where multiple attribute values are aggregated, become the main areas where water inrush points are concentrated.

At a 500 m radius, dangerous zones are properly integrated with surrounding areas, forming continuous risk belts where water inrush points are predominantly concentrated. The identification accuracy reaches the highest value of 89.3%. Safe zones are fully separated from water inrush points, achieving an identification rate of 0%. Transitional zones, with clearly defined risk classification standards, show a reduced identification rate, with only 10.7% of water inrush points falling within them.

At a 900 m radius, overall regional trends dominate risk determination, and local details are excessively generalized. Water inrush points associated with small-scale structures such as minor faults or dense fracture zones are obscured, causing the identification accuracy to drop slightly to 82.1%. The area of transitional zones is simplified, and their identification rate increases to 14.3%. Meanwhile, the safe zones shrink due to homogenization effects, leading to minor misclassifications and a small rise in identification rate to 3.6%.

Considering spatial morphological characteristics, area statistics, and water inrush point identification accuracy, the 500 m radius emerges as the optimal choice for local standardization. In terms of spatial morphology, zoning boundaries are more regular and continuous, balancing local heterogeneity with regional trends while avoiding the fragmentation seen at 100 m and the overgeneralization at 900 m. In terms of area distribution, the proportions of safe, transitional, and dangerous zones align well with actual risk gradients. Most importantly, in terms of accuracy, the identification rate of water inrush points is the highest, with 89.3% captured within dangerous zones, while misclassification rates in transitional and safe zones are significantly lower than those under the 100 m and 900 m radii.

The suitability of the 500 m radius is not accidental but is intrinsically linked to the geological structure scale and hydrogeological characteristics of the study area:

(1)

Consistency with the sampling precision and resolution of mine data.

Local evaluation relies on detailed data such as boreholes and geophysical surveys, and a 500 m radius matches well with the data acquisition scale. The typical spacing of exploration boreholes in mines ranges from 300 to 500 m, meaning that within a 500 m evaluation unit, at least one to two boreholes can be included to provide measured values of key parameters such as aquiclude thickness and coal seam thickness. If the radius is reduced to 100 m, some evaluation units may lack borehole control, leading to large interpolation errors. Conversely, if the radius is increased to 900 m, parameter averaging would obscure high-risk features such as local aquiclude thinning.

(2)

Balancing evaluation accuracy and computational efficiency.

Local evaluation must strike a balance between capturing “local heterogeneity” and reflecting “regional trends.” A radius that is too small (e.g., 100–200 m) would result in a sharp increase in the number of evaluation units, raising the burden of data processing and computation, while sparse data within units would cause greater fluctuations in results. A radius that is too large (e.g., 800–1000 m) would essentially become a “quasi-global evaluation,” losing the ability to capture local details. The 500 m radius provides an optimal balance: it ensures effective identification of local features while keeping the computational workload within an acceptable range for engineering applications.

6.4. Comparison of Models

To further verify the superiority of the local evaluation model, its results were compared and validated against those obtained from the traditional water inrush coefficient method and the global evaluation method.

$$T_S={\displaystyle \frac{P}{M}}$$

(30)

where Ts is the water inrush coefficient (MPa/m); P is the aquifer water pressure (MPa); and M is the thickness of the aquiclude (m).

Based on the threshold values of the water inrush coefficient, the evaluation area is divided into three zones: Safe zone (Ts ≤ 0.06 MPa), Dangerous zone (0.06 ≤ Ts ≤ 0.1 MPa/m), and Extremely dangerous zone (Ts ≥ 0.1 MPa/m). The zoning map of the water inrush coefficient was thus obtained, as shown in the figure.

From the evaluation results (Figure 21), it can be seen that the study area is dominated by safe zones, with only small parts of the northeast, northwest, and central regions classified as dangerous zones. The traditional water inrush coefficient method relies solely on the single indicator of “water pressure/aquiclude thickness,” while completely ignoring key controlling factors such as faults and coal seam burial depth. As a result, only 1 of the 28 documented water inrush points in the Dongjiahe Coal Mine was identified, yielding an accuracy of just 3.6%. This outcome highlights the inherent limitation of a single-factor approach, which cannot capture the coupled mechanisms of water inrush and therefore fails to provide reliable predictions of high-risk areas.

In contrast, the global evaluation model reveals a general trend of increasing risk from south to north across the study area. However, among the 28 water inrush points, only 6 fall within relatively dangerous zones, and none are located in dangerous zones. This clear spatial mismatch between the delineated dangerous/relatively dangerous zones and actual water inrush events demonstrates that the global evaluation method is unable to accurately capture the true distribution of risks, resulting in unreliable zoning outcomes that limit its effectiveness in guiding water inrush risk prevention and control.

The local evaluation method proposed in this study, which integrates MAHP with a moving-window approach, exhibits much finer precision in risk zoning. Taking the 500 m local standardization radius as an example, 25 out of the 28 known water inrush points were precisely captured within dangerous zones, significantly improving identification accuracy. Moreover, the localized analysis refined the boundaries and extent of dangerous zones, avoiding the drawback of excessively large hazard areas common in global evaluations. Consequently, the spatial distribution of high-risk zones is more consistent with actual geological conditions, enhancing both the reliability and practical applicability of the model.

7. More Applications

To further verify the reliability and applicability of the proposed method that combines MAHP with the moving-window approach, it was applied to the evaluation of floor water inrush risk in the Yangcheng Coal Mine. By fully reproducing the workflow of “indicator selection–local standardization–weight calculation–risk zoning,” a zoning map of water inrush risk for the Yangcheng Coal Mine was obtained (Figure 22).

The evaluation model developed in this study was compared with the previously proposed PCLRA-IAHP vulnerability index model. Although the PCLRA-IAHP model [20] can classify risk levels based on vulnerability indices, it is constrained by global weight allocation and fixed evaluation units. As a result, its risk boundaries tend to be overly smoothed, producing large, continuous relatively dangerous and dangerous zones, thereby masking the heterogeneity caused by local geological structures.

In contrast, the local evaluation model constructed in this study achieves refined delineation of risk zones through the dual mechanism of “dynamic adjustment of local weights + moving evaluation units.” While maintaining stable identification accuracy of water inrush points, the model avoids the unreasonable expansion of dangerous zones caused by the homogenization of global weights through dynamic adjustment of local weights. Meanwhile, the moving-window approach under local standardization allows for the identification of localized hydrogeological anomalies, ensuring that the spatial distribution of water inrush risk zones is more consistent with actual conditions and thus enhancing the targeting of water prevention and control efforts.

The comparative analysis of different models not only demonstrates the effectiveness of the proposed method in the Yangcheng Coal Mine but also validates the reliability of the combined MAHP and moving-window approach through cross-mine application. This indicates that the method, while performing local standardization and dynamic weight adjustment, is not restricted by the geological characteristics of a single mine. Instead, it better reveals the spatial patterns of water inrush risk across different regions. Therefore, the local evaluation model based on the integration of MAHP and moving-window techniques is a practical, rational, and essential approach for floor water inrush risk assessment.

8. Conclusions

(1)

This study developed a floor water inrush risk assessment method that integrates the Monte Carlo Analytic Hierarchy Process (MAHP) with a moving-window approach. By employing the Beta-PERT probability distribution to characterize uncertainties in expert judgment, the MAHP extends a single judgment matrix into a set of random matrices. This reduces subjective interference, addresses the strong subjectivity and insufficient weight stability inherent in traditional AHP, and ensures that the derived weights better reflect the actual influence of the indicators.

(2)

A local evaluation method based on circular moving windows was proposed. Through local standardization and local weight calculation within the window, dynamic spatial adjustment of weights was achieved. This overcomes the limitations of conventional global evaluation methods, which often ignore local variations and rely on fixed weights, thereby yielding results that better align with site-specific geological conditions.

(3)

To determine the appropriate radius for local standardization, evaluation results for 100 m, 500 m, and 900 m radii were compared. The findings indicate that a 500 m radius provides the optimal scale for the study area, as it balances overall spatial continuity with local detail, produces a reasonable proportion of safe, transitional, and hazardous zones, and achieves the highest identification accuracy of water inrush points. This radius avoids the excessive fragmentation observed at 100 m and the detail-masking effect of macro trends at 900 m.

(4)

Compared with the traditional water-inrush coefficient method and global evaluation models, the proposed method demonstrates significant advantages. Traditional approaches, which rely on a single indicator such as “water pressure/isolating layer thickness,” identified only 3.6% of the 28 water inrush points in the Dongjiahe Coal Mine, failing to capture the combined effects of multiple factors. In contrast, the proposed model integrates six core indicators, and through local standardization and dynamic weight adjustment, increases the identification accuracy of water inrush points to 89.3% with a 500 m radius, while also providing more refined delineation of hazardous zone boundaries.

(5)

Cross-mine validation further confirmed the reliability and universality of the method. In its application to the Yangcheng Coal Mine, the method not only maintained high accuracy in identifying water inrush points but also achieved precise delineation of high-risk zones and refinement of hazardous zone boundaries. These outcomes provide a scientific, effective, and targeted technical foundation for mine water prevention and control, enriching and advancing the methodological framework for floor water inrush risk assessment in coal mines.

(6)

Although the proposed model performs well in the Dongjiahe and Yangcheng coal mines, its accuracy may decrease in areas lacking sufficient borehole or hydrogeological data. The relationship between mining methods and water inrush risk is also critical: longwall mining in deep coal seams often leads to higher stress concentration and fracture propagation in the floor, thereby increasing the likelihood of hydraulic connection with the underlying aquifers. Future studies should incorporate mining-induced effects and explore adaptive calibration techniques to further extend the applicability of this method to regions with limited data or complex geological conditions.